Multi-criteria PROMETHEE method based on possibility degree with Z-numbers under uncertain linguistic environment

Abstract

People make decisions based on their cognitive information about the objective world. Zadeh’s Z-number allows people to better express their cognition of the real world by considering the fuzzy restriction and reliability restriction of information. However, the Z-number is a complex construct, and some important issues must be discussed in its study. Here, a computationally simple method of ranking Z-numbers for multi-criteria decision-making (MCDM) problems is proposed, and a comprehensive possibility degree of Z-numbers is defined, as inspired by the possibility degree concept of interval numbers. The outranking relations of Z-numbers are also discussed on the basis of the proposed method. Then, a weight acquisition algorithm relative to the possibility degree of Z-numbers is presented. Finally, an extended Preference Ranking Organization Method for Enrichment Evaluation II (PROMETHEE II) based on the possibility degree of Z-numbers is developed for the MCDM problem under Z-evaluation, and a numerical example about the selection of travel plans is used to illustrate the validity of the proposed method. The applicability and superiority of the proposed method is demonstrated through sensitivity and comparative analyses along with other existing methods.

1 Introduction

Humans participate in relevant decision-making activities based on the information they perceive (Ji et al. 2018; Li and Wang 2017; Wang et al. 2017). However, the perceived information is usually fuzzy and partially reliable, which deeply affects humans’ decision-making activities (Hu et al. 2017; Tian et al. 2017; Wang et al. 2015, 2017, 2018, 2019; Zadeh 1965). Zadeh (2011) proposed the Z-number in consideration of the fuzzy restriction and information reliability. A Z-number, $Z$, is composed of an ordered pair, $\left( {A,B} \right)$, which is used to describe a real-valued uncertain variable, $X$. The component $A$ is a fuzzy restriction on the values of $X$, and $B$ reflects the reliability restriction of the first component. A Z-number can be denoted as ‘$X$ is $Z=(A,B)$’ or $(X,A,B)$. According to Zadeh (2011), $A$ and $B$ in the natural language can be converted into trapezoidal fuzzy numbers (Bakar and Gegov 2015) or triangular fuzzy numbers (TFNs) (Aliev et al. 2016a, b) for computation purposes. Therefore, studying the Z-number-based decision-making problem is meaningful under uncertain linguistic environments.

Decision makers (DMs) are often more willing to express their decision-making perspectives by using natural language terms rather than specific numerical scores due to the ambiguity of the decision-making process and its uncertainties. Recently, many scholars have conducted in-depth research on uncertain linguistic decision-making problems (Hu et al. 2018; Huang et al. 2018; Li et al. 2018; Mardani et al. 2015; Xue et al. 2016). Ding and Liu (2018) used the decision-making trial and evaluation laboratory method to identify critical success factors in emergency management, in which evaluation values were represented by two-dimensional uncertain linguistic variables. Liu et al. (2019) built a robot selection model by combining quality function development theory and the qualitative flexible multiple criteria method, by which the DMs expressed their views through interval-valued Pythagorean uncertain linguistic sets. Peng and Wang (2018) studied the applications of Z-numbers and cloud model to address multi-criteria group decision-making problems under uncertain linguistic environments. Peng et al. (2019) combined linguistic variables and Z-numbers to establish a multi-criteria game model.

Zadeh (2011) stressed that stating the problem described by Z-numbers is relatively easy, but solving for the Z-numbers is difficult in terms of computation. Many scholars have studied the generation and operation of Z-numbers (Kang et al. 2018a, b, c, d). For example, Yager (2012) studied specific underlying probability distributions to solve certain decision problems involving Z-numbers. Aliev et al. (2015) developed the basic arithmetic of discrete Z-numbers according to discrete fuzzy number theory (Casasnovas and Riera 2006; Chou 2003; Voxman 2001) and the general principle of Z-number calculation (Zadeh 2011). Aliev et al. (2016a, b) implemented a comprehensive study on continuous Z-numbers. Shen and Wang (2018) constructed a comprehensively weighted Z-distance measure that only considers the reliability restriction and the underlying probability distribution of Z-numbers. The above studies focused on the direct calculation of Z-numbers according to the basic properties of the Z-number. However, these methods are complicated because of the need to satisfy the requirements of goal programming and convolution operations (Peng and Wang 2017).

Some scholars have attempted to simplify the operations of Z-numbers by converting them into simpler forms. Kang et al. (2012a, b) developed a typical method for converting the Z-number into a trapezoidal fuzzy number or a triangular fuzzy number. Kang et al. (2012a, b) and Kang et al. (2018a, b, c, d) constructed a formula for converting the Z-number into a crisp value. Aliyev (2016) proposed a single-distance measure by considering the Z-number as a pair of two classical fuzzy numbers. Different from the explanations of Aliev et al. (2015); Aliev et al. (2016a, b); Yang and Wang (2018), Kang et al. (2018a, b, c, d) regarded the Z-number as an ordered pair of two fuzzy numbers, and they proposed an improved fuzzy measure for calculating the uncertainty of this Z-number. The above conversion methods effectively reduced the complexity involved in Z-information fusion and hence can be applied to many practical decision problems (Kang et al. 2018a, b, c, d; Tavakkoli-Moghaddam et al. 2015; Wu et al. 2018; Yaakob and Gegov 2016). However, the above studies ignored the different effects of both fuzzy and reliability restrictions of the Z-number on the decision-making process.

The Preference Ranking Organization Method for Enrichment Evaluation (PROMETHEE) method developed by Brans et al. (1986) is one of the most applicable outranking methods for solving decision-making problems. Many studies on fuzzy multi-criteria decision-making (MCDM) have used the PROMETHEE method. Liu et al. (2017) performed a failure mode and effect analysis of a risk identification problem by combining the cloud model and PROMETHEE. Liang et al. (2018) proposed a projection-based PROMETHEE method with hesitant fuzzy linguistic term sets. Li and Wang (2017) extended the PROMETHEE method to hesitant probabilistic fuzzy environments. Peng et al. (2016) presented a novel MCDM method based on hesitant fuzzy sets and prospect theory. Tavakkoli-Moghaddam et al. (2015) investigated the problem of facility location selection under Z-evaluation by developing the Z-PROMETHEE method. Although the fuzzy PROMETHEE decision-making method has been thoroughly studied, the research on extending PROMETHEE by combining it with the Z-number and under Z-environments is still rare; hence, such research is necessary.

Here, a novel ranking method for Z-numbers is developed to deal with the MCDM problem under Z-evaluation. Firstly, the concept of possibility degree of TFNs is defined, as inspired by the possibility degree concept of interval numbers (Xu and Da 2003, 2002). Secondly, a joint possibility degree of Z-numbers is developed on the basis of the possibility degree of TFNs. In addition, a pairwise comparative matrix that reflects the additive preference relation is constructed to acquire the criteria weights (Xu 2001). Thirdly, an extended PROMETHEE method based on the proposed possibility degree of Z-numbers is presented for the MCDM problem, in which the evaluation values are described by using Z-numbers. Finally, as the most important research aspect, a numerical example about the selection of travel plans is used to illustrate the validity and feasibility of the proposed Z-PROMETHEE approach. Compared with those in the existing literature, some pivotal innovations can be derived from the present work as follows:

• 1. The possibility degree of two TFNs is developed, as inspired by the possibility degree concept of interval fuzzy numbers. Then, a comprehensively weighted possibility degree of two Z-numbers is constructed. This possibility degree is used to compare the fuzzy restriction and the reliability restriction of two Z-numbers without converting the Z-number into a fuzzy number or a crisp value.

• 2. For the MCDM problem with the Z-number as the evaluation value, if the criteria weights are expressed by using Z-numbers, then a method of converting the Z-weight vector into a real-weight vector is necessary. In light of the possibility degree of Z-numbers, a weight acquisition algorithm is introduced on the basis of the fuzzy complementary judgment matrix to obtain the real weight vector.

• 3. The possibility degree between two Z-numbers can reveal their partial order relationship. The PROMETHEE II method, combined with the possibility degree of Z-numbers, is used to present a Z-valued multi-criteria PROMETHEE method under uncertain linguistic environments. The extended Z-PROMETHEE method can provide the full order of all the alternatives. Moreover, a travel example is used to illustrate its effectiveness

The remainder of this paper is constructed as follows. In Sect. 2, some basic concepts are reviewed for subsequent discussions. In Sect. 3, a possibility degree definition of Z-numbers is developed to construct their outranking relations. Furthermore, a Z-PROMETHEE approach based on the possibility degree concept of Z-numbers is presented for MCDM in Sect. 4. In Sect. 5, a numerical example is used to illustrate the feasibility of the proposed method. Sensitivity and comparative analyses are implemented to verify the validity and reasonability of the proposed approach. The conclusion is presented in Sect. 6.

2 Preliminaries

For convenience of subsequent discussions, some basic concepts are presented for background information such as triangular fuzzy number, continuous Z-number, and interval number.

2.1 Continuous fuzzy number and triangular fuzzy number

Definition 1

(Aliev et al. 2016a, b): Let X be a universe of discourse. The fuzzy set $A$ on X, whose membership function is the mapping of ${\mu _A}:R \to [0,1]$, is a continuous fuzzy number if it fulfils the following conditions:

• 1. $A$ is a normal fuzzy set;

• 2. $A$ is a convex fuzzy set;

• 3. $\alpha$-cut ${A^\alpha }$ of $A$ is a closed interval for any $\alpha \in [0,1]$;

• 4. The support supp (A) of $A$ is bounded.

Definition 2

(Abbasbandy and Hajjari 2009): Let X be a universe of discourse. The membership function of the TFN A = (a, b, c) is

$${\mu _A}(x)\left\{ {\begin{array}{*{20}{c}} 0&{x<a} \\ {\frac{{x - a}}{{b - a}}}&{a \leq x<b} \\ 1&{x=b} \\ {\frac{{c - x}}{{c - b}}}&{b \leq x<c} \\ 0&{x>c} \end{array}} \right..$$

(1)

Evidently, the TFN is a type of continuous fuzzy number.

2.2 Z-number and continuous Z-number

Definition 3

(Zadeh 2011): A Z-number is an ordered pair of fuzzy numbers, $(A,B)$, which is used to characterise a real-valued uncertain variable X. The first component $A$, which is allowed to be taken by $X$, plays a role in the fuzzy restriction of values. The second component B is a reliability restriction of the first component. A Z-number is usually expressed as

‘X is $(A,B)$’, ‘X is $Z=(A,B)$’ or ‘$(X,A,B)$’.

Definition 4

(Aliev et al. 2016a, b): A continuous Z-number is an ordered pair Z = (A, B), in which some conditions need to be satisfied as follows:

• 1. $A$ is a continuous fuzzy number whose membership function is the mapping of ${\mu _A}:R \to [0,1]$, where ${R_X}$ is the support supp (A) of $A$;

• 2. $B$ is a continuous fuzzy number whose membership function is the mapping of ${\mu _B}:[0,1] \to [0,1]$.

2.3 Possibility degree of interval numbers

Definition 5

(Xu and Da 2003): Let X be a universe of discourse. An interval number a on X can be defined as

$$a=[{a^ - },{a^+}]=\left\{ {x|{a^ - } \leq x \leq {a^+}} \right\}.$$

(2)

If ${a^ - }={a^+}$, then the interval number $a=[{a^ - },\,{a^+}]$ will degenerate to a real number. Moreover, for any two interval numbers $a=\left[ {{a^ - },{a^+}} \right]$ and $b=\left[ {{b^ - },{b^+}} \right]$, $a$ is strictly equivalent to $b$ marked as $a=b$ if ${a^ - }={b^ - }$ and ${a^+}={b^+}$.

Definition 6

(Gao 2013; Xu 2001; Xu and Da 2003): Let $a=[{a^ - },\,{a^+}]$ and $b=[{b^ - },{b^+}]$ be any two interval numbers. The possibility degree of $a \geq b$ is defined as

$$p\left( {a \geq b} \right)=\hbox{max} \left\{ {1 - \hbox{max} \left( {\frac{{{b^+} - {a^ - }}}{{({b^+} - {b^ - })+({a^+} - {a^ - })}},0} \right),0} \right\}.$$

(3)

For any real number a and any interval number $b=\left[ {{b^ - },{b^+}} \right]$, the possibility degree formula is also applicable to the calculation of the possibility degree of $a \geq b$ or $b \geq a$, provided that the real number a is viewed as $a=\left[ {{a^ - },{a^+}} \right]$.

According to Xu and Da (2003), the possibility degree between any two real numbers can be defined. However, some discordant points in the properties of the possibility degree may exist. For example, obtaining $p\left( {a \geq b} \right)=0$ is inappropriate when $a$ and b are real numbers and equal, as the definition will not satisfy the reflexivity condition (i.e. $p\left( {a \geq b} \right) \ne \frac{1}{2}$). Therefore, the possibility degree of any two real numbers has been redefined according to Gao (2013).

Definition 7

(Gao 2013): Let a and b be any two real numbers. The possibility degree of $a \geq b$ is defined as

$$P(a \geq b)=\left\{ {\begin{array}{*{20}{c}} 0&{a<b} \\ {0.5}&{a=b} \\ 1&{a>b} \end{array}} \right..$$

(4)

Theorem 1

(Gao 2013): Let $a=\left[ {{a^ - },{a^+}} \right]({a^ - } \leq {a^+})$, $b=\left[ {{b^ - },{b^+}} \right]({b^ - } \leq {b^+})$ and $c=\left[ {{c^ - },{c^+}} \right]({c^ - } \leq {c^+})$ be any three interval numbers. Some properties of the possibility degree are satisfied as follows:

• 1. Normative: $0 \leq p(a \geq b) \leq 1$;

• 2. Complementary: $p(a \geq b)+p(b \geq a)=1$;

• 3. Reflexivity: $p(a \geq b)=p(b \geq a)=0.5$ if a = b;

• 4. Transitivity: if $p(a \geq b) \leq 0.5$ and $p(b \geq c) \leq 0.5$, then $p(a \geq c) \leq 0.5$.

3 Outranking relations of Z-numbers

A novel concept named possibility degree of Z-numbers is proposed on the basis of two closely connected subsections. Furthermore, the outranking relations between the Z-numbers are defined on the basis of the possibility degree of Z-numbers.

3.1 Possibility degree of TFNs

Definition 8

Let $\tilde {a}=\left( {{a_1},{a_2},{a_3}} \right)$ and $\tilde {b}=\left( {{b_1},{b_2},{b_3}} \right)$ be any two TFNs. Some comparative relations can be defined as follows:

• 1. If ${a_1}={b_1}$, ${a_2}={b_2}$ and ${a_3}={b_3}$, then $\tilde {a}$ is strictly equivalent to $\tilde {b}$, and they are marked as $\tilde {a}=\tilde {b}$.

• 2. If ${a_1} \geq {b_3}$, then $\tilde {a}$ is strictly larger than $\tilde {b}$, and it is marked as ${b^ - },{b^+}$.

Definition 9

Let $\tilde {a}=({a_1},{a_2},\,{a_3})$ and $\tilde {b}=({b_1},{b_2},\,{b_3})$ be any two TFNs. The possibility degree of $\tilde {a} \geq \tilde {b}$ is defined as follows:

$$p(\tilde {a} \geq \tilde {b})=\int_{0}^{1} {{p^\alpha }(\tilde {a} \geq \tilde {b})d\alpha } ,$$

(5)

where ${p^\alpha }(\tilde {a} \geq \tilde {b})$ is the possibility degree of the cut set $\left[ {{a^ - },{a^+}} \right]$ of $\tilde {a}$ and the cut set $\left[ {{b^ - },{b^+}} \right]$ of $\tilde {b}$ in $\alpha$ level (Yao and Chiang 2003; Yao et al. 2003), as shown in Fig. 1. The analytic solution of the possibility degree of TFNs is shown in the Appendix A.

Fig. 1

Possibility degree of two TFNs

Note 1 The TFNs in Definition 9 are regular fuzzy numbers, which indicates that the range of the integration interval is from 0 to 1. If the uncertain information is expressed by irregular fuzzy numbers (e.g. the maximum membership is less than one), then the cut set of the irregular fuzzy number is assumed to be a crisp value when the level of cut set is greater than its maximum membership. For example, for an irregular fuzzy number $(1,2,3;0.5)$ with the maximum membership of $0.5$, the interval of the cut set will always be $\left[ {2,2} \right]$ or when the level $\alpha$ of the cut set belongs to $\left( {0.5,1} \right]$. Therefore, Eq. (5) in Definition 9 can be used to rank two irregular fuzzy numbers.

Example 1

Let $\tilde {a}=(1,2,3)$ and $\tilde {b}=(2,3,4)$ be two TFNs.

According to Definition 9,

$${\tilde {a}^\alpha }=\left[ {1+\alpha ,3 - \alpha } \right]$$

$${\tilde {b}^\alpha }=\left[ {2+\alpha ,4 - \alpha } \right];$$

$${p^\alpha }(\tilde {a} \geq \tilde {b})=\hbox{max} \left\{ {1 - \hbox{max} \left\{ {\frac{{\left( {4 - \alpha } \right) - \left( {1+\alpha } \right)}}{{\left[ {\left( {4 - \alpha } \right) - \left( {2+\alpha } \right)} \right]+\left[ {\left( {3 - \alpha } \right) - \left( {1+\alpha } \right)} \right]}}} \right\},0} \right\};$$

$$p(\tilde {a} \geq \tilde {b})=\int_{0}^{1} {{p^\alpha }(\tilde {a} \geq \tilde {b})d\alpha } =0.0767.$$

The possibility degree between TFNs can be directly computed by adopting the formula in Appendix A.

$$p(\tilde {a} \geq \tilde {b}){\text{=}}\frac{{{\text{3-2}}}}{{\left( {4 - 2} \right){\text{+}}\left( {3 - 1} \right)}}{\text{+}}\frac{{{\text{3-2}}}}{{\left( {4 - 2} \right){\text{+}}\left( {3 - 1} \right)}}\ln \frac{{3 - 2}}{{\left( {3 - 2} \right)+\left( {3 - 2} \right)}}=\frac{1}{4}+\frac{1}{4}\ln \frac{1}{2}={\text{0.0767}}$$

Definition 10

Let $\tilde {a}=({a_1},{a_2},{a_3})$ and $\tilde {b}=({b_1},{b_2},{b_3})$ be any two TFNs. Some comparative relations can be defined as follows:

• 1. If $p(\tilde {a} \geq \tilde {b})=p(\tilde {b} \geq \tilde {a})=0.5$, then $\tilde {a}$ is indifferent to $\tilde {b}$, and it is marked as $\tilde {a}\sim \tilde {b}$.

• 2. If $p(\tilde {a} \geq \tilde {b})>0.5$, then $\tilde {a}$ is weakly larger than $\tilde {b}$, and it is marked as $\tilde {a} \succ \tilde {b}$.

Theorem 2

Let $\tilde {a}=({a_1},{a_2},{a_3})$ and $\tilde {b}=({b_1},{b_2},{b_3})$ be any two TFNs. Some properties of the possibility degree of TFNs are satisfied as follows:

• 1. Normative: $0 \leq p(\tilde {a} \geq \tilde {b}) \leq 1$;

• 2. Complementary: $p(\tilde {a} \geq \tilde {b})+p(\tilde {b} \geq \tilde {a})=1$;

• 3. Reflexivity: $p(\tilde {a} \geq \tilde {b})=p(\tilde {b} \geq \tilde {a})=0.5$ if $\tilde {a}=\tilde {b}$.

Proof

• 1. On the basis of Definition 9 and the first property (normative property) of Theorem 1,

$\forall \alpha \in \left[ {0,1} \right],\;0 \leq {p^\alpha }(\tilde {a} \geq \tilde {b}) \leq 1$. Consequently, $\int_{0}^{1} {0d\alpha } \leq p(\tilde {a} \geq \tilde {b})=\int_{0}^{1} {{p^\alpha }(\tilde {a} \geq \tilde {b})d\alpha } \leq \int_{0}^{1} {1d\alpha }$.

Therefore, $0 \leq p(\tilde {a} \geq \tilde {b}) \leq 1$.

Thus, the first property (normative property) is proven.

• 2. In accordance with Definition 9 and the second property (complementary property) of Theorem 1,

$\forall \alpha \in \left[ {0,1} \right],\;{p^\alpha }(\tilde {a} \geq \tilde {b})+{p^\alpha }(\tilde {b} \geq \tilde {a})=1$. Consequently, $\begin{gathered} p(\tilde {a} \geq \tilde {b})+p(\tilde {b} \geq \tilde {a})=\int_{0}^{1} {{p^\alpha }(\tilde {a} \geq \tilde {b})d\alpha } +\int_{0}^{1} {{p^\alpha }(\tilde {b} \geq \tilde {a})d\alpha } \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=\int_{0}^{1} {\left[ {{p^\alpha }(\tilde {a} \geq \tilde {b})+{p^\alpha }(\tilde {b} \geq \tilde {a})} \right]d\alpha } \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=\int_{0}^{1} {1d\alpha } \hfill \\ \end{gathered}$.

Therefore, $p(\tilde {a} \geq \tilde {b})+p(\tilde {b} \geq \tilde {a})=1$.

Thus, the second property (complementary property) is proven.

• 3. According to Definition 9 and the third property (reflexivity) of Theorem 1,

if $\tilde {a}=\tilde {b}$, then $\forall \alpha \in [0,1],{p^\alpha }(\tilde {a} \geq \tilde {b})=0.5$ and ${p^\alpha }(\tilde {b} \geq \tilde {a})=0.5$ Consequently, $p(\tilde {a} \geq \tilde {b})=\int_{0}^{1} {{p^\alpha }(\tilde {a} \geq \tilde {b})d\alpha } =\int_{0}^{1} {{\text{0.5}}d\alpha }$ and $p(\tilde {b} \geq \tilde {a})=\int_{0}^{1} {{p^\alpha }(\tilde {b} \geq \tilde {a})d\alpha } =\int_{0}^{1} {{\text{0.5}}d\alpha }$.

Therefore, $P(\tilde {a} \geq \tilde {b})=P(\tilde {b} \geq \tilde {a})=0.5$ if $\tilde {a}=\tilde {b}$.

Hence, the reflexivity property of Theorem 1 is proven.

Remark 1

The normative, complementary and reflexivity properties of the defined possibility degree of TFNs have been discussed in Theorem 2. Here, the transitivity property is demonstrated below.

A classic example is shown in Fig. 2. In many studies of fuzzy MCDM, a sequence of TFNs is often used as an uncertain information expression to evaluate alternatives. A TFN is a special interval fuzzy number. The TFNs in such a sequence are usually partially intersecting or non-intersecting.

Fig. 2

Sequence of TFNs

The sequence of TFNs shown in Fig. 2 is represented by ${A_i},i=1,2,3,4$. For any three different TFNs such as ${A_i}$, ${A_j}$ and ${A_k}$, finding $p\left( {{A_i} \geq {A_j}} \right)<0.5$ is easy if and only if $i<j$ (see brief proof in Appendix B). Thus, if $p\left( {{A_i} \geq {A_j}} \right)<0.5$ and $p\left( {{A_j} \geq {A_k}} \right)<0.5$, then $i<j$ and $j<k$. Consequently, $i<k$ is satisfied. Therefore, $p\left( {{A_i} \geq {A_k}} \right)<0.5$.

3.2 Possibility degree of Z-numbers

Definition 11

Let ${Z_1}=({A_1},{B_1})$ and ${Z_2}=({A_2},{B_2})$ be any two Z-numbers where all the elements in $\left\{ {{A_1},{B_1},{A_2},{B_2}} \right\}$ are TFNs. Some comparative relations can be defined as follows:

• 1. If ${A_1}={A_2}$ and ${B_1}={B_2}$, then Z₁ is absolutely equivalent to Z₂, and they are marked as ${Z_1} \equiv {Z_2}$.

• 2. If ${A_1}\sim {A_2}$ and ${B_1}\sim {B_2}$, then Z₁ is strictly equivalent to Z₂, and they are marked as ${Z_1}={Z_2}$.

• 3. If ${A_1}>{A_2}$ and ${B_1}>{B_2}$, then Z₁ is absolutely larger than Z₂, and they are marked as ${Z_1} \gg {Z_2}$.

• 4. If ${A_1} \succ {A_2}$ and ${B_1} \succ {B_2}$, then Z₁ is strictly larger than Z₂, and they are marked as ${Z_1}>{Z_2}$.

Definition 12

Let ${Z_1}=({A_1},{B_1})$ and ${Z_2}=({A_2},{B_2})$ be any two Z-numbers where all the elements in $\left\{ {{A_1},{B_1}{A_2},{B_2}} \right\}$ are TFNs. The possibility degree of ${Z_1} \geq {Z_2}$ can be defined as

$$p({z_1} \geq {z_2})=\omega p({A_1} \geq {A_2})+(1 - \omega )p({B_1} \geq {B_2}),$$

(6)

where the value of $\omega$ lies in the interval of [0,1], and it represents the concern degree of a DM towards the first component $A$ of the Z-number. The equivalent formula is given by

$$p({Z_1} \geq {Z_2})=\omega \int_{0}^{1} {{p^\alpha }({A_1} \geq {A_2})d\alpha } +\left( {1 - \omega } \right)\int_{0}^{1} {{p^\beta }({B_1} \geq {B_2})d\beta } .$$

(7)

The parameter $\omega$ in Eq. (6) can reflect the varying preferences of different DMs. When $0<\omega <0.5$, a DM perceives the reliability of an information as more important than the other properties. When $\omega =0.5$, the ambiguity and reliability of information are equally significant for the DM. When $0.5<\omega <1$, the DM is more concerned on the ambiguity of the information. In particular, $\omega =0$ indicates that the DM only considers the reliability restriction of the information, whereas $\omega =1$ indicates that the DM is only concerned with the fuzzy restriction of the information.

A Z-number simultaneously considers the ambiguity and reliability properties of an information. According to Zadeh (2011), the first component of Z-number reflects the fuzzy restriction, whereas the second component plays a role in reliability restriction. These two characteristics must be considered when ranking Z-numbers. Furthermore, different DMs have varying risk preferences towards fuzziness and reliability. Therefore, the associated possibility degree formula that has been developed is rational.

Example 2

Let ${Z_1}=\left( {(0.1,0.2,0.3),(0.2,0.3,0.4)} \right)$ and ${Z_2}=\left( {\left( {0.2,0.3,0.4} \right),\left( {0.1,0.2,0.3} \right)} \right)$ be two Z-numbers. Then, $p({Z_1} \geq {Z_2}){|_{\omega =0.5}}=\omega p({A_1} \geq {A_2})+\left( {1 - \omega } \right)p({B_1} \geq {B_2})=0.5 \times 0.0767+\left( {1 - 0.5} \right) \times 0.9233=0.5,$$p({Z_1} \geq {Z_2}){|_{\omega =0.4}}=0.5847$ and $p({Z_1} \geq {Z_2}){|_{\omega =0.6}}=0.4153$.

Definition 13

Let ${Z_1}=({A_1},{B_1})$ and ${Z_2}=({A_2},{B_2})$ be any two Z-numbers where all the elements in $\left\{ {{A_1},{B_1},{A_2},{B_2}} \right\}$ are TFNs. Some comparative relations can be defined as follows:

• 1. If $p({Z_1} \geq {Z_2})=p({Z_2} \geq {Z_1})=0.5$, then Z₁ is indifferent to Z₂, and it is marked as ${Z_1}\sim {Z_2}$.

• 2. If $p({Z_1} \geq {Z_2})>0.5$, then Z₁ is weakly larger than Z₂, and it is marked as ${Z_1} \succ {Z_2}$.

Theorem 3

Let ${Z_1}=({A_1},{B_1})$ and ${Z_2}=({A_2},{B_2})$ be any two Z-numbers where the components $A$ and $B$ are TFNs. Some properties about the possibility degree of Z-numbers are satisfied as follows:

• 1. Normative: $0 \leq p({Z_1} \geq {Z_2}) \leq 1$;

• 2. Complementary: $p({Z_1} \geq {Z_2})+p({Z_2} \geq {Z_1})=1$;

• 3. Reflexivity: $p({Z_1} \geq {Z_2})=p({Z_2} \geq {Z_1})=0.5$ if ${Z_1}={Z_2}$.

Proof

• 1. In accordance with Definition 12 and the first property (normative property) of Theorem 2,

${\text{0}} \leq p({A_1} \geq {A_2}) \leq {\text{1}}$ and $0 \leq p({B_1} \geq {B_2}) \leq 1$ Consequently, $\omega \times 0+(1 - \omega ) \times 0 \leq p({Z_1} \geq {Z_2})=\omega p({A_1} \geq {A_2})+(1 - \omega )p({B_1} \geq {B_2}) \leq \omega \times 1+(1 - \omega ) \times 1.$

Therefore, the first property (normative property) is proven.

• 2. According to Definition 12 and the second property (complementary property) of Theorem 2,

$p({A_1} \geq {A_2})+p({A_2} \geq {A_1})=1$ and $p({B_1} \geq {B_2})+p({B_2} \geq {B_1})=1$. Consequently,

$$\begin{gathered} p({Z_1} \geq {Z_2})+p({Z_2} \geq {Z_1}) \hfill \\ =\omega p({A_1} \geq {A_2})+(1 - \omega )p({B_1} \geq {B_2})+\omega p({A_2} \geq {A_1})+(1 - \omega )p({B_2} \geq {B_1}) \hfill \\ =\omega \left[ {p({A_1} \geq {A_2})+p({A_2} \geq {A_1})} \right]+(1 - \omega )[p({B_1} \geq {B_2})+p({B_2} \geq {B_1})] \hfill \\ =\omega +(1+\omega ) \hfill \\ =1 \hfill \\ \end{gathered}$$

Hence, the second property (complementary property) is proven.

• (i) On the basis of Definition 12 and the third property (reflexivity property) of Theorem 2,

if ${Z_1}={Z_2}$, then $p({A_1} \geq {A_2})=0.5$, $p({A_2} \geq {A_1})=0.5$, $p({B_1} \geq {B_2})=0.5$ and $p({B_2} \geq {B_1})=0.5$. Consequently, $p({Z_1} \geq {Z_2})=\omega p({A_1} \geq {A_2})+(1 - \omega )p({B_1} \geq {B_2})=\omega \times 0.5+(1 - \omega ) \times 0.5.$ and $p({Z_2} \geq {Z_1})=\omega p({A_2} \geq {A_1})+(1 - \omega )p({B_2} \geq {B_1})=\omega \times 0.5+(1 - \omega ) \times 0.5.$

Therefore, the third property (reflexivity property) is proven.

Remark 2

Let ${Z_1}=\left( {{A_1},{B_1}} \right)$, ${Z_2}=\left( {{A_2},{B_2}} \right)$ and ${Z_3}=\left( {{A_3},{B_3}} \right)$ be any three Z-numbers, in which ${A_1}=(a_{1}^{i},a_{2}^{i},a_{3}^{i})(i=1,2,3)$ and ${B_1}=(b_{1}^{i},b_{2}^{i},b_{3}^{i})(i=1,2,3)$ are TFNs. Moreover, $p\left( {{A_1} \geq {A_2}} \right)<0.5$, $p\left( {{A_2} \geq {A_3}} \right)<0.5$, $p({B_1} \geq {B_2})<0.5$ and $p({B_2} \geq {B_3})<0.5$ are satisfied. Consequently, $p({Z_1} \geq {Z_2}) \leq 0.5$, $p({Z_2} \geq {Z_3}) \leq 0.5$ and $p({Z_1} \geq {Z_3}) \leq 0.5$.

Example 3

Let ${Z_1}=\left( {\left( {1,2,3} \right),\left( {0.2,0.3,0.4} \right)} \right)$, ${Z_2}=\left( {\left( {2,3,4} \right),\left( {0.4,0.6,0.7} \right)} \right)$ and ${Z_3}=\left( {\left( {3,4,5} \right),\left( {0.7,0.8,1} \right)} \right)$ be three given continuous Z-numbers.

According to Definition 12, $p({Z_1} \geq {Z_2})=0.0384<0.5$, $p({Z_2} \geq {Z_3})=0.0442<0.5$ and $p({Z_2} \geq {Z_3})=0<0.5$.

4 Z-PROMETHEE approach for solving MCDM problems

The possibility degree of Z-numbers can meaningfully solve the MCDM problem based on Z-numbers. The possibility degree of Z-numbers can also reflect the difference between two Z-numbers. An extended Z-PROMETHEE approach is therefore developed as follows.

For a MCDM problem using Z-numbers, let $A=\{ {a_i}|i=1,2, \ldots ,m\}$ be a set that includes all the provided alternatives; $c=\{ {c_j}|j=1,2, \ldots ,n\}$ be the collection of criteria; $D={[{z_{ij}}]_{m \times n}}={\left[ {({A_{ij}},{B_{ij}})} \right]_{m \times n}}$ be the decision-making matrix, in which ${z_{ij}}=({A_{ij}},{B_{ij}})\,$ denotes the evaluation of alternative ${a_i}$ under the criteria ${c_j}$; and $W={[{Z_j}]_{1 \times n}}={\left[ {({A_j},{B_j})} \right]_{1 \times n}}$ be the weight matrix, in which ${z_{ij}}=({A_j},{B_j})\,$ reflects the importance of criteria ${c_j}$.

Step 1. Normalise the decision-making matrix.

Different criteria require different scales. Moreover, two different sets of criteria exist (i.e. benefit criteria and cost criteria). For discussion purposes, the linear transformation (Kang et al. 2018a, b, c, d; Yaakob and Gegov 2016) is used to eliminate the effects of the differentiations.

$$A_{{ij}}^{N}=\left\{ {\begin{array}{*{20}{l}} {\left( {\frac{{a_{{ij}}^{1}}}{{c_{j}^{+}}},\frac{{a_{{ij}}^{2}}}{{c_{j}^{+}}},\frac{{a_{{ij}}^{3}}}{{c_{j}^{+}}}} \right)}&{j \in B} \\ {\left( {1 - \frac{{a_{{ij}}^{3}}}{{c_{j}^{+}}},1 - \frac{{a_{{ij}}^{2}}}{{c_{j}^{+}}},1 - \frac{{a_{{ij}}^{1}}}{{c_{j}^{+}}}} \right)}&{j \in C} \end{array}} \right.,$$

(8)

where $B$ and C are the collections of benefit criteria and cost criteria, respectively, and $C_{j}^{+}=\mathop {\hbox{max} }\limits_{i} \left\{ {a_{{ij}}^{3}} \right\}$. Thus, the normalised matrix can be denoted as ${D^N}={\left[ {z_{{ij}}^{N}} \right]_{m \times n}}={\left[ {\left( {A_{{_{{ij}}}}^{N},{B_{ij}}} \right)} \right]_{m \times n}}$.

Step 2. Compute the criteria weights.

When the importance of the criteria is evaluated by using Z-numbers, an appropriate method for acquiring the criteria weight vector must be developed under Z-environment. Xu (2001) proposed an algorithm for the priority of fuzzy complementary judgment matrix. The discussion in Sect. 3 suggests that the possibility degree of Z-numbers is suitable in Xu’s algorithm. Hence, the criteria weights can be obtained as follows:

$${w_i}=\frac{{\sum\nolimits_{{j=1}}^{n} {p({c_i},{c_j})+\frac{n}{2} - 1} }}{{n(n - 1)}},\,i=1,2, \ldots n,$$

(9)

where $p({c_i},{c_j})=p({z_i} \geq {z_j})=\omega p({A_i} \geq {A_j})+(1 - \omega )p({B_i} \geq {B_j})$; w_i reflects the importance of criteria ${c_i}$; and $\sum\nolimits_{{i=1}}^{n} {{w_i}=1}$.

Step 3. Calculate the priority index $\psi \left( {{a_i},{a_k}} \right)$ of the alternative ${a_i}$ over the alternative ${a_k}$.

$$\psi ({a_i},{a_k})=\frac{{\sum\nolimits_{{j=1}}^{n} {{w_j}{p_j}({a_i},{a_k})} }}{{\sum\nolimits_{{j=1}}^{n} {{w_j}} }},$$

(10)

where ${p_j}({a_i},{a_k})=p({z_{ij}} \geq {z_{kj}}) - 0.5$. If ${p_j}\left( {{a_i},{a_k}} \right)>0$, which indicates that $p({z_{ij}} \geq {z_{kj}})>0.5$, then ${a_i}$ is better than relative to ${c_j}$. Thus, ${a_i}$ is undifferentiated from ${a_k}$ for criterion ${c_j}$ if ${p_j}({a_i},\,{a_k})=0$ (i.e. ${p_j}({z_{ij}},\,{z_{kj}})=0.5$). In addition, ${a_i}$ is inferior to ${a_k}$ under ${c_j}$ if the condition is ${p_j}\left( {{a_i},{a_k}} \right)<0$, which indicates that ${p_j}({Z_{ij}} \geq {Z_{kj}})<0.5$.

Step 4. Compute the outgoing flow, the incoming flow and the net flow of alternative ${a_i}$.

• (i) Outgoing flow:

$${\phi ^+}\left( {{a_i}} \right)=\sum\nolimits_{{k=1}}^{m} {\psi \left( {{a_i},{a_k}} \right)}$$

(11)

• (ii) Incoming flow:

$${\phi ^ - }\left( {{a_i}} \right)=\sum\nolimits_{{k=1}}^{m} {\psi \left( {{a_k},{a_i}} \right)}$$

(12)

• (iii) Net flow:

$$\phi \left( {{a_i}} \right)={\phi ^+}\left( {{a_i}} \right) - {\phi ^ - }\left( {{a_i}} \right)$$

(13)

Step 5. Rank all of the provided alternatives.

The ranking of alternatives can be acquired in light of each alternative’s net flow. The larger $\phi \left( {{a_i}} \right)$ is, the better ${a_i}$ will be.

5 Illustrative example

The living standards of people in China have further improved with the prosperity of the Chinese economy. In accordance with Maslow’s hierarchy of needs (Maslow 1972), human beings pursue higher spiritual enjoyment to enhance their happiness. The Chinese government has attempted to increase statutory holidays to encourage consumption, indicating a solution akin to ‘two birds hit with one stone’. On the one hand, the economy of China has become increasingly dynamic. On the other hand, the life quality of the people has also been greatly improved.

The celebration of the National Day of China is the longest festival in the country. During National Day, many people prefer to go on a short trip with family or friends. To enhance the planned tour, the most suitable travel option should be considered. The selection of travel plans often involves some major factors (Gardashova 2014; Kang et al. 2018a, b, c, d), such as price, service and destination. When evaluating the different travel plans, uncertainties are important aspects of the decision information. On the one hand, the evaluation values of travel planning by using the above criteria are usually fuzzy and imprecise. On the other hand, the reliability of decision information must be considered due to the subjectivity of the evaluation. The issue of travel plan selection can be described appropriately by using Z-numbers combined with a natural language (Zadeh 2011).

A particular example on travel plan selection is used to explain the proposed method. Moreover, to evaluate the different travel plans, the five most critical criteria are determined: ${c_1}$ (basic budget), ${c_2}$ (location preference), ${c_3}$ (scenic security), ${c_4}$ (scenic service) and ${c_5}$ (invisible consumption). The decision matrix with linguistic values shown in Table 1 is based on these five criteria. The codebooks of linguistic terms are shown in Tables 2 and 3.

Table 1 Decision matrix with linguistic values

Table 2 Codebook of linguistic terms for fuzzy restriction

Table 3 Codebook of linguistic terms for reliability restriction

5.1 Application of the proposed approach

A numerical example is used to illustrate the feasibility of the proposed approach. The particular procedure is as follows.

Note 2. The DM’s risk preference parameter $\omega$ is set to be equal to 0.5.

Step 1. Normalise the decision-making matrix.

For simplicity, criteria ${c_1}$ and ${c_5}$ denote the cost criteria, whilst criteria ${c_2}$, ${c_3}$ and ${c_4}$ represent the benefit criteria. Therefore, the decision matrix can be normalised by using Eq. (8).

Step 2. Compute the criteria weights.

On the basis of Eq. (9) in Sect. 3, the weight values of the criteria are calculated (Table 4).

Table 4 Criteria weight distribution matrix

Step 3. Construct the possibility degree matrix under each criterion and calculate the priority index $\psi \left( {{a_i},{a_k}} \right)$ of alternative ${a_i}$ over alternative ${a_k}$. The obtained results are shown in Table 5.

Table 5 Priority index matrix

Step 4. Compute the outgoing flow, incoming flow and net flow of each alternative (Table 6).

Table 6 Flow matrix

Step 5. Rank all of the provided alternatives.

On the basis of Table 6, the order of all the provided alternatives is obtained.

$${a_6} \succ {a_4} \succ {a_2} \succ {a_3} \succ {a_8} \succ {a_7} \succ {a_5} \succ {a_1}$$

(14)

5.2 Sensitivity analysis

A sensitivity analysis of $\omega$ for the possibility degree between Z-numbers is implemented to determine the influence of this parameter to the ranking result. As stated in Definition 12, the value of $\omega$ reflects the concern degree towards the fuzzy restriction $A$ of a Z-number. For simplicity, the values of $\omega$ are acquired in the collection of $\left\{ {\omega |\omega =0.1k,0 \leq 10,k \in N} \right\}$. The results are shown in Tables 7 and 8.

Table 7 Ranking results when $0 \leq \omega <0.5$

Table 8 Ranking results when $0<\omega \leq 0.5$

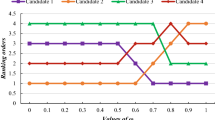
As shown in Tables 7 and 8, the ranking results of all travel plans change as $\omega$ changes. When $0 \leq \omega \leq 0.2$, the optimal travel plan is ${a_2}$; when $0.5<\omega \leq 1$, the optimal travel plan is ${a_6}$. Therefore, $\omega$ affects the ranking of travel plans, which preliminarily illustrates the rationality of setting the $\omega$ parameter. The ranking diagram of all travel plans under different $\omega$ values is shown in Fig. 3.

Fig. 3

Ranking results of all travel plans under different $\omega$ values

As shown in Fig. 3, the ranking results of all travel plans vary when $\omega$ takes different values. In the diagram, the optimal travel plan is ${a_2}$ when $0 \leq \omega \leq 0.2$. The DM at this time pays more attention to the reliability restriction rather than the fuzzy restriction of information. Consequently, the criteria, including ${c_2}$ and ${c_5}$, become even more important. Criteria ${c_2}$ and ${c_5}$ considerably affect the travel plan rankings compared with the ${c_1}$, ${c_3}$ and ${c_5}$. Moreover, on the basis of Table 1, the reliability restriction of the evaluation values of travel plan ${a_2}$ under criteria ${c_2}$ and ${c_5}$ is more positive than those of the other travel plans. Thus, the optimal travel plan is ${a_2}$ when $0 \leq \omega \leq 0.2$.

As shown in Fig. 3, the optimal travel plan becomes ${a_6}$ when $\omega$ is larger than 0.3. The increase in $\omega$ indicates that the DM has focused on the fuzzy restriction of information whilst reducing the concern for information reliability, thereby providing a two-pay impact on the ranking of travel plans. On the one hand, the weight of criterion ${c_1}$ continues to increase. Moreover, as shown in Table 1, the evaluation value of travel plan ${a_6}$ under criterion ${c_1}$ is better than any other travel plans. Therefore, the increase in $\omega$ is a positive contribution to ${a_6}$, which becomes the optimal option. On the other hand, the fuzzy restriction of the evaluation values of travel plan ${a_6}$ under the other criteria is generally better than those of the other travel plans. Thus, travel plan ${a_6}$ is the optimal solution. Consequently, travel plan ${a_6}$ is more likely to be the most satisfactory plan when DMs focus on information reliability.

The proposed Z-PROMETHEE approach shows good stability and feasibility when $\omega$ is used as a parameter in sensitivity analysis. On the one hand, the ranking results are relatively consistent when $\omega$ lies in some intervals. On the other hand, the ranking results change when $\omega$ changes. This finding is generally consistent with our expectation. Therefore, setting $\omega$ as a parameter is necessary to rationally reflect a DM’s preference. Consequently, the decision-making method based on the possibility degree of Z-numbers can be effectively applied to actual decision scenarios.

6 Comparative analysis

Other methods are for comparison with the proposed method. Here, the comparative analysis has two components. The first component compares the proposed method with the existing method, whilst the second component compares the proposed method with the previously developed PROMETHEE method.

Part I: Comparison of the proposed method with existing methods of Z-information fusion.

Method I. Yaakob and Gegov (2016) presented a TOPSIS method in Z-environments by converting the Z-number into a classical fuzzy number (Kang et al. 2018a, b, c, d). The following formula is used to convert the reliability restriction $B$ of the Z-number into a real number:

$$\alpha =\frac{{\int {x{\mu _B}dx} }}{{\int {{\mu _B}dx} }}.$$

(15)

Method II. The method proposed by Kang et al. (2012a, b) is based on another conversion concept, and it is expressed as

$$\begin{gathered} P(\tilde {A} \otimes \tilde {B}) \hfill \\ =P(\tilde {A}) \times (\tilde {B}) \hfill \\ =\frac{1}{6}({a_1}+4 \times {a_2}+{a_3}) \times \frac{1}{6}({b_1}+4 \times {b_2}+{b_3}) \hfill \\ \end{gathered}$$

(16)

Method III. Kang et al. (2018a, b, c, d) argued that a Z-number can be evaluated by using a real value based on utility theory. The utility formula of a Z-number is

$$\begin{array}{*{20}{l}} {}&{TU\left( Z \right)} \\ =&{TU\left( {\tilde {A},\tilde {R}} \right)} \\ =&{\int_{0}^{1} {\int_{0}^{1} {\int_{{ - \frac{1}{2}}}^{{\frac{1}{2}}} {\int_{{ - \frac{1}{2}}}^{{\frac{1}{2}}} {\left\{ {\begin{array}{*{20}{l}} {\left[ {\frac{{{{\tilde {A}}^ - }\left( \alpha \right)+{{\tilde {A}}^+}\left( \alpha \right)}}{2}+x\left( {{{\tilde {A}}^+}\left( \alpha \right) - {{\tilde {A}}^ - }\left( \alpha \right)} \right)} \right]{e^{ - {{\left[ {{{\tilde {A}}^+}\left( \alpha \right) - {{\tilde {A}}^ - }\left( \alpha \right)} \right]}^2}}}} \\ { \times \left[ {\frac{{{{\tilde {R}}^ - }\left( \beta \right)+{{\tilde {R}}^+}\left( \beta \right)}}{2}+x\left( {{{\tilde {R}}^+}\left( \beta \right) - {{\tilde {R}}^ - }\left( \beta \right)} \right)} \right]{e^{ - {{\left[ {{{\tilde {R}}^+}\left( \beta \right) - {{\tilde {R}}^ - }\left( \beta \right)} \right]}^2}}}} \end{array}} \right\}dxdyd\alpha d\beta } } } } } \end{array}.$$

(17)

Method IV. The decision-making method developed by Aliyev (2016) is based on their proposed distance measure for Z-numbers, and it is expressed as

$$D({Z_1},{Z_2})=\frac{1}{{n+1}}\sum\limits_{{k=1}}^{n} {\left\{ {\left| {a_{{1{a_k}}}^{L} - a_{{2{a_k}}}^{L}} \right|+\left| {a_{{1{a_k}}}^{R} - a_{{2{a_k}}}^{R}} \right|} \right\}} +\frac{1}{{m+1}}\sum\limits_{{k=1}}^{m} {\left\{ {\left| {b_{{1{a_k}}}^{L} - b_{{2{a_k}}}^{L}} \right|+\left| {b_{{1{a_k}}}^{R} - b_{{2{a_k}}}^{R}} \right|} \right\}} .$$

(18)

The rankings acquired from the abovementioned four methods are shown in Table 9.

Table 9 Rankings acquired from different methods

The four other methods, which result in the different rankings, can be further explained as follows.

As shown in Table 9, the ranking result obtained by Aliyev (2016) is somewhat identical to that of the proposed method. In addition, the optimal travel plans of the two methods are the same. The ranking method developed by Aliyev (2016) and the proposed ranking method are used to compare the fuzzy restriction and the reliability restriction of the Z-numbers based on the cut-set theory of trapezoidal/triangular fuzzy numbers. However, Aliyev considered a Z-number as a pair of equally important trapezoidal/triangular fuzzy numbers. This approach is inconsistent with that of actual decision-making. In general, DMs have different risk preferences and different degrees of emphasis towards information reliability. Therefore, the ranking result generated by Aliyev (2016) may deviate from actual decision-making.

The ranking result generated in Yaakob’s method is somewhat inconsistent with the proposed method. Yaakob and Gegov (2016) presented an extended Z-TOPSIS based on the conversion method of Kang et al. (2012a, b). The conversion method shows two characteristics. Firstly, it fully retains the information of fuzzy restriction $A$ in the Z-number. Secondly, reliability restriction $B$ is converted into a real number. Although this conversion method has attempted to reduce the complexity of comparing Z-numbers, it results in the information loss of Z-numbers to some extent in relation to the reliability restriction. Therefore, the ranking result produced by the above decision-making method is unconvincing.

The optimal travel plans acquired by the methods of Kang et al. (2018a, b, c, d); Kang et al. (2012a, b) are inconsistent with that of the proposed method. The extant two methods developed two formulas to convert the Z-number into a real value. Consequently, some unreasonable decision results may arise if these two ranking methods are followed. For example, no difference exists between ${Z_1}=((0.1,0.2,0.3),(0.4,0.5,0.6))$ and ${Z_2}=((0.4,0.5,0.6),(0.1,0.2,0.3))$ when the methods by Kang et al. (2018a, b, c, d); Kang et al. (2012a, b) are adopted. Obviously, the decision results do not accord with actual decision-making. In fact, the fuzzy restriction and reliability restriction of Z-numbers represent completely different meanings. Therefore, their ranking results may have some deviation from the actual decision-making.

The proposed method based on the possibility degree of Z-numbers does not convert the Z-number into a classical fuzzy number or crisp value. Furthermore, it can cater to the different risk preferences of DMs by adjusting the decision preference parameter. Therefore, the proposed method of ranking Z-numbers based on the possibility degree is more applicable when considering the risk preferences of DMs.

Part II: Comparison of the proposed method with the existing PROMETHEE methods.

Method I. Chen et al. (2011) developed an extended multi-criteria PROMETHEE approach based on Zadeh’s fuzzy logic. In their approach, TFNs were used as the uncertain information for criteria and alternative evaluation. The maximum set and minimum set method proposed by Chen (1985) was used to rank TFNs when the net flow of each alternative was calculated.

Method II. Tavakkoli-Moghaddam et al. (2015) proposed an extended multi-criteria Z-PROMETHEE group decision-making method. Criteria evaluation was conducted by using the Z-number, and the alternative evaluation under each criterion was expressed by TFNs. The conversion method in Kang et al. (2012a, b) was initially used to convert the Z-information of the evaluation criteria into TFNs, and the subsequent steps of their Z-PROMETHEE method were the same as those performed by Chen et al. (2011).

A comparison of different sets of evaluation information from the various PROMETHEE methods is shown in Table 10.

Table 10 Comparison of evaluation information among different PROMETHEE methods

The rankings acquired from the different methods are shown in Table 11.

Table 11 Rankings acquired from different methods

Z-numbers consider the fuzzy restriction and the reliability restriction of the decision information, and this approach differs from those that use traditional fuzzy sets. To effectively compare and analyse the extended PROMETHEE approaches under different information situations, the information for alternative evaluation is obtained and adjusted. Firstly, the reliability restrictions of the evaluation information of the alternatives and the criteria were ignored, and only the fuzzy restriction was considered when all the provided alternatives were sorted by the fuzzy PROMETHEE method of Chen et al. (2011). For example, for the evaluation $((115,120,125),VU)$ of ${a_{\text{1}}}$ under ${c_1}$, the reliability ‘VU’ was removed, and only the fuzzy restriction $(115,120,125)$ was retained. Secondly, in the Z-PROMETHEE method of Tavakkoli-Moghaddam et al. (2015), the evaluation information of the criteria was adjusted to render it fully reliable, and only the fuzzy restriction was retained. For instance, after removing the reliability restriction during criteria evaluation, all of the criteria except ${c_1}$ were regarded equally important because their fuzzy restriction was ‘S’.

As shown in Table 11, the best and worst alternatives (i.e. ${a_6}$ and ${a_{\text{1}}}$, respectively) derived from the two existing PROMETHEE methods are the same as those obtained by the proposed method. Thus, the proposed method and the existing methods are consistent to some extent.

However, some inconsistencies exist between the proposed method and the existing PROMETHEE methods. Firstly, ${a_{\text{3}}}$ and ${a_{\text{7}}}$ have different priorities when the two existing PROMETHEE methods are used to rank the alternatives. Although the fuzzy restriction of the evaluation information of all the criteria is the same except for ${c_1}$, the reliability restrictions of the evaluation information of ${c_2}$ and ${c_5}$ are higher. Consequently, ${c_2}$ and ${c_5}$ are more important. Moreover, Table 1 shows that the evaluations of ${a_{\text{3}}}$ under ${c_2}$ and ${c_5}$ are better than those of ${a_{\text{7}}}$. Therefore, the existing Z-PROMETHEE methods yielded ${a_{\text{3}}}$ with a higher priority compared that of the fuzzy PROMETHEE method. Secondly, the priority of ${a_{\text{8}}}$ obtained by the proposed method is lower than the priority of ${a_{\text{8}}}$ generated by the two existing methods, particularly because the two existing methods did not consider the reliability of their alternatives’ evaluation information. Evidently, as shown in Table 1, the reliability restriction of the evaluation information of ${a_{\text{8}}}$ under most criteria is very low. Therefore, ${a_{\text{8}}}$ in the proposed approach has a lower priority than the previously developed PROMETHEE methods.

The fuzzy PROMETHEE method proposed by Chen et al. (2011) did not consider the influence of information reliability on MCDM problems. In addition, in the Z-PROMETHEE method of Tavakkoli-Moghaddam et al. (2015), only the criteria were evaluated by the Z-number, whereas the alternative evaluation was expressed by TFNs. The comparative analysis shows that the proposed PROMETHEE method is better than the existing method when the information of the alternatives and the criteria are evaluated by using a Z-number. Furthermore, the proposed PROMETHEE approach is based on the comprehensively weighted possibility degree of Z-numbers, which considers the different effects of fuzzy and reliability restrictions of information during actual decision-making. The previously developed Z-PROETHEE method converted the Z-number into a TFN, which caused information loss to some extent. Overall, the proposed PROMETHEE method is better than the existing PROMETHEE methods.

On the basis of the comparative analysis, some conclusions about the proposed method can be drawn.

• 1. Adopting the different preferences of DMs indicates good applicability. The numerical example shows that although the decision matrix does not change all the time, the ranking results can vary when $\omega$ changes. In other words, even if two DMs use the same Z-evaluation, their expressions can still differ because of their varying preferences. The proposed ranking method is valid and therefore applicable in this case.

• 2. The information loss of Z-numbers can be reduced to some extent. In particular, the proposed approach does not convert the Z-number into a classical fuzzy number and/or a real number but instead considers the relation between two components of the Z-number. Thus, the proposed method is more faithful to the original concept of the Z-number, and it reduces information distortion.

• 3. Each extended PROMETHEE method has its own application scope. When the reliability restriction of an information is difficult to obtain under certain decision-making environments, using the traditional fuzzy PROMETHEE decision-making method may be more appropriate. The existing Z-PROMETHEE approach only considered the reliability restriction during criteria evaluation but not during alternative evaluation, which indicates research deficiency. By contrast, as an innovative work, the proposed PROMETHEE method simultaneously considers the reliability restriction during both alternative evaluation and criteria evaluation. Therefore, the proposed PROMETHEE is superior to the existing Z-PROMETHEE methods.

7 Conclusions

Z-number simultaneously considers the ambiguity and the reliability of an information. To fully use Z-numbers, efficient methods for Z-information fusion must be developed to support decision-making activities. A novel concept called the possibility degree of Z-numbers is proposed on the basis of the possibility degree concept of interval numbers to discuss the outranking relations of Z-numbers. The possibility degree formula for the Z-numbers is constructed in two steps. Firstly, the possibility degree of TFNs based on cut-set theory and the possibility degree of interval numbers is defined to serve as the basis of the proposed method. Secondly, the possibility degree formula of the Z-numbers is constructed by combining the possibility degrees of two restriction components of the Z-number by using a single adjustable risk preference parameter. In addition, the numerical example also illustrates the effectiveness of the proposed method to enhance the practical application of cognitive information during decision making under Z-evaluation.

The topics about the possibility degree of Z-numbers are worth studying in future research. Firstly, parameter determination, as a manner of reflecting the varying preferences of different DMs, continues to be important, especially in group decision making. The possible future direction is to determine the value of the risk preference parameter by using intelligent optimisation algorithms. Secondly, considering that Z-numbers can much better describe the objective world when combined with natural language, the proposed ranking method for Z-numbers may play a significant role in the fields of computing with words, artificial intelligence and cognitive computing.

Appendices

Appendix A. Special computation of the possibility degree of triangular fuzzy numbers

Let $\tilde {a}=({a_1},{a_2},{a_3})$ and $\tilde {b}=({b_1},{b_2},{b_3})$ be any two TFNs. The possibility degree of $\tilde {a} \geq \tilde {b}$ can be computed as follows:

If ${a_1}={a_2}$, ${a_2}={a_3}$, ${b_1}={b_2}$ and ${b_2}={b_3}$, then

$$p(\tilde {a} \geq \tilde {b})=\left\{ {\begin{array}{*{20}{c}} 0&{{a_2}<{b_2}} \\ {0.5}&{{a_2}={b_2}} \\ 1&{{a_2}>{b_2}} \end{array}} \right.$$

Otherwise,

$p(\tilde {a} \geq \tilde {b})=\left\{ {\begin{array}{*{20}{c}} 0&{{a_2}<{b_2}\,{\text{and}}\,{a_3} \leq {b_1}} \\ {\frac{{{a_3} - {b_1}}}{{({b_3} - {b_1})+({a_3} - {a_1})}}+\frac{{{b_2} - {a_2}}}{{({b_3} - {b_1})+({a_3} - {a_1})}}\ln \left( {\frac{{{b_2} - {a_2}}}{{({b_2} - {b_1})+({a_3} - {a_1})}}} \right)}&{{a_2}<{b_2}\,{\text{and}}\,{a_3}>{b_1}} \\ {\frac{{{a_3} - {b_1}}}{{({b_3} - {b_1})+({a_3} - {a_1})}}}&{{a_2}={b_2}} \\ {\frac{{{a_3} - {b_1}}}{{({b_3} - {b_1})+({a_3} - {a_1})}}+\frac{{{a_2} - {b_2}}}{{({b_3} - {b_1})+({a_3} - {a_1})}}\ln \left( {\frac{{{a_2} - {b_2}}}{{({a_2} - {a_1})+({b_3} - {b_2})}}} \right)}&{{a_2}>{b_2}\,{\text{and}}\,{b_3}>{a_1}} \\ 1&{{a_2}<{b_2}\,{\text{and}}\,{b_3}>{a_1}} \end{array}} \right.$

Appendix B. Proof for the conclusion in Remark 1.

As shown in Fig. 2, two TFNs, denoted by ${A_i}$ and ($i<j$), exist.

If ${A_i}$ and ${A_j}$ are non-intersecting (e.g. ${A_3}$ and ${A_4}$), then ${p^\alpha }({A_i} \geq {A_j})=0,\,\forall \alpha \in [0,1]$ Consequently, $p({A_i} \geq {A_j})<0.5$ is satisfied according to Definition 9.

If ${A_i}$ and ${A_j}$ are partially intersecting (e.g. ${A_1}$ and ${A_2}$), whose cut sets under level $\alpha$ are $\left[ {A_{{i\alpha }}^{ - },A_{{i\alpha }}^{+}} \right]$and $\left[ {A_{{j\alpha }}^{ - },A_{{j\alpha }}^{+}} \right]$, then ${p^\alpha }({A_i} \geq {A_j})=\left\{ {\begin{array}{*{20}{l}} 0&{A_{{i\alpha }}^{+} - A_{{j\alpha }}^{ - } \leq 0} \\ {\frac{{A_{{i\alpha }}^{+} - A_{{j\alpha }}^{ - }}}{{(A_{{j\alpha }}^{+} - A_{{j\alpha }}^{ - })+(A_{{i\alpha }}^{+} - A_{{i\alpha }}^{ - })}}}&{A_{{i\alpha }}^{+} - A_{{j\alpha }}^{ - }>0} \end{array}} \right.$. Furthermore, the following is obtained:

$\frac{{A_{{i\alpha }}^{+} - A_{{i\alpha }}^{ - }}}{{(A_{{j\alpha }}^{+} - A_{{j\alpha }}^{ - })+(A_{{i\alpha }}^{+}+A_{{i\alpha }}^{ - })}} \leq \frac{{A_{{i\alpha }}^{+} - A_{{j\alpha }}^{ - }+\left[ {\frac{{A_{{j\alpha }}^{+}+A_{{j\alpha }}^{ - }}}{2} - \frac{{A_{{i\alpha }}^{+}+A_{{i\alpha }}^{ - }}}{2}} \right]}}{{(A_{{j\alpha }}^{+} - A_{{j\alpha }}^{+})+(A_{{i\alpha }}^{+} - A_{{i\alpha }}^{ - })}}=\frac{{\frac{1}{2}\left[ {(A_{{j\alpha }}^{+} - A_{{j\alpha }}^{ - })+(A_{{i\alpha }}^{+} - A_{{i\alpha }}^{ - })} \right]}}{{(A_{{j\alpha }}^{+} - A_{{j\alpha }}^{ - })+(A_{{i\alpha }}^{+} - A_{{i\alpha }}^{ - })}}=0.5.$Consequently, ${p^\alpha }({A_i} \geq {A_j}) \leq 0.5,\forall \alpha \in \left[ {0,1} \right]$ is always true. Therefore, $p({A_i} \geq {A_j})<0.5$ is satisfied according to Definition 9.

On the basis of the above definitions, the relevant conclusion can be obtained.