1 Introduction

Vehicle active suspension plays an important component of the automobile assisted driving technology in improving the driving safety, the road-holding capability and the passenger ride comfort [1, 2]. However, many irresistible phenomena threat to the safety and stability of vehicle active suspension, such as the irregular road disturbances and structure friction loss. To offset the persistent vehicle body’s vibration and satisfy the control performance requirement of the vehicle active suspension, various active control schemes have been proposed in recent decades aiming to achieve the tradeoff among the conflicting performance requirements including the road-holding ability, ride comfort, suspension deflection and energy consumption [3]. More recently, combining active vibration control strategies with advanced optimal control technologies to offset the irregular vehicle body’s vibration has been attracted continuing attention, such as linear quadratic optimal control [4], approximate optimal active control [5] and optimal preview active control [6].

With advantages of convenient maintenance and flexible structure, the researches on networked control system (NCSs) have become important topics in the automatic control domain [7, 8], such as stability analysis [9], controller design [10, 11], and fault-tolerant diagnosis and control [12,13,14]. Then, the networked vehicle active suspension is an inevitable trend by using the technologies of advanced actuator and communication network. However, due to the complexities of active suspension actuator and communication network, control delay is inevitable in practical vehicle engineering [15]. On the one hand, while the advanced suspension actuator implements the control strategies, the control delay will be induced from building up the required control force, such as pneumatic [16, 17] and hydraulic systems [18, 19]. On the other hand, in communication network, control delay mainly results from transmitting the control signals from vehicle implementing agency to actuator. Unfortunately, the control delay usually brings about the deterioration of control performance, even the instability of vehicle active suspension. Taken the control delay and external road disturbances into account, the design problem of vibration control strategy for networked vehicle active suspension is crucially important for development of the vehicle initiative safety system. The aim of this paper is to seek a disturbance attenuation controller to reduced the road-induced vibration of the vehicle active suspension and compensate the random control delay.

The disturbance attenuation control problem for networked vehicle active suspension is discussed in this paper, in which the random control delay and the external road disturbances with Gaussian white noise are considered. First, the T–S fuzzy model for networked vehicle active suspension is established, where the appearing probabilities of control delay are defined as the membership function. After that, a delay-free transformation system and a corresponding reformed performance index are designed based on an introduced transformation vector. By employing the optimal control theory and a Kalman filter, a physically realizable disturbance attenuation controller is proposed. Finally, the effectiveness of proposed control scheme is illustrated by discussing the sprung mass acceleration, the suspension deflection and the tyre deflection under different situations with control delay.

The rest of this paper is organized as follows. The attenuation control problem for networked vehicle active suspension is presented in Sect. 2. The main result of this paper is proposed in Sect. 3 where the optimal disturbance attenuation controller is developed. By employing a simple vehicle active suspension, some simulation results are given in Sect. 4. Some findings and concluding remarks are concluded in Sect. 5.

2 Problem Description

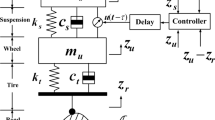
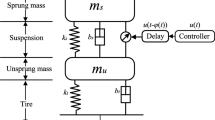
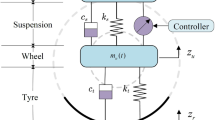
In this section, we discuss a simple vehicle active suspension displayed in Fig. 1. Tanking the random control delay into account, the dynamic equations of the two-dimensional vehicle active suspension are described as

$$\begin{aligned}&{m_s \ddot{z}_s (t) + c_s [\dot{z}_s (t) - \dot{z}_u (t)] + k_s [z_s (t) - z_u (t)] = u(t-\tau )}, \nonumber \\&m_u \ddot{z}_u (t) + c_s [\dot{z}_u (t) - \dot{z}_s (t)] + k_s [z_u (t) - z_s (t)] \nonumber \\&\quad + k_t [z_u (t) - z_r (t)] + c_t [\dot{z}_u (t) - \dot{z}_r (t)] = - u(t-\tau ), \end{aligned}$$
(1)

where \(m_s(t)\) and \(z_s(t)\) denote the mass and displacement of sprung components; \(z_s(t)\) and \(z_u(t)\) are the mass and displacement of unsprung components; \(k_t\) and \(c_t\) denote the compressibility and damping of the pneumatic tyre; \(c_s\) and \(k_s\) stand for the damping and stiffness of vehicle active suspension, respectively. u(t) is the control force with control delay \(\tau\), and \(z_r\) denotes the road irregularities acting on the vehicle active suspension.

Fig. 1
figure 1

The simple quarter vehicle active suspension

Full size image

Defining the following vehicle suspension system state

$$\begin{aligned} \bar{x}(t) = \left[ {\begin{array}{*{20}c} {x_1 (t)} \\ {x_2 (t)} \\ {x_3 (t)} \\ {x_4 (t)} \\ \end{array}} \right] = \left[ {\begin{array}{*{20}c} {z_s (t) - z_u (t)} \\ {z_u (t) - z_4 (t)} \\ {\dot{z}_s (t)} \\ {\dot{z}_u (t)} \\ \end{array}} \right] , \end{aligned}$$
(2)

the continuous-time state space of vehicle active suspension can be written as

$$\left\{ {\begin{array}{*{20}l} {\dot{\bar{x}}(t) = \bar{A}\bar{x}(t) + \bar{B}u(t - \tau ) + \bar{D}v(t),} \hfill \\ {y_{c} (t) = C\bar{x}(t) + Eu(t - \tau ),} \hfill \\ \end{array} } \right.$$
(3)

where \(x_1\) denotes the suspension deflection, \(x_2\) is the tyre deflection, \(x_3\) and \(x_4\) represent the velocities of sprung mass and unsprung mass, respectively; \(y_c(t)\) is the controlled output; \(v(t) = \dot{z}_r (t)\), and

$$\begin{aligned} \bar{A}= \left[ {\begin{array}{*{20}c} 0 &{}\quad 0 &{}\quad 1 &{}\quad { - 1} \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ {- \frac{{ k_s }}{{m_s }}} &{}\quad 0 &{}\quad { -\frac{{ {\mathrm{c}}_s }}{{m_s }}} &{}\quad {\frac{{c_s }}{{m_s }}} \\ {\frac{{k_s }}{{m_u }}} &{}\quad {-\frac{{ k_t }}{{m_u }}} &{}\quad {\frac{{c_s }}{{m_u }}} &{}\quad {- \frac{{ (c_s + c_t )}}{{m_u }}} \\ \end{array}} \right] ,\nonumber \\ \bar{B} = \left[ \begin{array}{l} 0 \\ 0 \\ \frac{1}{{m_s }} \\ - \frac{1}{{m_u }} \\ \end{array} \right] ,\; \bar{D}_v = \left[ \begin{array}{l} 0 \\ - 1 \\ 0 \\ \frac{{c_t }}{{m_u }}\; \end{array} \right] ,\,\nonumber \\ C = \left[ \begin{array}{l} - \frac{{k_s }}{{m_s }}\quad 0\quad - \frac{{c_s }}{{m_s }}\quad \frac{{c_s }}{{m_s }} \\ \quad 1\quad \;\,0\quad \quad 0\quad \quad \;0 \\ \quad 0\quad \;\,1\quad \quad 0\quad \quad \;0 \\ \end{array} \right] ,\, E = \left[ {\begin{array}{*{20}c} {\frac{1}{{m_s }}} \\ 0 \\ 0 \\ \end{array}} \right] . \end{aligned}$$
(4)

Considering the vehicle active suspension under an in-vehicle network, the following fuzzy rule is defined based on the random control delay \(\tau\), which is in the form as

$$\begin{aligned} \begin{array}{l} \hbox {IF}\quad \quad \quad \left( {m - 1} \right) T < \tau \le mT,\\ \hbox {THEN}\quad \;x\left( {k + 1} \right) = Ax\left( k \right) +Dv(k)+ Hu\left( {k - m} \right) , \end{array} \end{aligned}$$
(5)

where T denotes the sampling period, the random control delay \(\tau\) is evaluated between two adjacent sampling periods with \(\left( {m - 1} \right) T \le \tau < mT\), \(A={\mathrm{e}^{\bar{A}T}}\), \(H=\int _0^T {{\mathrm{e}^{\bar{A}t}}{\mathrm{d}}t\bar{B}}\) and \(D = \int _0^T {{\mathrm{e}^{\bar{A}t}}{\mathrm{d}}t\bar{D}}\).

Defining the appearing probabilities of control delay as membership function to fuzzily fuse the subsystems (5), the global model of networked vehicle active suspension with random control delay can be formulated as

$$\left\{ {\begin{array}{*{20}l} {x(k + 1) = Ax(k) + \sum\limits_{{i = 1}}^{M} {\mu _{i} Hu(k - i)} + Dv(k),} \hfill \\ {y_{c} (k) = Cx(k) + \sum\limits_{{i = 1}}^{M} {\mu _{i} Eu(k - i),} } \hfill \\ \end{array} } \right.$$
(6)

where M is the number of switch subsystems, \({\mu _i}\) denotes the appearing probability of the control delay with the following constrains

$$\begin{aligned} {\mu _m} = P\left[ {\left( {m - 1} \right) T< \tau < mT} \right] \in \left[ {\begin{array}{ll} 0&1 \end{array}} \right] , \sum \limits _{i = 1}^M {{\mu _i} = 1.} \end{aligned}$$
(7)

For the external road disturbances, as stated in [5], based on the ground displacement power spectral density (PSD) under different road roughnesses, the road disturbance v(t) can be viewed as the output of the following exosystem

$$\begin{aligned} \left\{ \begin{array}{l} \dot{w}(t) = \bar{G}_v w(t), \\ v(t) = F_v w(t), \\ \end{array} \right. \end{aligned}$$
(8)

where \(\bar{G}_v \in R^{2p \times 2p}\), \(F_v \in R^{1 \times 2p}\), and

$$\begin{aligned} \bar{G}_v = \left[ {\begin{array}{*{20}c} {\mathbf{{0}}} &{}\quad {\mathbf{{I}}} \\ {\tilde{G}} &{}\quad {\mathbf{{0}}} \\ \end{array}} \right] , \nonumber \\ F_v = [\underbrace{\begin{array}{*{20}c} {0,} &{} { \ldots ,} &{} {0,} \\ \end{array}}_p\;\;\underbrace{\begin{array}{*{20}c} {1,} & { \ldots ,} &{} 1 \\ \end{array}}_p], \nonumber \\ \tilde{G}=& {\mathrm{diag}}\left\{ {\begin{array}{*{20}c} { - \omega _1^2 ,\;} & { \ldots ,} &{} { - \left( \omega _1 + (p-1) \frac{2 \pi v_0}{l}\right) } \\ \end{array}} \right\} . \end{aligned}$$
(9)

in which the considered frequency range of road disturbances is arranged in \(\left[ {\omega _1 ,\omega _2 } \right] = \left[ {\beta _1 \omega _n ,\beta _2 \omega _n } \right]\) with \(0< \beta _1< 1 < \beta _2\); \(p \in \left[ {\left( {\omega _2 - \omega _1 } \right) l/2\pi v_0 + 1,\left( {\omega _2 - \omega _1 } \right) l/2\pi v_0 + 2} \right)\) restricts the frequency of road roughness; l is the road length.

Taken the measurement noise into account, the discrete-time form of Eq. (8) can be described as following equation with the sampling period T

$$\left\{ {\begin{array}{*{20}l} {w(k + 1) = G_{v} w(k) + H_{v} m(k),} \hfill \\ {v(k) = F_{v} w(k) + n(k),} \hfill \\ \end{array} } \right.$$
(10)

where \(G_v = e^{\bar{G}_vT}\), m(k) and n(k) denote the discrete-time Gaussian white-noise processes with zero-mean values

$$\begin{aligned} E[m(k)m^T (j)] = \bar{Q}\delta _{kj} ,E[n(k)n^T (j)] = \bar{R}\delta _{kj} , \nonumber \\ \mathop {\mathrm{cov}} [m(k)n^T (j)]= 0,\forall k,j. \end{aligned}$$
(11)

In general, the performance requirements include the suspension deflection, the sprung mass acceleration and the tyre deflection. In order to trade off between performance requirements and energy consumption, the following average performance index is chosen as

$$\begin{aligned} \begin{array}{l} J = \mathop {\lim}\limits _{N \rightarrow \infty } \frac{1}{N}\sum \limits _{k = 0}^N {\left[ {{\mathrm{y}}_c ^T (k)Qy_c (k) + u^T (k)Ru(k)} \right] }, \\ \end{array} \end{aligned}$$
(12)

where \(Q \in R^{3\times 3}\) is positive-semi-definite matrix, and R is a positive real number.

Then, the disturbance attenuation control problem for networked vehicle active suspension with random control delay and measurement noise can be formulated to find a controller \(u^ * ( \cdot )\) to minimize the performance index (12) under the constrains of (6) and (10).

3 Design of Optimal Disturbance Attenuation Controller

3.1 Reformation of Disturbance Attenuation Control Problem

Due to the control delay items \(\sum \nolimits _{i = 1}^M {\mu _i Hu(k - i)}\), it is difficult to design the optimal disturbance attenuation controller. In order to resolve this problem, the following transformation vector is introduced as

$$\begin{aligned} z(k) = x(k) + \sum \limits _{i = 1}^M {{\mu _i}\sum \limits _{j = k - i}^{k - 1} {{A^{k - j - 1 - i}}H} u(j)}, \end{aligned}$$
(13)

vehicle active suspension (6) can be reformulated as

$$\begin{aligned} z\left( {k + 1} \right) = Az\left( k \right) + Bu\left( k \right) + Dv\left( k \right) ,\nonumber \\ {y_c}\left( k \right) = Cz\left( k \right) + \varGamma (k), \end{aligned}$$
(14)

where

$$\begin{aligned} B = \sum \limits _{i = 1}^M {{\mu _i}{A^{ - i}}H,} \,\nonumber \\ \varGamma (k) = \sum \limits _{i = 1}^M {\mu _i \left( {Eu(k - i) - \sum \limits _{j = k - i}^{k - 1} {CA^{k - j - 1} } Hu(j)} \right) }. \end{aligned}$$
(15)

Substituting the second formula \(y_c(k)\) of (14) into the performance index (12), it can be reformulated as

$$\begin{aligned} J = \mathop {\lim}\limits _{k \rightarrow \infty } \frac{1}{N}\sum \limits _{k = 0}^N {\left( {z^T (k)C^T QCz(k)} \right. } \nonumber \\&+\,\left. u^T (k)Ru(k) + \varGamma ^T (k)Q\varGamma (k) + 2z^T (k)C^T Q\varGamma (k) \right) , \end{aligned}$$
(16)

Expanding superposition and summarizing the same item, one has

$$\begin{aligned}& \mathop {\lim}\limits _{k \rightarrow \infty } \sum \limits _{k = 0}^N {\left( {\varGamma ^T (k)Q\varGamma (k)} \right) } = \mathop {\lim}\limits _{k \rightarrow \infty } \sum \limits _{k = 0}^N {\left( {u^T (k)R_{uu} u(k)} \right) ,} \nonumber \\& \mathop {\lim}\limits _{k \rightarrow \infty } \sum \limits _{k = 0}^N {\left( {z^T (k)C^T Q\varGamma (k)} \right) } \nonumber \\&\quad = \mathop {\lim}\limits _{k \rightarrow \infty } \sum \limits _{k = 0}^N {\left( {z^T (k)Q_{zu} u(k) + w^T (k)Q_{wu} u(k)} \right) ,} \end{aligned}$$
(17)

where

$$\begin{aligned} R_{uu} = \sum \limits _{i = 1}^M {\mu _i } \left( {E^T QE - \sum \limits _{j = 1}^i {\left( {\left( {CA^{ - j} B} \right) ^T QCA^{ - j} H} \right) } } \right) , \nonumber \\ Q_{zu} = \sum \limits _{i = 1}^M {\mu _i } \left( {\left( {CA^i } \right) ^T QE - \sum \limits _{j = 1}^i {\left( {\left( {CA^i } \right) ^T QCA^{j - 1 - i} H} \right) } } \right) , \nonumber \\ Q_{wu} = \sum \limits _{i = 1}^M {\mu _i } \left( {\left( {\sum \limits _{j = 1}^i {CA^{i - j} DFG^{j - 1} } } \right) ^T QE} \right. \nonumber \\&\left. - \sum \limits _{j = 1}^i {\sum \limits _{t = 0}^{i - j} {\left( {\left( {CA^t DFG^{j - 1} } \right) ^T QCA^{t + j - i - 1} H} \right) }}\right) . \end{aligned}$$
(18)

Then the introduced average quadratic performance index (12) can be reformulated as

$$\begin{aligned} J = \mathop {\lim}\limits _{k \rightarrow \infty } \frac{1}{N}\sum \limits _{k = 0}^N {\left( z^T (k)C^T QCz(k)\right. } \nonumber \\&\left. +\, z^T (k)Q_{zu} u(k) + u^T (k)\tilde{R}u(k) + w^T (k)Q_{wu} u(k)\right) , \end{aligned}$$
(19)

where \(\tilde{R} = R_{uu} + R\).

Therefore, the disturbance attenuation control problem can be reformulated to find a controller \(u^ * ( \cdot )\) to minimize the performance index (16) under the constrains of (10) and (14).

Remark 1

Noted the designed real number \(\tilde{R}\), the absolute value of component \(R_{uu}\) is in the range of [0, 1] based on the small values of matrices A, B, C and H. Therefore, the value of R could set a reasonable value to ensure the existence of \(\tilde{R}^{-1}\), which is larger than the absolute value of \(R_{uu}\)

3.2 Optimal Disturbance Attenuation Controller

The main results are described in the following theorem, which include a physical realizable disturbance attenuation controller with a Kalman filter for estimating the road disturbances.

Theorem 1

Consider the disturbance attenuation control problem for theT–Sfuzzy networked vehicle active suspension (6) subject to the persistent irregular road disturbance (10) with respect to the average quadratic performance index (12), the disturbance attenuation controller can be designed as

$$\begin{aligned} u(k) = - \tilde{R}^{ - 1} \left( {K_1 z(k) + K_2 \hat{w}(k)} \right) , \end{aligned}$$
(20)

where

$$\begin{aligned} S = (I + B^T PB\tilde{R}^{ - 1} )^{ - 1} , \; K_1 = Q_{zu}^T + SB^T PA_1 , \nonumber \\ K_2 = Q_{wu}^T + SB^T (P(D_v F_v - B\tilde{R}^{ - 1} Q_{wu}^T ) + P_1 G_v ), \end{aligned}$$
(21)

in whichPis the unique solution of the following Riccati equation

$$\begin{aligned} P &=& \left( C^T QC - Q_{zu} \tilde{R}^{ - 1} Q_{zu}^T \right) \nonumber \\&&\quad + A_1^T P(I + B\tilde{R}^{ - 1} B^T P)^{ - 1} A_1 , \end{aligned}$$
(22)

and\(P_1\)is the unique solution of the following Stein equation

$$\begin{aligned} P_1 = A_1 P\left( D_v F_v - B\tilde{R}^{ - 1} Q_{wu}^T \right) \nonumber \\&+ A_1 (I - PB\tilde{R}^{ - 1} B^T )P_1 G_v - Q_{zu} \tilde{R}^{ - 1} Q_{wu}^T , \end{aligned}$$
(23)

with\(A_1 = A - B\tilde{R}^{ - 1} Q_{zu}^T\).

Meanwhile,\(\hat{w}(k)\)is the estimation of road disturbance statew(k), which can be obtained from the following Kalman filter

$$\begin{aligned} \hat{w}(k + 1|k + 1) = G_v \hat{w}(k|k) \nonumber \\&+K(k + 1)(v(k + 1) - F_v \hat{w}(k + 1|k)), \end{aligned}$$
(24)

where

$$\begin{aligned} \hat{w}(k + 1|k) = G_v w(k|k), \nonumber \\ K(k + 1) = \bar{P}(k + 1|k)F_v^T (F_v \bar{P}(k + 1|k) + \bar{R})^{ - 1} , \nonumber \\ \bar{P}(k + 1|k) = G_v \bar{P}(k|k)G_v^T + H_v \bar{Q}H_v^T , \nonumber \\ \bar{P}(k + 1|k + 1) = \left( {I - K(k + 1)F_v } \right) \bar{P}(k + 1|k), \end{aligned}$$
(25)

Proof

Applying the optimal theory to disturbance attenuation control problem, the disturbance attenuation controller can be designed as

$$\begin{aligned} u(k) = - \tilde{R}^{ - 1} \left( {Q_{zu}^T z(k) + Q_{wu}^T w(k) + B^T \lambda (k + 1)} \right) . \end{aligned}$$
(26)

Then the following TPBV problem is introduced

$$\begin{aligned} \left\{ \begin{array}{l} z(k + 1) = A_1 z(k) + \\ (D_v F_v - B\tilde{R}^{ - 1} Q_{wu}^T )w(k) - B\tilde{R}^{ - 1} B^T \lambda (k + 1), \\ \lambda (k) = (C^T QC - Q_{zu} \tilde{R}^{ - 1} Q_{zu}^T )z(k) \\ + A_1^T \lambda (k + 1) - Q_{zu} \tilde{R}^{ - 1} Q_{wu}^T w(k), \\ z(0) = x_0 ,\lambda (\infty ) = 0. \\ \end{array} \right. \end{aligned}$$
(27)

By defining the following vector \(\lambda (k)\)

$$\begin{aligned} \lambda (k) = Pz(k) + P_1 w(k), \end{aligned}$$
(28)

the above TPBV problem can be obtained.

Rearranging (26), (27) and (28), we have

$$\begin{aligned} B^T \lambda (k + 1) = SB^T \left[ {PA_1 z(k)} \right. \nonumber \\&+\left. \left( {P\left( {D_v F_v - B\tilde{R}^{ - 1} Q_{wu}^T } \right) + P_1 G_v } \right) w(k) \right] . \end{aligned}$$
(29)

Substituting (29) into (26), the disturbance attenuation controller can be obtained as

$$\begin{aligned} u(k) = - \tilde{R}^{ - 1} \left( {K_1 z(k) + K_2 w(k)} \right) . \end{aligned}$$
(30)

Rearranging (28) and the first formula of (27), we have

$$\begin{aligned} z(k + 1) = S\left\{ {A_1 z(k)} \right. \nonumber \\&+\left. {\left( {D_v F_v - B\tilde{R}^{ - 1} Q_{wu}^T - B\tilde{R}^{ - 1} B^T P_1 G_v } \right) w(k)} \right\} . \end{aligned}$$
(31)

Thus we have

$$\begin{aligned} \lambda (k) = \left( {C^T QC - Q_{zu} \tilde{R}^{ - 1} Q_{zu}^T } \right) z(k) \nonumber \\&+\, A_1 \left( {Pz(k + 1) + P_1 w(k + 1)} \right) - Q_{zu} \tilde{R}^{ - 1} Q_{wu}^T w(k) \nonumber \\ = \{ (C^T QC - Q_{zu} \tilde{R}^{ - 1} Q_{zu}^T ) \nonumber \\&+\, A_1 P(I + B\tilde{R}^{ - 1} B^T P)^{ - 1} A_1 \} z(k) \nonumber \\&+\, \{ A_1 P(D_v F_v - B\tilde{R}^{ - 1} Q_{wu}^T ) - Q_{zu} \tilde{R}^{ - 1} Q_{wu}^T \nonumber \\&+\, A_1 (I - PB\tilde{R}^{ - 1} B^T )P_1 G_v \} w(k). \end{aligned}$$
(32)

Noting the parameters for the items of z(k) and w(k) in (28) and (32), the Riccati equation (22) and Stein equation (23) are obtained.

Meanwhile, it should be noted that the disturbance attenuation controller (30) is physical unrealizable caused by the disturbance state w(k). Then by applying the Kalman filter theory, the Kalman filter (24) is designed under the assumption (11). Substituting the estimated value \(\hat{w}(k)\) for w(k) into the controller (30), the optimal disturbance attenuation controller (20) is designed. The proof is completed. \(\square\)

4 Simulation Results

In this section, by employing a simple active vehicle suspension, experimental results will be discussed detailed to show the abilities for offsetting the irregular road disturbance and compensating the random control delay of the proposed optimal disturbance attenuation controller (20).

The parameters of vehicle active suspension are listed in Table 1. Thus the matrices A, B, C and D in Eq. (14) are obtained as

$$\begin{aligned} A = \left[ {\begin{array}{*{20}c} 0.8754 &{}\quad 0.2627&{}\quad 0.0734&{}\quad -\,0.0661\\ 0.1110&{}\quad 0.7358&{}\quad 0.0059&{}\quad 0.0668\\ -\,0.3290&{}\quad -\,0.0628&{}\quad 0.9779&{}\quad 0.0206\\ 2.5350&{}\quad -\,6.0630&{}\quad 0.1760&{}\quad 0.5589\\ \end{array}} \right] , \nonumber \\ H = 10^{ - 4} \times \left[ {\begin{array}{*{20}c} 0.0292 \\ -\,0.0260\\ 0.0770\\ -\,0.5934\\ \end{array}} \right] , D = \left[ {\begin{array}{*{20}c} -\,0.0073\\ -\,0.0727\\ 0.0015\\ 0.2651\\ \end{array}} \right] , \nonumber \\ C = \left[ {\begin{array}{*{20}c} -\,4.4838&{}\quad 0&{}\quad -\,0.1149&{} \quad 0.1149\\ 1.0000&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1.0000&{}\quad 0&{}\quad 0\\ \end{array}} \right] , \nonumber \\ E = 10^{ - 3} \times \left[ {\begin{array}{*{20}c} 0.1050\\ 0 \\ 0 \\ \end{array}} \right] . \end{aligned}$$
(33)

Meanwhile, the road displacement input is generated from the exosystem in Eq. (10) based on the parameters shown in Table 2. The curve of the random road disturbances input is shown in Fig. 2. In order to established the T–S fuzzy networked vehicle active suspension, the probability distributions of control delay \(\tau\) are given in Table 3. At the same time, the designed performance index (12) is set as \(Q = {10^7} \times {\mathrm{diag}}\left\{ {1,\;2,\;5} \right\} , R = 215.07\) (Fig. 2).

Fig. 2
figure 2

The curve of random road disturbances

Full size image
Table 1 Parameters of vehicle active suspension [16]
Full size table
Table 2 Parameters of random road roughness
Full size table
Table 3 Probability distributions of actuator time delay
Full size table

In order to show the abilities of offsetting the irregular road disturbance and compensating the random control delay more clearly, the control performances will be discussed by applying the proposed controller to the above vehicle active suspension. Specially, considering an open-loop vehicle active suspension and ones under proposed control scheme with control delay \(\tau = 15\), 24, 45 ms, the comparison curves of the sprung mass acceleration, the suspension deflection, the tyre deflection and the control force are displayed in Figs. 3, 4, 5 and 6.

Fig. 3
figure 3

The curve of sprung mass acceleration under different situations

Full size image
Fig. 4
figure 4

The curve of suspension deflection under different situations

Full size image
Fig. 5
figure 5

The curve of tyre deflection under different situations

Full size image
Fig. 6
figure 6

The curve of control force under different situations

Full size image

From Figs. 3, 4 and 5, by applying the proposed control scheme, it can be observed that the values of the suspension deflection, the sprung mass acceleration and the tyre deflection could be converged to a small range rapidly under control delays \(\tau = 15\), 24, 45 ms. Meanwhile, although the control delays increase, the values of the sprung mass acceleration, suspension deflection and tyre deflection can be arranged in the range of \((-\,0.25,0.25)\), \((-\,0.05,0.05)\) and \((-\,0.025,0.025)\), respectively. Then the control performance can be improved effectively under the proposed control scheme. Meanwhile, from Fig. 6, the trajectories of control schemes are similar under the situations with control delays \(\tau = 15\), 24, 45 ms.

After that, in order to demonstrate the ability of improving the control performance under control delays, the root-mean-square (RMS) values of control performance requirements are displayed in Tables 4, 5 and 6 including the sprung mass acceleration, suspension deflection and tyre deflection are displayed in Tables 4, 5 and 6 under different situations with control delays \(\tau = 15\), 24, 34, 45 and 56 ms, in which the decrement rate (DR) of the closed-loop (CL) response relative to the OL vehicle active suspension are given. For example, while control delay \(\tau = 15\) ms, the RMS values of sprung mass acceleration, suspension deflection and tyre deflection under proposed controller are 0.0840, 0.0215 and 0.0129. Compared to OL system, the decrement rate are 52.24%, 45.15% and 34.18%.

Table 4 RMS values of the sprung mass acceleration under difference situations
Full size table
Table 5 RMS values of the suspension deflection under difference situations
Full size table
Table 6 RMS values of the tyre deflection under difference situations
Full size table

In summary, the proposed control scheme is efficient to improve the control performance, offset the road disturbance and compensate the control delay.

5 Conclusion

The disturbance attenuation control scheme for T–S fuzzy networked vehicle active suspension was developed in this paper. A T–S fuzzy model of networked vehicle active suspension was established based on the appearing probabilities of control delay. The gain matrices of the disturbance attenuation control scheme were designed by solving a TPBV problem formulated from a delay-free transformation system and an equivalence performance index. Meanwhile, the road disturbance state were estimated from a Kalman filter under white noise. The simulation results have shown that under the proposed control scheme with different control delays, the values of control performance including suspension deflection, sprung mass acceleration and tyre deflection can be effectively reduced, and the road disturbances can be significantly offset.