Introduction

Wetland ecosystems, the area of marsh or fen, whether natural or artificial, fresh or salty, play an important role and provide support to millions of peoples who live surrounding it. Wetland is the primary habitat for a range of various species, fish, birds and sustains a variety of flora and fauna. The Sundarbans is located in the Bay of Bengal on the Ganges, the Brahmaputra and Meghna Delta (Ghosh et al. 2015). The Sundarbans (21\(^\circ\) 32′ to 22\(^\circ\) 40′ N and 88\(^\circ\) 05′ to 89\(^\circ\) 51′ E) covers the area 10,000 km\(^{2}\) approximately, lies between Bangladesh (62%) and India (38%) and is the largest mangrove on the earth (Spalding et al. 2010). Mangroves at land–sea interface are a highly diverse and productive ecosystem that protect the coastal areas from cyclones and tsunamis (Dahdouh-Guebas et al. 2005). It provides nutrients recycle, growth of coral reefs, reef fish, provides food for the countless organism and collectively has great economic value (Nagelkerken et al. 2008). Indian Sundarbans with varying freshwater inputs has 24 mangrove taxa of 9 different families (Barik and Chowdhury 2014). The biodiversity of Sundarbans has more than 200 other plant species, birds, fish, reptiles, mammals and a number of phytoplankton, zooplankton, benthic invertebrates, bacteria, fungi, etc. (Gopal and Chauhan 2006). A total of 46 taxa of phytoplankton belonging to six major classes algal groups Bacillariophyceae (Diatoms), Chlorophyceae (Green algae), Cyanophyceae ( Blue-green algae), Pyrrophyceae (Dinoflagellates) and Chrysophyceae are recorded in the estuarine water of Sundarbans (Manna et al. (2010). Sundarbans mangrove is suffering from toxic algal bloom dominated by diatoms (Bacillariophyceae) followed by Dinoflagellates and Cyanophyceae. Excessive growth of HAB is a severe threat for the wetland ecosystem and in large for the aquatic ecosystem. Study shows that toxic Dinoflagellates and Cyanophyceae have deteriorated the water quality of Sundarbans estuary. This kind of occurrence puts the survival of mangroves into question. Control of such blooms is important for the conservation of the Sundarbans ecosystem.

In the past few decades, HABs have become increasingly prevalent worldwide concern. There are several TPP species, including Pseudo-nitzschia sp., Gambierdiscus toxicus, Prorocentrum sp., Ostrepsis sp., Coolie monotis, Gymnodinium breve, Chrysochromulina polylepis, P. parvum, etc. that have become major threat for aquatic ecosystem due to the excessive growth (Hallegraeff 1993). Such TPP can contaminate fish or destroy higher trophic species. Therefore, it is very important to understand the causes and possible impacts of toxic phytoplankton on algae blooms and also their potential control mechanisms in the area of aquatic and marine ecology. Several papers based on HABs reflect the growing interest in biological stoichiometry strategies and management (Zingone and Enevoldsen 2000; Anderson and Garrison 1997; Blaxter and Southward 1997; Elser et al. 2012; Franks 1997; Truscott and Brindley 1994; Wyatt 1988). Chattopadhyay et al. (2000) have investigated the mechanism of explaining the cyclical behavior of bloom system using different kinds of toxin release processes in plankton interaction. The effect of toxic substances and time delay on the dynamics of diffusive plankton system modeling the HABs was studied by Zhao and Wei (2015). The space-time structure for promoting plankton distribution due to the existence of TPP was studied by Roy et al. (2007), (2006), Roy (2008) with the ease of field observations. They addressed the role of toxic phytoplankton in determining and preserving the composition of the total phytoplankton and zooplankton community in Bengal Bay. Yang and Fu (2008) have explored a tri-trophic food chain model with functional form II and the existence of global solutions of cross-diffusion-type model is examined when the spatial dimension is less than six. A tool for monitoring, preventing and regulating HABs has been studied by Anderson (2009). Chakraborty et al. (2012) clarified the role of zooplankton prevention in the sustainability and prevailing of poisonous phytoplankton and noted that high prevention contributes to the coexistence of TPP, NTP and zooplankton. Scotti et al. (2015) identified the characteristic of toxicity and zooplankton predation in toxic prey persistence and found that toxic prey could destabilize coexistence spatially homogeneous and spatial patterns. Bairagi et al. (2008) have proposed interacting nutrient-plankton dynamics and suggested that interactions among these species are very complex and situation-specific. Model for interacting TPP, NTP and zooplankton recognized that the populations are independent in the magnitude of the steady-state component (Banerjee and Venturino 2011). Chakraborty and Das (2015) studied two zooplankton and one phytoplankton toxicity-based model and found that the toxin coefficient plays a significant role in the existence of Hopf bifurcation around the interior equilibrium. Chatterjee and Pal (2016) investigated the effect of toxin in nutrient-plankton model and observed that toxic phytoplankton may change the steady-state behavior. De Silva and Jang (2017) observed that the mutual interference of zooplankton diminishing HABs.

Many researchers have employed the predator–prey interaction models to study the spatiotemporal dynamics in plankton system (Dhar and Baghel 2016; Malchow et al. 2002; Pascual 1993; Petrovskii and Malchow 1999, 2001; Thakur et al. 2016). Spatiotemporal patterns in plankton dynamics with the sequence of chaotic spiral, strip and spot patterns are studied by Rao (2013). Wang et al. (2016) examined a spatial model with self and cross-diffusion and observed that direction of cross-diffusion influence the spatial distribution as well as population density. Thakur et al. (2017) have proposed a diffusive three species plankton model with toxic effect for the wetland ecosystem. Chaudhuri et al. (2012) studied toxic phytoplankton-induced spatiotemporal patterns and observed that the populations become inhomogeneous in presence of toxin-producing phytoplankton. Chakraborty et al. (2015) observed the spatiotemporal oscillation for certain toxicity level through a diffusive nutrient-plankton model system. In the current manuscript, we have considered a three-species system composed of NTP, TPP and zooplankton and tried to identify the parameters that are responsible for the good health of Sundarban mangrove wetland. We assume that toxic phytoplanktons are capable of defending their predators. For this purpose, a basic functional response of MH type in the form of \(\phi (x)=\dfrac{mx}{(a+bx+x^2)}\) is considered which is suggested by Andrews (1968). Later, a revised MH functional response established by Sokol and Howell (1981) in the form of \(\phi (x)=\dfrac{mx}{(a+ix^2)}\) to give the better description of defense phenomenon. Thakur and Ojha (2020a) have modeled a phytoplankton–zooplankton interaction under the influence of toxicity and adaptation. They have obtained the complex spatiotemporal pattern of the plankton system by using MH functional response. Pal et al. (2009a) have analyzed a model using a simplified form of MH function and studied the inhibitory effect in toxic phytoplankton–zooplankton dynamics. Han and Dai (2019) proposed a model with Allee effect and cross-diffusion in a toxic-phytoplankton and zooplankton system and explored the impact of Allee effect and toxin liberation rate on pattern via simplified MH functional response.

A well-known truth is that time delays exist in every biological process and influence the dynamics of the aquatic as well as marine ecosystem and its whole community. The time delay consequences for plankton system have also been successfully deliberated by several authors by using different functional responses (Mondal et al. 2020; Roy et al. 2016; Thakur and Ojha 2020b; Thakur et al. 2020). Recently, Thakur et al. (2020) have established the plankton–fish model with multiple gestation delay and demonstrated that the two equal gestation delay may promote the chaotic phenomenon in the plankton system. Mondal et al. (2020) noted that increment in gestation delays can lead to stationary points destabilization by creating limit cycles. The effect of time delay in top predator gestation has been studied by Ojha and Thakur (2020). For that purpose, they have considered a simple three species system in which phytoplankton acts as a prey species and equipped with toxicity whereas zooplankton and fish act as middle and top predators, respectively. Misra and Raveendra Babu (2016) proposed a mathematical model to study the effect of toxicant in a three-species food chain system incorporating delay in toxicant uptake process by prey population. Kumar et al. (2018) analyzed stability and Hopf-bifurcation dynamics of a food chain system for both pest and the natural enemy with dual gestation delay and observed that the natural enemy free steady state is stable if the gestation delay for the pest is sufficiently low otherwise system observed oscillating behavior. Sharma et al. (2016) studied a mathematical model for plankton–fish interaction in the context of obtaining the impact of quadratic harvesting and time delay. Further, they conclude that induction of stability by harvesting of a top predator in the plankton food chain can be destabilized by digestion delay.

Most modeling methods were focused on wastewater treatment and assumed the spatial structure of the wetland did not influence temporal dynamics (Rahman et al. 2018). This study offers an important insight into local welfare services and the values of mangroves, enabling them to inform policies on protection and better exploitation of mangrove resources. With this motivation, we consider three interacting components consisting of NTP, TPP and zooplankton in our model system and incorporating competition between TPP and NTP and observe its consequences on the dynamical system. We assume that the local growth of the prey is logistic and that the predator shows the Holling type II functional response for NTP and MH-type functional for TPP. Because some zooplanktons have the ability to discriminate between toxic and non-toxic phytoplankton and first feed on non-toxic phytoplankton but gradually move to the toxic one if non-toxic resources become limited (Chakraborty et al. 2012). The principal objective of this paper is the analysis of spatial–temporal interactions and patterns. Also, the role of dual delay on NTP, TPP and zooplankton system is well established numerically. The paper is organized into eight sections as follows: "The mathematical model" section addresses the system model and parameter description. In the absence and the presence of diffusion, the model system is analyzed in "Analytical methodologies" section. The conditions for Turing instabilities have been presented in "Turing instability" section. In "Numerical results" section, we have exhibited the numerical simulation results. In "The mathematical model with time delay" section, we have discussed the population dynamics with time delay. In "Discussion" section, the results are discussed. Finally, in "Conclusion" section conclusions of the work are presented.

The mathematical model

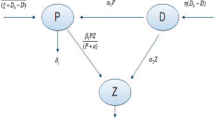
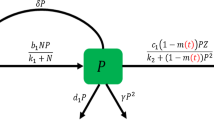
In this section, we have proposed a mathematical model for structuring diffusion-induced plankton system that deals with a combination of NTP, TPP with a zooplankton population for an aquatic ecosystem. Zooplankton is considered as a single predator in our study that predates NTP and TPP both, where the predation of TPP indirectly affects the population of zooplankton. We have discussed the situation that arises when the prey population shows the competing effect, and this competition is described as the adverse consequences on one species to another together with spatial interaction. Kretzschmar et al. (1993) have studied a basic two prey (i.e., NTP and TPP) one predator (i.e., zooplankton) model based on Lotka–Volterra equations in which both the preys are modeled as Holling type II functional response and competing for the same resource. Several experimental outcomes reveal that whenever NTP abundance is high, zooplankton prefer to graze on NTP and avoid ingesting toxic species (Pal et al. 2010; Schultz and Kiørboe 2009). It has also observed that, zooplankton graze on TPP only when NTP abundance becomes very low or nil. Therefore, zooplankton shows an avoidance tendency to graze on TPP in the presence of NTP. Moreover, TPP has no significant influence on the predation of NTP, but NTP abundance greatly reduces the ingestion of TPP (Schultz and Kiørboe 2009). Therefore, consumption of NTP population by zooplankton gives the gain in zooplankton growth but the consumption of TPP population gives a reduction in zooplankton growth due to the ingestion of toxic substances together with TPP population. Although it is well known that TPP has a negative effect in zooplankton dynamics, there is still not an exact functional form describe to explain decrease in zooplankton grazing due to TPP biomass. However, different authors modeled NTP-TPP phenomenon by different functional forms (Chakraborty et al. 2012; Roy 2008; Thakur et al. 2016). We have considered two different types of response functions for NTP and TPP population. Holling type II functional response is used as a grazing function for NTP whereas MH-type functional response is used for TPP population. One more important factor that has been considered in our study is the interspecific competition coefficients of zooplankton that express the self-limitation of zooplankton (Thakur et al. 2017). For the model formulation, NTP population is represented by \(P_1(t)\), TPP population is represented by \(P_2(t)\) and zooplankton is represented by Z(t). We would like to impose a brief description of the model system which is based on the following ecological assumptions:

  1. (i)

    The dynamics of entire community arises due to the coupling of three interacting populations: NTP \(P_1(t)\), TPP \(P_2(t)\) and zooplankton Z(t).

  2. (ii)

    In the absence of zooplankton Z(t), the population of NTP \(P_1(t)\) and TPP \(P_2(t)\) increases logistically with the intrinsic growth rate \(r_1\), \(r_2\) (\(r_1, r_2 > 0\)) and carrying capacity \(K_1\), \(K_2\) (\(K_1, K_2 > 0\)).

  3. (iii)

    The relationship between (\(P_1, Z\)) is defined by Holling type II functional response, and the relationship between (\(P_2, Z\)) is defined by MH-type functional response.

  4. (iv)

    Zooplankton predates its favorite food NTP at a rate of \(w_1\) with the maximum conversion rate \(\gamma _1\) and predates its unfavorite food TPP at a rate of \(w_2\) with the reduction rate \(\gamma _2\). In the absence of their favorite food, zooplankton will die out as their natural death rate m.

  5. (v)

    For the spatial distribution, we have incorporated the diffusion coefficient with each species where at any point (x, y) and time t, the dynamics of NTP is denoted by \(P_1(x,y,t)\), the dynamics of TPP is denoted by \(P_2(x,y,t)\) and the dynamics of zooplankton denoted by Z(x, y, t).

With the above assumption, we have proposed a reaction-diffusion model system for plankton–zooplankton interaction as follows:

$$\begin{aligned} \frac{\partial P_1}{\partial t}&=r_1P_1\bigg (1-\frac{P_1+\alpha _1P_2}{K_1}\bigg )-\frac{w_1P_1Z}{d_1+P_1}+D_1\nabla ^2 P_1,\nonumber \\ \frac{\partial P_2}{\partial t}&=r_2P_2\bigg (1-\frac{P_2+\alpha _2P_1}{K_2}\bigg )-\frac{w_2P_2Z}{d_2+b_1P^2_2}+D_2\nabla ^2 P_2,\nonumber \\ \frac{\partial Z}{\partial t}&=\frac{\gamma _1P_1Z}{d_1+P_1}-\frac{\gamma _2P_2Z}{d_2+b_1P^2_2}-mZ-m_1 Z^2+D_3\nabla ^2 Z, \end{aligned}$$
(2.1)

with initial conditions and zero-flux boundary conditions

$$\begin{aligned}&P_1(x, y, 0)>0, \ P_2(x, y, 0)>0, \ Z(x, y, 0)>0, \ \text {for} \ (x,y)\in \varOmega , \end{aligned}$$
(2.2)
$$\begin{aligned}&\quad \frac{\partial P_1}{\partial n} = \frac{\partial P_2}{\partial n} = \frac{\partial Z}{\partial n} =0, \ \text {for} \ (x,y)\in \partial \varOmega , \ t>0, \end{aligned}$$
(2.3)

where \(D_1, \ D_2\) and \(D_3\) are the diffusion coefficients of NTP, TPP and zooplankton populations, respectively, n is the outward normal to \(\partial \varOmega\). \(\nabla ^2= \frac{\partial ^2}{\partial x^2}\) denotes the 1D Laplacian operator whereas \(\nabla ^2= \frac{\partial ^2}{\partial x^2} + \frac{\partial ^2}{\partial y^2}\) denotes the 2D Laplacian operator. A brief description of parameters presented in Table 1.

Analytical methodologies

Non-spatial model system

In this subsection, we have discussed the nonnegative equilibrium points and their stability properties of the model system in absence of diffusion and the reduced system of ordinary differential equations is as follows:

$$\begin{aligned} \frac{dP_1}{dt}&=r_1P_1\bigg (1-\frac{P_1+\alpha _1P_2}{K_1}\bigg )-\frac{w_1P_1Z}{d_1+P_1},\nonumber \\ \frac{d P_2}{d t}&=r_2P_2\bigg (1-\frac{P_2+\alpha _2P_1}{K_2}\bigg )-\frac{w_2P_2Z}{d_2+b_1P^2_2},\nonumber \\ \frac{d Z}{d t}&=\frac{\gamma _1P_1Z}{d_1+P_1}-\frac{\gamma _2P_2Z}{d_2+b_1P^2_2}-mZ-m_1 Z^2, \end{aligned}$$
(3.1)

with

$$\begin{aligned} P_1(0)>0,P_2(0)>0, Z(0)>0. \end{aligned}$$
(3.2)
Table 1 Definition of the parameters used in the model system (2.1)
Full size table

Boundedness solution

Lemma 1

Assume that u(x, t) is defined by (Hale and Waltman 1989)

$$\begin{aligned} \frac{\partial u}{\partial t} =&D_1\varDelta u + ru(1-\frac{u}{K}), \ x \in \varOmega , \ t>0,\nonumber \\ \frac{\partial u}{\partial v} =&0, \ x \in \partial \varOmega , \ t>0,\nonumber \\ u(x,0) =&u_0(x)>0, \ x \in \varOmega .\nonumber \\&\text {Then}, \ \underset{t \rightarrow \infty }{\lim } u(x,t)=K. \end{aligned}$$
(3.3)

Theorem 1

All the solutions of model system (2.1) are nonnegative and defined for all \(t>0\). Furthermore, the nonnegative solution \((P_1(x,t),P_2(x,t),Z(x,t))\) of (2.1) satisfies, \(\underset{t \rightarrow \infty }{\lim } \sup \max P_1(x,t)\le K_1\),\(\underset{t \rightarrow \infty }{\lim } \sup \max P_2(x,t)\le K_2\), \(\underset{t \rightarrow \infty }{\lim } \sup \max Z(x,t)\le \frac{\gamma _1P_1}{m_1(d_1+P_1)}\).

Proof

From the first equation of model system (2.1), we obtain

$$\begin{aligned} \frac{\partial P_1}{\partial t}\le D_1\varDelta P_1 +r_1 P_1\bigg (1-\frac{P_1}{K_1}\bigg ). \end{aligned}$$
(3.4)

By using comparison principle, for any arbitrary \(\varepsilon _1>0\), there exists \(T_1>0\) such that \(t>T_1\), we have

$$\begin{aligned} P_1(x,t)\le K_1+\varepsilon _1. \end{aligned}$$
(3.5)

Thus,

$$\begin{aligned} \underset{t \rightarrow \infty }{\lim } \sup \underset{x \epsilon {\bar{\varOmega }}}{\max }P_1(x,t)\le K_1. \end{aligned}$$
(3.6)

From second equation of model system (2.1), we have

$$\begin{aligned} P_2(x,t)\le K_2+\varepsilon _2. \end{aligned}$$
(3.7)

Thus,

$$\begin{aligned} \underset{t \rightarrow \infty }{\lim } \sup \underset{x \epsilon {\bar{\varOmega }}}{\max }P_2(x,t)\le K_2. \end{aligned}$$
(3.8)

Similarly from third equation of model system (2.1), we have

$$\begin{aligned} \frac{\partial Z}{\partial t} \le D_3\varDelta Z+Z \bigg (\frac{\gamma _1P_1}{(d_1+P_1)}-m_1 Z\bigg ). \end{aligned}$$
(3.9)

Therefore,

$$\begin{aligned} Z(x,t)\le \frac{\gamma _1P_1}{m_1(d_1+P_1)}+\varepsilon . \end{aligned}$$
(3.10)

This implies,

$$\begin{aligned} \underset{t \rightarrow \infty }{\lim } \sup \underset{x \epsilon {\bar{\varOmega }}}{\max }Z(x,t)\le \frac{\gamma _1P_1}{m_1(d_1+P_1)}. \end{aligned}$$
(3.11)

\(\square\)

Stability properties with equilibria analysis

The non-spatial model system (3.1) has six nonnegative equilibrium state, namely \(E_0(0,0,0)\), \(E_1(K_1,0,0)\), \(E_2(0,K_2,0)\), \(E_3(\tilde{P_1},\tilde{P_2},0)\), \(E_4(\bar{P_1},0,\bar{Z})\) and \(E_5(P_1^*,P_2^*,Z^*)\), as follows:

  1. (i)

    The trivial equilibrium point \(E_0 = (0, 0, 0)\) always exists.

  2. (ii)

    The axial equilibrium point \(E_1 = (K_1, 0, 0)\) exists on the boundary of the first octant.

  3. (iii)

    The axial equilibrium point \(E_2 = (0, K_2, 0)\) exists on the boundary of the first octant.

  4. (iv)

    The planar equilibrium point \(E_3 = (\tilde{P_1},\tilde{P_2}, 0)\) exists on the \(P_1P_2\)-plane, where \(\tilde{P_1}=\dfrac{(K_1-\alpha _1K_2)}{(1-\alpha _1\alpha _2)}\), \(\tilde{P_2}=\dfrac{(K_2-\alpha _1K_1)}{(1-\alpha _1\alpha _2)}\), if \(\alpha _1<\dfrac{K_1}{K_2}<\dfrac{1}{\alpha _2}.\)

  5. (v)

    The planar equilibrium point \(E_4 =(\bar{P_1},0,\bar{Z})\) exists on the \(P_1Z\)-plane, where \(\bar{P_1}\) and \(\bar{Z}\) are the positive solution of the following equations:

    $$\begin{aligned}&r_1\bigg (1-\frac{\bar{P_1}}{K_1}\bigg )-\frac{w_1\bar{Z}}{d_1+\bar{P_1}}=0, \end{aligned}$$
    (3.12)
    $$\begin{aligned}&\quad \dfrac{\gamma _1\bar{P_1}}{d_1+\bar{P_1}}-m-m_1\bar{Z}=0. \end{aligned}$$
    (3.13)

    From Eq. (3.12), we have

    $$\begin{aligned} \bar{Z}=\dfrac{r_1}{w_1}\bigg (1-\dfrac{\bar{P_1}}{K_1}\bigg )(d_1+\bar{P_1}). \end{aligned}$$
    (3.14)

    Putting the value of \(\bar{Z}\) from Eq. (3.14) into Eq. (3.13), we get

    $$\begin{aligned}&m_1r_1\bar{P_1}^3+m_1r_1(2d_1-K_1)\bar{P_1}^2+\{w_1K_1(\gamma _1-m)\nonumber \\&\quad +m_1r_1d_1(d_1-2K_1)\}\bar{P_1}-d_1K_1(m_1r_1d_1+mw_1)=0. \end{aligned}$$
    (3.15)

    According to Descartes rule of sign, Eq. (3.15) has a unique positive real root if

    $$\begin{aligned} K_1<2d_1. \end{aligned}$$
    (3.16)

    And \(\bar{Z}\) is exists, If

    $$\begin{aligned} \bar{P_1}<K_1. \end{aligned}$$
    (3.17)

    This shows that \(E_4 =(\bar{P_1},0,\bar{Z})\) exists under the condition of (3.16) and (3.17).

  6. (vi)

    The interior equilibrium point \(E_5 = (P_1^*,P_2^*,Z^*)\) exists by following (Dubey and Upadhyay 2004). In this case, \(P_1^*,P_2^*\) and \(Z^*\) are the positive solutions of following equations:

    $$\begin{aligned}&r_1\bigg (1-\frac{P_1^*+\alpha _1P_2^*}{K_1}\bigg )-\frac{w_1Z^*}{d_1+P_1^*}=0, \end{aligned}$$
    (3.18)
    $$\begin{aligned}&\quad r_2\bigg (1-\frac{P_2^*+\alpha _2P_1^*}{K_2}\bigg )-\frac{w_2Z^*}{d_2+b_1P_2^{*2}}=0, \end{aligned}$$
    (3.19)
    $$\begin{aligned}&\quad \frac{\gamma _1P_1^*}{d_1+P_1^*}-\frac{\gamma _2P_2^*}{d_2+b_1P_2^{*2}}-m-m_1 Z^*=0. \end{aligned}$$
    (3.20)

    From Eq. (3.18), we obtain

    $$\begin{aligned} Z^*=\frac{r_1}{w_1}\bigg (1-\frac{P_1^*+\alpha _1P_2^*}{K_1}\bigg )(d_1+P_1^*), \end{aligned}$$
    (3.21)

    \(Z^*>0\) if \(P_1^*+\alpha _1P_2^*<K_1.\). Putting the value of \(Z^*\) from Eq. (3.21) in Eqs. (3.19) and (3.20), we obtain

    $$\begin{aligned} G_1(P_1^*, P_2^*)&=r_2\bigg (1-\frac{P_2^*+\alpha _2P_1^*}{K_2}\bigg )-\frac{w_2r_1}{w_1(d_2+b_1P_2^{*2})}\nonumber \\&\quad \bigg (1-\frac{P_1^*+\alpha _1P_2^*}{K_1}\bigg )(d_1+P_1^*)=0, \end{aligned}$$
    (3.22)
    $$\begin{aligned} G_2(P_1^*, P_2^*)&= -m-\frac{m_1r_1}{w_1}\bigg (1-\frac{P_1^*+\alpha _1P_2^*}{K_1}\bigg )(d_1+P_1^*)\nonumber \\&\quad +\frac{(\gamma _1P_1^*)}{d_1+P_1^*}-\frac{\gamma _2P_2^*}{d_2+b_1P_2^{*2}}=0. \end{aligned}$$
    (3.23)

    From Eq. (3.22) when \(P_2^*=0\), then \(P_1^*= P_{1a}\) where

    $$\begin{aligned} P_{1a}>0 \ \text {if} \ r_1d_1w_2>r_2d_2w_1. \end{aligned}$$
    (3.24)

    Putting \(P_1^*=0\) in Eq. (3.22), we note that \(G_1(0, P_2^*)=0\) has a unique root \(P_{2a}\), which is solution of the following equation:

    $$\begin{aligned}&r_2b_1P_2^{*3}-r_2b_1K_2P_2^{*2}+\bigg (r_2d_2-\dfrac{w_2r_1d_1\alpha _1K_2}{w_1K_1}\bigg )P_2^*\nonumber \\&-\bigg (r_2d_2-\dfrac{w_2r_1d_1}{w_1}\bigg )K_2=0. \end{aligned}$$
    (3.25)

    It may be noted here that Eq. (3.25) has one or three positive roots. Eq. (3.25) can be rewritten as

    $$\begin{aligned} P_2^{*3}+r_1P_2^{*2}+r_2P_2^*+r_3=0, \end{aligned}$$
    (3.26)

    where

    $$\begin{aligned} r_1&=-r_2b_1K_2, \\ r_2&=\bigg (r_2d_2-\dfrac{w_2r_1d_1\alpha _1K_2}{w_1K_1}\bigg ),\\ r_3&=-\bigg (r_2d_2-\dfrac{w_2r_1d_1}{w_1}\bigg )K_2. \end{aligned}$$

    Thus, Eq. (3.25) has a unique real positive root \(P_{2a}\) (other two roots are complex conjugate) if

    $$\begin{aligned} \dfrac{b^2}{4}+\dfrac{a^3}{27}>0, \end{aligned}$$
    (3.27)

    where

    $$\begin{aligned} a=\dfrac{1}{3}(3r_2-r_1^2),~~~ b=\dfrac{1}{27}(2r_1^3-9r_1r_2+27r_3). \end{aligned}$$

    Also, we have

    $$\begin{aligned} \frac{dP_1^*}{dP_2^*}=-\frac{\partial G_1}{\partial P_2^*}/\frac{\partial G_1}{\partial P_1^*}. \end{aligned}$$

    We noted that \(\frac{dP_1^*}{dP_2^*}<0,\) if

    $$\begin{aligned}&\text {either}~~(i) \frac{\partial G_1}{\partial P_1^*}>0~~and ~~\frac{\partial G_1}{\partial P_2^*}>0,\nonumber \\&\quad \text {or}~~(ii) \frac{\partial G_1}{\partial P_1^*}<0~~and ~~\frac{\partial G_1}{\partial P_2^*}<0, \end{aligned}$$
    (3.28)

    holds. From Eq. (3.23) when \(P_2^*=0\), then \(G_2(P_1^*, 0)=0\) has a root \(P_{1b}\), which is solution of the following equation

    $$\begin{aligned}&\frac{m_1r_1}{w_1K_1}P_1^{*3} -\frac{m_1r_1}{w_1}\bigg (1-\frac{2d_1}{K_1}\bigg )P_1^{*2}-\bigg \{\frac{m_1r_1d_1}{w_1}\bigg (2-\frac{d_1}{K_1}\bigg )\nonumber \\&\quad +(m-r_1)\bigg \}P_1^*-d_1\bigg (m+\frac{m_1r_1d_1}{w_1}\bigg )=0. \end{aligned}$$
    (3.29)

    Hence, \(P_{1b}\) has a unique positive root of Eq. (3.29) if

    $$\begin{aligned} K_1<2d_1. \end{aligned}$$
    (3.30)

    Also, we have \(\frac{dP_1^*}{dP_2^*}=-\frac{\partial G_2}{\partial P_2^*}/\frac{\partial G_2}{\partial P_1^*}\). We noted that \(\frac{dP_1^*}{dP_2^*}>0,\) if

    $$\begin{aligned}&\text {either} \ (i) \ \frac{\partial G_2}{\partial P_1^*}>0 \ \text {and} \ \frac{\partial G_2}{\partial P_2^*}>0,\nonumber \\&\quad \text {or} \ (ii) \ \frac{\partial G_2}{\partial P_1^*}<0 \ \text {and} \ \frac{\partial G_2}{\partial P_2^*}<0, \end{aligned}$$
    (3.31)

    holds.                                                                                                                                                                                                                                                                                                                                                           We noted that the two isocline Eqs. (3.22) and (3.23) intersect at a unique point \((P_1^*, P_2^*)\) if in addition to the condition Eqs. (3.27), (3.28), (3.30) and (3.31), the inequality \(P_{1b}<P_{1a}\) holds.

The local stability of each equilibrium point is now discussed by deriving the variance matrices and using the Routh Hurwitz criterion. The findings were obtained below:

  1. (i)

    \(E_0(0, 0, 0)\) is a saddle point. There is unstable manifold along \(P_1, P_2\)-direction and stable manifold along Z-direction.

  2. (ii)

    \(E_1(K_1, 0, 0)\) is locally asymptotically stable if \(\dfrac{K_2}{\alpha _2}<K_1<\dfrac{md_1}{(\gamma _1-m)}, \gamma _1>m\). It is a saddle point if the inequality opposes.

  3. (iii)

    \(E_2(0, K_2, 0)\) is locally asymptotically stable if \(K_1<\alpha _1K_2\). It is a saddle point if the inequality opposes.

  4. (iv)

    \(E_3(\tilde{P_1}, \tilde{P_2}, 0)\) is stable or unstable in the positive direction orthogonal to the \(P_1P_2\)-plane, i.e., Z-direction depending on whether \(\lambda _3=\dfrac{\gamma _1\tilde{P_1}}{d_1+\tilde{P_1}}-\dfrac{\gamma _1\tilde{P_2}}{d_2+b_1\tilde{P_2}^2}-m\) is negative or positive, respectively.

  5. (v)

    \(E_4(\bar{P_1}, 0, \bar{Z})\) is stable or unstable in the positive direction orthogonal to the \(P_1Z\)-plane, i.e., \(P_2\)-direction depending on whether \(\lambda _3=r_2-\dfrac{\alpha _2r_2\bar{P_1}}{K_2}-\dfrac{w_2\bar{Z}}{d_2}\) is negative or positive, respectively, if \(w_1K_1\bar{Z}<r_1(d_1+\bar{P_1})^2\).

  6. (vi)

    The variational matrix along \(E_5(P_1^*, P_2^*, Z^*)\) is given by

    $$\begin{aligned} M=\begin{pmatrix} \varrho _{11} &{} \varrho _{12} &{} \varrho _{13}\\ \varrho _{21} &{} \varrho _{22}&{} \varrho _{23}\\ \varrho _{31} &{} \varrho _{32} &{} \varrho _{33} \end{pmatrix}\\= & {} \small { \begin{pmatrix} P_1^*\bigg (-\dfrac{r_1}{K_1}+\dfrac{w_1Z^*}{(d_1+P_1^*)^2}\bigg ) &{} -\dfrac{\alpha _1r_1P_1^*}{K_1} &{} \dfrac{-w_1P_1^*}{(d_1+P_1^*)}\\ \\ -\dfrac{\alpha _2r_2P_2^*}{K_2} &{} P_2^*\bigg (-\dfrac{r_2}{K_2}+\dfrac{2b_1w_2P_2^*Z^*}{(d_2+b_1P_2^{*2})^2}\bigg ) &{} \dfrac{-w_2P_2^*}{(d_1+b_1P_2^{*2})} \\ \\ \dfrac{\gamma _1d_1Z^*}{(d_1+P_1^*)^2} &{}~~~~ -\dfrac{(d_2-b_1P_2^{*2})\gamma _2Z^*}{(d_2+b_1P_2^{*2})^2}&{} -m_1 Z^* \end{pmatrix}}. \end{aligned}$$

    The characteristic equation for the above matrix M is given by

    $$\begin{aligned} \nu ^3+A_1\nu ^2+A_2\nu +A_3=0, \end{aligned}$$

    where

    $$\begin{aligned} A_1&=-(\varrho _{11}+\varrho _{22}+\varrho _{33}),\\ A_2&=\varrho _{22}\varrho _{33}-\varrho _{23}\varrho _{32}+\varrho _{11}\varrho _{33}-\varrho _{13}\varrho _{31}+\varrho _{11}\varrho _{22}\\&-\varrho _{12}\varrho _{21},\\ A_3&=-\varrho _{11}\varrho _{22}\varrho _{33}+\varrho _{11}\varrho _{23}\varrho _{32}+\varrho _{12}\varrho _{21}\varrho _{33}-\varrho _{12}\varrho _{23}\varrho _{31}\\&-\varrho _{13}\varrho _{21}\varrho _{32}+\varrho _{13}\varrho _{22}\varrho _{31}. \end{aligned}$$

Theorem 2

Assume that the \(E_5(P_1^*, P_2^*, Z^*)\) is positive equilibrium point of the system (3.1). Therefore, the equilibrium point \(E_5(P_1^*, P_2^*, Z^*)\) is locally asymptotically stable when \(A_1>0, \ A_3>0\) and \(A_1A_2-A_3>0\) is satisfied.

The proof of the theorem follows from the Routh–Hurwitz criterion, hence omitted.

Theorem 3

If the following inequalities hold

$$\begin{aligned}&w_1K_1Z^*<r_1d_1(d_1+P_1^*), \end{aligned}$$
(3.32)
$$\begin{aligned}&\quad w_2b_1K_2P_2^*Z^*<r_2d_2(d_2+b_1P_2^{*2}), \end{aligned}$$
(3.33)
$$\begin{aligned}&\quad \bigg (\dfrac{\alpha _1r_1}{K_1}+\dfrac{\alpha _2r_2}{K_2}\bigg )^2<\bigg (\dfrac{r_1}{K_1}-\dfrac{w_1Z^*}{d_1(d_1+P_1^*)}\bigg )\nonumber \\&\quad \times \bigg (\dfrac{r_2}{K_2}-\dfrac{w_2b_1P_2^*Z^*}{d_2(d_2+b_1P_2^{*2})}\bigg ), \end{aligned}$$
(3.34)
$$\begin{aligned}&\quad \bigg (\dfrac{w_2}{d_2}+\dfrac{w_1\gamma _2(d_1+P_1^*)(d_2-b_1P_2^*)}{\gamma _1d_1d_2(d_2+b_1P_2^{*2})}\bigg )^2<\bigg (\dfrac{r_2}{K_2}-\dfrac{w_2b_1P_2^*Z^*}{d_2(d_2+b_1P_2^{*2})}\bigg )\nonumber \\&\quad \times \bigg (\dfrac{w_1m_1(d_1+P_1^*)}{\gamma _1d_1}\bigg ). \end{aligned}$$
(3.35)

Then, the positive equilibria \(E_5\) is globally asymptotically stable with regard to the all solutions within the positive octant.

Proof

We take into account the positive definite function of the positive equilibrium \(E_5(P_1^*,P_2^*,Z^*)\) as

$$\begin{aligned} V(P_1,P_2,Z)&=\bigg (P_1-P_1^*-P_1^*\ln \frac{P_1}{P_1^*}\bigg )+\bigg (P_2-P_2^*-P_2^*\ln \frac{P_2}{P_2^*}\bigg )\nonumber \\&+c\bigg (Z-Z^*-Z^*\ln \frac{Z}{Z^*}\bigg ), \end{aligned}$$
(3.36)

where the positive constant c to be selected appropriately. Differentiating Eq. (3.36) with respect to time t along the solution of the model system (3.1), after some algebraic manipulations, we get

$$\begin{aligned} \frac{dV}{dt}=&-\frac{1}{2}m_{11}(P_1-P_1^*)^2+m_{12}(P_1-P_1^*)(P_2-P_2^*)\nonumber \\&-\frac{1}{2}m_{11}(P_1-P_1^*)^2+m_{13}(P_1-P_1^*)(Z-Z^*)\nonumber \\&-\frac{1}{2}m_{22}(P_2-P_2^*)^2+m_{23}(P_2-P_2^*)(Z-Z^*)\nonumber \\&-\frac{1}{2}m_{22}(P_2-P_2^*)^2-\frac{1}{2}m_{33}(Z-Z^*)^2-\frac{1}{2}m_{33}(Z-Z^*)^2, \end{aligned}$$
(3.37)

where

$$\begin{aligned} m_{11}&=\frac{r_1}{K_1}-\frac{w_1Z^*}{(d_1+P_1^*)(d_1+P_1)},\\ m_{22}&=\frac{r_2}{K_2}-\frac{w_2b_1Z^*(P_2+P_2^*)}{(d_2+b_1P_2^2)(d_2+b_1P_2^{*2})}, \\ m_{33}&=cm_1,\\ m_{12}&=-\bigg (\frac{\alpha _1r_1}{K_1}+\frac{\alpha _2r_2}{K_2}\bigg ),\\ m_{13}&=-\frac{w_1}{(d_1+P_1)}+\frac{c\gamma _1d_1}{(d_1+P_1^*)(d_1+P_1)},\\ m_{23}&=-\frac{w_2}{(d_2+b_1P_2^2)}-\frac{c\gamma _2(d_2-b_1P_2P_2^*)}{(d_2+b_1P_2^2)(d_2+b_1P_2^{*2})}. \end{aligned}$$

Sufficient condition for \(\frac{dV}{dt}\) to be negative is that the following inequalities hold:

$$\begin{aligned}&m_{11}>0, \end{aligned}$$
(3.38)
$$\begin{aligned}&m_{22}>0, \end{aligned}$$
(3.39)
$$\begin{aligned}&m^2_{12}<m_{11}m_{22}, \end{aligned}$$
(3.40)
$$\begin{aligned}&m^2_{13}<m_{11}m_{33},\end{aligned}$$
(3.41)
$$\begin{aligned}&m^2_{23}<m_{22}m_{33}. \end{aligned}$$
(3.42)

By choosing \(c=\frac{w_1(d_1+P_1^*)}{\gamma _1 d_1}\), we note that \(m_{13} = 0\), and thus condition (3.41) is automatically satisfied. It is easy to see that (3.32) \(\Rightarrow\) (3.38), (3.33) \(\Rightarrow\) (3.39), (3.34) \(\Rightarrow\) (3.40) and (3.35) \(\Rightarrow\) (3.42). \(\square\)

Spatial model system

In this section, we discuss the stability of interior equilibrium of the diffusive model system. In order to derive the condition of stability, we linearized the model system (2.1) about the equilibrium point \(E_5(P_1^*, P_2^*, Z^*)\) with small perturbation \(\bar{X}(x,t), \bar{Y}(x,t)\) and \(\bar{Z}(x,t)\) as \(P_{1}=P_1^*+\bar{X}(x,t), P_{2}=P_2^*+\bar{Y}(x,t)\) and \(Z=Z^*+\bar{Z}(x,t)\). The linearized form of model system is obtained as:

$$\begin{aligned} \frac{\partial \bar{X}}{\partial t} =&a_{11}\bar{X}+a_{12}\bar{Y}+a_{13}\bar{Z}+D_1 \bigg (\frac{\partial ^2}{{\partial x}^2}+\frac{\partial ^2}{{\partial y}^2}\bigg ) \bar{X},\nonumber \\ \frac{\partial \bar{Y}}{\partial t} =&a_{21}\bar{X}+a_{22}\bar{Y}+a_{23}\bar{Z}+D_2 \bigg (\frac{\partial ^2}{{\partial x}^2}+\frac{\partial ^2}{{\partial y}^2}\bigg )\bar{Y},\nonumber \\ \frac{\partial \bar{Z}}{\partial t}=&a_{31}\bar{X}+a_{32}\bar{Y}+a_{33}\bar{Z}+D_3 \bigg (\frac{\partial ^2}{{\partial x}^2}+\frac{\partial ^2}{{\partial y}^2}\bigg )\bar{Z}. \end{aligned}$$
(3.43)

Suppose that the solution of system (3.43) is

$$\begin{aligned} \left( \begin{array}{l} \bar{X} \\ \bar{Y} \\ \bar{Z} \\ \end{array} \right) = \left( \begin{array}{l} p \\ q \\ r \\ \end{array} \right) \exp (\tau t)\cos (\sqrt{{\lambda _{ix}}} x)\cos (\sqrt{{\lambda _{iy}}} y), \end{aligned}$$
(3.44)

where \(\lambda _{ix}\) and \(\lambda _{iy}\) are the components of wave number along x- and y-directions, respectively, and p, q and r are sufficiently small constants. \(R/n\pi\) is the critical wavelength and \(\sqrt{{\lambda _i}}= n\pi /R\) is wave number, R is the length of the system, \(2\pi /n\) is the period of cosine and \(\tau\) is the frequency, respectively. The characteristic equation of the linearized system is given by

$$\begin{aligned} {\tau }^3+\rho _1{\tau }^2+\rho _2{\tau }+\rho _3=0, \end{aligned}$$
(3.45)

where

$$\begin{aligned} \rho _1&=(D_1+D_2+D_3)\lambda _i+A_1,\nonumber \\ \rho _2&=A_2-((a_{22}+a_{33})D_1+(a_{11}+a_{33})+(a_{11}+a_{22}))\lambda _i\nonumber \\&+(D_1D_2+D_2D_3+D_3D_1)\lambda _i^2,\nonumber \\ \rho _3&=A_3+((a_{22}a_{33}-a_{23}a_{32})D_1+(a_{11}a_{33}-a_{13}a_{31})D_2\nonumber \\&+(a_{11}a_{22}-a_{12}a_{21})D_3)\lambda _i-(a_{33}D_1D_3+a_{22}D_1D_3\nonumber \\&+a_{11}D_2D_3)\lambda _i^2+D_1D_2D_3\lambda _i^3. \end{aligned}$$
(3.46)

Theorem 4

The positive equilibrium point \(E_5(P_1^*, P_2^*, Z^*)\) is locally asymptotically stable in the presence of diffusion if and only if:

  1. (i)

    \(\rho _1>0\),

  2. (ii)

    \(\rho _3>0\),

  3. (iii)

    \(\rho _1\rho _2-\rho _3>0\).

From Eq. (3.45) and using the Routh–Hurwitz criterion, the above theorem follows immediately.

Theorem 5

If the positive equilibrium point \(E_5\) of the model system (3.1) is globally asymptotically stable, then corresponding uniform steady state of model system (2.1) remains globally asymptotically stable.

Proof

For stability behavior of the system (2.1), we define a positive definite function \(V_{1}(t)\) given by

$$\begin{aligned} V_1(t)=\iint _\varOmega V(P_1,P_2,Z)dA. \end{aligned}$$
(3.47)

Calculating the derivative of \(V_1(t)\) along the solution of model system (2.1), we get

$$\begin{aligned} \frac{dV_1}{dt}&=\iint _\varOmega \frac{dV}{dt}dA+\iint _\varOmega \bigg (D_1\frac{\partial V}{\partial P_1}\nabla ^2P_1+D_2\frac{\partial V}{\partial P_2}\nabla ^2P_2\nonumber \\&+D_3\frac{\partial V}{\partial Z}\nabla ^2Z\bigg )dA,\nonumber \\ \frac{dV_1}{dt}&= I_1+I_2, \end{aligned}$$
(3.48)

where

$$\begin{aligned} I_1&=\iint _\varOmega \frac{dV}{dt}dA,\\ I_2&=\iint _\varOmega \bigg (D_1\frac{\partial V}{\partial P_1}\nabla ^2P_1+D_2\frac{\partial V}{\partial P_2}\nabla ^2P_2+D_3\frac{\partial V}{\partial Z}\nabla ^2Z\bigg )dA. \end{aligned}$$

Using Green’s first identity in the plane

$$\begin{aligned} \iint _\varOmega F\nabla ^2 G dA= \int _{\partial \varOmega }\frac{\partial G}{\partial \nu }dS-\iint _\varOmega (\nabla F.\nabla G)dA. \end{aligned}$$
(3.49)

Using similar study as in ( Upadhyay et al. 2010), we have

$$\begin{aligned} \iint _\varOmega \frac{\partial V}{\partial P_1}\nabla ^2P_1 dA&=-\iint _\varOmega \frac{\partial ^2 V}{\partial P_1^2}\bigg (\bigg (\frac{\partial P_1}{\partial x}\bigg )^2+\bigg (\frac{\partial P_1}{\partial y}\bigg )^2\bigg )dA\\&\le 0,\\ \iint _\varOmega \frac{\partial V}{\partial P_2}\nabla ^2P_2 dA&=-\iint _\varOmega \frac{\partial ^2 V}{\partial P_2^2}\bigg (\bigg (\frac{\partial P_2}{\partial x}\bigg )^2+\bigg (\frac{\partial P_2}{\partial y}\bigg )^2\bigg )dA\\&\le 0,\\ \iint _\varOmega \frac{\partial V}{\partial Z}\nabla ^2ZdA&=-\iint _\varOmega \frac{\partial ^2 V}{\partial Z^2}\bigg (\bigg (\frac{\partial Z}{\partial x}\bigg )^2+\bigg (\frac{\partial Z}{\partial y}\bigg )^2\bigg )dA\\&\le 0. \end{aligned}$$

This shows that \(I_2\le 0.\) From above analysis, we note that if \(I_1\le 0,\) then \(\frac{dV_1}{dt}<0.\) \(\square\)

Turing instability

In this section, we have derived the required conditions for the existence of Turing instability of the spatial phytoplankton–zooplankton system (2.1). Due to spatial diffusion, the occurrence of Turing instability changes the stable equilibrium to the unstable one. Mathematically, Turing instability requires at least one of the roots of the characteristic Eq. (3.45) has a non-negative real part or in the other hands, \(Re(\tau ) >0\) for some \(\lambda _i>0\).

Theorem 6

If the following conditions

  1. (i)

    \(b_1>0\), \(b_1{^2}>3b_0b_2\),

  2. (ii)

    \(\rho _3(\lambda _{i(cr)})=\frac{2b_1^{3}-9b_0b_1b_2-2(b_1^{2}-3b_0b_2)^{\frac{3}{2}}+27A_3b_0^2}{27b_0^3}<0\),

  3. (iii)

    \(\psi (\lambda _{i(cr)})=\frac{2c_1^{3}-9c_0c_1c_2-2(c_1^{2}-3c_0c_2)^{\frac{3}{2}}+27c_4c_0^2}{27c_0^3}<0\),

satisfy. Then, Turing instability takes place around interior equilibrium \(E_5\) of spatial system (2.1).

Proof

For diffusion driven instability, it is necessary to satisfy at least one of following conditions, which is given below:

$$\begin{aligned} \rho _1(\lambda _i)<0, \ \rho _3(\lambda _i)<0, \rho _1(\lambda _i)\rho _2(\lambda _i)-\rho _3(\lambda _i)<0, \end{aligned}$$

where \(\rho _1, \ \rho _2, \ \rho _3\) are defined in Eq. (3.46). Since \(D_1, \ D_2, \ D_3\) and \(\lambda _i\) are positive. Therefore, diffusion-driven instability cannot satisfy the condition \(\rho _1(\lambda _i)<0\). Hence, we look out for the conditions \(\rho _3(\lambda _i)<0, \ \rho _1(\lambda _i)\rho _2(\lambda _i)-\rho _3(\lambda _i)<0\). We have

$$\begin{aligned} P(\lambda _i)=\rho _3(\lambda _i)=b_0\lambda _i^3+b_1\lambda _i^2+b_2\lambda _i+A_3, \end{aligned}$$
(4.1)

where

$$\begin{aligned} b_0&=D_1D_2D_3,\\ b_1&=-a_{11}D_2D_3-a_{22}D_1D_3-a_{33}D_1D_2,\\ b_2&=D_1(a_{22}a_{33}-a_{23}a_{32})+D_2(a_{11}a_{33}-a_{13}a_{31})\\&+D_3(a_{11}a_{22}-a_{12}a_{21}). \end{aligned}$$

If \(P(\lambda _i)\) has a minimum, then one can find by simple manipulations that

$$\begin{aligned} \frac{dP}{d\lambda _i}=3b_0\lambda _i^{2}+2b_1\lambda _i+b_2=0, \ \text {gives} \ \lambda _{i(cr)}=\frac{-b_1 \pm \sqrt{ b_1^2-3b_0b_2}}{3b_0}, \end{aligned}$$

where \(\frac{d^2P}{d\lambda _i^2}>0.\) Hence \(b_1>0\) and \(b_1{^2}>3b_0b_2,\) then one can clearly observe occurrence of Turing instability if

$$\begin{aligned} P(\lambda _{i(cr)})=\dfrac{2b_1^{3}-9b_0b_1b_2-2(b_1^{2}-3b_0b_2)^{\dfrac{3}{2}}+27A_3b_0^2}{27b_0^3}<0. \end{aligned}$$

Again from Eq. (3.45), we have \(\psi (\lambda _i)=\rho _1(\lambda _i)\rho _2(\lambda _i)-\rho _3(\lambda _i)\). Some algebraic calculations lead us

$$\begin{aligned} \psi (\lambda _i)=c_0\lambda _i^3+c_1\lambda _i^2+c_2\lambda _i+c_3, \end{aligned}$$
(4.2)

where

$$\begin{aligned} c_0&=(D_2+D_3)(D_1D_1+D_1D_2+D_2D_3+D_1D_3),\\ c_1&=-a_{11}(D_2+D_3)(2D_1+D_2+D_3)-a_{22}(D_1+D_3)\\&\times (D_1+2D_2+D_3)-a_{33}(D_1+D_2)(D_1+D_2+2D_3),\\ c_2&=D_1(a_{22}a_{22}-a_{33}a_{33}) +D_2(a_{11}a_{11}-a_{33}a_{33})\\&+D_3(a_{11}a_{11}-a_{22}a_{22})+2(a_{11}a_{22}+a_{11}a_{33} +2a_{22}a_{33})\\&\times (D_1+D_2+D_3),\\ c_3&=A_1A_2-A_3>0. \end{aligned}$$

If \(\psi (\lambda _i)\) has a minimum, then

$$\begin{aligned} \frac{d\psi }{d\lambda _i}=3c_0\lambda _i^{2}+2c_1\lambda _i+c_2=0, \end{aligned}$$

where \(\dfrac{d^2\psi }{d\lambda _i^2}>0.\) This minimum is reached for the solution at

$$\begin{aligned} \lambda _{i(cr)}=\frac{-c_1 \pm \sqrt{ c_1^2-3c_0c_2}}{3c_0}. \end{aligned}$$
(4.3)

If we choose \(c_1<0\) and \(c_2<0\), then straightforward calculations show that Turing instability occur if

$$\begin{aligned} \psi (\lambda _{i(cr)})=\frac{2c_1^{3}-9c_0c_1c_2-2(c_1^{2}-3c_0c_2)^{\frac{3}{2}}+27c_3c_0^2}{27c_0^3}<0. \end{aligned}$$

\(\square\)

Fig. 1
figure 1

The graph of the function \(P(\lambda _i)\) for the set of parameter values given in Eq. (4.4) with \(D_1=D_2=0.01\) and a \(D_3=10\) b \(D_3=10, 20, 30\)

Full size image

Now, consider the following set of parameter values for which above mentioned conditions for Turing instability hold:

$$\begin{aligned}&r_1=0.4632, \ r_2=0.4425, \ K_1=505, \ K_2=505,\nonumber \\&\quad w_1=0.6625, \ w_2=0.435, \ \alpha _1=0.002, \ \alpha _2=0.001,\nonumber \\&\quad d_1=45, \ d_2=30, \ \gamma _1=0.516, \ \gamma _2=0.45, \ m=0.309,\nonumber \\&\quad m_1=0.001, \ b_1=0.49. \end{aligned}$$
(4.4)

For this set of parameter values, we have obtained the positive equilibrium point \(( P_1^*, P_2^*, Z^*)\). For \(D_1=D_2=0.01, D_3=10\) and using the above set of parameter values, we have obtained the critical values \(\lambda _{i(cr)}\) as \((35.7149, -8.7742)\) and corresponding value of \(P(\lambda _{i(cr)})\) as \((-39.5637, 4.4509)\) (c.f., Fig. 1a). The graph of \(P(\lambda _{i})\) vs. \(\lambda _{i}\) has been plotted for different values of \(D_3\) in Fig. 1b. The positive values of \(\lambda _{i}\) for which \(\rho _3=P(\lambda _{i})<0\), the plankton system (2.1) is unstable.

Fig. 2
figure 2

a, b Time series for the non-spatial model system (3.1) at \(m_1=0.001\), \(m_1=0.0001\). c Bifurcation diagram of the non-spatial model system (3.1) for \(m_1\) vs. Max(Z)

Full size image
Fig. 3
figure 3

Bifurcation diagram of the non-spatial model system (3.1) for \(\alpha _1\) vs. Max(\(P_1\)), Max(\(P_2\)) and Max(Z) at fixed \(\alpha _2=0.2\)

Full size image
Fig. 4
figure 4

Bifurcation diagram of the non-spatial model system (3.1) for \(\alpha _2\) vs. Max(\(P_1\)), Max(\(P_2\)) and Max(Z) at fixed \(\alpha _2=0.5\)

Full size image
Fig. 5
figure 5

a, b Phase space diagram for the non-spatial model system (3.1) at \(b_1=0.49\), \(b_1=2\). c Bifurcation diagram of the non-spatial model system (3.1) for \(b_1\) vs. Max(Z)

Full size image
Fig. 6
figure 6

Spatiotemporal pattern of NTP, TPP and zooplankton of the model system (2.1) for fixed \(x=100\) and a \(t=200\), b \(t=300\) at \(m_1= 0.0001\)

Full size image
Fig. 7
figure 7

Spatiotemporal pattern of NTP, TPP and zooplankton of the model system (2.1) for fixed \(t=100\) and a \(x= 200\), b \(x=300\) at \(m_1=0.0001\)

Full size image
Fig. 8
figure 8

Spatiotemporal pattern of NTP, TPP and zooplankton of the model system (2.1) for a \(x=100, \ t=100\), b \(x=200, \ t=200\) at \(m_1= 0.0001\)

Full size image
Fig. 9
figure 9

Snapshots NTP, TPP and Zooplankton of model system (2.1) for \(D_1=D_2=0.1\) with a \(D_3=0.3\), b \(D_3=1.36\), c \(D_3=1.361\), d \(D_3=1.6\)

Full size image
Fig. 10
figure 10

Snapshots NTP, TPP and Zooplankton of model system (2.1) for \(D_1=D_2=0.1, \ D_3=1.6\) with a \(t=100\), b \(t=150\), c \(t=1000\)

Full size image
Fig. 11
figure 11

Snapshots NTP, TPP and Zooplankton of model system (2.1) for \(D_1=D_2=0.1, \ D_3=1.36\) with a \(b_1=0.49\), b \(b_1=0.69\)

Full size image
Fig. 12
figure 12

Time series for the model system (6.1) for different cases of \(\tau _1\) and \(\tau _2\)

Full size image

Numerical results

In this section, model system (2.1) with and without diffusion is investigated numerically to validate our theoretical findings. The system without diffusion is studied to understand the behavior of some control parameters that affect the plankton dynamics. Model system with diffusion is investigated for both one- and two-dimensional cases. For one-dimensional case, the complex spatiotemporal pattern is plotted for different values of time and space. The spatiotemporal dynamics is analyzed by observing the effect of time, space vs. density plot of plankton populations. For two-dimensional cases, spatial distribution of plankton population is presented by snapshots. All the numerical results are plotted by using MATLAB. The snapshots of the model system (2.1) are plotted by semi-implicit (in time) finite difference method (Garvie 2007). The step lengths \(\varDelta x\) and \(\varDelta y\) of the numerical grid are chosen sufficiently small so that the results are numerically stable. Application of the finite difference method gives rise to a sparse, banded linear system of algebraic equations. The resulting linear system is solved by using the GMRES algorithm for the two-dimensional case.

For the non-spatial model system (3.1), we have plotted the time series, phase space diagram along with bifurcation representation for a different range of parametric values. For this simulations, we have considered the following set of parameter values as mentioned in Eq. (4.4) at which the system (3.1) is locally asymptotically stable (c.f., Fig. 2a). As we decrease the value of intraspecific interference parameter \(m_1\) from 0.001 to 0.0001, the system loses its stability and becomes unstable (c.f., Fig. 2b). Time series in Fig. 2 clearly show that intraspecific interference of zooplankton strongly affected the system dynamics. It reveals that the low value of intraspecific interference \(m_1\) destabilizes the dynamics of the plankton system. In Fig. 2c, we have generated the bifurcation diagram between intraspecific interference parameter \(m_1\) in the range [0.0001, 0.002] and population of Z. The population of \(P_1\) and \(P_2\) with respect to \(m_1\) are not plotted here, yet they are similar. Later, we have generated the bifurcation diagram for intraspecific competition coefficients \(\alpha _1\) and \(\alpha _2\). For this, we have chosen a window \(\alpha _1\in [0, 0.6]\) for fixed \(\alpha _2=0.2\) and generated the bifurcation diagram for \(\alpha _1\) vs. population of \(P_1\), \(P_2\) and Z, respectively (c.f., Fig. 3). For this range of \(\alpha _1\), it has been observed that the increasing value of \(\alpha _1\) makes the system stable to unstable but after a certain range, it regains stability. Similarly, we have chosen a window \(\alpha _2\in [0, 0.6]\) for fixed \(\alpha _1=0.5\) and generated the bifurcation diagram for \(\alpha _2\) vs. population of \(P_1\), \(P_2\) and Z, respectively (c.f., Fig. 4). For this range of \(\alpha _2\), it has been observed that the increasing value of \(\alpha _1\) makes the system stable to unstable. If we compare the bifurcation diagram 3 and 4, one can clearly observe the low value of \(\alpha _1\) gives rise to zooplankton density whereas low value of \(\alpha _2\) slightly decreases the zooplankton density. In addition, a high value of \(\alpha _2\) tends to the extinction of zooplankton stable equilibrium. Further, we have also observed the impact of inhibitory effect \(b_1\) on system dynamics. For fixed \(\alpha _1=0.5, \ \alpha _2=0.2\), we have drawn phase space diagram at \(b_1=0.49\) and \(b_1=2\). A stable limit cycle has appeared after a stable focus with an increasing value of \(b_1\) (c.f., Fig. 5a, b), since the inhibitory effect of TPP mainly affected the dynamics of zooplankton. Hence, a bifurcation diagram is plotted between \(b_1\) and the population of Z in Fig. 5c. We see that the populations of Z are oscillating as \(b_1\) crosses its threshold value.

For the spatial model system (2.1), we have chosen the same set of parameters value as given in Eq. (4.4) and plotted the spatiotemporal pattern with the following diffusion coefficients \(D_1=D_2=10^{-4}\) and \(D_3=10^{-3}\). The considered initial conditions for the spatial dynamics are as mentioned below:

$$\begin{aligned}&P_1(x,0)=P_1^*+\varepsilon _1\sin \bigg (\frac{2\pi (x-x_0)}{S}\bigg ),\nonumber \\&\quad P_2(x,0)=P_2^*+\varepsilon _1\sin \bigg (\frac{2\pi (x-x_0)}{S}\bigg ),\nonumber \\&\quad Z(x,0)=Z^*+\varepsilon _1\sin \bigg (\frac{2\pi (x-x_0)}{S}\bigg ), \end{aligned}$$
(5.1)

where \(\varepsilon _1=5\times 10^{-4}, \ x_0=0.1, \ S=0.2\) and \(( P_1^*, P_2^*, Z^*)=(72.1687, 504.6492, 70.0499)\).

Now, we have presented the pattern formation for the one-dimensional case in Figs. 6, 7, 8 with the above introduced initial conditions and parameters value of Eq. (4.4). Further, we decrease the value of zooplankton’s intraspecific interference coefficient from \(m_1=0.001\) to \(m_1=0.0001\) and observe the significant changes in the dynamics of NTP, TPP and zooplankton. Firstly, we have checked the effect of space, time, and then space-time in both of the proposed reaction-diffusion systems (2.1). To elaborate the effect of space with varying time, we fixed space in the interval \(0 \le x \le 100\) and increase the value of time from \(t=200\) to \(t=300\) (c.f., Fig. 6). In Fig. 6a, we observed that at \(t=200\), all the species (NTP, TPP and zooplankton) shows chaotic oscillation in space only. In Fig. 6b, we observed that at \(t=300\), NTP and zooplankton reduce its complexity whereas TPP remains in its old stage. Now, to elaborate the effect of time with varying space, we fixed time in the interval \(0 \le t \le 100\) and increase the value of space from \(x=200\) to \(x=300\) (c.f., Fig. 7). In this case, NTP and zooplankton show chaotic oscillations in space and time both whereas TPP shows complex spatiotemporal patterns in space only. Further, we observed that increasing the value of space increases the complexity in all the species. To elaborate the effect of space-time both, first we fixed \(0\le x\le 100\) and \(0\le t\le 100\) then we fixed \(0\le x\le 200\) and \(0\le t\le 200\) (c.f., Fig. 8). If we compare Fig. 8a to b, we observed that the density of NTP and zooplankton slightly stabilize with respect to time but increase the complexity with respect to space whereas the density of TPP increases the complexity with respect to space only.

After substantiating the appearance of Turing instability and plotting different spatiotemporal patterns with respect to time and space, now, we have investigated the various Turing patterns of the two-dimensional spatial systems to know how the different diffusion coefficients and time intervals affect the spatial distribution of plankton system (2.1). To explore the formation of the patterns, firstly, we have presented the snapshot for NTP, TPP and zooplankton for different diffusion coefficients in Fig. 9. During the formation of patterns, different types of dynamical outcomes such as mixture, stripes and spots have been seen and it also is found that the density distribution of NTP, TPP and zooplankton are always followed the same type of distribution. Initially, in the examination of diffusion coefficient, we fixed the diffusion coefficient of NTP and TPP at \(D_1=D_2=0.1\) and do a variation in diffusion coefficient of zooplankton \(D_3\) where the other parameters are mentioned in Eq. (4.4) and initial distribution of population is taken as \(P_1(x, y, 0)= P_1^*+0.1\)randn, \(P_2(x, y, 0)= P_2^*+0.1\)randn and \(Z(x, y,0)= Z^*+0.1\)randn. We observed from Fig. 9a, when \(D_3=0.3\), a stable pattern has appeared for the NTP population whereas an irregular patchy pattern has appeared for TPP and zooplankton density. Now, as we strengthen the value of diffusion coefficient of zooplankton from \(D_3=0.3\) to \(D_3=1.36\), it is very fascinating to see that the whole square domain of NTP changes into yellow color and the whole square domain of TPP changes into blue color, which ensures that TPP population less than the population of NTP as \(D_3\) increased. Further, the interconnected stripe and spot patterns for NTP, TPP and Zooplankton population are appeared at \(D_3=1.36\) (c.f., Fig. 9b). Now, as we slightly increase the value of \(D_3\) from \(D_3=1.36\) to \(D_3=1.361\), the population of TPP and zooplankton shows minor changes in their distribution from the previous patterns but the population of NTP shows major changes since the color of the whole square domain of NTP changes into a mixture of yellow and blue color which indicates the reduction in the density of NTP. In this case, we have found the plankton domain emergence with a mixture of stripe and spot patterns (c.f., Fig. 9c). At the large diffusion coefficient of \(D_3=1.6\), the model system depicts a transition from the stripe–spot mixture to spot replication (c.f., Fig. 9d). In this spot pattern, we have found that the NTP and zooplankton populations are in the isolated zone with low density whereas TPP is in the isolated zone with high density. Therefore, in this simulation, increasing the value of diffusion coefficient \(D_3\) leads to a sequence of pattern “irregular patchy pattern \(\longrightarrow\) stripe–spot mixture \(\longrightarrow\) spot.” Now, we have examined the consequences of time intervals on the density of NTP, TPP and zooplankton population by keeping all diffusion coefficient constant as \(D_1=D_2=0.1, \ D_3=1.6\). Initially, at \(t=100\), the spatial distribution consists of an irregular patchy pattern where \(t=150\) spatial distribution consists of a mixture of stripes and spots (c.f., Fig. 10a, b). It is remarkable that a minor change in time interval clears the occurrence of spots with strips. As we increase the value of time from \(t=150\) to \(t=1000\), we have observed the mixture of spots and stripes goes into a clear spot pattern and finally, the spatial distribution consists of spots only (c.f., Fig. 10c). The density distribution consequences for the parameter \(b_1\) is also studied under the Turing domain of the system (2.1). In Fig. 11, a mixture of stripe–spot pattern switches to spot pattern only when the value of inhibitory effect takes from \(b_1=0.49\) to \(b_1=0.69\).

The mathematical model with time delay

In order to generalize the proposed non-spatial model system (3.1), we have introduced two constant delay parameters \(\tau _1\) and \(\tau _2\). Since the interaction among NTP, TPP and zooplankton are not an immediate process. During the conversion process of food (i.e., NTP), a time lag is required for the reproduction by the zooplankton gestation. Therefore, we have introduced discrete time delay \(\tau _1\) in zooplanktons growth term. Further, we have assumed that the zooplanktons death due to predation of TPP needs some time lag. For this assumption, we have introduced discrete time delay \(\tau _2\) in the extra morality term in the zooplankton dynamics. Hence the corresponding delayed phytoplankton–zooplankton system takes the following form:

$$\begin{aligned} \frac{d P_1}{d t}&=r_1P_1\bigg (1-\frac{P_1+\alpha _1P_2}{K_1}\bigg )-\frac{w_1P_1Z}{d_1+P_1},\nonumber \\ \frac{d P_2}{d t}&=r_2P_2\bigg (1-\frac{P_2+\alpha _2P_1}{K_2}\bigg )-\frac{w_2P_2Z}{d_2+b_1P^2_2},\nonumber \\ \frac{d Z}{d t}&=\frac{\gamma _1P_1(t-\tau _1)Z(t-\tau _1)}{d_1+P_1(t-\tau _1)}-\frac{\gamma _2P_2(t-\tau _2)Z(t-\tau _2)}{d_2+b_1P^2_2(t-\tau _2)}\nonumber \\&-mZ-m_1 Z^2. \end{aligned}$$
(6.1)

For this system, we have validated all the possible combination of \(\tau _1-\tau _2\) in five different cases by using the same parameter set given in Eq. (4.4), as follows:

  1. (i)

    Case I, when both \(\tau _1=\tau _2=0\): In this case, the system is LAS (locally asymptotically stable) about the coexisting equilibria \(E^*(P_1^*, P_2^*, Z^*)=(210.2, 504.4, 103.8)\) (c.f., Fig. 12 (Case I: \(\tau _1=\tau _2=0\))).

  2. (ii)

    Case II, when \(\tau _1>0, \ \tau _2=0\): In this case, the system is LAS for \(\tau _1=1.5\) and unstable for \(\tau _1=3\). Therefore, the system experiences the Hopf-bifurcation scenario around \(\tau _1=\tau _1^*=1.791\) (c.f., Fig. 12 (Case II: \(\tau _1>0, \ \tau _2=0\))).

  3. (iii)

    Case III, when \(\tau _1=0, \ \tau _2>0\): In this case, the system is LAS for all \(\tau _2>0\). Therefore, the system does not experience the Hopf bifurcation for any value of \(\tau _2\) (c.f., Fig. 12 (Case III: \(\tau _1=0, \ \tau _2>0\))).

  4. (iv)

    Case IV, when \(\tau _1\in (0,\tau _1^*), \ \tau _2>0\): In this case, we have chosen an arbitrary value of \(\tau _1\) within its stability region (0,1.791) for the free parameter \(\tau _2\). We have taken \(\tau _1=1\) and observed, the system is LAS for all \(\tau _2>0\) (c.f., Fig. 12 (Case IV: \(\tau _1=1, \ \tau _2>0\))).

  5. (v)

    Case V, when \(\tau _1>0, \ \tau _2\in (0,\tau _2^*)\): In this case, we have chosen an arbitrary value of \(\tau _2\) within its stability region (0,10) for the free parameter \(\tau _1\). We have taken \(\tau _1=2\) and observed, the system is LAS for \(\tau _1=1.25\) and unstable \(\tau _1=3.5\). Therefore, the system experiences the Hopf-bifurcation scenario around \(\tau _1=\tilde{\tau _1}^*=2.256\) (c.f., Fig. 12 (Case V: \(\tau _1>0, \ \tau _2=2\))).

Discussion

Eutrophication and the presence of toxic phytoplankton in Sundarbans estuary have deteriorated the water quality. The structure of mangrove is unique and driven by marine and terrestrial. Most of the study focused on the treatment of wastewater, and very little attention has been given to disturbance occurred by toxin-producing phytoplankton and the presence of pollutant chemicals in the sediments of Sundarbans. Bio invasion in the world heritage Sundarbans ecosystem dynamics has put a question mark on their sustainability. Fresh and marine water HABs have a significant concern toward the aquatic food chains and population of humans. Therefore, a considerable investigation into all aspects is needed to verify essential blooming factors. Many researchers have focused on the study of plankton dynamics with different assumptions in which the role of HABs has been widely recognized. Chattopadhyay et al. (2004) had proposed a mathematical model for a three-dimensional plankton system that shows the interaction among NTP, TPP and zooplankton population. They incorporated two types of predation form, one describes the predation rate for NTP population which follows the simple law of mass action whereas another describes the predation rate for TPP population which follows the Holling type II functional form. Further, they assume NTP and TPP share the same carrying capacity. Roy et al. (2006) incorporated competing effects between NTP and TPP population by using Holling type II functional response for both groups of phytoplankton and studied some biological factors that regulate the overall dynamical behavior. Roy (2008) further studied this model with spatial movements in the subsurface water and described how a non-homogeneous biomass distribution of competing phytoplankton and grazer zooplankton emerges over space and time in the presence of toxic species. Pal et al. (2009b) modify the above study by assuming different carrying capacity for NTP and TPP and considering Beddington functional response as predation form rather than Holling type I or type II functional response. Recently, Thakur et al. (2016) investigated the role of HABs in three interacting species model (i.e., NTP, TPP and zooplankton) over the space and time. This study is further extended by Thakur et al. (2017) by taking one crucial parameter, the intraspecific interference coefficient between zooplankton populations for Sundarban mangrove wetland. In this paper, a mathematical model with three interacting components, NTP, TPP and zooplankton with spatial diffusion is established to study the dynamical complexity, where NTP and TPP both forms a prey and zooplankton forms a predator. The developed model system describes an ecosystem that contains a one-zooplankton two-phytoplankton population under the influence of toxicity which is released by the TPP population. Two different types of response functions are assumed to define the interaction among species. Holling type II functional form is used to express the mathematical structure of NTP and zooplankton whereas MH-type functional form is used to express the mathematical structure of TPP and zooplankton. Here, the MH-type response function is used to explain the phytoplankton toxicity over the range of zooplankton density. Additionally, the assumption of some important parameters such as competing and intraspecific interference coefficient together with spatial diffusion in the same model fascinates the plankton system. Further, analytical and numerical solution is well presented for the study of temporal and spatial properties of the model system, and some reasonable findings are obtained.

Firstly, a detailed study of stability analysis along with all feasible equilibria for the model system (2.1) has been done in the presence as well as in the absence of diffusion. Then, to substantiate our analytical findings, numerical validation is presented with the help of MATLAB. Numerical results indicate that the behavior of the non-spatial system is affected by the control parameters such as intraspecific interference coefficient \(m_1\), intraspecific competition coefficient \(\alpha _1, \alpha _2\) and inhibitory effect \(b_1\). Since a low value of\(m_1\) may arise the oscillatory behavior in a non-spatial model system (3.1) and changed the stable state to an unstable state. This can be seen in the time series and bifurcation diagram presented in Fig. 2. The bifurcation diagram 3 reveals that a low intraspecific competition coefficient of NTP (i.e., \(\alpha _1\)) stabilizes the dynamics and after the first critical value of \(\alpha _1\), the system losses its stability, and periodic oscillation appears. Further, at the second critical value of \(\alpha _1\), the system regains its stability. It is also observed that a low value of \(\alpha _1\) increases the density of NTP and zooplankton and decreases the density of TPP but a high value of \(\alpha _1\) decreases the density of NTP and zooplankton and increases the density of TPP. Hence, increasing intraspecific competition of NTP implies a similar kind of behavior for NTP and zooplankton but the opposite kind of behavior is obtained for TPP. A destabilization effect of intraspecific competition coefficient of TPP (i.e., \(\alpha _2\)) is observed in Fig. 4. It is also noticed that \(\alpha _2\) is mainly affected by the population of TPP since the increasing value of \(\alpha _2\) decreases the density of TPP. Fig. 5 depicts the occurrence of the limit cycle after a stable state as we increase the value of \(b_1\). From a biological sense, this result is very reasonable that a high inhibitory effect bifurcates the population at the critical value of \(b_1 = b_{1c}\). Additionally, we have explored the spatial distribution in one dimensional as well as two dimensional along with a different diffusion coefficient. In the case of a diffusive system (2.1), our observation reveals that the low diffusion of NTP and TPP and high diffusion of zooplankton result in the existence of Turing instability, and this instability supports the patchiness in the aquatic ecosystem (c.f., Fig.1). Biologically, Turing instability indicates that the diffusion coefficient supports the violation of sustainability conditions in spatial distribution. Pattern formation for the 1D case, we mainly study the effect of mechanisms like intraspecific interference coefficient \(m_1\). For a particular set of parameter values, we have plotted the spatiotemporal pattern to understand the effect of space, time and space-time both evolution for a small value of \(m_1\). In Figs. 6, 7, we have considered \(m_1\) = 0.0001 and noticed that on increasing the value of time and space from 200 to 300, the system exhibits irregular chaotic oscillation in space only and irregular chaotic oscillation in space and time both. Whereas on increasing the value of time-space together, we found chaotic dynamics with respect to space and time both for NTP and zooplankton and chaotic dynamics with respect to space only for TPP (c.f., Fig. 8). The overall observation of Figs. 6, 7, 8 is that increasing time decreases the complexity but increasing space increases the complexity. It is remarkable that the low value of \(m_1\) helps all the species to show a significant dynamical behavior with chaotic fluctuation in spatiotemporal patterns. Finally, snapshots for the 2D case are presented to explore the different Turing patterns of the reaction-diffusion system (2.1). Irregular patchy pattern, a mixture of stripe–spot and spot patterns is observed for different diffusion coefficients of zooplankton (c.f., Fig. 9) and stripe–spot and spot patterns are observed for different time intervals (c.f., Fig. 10). Mixture of stripe–spot and spot patterns are observed for intensity of inhibitory effect \(b_1\) (c.f., Fig. 11). The two-dimensional simulation result suggests that the patterns are diffusion and time-dependent and become a patchy reason for the aquatic ecosystem. Also, the transformation of stripes into spots shows the high and low density of the plankton species. For more realistic outcomes, we have studied the effect of two feedback delays on the system dynamics numerically. From Fig. 12, destabilization effect is observed with respect to gestation delay \(\tau _1\) of zooplankton (see Case II & IV). Further, the incorporation of \(\tau _2\) does not affect the system’s stability, and the system remains stable with varying \(\tau _2\) (see Case III & V). Hence, \(\tau _1\) strongly affects the system dynamics as compared to \(\tau _2\). Since one can clearly see a bifurcation point corresponding to \(\tau _1\) whereas no bifurcation point is observed corresponding to \(\tau _2\).

Conclusion

In this paper, we have proposed a three species interacting model with spatial interaction and competing effects for Sundarban mangrove wetland. Phytoplankton groups mainly Dinoflagellates and Cyanophyceae produces neurotoxin which is toxic to the zooplankton. Sundarban mangrove wetland is suffering from algal bloom due to the presence of such toxics. Toxin produced by phytoplankton depletes the quality of water, and cause problems to fishes and invertebrates. Our analytical results show under certain conditions the plankton dynamics is stable and maintain the steady state. Diffusion stabilizes the system dynamics and solution converges to its equilibrium faster than the non-spatial system. Our numerical findings show that the increasing value of inter-specific competition coefficient of NTP leads to increase in TPP density and reduction in zooplankton density that may cause algal blooms and bad health of the wetland system (c.f., Fig. 3). Spatiotemporal patterns show the spatially periodic patterns with high density of TPP, irrespective of increase in time or space (c.f., Figs. 6, 7, 8). The spatial distribution of plankton system is explored by plotting the snapshot for increasing value of time and diffusion coefficient of zooplankton and observed that the density distribution of NTP, TPP and zooplankton. The system shows sequence of irregular patchy to stripe–spot mixture to spot patterns (c.f., Figs. 9, 10). Some other parameters such as intraspecific interference of zooplankton, inhibitory effect of TPP and gestation delay are also responsible algal bloom and bad health of wetland in Sundarban region. Our study suggests that controlling such parameters may reduce the algal blooms and can be maintained the good health of Sundarban mangrove wetland.