Introduction

Articulated robotic arms are advantageous to traditional machine tools for machining large workpieces with complex features [1, 2]. For example, the application of robotic machining has been rapidly growing in aircraft fuselage assembly and wind turbine manufacturing processes. Avoiding unstable vibrations, known as chatter, is among the most critical challenges in designing high-performance machining processes, and this problem is more critical in robotic machining due to their much higher compliance compared to machine tools [3, 4]. Highly effective chatter modeling and avoidance methods that have been developed in the past decades are now being used by the industry to design high-performance chatter-free machining operations in machine tools [5]. The available methods however face major difficulties when applied to robotic machining, mainly due to the nonlinearity and pose-dependency of the vibration response in robots, which is negligible in machine tools.

Dynamics of the milling process includes a natural delayed feedback loop which may destabilize the process vibrations and lead to chatter and consequently damages to the tool or workpiece [6]. Modeling chatter dynamics by Delay Differential Equations (DDE) and solving them to identify chatter-free machining parameters has been studied extensively [5]. Frequency-domain method of Budak and Altintas [7] and discrete time-domain methods of Insperger and Stepan [8] and Ding et al. [9] are the two approaches that are widely used for chatter modeling in machine tools. In both of these approaches, accurate estimations of the Frequency Response Function (FRF) or the modal parameters extracted from the FRF at the tool-tip are required. The results of stability analysis by these methods are usually presented in the form of Stability Lobes Diagram (SLD) which shows the combinations of axial cutting depth and spindle speed that lead to stable vibrations, and the accuracy of the resulting SLD are directly correlated with the accuracy of the FRF used to compute them. Both of the frequency and discrete-time domain approaches, which were initially developed for machine tools, have also been adopted for robotic milling processes. Pan et al. [10] and Wang et al. [11] used the frequency-domain approach to predict chatter in robotic milling, focusing on the stability of the low-frequency modes of the robots’ structure. The flexible components that cause chatter in machine tools are usually the tool, holder, and the spindle, but the flexibility of revolute joints is the main source of chatter in robotic machining. Therefore, robotic machining is more prone to chatter in low-frequency modes (typically lower than 50 Hz), especially when lower spindle speeds are used. While the high-frequency modes associated with the flexibility in the tool, holder, and spindle remain relatively unchanged in the workspace of the machine tool or the robot, the parameters of low-frequency modes associated with the robot’s joints vary by the robot’s pose and the forces applied to it [12]. Multi-Body Dynamics (MBD) models with elastic joints can be applied to model the robot’s tool-tip FRF in arbitrary postures [13, 14], although the identification of the inertial and joint elastic parameters for the MBD models requires extensive experiments. Besides, the large number of unknown parameters may make the model parameters globally unidentifiable. Data-driven methods are also used to model the pose-dependency of the FRF, but the trained model shows a large variance outside the range of postures that are used for training [15,16,17]. Mousavi et al. [18, 19] developed a Multi-Body Dynamics (MBD) model with elastic joints and links to predict the posture-dependent FRF of the robot and employed the predicted FRF in the frequency-domain method to develop the stability lobes diagram. The FRF at the tool-tip (robot’s TCP) can also be measured by impulse hammer test instead of MBD modeling. The measured FRF is more accurate than MBD modeling but it is only applicable to the measurement posture. For instance, Li et al. [20] used impulse hammer to measure the FRF and used them in the frequency-domain method to obtain the SLD of the machining robot; they showed that cross-FRF contribute to the system dynamics much more significantly in robots than in machine tools. Cordes et al. [21] also used the FRF measured by hammer test in both the frequency-domain approach and Semi Discretization method. They showed that the low-frequency posture-dependent modes of the robot can be neglected in high-speed robotic milling; yet, the stability in low-speed milling is governed by the low-frequency modes.

Experimentally measured FRF are usually obtained by impulse hammer tests conducted in idle conditions. In this paper, idle condition represents the situation in which the robot is at rest and operational condition is referred to the conditions in which milling operation is performed and the tool-tip is subjected to cutting forces. Different methods can be applied to measure the FRF under operational conditions in CNC milling and turning. Minis et al. [22] designed a specialized workpiece with randomly distributed channels to provide random cutting forces during turning process. Ozsahin et al. [23] employed a similar idea to measure in-process FRF in milling. Inverse stability analysis can also be used to determine the FRF under operational conditions. In this approach, experimentally identified chatter stability limits are substituted in the theoretical model of chatter to inversely determine the modal parameters. Ozsahin et al. [24] presented a method based on this inverse approach and showed that the parameters of the flexible mode can be identified based on the limiting cutting depths at two relatively close spindle speeds. Grossi et al. [25] augmented the inverse method by combining it with speed ramp-up technique to improve the accuracy of the identified FRF in a wide range of spindle speeds. Both of these two works confirmed the substantial variation of the FRF under operational conditions from those measured in idle conditions. However, compared to robots, the change in machine tools’ vibration response due to operational conditions is relatively low because of their high rigidity. Therefore, idle FRF are reasonably accurate for predicting stability diagrams in machine tools. For robots, nonlinear mechanisms such as strain hardening/softening, friction and hysteresis effects in the robot’s revolute joints are minimally active in idle conditions but become prevalent under operational loads [12, 26,27,28]. We studied the effect of such nonlinearities on chatter stability in robotic machining and showed that the vibration response at the TCP depends not only on the robot’s posture but also the level and type of the applied forces in operation [29, 30]. Idle and in-process FRF can be different even without the operational loads. This was shown in Tunc and Gonul’s study where they observed a significant variation in the FRF measured by impulse hammer test conducted on the idle robot and when it moves at a constant speed [31]. The FRF measured in idle condition are therefore not representative of the vibration response under operational conditions and new FRF measurement methods need to be developed for chatter analysis in robotic machining.

In this paper, we present new methods for the experimental estimation of the robot’s FRF during the milling process.The FRF that are measured in-process represent the dynamics of the system linearized about the operational condition and account for the structural nonlinearities, feed motion, and any other unknown sources that may affect the system dynamics during machining. Operational Modal Analysis (OMA), which estimates the modal parameters from vibration response to ambient noise excitation, can potentially be applied to estimate in-process FRF [32]; however, because the mode shapes resulting from OMA are not mass-normalized due to the lack of input measurement, the resulting FRF are not applicable for chatter stability analysis. Besides, the modal parameters resulting from OMA represent the dynamics of the closed-loop (regenerative) system and not the robot’s (or machine tool’s) structural dynamics [33, 34]. Alternatively, milling forces that are measured by dynamometers during the process can be used as the excitation source for in-process FRF estimation [23, 35]. The FRF estimated by this method are not affected by the feedback loop in the process and are scaled to the physical unit; therefore, they are applicable for stability analysis. However, because the milling forces are periodic at the spindle rotation frequency, the resolution of the resulting FRF is limited to the spindle rotation frequency, which is not sufficient for the accurate identification of vibration modes. Besides, the milling forces simultaneously excite the system in multiple directions with correlated forces. The correlation of milling forces is not important when this method is applied to machine tools but becomes important in robots. Because the vibration response of the machine tool in each Cartesian direction is uncoupled from others, FRF in each direction can be estimated as a single-Input-Single-Output [23, 35]. However, the robot’s TCP vibration response is strongly coupled between all three Cartesian directions and therefore the FRF matrix must be estimated as Multi-Input Multi-Output (MIMO), which requires uncorrelated simultaneous excitation. To overcome these problems, we present two in-process FRF measurement methods that are effective in robotic machining. The first method uses the forces measured during milling porous materials. Because of the random distribution of the material in this method, the measured forces include a strong random component, which improves the resolution and bandwidth of the measured FRF and removes the correlation between milling forces in various directions. In the second method, forces measured during milling homogeneous materials are used, but the spindle speed is swept in the frequency range of interest to arbitrarily increase the resolution of the measured FRF. Forces measured in multiple (at least three) milling operations with various cutter-workpiece engagements are used to obtain a set of uncorrelated excitation forces. The presented methods are applied to measure the in-process FRF of a 6-axis machining robot and construct the corresponding SLD. Experimental validations confirm that the resulting SLD are more accurate than those obtained based on idle FRF. The first approach only requires one test under constant spindle speed and provides a quick method to identify the FRF in a wide range of frequencies with all the nonlinear effects included. The second approach requires more effort and multiple tests with varying spindle speeds, but the measured FRF have a better resolution and a higher coherence than the first method. Moreover, since the level of cutting forces can be controlled in the second approach, it is more suitable for studying nonlinearities in system dynamics.

A brief description of chatter modeling and the importance of FRF measurement for chatter analysis is presented in the next section. In “In-Process FRF Measurement” the two in-process FRF measurement methods are presented and applied to a 6-axis robotic machining setup. In “Stability Lobe Diagrams with In-Process FRF”, the resulting in-process measured FRF and their idle counterpart are used to plot the SLD of the robot and chatter tests are performed to confirm the enhanced chatter prediction accuracy when in-process FRF are used.

Dynamics of Regenerative Chatter in Milling

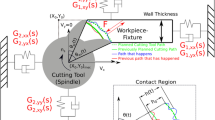
Consider the 6-DOF articulated robotic arm performing milling operation shown in Fig. 1. The robot is subjected to milling forces generated at its TCP (tool-tip) in the feed (X), normal (Y ), and axial (Z) directions. Milling forces are commonly modeled by linear models which describe them as a combination of periodic forces proportional to feedrate and transient forces proportional to the TCP’s present and past elastic oscillations [36]:

$$\mathbf{F}(t)=\mathbf{F}_{p}(t)+a {K_{tc}} [\alpha (t)] \left\{ {{\mathbf{X}} - {{\mathbf{X}}^{\tau} }} \right\}$$
(1)

where F(t) is the total forces applied at the TCP, and Fp(t) = Fp(t + τ) represents periodic forces with tooth-passing period, τ, as the principal period. Tooth-passing period, τ = 2π/NΩ, is inversely proportional to spindle speed (Ω) and the number of the cutting edges of the tool (N). The second term in Eq. 1 represents the transient regenerative forces, which are generated by the inherent feedback from the TCP vibrations into the machining forces that cause them. Since the detailed discussion of modeling the regenerative forces is available in chatter literature such as [36, 37] and [7], only a high-level summary of the model is provided here.

Regenerative forces are proportional to the elastic displacement of the TCP in Cartesian frame, \({\mathbf {X}} = {\left [ {x(t)\,\,y(t)\,\,z(t)} \right ]^{T}}\), and its value one tooth-passing period prior, \({\mathbf {X}^{\tau }} = {\left [ {x(t- \tau )\,\,y(t- \tau )\,\,z(t- \tau )} \right ]^{T}}\). This delayed term represents the modulation of the milling forces due to the surface undulations left by the previous tooth. The constant Ktc is the force coefficient in the tangential direction [37] and a is the axial cutting depth, as shown in Fig. 1d. The matrix [α(t)] = [α(t + τ)] represents the periodic variation of the regenerative forces and their directions as the spindle rotates; therefore, its entries are periodic at the tooth-passing period, τ:

$$\left[ {\alpha (t)} \right] = \left[ {\begin{array}{*{20}{c}} {{\alpha_{xx}}}&{{\alpha_{xy}}}&{{\alpha_{xz}}} \\ {{\alpha_{yx}}}&{{\alpha_{yy}}}&{{\alpha_{yz}}} \\ {{\alpha_{zx}}}&{{\alpha_{zy}}}&{{\alpha_{zz}}} \end{array}} \right]$$
(2)

where

$${\alpha_{xx}} = \sum\limits_{j = 1}^{N} {g(\varphi_{j}) \sin {\varphi_{j}}\sin \gamma \left( { - \cos {\varphi_{j}} - {k_{rc}}\sin {\varphi_{j}}\sin \gamma - {k_{ac}}\sin {\varphi_{j}}\cos \gamma } \right)},$$
$${\alpha_{xy}} = \sum\limits_{j = 1}^{N} {g(\varphi_{j}) \cos {\varphi_{j}}\sin \gamma \left( { - \cos {\varphi_{j}} - {k_{rc}}\sin {\varphi_{j}}\sin \gamma - {k_{ac}}\sin {\varphi_{j}}\cos \gamma } \right)},$$
$${\alpha_{xz}} = \sum\limits_{j = 1}^{N} { - g(\varphi_{j}) \cos \gamma \left( { - \cos {\varphi_{j}} - {k_{rc}}\sin {\varphi_{j}}\sin \gamma - {k_{ac}}\sin {\varphi_{j}}\cos \gamma } \right)} ,$$
$${\alpha_{yx}} = \sum\limits_{j = 1}^{N} {g(\varphi_{j}) \sin {\varphi_{j}}\sin \gamma \left( {\sin {\varphi_{j}} - {k_{rc}}\cos {\varphi_{j}}\sin \gamma - {k_{ac}}\cos {\varphi_{j}}\cos \gamma } \right)},$$
$${\alpha_{yy}} = \sum\limits_{j = 1}^{N} {g(\varphi_{j}) \cos {\varphi_{j}}\sin \gamma \left( {\sin {\varphi_{j}} - {k_{rc}}\cos {\varphi_{j}}\sin \gamma - {k_{ac}}\cos {\varphi_{j}}\cos \gamma } \right)},$$
$${\alpha_{yz}} = \sum\limits_{j = 1}^{N} { - g(\varphi_{j}) \cos \gamma \left( {\sin {\varphi_{j}} - {k_{rc}}\cos {\varphi_{j}}\sin \gamma - {k_{ac}}\cos {\varphi_{j}}\cos \gamma } \right)} ,$$
$${\alpha_{zx}} = \sum\limits_{j = 1}^{N} {g(\varphi_{j}) \sin {\varphi_{j}}\sin \gamma \left( { - {k_{rc}}\cos \gamma - {k_{ac}}\sin \gamma } \right)} ,$$
$${\alpha_{zy}} = \sum\limits_{j = 1}^{N} {g(\varphi_{j}) \cos {\varphi_{j}}\sin \gamma \left( { - {k_{rc}}\cos \gamma - {k_{ac}}\sin \gamma } \right)} ,$$
$${\alpha_{zz}} = \sum\limits_{j = 1}^{N} { -g(\varphi_{j}) \cos \gamma \left( { - {k_{rc}}\cos \gamma - {k_{ac}}\sin \gamma } \right)}.$$

The parameters krc and kac are force coefficients in the radial and axial directions, respectively, γ is the cutting edge angle, and \(\varphi _{j}={\Omega } t+(j-1)\frac {2\pi }{N}\) is the immersion angle of tooth j, as shown in Fig. 1c. The Heaviside function g(φj) determines whether this angle is within the cutting immersion angle range bounded by the start and exit angles, φst and φex, respectively:

$$g(\varphi_{j})=u(\varphi_{j}-\varphi_{st})-u(\varphi_{j}-\varphi_{ex})$$
(3)

with u(⋅) being unit step function. Depending on the axial depth of cut (a) and spindle speed (Ω = 2π/Nτ), the transient component of the forces may decay or grow, leading to stable or unstable vibrations. In stable cuts, the transient vibrations decay and settle at an equilibrium state; thus, steady-state TCP oscillations only include the periodic response induced by Fp(t). In unstable cuts, the transient vibrations cannot be suppressed by the system’s damping and they are superimposed on the aforementioned periodic response; this situation in which bifurcation occurs to the equilibrium state is usually referred to as chatter.

Fig. 1
figure 1

(a) Configuration of the KUKA KR90 R3100 robotic milling system. (b) the experimental setup used to measure in-process FRF. (c) and (d) 3DoF model of milling system

Full size image

Budak and Altintas [7] showed that the average of the periodic [α(t)] is sufficient for accurate chatter stability analysis in common machining applications, because its harmonic components are filtered by structural dynamics. They presented Zero-Order Approximation (ZOA) chatter analysis method where the periodic [α(t)] is approximated by \(\left [ {{{\mathbf {\alpha }}_{0}}} \right ]\), its average over one principal period [7]. In most of common machining applications, the dynamics of vibration response at the TCP can be assumed Linear-Time-Invariant [38]; therefore the milling forces and the resulting oscillations in the Laplace domain can be mapped to one another via the system transfer function, as follows:

$$\mathbf{X}(s)=\mathbf{H}(s)\mathbf{F}(s)$$
(4)

where H(s) is the transfer function between Cartesian forces and oscillations at the TCP, assuming the system is linearized about its periodic response. Transforming Eq. 1 to Laplace domain and substituting X(s) from Eq. 4 leads to the following characteristic equation:

$$\det \left[ {{\mathbf{I}} - a K_{tc}[{\alpha_{0}}]\left( {1 - {e^{- s \tau }}} \right) {\mathbf{H}}}(s) \right] = 0$$
(5)

For any given axial depth of cut, a, and spindle speed Ω = 2π/Nτ, stability of regenerative vibrations is determined according to the Nyquist criterion applied to the characteristic equation.

Discretization methods such as Semi-Discretization Method (SDM) or Full-Discretization Method (FDM) are also used to study the stability of vibrations in machining. With these methods, the time-periodic characteristics of the directional coefficients [α(t)] can be maintained in the solution. By discretizing the continuous-time equation, we are able to approximate the distributed-parameter system in Eq. 1 by a lumped-parameter system described by its state transition matrix, Φ as follows:

$$\mathbf{u}_{k+1}=\mathbf{\Phi}\mathbf{u}_{k}; k=1,2,..$$
(6)

where uk is the state vector of the approximate lumped-parameter system. This lumped-parameter system is asymptotically stable if and only if all of the eigenvalues of the state-transition matrix Φ are inside the unit circle on the complex plane. The dimension and composition of the state vector and its corresponding transition matrix vary by the applied discretization method (e.g. SDM, FDM). Nonetheless, state transition matrix depends on cutting parameters (e.g. depth of cut and spindle speed) as well as the modal parameters at the TCP.

Because the directional coefficients [α(t)] are approximated by their average in ZOA, Hopf-bifurcation is the only type of stability loss that is predicted by this method. Using discretization methods however, both Hopf and period-doubling bifurcations of the system dynamics can be predicted.

Both of the discussed frequency domain (ZOA) and discrete-time domain (SDM, FDM) approaches for predicting chatter stability require the TCP FRF or the modal parameters extracted from them. The transfer function H(s), or equivalently the Frequency Response Function H(iω), is usually determined by impulse hammer tests at the TCP while the machine tool or the robot is idle. While the TCP FRF measured in idle conditions remain relatively unchanged under operational (machining) loads in machine tools, it varies significantly in robotic machining, leading to inaccurate predictions of chatter stability. New in-process FRF measurement methods are presented in the next section to enhance the accuracy of chatter predictions by incorporating the true in-process dynamics of the robot in stability analysis.

In-Process FRF Measurement

The robotic milling setup used in this work, shown in Fig. 1, is a KUKA KR90 R3100 robotic arm equipped by a Powertech 400 Hiteco milling spindle with HSK 63F holder interface. Figure 2 shows the FRF measured by impulse hammer tests in Cartesian coordinates at the robot’s TCP (tool-tip) in the posture shown in Fig. 1. Excitation force was applied by a Kistler instrumented hammer and the resulting accelerations were measured using PCB piezoelectric accelerometers. This method of measuring TCP FRF has been adopted from machine tools where the FRF measured by hammer tests remain relatively unchanged under operational loads. However, these FRF could lead to incorrect stability prediction since, unlike in machine tools, FRF of the robot vary significantly by operational conditions [29, 30]. Figure 3 shows an example of FRF variations by operational conditions (i.e. excitation force). The TCP FRF in this figure are measured using sinusoidal excitation forces with different force amplitudes applied by a shaker, which are then compared to the FRF measured by transient forces applied by an instrumented hammer [29]. Because the sinusoidal excitation forces excite the structural nonlinearities in the robot joints, the FRF peaks are systematically distorted by increasing the force amplitude. Considering such nonlinearities, it is expected that the robot FRF also change during the milling process where high amplitude periodic cutting forces replace the shaker forces.

Fig. 2
figure 2

Measured FRF of the KUKA robotic milling system using impulse hammer tests in idle condition

Full size image
Fig. 3
figure 3

Variation of FRF measured using impulse hammer test and sinusoidal excitation force with different amplitudes [29]

Full size image

Considering the FRF variation due to structural nonlinearities, feed motion or other unknown factors, we aim to predict the stability diagrams using the FRF that are measured during the milling operation, rather than in idle conditions. The milling forces are used as excitation forces and the corresponding vibrations are measured to determine the in-process FRF. Because chatter-free milling forces are periodic at the tooth-passing frequency (Fp(t) in Eq. 1), they only excite the tooth-passing frequency and a few of its harmonics. Therefore, the resolution of the FRF estimated by those forces would be limited to the first few harmonics of tooth-passing frequency. Two approaches are considered to increase the bandwidth and resolution of the estimated FRF: i) milling porous material, and ii) milling homogeneous materials with varying spindle speed. In milling of porous materials, the random distribution of the pores adds a strong random component to the periodic milling forces, extending the bandwidth and resolution of excitation. In the second approach, the periodic content of the milling force at the tooth passing frequency is used for excitation, but the spindle rotation frequency is gradually swept across the frequency range where the flexible modes are located. The implementation of these two approaches are presented in the following sections. In the conducted experiments, cutting forces and the resulting vibrations in feed, normal and axial directions were measured using a table dynamometer beneath the workpiece and accelerometers located at the non-rotating part of the spindle, respectively, as shown in Fig. 1. The data acquisition was carried out using CompactDAQ NI-9234 modules and the sampling rate was set to 10240 Hz.

Milling of Porous Material

The porous material used in this work is an Aluminum foam workpiece shown in Fig. 4. The random distribution of pores with random sizes enriches the frequency spectra of the periodic machining forces by superimposing a strong random content on them. The frequency spectra of cutting forces in milling of Aluminum foam and a homogeneous material (Acetal Copolymer) in similar conditions are shown in Fig. 4. Although the periodic content of the two signals have similar amplitudes, the average level of cutting forces at non-harmonic frequencies is considerably increased in the case of Aluminum foam.

Fig. 4
figure 4

Left: Aluminum foam sample with density 0.36 g/cm3. The middle channel shows the surface after machining. Right: PSD of cutting forces in Aluminum foam milling (820 rev/min -0.1 mm/tooth -2 mm depth of cut) compared to Acetal milling (800 rev/min - 0.15 mm/tooth - 2 mm depth of cut)

Full size image

Full immersion (φst = 0, φex = π) milling was performed on the Aluminum foam with an endmill that had a diameter of 12.7 mm and two cutting teeth (with γ = π/2). Axial cutting depth was a = 2 mm and the feed motion was at the rate of 0.1 mm/tooth in X direction. The spindle speed was kept constant at 820 rev/min. This spindle speed was selected to prevent aligning the spindle rotation frequency (13.7 Hz) and its harmonics with the flexible modes of the robot. Note, since the flexible modes are below 30 Hz, a higher spindle speed could also be used to bypass all the flexible modes. However, 820 rev/min was selected to measure data for a longer time (considering the feedrate) while the change in robot’s posture throughout the cut is minimum. The measured cutting forces are shown in Fig. 5-a to -c. The Power Spectral Density (PSD) of the forces are shown in Fig. 4.

Fig. 5
figure 5

(a)-(c): Measured cutting forces in full-immersion milling of Aluminum foam, in feed, normal and axial directions, respectively. (d)-(e) The correlation between cutting forces in foam and Acetal milling tests, respectively

Full size image

The FRF matrix between the inputs \(\mathbf {F}=\left [ F_{x}\,\,F_{y}\,\,F_{z} \right ]^{T}\) and outputs \(\mathbf {X}=\left [ x\,\,y\,\,z \right ]^{T}\) of the MIMO system is calculated as follows [39]:

$${\mathbf{H}}(\omega) = {{\mathbf{S}}_{{\mathbf{XF}}}}(\omega){\mathbf{S}}_{{\mathbf{FF}}}^{- 1}(\omega)$$
(7)

where

$$\begin{gathered} {\mathbf{H}}(\omega) = \left[ {\begin{array}{*{20}{c}} {{H_{xx}}(\omega)}&{{H_{xy}}(\omega)}&{{H_{xz}}(\omega)} \\ {{H_{yx}}(\omega)}&{{H_{yy}}(\omega)}&{{H_{yz}}(\omega)} \\ {{H_{zx}}(\omega)}&{{H_{zy}}(\omega)}&{{H_{zz}}(\omega)} \end{array}} \right], {{\mathbf{S}}_{\mathbf{XF}}}(\omega) = \left[ {\begin{array}{*{20}{c}} {{S_{x,F_{x}}}(\omega)}&{{S_{x,F_{y}}}(\omega)}&{{S_{x,F_{z}}}(\omega)} \\ {{S_{y,F_{x}}}(\omega)}&{{S_{y,F_{y}}}(\omega)}&{{S_{y,F_{z}}}(\omega)} \\ {{S_{z,F_{x}}}(\omega)}&{{S_{z,F_{y}}}(\omega)}&{{S_{z,F_{z}}}(\omega)} \end{array}} \right] \hfill \\ {{\mathbf{S}}_{{\mathbf{FF}}}}(\omega) = \left[ {\begin{array}{*{20}{c}} {{S_{F_{x},F_{x}}}(\omega)}&{{S_{F_{x},F_{y}}}(\omega)}&{{S_{F_{x},F_{z}}}(\omega)} \\ {{S_{F_{y},F_{x}}}(\omega)}&{{S_{F_{y},F_{y}}}(\omega)}&{{S_{F_{y},F_{z}}}(\omega)} \\ {{S_{F_{z},F_{x}}}(\omega)}&{{S_{F_{z},F_{y}}}(\omega)}&{{S_{F_{z},F_{z}}}(\omega)} \end{array}} \right] \hfill \\ \end{gathered}$$
(8)

Hp,q(ω) is the frequency response function between the output p and the input q, and Sp,q(ω) is the cross PSD between signals p and q. The PSD, Sp,q(ω), was estimated by Welch’s method and Hamming window with 50% overlap for averaging. In order to estimate the FRF matrix from Eq.7, the input signals (excitation forces) must be linearly independent to avoid singularity of the inputs matrix SFF. This condition is confirmed by calculating the coherence between the cutting forces. The coherence function between two forces Fm and Fn is calculated as follows [39]:

$${C_{F_{m},F_{n}}}(\omega) = \frac{{{{\left| {{S_{F_{m},F_{n}}}(\omega)} \right|}^{2}}}}{{{S_{F_{m},F_{m}}}(\omega){S_{F_{n},F_{n}}}(\omega)}}, m,n=x,y,z$$
(9)

The coherence between foam milling forces are shown in Fig. 5-d, which indicate that the forces are largely uncorrelated and therefore suitable for identification in Eq. 7. In Fig. 5, for comparison, the coherence between milling forces in homogeneous material (Acetal) are also shown in part (e). Homogeneous material milling forces are linearly dependent at tooth passing frequency and its harmonics. Even at other frequencies, the lateral forces have higher correlation compared to the forces in foam milling. According to the coherence plots in Figs. 5-e and 4, foam milling provides less correlated forces with higher amplitude random content. The force and acceleration signals measured during milling Aluminum foam were used in Eq. 7 to estimate the in-process FRF shown in Fig. 6. The dashed lines show the identified FRF and the solid lines are the FRF fitted by modal analysis. The zoom window shows the most flexible modes in feed (X) and normal (Y ) directions. It will be shown in “Stability Lobe Diagrams with In-Process FRF” that these modes become unstable during machining and cause chatter; therefore, we are mainly interested in the accurate estimation of the FRF in the vicinity of these modes.

Fig. 6
figure 6

Calculated FRF in Cartesian coordinates using the signals obtained from milling of Aluminum foam

Full size image

As shown in Fig. 6, the frequencies of the most flexible modes of the robot are below 30 Hz. Variance of the estimated FRF in this range is studied using the multiple coherence function between the output p and the inputs F defined as follows [40]:

$${C_{{p},{\mathbf{F}}}}(\omega) = \frac{{\mathbf{S}_{{p,\mathbf{F}}}^{H}(\omega)\mathbf{S}_{{\mathbf{FF}}}^{- 1}(\omega){\mathbf{S}_{p,{\mathbf{F}}}}(\omega)}}{{{S_{{p}{p}}}(\omega)}}, p=x,y,z$$
(10)

where

$${\mathbf{S}_{p,{\mathbf{F}}}}(\omega) = {\left[ {\begin{array}{*{20}{c}} {{S_{p,F_{x}}}}&{{S_{p,F_{y}}}}&{{S_{p,F_{z}}}} \end{array}} \right]^{T}}$$
(11)

The superscript H stands for Hermitian transpose. The calculated multiple coherence function, between the x, y and z vibrations and the input forces, are shown in Fig. 7. The coherence function is close to unity in the vicinity of the flexible modes, confirming the acceptable variance of the estimated FRF in this range. Because the axial machining forces are usually significantly smaller than the lateral forces, the measured signals in z direction have a lower Signal to Noise Ratio and consequently the coherence in that direction is lower than in lateral directions.

Fig. 7
figure 7

Multiple coherence functions corresponding to the FRF measured in foam milling test

Full size image

Speed-Sweep Milling of Homogeneous Materials

In the previous section, the in-process FRF were estimated during milling porous materials. Using this approach, all of the flexible modes of the system can be identified with a single test. However, since the excitation energy is distributed over a wide range of frequencies, variance of the estimated FRF close to the less flexible modes may be poor. Spindle speed sweep tests proposed in this section enable concentrating the excitation energy in the frequency range of interest to improve the estimation variance in the vicinity of the specific mode(s) that are more prone to chatter. In this approach, the periodic component of the cutting forces (Fp(t) in Eq. 1) is used for excitation by sweeping the tooth-passing frequency across the frequency range of interest, i.e. where the flexible mode(s) of the system are located. To remove the correlation between the periodic milling forces in various directions, multiple (minimum three) cutting tests with different radial engagement conditions are conducted to form a full-rank matrix of inputs in Eq. 7. In this approach, the MIMO FRF are estimated using the same equation as Eq. 7, except that the SFX and SFF are defined as follows:

$$\begin{array}{l} {{\textbf{S}}_{{\textbf{XF}}}} = \left[ {\begin{array}{*{20}{c}} {{{\textbf{S}}_{{\textbf{XF}},1}}}&{{{\textbf{S}}_{{\textbf{XF}},2}}}&{{{\textbf{S}}_{{\textbf{XF}},3}}} \end{array}} \right],\\ {{\textbf{S}}_{{\textbf{FF}}}} = \left[ {\begin{array}{*{20}{c}} {{{\textbf{S}}_{{\textbf{FF}},1}}}&{{{\textbf{S}}_{{\textbf{FF}},2}}}&{{{\textbf{S}}_{{\textbf{FF}},3}}} \end{array}} \right] \end{array}$$
(12)

where the digits in the subscript denote the index of the conducted test. We used three different milling modes (i.e. radial engagements) that generate cutting forces with a different phase and/or amplitude in each test. The three milling tests were 1) central-milling (φst = 0.38π, φex = 0.61π), 2) down-milling (φst = 0.77π, φex = π) and 3) up-milling (φst = 0, φex = 0.23π). The axial cutting depth was 2 mm in all of the tests. The workpiece was Acetal Copolymer. The spindle speed in each test swept from 450 rev/min to 690 rev/min over nearly 60 seconds, which corresponds to the tooth passing frequency increasing from 15 to 23 Hz. This is the range in which the flexible chatter-prone modes of the system are located, as will be shown in “Stability Lobe Diagrams with In-Process FRF”. Figure 8 shows the spectrogram (using short-time Fourier transform) of the cutting forces in test 2, i.e. the down-milling test. As expected, most of the excitation energy is concentrated between 15 and 23 Hz and its harmonics. The high energy at the spindle rotation frequencies is due to runout. The measured cutting forces in the three milling modes are shown in Fig. 9. The PSD of the cutting forces are also shown in the same figure. It can be seen that excitation power is uniformly distributed across the frequency range of interest.

Fig. 8
figure 8

Spectrogram of the cutting forces in down-milling (test 2) speed-sweep test

Full size image
Fig. 9
figure 9

Measured cutting forces and their power spectral densities in speed sweep tests

Full size image

The coherence functions between the cutting forces are shown in Fig. 10, which indicates that the forces in each test are totally correlated, as expected for milling of a homogeneous material. However, since three different milling modes are used, the matrix of inputs SFF in Eq. 12 has three significant (non-zero) singular values, therefore it is full-rank and the FRF of the MIMO system can be estimated. The in-process FRF estimated in speed-sweep tests are presented in Fig. 11. As shown in this figure, the modes in the target range are well-identified. The results of two series of speed sweep tests with the same cutting parameters are presented in Fig. 11 to confirm the repeatability of FRF estimations. Note that the multiple coherence function as defined in Eq. 10 cannot be used for the speed sweep tests, because signals from different tests are being used.

Fig. 10
figure 10

Coherence of measured cutting forces in speed sweep tests, and the singular values of the the matrix of input forces SFF

Full size image
Fig. 11
figure 11

Measured in-process FRF using speed sweep tests. Solid lines: first series, Dashed lines: second series

Full size image

Calibration of TCP FRF

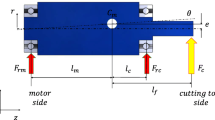
The FRF estimated in the previous sections were based on input forces at the tool-tip (TCP) and the vibrations response at the spindle housing. However, the transfer function H(s) in Eq. 5 maps the forces at the tool-tip to the vibration response at the tool-tip as well. Considering that the flexible modes of the robot are mainly associated with the flexibility of the robot’s joints, it can be assumed that the vibration of the spindle-holder-tool assembly at these modes is a rigid-body motion. With this assumption, we can multiply the resulting in-process FRF by a constant coefficient to calibrate them to represent the TCP FRF. Figure 12-a illustrates the rigid body motion of the assembly. It is assumed that the joints of the robot have small rotational displacements. Due to the joints’ displacement, the rigid body motion of the assembly includes translational and rotational displacements. As a result, the absolute displacements at the tool-tip and sensor locations are different. With reference to Fig. 12, the calibration coefficient for the FRF in the vicinity of each mode is determined as follows:

  1. 1.

    The two FRF HST and HTT are measured by applying hammer impulse at the tool-tip (point T) and measuring the response at the sensor’s location (point S) and tool-tip, respectively (Fig. 12-a).

  2. 2.

    Modal fitting is applied to the measured FRF, HST and HTT, to find the corresponding mode shape between points S and T (Fig. 12-c):

    $${H_{pq}} (\omega ) = \frac{{{\phi_{p}}{\phi_{q}}}}{{{\omega_{n}^{2}} - {\omega^{2}} + i2\xi \omega {\omega_{n}}}}\,\,{\text{for}}\,\,p,q = S,T$$
    (13)
  3. 3.

    The FRF HST is calibrated by the mode shape ratio such that the calibrated HST matches HTT, and as a result, the total displacement of the two points is equal (Fig. 12-d):

    $${H_{TT}}(\omega ) \simeq H_{ST}^{calibrated}(\omega ) = \frac{{{\phi_{T}}}}{{{\phi_{S}}}}{H_{ST}}(\omega )$$
    (14)

The same coefficient, \(\frac {\phi _{T}}{\phi _{S}}\), is used to calibrate the in-process FRF obtained in the previous sections. The calibrated in-process FRF are used in frequency and discrete-time chatter analysis methods to develop the robot’s stability lobe diagrams in the next section.

Fig. 12
figure 12

Calibration of identified in-process FRF. (a) illustration of the rigid body motion of the spindle-holder-tool assembly due to rotational displacements at the joints, (b) measured and calibrated FRF, (c) mode-shape before calibration and (d) after calibration

Full size image

Stability Lobe Diagrams with In-Process FRF

Acetal Copolymer workpiece was milled with an end mill that has a diameter of 12.7 mm and two cutting teeth with γ = π/2. The cutting force coefficients were determined experimentally as Ktc = 119 MPa and krc = 0.17 and kac = 0.33 [37]. Stability of vibrations during machining is determined by monitoring the cutting forces and the spindle vibrations. Both types of Hopf and period-doubling bifurcations are checked in each test. Hopf bifurcation was identified according to the Fast Fourier Transformation (FFT) of the cutting forces and spindle vibrations, and period-doubling was identified according to the time-history of the measured signals.

At each tested spindle speed, the cutting depth was increased incrementally until a dominating peak that is not a harmonic of spindle rotation frequency was observed in the signals’ FFT. This cutting depth was then determined as the border of Hopf bifurcation at the tested spindle speed. An example of Hopf bifurcation detection is shown in Fig. 13. The measured force and vibration signals in feed direction and their frequency spectra at axial cutting depths of 1.5 and 2 mm are shown in Fig. 13. The displacement was obtained by numerically integrating the measured accelerations. At 1.5 mm depth, the FFT plots show peaks at the harmonics of spindle and tooth passing frequencies, i.e. ft/2 and ft, respectively. However, at 2 mm depth, the amplitude of force and vibration signals grow and the FFT plots (especially the FFT of vibrations) show a dominant peak at the chatter frequency fc ≈ 18 Hz. This point is identified as chatter emanating from Hopf bifurcation. Stable and unstable cuts were primarily distinguished by their corresponding vibration and force signals measured by accelerometers and the dynamometer, respectively. Nonetheless, the machined surface was also inspected visually for further confirmation of vibration stability/instability. Figure 14 shows examples of the surfaces machined under stable and unstable conditions. Cases (a) and (b) correspond to stable conditions as only feed marks are observed on the surface. When the system is unstable, the feed marks are distorted by unstable vibrations as shown in cases (c) and (d).

Fig. 13
figure 13

Detection of Hopf bifurcations using measured force and vibrations signals (in feed direction). Half-immersion down-milling at spindle speed of 900 rev/min and feedrate of 0.15 mm/tooth

Full size image
Fig. 14
figure 14

Cutting surfaces of Acetal Copolymer workpiece. (a) stable, 800 rev/min, 1.5 mm. (b) stable, 1200 rev/min, 2 mm. (c) unstable, 800 rev/min, 2 mm. (d) unstable, 900 rev/min, 2.5 mm

Full size image

For period doubling bifurcations, the time history of displacement is observed. Figure 15 shows samples of chatter as a result of period doubling bifurcation compared to Hopf bifurcation. The orange dots are the same signal sampled at tooth passing frequency. At 1100 rev/min spindle speed, the system is stable at 0.5 mm depth, but at 2.5 mm depth, the sampled signals forms two parallel branches indicating period doubling [41]. Note that the two branches are expected to be straight in the time history of the signals. However, the branches are not straight during the cut. This could be due to i) small variations in spindle speed during operation, and ii) small variations in natural frequency as the robot’s posture changes during the cut. Periodic oscillations emanating from period-doubling bifurcation were observed until 4 mm depth of cut, at which point they loose stability. On the contrary, at 1200 rev/min the system goes through Hopf bifurcation without observing any period doubling bifurcations.

Fig. 15
figure 15

Displacements at the spindle speeds 1100 rev/min and 1200 rev/min. Orange dots represents sampled signals at the tooth passing frequency

Full size image

Similar chatter tests are conducted at several speeds and axial depth of cut values and the summary of results is shown in Fig. 16. The circles and crosses stand for stable and chatter due to Hopf bifurcation, respectively. The square signs show chatter due to period doubling bifurcation. In Fig. 16, the stability diagrams calculated based on Nyquist criteria using idle (hammer test) FRF and in-process FRF are also shown. The experimental results agree with SLD obtained from in-process FRF but there are considerable discrepancies between them and the SLD developed by hammer test FRF. The rightmost lobe in the SLD associated with hammer FRF show the Hopf bifurcation limit of the mode at 20 Hz, which is lightly damped in the hammer test FRF but heavily damped in the in-process FRF. The experimental results clearly show that this mode is indeed stable during the process and it does not cause chatter. The force and acceleration signals (in normal direction) measured under 1600 and 2000 rev/min are presented in Figs. 17 and 18, respectively. The SLD with idle FRF suggests that, at these spindle speeds, the system is unstable at cutting depth of 3 mm. However, the measured signals indicate that chatter occurs at a higher cutting depth. The FFTs of vibration signals at 1600 and 2000 rev/min are also presented in Fig. 19. Chatter and tooth passing frequencies are shown as fc and ft, respectively. In both cases, it can be seen that the chatter frequencies are between 17.5-18 Hz which correspond to the mode in normal direction (Y ). There is no peak in the vicinity of 20 Hz, confirming that this mode is mostly damped and does not cause chatter.

Fig. 16
figure 16

Stability diagram of half-immersion down-milling of Acetal workpiece using a tool with 12.7 mm diameter and two teeth. The abbreviation SS stands for speed sweep tests

Full size image
Fig. 17
figure 17

Measured cutting force and acceleration in normal direction at spindle speed of 1600 rev/min

Full size image
Fig. 18
figure 18

Measured cutting force and acceleration in normal direction at spindle speed of 2000 rev/min

Full size image
Fig. 19
figure 19

FFT of vibrations signal in chatter tests at 1600 and 2000 rev/min

Full size image

As shown in Fig. 16, period doubling bifurcations are not predicted by the ZOA method and Nyquist criterion, because the average values of directional coefficients are used. Semi-discretization Method (SDM) considers the periodicity of the directional coefficients and therefore is able to predict period-doubling bifurcation, however SDM requires modal fitting of the measured FRF. Considering non-proportional damping in the system, the modal decomposition of the FRF is expressed as follows [42]:

$$H_{pq}(\omega)=\sum\limits_{r=1}^{n}\left( \frac{{\Psi}_{p r}^{\mathrm{R}} {\Psi }_{q r}^{\mathrm{L}}}{i \omega-\lambda_{r}}+\frac{\bar{{\Psi }}_{p r}^{\mathrm{R}} \bar{{\Psi }}_{q r}^{\mathrm{L}}}{i \omega-\bar{\lambda}_{r}}\right) , \lambda_{r}=-\omega_{\mathrm{n}, r} \zeta_{r} \pm i \omega_{\mathrm{n}, r} \sqrt{1-{\zeta_{r}^{2}}}$$
(15)

where ωn is the natural frequency, ζr is the damping ratio, ΨR is the normalized right eigenvector, and ΨL is the normalized left eigenvector and n is the number of modes. The procedure in [21] was followed to identify these modal parameters from in-process FRF. The fitting procedure was applied to the FRF measured in speed sweep tests. Two flexible modes were assumed to be present in the frequency range of interest. The identified parameters of these mode are presented in Table 1. Figure 20 shows the fitted FRF, calculated using the identified modal parameters in Table 1, and compares them against the measured FRF.

Table 1 Identified modal parameters of the system flexible modes
Full size table
Fig. 20
figure 20

Amplitude of fitted and measured FRF in the speed sweep tests (FRF are calibrated to represent the dynamics at the tool tip)

Full size image

The modal parameters shown in Table 1 are used in SDM method [8, 21] to predict the SLD shown by the dotted line in Fig. 16. Except for around 1100 rev/min, the SLD agrees with the ones obtained from ZOA and Nyquist method with in-process FRF. The notch close to 1100 rev/min in the SLD from SDM is the period-doubling bifurcations limit, which is not predicted by the ZOA method. Consistent with the SLD from SDM, period doubling was observed around 1100 rev/min in the experiments, although the experimental results suggest a wider region of period doubling bifurcation.

Overall, compared to idle FRF, the stability diagrams associated with the in-process FRF agree better with the experimental results. The discrepancies between the experimental results and the SLD are mainly because of the different cutting speed and depth values that were used in FRF estimation and chatter tests. The FRF were measured under fixed spindle speed and cutting depth, but those values are different at each one of the tested points shown in Fig. 16.

Conclusions

Two new methods were presented for in-process measurement of TCP FRF in machining robots. The presented methods leverage the machining forces as the input to the system and estimate the FRF from the forces and vibrations measured during the process. The application of porous materials to randomize the machining forces and spindle speed sweep technique are shown to be effective in achieving broadband and uncorrelated excitation. The measured in-process FRF yield more accurate predictions of chatter-free machining parameters than the FRF measured by impulse hammer test when the robot is idle.

When a table dynamometer was used to measure the input (machining) forces, this method can only measure the FRF in the posture that positions the TCP at the dynamometer. Nonetheless, if the machining robot is equipped with a wrist force sensors or a rotary dynamometer, the presented method can be applied in arbitrary postures as well.