Position-dependent FRF identification without force measurement in milling process

Abstract

Frequency response functions (FRFs) are one of the most useful methods for representing machine tool dynamics under force excitation. FRFs are usually obtained empirically through output measurements, and force excitations are controlled by an external device such as hammers or shakers. This study offers an operational identification method that utilizes the calculation of force applied during the process as an input for FRF identification. Force excitation is provided through the face milling of a thin-walled workpiece, and acceleration measurements are taken during the process. The FRF is calculated at a designated position by sampling workpiece-cutting tool contacts as individual tap tests and substituting a force calculation as input. Force coefficients need to be known for the force calculation. An experimental force coefficient identification method is proposed. In that case, a similar thin-walled workpiece at a point with known FRF and acceleration measurements is utilized. Results are confirmed with FRFs obtained in the same location for both FRF identification and force coefficient identification approaches.

1 Introduction

Frequency response function (FRF) is one of the most common methods for explaining the behavior of the machine tool structure under force excitation.

For most applications in milling, FRF is obtained empirically by measuring the vibrations under excitation. Utilization of excitation devices, signal types, and methods have great variety in the literature. The most common method of FRF identification is the utilization of external excitation devices such as hammers and shakers [1, 2]. These devices can provide different types of excitations, such as impulse excitation, harmonic excitation, and harmonic sweep excitation [1]. Methods involving hammers and shakers are highly automated processes and are widely used. Such methods are excellent for precise excitation applications. However, the dynamics of the machine tool structure are known to change during operation, and external force implementation can be challenging during operation. Bediz et al. [3] developed an impulse excitation device that is tailored for micro-milling cutting tools. Furthermore, their excitation character can be insufficient [4]. An alternative approach is to rely on internal excitation methods, i.e., the force is created during the process. Internal excitation applications have the potential to more accurately identify the changing machine tool dynamic behavior during operation. However, controlling the desired excitation input is more challenging since the milling force depends on both the system and process parameters.

Basic internal methods aim to obtain impact-like excitations. Li et al. [5] utilized the inertia of the machine itself for excitation to identify the structure of the machine tool in the range below 500 Hz, where the main structural mode frequencies are located. The main purpose of the work is to show differences in the dynamics of the worktable at different speeds and locations. The method provides mode frequencies and damping ratios. The author also lists the modal parameters that shift during operation. Li et al. [6] has developed another inertia-based application. In this application, multiple axes are moved simultaneously to obtain more accurate results. The results show no significant nonlinearity [6]. Inertia-based methods are suitable for the identification of structural dynamics, but since the force is not applied at the workpiece, they are not able to identify the tooltip FRF directly.

One common approach for internal excitation is to utilize milling forces. However, the frequency content of the milling forces in conventional operation contains only the harmonics of the spindle speed and tooth passing frequency. This is not suitable for identification since a candidate mode may not be excited in between the two consecutive harmonics. Thus, milling force excitation methods aim to create white noise with desired stochastic and frequency domain characteristics by manipulating process parameters, such as variable feed rates and spindle speeds. Furthermore, special workpieces such as channels or single walls are designed. Özşahin et al. [7] used a workpiece with random channels and cut this workpiece with a feed direction perpendicular to the wall to achieve random excitation. The excitation method is confirmed by the coherence function. Dynamometer measurements are taken as input, and a laser vibrometer is used on the cutting tool. Wang et al. [8] also used a constructed workpiece with a channel-like profile. However, the author used only modal shapes, and for heavy machines, an approach with randomized channels. Li et al. [4] used a single workpiece to identify machine tools. This method assumes an impulse model for the excitation depending on angular velocity, feed rate, and wall thickness. They also provided some simplified calculations to estimate the frequency range where the excitation is effective [4]. The method aims to achieve white noise for the application of OMA methods. To obtain an even better random signal for operational modal analysis (OMA), Cai et al. [9] designed a workpiece with a randomized shape. Berthold et al. [10] applied the same principle without a specially designed workpiece and have shown that the same white noise requirement can be obtained without a special workpiece. Berthold et al. [11] compared EMA and OMA methods, questioning the position dependence and time invariance of the system and identifies regions (position of spindle and table) with constant FRF on the machine tool, while the above-mentioned randomized milling force excitation methods do not require a force measurement. However, they generally identify a relatively low-frequency (0–500 Hz) region, which is related to machine tool feed axis dynamics.

Besides the randomized approach, deterministic milling forces can be utilized as internal excitation inputs. Iglesias et al. [12] used a simple spindle speed sweeping method to excite the desired frequency range for identification. Force and acceleration measurements were performed. This method provides excellent control over the excitation frequency and is very intuitive to use. A major drawback of this method is that the excitation of higher frequencies can be limited by the spindle speed, and the excitation amplitude can be a limiting factor. Unlike the output only methods, calculated milling forces can be used for FRF identification. Cai et al. [13] eliminated force measurement and utilized calculated milling forces. A conventional static chip thickness based milling force model is utilized, and a constant single wall is face milled with varying feed and spindle angular speeds. In this way, a similar white noise excitation is created. However, this method requires the previously known force coefficients. Pawelko et al. [14] approached the same problem from the other side and used FRF measurements for force coefficients identification and have listed several error factors. The method used is based on the representation of the force model in the frequency domain, and the dynamics of the workpiece are assumed to be rigid. Observer-based cutting force estimation is an alternative approach. Aggarwal et al. [15] used the spindle motor measurements (current) along with the spindle structure inefficiencies to calculate the tangential force coefficients. Zhou et al. [16] used the Kalman filter and the results of tap tests to calculate the force. The Kalman filter works to eliminate interference and bandwidth problems. Yamato et al. [17] also used motor current along with encoder values and applied feed drive system modeling to obtain a force estimate.

Literature also involves approaches that rely on dynamic chip regeneration and chatter limit for identification [18]. These methods rely on identification of chatter stability limit and chatter frequencies experimentally. Since chatter stability limit and chatter frequency are functions of the point FRF, a mathematical expression can be obtained to identify tool point FRFs. Quintana et al. [19] propose an experimental method of calculating the chatter stability limit by gradually increasing axial depth by utilizing a sloped workpiece. Grossi et al. [20] utilized a speed–ramp cutting process with constant feed per tooth and utilized chatter stability for FRF identification.

This study proposes a complete FRF identification method with internal excitation. The milling forces are not measured but calculated based on a mechanistic force model. Therefore, accurate force coefficients are required for accurate FRF identification. The proposed methodology can be classified as (i) force coefficient identification with a known point FRF and (ii) FRF identification at different positions with the calculated milling force. The major contribution of the study for force coefficient identification is the two-part recursive least squares method, where acceleration measurement of each individual tool workpiece engagement of a single-wall workpiece is utilized. In both force coefficient identification and FRF identification steps, each individual tool–workpiece engagement is sampled and processed as a single tap test result. Since the input milling force is calculated, its time axis has to be synchronized with the measurement time of the acceleration. The synchronization of a single engagement is much easier and less sensitive to errors than the synchronization of multiple engagements as used in literature. Furthermore, the effect of synchronization errors increases with increasing identification frequency. Therefore, a single engagement allows FRF identification up to a higher frequency range. The given method is verified on a CNC milling machine, and it is shown that the varying FRF of the fixture-workpiece at different positions can be monitored. The study starts with the mathematical model of the milling process in Section 2. In Section 3, identification steps are explained, and both force coefficient identification and FRF identification methods are detailed. In Section 4, the proposed methods are verified through experimental tap tests. In Section 5, the conclusion is given with the strengths of the method and improvement areas.

2 Milling process dynamics

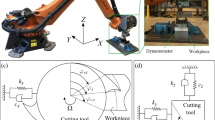
The milling dynamics model utilized in this study is explained with Fig. 1. As shown in Fig. 1, structural flexibility of the cutting tool attached to the spindle, (functions G_{2, yy}(s), G_{2, yx}(s), G_{2, xx}(s), G_{2, xy}(s)) and the workpiece attached to the table of machine tool (functions G_{1, xx}(s), G_{1, xy}(s), G_{1, yy}(s), G_{1, yx}(s)) can be represented by transfer functions in X and Y directions. Due to this flexibility, milling force causes deflection at both the cutting tool and the workpiece. The thickness of the chip removed changes as a result of this deflection, and it is defined as “dynamic chip thickness.” This phenomenon is depicted in the figure with the planned ideal and the real path the cutting tool takes on the workpiece. Since milling force is based on the thickness of the chip removed and deflections change the thickness, there is a feedback mechanism between the amount of chip removal and the milling force applied. This section intends to explain the model of milling process dynamics and the theoretical basis of the identification methods. For the milling operation shown in Fig. 1, tangential and radial milling forces can be expressed as Eqs. 1 and 2 [21].

$${F}_r(t)=\left[{K}_{\textrm{rc}}h(t)+{K}_{\textrm{re}}\right]{a}_pg(t)$$

(1)

$${F}_t(t)=\left[{K}_{\textrm{tc}}h(t)+{K}_{\textrm{te}}\right]{a}_pg(t)$$

(2)

Fig. 1

Milling dynamics and chip regeneration

where K_tc (N/mm²) is the tangential milling force coefficient, K_rc (N/mm²) is the radial milling force coefficient, K_te (N/mm) is the tangential edge force coefficient, and K_re (N/mm) is the radial edge force coefficient. a_p (mm) is axial depth of cut, h(t) (mm) is the instantaneous total chip thickness, and g(t) is the window function which defines whether the teeth in the cutting region or outside of it and it can be defined as shown in Eq. 3.

$$g(t)=\left\{\begin{array}{cc}1,& {\theta}_{\textrm{ex}}\ge \text{mod}\left(\theta (t),2\pi \right)\ge {\uptheta}_{\textrm{st}}\\ {}0,& \textrm{otherwise}\end{array}\right.$$

(3)

Instantaneous total chip thickness can also be expressed as Eq. 4.

$$h(t)=\underset{h_0}{\underbrace{c\sin \theta (t)}}+\underset{h_d(t)}{\underbrace{\left[x(t)-x\left(t-\tau \right)\right]\sin \theta (t)+\left[y(t)-y\left(t-\tau \right)\right]\cos \theta (t)}}$$

(4)

where c (mm/rev) is the feed, τ (s) is the time delay between consecutive cutting tool–workpiece contact, θ(t) is immersion angle of the insert, x(t) and y(t) are the current vibrations in X and Y directions, x(t − τ) and y(t − τ) are the vibrations of the system one delay before. Equation 4 can be separated into two parts for analyzing the effect of the milling force applied. The first term h₀ represents the static chip thickness and the rest of the equation, and h_d(t) represents the dynamic chip thickness.

The axial depth and angular speed of cutting tool are kept constant, and the helix angle is omitted. The cutting tool is selected according to this assumption.

The radial and tangential forces can be transformed to X-Y coordinates as follows:

$$\boldsymbol{F}(t)=\left[\begin{array}{c}{F}_x(t)\\ {}{F}_y(t)\end{array}\right]={\boldsymbol{F}}_{\boldsymbol{d}}(t)+{\boldsymbol{F}}_{\boldsymbol{s}}(t)$$

(5)

$${\boldsymbol{F}}_{\boldsymbol{d}}\left(\boldsymbol{t}\right)={a}_p{K}_{tc}\boldsymbol{A}(t)\left[\boldsymbol{x}(t)-\boldsymbol{x}\left(t-\tau \right)\right]$$

(6)

$${\boldsymbol{F}}_{\boldsymbol{s}}\left(\boldsymbol{t}\right)={a}_p{K}_{tc}c{\boldsymbol{A}}_{\boldsymbol{p}}(t)+{a}_p{K}_{te}{\boldsymbol{A}}_{\boldsymbol{p},\textbf{2}}(t)$$

(7)

where F(t) is the total milling force which consist of dynamic and static forces, F_d(t) and F_s(t), respectively. x(t) = [x(t) y(t)]^T = x₁(t) + x₂(t) is the displacement vector in X-Y directions and is formed by the workpiece and cutting tool displacements x₁(t) and x₂(t), respectively.

A _p(t) and A_p,2(t) are the transformation matrices which can be expressed as Eq. 8, 9, 10, 11, 12, 13, and 14.

$$\boldsymbol{A}(t)=\frac{1}{2}\left[\begin{array}{cc}{a}_{xx}(t)& {a}_{xy}(t)\\ {}{a}_{yx}(t)& {a}_{yy}(t)\end{array}\right]\qquad {\boldsymbol{A}}_{\boldsymbol{p}}(t)=\frac{1}{2}\left[\begin{array}{c}{a}_{xx}(t)\\ {}{a}_{yx}(t)\end{array}\right]\qquad {\boldsymbol{A}}_{\boldsymbol{p},\textbf{2}}(t)=\left[\begin{array}{c}{a}_{xx,2}(t)\\ {}{a}_{yx,2}(t)\end{array}\right]$$

(8)

$${a}_{xx}(t)=-g(t)\left[\left(\sin 2\theta (t)\right)+\frac{K_{\textrm{rc}}}{K_{tc}}\left(1-\cos 2\theta (t)\right)\right]$$

(9)

$${a}_{xx,2}(t)=-g(t)\left[\left(\cos \theta (t)\right)+\frac{K_{\textrm{re}}}{K_{\textrm{te}}}\left(\sin \theta (t)\right)\right]$$

(10)

$${a}_{xy}(t)=-g(t)\left[\left(1+\cos 2\theta (t)\right)+\frac{K_{\textrm{rc}}}{K_{\textrm{tc}}}\sin 2\theta (t)\right]$$

(11)

$${a}_{yx}(t)=g(t)\left[\left(1-\cos 2\theta (t)\right)-\frac{K_{\textrm{rc}}}{K_{\textrm{tc}}}\sin 2\theta (t)\right]$$

(12)

$${a}_{yx,2}(t)=g(t)\left[\left(\sin \theta (t)\right)-\frac{K_{\textrm{re}}}{K_{\textrm{te}}}\cos \theta (t)\right]$$

(13)

$${a}_{yy}(t)=g(t)\left[\left(\sin 2\theta (t)\right)-\frac{K_{\textrm{rc}}}{K_{\textrm{tc}}}\left(1+\cos 2\theta (t)\right)\right]$$

(14)

Based on the transformation, the static milling force can be expressed in terms of axial depth a_p, geometry matrix L(t), and milling force coefficients K as follows:

$${\boldsymbol{F}}_{\boldsymbol{s}}(t)=-{a}_p\underset{L(t)}{\underbrace{g(t)\left[\begin{array}{cccc}c\cos \left(\theta (t)\right)\sin \left(\theta (t)\right)& c{\sin}^2\left(\theta (t)\right)& \cos \left(\theta (t)\right)& \sin \left(\theta (t)\right)\\ {}-c{\sin}^2\left(\theta (t)\right)& c\cos \left(\theta (t)\right)\sin \left(\theta (t)\right)& -\sin \left(\theta (t)\right)& \cos \left(\theta (t)\right)\end{array}\right]}}\left[\begin{array}{c}{K}_{\textrm{tc}}\\ {}{K}_{\textrm{rc}}\\ {}{K}_{\textrm{te}}\\ {}{K}_{\textrm{re}}\end{array}\right]$$

(15)

Block diagram representation of system model is shown in Fig. 2, where G(s) is the transfer function including the workpiece and cutting tool dynamics.

Fig. 2

Milling dynamics, representation of chip regeneration in block diagram

Based on the transfer functions given in Fig. 1 and the block diagram given in Fig. 2, displacement vector x(s), which represents the workpiece x₁(s) and tool x₂(s) vibrations in X and Y directions can be written as follows:

$$\boldsymbol{x}(s)=\boldsymbol{G}(s)\cdot \boldsymbol{F}(s)$$

(16)

where

$$\boldsymbol{x}={\underset{{\boldsymbol{x}}_{\textbf{1}}}{\underbrace{\left[\begin{array}{cc}{x}_{1x}& {x}_{1y}\end{array}\right]}}}^{\boldsymbol{T}}+{\underset{{\boldsymbol{x}}_{\textbf{2}}}{\underbrace{\left[\begin{array}{cc}{x}_{2x}& {x}_{2y}\end{array}\right]}}}^{\boldsymbol{T}}$$

(17)

$$\boldsymbol{G}(s)=\left[\begin{array}{cc}{G}_{1, xx}& {G}_{1, xy}\\ {}{G}_{1, yx}& {G}_{1, yy}\end{array}\right]+\left[\begin{array}{cc}{G}_{2, xx}& {G}_{2, xy}\\ {}{G}_{2, yx}& {G}_{2, yy}\end{array}\right]={\boldsymbol{G}}_{\textbf{1}}(s)+{\boldsymbol{G}}_{\textbf{2}}(s)$$

(18)

Merging Eqs. 16 and 18 for machine tool dynamics and Eq. 8 for force calculation including dynamic chip thickness, Eq. 19 can be obtained as below:

$${\boldsymbol{x}}_{\textbf{1}}(s)={\boldsymbol{F}}_{\boldsymbol{s}}(s)\frac{{\boldsymbol{G}}_{\textbf{1}}(s)}{1+\left(1-{e}^{- s\tau}\right)\boldsymbol{G}(s){a}_p{K}_{tc}\boldsymbol{A}(s)}$$

(19)

In Eq. 19, the static force term, F_s(s) can be calculated by using Eq. 15 with the known static chip thickness, known force coefficients, and tool workpiece engagement conditions. Furthermore, the workpiece displacement x₁(s) can be known by the acceleration measurement. In addition to the workpiece-fixture assembly transfer function G₁(s), the displacement, x₁(s), also depends on the tool assembly transfer function, G₂(s), which is represented in G(s). The coupling of the workpiece and tool displacements is due to the previous vibration marks left on the surface during the previous engagement, which are modeled with the time delay τ[s]. During stable cutting, steady state vibrations occur at the harmonics of spindle speed frequency. The vibrations occurring at two consecutive cutting tool–workpiece engagements are the same, and the effect of time delay τ(s) is negligible, as shown in Eq. 20.

$$\boldsymbol{x}(s)\left(1-{e}^{- s\tau}\right)\approx 0$$

(20)

Therefore, neglecting the dynamic chip thickness, the static chip thickness-based force calculation can accurately represent applied force in given conditions of this article.

$$\frac{{\boldsymbol{x}}_{\textbf{1}}(s)}{{\boldsymbol{F}}_{\boldsymbol{s}}(s)}\approx {\boldsymbol{G}}_{\textbf{1}}(s)=\left[\begin{array}{cc}{G}_{1, xx}(s)& {G}_{1, xy}(s)\\ {}{G}_{1, yx}(s)& {G}_{1, yy}(s)\end{array}\right]$$

(21)

Non-diagonal cross-terms (G_{1, xy}, G_{1, yx}) can be neglected since they are relatively small compared to diagonal elements. This is verified through the tap test results shown in Section 4. This means Eq. 21 is simplified to Eq. 22 in frequency domain, and this equation allows identifications in later sections. However, due to practical considerations, direct application of Eq. 22 is not possible, and that is where identification procedures come in in the next section.

$${\boldsymbol{x}}_{\textbf{1}}(s)=\left[\begin{array}{c}{x}_1(s)\\ {}{y}_1(s)\end{array}\right]\approx \cdot \left[\begin{array}{cc}{G}_{1, xx}(s)& 0\\ {}0& {G}_{1, yy}(s)\end{array}\right]{\boldsymbol{F}}_{\boldsymbol{s}}(s)$$

(22)

3 Identification procedure

The steps for identification are summarized in Fig. 3. In the force coefficients identification step, point FRF and acceleration measurements obtained during a particular single wall milling process are taken as inputs. Point FRF and process parameters are used to calculate acceleration by using the milling force model that is introduced in the previous section. A two-part recursive least squares method is used to identify the force coefficients by utilizing both the measured and calculated accelerations. In the FRF identification step, force coefficients, acceleration measurements from another particular milling process, and process parameters are taken as inputs. By using force coefficients, process parameters, and the milling force model, milling force is calculated, and FFT of both acceleration measurement and force calculation are used for FRF identification. Note that if the force coefficients are known, the FRF identification can be processed without the first step.

Fig. 3

Identification approach summarized for force coefficients and FRF of machine tool

The outline of this section is as follows: Section 3.1 provides the application of milling force model for identification methods. Section 3.2 explains the force coefficients identification method. Section 3.3 explains FRF identification.

3.1 Excitation using milling forces

3.1.1 Workpiece and process parameter design

During a conventional milling process with high angular engagement, milling forces excite the machine tool structure at the tooth passing frequency and its several higher harmonics. Therefore, especially for slot milling operations, frequency content of the milling forces is limited and not well suited for structural identification. However, this limitation can be overcome by decreasing the radial depth of cut. By doing that, due to low angular engagement, force excitation takes very short time and the force is impulse-like. Thus, frequency content of the excitation force increases. This enables the identification at a higher frequency range. For that purpose, a single walled workpiece, as shown in Fig. 4 can be machined.

Fig. 4

Static chip thickness model of workpiece gives a single wall aligned with X axis, and the wall is cut through X direction. Picture of cutting tool is provided

The force spectrum of a single walled workpiece is illustrated in Fig. 5. Here, the continuous curves (envelopes) represent the FRF of a force pulse occurring due to a single engagement, and discrete vertical lines (harmonics) represent the FRF of force pulses due to multiple engagements formed during a particular interval. Note that, the distance between vertical lines corresponds to the spindle frequency. The envelope of the excitation consists of diminishing lobes at certain zero-touching frequencies. The width of the first lobe where the envelope of excitation reaches zero magnitude, is defined as follows:

$${f}_{zc}=\frac{1}{\Delta T}={\left(\frac{\theta_2-{\theta}_1}{\frac{n_S}{60}\cdot 2\pi}\right)}^{-1}\cong {\left(\frac{L}{\frac{n_S}{60}\cdot \pi \cdot D}\right)}^{-1}$$

(23)

Fig. 5

Effects of angular speed and wall thickness on milling force spectrum, tool diameter 65 [mm], axial depth of cut: 2.9 [mm], K_tc = 1319 (N/mm²), K_rc = 788 (N/mm²)

Here, for small engagement angles, distance cutting edge travels during the cut can be assumed to be the wall thickness L

Equation 23 and Fig. 5 demonstrate that frequency range of the first lobe, i.e.. the width of the first lobe can be increased by decreasing the engagement duration, ∆T. This is possible by either increasing angular speed or decreasing the wall thickness, but both actions reduce amplitude of excitation. For example, at the zero frequency, force calculation with 4 (mm) wall cut has twice the force amplitude of force calculation with 2 (mm) wall cut. However, the frequency range of the first lobe where the amplitude vanishes is also almost halved. Likewise, increasing angular speed of the cutting tool from 3000 to 6000 rpm has the same effect. Note that for this study, only a particular portion of the first lobe with high enough amplitude is to be utilized as very low force excitations result in low signal-to-noise ratio.

3.1.2 Synchronization problem

If multiple tool–workpiece engagements are utilized instead of a single engagement, the frequency content of the excitation force is dominated by the spindle harmonics, which creates two major issues. The first issue is candidate mode may not be excited in between the two consecutive harmonics. The second issue is that any application of an identification procedure without considering harmonics can result in an incoherent outcome due to divisions by small numbers. Both of these issues are handled with analyzing tool–workpiece engagements as individual excitations. A single engagement that is sampled from measured acceleration data and force calculation together can be considered as an equivalent tap test.

The synchronization of the calculated force and measured acceleration is necessary since their time axes are different. Synchronization is done by defining an acceleration threshold. A threshold value is defined, which should be higher than the background noise and smaller than the measured acceleration values. A trial-and-error approach is utilized such that the known point FRF is identified back. As a result, the threshold is determined as (10 m/s²). Figure 6 illustrates an example engagement. The calculated force (blue) is synchronized with the measured acceleration (orange) at the threshold value shown by the black vertical line. Note that for the accurate identification, the acceleration should be damped out in the prescribed interval in between the two consecutive engagements. The corresponding frequency domain representation is obtained by FFT and shown in Fig. 7. Single engagement provides the excitation at all frequencies rather than excitation at spindle harmonics only.

Fig. 6

An engagement sampled

Fig. 7

An engagement sampled in frequency domain

3.2 Force coefficient identification utilizing two part least squares

In the literature, force coefficients are available for the workpiece material used in this study. However, force coefficients are known to change based on process parameters (angular speed, feed rate, and depth of cut) as well as wear and cutting-edge geometry [21]. Therefore, in order to obtain accurate force calculations, first, the coefficients are identified, with particular process parameters, then by keeping those parameters constant and close to the identification parameters (i.e., spindle speed and feed rate) the FRF is identified accurately with the calculated forces.

For the identification of cutting force coefficients, expensive measurement equipment’s (dynamometers) are required. However, the proposed identification method can be applied for the fast and reliable identification of cutting force coefficients without the requirement of complicated equipment.

3.2.1 Displacement response in frequency domain

The displacement response in frequency domain can be expressed in terms of unknown milling force coefficients, by inserting the milling force equation (15) into the milling dynamics equation (22) and then applying Fourier transform, as follows:

$$\textbf{x}{\left(\boldsymbol{\upomega} \right)}_{2\textrm{n}\times 1}\cong \textbf{H}{\left(\boldsymbol{\upomega} \right)}_{2\textrm{n}\times 4}\textbf{K}$$

(24)

Here, ω is the frequency array defined for the range of interest [ω₁, ω_n], x is the displacement in X and Y axes, and K is the milling force coefficients defined as follows:

$${\boldsymbol{\omega}}_{n\times 1}={\left[{\omega}_1,{\omega}_2,,\dots, {\omega}_i,\dots {\omega}_n\right]}^T$$

(25)

$$\boldsymbol{x}\left({\omega}_i\right)=\left|\begin{array}{c}x\left({\omega}_i\right)\\ {}y\left({\omega}_i\right)\end{array}\right|$$

(26)

$$\textbf{K}=\left[\begin{array}{c}{K}_{tc}\\ {}{K}_{rc}\\ {}{K}_{te}\\ {}{K}_{re}\end{array}\right]$$

(27)

The matrix H(ω)_2n × 4 which can be named as the regression matrix in least square problem consist of the FRF of the X and Y axes and the Fourier transform of the geometry matrix L(t) defined in Eq. 15.

$$\boldsymbol{H}{\left({\omega}_i\right)}_{\textbf{2}\times 4}=\left[\begin{array}{cc}{G}_{xx}\left({\omega}_i\right)& 0\\ {}0& {G}_{yy}\left({\omega}_i\right)\end{array}\right]{a}_p\underset{\boldsymbol{L}\left({\boldsymbol{\omega}}_{\boldsymbol{i}}\right)}{\underbrace{\left[\begin{array}{cccc}c{L}_{tc,x}\left({\omega}_i\right)& c{L}_{rc,x}\left({\omega}_i\right)& {L}_{te,x}\left({\omega}_i\right)& {L}_{re,x}\left({\omega}_i\right)\\ {}c{L}_{tc,y}\left({\omega}_i\right)& c{L}_{rc,y}\left({\omega}_i\right)& {L}_{te,y}\left({\omega}_i\right)& {L}_{re,y}\left({\omega}_i\right)\end{array}\right]}}$$

(28)

3.2.2 Identification algorithm

The unknown coefficients K can be derived from Eq. 24 by using least squares optimization. However, for small radial engagements, the regression matrix H(ω) becomes ill conditioned. This can be illustrated for θ(t) = 90° case. Considering small angle difference between the entry and exit tool work piece engagement, so that sinθ ≈ 0 and cosθ ≈ 1,and updating the terms of the geometry matrix L(t) in Eq. 15, the resulting regression matrix H(ω) reduces to two dependent columns as follows.

$$\textbf{H}\left(\boldsymbol{\upomega} \right)=\left[\begin{array}{cccc}{\textbf{0}}_{n\times 1}& c{L}_{rc,x}\left(\boldsymbol{\omega} \right){G}_{xx}\left(\boldsymbol{\omega} \right)& {\textbf{0}}_{n\times 1}& {L}_{rc,x}\left(\boldsymbol{\omega} \right){G}_{xx}\left(\boldsymbol{\omega} \right)\\ {}c{L}_{tc,y}\left(\boldsymbol{\omega} \right){G}_{yy}\left(\boldsymbol{\omega} \right)& {\textbf{0}}_{n\times 1}& {L}_{tc,y}\left(\boldsymbol{\omega} \right){G}_{yy}\left(\boldsymbol{\omega} \right)& {\textbf{0}}_{n\times 1}\end{array}\right]$$

(29)

In order to handle the rank deficiency problem, it is proposed to solve the coefficients in two parts. First, two intermediate milling force coefficients (K_{A, k} and K_{B, k}) are defined for a particular feed per tooth c_k

$${K}_{A,k}={c}_k{K}_{rc}+{K}_{re}$$

$${K}_{B,k}={c}_k\ {K}_{tc}+{K}_{te}$$

(30)

In the first part the intermediate coefficients are solved with the reduced regression matrix as follows:

$${\left[\begin{array}{c}x\left(\boldsymbol{\omega} \right)\\ {}y\left(\boldsymbol{\omega} \right)\end{array}\right]}_{2n\times 1,\textrm{k}}\cong {a}_p{\left[\begin{array}{cc}{L}_{rc,x}\left(\boldsymbol{\omega} \right){G}_{xx}\left(\boldsymbol{\omega} \right)& {\textbf{0}}_{n\times 1}\\ {}{\textbf{0}}_{n\times 1}& {L}_{tc,y}\left(\boldsymbol{\omega} \right){G}_{yy}\left(\boldsymbol{\omega} \right)\end{array}\right]}_{2n\times 2,\textrm{k}}{\left[\begin{array}{c}{K}_A\\ {}{K}_B\end{array}\right]}_k$$

(31)

where index k ∈ {1⋯m} represents the tests with m different feed per tooth. After obtaining m-many intermediate coefficients sets, the milling force coefficients can be obtained by least square optimization of Eq. 30 in the second part.

Figure 8 illustrates a set of cutting tests for coefficient identification. Here, m-many tests with different feed per tooth values c_k are utilized, and each test includes at least n-many tool-workpiece engagements. For each feed per tooth k ∈ {1⋯m}, the intermediate coefficients are identified recursively at each cutting tool–workpiece engagement j ∈ {1⋯n}. After obtaining m sets of intermediate coefficients, the milling force coefficients are obtained by the least square problem.

Fig. 8

Illustration of a set of cutting tests for force coefficients identification

The basic framework of the method is explained as follows:

Part-1:

For each j_th engagement sample:

• A. Isolate each individual cutting tool–workpiece engagement by windowing the measured acceleration into particular number of time frames, ${\ddot{x}}_j(t)$ and ${\ddot{y}}_j(t)$. Here, the subscript j is used to count the tool and the workpiece engagements

• B. Shift the time array such that time t_th corresponds to the acceleration threshold ${\ddot{x}}_j\left({t}_{\textrm{th}}\right)=\textrm{threshold}$. Here, threshold time t_th is selected to be 5% of the time interval Δt of the engagement.

• C. Apply zero padding. Since the time interval is small, it has to be increased to obtain the same frequency resolution with the point FRF. In this study the engagements are extended to 1 s, corresponding to 1-Hz frequency resolution

• D. Obtain the FFT of the measured acceleration in X and Y directions, dividing by −ω² form the displacement vectors: x_j(ω)_n × 1 and y_j(ω)_n × 1.

• E. Construct the time array of the window function g(t), synchronizing the time array such that the threshold time t_th, corresponds to when the tool engages with the workpiece.

• F. Form the geometry matrix L(t) in Eq. X and take the FFT to obtain the individual components of L(ω)

• G. Apply the least square problem to Eq. 31. Including both real and imaginary components as follows:

$${\left|\begin{array}{c}\operatorname{Re}\left[{x}_j\left(\omega \right)\right]\\ {}\operatorname{Im}\left[{x}_j\left(\omega \right)\right]\\ {}\operatorname{Re}\left[{y}_j\left(\omega \right)\right]\\ {}\operatorname{Im}\left[{y}_j\left(\omega \right)\right]\end{array}\right|}_{4n\times 1,\textrm{j}}\cong {a}_p{\left[\begin{array}{cc}\operatorname{Re}\left[{L}_{rc,x}\left(\omega \right){G}_{xx}\left(\omega \right)\right]& {\textbf{0}}_{n\times 1}\\ {}\operatorname{Im}\left[{L}_{rc,x}\left(\omega \right){G}_{xx}\left(\omega \right)\right]& {\textbf{0}}_{n\times 1}\\ {}{\textbf{0}}_{n\times 1}& \operatorname{Re}\left[{L}_{tc,y}\left(\omega \right){G}_{yy}\left(\boldsymbol{\omega} \right)\right]\\ {}{\textbf{0}}_{n\times 1}& \operatorname{Im}\left[{L}_{tc,y}\left(\omega \right){G}_{yy}\left(\omega \right)\right]\end{array}\right]}_{4n\times 2,\textrm{j}}{\left[\begin{array}{c}{K}_A\\ {}{K}_B\end{array}\right]}_j$$

(32)

The below recursive least square algorithm is solved at each j_th engagement

$${\textbf{P}}_{\textrm{j}}={\left({\textbf{H}}^{\textrm{T}}\textbf{H}\right)}^{-\textbf{1}}$$

$${\left[\begin{array}{c}{K}_A\\ {}{K}_B\end{array}\right]}_j={\textbf{P}}_{\textrm{j}}{\left[\textbf{H}\right]}^{\textrm{T}}\left[\ \begin{array}{cc}\operatorname{Re}\left[{x}_j\left(\omega \right)\right]& {\textbf{0}}_{n\times 1}\\ {}\operatorname{Im}\left[{x}_j\left(\omega \right)\right]& {\textbf{0}}_{n\times 1}\\ {}{\textbf{0}}_{n\times 1}& \mathit{\operatorname{Re}}\left[{y}_j\left(\omega \right)\right]\\ {}{\textbf{0}}_{n\times 1}& \mathit{\operatorname{Im}}\left[{y}_j\left(\omega \right)\right]\end{array}\right]$$

$${\textbf{P}}_{\textrm{j}+1}={\left({\textbf{P}}_{\textrm{j}}^{-\textbf{1}}+{\left[\textbf{H}\right]}^{\textrm{T}}\textbf{H}\right)}^{-\textbf{1}}$$

$${\textbf{J}}_{\textrm{j}+1}={\textbf{P}}_{\textrm{j}+1}\left[\textbf{H}\right]$$

$${\left[\begin{array}{c}{K}_A\\ {}{K}_B\end{array}\right]}_{j+1}={\left[\begin{array}{c}{K}_A\\ {}{K}_B\end{array}\right]}_j+{\textbf{J}}_{\textrm{j}+1}\left(\left[\ \begin{array}{cc}\mathit{\operatorname{Re}}\left[{x}_j\left(\omega \right)\right]& {\textbf{0}}_{n\times 1}\\ {}\mathit{\operatorname{Im}}\left[{x}_j\left(\omega \right)\right]& {\textbf{0}}_{n\times 1}\\ {}{\textbf{0}}_{n\times 1}& \mathit{\operatorname{Re}}\left[{y}_j\left(\omega \right)\right]\\ {}{\textbf{0}}_{n\times 1}& \mathit{\operatorname{Im}}\left[{y}_j\left(\omega \right)\right]\end{array}\right]-\textbf{H}{\left[\begin{array}{c}{K}_A\\ {}{K}_B\end{array}\right]}_j\right)$$

(33)

Here, P_j is the covariance matrix (alternatively called information matrix) at i_th engagement. In this application, matrix size is 2 × 2. H_4n × 2 is the regressor matrice (alternatively called basis matrice) which comes from the set of linear equations at Eq. 28. J_i + 1 is referred as Kalman gain because recursive least squares method works in a similar principle as Kalman filter.

The last engagement where j = n, is the intermediate coefficient output ${{\left[\begin{array}{cc}{K}_A& {K}_B\end{array}\ \right]}^T}_k$ of the k_th cutting test with the particular feed per tooth c_k value.

Part 2: for all engagements

After repeating part 1 for each k ∈ {1⋯m} and obtaining m-many intermediate coefficients for each feed per tooth, equation (30) can be re-defined as Eq. 34:

$$\left[\begin{array}{c}{K}_{\textrm{tc}}\\ {}{K}_{\textrm{te}}\end{array}\right]=\underset{{\textbf{H}}_1}{\underbrace{\left[\begin{array}{cc}{c}_1& 1\\ {}\vdots & \vdots \\ {}{c}_m & 1\end{array}\right]}}\left[\begin{array}{c}{K}_{B,1}\\ {}\vdots \\ {}{K}_{B,m}\end{array} \right]$$

$$\left[\begin{array}{c}{K}_{rc}\\ {}{K}_{re}\end{array}\right]={\textbf{H}}_1\left[\begin{array}{c}{K}_{A,1}\\ {}\vdots \\ {}{K}_{A,m}\end{array}\right]$$

(34)

Least square optimization to solve for force coefficients can be solved as below:

$$\left[\begin{array}{c}{K}_{tc}\\ {}{K}_{te}\end{array}\right]={\left({\textbf{H}}_{\textbf{1}}^{\mathrm{T}}\cdot {\textbf{H}}_{\textbf{1}}\right)}^{-\textbf{1}}\cdot {\textbf{H}}_{\textbf{1}}^{\mathrm{T}}{\boldsymbol{K}}_{\boldsymbol{B}}$$

(35)

$$\left[\begin{array}{c}{K}_{rc}\\ {}{K}_{re}\end{array}\right]={\left({\textbf{H}}_{\textbf{1}}^{\mathrm{T}}\cdot {\textbf{H}}_{\textbf{1}}\right)}^{-\textbf{1}}\cdot {\textbf{H}}_{\textbf{1}}^{\mathrm{T}}{\boldsymbol{K}}_{\boldsymbol{A}}$$

(36)

3.3 Identification of workpiece-fixture dynamics

Likewise, the force coefficient identification tests, a single wall is utilized for FRF identification. By knowing the milling force coefficients and the process parameters, it is possible to calculate the milling forces. The FRF identification utilizes the individual tool workpiece engagement and the corresponding force calculation. In this way, an equivalent tap test condition is formed for each engagement. At a desired identification position, N-many individual tool workpiece engagements are selected, and power spectral density is used for FRF identification.

The FRF identification steps for each individual engagement are explained as follows:

• A. Apply the steps A-B-C-D-E of the coefficient identification section. Note that the time range of the zero padding is not a must and does not depend on the known point FRF, but is selected according to the desired resolution of the identified FRF.

• B. Based on cutting parameters and the synchronized window function g(t_th), utilize Eq. 15 to calculate the milling force.

• C. Obtain the FFT of the sampled accelerations and the calculated force. Convert acceleration response into displacement.

• D. Obtain the spectral density function S₋₋(ω) of the calculated force and the cancellation

$${S}_{qq,j}\left(\omega \right)={q}_j\left(\omega \right)\cdot {q}_j{\left(\omega \right)}^{\ast }$$

(37)

$${S}_{qF,j}\left(\omega \right)={q}_j\left(\omega \right)\cdot {F}_{q,i}{\left(\omega \right)}^{\ast }$$

(38)

$${S}_{Fq,j}\left(\omega \right)={F}_{q,j}\left(\omega \right)\cdot {q}_j{\left(\omega \right)}^{\ast }$$

(39)

$${S}_{FF,j}\left(\omega \right)={F}_{q,j}\left(\omega \right)\cdot {F}_{q,j}{\left(\omega \right)}^{\ast }$$

(40)

Here, j is the index of the engagement, and q is either x or y displacement.

FRF can be calculated by utilizing the average of N-many spectral density functions as follows:

$$G\left(\omega \right)=\frac{S_{qq}\left(\omega \right)}{S_{qF}\left(\omega \right)}\equiv \frac{S_{Fq}\left(\omega \right)}{S_{FF}\left(\omega \right)}$$

(41)

The quality of estimation is assessed by the coherence function as follows:

$$C\left(\omega \right)=\frac{\mid {S}_{qF}\left(\omega \right)\mid }{\sqrt{S_{qq}\left(\omega \right){S}_{FF}\left(\omega \right)}}$$

(42)

4 Experimental verification

A Deckel FP5CC, 5-axis CNC milling machine that is in house retrofitted with Beckhoff controller and drive systems is utilized for the verification of the proposed method. In order to illustrate the proof of concept, a single walled block workpiece is milled and the FRF variation of the workpiece fixture which is mounted to the table from two points is identified. For the cutting tests, AL7075 aluminum alloy is used as the workpiece material. The cutting used tool is an EM90 63X6 022 EDPT 140408 (MBC cutting tools, Fig. 9) which is a square shoulder face milling tool with 63.3 (mm) diameter (with inserts) placed on it. It allows for 6 inserts but only one of them is used and neither the cutting tool nor the insert has a significant helix angle. The insert used is EDPX 140420-CKN20M (Rapid Maxtools) The insert has insignificant helix angle and 1 (mm) tool nose radius. As shown in Fig. 9, a two single walled workpiece are used, where the walls have rectangular profiles and the thickness of the walls are selected as 5 (mm) and 6 (mm). The height of walls is kept constant at 4 (mm).

Fig. 9

Accelerometer locations (1–3), tap test application positions (2–4), and tool given at top left side

Before the machining operations and identification, the workpiece–fixture dynamics are measured using tap testing. For the tap tests, a DYTRAN 5800B3T (10.30 mV/g) model impact hammer and a PCB 352C23 (5.12 mV/g) accelerometer at point 1 and a DYTRAN 3225F1 (10.23 mV/g) at point 3 are used. In Fig. 9, Points 1 and 3 represent the accelerometer measurement locations, and points 2 and 4 are the hammer impact excitation locations. Note that, since the accelerometer is mounted directly on the workpiece block, the identified FRF’s will reflect the flexibility of the fixture. Furthermore, since the aspect ratio of the single wall is small, the workpiece and fixture vibrations are assumed to be the same, and the identified FRF is named the workpiece–fixture FRF. For the given locations, measured point and cross FRFs are shown in Figs. 10 and 11 for the X and Y directions, respectively.

Fig. 10

Tap tests comparison XX(P₂P₁) vs. YX(P₄P₁) and the change of P₂P₁ along Y feed direction

Fig. 11

Tap tests comparison XY(P₂P₃) vs. YY(P₄P₃) and the change of P₄P₃ along the X feed direction

As seen in Fig. 10, cross FRF, P₄P₁, in-between the X-Y directions is significantly smaller than the FRF P₂P₁, in-between the X-X directions. However, in the Y direction, the diagonal FRF P₄P₃ is not always dominant, but comparable with the cross FRFs P₂P₃ at certain frequency intervals as shown in Fig. 11. Comparing both figures reveals P₂P₁ is the dominant FRF of the workpiece–fixture.

In order to illustrate the position dependency of the FRF, hammer impacts are applied at different locations without changing the accelerometer location. In Fig. 10, P₂P₁ at positions of Y = 140 (mm) and Y = 10 (mm) are different at the 1500–2000 (Hz) frequency range. This observation is used for verification of FRF identification (Section 4.2). Similarly, in Fig. 11, P₄P₃ at positions of X = 10 (mm) and X = 130 (mm) are tested. However, P₄P₃ can be observed to be independent of the movement of force excitation in X feed direction. Both P₂P₁ and P₄P₃ do not vary in the 500–1500 (Hz) frequency interval, which is to be used for coefficient identification.

4.1 Identification of cutting force coefficients

Force coefficients are identified along the X-axis. The AL7075 workpiece has a single wall of 6-mm thickness and 4-mm depth. The axial depth of cut is selected as 2.9 mm to prevent tool face contact. Three different tests with different feed per tooths are performed and the machining conditions for each test are given in Table 1. In each test, the tool center travels 32 (mm) and in order to eliminate the effect of transient vibrations, the engagements are selected after 20 mm travel of the tool center. The corresponding engagement positions are X = 20 (mm), 52 (mm), and 84 (mm). Only seven engagements are utilized for the recursive identification of the intermediate coefficients. Seven individual engagements correspond to 0.5–1 (mm) cut length. Finally, the width of the first spectral lobes is calculated with Eq. 23 as 1689 (Hz).

Table 1 Process and test parameters of force coefficient identification

As seen in Fig. 11, G_yy(ω) which is P₄P₃ do not vary along the X axis. On the other hand, G_xx(ω) which is P₂P₁, varies along the Y axis. However, the mode frequency between 500 and 1500 Hz remains constant. Therefore, the frequency range of 500 to 1500 (Hz) is selected as the reference point FRF of the identification algorithm and is applied for all three test positions. Note that the frequency content of the excitation force is above 1500 Hz.

Figure 12 gives the recursive calculation of the intermediate force coefficients (K_{A, j}, K_{B, j}) of each individual tool workpiece engagement, for j ∈ {1 : 7}. As seen from the figure, the coefficient estimations converge into a value after a few tool workpiece engagements. Table 2 represents the resulting identified K_A and K_B for the three tests. Those values correspond to the end values of Fig. 12 and increases with increasing feed per tooth values, as expected by its definition.

Fig. 12

Variations of force coefficients during recursive least squares

Table 2 Recursive least squares output

The performance of the method of force coefficient identification with the recursive least square is illustrated in Fig. 13. The real and imaginary values of the calculated acceleration that is expressed in Eq. 31 is compared with the FFT of the measured acceleration.

Fig. 13

Test 3, verification of intermediate force coefficients by comparing acceleration calculation to acceleration measurement. j indicates tool-workpiece engagements

Three tests with different chip thickness values offered 3 sets of K_A and K_B. Using Eqs. 35 and 36, force coefficients are identified and presented in the first row of the Table 3. The remaining rows represent the force coefficients taken from a milling force review study [21]. It is seen that the values found in this article are comparable to the results of the research studies.

Table 3 A set of force coefficients from [21]

4.2 Application of FRF identification method

A single-wall cutting test is performed in order to identify the position dependent FRF, G_xx(ω), along the Y- axis. As shown in Fig. 11, in the frequency range of 1500–3000 (Hz), the FRF P₂P₁ varies with the position. In order to increase the frequency content of the excitation force, the spindle speed is increased to 4800 (rpm) and the wall thickness is reduced to 5 mm. The corresponding width of the first lobe of the force spectrum is 3181 (Hz) which is above the desired identification range. The wall depth is the same as the previous part as 4 (mm) and the axial depth of cut is 2.9 (mm) preventing tool face contact. The feed rate is selected as 600 (mm/min) which corresponds to the compatible feed per tooths utilized in the previous part. The cutting test parameters are presented in Table 4

Table 4 Test parameters of FRF identification (D = 63.3 (mm), a_p = 2.9 (mm]), wall depth = 4 (mm))

The total cutting length is 148 (mm). The FRF is for 9 consecutive tool-workpiece engagements corresponding to around 1[mm] cutting length. In order to illustrate the FRF variations, the tool positions are selected at Y = 20 (mm), 52 (mm), and 84 (mm).

The acceleration responses corresponding to individual engagements are sampled and zero-padded to 1-s time interval in order to obtain 1 Hz frequency resolution. The force is calculated and synchronized with the acceleration measurement by utilizing the threshold time mentioned in Section 3.1.2.

Figure 14 shows the comparison of identified FRFs at three different positions with the corresponding measured tap tests P₂P₁ was given in Fig. 11. It can be seen that the identified FRFs fits the tap test results and capture the position dependent amplitude variation of the mode frequency at 1500–2000 (Hz). Figure 15 gives coherence values of identified FRFs. Coherence values are consistently higher than 0.8 for the given frequency range. This means that there is a strong linear relation between force calculation and acceleration measurement.

Fig. 14

FRF identification results of selected regions

Fig. 15

Coherence values of identified FRFs

In Fig. 14, at the frequency range of 0–500 (Hz), it can be seen that the method fails to obtain the point FRF reliably. This cannot be explained by coherence as the coherence at Fig. 15 is high. A part of this problem can be inferred from the sampling theorem that the minimum identification frequency is restricted by the time in between the two consecutive tool–workpiece engagements, i.e., the time between the acceleration responses. In this study, the time in between the two consecutive engagements is around 0.012 seconds, which corresponds to a minimum of 160 (Hz) minimum frequency value (twice the frequency). However, the frequency range of 160–500 (Hz) needs additional explanation.

5 Conclusion

In this study, a complete FRF identification method without force measurement is proposed to detect the position dependency of workpiece-fixture dynamics. The method is separated into two parts as (i) the force coefficients identification and (ii) FRF identification. For the force coefficient identification, acceleration measurements were taken during process of face milling the single walled workpiece. By using the mechanistic force model, the approach of sampling single engagements, and the two-part recursive least squares method, force coefficients of the particular workpiece material (AL7075) have been identified. For FRF identification, FRF was identified by measuring acceleration during the face milling process of another single walled workpiece made of the same material. Milling force excitation is calculated with process parameters and force coefficients. Overall, FRF was obtained thanks to the calculated force excitation, obtained acceleration measurements, and the approach of sampling single engagements.

The proposed method in this study has been confirmed to obtain FRF at different positions and in an analyzed frequency domain, accurately. Cutting parameters were selected for the system to be excited in the selected frequency domain. Force coefficient identification has been performed at a selected region of the workpiece with consistent FRF and accuracy of the identified force coefficients has been shown by comparison of acceleration results. It is shown that the proposed method can be applied both for the cutting force coefficient and FRF identification without and requirement of a complicated and expensive force measurement device. A major possible advantage is that the method offers in-process identification which allows to analyze FRF variation under operational conditions.

However, there are some limitations of the method that need to be mentioned. The force model utilized in this article is based on mechanistic milling force with constant force coefficients. Constant force coefficients are accurate at a certain range of process parameters because force coefficients are known to change based on process parameters. In addition, the mechanistic milling force model in this article does not include helix angle, runout, edge radius, and multiple tooth cutters. These factors can be included by updating the mechanistic milling force model. In order to make the application of the method offered in this study more convenient and reduce the computation burden, the threshold value that is used for synchronization of acceleration measurements with force calculation should be identified automatically, and this should be a future research topic. In terms of industrial applications, the study can be separated into two parts. Force coefficients identification has the most immediate potential as dynamometers are not present in most manufacturing plants, but chatter is a significant problem, and force coefficients are a factor in chatter. In addition, force coefficients are also a major determining factor for energy consumption. The FRF identification method in this study enables identification at process conditions. Moreover, the FRF identification method in this study can demonstrate the continuous change of FRF based on position even at machine tool setups where a similar feat would require impractical numbers of tap tests. Furthermore, the method offers control over the excitation power, frequency content, and position, which the available tap test equipment may not be able to offer. To sum up, possible application areas are local FRF identification of machine tool structure, prediction of excitation, and study of material force coefficients. Critical areas for future work include extending the milling force model for helix angle, runout, and automatization of threshold identification.