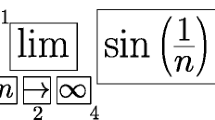A Pathway to a Student-Worded Definition of Limits at the Secondary-Tertiary Transition

Abstract

Over the last forty years of mathematics education research, a coherent body of knowledge has accumulated regarding the teaching of limits. On this basis, it remains a challenge to identify goals and design tasks compatible with ordinary teaching conditions. This paper reports on a teaching experiment carried out in France with year 12 students, which led to the formulation by the students of a correct formal definition of the infinite limit for sequences, with minimal background logical prerequisites and in the course of a 2-h session. On a more theoretical level, the teaching project was developed in the framework of didactic engineering, and provides opportunities to contribute to the ongoing work on its adaptation to the specific context of tertiary education. In the a priori analysis, we highlight the didactical potential of tasks of differentiation between neighboring concepts as a pathway to advanced mathematical concepts. In the a posteriori analysis, we focus on the nature and extent of teacher intervention in the shaping of a mathematical milieu that is conducive to the definition of an advanced mathematical concept.

Introduction

In their paper of 1996 On the understanding of the concept of limit, Cottrill and Dubinsky could already refer to a vast didactical literature highlighting the central role of this concept in advanced mathematical thinking, and documenting the wealth of difficulties students faced when confronted with the formal definition of limits. They noted rather pessimistically: “We have not, however, found any report of success in helping students to overcome these difficulties.” (Cottrill et al. 1996, p.174). Twenty years later, limits still play a central role in didactical research on the teaching and learning of advanced mathematical concepts, and the research literature on this topic has continued to be produced at an unabated pace. The general outlook, however, is brighter than reported in 1996. In particular, recent teaching experiments such as Roh and Lee’s (2017) proved reasonably successful in helping small groups of first year university students make sense of the formal definition of the notion of converging sequence given by the researchers; a success that was established by studying students’ ability to make sensible use of the formal definition in the context of a proof task.

The goal of this paper is twofold: on the one hand, it reports on the design and the implementation of a teaching session aiming for the formulation by students of a correct and formal definition of the notion of infinite limit for sequences, in ordinary teaching conditions in terms of group size (classes of 30 to 35 high school students) and teaching time (a 2-h session). On the other hand, this case-study gives us the opportunity to tackle two issues of general interest for the research on the teaching and learning of advanced mathematical concepts. In part 2, we will discuss the role of differentiation between neighboring concepts, both from an epistemological and a didactical perspective. In part 4, in addition to documenting the observed learning trajectories of the students in the four implementations, we will endeavor to analyze the multilayered role of the teacher in the session. To this end, we will use an adaptation of the framework developed by Cécile Ouvrier-Buffet for the design and analysis of Situations of Definition Construction (Ouvrier-Buffet 2006, 2011, 2013).

As far as instructional design is concerned, the session was designed within the theoretical framework of didactic engineering. We refer the reader to the paper of Artigue (1988) and Barquero and Bosch (2015) for general descriptions of this framework, and of its connections to both the theory of didactical situations (TDS) and the anthropological theory of the didactic (ATD). A recent survey emphasizing the challenges of the adaptation of this framework to tertiary education can be found in (González-Martín et al. 2014). As is standard in didactic engineering, the paper will report on it in two steps. In parts 2 and 3, we will present the preliminary analysis based on the research literature, then lay out the specifics of the session in a given teaching-context. On this occasion, we will highlight some key elements of the a priori analysis so as to justify our choices (such as: starting with infinite limits rather than with finite limits; using the question of the uniqueness of limits to trigger socio-cognitive conflict; using “not bounded above” as a stepping-stone for the target-definition), and to make explicit hypotheses as to their expected impact on the behavior of students in the teaching sessions. Part 4 will be devoted to the a posteriori analysis, whose main goal is to analyze the actual behavior of students in the experiment – which was carried out four times – and compare it to the hypothesized behavior. The essential feature of didactic engineering was underlined by Artigue:

Controlled realizations in classrooms should thus be given a prominent role in research methodologies for identifying, producing and re-producing didactic phenomena, for testing didactical construction. (Quoted in (Barquero and Bosch 2015, p.250))

To put it in a nutshell, the two-hour session was designed for students with an experience of limits involving numerical or graphical conjectures, and the use of a series of techniques (algebra of limits, limits of standard functions, squeeze theorem) that were given without proof. The session aims for two intertwined but distinct goals pertaining to the formal definition of the infinite limit: (1) make students realize that, in some contexts, their informal knowledge of limits is inadequate, and that these contexts require that a definition be established; (2) lead students to formulate a (correct) definition which they acknowledge to be correct. The classroom work alternates individual work of students (pairs of students, actually) and collective discussion under the guidance of the teacher. The two-hour session has three main phases: in phase 1, students are asked to sort a short list of sequences according to whether or not they tend to +∞; the collective discussion of the sorting is meant to trigger socio-cognitive conflict regarding the uniqueness of the limit; the main expected outcome of phase 1 is the acknowledgement of the need of a definition to settle the uniqueness issue. Students are then asked to write down tentative definitions for the infinite limit; we will call these candidate-definition. In phase 2, a sample of these candidate-definitions is collectively discussed, under the guidance of the teacher; the main expected outcome of phase 2 is not that the target-definition be formulated, but that standard misconceptions on limits be dispelled. In phase 3, the formal definition of “not bounded above” is used as a starting point, and students are encouraged to suggest a way to strengthen this condition in order to reach a condition which is both necessary and sufficient for a sequence to tend to +∞; in other words, a condition that is definitory of the target concept. On all four occasions, phase 3 led students to formulate a correct definition of the infinite limit. On three out of four occasions, the definitory condition suggested by the class was not the standard

$$ \forall M\in \mathbb{R}\kern0.5em \exists {n}_M\in \mathbb{N}\kern0.5em \forall n\in \mathbb{N}\kern0.5em n\ge {n}_M\Rightarrow {u}_n\ge \mathrm{A}, $$

but the unusual, yet logically equivalent

$$ \forall M\in \mathbb{R}\kern0.5em \exists {n}_M\in \mathbb{N}\kern0.5em \forall m\in \mathbb{N}\kern0.5em {u}_{n_M+m}\ge \mathrm{A}. $$

This case-study on limits will enable us to discuss two issues of general interest for research on Advanced Mathematical Thinking (AMT): As to the range of didactic strategies for the introduction of advanced mathematical concepts; and as to the form and level of teacher guidance in sessions which aim to introduce such concepts.

The specific challenges for the teaching of AMT concepts have long been analyzed from two main viewpoints. On the one hand, epistemological and didactical tools have been used to study the nature of the concepts and design adapted learning trajectories (Tall 1991). Along this line of investigation, we drew mainly on the work of Dorier, Robert and Rogalski on FUG concepts (Formalizing – Unifying – Generalizing concepts) (Dorier 1995; Robert 1998; Hache and Robert 2013) and their insertion in the “mathematical landscape” of students, even though we also took the genetic decomposition approach of Cottrill et al. (1996) into account. On the other hand, a more cognitive approach allows for the fine-grained analysis of the standard misconceptions about limits, and points to the dialectic between the (mathematical) definition of a concept, and the image of this concept students have constructed along their didactic trajectory. Of course, we are referring to the Tall and Vinner’s classic distinction between concept-image and concept-definition, a distinction which aims to capture the distance between mathematics as a mental activity and mathematics as a formal and deductive system:

We shall use the term concept image to describe the total cognitive structure that is associated with the concept, which includes all the mental pictures and associated properties and processes. (…) it needs not be coherent (…).” (Quoted in (Tall 1991, p.7))

In the design of this engineering we took both lines of investigation into account. First, from an epistemological viewpoint, it can be argued that some advanced mathematical concepts can also serve a purpose of conceptual clarification through conceptual differentiation; a purpose which calls for a task design which differs from the one adapted for concepts whose main purposes are formalization, unification, and generalization. For the fundamental concepts of mathematical analysis, a brief excursus into the history of mathematical analysis will help us back this claim. Second, from the cognitive viewpoint, explicit differentiation between neighboring concepts can lead to a re-organization of the loosely organized concept-image of students, and to the inclusion of the concept-definition as a part of the concept-image. More specifically, studies (see (Davis and Vinner 1986) and (Mamona-Downs 2001) for surveys) have consistently shown that students usually conflate three distinct mathematical properties of numerical sequences, namely:

• (1) Tending to positive infinity.

• (2) Not being bounded above.

• (3) Being strictly increasing (at least from a certain rank).

The main hypothesis underlying this engineering is that students can be entrusted the task of making explicit the differences between these three properties, and that this process of differentiation can lead to the formulation of a precise, formal definition of property (1). Hence, in this design, the misconceptions as to property (1) are not seen only as obstacles which the designer knows have to be overcome; they are also the explicit object of students’ work, and stepping-stones for the formulation of the target-definition.

This case-study on limits also provides an opportunity contribute to the ongoing work on the role of guidance – by a teacher, a lecturer, a manager-observer (Ouvrier-Buffet 2006) or a researcher – in experiments or engineerings designed in the framework of TDS or RME (Realistic Mathematics Education). As far as TDS is concerned, the survey paper of González-Martín et al. (2014, p.118) pointed out that for advanced mathematical concepts “the teacher can play a more active role” (than in primary or lower-secondary education). Although this paper provided no analysis of this aspect, one can be found in (Bloch and Gibel 2011). From the perspective of guided reinvention, in the analyses of Swinyard’s experiment (Swinyard 2011; Larsen and Swinyard 2012) the main research question also bore on students: “In the process of generating a precise definition of limit, what challenges do students experience, and how are such challenges resolved?” (Larsen and Swinyard 2012, p.466). Indeed, these detailed studies of how two pairs of 1^rst-year university students got to reason correctly about limits over a long period of time (10 sessions of 1 to 1 ½ hours) provided a wealth of information on which we drew. In the conclusion of the paper of 2011, the author acknowledged: “To be clear, Amy and Mike’s reinvention efforts were scaffolded in significant ways – as the researcher, I intervened on multiple occasions to guide them towards paths I felt might be productive.” (Swinyard 2011, p.112.) This scaffolding is described more explicitly in (Larsen and Swinyard 2012) and in (Martin et al. 2014).

In the second part of this paper, we endeavor to describe and analyze the learning trajectories of students on the one hand; the nature and role of teacher’s scaffolding on the other hand. The nature and extent of teacher intervention is of great theoretical significance, either in TDS or RME. TDS is a constructivist framework insofar as it relies on a theory of learning based on the tenet that new knowledge is gained when a new equilibrium is reached after a phase of destabilization of some previous knowledge (of lesser scope or depth). This destabilization is triggered when students engage in tasks for which their previous knowledge proves inadequate, inefficient, or inconsistent. New knowledge is to be constructed by students trough their interaction with a well-designed mathematical milieu and with peer-students. Ideally, the milieu sends enough feedback for students to gradually adjust to it and generate a consensual appropriate response, either in the form a new procedure (for situations of action), a new formulation (situations of formulation) or a rational argument (situation of validation). This central, ideal phase of the design is said to be adidactic insofar as it should take place without direct didactical intervention of the teacher (while pedagogical interventions – such as refocusing students on classroom work – remains part of the picture). Of course, the adidactic phase comes after a didactic phase of devolution – in which the task is entrusted to the students by the teacher – and is followed by a final didactic phase of institutionalization, in which the teacher is to alter the status (and, more often than not, the wording) of the response produced by the students in the adidactic phase and make it both public and decontextualized.

This approach proved fruitful for the teaching of mathematics at the primary and lower-secondary levels; its classic studies bear on fractions, decimals, or the enlargement of geometrical shapes. It’s adaptation to AMT, however, remains challenging. For a number of reasons, some pertaining to the nature of advanced mathematical concepts in general (Robert 1998; Artigue et al. 2007), some of which are specific to the limit concept and will be spelled out in the first part of the paper, we did not design a session with an adidactic core. Rather, we opted for a codidactic situation – also called situations with an adidactic dimension (Bloch and Gibel 2011; González-Martín et al. 2014), in which didactic teacher intervention is explicitly taken into account as an element which contributes to shaping the milieu. The level and nature of “scaffolding” and “guidance” is regarded as a didactic variable.

In the design, we endeavored to maintain what we considered to be the highest possible level of adidacticity, for two reasons, which reflect the dual nature of didactic engineering as both a protocol for instructional design - whose success is to be measured by what students manage to do/learn – and a research protocol – whose success is to be assessed through the empirical control of grounded hypotheses/forecasts regarding didactic phenomena. As far as instructional design is concerned, we are not willing to forsake the basic tenets of socio-constructivism as to how new knowledge is generated by rational agents. The basic principles are so general that they should be valid for kindergarten and university students alike. As far as testing research hypotheses is concerned, since our main hypothesis is that students can be entrusted with a task of conceptual differentiation between neighboring concepts, intrusive teacher intervention would blur the data and weaken the validation of this hypothesis. Even though the two perspectives concur to favor a high level of adidacticity, it should be noted that this can cause tensions among the various participants in the experiment. In particular, the goal of the researcher is to test hypotheses, which means that he/she must warrant that the conditions allow for falsification or verification alike. The teachers, however, need the two-hour session to lead to a definition of the infinite limit, and want to maintain a trusting relationship with the students; a relationship which depends on his/her support; a relationship which might be negatively affected should the students leave with the impression that the session was a failure.

For these reasons, the a posteriori analysis of the experiment will pay attention not only to the cognitive trajectory of the students – so as to compare it to the hypothesized trajectory – but also to the nature and level of teacher intervention. Teacher intervention can be studied from a variety of theoretical perspectives (Fischbein and Mariotti 1997; Stephan and Rasmussen 2002; Yackel 2002; Bartolini Bussi and Mariotti 2008; Bridoux 2016). Following Bloch and Gibel’s proposal for the study of codidactic situations (Bloch and Gibel 2011), we will pay a close attention to the evolution of the mathematical milieu, both it itself – as a growing set of examples / non-examples / counter-examples, diagrams, gestures, mathematical properties, and semiotic registers¹ – and in terms agency: ability to spot a counter-example, ability to generate a new diagram, ability to rephrase a property, etc. However, rather than using the formal scheme suggested by Bloch and Gibel, we will rely on the framework which Cécile Ouvrier-Buffet specifically developed for the design and analysis of Situations of Definition Construction (SDC).

Literature

Epistemological and Cognitive Aspects of the Limit Concept – Didactical Consequences

In the field of mathematics education, the teaching of limits has been one of the main focuses of attention for those working on advanced mathematical concepts. A whole chapter bore on this topic in the 1991 handbook on Advanced Mathematical Thinking (Tall 1991), and the topic was also a key example in the other chapters such as Vinner’s chapter on the role of definitions in teaching and learning of mathematics (Vinner 1991), and the chapter on research on teaching and learning of mathematics at an advanced level (Robert and Schwarzenberger 1991). Since then, publication has continued at an unabated pace. Since the work of Cornu (1991) and Robert (1983), research work has been carried out in many theoretical frameworks, some focusing on cognition (Pinto and Tall 2002) (Oerhtman 2009), some relying on genetic decomposition (Cottrill et al. 1996), and quite a few using the theory of didactic situations (Robert 83; Bloch and Gibel 2011). Except for a few papers, such as (Mamona-Downs 2001; Przenioslo 2005), most of them analyze empirical data collected in a great variety of contexts, ranging from the experimental – with very small groups of students working over a rather (or very) long period of time (Job 2011; Swinyard 2011; Martin et al. 2014) – to contexts closer to ordinary teaching conditions, either in the final years of secondary education (Bloch and Gibel 2011; Lecorre 2016) or in the first year of tertiary education (Robert 1983; Roh and Lee 2017). We feel that this collective endeavor on the part of the mathematics education community has yielded a rather coherent body of knowledge, at two levels. First, the analysis of misconceptions, errors, and obstacles has shed light on the range and the nature of the difficulties to be overcome. Second, since a wide range of tasks have been carefully designed and tried out, empirically grounded hypotheses can be made as to the likely impact of such and such teaching strategy.

In this paper, we will discuss several definitions of $\underset{n\to +\infty }{\lim }{u}_n=+\infty$. We will call “standard definition (implicative form)” the following:

$$ \forall M\in \mathbb{R}\exists {n}_M\in \mathbb{N}\forall n\in \mathbb{N}\kern0.5em n\ge {n}_M\Rightarrow {u}_n\ge M $$

The “standard definition (non implicative form²)”:

$$ \forall M\in \mathbb{R}\exists {n}_M\in \mathbb{N}\kern0.5em \forall n\in \left[{n}_M;+\infty \right]{u}_n\ge M $$

The “standard definition (additive form):

$$ \forall M\in \mathbb{R}\exists {n}_M\in \mathbb{N}\forall n\in \mathbb{N}\kern0.5em {u}_{n_M+n}\ge M $$

The “almost all definition” (adapted from (Roh and Lee 2017)):

∀M ∈ ℝ u_n ≥ M except for (at most) a finite number of terms.

The range of definitions can be extended by altering the formulation, in particular by substituting rhetorical formulations for formal ones.

Let us first discuss some of the epistemological aspects of the limit concept which have an empirically established cognitive impact on students’ access to this notion. We will restrict ourselves to the three aspects which will play a part in the design of the engineering.

First, from a cognitive viewpoint, limits can be seen either as processes or as objects, both being denoted by the single lim symbol; a situation for which Tall coined the term “procept” (Tall 1991). Using Robert’s classification of students’ “expressed models” (or conceptions) of what it means for a sequence to “tend to …”, the process aspect is related to the dynamical model (Robert 1982a, b), while the object aspect is related to the static/numerical model. Although this dynamic vs static terminology is widely used, it should not be seen as capturing a pre-mathematical vs mathematical dichotomy. Indeed, as highlighted by Larsen and Swinyard (2012) most definitions (except for maybe the “almost all definition”) have a dynamic side to them, an argument which strengthens the case for the procept nature of limits. Discussing finite limits, they distinguish between two processes, that of finding a limit candidate, and that of checking or verifying that a given number is the limit. With its intricate combination of nested quantifiers, the standard formal definition can be seen either from a static viewpoint – as expressing a property of a number with respect to a sequence – or from a dynamic viewpoint, as the description of a procedure for verification. In proofs and in theorems, at least in the case of finite limits, limits can be compared and calculated upon as if they were numbers, simply because they are numbers, even if the lim symbol is a reminder of the fact these numbers bear a very special relationship to some sequences.

A second change of viewpoints on limits is necessary to access the formal definition; a change which is actually a reversal of viewpoints. When it comes to making conjectures (i.e. finding a limit candidate), the behavior of the variable determines the behavior of the values of the function or sequence, and the asymptotic behavior is captured in narratives which ring – indiscriminately – of succession, of causality, and of implication (“when x tends to …, then f(x) does …”). This temporal precedence of the values taken by the variable over the values taken by the sequence or function is consonant with both the abstract mapping concept (with its input and output values), and with standard procedures used to make conjectures about limits, such as: to investigate the limit of f at x = a, work out f(x) for values of x which come ever closer to a; or: to study the limit of sequence (u_n), work out its values for n = 10, 100, 1000, 1,000,000 … and see what happens. In the formal definition, however, the constraint on the values of the function or sequence comes first; the constraint on the values of the variable comes second, and is dependent on the first (in a non-functional way, however). For instance, Swinyard (2011) reported on the various moves he made to – eventually – prompt students to switch from what he called the “x-first perspective” to the “y-first perspective”. On the basis of his case study, he suggested that studying limits of functions at infinity can trigger this change of viewpoints, whereas studying limits at a point is less likely to. In Roh and Lee’s engineering (Roh and Lee 2017), the “y-first perspective” was forced on students, since, from the outset, they were required to study the behavior of a few graphically given sequences using strips of various widths, to be placed parallel to the x-axis.

A third fact is consistently documented in the literature, regarding the asymptotic behavior of sequences: a large proportion of students (implicitly) assume that sequences with a limit (whether finite or infinite) display simple enough patterns in the neighborhood of +∞, in particular when it comes to variations. A crude but widely shared version of this general belief is that convergent sequences are monotonic (at least from a certain rank), a phenomenon which Robert called “monotonic reduction” (Robert 1982a; Davis and Vinner 1986). In her dissertation, for instance, Robert asked students in the first year of tertiary education if they deemed the following sentence to be true or false: “Every positive sequence which tends to 0 is a decreasing sequence” (Robert 1982a, p.169). She surveyed various populations of students – coming from standard to elite schools and universities – and got the incorrect answer (“True”) with proportions ranging from 20% to 70% (Robert 1982a, p.204). A slightly less crude belief is that, if a sequence is convergent, the distance between the terms of the sequence and the limit-value decreases – whereas the target definition only implies that the upper bound for the distance between the terms of the sequence and the limit-value decreases. It is quite likely that this belief is rooted in the standard pre-theoretical formulations – or in the rhetorical reformulations – of the notion of limit, such as: “In the real numbers, a number L is the limit of the sequence (x_n) if the numbers in the sequence become closer and closer to L and not to any other number.” (Wikipedia, art. Limit of a sequence, accessed nov. 9, 2017). Even if the literature provides less empirical data regarding sequences which tend to infinity, our hypothesis is that similar beliefs are also widespread, a phenomenon which could be studied by surveying the answers to a “True/False” question about the following statement: “if a sequence tends to +∞, then it is an increasing sequence (at least from a certain rank)” (Chorlay 2018). In the second part of this paper, the a posteriori analysis of the didactical engineering will confirm this hypothesis.

This phenomenon of “monotonic reduction” is not problematic only because it is a belief in something which is mathematical incorrect, but also because it can be an obstacle to the formulation of the definition. Indeed, if we restrict ourselves to sequences which are monotonic – at least from a certain rank – then, if L denotes a real number and (x_n) a real sequence, the following property:

$$ \forall \varepsilon \in {\mathbb{R}}^{+\ast}\forall N\in \mathbb{N}\exists n\in \mathbb{N}\kern0.5em n>N\kern0.50em and\mid {x}_n-L\mid <\varepsilon $$

does imply that ${\lim}_{n\longrightarrow +\infty }{x}_n=L$. In other words, if we restrict our attention to monotonic sequences, the concepts of (finite) limit and subsequential limit conflate. The situation is even worse for infinite limits since, for monotonic sequences, the following property:$\forall M\in \mathbb{R}\kern0.5em \exists n\in \mathbb{N}\kern0.5em {x}_n>M$does imply that ${\lim}_{n\longrightarrow +\infty }{x}_n=+\infty$. In other words, if we restrict our attention to monotonic sequences, “tending to +∞” and “not being bounded above” conflate; and the notion of infinite limit can be defined with two quantifiers instead of three.

On the basis of these well-documented difficulties, we made several choices and one key-hypothesis. We decided to design a teaching-session targeting the definition of the infinite limit, rather the definition of convergence. This should leave out two difficulties. First, since for infinite limits the lim symbol does not denote a number, the demanding shift of viewpoints between a process-aspect and an object-aspect should not be required from students; the challenge of the shift from an x-first finding-the-limit process and the y-first verifying-the-limit process partially remains, however. Second, the notion of distance – and its formal expression in terms of inequalities involving absolute values – will play no part. On the downside, the research literature makes it clear that focusing on infinite limits will lead to interferences with neighboring concepts. More specifically, our hypothesis is that, on the basis of their experience of limits, the three following mathematical properties are part of students’ concept image of the infinite limit:

• (1) Tending to positive infinity.

• (2) Not being bounded above.

• (3) Being strictly increasing (at least from a certain rank).

Of course, since (1), (2), and (3) are well-defined mathematical concepts, saying that they are part of students’ concept image – which, by definition, is not a set of well-defined concepts connected by proven properties – is a mere shortcut. All three mathematical properties are compatible with the usual procedures to conjecture whether or not a given sequence tends to +∞ (such as: work out values of the sequence for “large” values if n; look for patterns of growth), or with elementary procedures to prove some results about infinite limits (such as: if a sequence is bounded above, or decreasing, then it does not tend to +∞). Just as well, all three are compatible with the usual vague rhetorical description of what it means to tend to +∞ (“to become larger than any number”, “to grow ever larger” etc.). Thus, our hypothesis is based, on the one hand, on the epistemological analysis summarized above – which suggests that these are neighboring concepts –, and on the other hand, on the didactical analysis of the experience of limits students have – in terms of tasks, procedures and formulations – which builds up an image in which the three notions are connected.

On the basis of this hypothesis, the design of the engineering rests on a key choice: one can either attempt to design a path to the target definition of (1) which avoids encounters with the neighboring (2) and (3); or a path to (1) which gives an explicit role to (2) and (3). For instance, the first choice was made by Bloch (Bloch and Gibel 2011). Bloch’s design rests on the study of von Koch’s snowflake. Students were asked to numerically explore two sequences associated to the sequence of geometrical diagrams, namely the sequence of measures of their lengths, and the sequence of the measures of their areas. The definitions of limits – infinite for the length, finite for the area – was eventually given by the teacher, and showed to be an efficient tool to prove the conjectures made by the students as to the asymptotic behavior of the two sequences. Bloch’s choice was to work with only two sequences, both of which are strictly increasing, a context in which (1) and (2) conflate. Most designs, however, take the neighboring concepts into account: in Robert’s engineering (Robert 1983, p.441), students were to assess the statement “if a positive sequence is not bounded above, then it tends to +∞”; in their design, Roh and Lee (2017, p.40) included non-monotonic sequences in their list of examples of convergent sequences; Przenioslo’s design (2005) required that students discuss the validity of a range of arguments presented in (artificial) written dialogues between “students” in which the various elements of the concept image – including misconceptions – appear explicitly. In our design, we take the whole concept image into account and target not only a formulation of the formal definition of (1), but also an explicit distinction between (1), (2) and (3).

On the basis of this choice, the fact that the concept image of “infinite limit” is one which conflates (1), (2), and (3) can be seen either as an obstacle to overcome in order to reach a clear and distinct idea of (1), or as an obstacle and a stepping-stone in this process. As in Martin, Oehrtman and Swinyard (2014, p.132) and Zandieh and Rasmussen (2010), this design is based on the second alternative, since an epistemological analysis, suggest that concepts (2) and (3) are not only different from (1) – yet connected to (1) – but also potentially conducive to (1). This assumption rests on two arguments. First, (2) and (3) are, in a sense, simpler (1), at least in terms of the number of nested quantifiers in the formal definition: two quantifiers (∀∃) for (2), only one universal quantifier for “strictly increasing”, two for “strictly increasing (from a certain rank)” (with ∃∀, this time). From a formal viewpoint, the sequence of quantifiers in the target definition – namely ∀ ∃ ∀ – could be seen as a combinations of the sequences which appear in the (2), and (3), the ∀∃ sequence from (2) formally expressing the semantic element “become greater than any given number”, while the ∃∀ sequence which appears in the formal definition of (3) suggesting syntactic means to capture the semantic element “and remaining so”. Second, whereas the definition of (3) is consonant with a “dynamic”, “x-first” perspective on sequences, the definitions of “bounded above” and “not bounded” are consonant with a “static” and “y-first” perspective. This suggests that focusing students’ attention on (2) is more likely to lead to (1) than focusing on (3). Moreover, the study of Martin et al. (2014) showed that, even after the adoption of a y-first perspective, the inclusion in the definition of a first universal quantifier remained a major difficulty. Starting from the quantified version of the definition of (2) could help curtail this problem.

This survey of epistemological features which are specific to the limit concept and have a well-documented cognitive impact helped us explicit – and to some extent justify – some macro-choices for this instructional design: to study limits at infinity (even though we did not justify why we started with sequences rather than with functions defined in neighborhoods of +∞) so as to help the transition from an x-first to a y-first perspective; to study infinite limits rather than finite ones so as to accommodate a procept take on limits and avoid issues related to the notion of distance; to take into account the concept image of limits – with its likely conflation of three distinct mathematical concepts – both as an target of the engineering and as a provider of affordances (and not only constraints); to focus on the connection between “infinite limit” (1) and “not bounded above” (2), the latter concept being fairly familiar to the students (including the formal definition), bearing a simple enough logical relationship to the target concept (namely: (1) ⇒ (2) but the converse does not hold), and providing a ready-made y-first formulation which begins with a universal quantifier. However, these choices have a cost. In particular, focusing on infinite limits implies that the engineering will not be based on approximation problems, in spite of the fact that these constitute a major raison d’être for limits in mathematics. Moreover, didactical studies showed that approximation metaphors form a stable and widely shared core in students’ concept image of limits (Oerhtman 2009); a core which provides a stepping stone for instructional design (Martin et al. 2014).

Theoretical Perspectives on the Introduction of Advanced Mathematical Concepts

Beyond these very content-specific aspects, we need to take into account more general frameworks and results bearing on the teaching of advanced mathematical concepts. These results will either help us explicit and partially justify some macro-choices for the instructional design, or provide tools for the analysis of the empirical data. We will first argue for the potential of situations of conceptual differentiation as a pathway to advanced mathematical concepts, and contrast it with the other situations of concept-introduction considered in Robert’s framework (Hache and Robert 2013). We will then present some of the tools which we borrowed – and occasionally adapted – from Ouvrier-Buffet’s work on Situations of Definition Construction (SDC) (Ouvrier-Buffet 2006, 2011, 2013).

Conceptual Differentiation as a Pathway to Advanced Mathematical Concepts

In this paragraph, we shall use the term “concept” in a very general sense, to denote mathematical objects, properties, procedures, or frameworks (“frameworks” as in: Euclidean-synthetic geometry as distinguished from coordinate geometry). The challenge of the insertion of a new concept in the “mathematical landscape” of students (Hache and Robert 2013) depends not only on the intrinsic properties of the concept, but also on the long-term learning trajectory of students, as shaped by curricula. Taking both aspects into account helps to specify the relationship between the new concept and the concepts students encountered earlier. In her work, Robert distinguishes between four such relationships between “old” and “new” concepts. Identifying to which of the four types of concepts any new concept belongs helps to specify the affordances and constraints for the possible teaching strategies. Robert coined the terms extension without accident (or smooth extensions) and extension with accident (or rough extensions) to denote the first two types. In both cases, the new notion is (from a mathematical viewpoint) and is seen by students (from a cognitive viewpoint) as an extension of a notion which students are already familiar with. In some cases, the extension can be smooth, for instance when introducing the dot product in space geometry to students who studied the dot product in plane geometry before. More often than not, the extension is potentially tricky, and this is where a didactical analysis combining mathematical, epistemological and cognitive aspects is necessary to identify difficulties and affordances. Standard examples are the passage from counting numbers to decimals, and from plane to space geometry. A third type of concepts is that of Answers to a Problem. In such a case, the concept is not an extension of something students encountered earlier, but students have means to test or acknowledge the fact that the new concept does provide an answer to a problem which students can make sense of on the basis on their pre-existing knowledge. Whether the new concept has to be introduced by the teacher, or can be discovered by students as the efficient tool in a well-designed problem-solving task (as the Theory of Didactical Situation recommends), depends on the concept and the curriculum. For instance, the Pythagorean property can serve as a tool to work out lengths in many situations involving right-angles; it can be used to test whether or not some angles are right-angles. For instance, antiderivation and integration can be seen as means to work out areas under curves.

The fourth type of concept is what Robert, Rogalski and Dorier (1995) called FUG concepts: concepts which Formalize, Unify and Generalize a wealth of previously encountered concepts – and many others still unknown to the students. FUG concepts can also be characterized negatively, insofar as they cannot be seen as extensions of isolated items of knowledge, and probably cannot be introduced as efficient tools to solve a well-chosen specific problem that students can make sense of (if not solve). Although the notion of FUG concept has recently been used in the context of rather elementary mathematics – to discuss the introduction of the distributive law expressed with letters, in middle school (Constantin 2017) – the notion was first designed for the study of challenges which are common in higher secondary and in tertiary education, in the teaching of advanced mathematical notions. The main case-study relying on this approach is Dorier’s dissertation on the introduction of the axiomatic theory of vector spaces in the first year of tertiary education (Dorier 1995; Dorier 2000). The axiomatic description of vector spaces is, indeed, formal; it captures into a unified formalism a large variety of objects: some geometric objects (lines, planes), simultaneous linear equations and their solution sets, linear differential equations and their solution sets, matrices etc.; it provides general conceptual tools to handle these objects and many others: linear dependence/independence, basis, dimension, rank, kernel, duality etc. in any dimension and on any field. Such FUG concepts were generally introduced by mathematicians whose goal was explicitly to unify and generalize, on the basis of their extensive knowledge of mathematics as a whole – or of large parts thereof – in order to better organize the whole body of knowledge. This creates specific challenges for the teaching of such concepts. On the one hand, even if one could design a problem-solving situation for students to first come across the new concept, the problem-solving context could not bring across to the students the meaning and import of the concept. Moreover, the introduction of a new and very abstract terminology to describe a single problematic situation might make the new set of notions sound like unnecessary jargon. On the other hand, trying to emulate the historical emergence of the concept might lead to a long and extensive preliminary study of many specific cases. In the case of vector spaces, Dorier sought to trigger reflective abstraction by combining two levels of discourse: an object-level discourse, produced by students in a problem-solving context, and a meta-level discourse produced with students about the methods used in problem-solving. This meta-level discourse is to emerge under the guidance of the teacher, and can be prompted by questions about the various steps of the problem-solving endeavor, such as: What justifies them? How can the list of rules or moves be made minimal? How can they be reformulated in a more formal and context-free language?

We will take for granted that the formal definition of limits of sequences is not an extension of something already familiar to the students. We also doubt it can be successfully introduced as an Answer to a Problem, for reasons which belong to two categories.

First, we are aware of two attempts to introduce the concept of limit in a problem-solving situation, both of which leading to results that we deem unsatisfactory. We mentioned earlier what we consider to be the shortcomings of the snowflake engineering (Bloch and Gibel 2011). Another attempt is that of Job, in his dissertation (Job 2011). Year 12 students had to study a list of sequences, all increasing, none of which tending to $\sqrt{2}$. After sorting the sequences according to whether or not they were bounded above by $\sqrt{2}$, students were entrusted the task of deciding which, among those which were bounded above by $\sqrt{2}$, provided the best approximation of $\sqrt{2}$. Job’s work rested on the Lakatosian notion of proof-generated concept, and pursued two goals: to study whether or not students could (a) reach a sea-worthy definition of the limit of a convergent sequence in a problem-solving context, and (b) change their image of definitions in mathematics - from descriptions of objects to tools for proving. Job provided a thought-through analysis of why this attempt failed for either goal, in spite of the very propitious experimental conditions (a group of 12 high-achieving students who volunteered for seven 1-h sessions, under the guidance of the researcher).

A second argument rests on the history of mathematics, since, for centuries, problems were solved and theorems proved using reasoning which – for the twenty-first century reader – are consonant with the limit concept, without any definition of limits being singled out and made explicit. Let us mention two examples of different scales and from different periods. In Hellenistic mathematics, Euclid and Archimedes proved many theorems using a uniform formal proof-scheme: two magnitudes A and B can be proven to be equal if their difference is less than a sequence of magnitudes which is bounded above by a geometric sequence of magnitudes of common ratio ½ (Proposition I of Book X (Euclid 1908)). In 1713, in a letter to Hermann, Leibniz proved what is still usually called the Leibniz criterion for alternating series, and he proved it the way we still prove it (assuming the completeness of the set of real numbers) (Leibniz 1859, 272–275). However, he never considered that this well-known (since Antiquity), versatile and ubiquitous proof-scheme made it necessary to define a new notion such as “limit”. Let us mention here the work of Bob Burn (2005), who devised – but did not experiment – a teaching path going from the historical proof-scheme to the formal definition.

Consequently, we acknowledge the fact that the limit concept shares many essential properties with FUG concepts, and that this commonality implies similarities in terms of teaching strategies. However, we will not go as far as to say that the limit concept is a FUG concept, for both epistemological and didactical reasons. From a historical viewpoint, it is indeed Cauchy who, in his teaching at the Ecole royale polytechnique (Cauchy 1989), presented a systematic organization of the part of mathematics dealing with functions on the basis of the notion of limit of a variable quantity. This choice for the large scale deductive structure of function theory, which at the time had competitors of no lesser systematicity (as in Langrage (1813)), is, to a large extent, still reflected in today’s analysis: its fundamental concepts (continuity, derivation, integration, number and function series) are defined in terms of limits; the theory involves existence proofs (for real numbers, for functions which are solutions of functional equations) for the defined objects, which was one the main novelties in Cauchy’s exposition. This situation is very similar to that of the introduction of abstract vector spaces and creates a similar challenge for teaching: the raison d’être of limits, i.e. the reason why mathematicians value this notion, can probably not be grasped on the occasion of one problem-solving session, or even a short series thereof. On this basis, one could imagine designing a teaching sequence combining the Burn proposal and the Robert-Dorier approach, with a guided meta reflection on a gradually abstracted proof-scheme. This is not the choice we made, however; for two reasons. First, this approach might not take into account the cognitive difficulties to access the notion of limit, and might lead to a formulation of the definition of the notion of limit without inserting it properly in a restructured concept image. Second, our goal is to design a teaching sequence which is compatible with ordinary teaching conditions, in particular in terms of time.

A closer look at the history of mathematical analysis in the nineteenth century suggests another lead. Mathematicians introduce new concepts for a variety of reasons and purposes. One of the merits of the FUG approach is to remind us that not all concepts were introduced to solve new problems, or to solve older problems more efficiently, or even to help ascertain statements (as for proof-generated concepts). Concepts are also introduced to unify, generalize, simplify, and – more generally – streamline parts of mathematics as a body of knowledge. On some occasions, concepts are also made explicit in a process of conceptual differentiation; not to unify, but to distinguish between two hitherto conflated notions. It is well-known that, in the course of the nineteenth century, mathematicians learned to distinguish between point-wise and uniform properties in analysis – for continuity or for the convergence of sequences of functions – in cases where mathematicians of the former generation, such as Cauchy, saw no difference. In the second half of that century, the distinction between maximum and least upper bound gradually became standard (Chorlay 2012). At the turn of the twentieth century, mathematicians learned to systematically distinguish between local and global viewpoints, theorems and theories (Chorlay 2011).

In these three cases, at least two types of phenomena concurred to foster the differentiation process. On the one hand, a series of rational moves from mathematicians engaged in the streamlining of proofs; rational moves which the Lakatosian description of proof-generated concepts captures appropriately: search for exceptions and refusal of the monster-barring approach, search for hidden lemmas, and exploration of the realm of unintended objects falling under a seemingly innocuous definition (Lakatos 1976; Volkert 1987; Chorlay 2012). On the other hand, an evolution of the syntax of mathematics, and of the norms of proper mathematical writing: explicit use and ordering of quantifiers in the case of the point-wise / uniform differentiation; explicit statement of domain for every function and every functional equality in the case of the local/global differentiation (Chorlay 2011).

The point of this admittedly sketchy historical excursus³ is not only to remind us that conceptual differentiation is a well-documented drive for concept introduction in higher mathematics, on a par with unification and generalization, but also to show that it could be better suited for the introduction of the formal limit concept to students. First, the formalization of the concept took place in the course of the point-wise/uniform differentiation, and not in the Cauchy phase of unification. Second, and this is not specific to the case of the limit concept, it might be easier to insert a new notion in the mathematical landscape of students on the basis of its differentiating role than on the basis of its FUG role in higher mathematics. The need, felt by mathematicians on the basis of their extensive knowledge of mathematics, to unify, generalize and simplify is not something that can easily be emulated in a teaching protocol. And assuring students that a newly defined concept is very important – for mathematicians – and will – in the years to come – be of great use in their study of mathematics may have a motivational impact, but probably little cognitive impact. By contrast, the need for conceptual clarification does not require an extensive view of mathematics or a premonition of future benefits, but only the ability to spot specific inconsistencies in a mathematical milieu that can be designed for that purpose.

Tools for the Analysis of Situations of Definition Construction

Within the framework of the theory of didactical situation (TDS), Ouvrier-Buffet (2006, 2011, 2013) has been developing specific tools for the design and the analysis of what she termed “Situations of Definition Construction”. We will first present the elements of her framework which we will use for the analysis of this design, then suggest adaptations allowing for the study of student-teacher interaction in a codidactic situation. We will eventually sketch a comparison with other works which bear on defining as a mathematical activity.

Beyond the general framework of TDS, Ouvrier-Buffet relied on the theoretical constructs of Balacheff (Balacheff and Pedemonte 2016) to identify tools for the design and the analysis of situations of definition construction. Balacheff calls a conception of X a state of equilibrium of a cognitive subject with respect to a milieu which can be described in terms of four elements: a set P of problems for which X is regarded by the subject as a provider of solutions, and which in return give meaning to X; a set O of operators which enable the subject to alter the milieu; a system of representation L, which may use several semiotic registers; and a set Σ of controls which enable the subject to assess if the modification of the milieu by a given operator is possible (or not), and efficient (problem solved / problem not solved). This framework was first designed to study and compare the variety of conceptions – among students of the same age or at different levels of the educational system – of standard mathematical objects such as addition, decimals or symmetry. It was later used to characterize forms of engagement with mathematics, such as argumentation and proof (Balacheff and Pedemonte 2016). Along this line, Ouvrier-Buffet seeks to characterize three conceptions of defining as a mathematical activity.

To describe our classroom experiment, we will have no use for what she calls the Popperian conception of defining, which bears on large-scale and high-level problems such as the construction of a whole theory, or the selection of a theory among competing ones. By contrast, we will retain elements from what she calls the Aristotelian and the Lakatosian conceptions, both of which aim for concept-formation rather than theory-building. The Aristotelian conception of the defining activity targets problems of classification, in which a concept is to be delineated through the identification of invariant properties (displayed by all the instances of the concept) and specific differences (distinguishing it from neighboring concepts). Its controls express logical and linguistic requisites: a definition has to avoid metaphors and loosely defined terms; it has to avoid vicious circles resulting from a use of the definiendum (what is to be defined) in the definiens (that which defines); it has to capture a necessary and sufficient condition; it should be minimal. The operators can be derived from the controls: eliminate ill-defined terms, weaken conditions that are sufficient but not necessary etc.

On the basis of Lakatos’s Proof and Refutation (1976), Ouvrier-Buffet outlines a Lakatosian conception of the defining activity which also fosters concept-formation either through problems of classification, or through various forms of engagement with argumentation (e.g. exploring the scope of a conjecture, checking the correctness of a proof). A first class of operators has to do with examples: generate examples, counter-examples (to a statement), and non-examples (of the target concept); alter a definition (or a proof) to take non-examples (or counter-examples) into account. Among these operators, we will mainly have use for monster-barring, i.e. the strengthening of a definition aiming to exclude a non-example, or a whole class of these. Other operators do not bear directly on examples: some bear on proof (in particular: analyze the “proof” of an invalid theorem to spot a hidden Lemma); reformulate in a new framework or in a new semiotic setting; generate new conjectures or new problems (sub-problems, generalizations etc.). The controls derive from the operators. Clearly, the Aristotelian and Lakatosian conceptions of defining partially overlap.

Since our engineering rests on classification rather than proof and conjecture, large parts of the framework of Ouvrier-Buffet will not be directly of use, in particular the distinction between in-action definitions, zero-definitions and proof-generated definitions (Ouvrier-Buffet 2011). In particular, for lack of an engagement in proof and proof-analysis, we will not retain the term “zero-definition” to describe the tentative definitions written out then assessed by students in phase 2; we will use the more neutral term “candidate-definition”.

In situations of definition construction, Ouvrier-Buffet studied the impact of a key didactic variable, namely the degree of explicitness of the requirement that candidate-definitions be provided by students. Both empirical studies (Ouvrier-Buffet 2006, 2011) strongly suggest that even in the face of well-designed milieus and problematic situations (of classification or proof) an explicit request for definitions from the supervisor is a decisive component, either to trigger the shift from an in-action (meaning: implicit) definition to a zero-definition, or to allow for the inclusion into the milieu of (explicit) zero-definitions over which students can exert controls and apply operators.

Although this framework was first devised to provide tools for the design of SDCs and the analysis of the cognitive trajectories of students in SDCs, it also provides tools for the analysis of student-teacher interaction. In the a posteriori analysis of phases 2 and 3, we will sort out the various moves of the actors in terms of controls and operators, while paying attention to who exerts control or applies operators: teacher or students. In order to capture the specific role of the teacher, we will also distinguish between cases when he/she actually exerts control or applies operators, and cases when he/she hints at what students may consider doing in terms of controls and operators. This will help us ground our claim that the situation did elicit an active engagement of the students in the defining activity. In other words, that the behaviors of the students can be seen as gradually building up an adaptative response to the constraints of the milieu – with a teacher acting as a mediator between the students and the milieu and an orchestrator of the multiplicity of voices (Bartolini Bussi 1998, 2009; Bartolini Bussi and Mariotti 2008; Fischbein and Mariotti 1997) – as opposed to a series of unconnected and short-scale applications of the teachers’ instructions. More locally, it will provide tools to capture the variety of controls and operators used by the students (either with or without prompt from the teacher) or by the teacher.

Since these analytical tools were crafted in the framework of TDS, a systematic comparison with other frameworks could be fruitful. This holds in particular for the framework of Realistic Mathematics Education since genetic decomposition and guided reinvention were used in several key-studies on the limit concept (Cottrill et al. 1996; Swinyard 2011). It was also used for instructional design (Martin et al. 2014) in a constructivist perspective which is similar to ours. Moreover, general tools for the analysis of defining as a mathematical activity (DMA) were also designed in this framework by Zandieh and Rasmussen (2010). However, just as we will not use the totality of the tools provided by Ouvrier-Buffet because we chose a situation of classification and not one involving conjectures and proofs, this case-study does not lend itself easily to a description in terms of the DMA framework. First our situation is one of classification which involves neither modeling nor proving. Second, the DMA framework allows for the analysis of the diversity of the successive forms of engagements with definitions on a rather long time-scale (a 5-week course). In our engineering, students only commit to defining for only one hour, since the first half of the 2-h session is meant to lead students to acknowledge the need of a definition of the infinite limit. The second hour can be seen as an instance of the first of the four levels of defining activity, that of “situational activity” in which a concept-definition is to be created on the basis of a concept-image (Zandieh and Rasmussen 2010, p.60). Since this phase does not involving making use of a definition as a tool, we will only be dealing with definitions-of and not with definitions-for (Zandieh and Rasmussen 2010, p.58).

Layout of the Teaching Session – Elements of A Priori Analysis

Local Teaching Requirements and Constraints

In the final year of secondary education – year 12 in the French educational system – the curriculum requires that students majoring in mathematics and the sciences study a few formal definitions regarding limits. On this basis, they are expected to study and memorize the proofs of a few standard facts about limits, such as: “If an increasing sequences has limit l, then all its terms are less than or equal to l”, and “An increasing sequence with no upper bound tends to +∞”. On the whole, the encounter with a formal definition plays a very minor part in the range of tasks entrusted to students in their study of mathematical analysis. In high school, the focus is on the use of sequences and functions in modeling and problem-solving, and on the gradual expansion of the investigative means, thanks to new functions (rational, circular, logarithmic) or new procedures (derivation, integration). As far as limits are concerned, students are to be able to make conjectures about limits in a numerical or a graphical context, and to study the limit(s) of specific functions and sequences by choosing and using the right tool from a list of rules on the algebra of limits. These rules are usually studied before the definition is given. The official syllabus suggests that this limited display of more formal mathematics can serve two purposes: to show students that analysis is a deductive theory (on a par with, say, geometry); and to give an opportunity to use logic (in particular quantifiers).

From a more theoretical standpoint, this “in-depth study of the notion of limit of a sequence” – as the syllabus puts it – seems to be a rather isolated sample of analysis in a world of calculus. This is very similar to the Spanish situation which Barbé et al. (2005) analyzed in terms of praxeologies. In both cases, the calculus and the analysis praxeologies are present in the curriculum, yet they are almost completely disconnected in practice. This charge of “disconnection” calls for qualification, though, according to whose practice one considers. From the viewpoint of analysis – which, hopefully, is that of the teacher –, there are connections indeed: the definition of limits is a sample of a theory (mathematical analysis); a sample with a technological function, insofar as it enables one to prove theorems warranting some of the techniques used to handle and determine limits (algebra of limits, rules about limits and inequalities). However, assuming that the students’ perspective – grounded in their experience of school mathematics – is that of calculus, the specifics of this discourse on defining limits may not only be difficult to understand; the meaning of the whole endeavor might also be difficult to grasp. The definition of limit might appear to be useless – when it comes to dealing with the problem-solving and modeling tasks which are entrusted to students on a daily basis – in addition to being difficult to understand.

Prerequisites for the Session

There are two kinds of prerequisites for the session: a general familiarity with limits of sequences, and some familiarity with the formal characterization of some properties of sequences.

Actually, so as to keep the logical prerequisites to a minimum, only the formal expression of “bounded above” (at least one of them) and its negation play a significant part in the design. Working on the formal expressions of this property can provide opportunities to remind students of the meaning of the universal and the existential quantifiers, but also to come across and discuss expressions involving nested quantifiers. In particular, students should probably be aware of the fact that, on some occasions, the order of the quantifiers does matter (Durand-Guerrier and Arsac 2005), as can be illustrated by the fact that

$$ \forall n\in \mathbb{N}\kern0.5em \exists M\in \mathbb{R}\kern1.00em {u}_n<M $$

always holds, which does not mean that all sequences are bounded above. In the session, we endeavor to make this explicit by using the standard subscript convention; for instance, we express “not bounded above” as

$$ \forall M\in \mathbb{R}\kern0.5em \exists {n}_M\in \mathbb{N}\kern0.5em {u}_{n_M}\ge M. $$

We drew on the numerous elements gathered in the preliminary analysis to design a 2-h teaching session. We will describe the layout of the session and discuss some key didactic variables.

We will not expatiate on the choice of one of the variables, namely the fact that we decided right from the start that the specific work on the definition of infinite limits should not take more than one teaching session. The session was designed with the two teachers who would implement them, and the fact that they were not willing to spend more than the usual 2 h they usually spend on the definition of limits was an external constraint. This constraint, however, was in keeping with our research goal, since we aimed for a formulation of the definition by students – as was achieved by Swinyard (2011) and (Martin et al. 2014) but with a very small group of students and over a long period of time – within a time scale similar to that of (Robert 1983), (Bloch and Gibel 2011), and (Roh and Lee 2017).

The layout of the session has three main phases:

• Phase 1: Students are required to sort sequences according to whether or not they tend to +∞. Collective discussion on the sorting. Collective discussion on the connections between limit, variations and upper bounds. Collective discussion on the issue of uniqueness of a limit. Collective discussion on the need for a definition.

• Phase 2: Students are asked to write down possible definitions – we will call them candidate-definitions – of “$\underset{n\to +\infty }{\lim }{u}_n=+\infty$”, for an unspecified sequence denoted by (u_n). Collective assessment of the candidate-definitions.

• Phase 3: Under teacher guidance, formal reformulation of “not bounded above”; acknowledgement of the fact that it is a necessary but not sufficient condition for “$\underset{n\to +\infty }{\lim }{u}_n=+\infty$”. Collective work on the strengthening of this condition in order to find a necessary and sufficient (hence definitory) condition.

Phase 1

In the sorting task entrusted to students in the first phase, four didactic variables can be identified: two bear on the list of sequences to be sorted, namely, (1) the way they are given (e.g. by formulas or scatter-plots), and (2) the specific properties of each one of them; a third variable bears on the role of argumentation and justification in the sorting task; the nature and level of teacher intervention is a fourth variable. In this part, we will discuss (2), (3), and (4). Variable (1) will be discussed in the a posteriori analysis, so as to shed light on a general issue about situations of definition construction.

In phase one, students are first asked to work in pairs for 15 to 20 min, and study the following sequences:

$$ {\displaystyle \begin{array}{l}\kern0.48em {a}_n=\frac{n}{100}-100\kern0.5em {b}_n={3}^n-1000\kern0.5em {c}_n=100n-{n}^2\kern0.5em {d}_n=\sqrt{\sqrt{n}}\\ {}\begin{array}{cccc}{e}_n={\left(-1\right)}^n\times n& {f}_n=10\ 000-1000\times {\left(\frac{2}{3}\right)}^n& {g}_n={\left(-1\right)}^n+n& \left(\mathrm{in}\ 2016\right)\end{array}\\ {}\kern2.28em \begin{array}{ccc}{g}_n={\left(-1\right)}^n\times 10+n& \left(\mathrm{in}\ 2017\right)& {h}_n=\left({\left(-1\right)}^n+1\right)\times n\end{array}\\ {}\kern2.879999em \begin{array}{cc}{i}_n=10\ 000+1000\times \cos (n)& {j}_n=\end{array}\left({\left(-1\right)}^n+2\right)\times n\end{array}} $$

Students are also given a worksheet with a three-column table, and instructed to: “place each sequence in one of the columns. If you place one of them in the middle-column, explain why”. The columns were labeled:

I think the sequence tends to +∞

I don’t know

I think the sequence does not tend to +∞

We had several reasons not to ask students to “prove” or “justify” all their answers. First, the techniques they had studied only enabled them – in theory – to fully justify their answers for some of the sequences. And even among these, this justificatory task ranged from the familiar to the tricky.

What students are expected to provide are not – at least not always and not necessarily – proofs, but decisions, as characterized in (Balacheff 1987). To the standard distinction in TDS between situations of action, situations of formulation, and situations of validation, Balacheff suggested that a fourth kind of situations be added, halfway between formulation and validation:

[a situation of decision] requires the mobilization of means of decision, hence means of validation, without any explicit proof be demanded. What is to be produced is a valid proposition, not the proof of validity. In the situation of decision, the intellectual operations of hypothetico-deductive reasoning (…) may be come into play, without any proof being displayed. The logical and semantic controls function locally in the process of finding the solution. Eventually, as mathematicians, we recognize in it an organization which is of a demonstrative type, but here, for the subject, it is a tool and not an object. (Balacheff 1987, p.153. Our translation)

Among the sequences, two subgroups play different but central parts in the design. Sequences f, g and j are meant to foster conceptual differentiation between infinite limit and variations: sequence f does not tend to +∞ – since it is bounded above – in spite of the fact that it is strictly increasing; sequences g and j do tend to +∞, in spite of the fact that they are not increasing, not even from a certain rank. Thus, neither of the properties “being an increasing sequence (at least from a certain rank)” and “tending to +∞” implies the other. Sequences g and j differ in so far as the size of the “oscillations” is bounded for g and not bounded for j. This can be used to show that no combination of conditions such as “not bounded above + bounded oscillations” is definitory for the infinite limit.

From a more general didactical viewpoint, challenging students’ image of the infinite limit by displaying “boundary examples” (Watson and Mason 2001; Chorlay 2015), or “wedges” (Dawkins and Roh 2016) is a standard move in sessions aiming to trigger a defining activity (Ouvrier-Buffet 2006).

Sequences e – which goes 0, −1, 2, −3, 4, −5, … – and h – which goes 0, 0, 4, 0, 8, 0, 12, … – are meant to trigger socio-cognitive conflict, for several reasons, and with several expected benefits.

The decision as to these two sequences cannot be justified by students on the basis of the course on limits they were exposed to on earlier occasions. Indeed, in the course on limits, the theorem on uniqueness of limits is usually not stated in year 11; in the classes where the experiment was carried out it had not been stated in year 12 until then either. Students do not generally feel the need for any such statement, all the more since the definite article “the” is usually used right from the start by teachers when informally introducing limits. The fact that uniqueness seems to “go without saying” is confirmed by the fact that many year 12 textbooks in France do not even mention it. Needless to say this theorem – as any theorem about limits – cannot be proved before a definition is available.

We also claim that the sorting decision for sequences e and h cannot be made on the basis of purely mathematical arguments. In other words, we claim that, in the absence of a definition, deciding that sequences e and h do tend to +∞ and to −∞ (for e) or 0 (for h) is not mathematically incorrect. First, defining and using in proofs a notion of “limit” which does not imply uniqueness is mathematically correct, since it corresponds to the contemporary notion of subsequential limit.⁴ One could argue that the conceptual differentiation between “limit” and “subsequential limit” is one of the various conceptual differentiations which we target in this design; we would not go as far as saying that, since at no point will it be necessary to carry out explicit work on the concept of subsequential limit. Second, it so happens that prominent mathematicians chose definitions for the word “limit” which do not imply uniqueness. For instance, in his Analyse algébrique of 1821, Cauchy wrote:

When a variable quantity converges to a fixed limit, it is often convenient to denote this limit with a specific notation. This is what we will do, by writing the abbreviation lim before the aforesaid variable quantity. Occasionally, when one or several variables converge to fixed limits, an expression involving these variables converges at the same time to several different limits. We will then denote either of these limits using double parentheses placed after the abbreviation lim, thus bracketing the expression at play. Let us assume, for instance, that a positive or negative variable represented by x converges to the limit 0, (…) then the expression $\mathit{\lim}\left(\left(\frac{1}{x}\right)\right)$ admits two values, namely +∞ and −∞; and $\mathit{\lim}\left(\left(\mathit{\sin}\frac{1}{x}\right)\right)$ has an infinity of values between -1 and 1. (Cauchy 1989, p.26. Our translation)

This acceptance of ambiguous symbols by Cauchy was not restricted to limits, since his function concept allowed for multivalued functions: $\sqrt{4}=\pm 2$, arctan0 = kπ for all integers k etc. This function concept was by no means specific to Cauchy: it was first promoted by Euler, in the context of the controversy on the logarithm(s) of negative or complex variables, and remained a widespread convention in the mathematical community until the turn of the twentieth century.

The fact that students do not have rational means to decide how to sort sequences e and h has two consequences, both of which play a crucial part in the design.

First, our goal is to trigger socio-cognitive conflict – in the form of dissensus among students in the collective discussion phase – triggering the recognition of the need for something that is not yet available in the didactical milieu. Something that could be either a definition, or at least a convention as to whether the word “limit” should be used only in the cases where there is one such object, or, just as well, in cases where a sequences “tends” to several such objects. It is important that the sequences e and h themselves display general patterns which are quite easy to grasp, since the goal is to show that the inability to decide how to sort them does not stem from the difficulty to understand their behavior, but, rather, from the lack of a settled rule governing the use of the word “limit” in the classroom.

Second, from a mathematical viewpoint, the need to settle the uniqueness issue is a cornerstone for the conceptual differentiation between “infinite limit” and “not bounded above”. Indeed, if one does not require that the definition of the word “limit” imply uniqueness, that is, if one chooses to use the word “limit” to denote what is now conventionally called subsequential limit, then the definition of “infinite limit” becomes:

$$ \forall M\in \mathbb{R}\kern0.5em \forall N\in \mathbb{N}\kern0.5em \exists {n}_N\in \mathbb{N}\kern0.5em {n}_N>N\kern0.5em and\kern0.5em {u}_{n_N}\ge M, $$

a property which happens to be equivalent to the seemingly weaker property

$$ \forall M\in \mathbb{R}\kern0.5em \exists n\in \mathbb{N}\kern0.5em {u}_n\ge M. $$

Thus, if one does not require uniqueness, “infinite limit” thoroughly conflates with “not bounded above”.

This analysis has an impact on the fourth variable, which bears on the nature and extent of teacher intervention. In the sorting task, we hypothesize that the properties of the listed sequences and the experience of limits students have will lead to a dissensus if the teacher assumes a neutral role, only warranting that decisions are not based on an incorrect understanding of the behavior of the various limits. Before launching the second phase, the teacher has to briefly change roles. Since the requirement of uniqueness is a convention, it cannot be derived from a rational analysis of the collection of sequences. The teacher will add this requirement to the milieu without trying to justify it: it will be required that the definition of “infinite limit” be such that uniqueness holds.

To sum up, at the end of the first phase, we expect that the collective discussion about the sorting task will lead to a consensus – within the collective comprising the students and the neutral teacher – on the following point:

• The property “being increasing (at least from a certain rank)” is neither a necessary nor a sufficient condition for a sequence to tend to +∞.

• Our current use of the word “limit” does not allow for a rational and consensual sorting decision for seemingly innocuous sequences such as e and h. Writing a definition for “infinite limit” could be a way to settle this issue.

• If we chose a definition of “infinite limit” which either requires or implies uniqueness – that is, a definition for which sequences e and h do not tend to infinity; a definition for which sequences e and h are non-examples of sequences with limit +∞ – then “not bounded above” would not be a sufficient condition for “infinite limit”, even though it is clearly a necessary condition.

Phases 2 and 3

In phase 2, students are first asked to write down what their definition for the infinite limit would be; the definition should warrant uniqueness. We let them work in pairs, and give them about five minutes. Then, a sample of the candidate-definitions is selected by the teacher and displayed for collective discussion (after a short phase of individual reading). Again, students are asked to assess the candidate-definitions and decide whether each one of them should be accepted or rejected as a definition for the infinite limit.

On the basis of the preliminary analysis, we did not expect anyone to come up with the target definition, either expressed formally as in

$$ \forall M\in \mathbb{R}\kern0.5em \exists N\in \mathbb{N}\kern0.5em \forall n\in \mathbb{N}\kern0.5em n>N\kern0.5em {\displaystyle \begin{array}{cc}\Rightarrow & {u}_n\ge M.\end{array}} $$

or in a logically equivalent rhetorical formulation such as: “for any number M there is a rank after which all terms of the sequence are greater than M”. Of course, we would not have considered rhetorical wordings such as “the sequence takes on arbitrarily large values”, “the sequences becomes greater than any chosen constant”, “the values becomes ever larger” to constitute satisfactory definitions; not because of the rhetorical formulation, not even because the quantification is not as explicit as it could be, but because these sentences define “not bounded above” or “increasing”, but not “infinite limit”. In other words, whether in a formal or in a rhetorical register, we did not expect the third quantifier “… ∀ n ∈ ℕ…” (or “all the terms of the sequence after a certain rank”) to come up in the candidate-definitions. Overcoming this obstacle would be the goal of phase 3.

A thorough a priori analysis of the preliminary stage of phase 2 – in which pairs of students write down candidate-definitions – would involve an analysis of the range of possible answers in terms of content and form, and of its relationship with the state of the milieu at the end of phase 1. We will not provide this analysis, for two reasons. First, we feel the preliminary analysis based on the literature is sufficient to back up the assumption that students will not reach anything qualifying as a definition. Second, the range of candidate-definitions provided by the students will allow for the unfolding of the engineering as long as it displays various combinations and expressions of “increasing” and “not bounded above”. Again, the preliminary analysis warrants the assumption that it will.

The role of the preliminary stage of phase 2 is twofold: to initiate a shift in tasks (from sorting to defining), and to enrich the milieu through the introduction of candidate-definitions.

The task of assessing candidate-definition is, in itself, an unusual task in the French educational system; a task which we can safely assume a large majority of the students had never been assigned before. On a more local scale, the students had – until then – spent most of the session working on a collection of sequences, so as to study their asymptotic behavior. In phase one, sequences were the object of study, while students’ patchy knowledge of limits provided tools for this study. Making candidate-definitions the object of study involves a complete shift of focus which we thought requires some time.

Even if the preliminary analysis left us little hope that the local mathematical milieu could possibly lead some students to the formulation of the target definition, we assumed it was rich enough to enable students to rationally assess (and reject) a few candidate-definitions. In the a posteriori analysis we will have to pay a close attention to the ability of students to make use of the affordances of this milieu for the assessment task. The milieu comprises 11 sequences, some being examples of sequences which tend to +∞, some being non-examples. Beyond this fundamental feature, each of them displays a combination of properties – in terms of sign, variations, upper or lower bounds – which could play a significant part when assessing a candidate-definition, or comparing and contrasting candidate-definitions. In phase one, these properties were not the object of study, even though they were facts which the teacher made explicit in order to stress logical connections between properties. Only the a posteriori analysis will enable us to be confident that drawing, in phase 1, the attention of the students on a few facts and connections which the teacher deemed relevant actually generated argumentative resources (and constraints) for students to make use of (and take into account) in phase 2.

To sum up, at the end of the second phase, we expect that the collective discussion of phase 2 will have:

• Triggered an active engagement of the students in a non-standard task, namely a defining task; or, more precisely, the task of assessing candidate-definitions.

• Led to a consensus – within the collective comprising the students and the neutral teacher – on the following points: “not bounded above” cannot be accepted as definitory for “infinite limit” since the former is a necessary but not a sufficient for the latter. However, it is our best guess yet, since (1) it is a bona fide mathematical property, something that can be defined mathematically - as opposed to mere images such as “infinitely large” etc., (2) at least it is a necessary condition - as opposed to “increasing (at least from a certain rank)”, which is neither necessary nor sufficient.

In particular, our hypothesis is that in this teaching context – with high school students with no experience of analysis as a deductive theory, no experience of definition construction, and very little experience of nested quantifiers – the outcome of phase 2 will be substantial but negative: rejection of “increasing”; qualified rejection of “not bounded above”. Thus, the design has a third phase for which we identify two non-independent key didactic variables: the nature of teacher intervention, and the semiotic registers. First, once the negative results have been reached, the teacher will be at liberty to explicitly ask students to focus on “not bounded above” and ask for ways to strengthen into a necessary and sufficient condition for the infinite limit. Second, should students have used only rhetorical formulations until then, the teacher will be at liberty to ask them to rephrase in the formal register. This choice rests on the elements gathered in the preliminary analysis with respect to the specific affordance of the definition of “not bounded above”. Moreover, in the a posteriori analysis, we will show that the affordances of the formal register enable students to tinker with candidate-definitions in order to generate new ones. Our experimental results will show that this path is viable and fairly robust.

Admittedly, since we did not change these variables throughout the four experiments, we cannot claim that working in the formal register is necessary or even more likely to lead to the formulation of a correct definition than remaining in the rhetorical register. In particular, it seems possible for the “almost all definition” to emerge in the rhetorical register. Nevertheless, this definition did not emerge in (Martin et al. 2014); in (Roh and Lee 2017), it was given by the lecturer for students to assess. Also, the results of (Martin et al. 2014) suggest that a version of the definition could be reached in a mixed formal-rhetorical register, by first strengthening “for any real number M, there exists an nfor which u_n ≥ M” into “for any real number M, there exists an nafter whichu_n ≥ M”. The latter candidate-definition is incorrect due to the use of the same letter n to denote both a number and all its successors, but it could in turn be modified into a correct definition expressed in the mixed register. We do not deem it likely that this path could have been taken if students had started from a purely rhetorical version of “not bounded above” such as “the sequence becomes greater than any given number”, since we do not consider formulations such as “the sequence becomes greater than any given number and remains so” as qualifying as a definition.

In order to strengthen the condition “not bounded above” so as to make it not only necessary but also sufficient for “infinite limit”, students will be asked to remind the teacher of formal expression for “bounded above”:

$$ \exists M\in \mathbb{R}\kern0.5em \forall n\in \mathbb{N}\kern0.5em {u}_n<M, $$

then asked to express its negation:

$$ \forall M\in \mathbb{R}\kern0.5em \exists n\in \mathbb{N}\kern0.5em {u}_n\ge M, $$

Although there is no logical necessity for it, we will use subscripts in order to be more explicit on the relations between the variables:

$$ \forall M\in \mathbb{R}\kern0.5em \exists {n}_M\in \mathbb{N}\kern0.5em {u}_{n_M}\ge M. $$

As regards phase 3, our main hypotheses are that (1) in the given teaching-context, the students can suggest one of the correct definitions in their endeavor to strengthen “not bounded above; and (2), in the process of collectively assessing the newly generated candidate-definition, they will be able to select this strengthening as definitory for “infinite limit” on the ground that it is the only one compatible with three constraints afforded by the milieu:

• One should work in the setting of formal logic.

• Sequence h – which (starting from n = 1) goes 0, 4, 0, 8, 0, 12, … – is a non-example of “infinite limit”, because of the uniqueness requirement.

• Sequence j – which takes value 3n for even values of n, and value n for odd values of n – is an example of “infinite limit”, which implies that “increasing (at least from a certain rank)” cannot play any part in the target definition.

The a posteriori analysis will show that students tend to come up with the additive form of the standard definition.

A Posteriori Analysis

This lesson plan was tried out twice in 2016 and twice in 2017, with year 12 science majors, in standard teaching conditions in a French high school: a two-hour session, in classes of 30 to 35 students. The teaching took place in November, while the chapter on the algebra of limits and its list of admitted rules had been studied in September. At the beginning of the session, the teacher explained that they were going to resume work on limits. Of course, the fact that the final aim of the session is the formulation of a definition of the infinite limit was not mentioned, since one of the objectives of phase one is to lead students to express – or at least acknowledge – the need of a definition. The two teachers (denoted 1 and 2) were experienced teachers who were involved in the design of the session right from the start. This a posteriori analysis will bear only on the collective phases, which were audio recorded. “2016–1” will denote the experiment carried out in 2016 in the class of teacher #1, etc.

Emergence of the Need for a Sorting Criterion in the Case of “Multiple” Limits

In the collective discussion of phase 1, the sorting of sequences such as e_n = (−1)ⁿ × n, h_n = ((−1)ⁿ + 1) × n, and j_n= ((−1)ⁿ + 2) × n was meant to trigger dissensus among students, which, in turn, was to lead them to take a step back and begin discussing their understanding of limits beyond the case of such and such sequence. The first goal was reached consistently in the four experiments. However, whether or not that led students to voice, or at least acknowledge, the need for a “definition” calls for a nuanced answer.

Let us take the example of the discussion of (e_n) in 2016–1. Working in pairs, students were asked to sort the sequences in one of the three categories: tends to +∞ / does not / I don’t know.

Teach.: So, what about e _n ? Whose turn will it be … Mathias and Louis-Maxime, what did you do with this one?

Mattias: we said the values oscillate between the positive and the negative, so it tended to +∞ and −∞ … we didn’t consider that it tended … so: “we don’t know”

Teach.: Did everyone hear the arguments, the hesitations of Louis-Maxime and Mattias? (…) repeat what you said Mattias.

Mattias: It tends to +∞ and −∞

Teach. : yes, but it does do not do this [gesture], it does this, that, this … OK ? and so …

Mattias: If one says that we can have … have both, one could say that it tends to infinity, but if it has to be … to tend only to infinity then

Teach.: positive infinity

Mattias: that’s what we say.

The student was aware that the sorting problem did not stem from a lack of understanding of the behavior of (e_n); but from the fact that, in spite of a clear understanding of this behavior, the lack of a convenient “tends to +∞ and −∞” made it difficult to sort. The students spotted the fact that the issue lay in the uniqueness, and that the sorting task could be carried out if some convention was settled regarding the use of the phrase “tends to +∞”. From a grammatical viewpoint, his use of the neutral “one” instead of the “we” he used to express the view of his group is probably indicative of the implicit reference to a shared convention.

Teach.: yes, with “positive”. So, we leave it here [in the “I don’t know column”] because we don’t know what to say. Did some of you sort (e_n) in another column? OK, Augustin.

Augustin: we said it did not tend to +∞.

Teach.: so you sorted it here, why ?

Augustin: … because it does not tend to +∞.

Teach.: hmmmm, we’ve reached heights in argumentation ! … Isabel?

Isabel: well, we know it does [gestures].

Teach.: this sort of … come and go, OK

Isabel: well, it tends … so … it’s sure we cannot sort it in the same categories as the others and, in math, its either yes or no, so, by deduction …

Student [in the background]: and who says it’s “either yes or no”!

Teach.: so, in math its either yes or no …

Student [in the background]: it can be “greater than or equal to”

Teach.: … either true or false … so one cannot say, given what math is, on cannot say that sometimes it would do this and sometimes …

Isabel: there is no limit, so if there is no limit then it does not tend to infinity.

Here also, Isabel took a step back and proceeds “by deduction” to justify her sorting decision – “does not tend to +∞” – on the basis of her general understanding of mathematics. In the background, a student attempted to challenge the meta argument by remarking that in math class we sometimes use expressions which cover several exclusive cases. In the next minutes, the teacher asked the students whether they agree or disagree with Isabel’s argument. On the whole, this argument failed to convince part of the class, either because of its intrinsic nature, or because it is meant to support her conclusion (“there is no limit, so if there is no limit then it does not tend to infinity”); a conclusion which was met with disbelief. In an attempt to counter Isabel’s deduction, another student explained:

Romain: … that is, in math, when we see a curve and it has limits, well, then, the curve cannot go beyond.

Teach.: you mean, something like this [gesture for the horizontal asymptote]

Romain: that’s it.

Teach.: OK, it would be bounded then

Romain: if it does not tend to infinity, then it is bounded.

Romain’s explanation was clearly based on a series of common misconceptions about limits, yet it attempted to conjure up a general property of limits, and sketched a deduction: sequences (or functions) with (finite) limits are bounded; so, since sequence e is not bounded, it tends to infinity. At this point – and, more generally, throughout phase 1 – the teacher did not prompt students to precisely word the logical connections between the various properties. However, and from this point onward, the term “bounded” would be part of the mathematical milieu. On other occasions, students began to toy with other properties in the course of their argumentations. For instance, in 2017–1, in order to defend his sorting of sequence e in the “tends to +∞” column, student Kian mentioned that “the fact that it is not strictly increasing does not prevent it from tending to +∞. (…) it tends to both +∞ and −∞.” In the 2017–2 experiment, when discussing h_n = ((−1)ⁿ + 1) × n, a student suggested a way out of the apparent dead-end by enriching the phrase “tend to +∞”: “I have a question. Could we say that it tends … with a condition for n? If it tends … it tends for all n-s, not under some condition; here it tends to positive infinity, but for some n-s, even or odd.”

On all four occasions, robust dissensus settled when it came to sorting those of the sequences which have “several” limits (whether finite or infinite), a fact which can be ascertained in two ways. First, it was never the case that all groups sorted them in a single category during the first phase of autonomous work. Second, even after occasionally heated exchanges of arguments among groups, no consensual decision was reached; for instance, in 2017–1, after 5 min of discussion of d, a final vote led to: 4 groups in favor of “does not tend to +∞”, 9 groups in favor of “tends to +∞”, and 4 groups opting for the “we don’t know” column.

By contrast, consensus was soon reached on where the hitch lies: a decision has to be made to clarify the sorting criterion, a decision bearing on whether or not a sequence can be said to tend to several limits. In our design, we deemed it possible that, at this point, students might realize that, in their curriculum, they had never been given a bona fide definition of limits; and that this is what failed them in this instance. The four experiments showed a range of reactions.

In 2017–2, on the basis of the failure to reach consensus on the sorting of ((−1)ⁿ + 1) × n, a student suggested the following move:

Student: We need a definition of what it means to tend to infinity.

Teach. [to the rest of the class]: shhh … Listen to what your classmate has to say.

Student: We don’t know what it means “tend to infinity” [inaudible].

On this occasion, the teacher could validate this need without meeting any particular reactions from the class. In 2016–1, students fully agreed that they did not know enough about limits to make some decisions, but the fact that what they needed was a “definition” was partially induced by the teacher in her request for more context-free formulations:

Teach.: (…) so, eventually, what do we need to decide; to cut short; to know.

Emmanuel: what it is to tend to infinity.

Teach.: yes, Emmanuel, what we call …

Emmanuel: we call the limit … to reach the limit …

Teach.: (…) so what do we need; what do we need to do to …

Student: define.

In 2016–2, things seemed to run just as smoothly, but actually failed to convince part of the class:

Teach.: So, in these cases of uncertainty, how will we be able to cut short? Yes

Student: Work out the value for n equals infinity.

Teach.: Well, we carried out these calculations, still you disagree among classmates … you all have the calculations – remember what we said – you all observed the same things yet you drew different conclusions. So, we have the calculations; what do we need to decide?

Simone: Define in which case we have the +∞ limit; can we consider that if a sequence has limit +∞, even if it also has a limit which is 0 or −∞.

Teach.: Indeed, and what Simone just said – which is very important – is that we need to define what’s going on, what’s happening. And, in this case, the notion we need to define is the one which we’ve been working with intuitively since the beginning; it is the notion of “tends to +∞”, and this notion has to be defined. Does everyone understand the necessity to formulate a definition? Sharon, I can see your shaking your head; why not?

Sharon: why “define”?

The teacher then asked students to explain, for the benefit of Sharon, why we needed a definition. The few reactions merely elaborated on the need to settle the uniqueness issue. Sensing that it failed to convince many of the need for a definition, the teacher tried to prompt students to reflect on the current dead-end from a higher standpoint by asking: “how does mathematics work?”, a question which elicited nothing but nonplussed silence. A student summoned up the courage to question this “need”:

Simon: Well, actually, I don’t understand why we need to define … the infinite limit. We know what it is.

Indeed, the exchange that followed shows that the fact that everyone agreed on the behavior of sequences such as e or f – they tend to positive infinity (possibly: among other things) – warranted Simon’s contention to the effect that – in a sense – we can tell when a sequence tends to +∞. He regarded the need for a convention on the uniqueness issue as a complement to this prior and consensual item of knowledge, and not as reason to forsake it by going back to the root. Maybe he would have been convinced by a slightly different formulation. In 2016–1, for instance, way into the second phase it dawned on one student that what they were trying to do was to define “tend to +∞ only”; the class regarded this formulation as a welcome clarification.

At any rate, even on the occasion where some students failed to be convinced that the necessary convention as to uniqueness required that a “definition” be written out, they engaged in phase two without any difficulty. A complete list of the candidate-definitions provided by the students in the two experiments of 2016 can be found in the Appendix. As explained above, we will not analyze these data in this paper.

The Pathway to the Definition in the 2016–1 Experiment

Students were handed out a selection of candidate-definitions (CD 1 to 5, see Table 1 below); they were given five minutes to read them and prepare arguments for the collective discussion. The goal of the collective discussion would be to decide whether or not either one of them should be accepted as definition of “tending to +∞”. The definition should accommodate sequences g and j, but rule out e and h; it should imply uniqueness of the limit.

Table 1 Candidate-definitions selected for collective discussion in 2016–1

In what follows, our goal is first to provide an overview of the pathway which led to the formulation of two mathematically correct definitions of the infinite limit. Since phases 2 and 3 took 55 min in total, it is possible to give a fairly comprehensive account of the exchange of arguments, so as to back up our claim as to the actual engagement of the students in the defining process, and provide a fine-grained description of the level and nature of teacher guidance. However, the description below has been streamlined and edited. In particular, we left out 5 min of the collective dialogue which bore on the nature and meaning of the dependence between the threshold value M and the index n_M; this issue will be discussed later. We also left out a short episode with students who remained unsure as to why sequences such as e_n = (−1)ⁿ × n or h_n = ((−1)ⁿ + 1) × n ought be considered non-examples in spite of the fact that they clearly tend to +∞ (among other limits). Even so, we did not select only those episodes which were mathematically correct and efficiently advanced the defining process. Indeed, dead-ends, move-backs, and incorrect or loosely-worded statements are central to the analysis of the pathway, both to document the role of the teacher, and to test our global hypotheses as the pivotal roles of a concept (“not bounded above”) and a semiotic register (that of predicate logic, with its formal and mixed variants).

In the boxes below, the italicized texts on the left-hand side are transcriptions from the audio-recordings. For lack of space, summaries occasionally replace transcription extracts. On the right-hand side, the analysis of the successive moves of the actors rests on the adaptation of Ouvrier-Buffet’s tools described above: C stands for “control” (i.e. assessment of the current state of the milieu – usually after its alteration by the use of some operator – with regard to the target problem), O stands for “operator” (action on the milieu). In order to distinguish between the cases when the controls and operators were actually carried out, and those when they were only referred to or hinted at, we use HC and HO to code for the latter. To distinguish between types of agents (students or teacher), teacher interventions are underscored. The analysis on the right-hand side does not aim to capture all that can be seen as didactically relevant in the session, but that which can be captured within this specific framework.

Teach.: So, let’s go; try to concentrate. So, Angèle [raising her hand], what do you think of the first suggestion: “For a sequence to tend to + ∞, we need to have ∀ n ∈ ℕ,  un + 1 > un”? Angèle: I think it’s incorrect, since a sequence can be decreasing then increasing.
	C: Spot that a condition is too strong / not necessary. This student came up with a similar argument in phase 1, then used the operator “weaken the condition” by suggesting that “increasing” should be replaced by “increasing in its last part”.

Teach.: (…) Are there others among you with arguments … Mattias. Mattias: If we consider f n , we can see that it’s increasing, yet it tends to 10,000. Teach.: Yes. So the sequences in our collection can be used as … as what? Mattias: examples. Teach.: counter-examples.
	C: Spot a non-example from the list of sequences which is compatible with CD1.. This student makes relevant use of the list of sequences from phase 1; however, he does not express the type of control he exerted in the framework of logic (“increasing” not sufficient). O: Reject CD1

Victor: In #2 it’s written that it is increasing and not bounded above, and we said that increasing is not a factor, so …

C: Spot that a condition is too strong / not necessary. Victor is referring to Angèle’s argument. Again, the wording in terms of “factors” remains pre-logical. As far as operators are concerned, rather than rejecting CD2 right away students suggested it be “qualified” (in French: “nuançons”) with a mention of the behavior “towards the end”.

Teach.: (…) What’s the difference between these two sentences, between the first one and the second one? What difference in terms of form, so to speak? Student: The first one is a little more vague. Teach.: No, it’s not vague; everyone understood it right away. Maxime. Maxime: In the second one something is added. Well … for instance in the first one we can say that the fact that u n + 1 is greater than or equal to u n , well it can still be bounded above, hence not tend to + ∞, whereas in the second one, it is said it’s not bounded above, so, well… Teach.: So what? … Angèle. Angèle: The first one is a necessary condition.	HC: Compare the logical forms of the CD1 and CD2.
	C: A condition of the form “A and B” is stronger than “A”. C (likely): Adding “and bounded above” is efficient in so far as it does rule out sequence f.
	C: Analysis of the logical connection between the properties mentioned in CD1 and CD2 in terms of necessary/sufficient condition. Angèle is wrong, however, since “increasing” is not a necessary condition. C: In CD2, “if and only if” expresses a necessary and sufficient condition. O: Split the “if and only if” statement into two converse implications. HC: Assess the validity of the two statements independently. C: Several students acknowledge the validity of “If a sequence is increasing and not bounded above, then it tends to +∞”. No one dissents.

Teach.: OK, so what about #3, what do you make of it. #3 is “The sequence (un) tends to + ∞ when it is not bounded above.” Rémi. Rémi: It looks good to me because … it’s a necessary and sufficient condition. Teach.: So, first, is it the case that this sentence states a necessary and sufficient condition? … it’s not very clear to me. This “when”, in maths … who wrote this sentence? … it’s you Rémi! What did you mean by “when”? Rémi: I meant to say “if”. Teach.: So let’s write down what you meant to say: “If (un) is not bounded above, then it tends to + ∞”. Now that’s written in such a way that we can understand what is the sufficient condition. So what do you think? … Isabelle. Isabelle: We saw that in the case of a sequence which does this [oscillating gesture], on the one hand it tends to infinity, and on the other hand also to negative infinity. Teach.: That was e n in the list. Isabelle: It wasn’t bounded above but it didn’t have to tend to + ∞, because it wasn’t bounded below either. Teach.: So you think it needs to be bounded below to tend to + ∞. Isabelle: I think so, yes.
	C: Consider the logical form of the definition. Check that – as it should – it states a necessary and sufficient condition.
	C: Spot a vague wording. HO: Ask for a more precise rewording.
	O: Select an explicit logical connector.
	C: Spot that CD3 accommodates non-examples.
	C: Spot a property (“not bounded below”) of the non-example being discussed.
	O: Complement the CD with the negation of “not bounded below” to rule out the non-example. The data do not allow us to distinguish between two possible motives for Isabelle’s move: it could be a case of monster-barring (to rule out sequence (en)), specifically). It could also be the case that Isabelle holds it to be the case (as part of her concept-image) that sequences that tend to +∞ are bounded below, hence this requirement can be added to the CD. In the three other experiments, this specific operator was used by students as a monster-barring move.

Rochelle: Couldn’t we put it in the necessary position?

O: Generate a new statement by considering the converse of an implication. C: Statement considered valid by the whole class.

Teach.: Let’s take a quick look at #4 “the sequence increases while getting ever closer to + ∞ but without ever reaching it.” What do you make of that? (…) “increasing”, what did we say earlier? That it’s not a condition we would consider any more. So this one doesn’t look … should be keep it? [hubhub] It’s not really a definition, “it comes ever closer”, what can it mean? Student: the ordinate. [The teacher then asked those who wrote CD4 to reformulate] Emmanuel: It means the sequence is increasing and hmmm… well, I could’ve replaced by un + 1 ≥ un. Teach.: Sure, but “increasing” and un + 1 ≥ unthat’s the same, agreed? So: “increases and comes ever closer to + ∞” … Emmanuel: It means it cannot go down again. Teach.: [to the class] Does that sound relevant to you: “cannot go down again”? Student: well, actually, it can go down a little. Teach.: “go down a little”? … Student: well … before going over.
	C: Spot a condition that has already been acknowledged to be neither necessary nor sufficient. C: Spot undefined terms in the CD. HO: Ask for clarification.
	O: Reformulate.
	HO: Reformulate.
	O: Rephrase in the formal register.
	C: Ill-defined term still here.
	O: Rephrase ill-defined term.
	C: Spot that the condition is too strong (possibly with example (gn) in mind).

After a quick and consensual rejection of CD5, a pair of students suggested a new CD:

Teach.: So, another pair of students has a new definition to suggest, let’s call it definition 6. Let’s see what’s on your worksheet: [copying onto the blackboard] ∀M ∈ ℝ  ∃ n ∈ ℕ  un > M [The teacher rephrased as “not bounded above”] Teach.: So, is the idea of not being bounded above an important one in order to capture “tending to + ∞”? Shall we keep it? … We said earlier that, if it’s not a sufficient condition, it means we have to … to what? … We need another one, we need to add an extra condition, agreed? So, what would you suggest? [A student suggested adding “and bounded below”, explicitly targeting non-example (en)]
	O: Suggest a new CD. O: Change semiotic registers formal → rhetorical.
	C: Spot a necessary but not sufficient condition. HO: Strengthen the condition.
	O: Add an extra condition. Monster-barring.

The teacher reformulated “not bounded above” by stressing that, for any M, it only warrants the existence of one index n such that un > M. She drew a scatter-plot with two horizontal lines at heights denoted by M and M’ to show that even if the sequence becomes greater than any M for some index, the condition says nothing as to its “future” behavior. Again, she asked for ways to strengthen “not bounded above” and capture the loosely-stated “remain greater than M”. The students went round in circles: some suggested “increasing”; some remarked that even after becoming greater than M, the sequence could “go down a little” and still tend to +∞.
	O: Change semiotic registers. Generate an example.
	HO: Strengthen. Reformulate.
	O: Strengthen.
	C: Condition too strong.

Maxime: un + 1 > M [oral emphasis on “+1”] Teach.: I need a complete sentence here. [being dictated to, the teacher wrote on the blackboard] ∀M ∈ ℝ  ∃ n ∈ ℕ We’ll call it n M to say that is depends on M, because every time I pick an M, it doesn’t have to be the same, right? So… $\forall M\in \mathbb{R}\kern1em \exists {n}_M\in \mathbb{N}\kern0.5em s.t.{u}_{n_M}>M$ $and\kern0.50em {u}_{n_M+1}>M$ Teach.: [to the class] So, what do you think … you can draw if it helps … [to Maxime] you wanted to prevent it from going down, is that it?	O: Add a condition.
	O: Use the affordances of the formal register to make relationships between variables more explicit.
	HO: Ask for clarification.
Maxime: Yes, but it means that afterward, u n + 1 becomes u n , and the next u n + 1 will still be greater …	O: Switch to the rhetorical register to express the intended meaning of the formal proposition. A similar attempt to formally capture the “for all terms after un” – reminiscent of the proof-by-induction scheme – was also observed in (Martin et al. 2014, 138).
Teach.: So, you agree that this will not do because here there’s only one … [to the class] Do you guys see what Maxime is trying to do?
	C: Condition too weak. O: Focus on the part of the formal proposition which fails to capture the intended meaning.
Maxime: u n +  x	O: Use the affordances of the formal register to introduce a new indeterminate in order to additively express “as from rank n” or “for ranks greater than n”.

A student had a hard time making sense of this x. Teach.: That’s a good question; indeed, this sentence isn’t precise enough. [to Maxime] Did you mean to say “there is a un + xfor which is remains greater”? Maxime: Whichever Teach.: So, would “for all x in ℕ” suit you?
	C: Variable x not quantified. HO: Quantify. O: Quantify. O: Reformulate in the formal register (possibly overinterpreting Maxime’s informal answer).

Teach.: Paul, you wanted to bring an improvement. What do you suggest? Paul: [inaudible] Teach.: Give me a complete sentence please. [being dictated to, the teacher wrote on the blackboard] $\forall M\in \mathbb{R}\kern0.5em \exists {n}_M\in \mathbb{N}\kern0.5em s.t.{u}_{n_M+x}>{u}_{n_M}>M$	Indeed, right after Maxime introduced variable x, Paul suggested the CD could be improved.
	C – O: Spot that the conditions can be rephrased more economically. Of course this formulation is incorrect for x = 0. The student also forgot the quantification on x.

Teach.: OK, that’s an improvement … can’t we do even better? Go ahead, I’m sure you can find it. I am. Don’t you find this a little too complicated? Maxime, this “ ${u}_{n_M+x}$ ” … can’t you think of a much simpler way to say this? Maxendre … [being didacted to, the teacher wrote on the blackboard] ∀M ∈ ℝ  ∃ nM ∈ ℕ s. t.  ∀ n > nMun > M
	HO: Simplify.
	O: Replace the additive formulation of “greater than” (“greater than nM” being captured by “nM + something”, “something” being assumed to be positive) by a direct formulation.

Comparison with the Other Experiments

A Robust Pathway

The global pathway described above is structurally similar to those observed in the three other experiments. The list of operators and controls exerted by students (without explicit prompts) show an active engagement in the defining process, mostly through a (usually) relevant use of the list of examples and non-examples provided by the first phase: spotting that a condition is too strong (since it rules out examples) or too weak (since it accommodates non examples); strengthening a condition to bar a “monster” (e.g. “not bounded above” → “not bounded above and bounded below”); weakening a condition that is too strong (e.g. “increasing” → “increasing from a certain rank”, “globally increasing”). Other operators and controls were usually exerted by students when asked by the teacher, in particular when it came to making logical aspects explicit: replacing rhetorical formulations such as “when” by implications; distinguishing between ⇒, ⇐, and ⇔; specifying whether newly introduced variables were to be quantified universally or existentially; spotting undefined terms and asking for reformulation and clarification.

The teacher plays a key role at the transition between phases 2 and 3: asking the class to focus on “not bounded above”; asking the class to suggest ways to strengthen this condition; underlining the fact that the existential quantifier in “∃n_M ∈ ℕ” puts no constraints on the “future” behavior of the sequence. These moves are clearly of a didactic nature. Nevertheless, our analysis is that they are not completely on the didactic side: firstly, the teachers focused students’ attention on elements which were already in the milieu, without introducing any new elements. Secondly, all the moves, even when hinted at by the teacher, were carried out by students. Thirdly, all the types of moves carried out in phase 3 had been carried out earlier (strengthen a condition, use the formal logical register etc.).

It should be mentioned that in the 2017–1 experiment, on one occasion, the teacher acted in a way which could not be regarded by the students as part of a shared response – from the collective formed by the students and the teacher – to the challenges of the milieu with respect to the problem. At some point during phase 2, a student attempted to distinguish between the behaviors of ((−1)ⁿ + 1) × n and ((−1)ⁿ + 2) × n by suggesting that “bounded below and not bounded above” was to be considered separately for the subsequence of even indices and that of odd indices. This interesting operator is somewhat specific to definitions of properties of sequences: replace “condition X on (u_n)” by “condition X on (u_2n) and on (u_2n + 1)”; it can serve as a template for a whole range of new operators seeking to apply some condition to some/all subsequences. On this occasion, the teacher deemed this to be a rather sterile and time-consuming path and cut short, arguing that she could generate at will new examples and non-examples by weaving together not two but three or more simple patterns.

In the a priori analysis we claimed that – at least for phase 3 – it was more likely that a correct definition would be formulated if work took place at least partly in the formal register. The a posteriori analysis provides elements to refine this claim. This also gives us the opportunity to give an overview of phase 3 in the three other experiments, thus grounding our claim of robustness of the engineering.

As far as purely logical aspects are concerned, nothing in the four experiments suggests that the rhetorical “for all” and “there exist” cannot be used as easily and efficiently as the corresponding symbols which serve as a mere shorthand. What is decisive is the explicit introduction of variables (from a mathematical viewpoint) denoted by letters (from a semiotic viewpoint) in order to express properties such as “(not) bounded above/below”, or “(strictly) increasing (from a certain rank)”. As hypothesized in the a priori analysis, working only with these rhetorical formulations proved adequate when it came to rejecting candidate-definitions, but led to an apparent dead-end, with a long list of ruled-out combinations of these properties, and no clue as to how to get out of this predicament. The introduction of variables to express these properties has at least two benefits. Firstly, it provides opportunities to express the fact that some variables depend on others. Of course, in “$\forall M\in \mathbb{R}\kern1em \exists {n}_M\in \mathbb{N}\kern0.5em s.t.{u}_{n_M}>M$” it is not necessary, from a logical viewpoint, to write n_M rather than n. For students with almost no experience of nested quantifiers, however, it is probably helpful. Secondly – and more importantly – the introduction of variables to denote sequences allows for a clear distinction between the values of the sequences and the ranks (i.e. the “u”s and the “n”s), and gives students the opportunity to exert controls and carry out operators on either one of them. In the 2016–1 experiment, the path from “u_n” to “u_n + 1”, then “u_n + x”, and eventually “u_p (with p ≥ n)” led to the standard definition. Variants of this path were observed in the other experiments.

In phase 3 of the 2016–2 experiment, the teacher gave students 5 min to work in pairs and try to write down new candidate-definitions by strengthening “not bounded above”. He spotted that a pair of students introduced “u_n + i”, and asked them to write their candidate-definition on the blackboard. They wrote

$$ \forall M,\exists n\ \mathrm{and}\ i\ \mathrm{such}\ \mathrm{that}\ {u}_n>M\ \mathrm{and}\ {u}_{n+i}>M $$

When asked to explain their idea to the class, the students said “for all i u_n + i > M”. The teacher pinpointed the discrepancy between the written expression – in which variable i is existentially quantified – and the oral explanation. When asked to choose between ∃ and ∀, the students made the relevant choice by selecting the universal quantification. This episode possibly illustrates a fact observed on several occasions: when students introduced new variables, they usually did not quantify, thus introducing free variables (i.e. indeterminates). It can be hypothesized that they regarded this as capturing the same intended meaning as a universal quantifier. However, our data is too scarce for us to investigate this hypothesis.

A very similar chain of formulas was observed in the 2017–1 experiment. In phase 2, students had introduced in the milieu the additive notation “u_n + 2” in their attempt to split a sequence into its subsequences of even and odd indices (respectively). In phase 3, a student used this template to introduce “u_n + m” (with an unquantified m). When the teacher asked the class if they thought this move was relevant, another student ventured “u_{n + infinity}”. The teacher rejected this notation, and students readily suggested that variable m should be universally quantified.

Only in the 2017–2 experiment did students suggest “for all m > n” without first toying with the additive form “u_n + …”.

These results suggest that working with sequences rather than functions (defined on domains including intervals of the [a, +∞) type) provided specific opportunities for students to reach a correct definition. Of course, the additive “f(x + y) for all y ∈ ℝ⁺” is equivalent to “f(y) for all y ≥ x”. However, it is less likely that the additive notations would have been introduced in the non-discrete context, since in the discrete context students used them either to echo the proof-by-induction scheme or to denote sub-sequences.

A Window of Opportunity for the “Almost all” Definition in the 2017–1 Experiment

In the 2017–1 experiment, the teacher decided to curtail an exchange of arguments which was heading toward the standard definition of the infinite limit, and which might have branched out onto a path to the “almost all” definition.

During phase 2, the teacher had taken the opportunity offered by the assessment of the candidate-definition “A sequence tends to +∞ iff it’s bounded below and not bounded above”, to get the formal definitions of these two properties written formally on the blackboard. By the end of phase 2, students were trying to find ways to capture the notion of global behavior of a sequences, toying with expressions such as “on average”, “as a whole”, “all in all”. They also mentioned that the “first” values do not really “matter”, since only what happens “as n tends to infinity” was to be taken into account.

Antoine: [inaudible]

Teach.: “the mean line should be increasing” … we said “increasing” could not play any part, but I understand what you mean. You mean to say that globally it should increase [in the background, several students approve] … we agreed that “not bounded above” is a necessary condition. If it’s not a sufficient condition, it means we need to add a little something [several students approve]. So, if it’s not bounded above, it means that, if I consider a number, there is a value which is greater. If we want the sequence to tend to +∞, what should we add?

Victor: We could say that there is an infinity of ranks for which all the values which are above … are above.

[Silence in the class. Some giggles]

Teach.: I see what you mean, but I’m not a hundred percent sure. Let us write down what you said. It went like: (u_n) tends to +∞ … [to the rest of the class] I assure you it’s meaningful, you just need to see in written form. Victor, come again please.

Victor [dictating to the teacher]: … if there is an infinity of ranks … for which …

Teach.: Try to avoid using “above” twice! “for which” …

Victor: for which, all the following ranks are greater than this one

Teach.: Than this one?

Victor: Than the value for this rank

[In the background, some students complain they don’t understand what “rank” means. Others offer support: “go Victor”]

In his attempt to capture the idea of global behavior, Victor introduced into the milieu an expression which had not been used earlier, neither by the teacher nor by another student: “an infinity of ranks”. It is the only instance in the four experiments when a student suggested a formulation which could possibly have led to what we termed the “almost all” definition. In the literature, Roh and Lee’s experiment (2017) targeted this definition of convergence (at least as a provisional but correct one) by asking students to assess and compare two candidate-definitions (provided by the lecturer): some property holds for infinitely many values of the sequence vs there are only finitely many values for which it does not hold.

This excerpt also illustrates how difficult it is to work purely in the rhetorical register: it is quite likely that the two “above” in Victor’s first proposal referred either to the ranks (for the first one: for all n > n_M) or to the values (for the second one: ${u}_n>{u}_{n_M}$). Similarly, in his “all the following ranks are greater than this one”, he probably meant to “greater than the corresponding value” (and not the rank), as he partially made explicit when asked for clarification. We can also notice that Victor’s proposal also introduced into the milieu the notion of behavior “from a certain rank”, which is a key element of the correct definition; which is not the case for “an infinity of ranks”.

Victor: Maybe with letters …

Teach.: Maybe it would be easier with letters? Didn’t I just write it down with letters?

Victor: Yes, but with …

Teach.: Quantifiers?

Victor: Yes

Teach.: Well, yes, if you can do it the quantified way, maybe it’ll be easier. Indeed, we can feel that the French language isn’t helping here. Antoine, you wanted to try?

Antoine: That’s just the definition of an increasing sequence.

Teach.: … no, I don’t think so. At any rate, I don’t think it’s what he means to say. Victor?

Victor: There’s an infinity of ns for which it’s greater than u _n .

Teach.: But I can’t write this

Victor: Well … such that for all n greater than n

Our data does not allow us to determine whether Victor regarded “an infinity of ranks” and “for all ranks after a given one” as two distinct notions to be articulated, or just conflated them. However, when the teacher rejected “an infinity of n” as a legitimate mathematical expression, he directly rephrased as “for all … greater than …”.

Teach.: “n greater than n”, really?

Victor: m

Teach.: Oh, I didn’t hear the difference.

Victor: Or p

Teach.: Let’s say p rather than m! [In the background, some students ask “what is p?”] p greater than n …

Victor: u _p greater than u _n ; greater than or equal to.

Teach.: We don’t need to go into that for now. … So “there exists p”

Victor: No, there exists n

Student1 [in the background]: No, it’s the other way round.

Student2 [in the background]: exists infinity n.

In this episode, Victor’s reworking of the formal definition of “not bounded above” led to the correct:

$$ \forall M\in \mathbb{R}\kern0.5em \exists n\in \mathbb{N}\kern0.5em \forall p>n\kern0.5em {u}_p\ge {u}_n>M $$

However, the teacher chose to cut short, maybe sensing that the rest of the class was not keeping track.

The Cost of Instantiation and the Impact of the Graphic Register

In the design of the engineering, students were to work either in the formal register – with sequences given by formulas, and properties expressed in a school-version of predicate logic – and the rhetorical register – either orally or in written form. An occasional use of the numerical register was considered, for instance to provide “0 -1 2 -3 4 -5 6 …” as an alternative to “(−1)ⁿ × n”. In the experiments, working in these semiotic registers provided enough affordances for students to go through phases 1 and 2 as planned. In particular, our account of phase 2 and the list of candidate definitions in the appendix show that, in spite of the fact that students had first worked with a short list of sequences, they did not engage in the task of painstakingly explaining why each one of them tends to +∞ (or doesn’t); rather, they engaged in the expected task, that of defining “tending to +∞” in general, and used the examples and non-examples to put candidate-definitions to the test.

However, in the four experiments, the teachers eventually resorted to the graphic register as well. They did so at the beginning of phase 3, usually in order illustrate on a scatter plot the respective roles of M and n_M in the formal definition of “bounded above” and the insufficiency of this property to capture the notion of asymptotic behavior. In the experiments, on the whole, this move did not hinder the emergence of correct definitions. However, the teachers did not stop the collective work as soon as he/she deemed that a correct definition had been put forth by one student; rather, they went on asking the class for their assessment of the new candidate-definition. The use of scatter-plots to assess a candidate-definition had two main adverse consequences.

Students’ difficulties with the universal quantifier have been noted on many occasions, even without the added complexity of a sequence of nested quantifiers. In the context of finite limits, Larsen and Swinyard (2012) stressed that the first universal quantifier can be interpreted in several ways which are not equivalent from a cognitive viewpoint: when it comes to verifying that a limit candidate is the limit, the first universal quantifier can be used to refer to an iterative process or procedure, thus capturing the idea of “infinitely close”; rhetorical reformulations such as “for any chosen ε” capture a more static idea of “arbitrary closeness”. Martin et al. (2014) mentioned a third viewpoint captured by standard rhetorical formulations such as “sufficiently close”. He also showed that these formulations were not transparent to many 1^rst-year calculus students, who did not associate with them any of the correct viewpoints but rather with a pre-mathematical idea of “very very small”. In our engineering, the initial universal quantifier emerged as a part of the formal definition of “not bounded above”, a definition which was usually reached in three steps: start from the formal definition of “bounded above”, negate it (students usually suggested “there is no M such that for all n, u_n ≤ M”) then reformulate with a universally quantified M. When shifting to the graphic register, however, the threshold value M was typically instantiated by a tick on the (unmarked) y-axis, possibly with a horizontal line at height M. The teachers meant this instantiation to be generic (as opposed to specific instantiations, as in: “for example, let’s say M = 10”) but it is likely that many students read off the tick or the line as denoting a given M (as opposed to the generic “any given M”). This may account for what happened in the 2017–2 experiment, when a student rejected a correct definition:

Student: Here, we didn’t say the sequence was increasing, am I right?

Teach.: Indeed

Student: So, what if it goes over M, then decreases and sticks to M without going below …?

For finite limits, a similar shift towards an existential reading of the first variable in the graphic register was also documented in the experiment of Martin et al. (2014). Even though the graphic register probably fosters this shift in interpretation, the blurring of the meaning of the universal quantifier through instantiation can also take place in the rhetorical register. For instance, in the 2017–2 experiment, students discussed for quite some time whether or not “For any real number M” and “Let M be a real number” (generic instantiation) were correct and equivalent interpretations of “∀M ∈ ℝ”.

The use of scatter-plots can have a second adverse consequence. From a logical viewpoint, it goes without saying that the following (equivalent) implications are true:

$$ {\displaystyle \begin{array}{c}\underset{n\to +\infty }{\lim }{u}_n=+\infty \Rightarrow \left({u}_n\right)\ is\ not\ bounded\ above\\ {}\forall M\in \mathbb{R}\exists n\in \mathbb{N}\forall p\ge n\kern0.50em \ \ {u}_p\ge M\kern0.5em \Rightarrow \kern0.5em \forall M\in \mathbb{R}\exists n\in \mathbb{N}\ \ \ \ {u}_n\ge M.\end{array}} $$

In this engineering, however, the heuristic process flows in the opposite direction, since students are to tinker with the definition of “not bounded above” and strengthen it into a definition of the infinite limit. To support students’ work in the experiments, the teachers drew scatter plots either to illustrate examples such as (−1)ⁿ + n, or non-examples such as(−1)ⁿ × n. These instantiations might actually hinder the emergence of a correct definition, and did so on one occasion. Indeed, for a given sequence (u_n) with infinite limit, and a given real number M, the fact that some natural number n is such that u_n ≥ M, does not imply that this number n is such that ∀p ≥ n u_p ≥ u_n ≥ M. In other words, for any given M the set {n ∈ ℕ such that u_n ≥ M } can be strictly larger than {n ∈ ℕ such that ∀ p ≥ n u_p ≥ M}; the equality of both sets for all Ms would imply that the sequence is increasing. Even if the students never expressed it this way, some were troubled by the fact that, even though they agreed that the goal was to precisely formulate the hitherto vague idea of “not going down below M”, it remained that for any given n_M such that ${u}_{n_M}\ge M$, the definition had to allow the sequence to “sink below M” for some n greater than n_M. This happened in the 2016–2 experiment, when student Angèle questioned the validity of Maxime’s candidate-definition: $\forall M\in \mathbb{R}\kern0.5em \exists {n}_M\in \mathbb{N}\kern0.5em s.t.{u}_{n_M}>M\ and\forall x\in \mathbb{N}\kern0.5em {u}_{n_M+x}>M$.

Teach.: (…) who wants to keep this definition ? … Angèle doesn’t agree … panic in the classroom! [Her classmates know Angèle to be excellent in maths]

Angèle: Well yes, but it what if ${u}_{n_M+1}$ is not greater than M ?

Teach.: What do you mean? What’s your sentence, because if you all give me just bits it’s not going to work. Well?

Angèle: It’s every u _n greater than M, and u _n + 1 …

Teach.: Should I leave the first part of the sentence unchanged?

Angèle: I don’t know.

The final line shows that Angèle was focusing on the final part of the definition while paying little attention to the string of nested quantifiers. In this experiment, the teacher did not have to cross the thin line between scaffolding and lecturing since Angèle herself managed to identify and express the fact that, for a given sequence and a given threshold value M, an n_M which works for “not bounded above” does not necessarily work the infinite limit:

Angèle: It’s not necessarily thefirst [oral emphasis] n which goes above, … not the first term.

Teach.: No, not the smallest. We did not write “the smallest”, we wrote “the exists”. On the graph, as I said, I had to make a choice and, here, indeed, it’s the first; but any one after that one would work just as well.

Our data does not allow us to determine whether this convinced Angèle, or if she stopped voicing dissent because she felt the teacher wanted the class to validate the candidate definition.

Discussion and Perspectives

As we highlight some key features of this case study, from the practical and the theoretical viewpoints, we will endeavor to point to some of its blind spots so as to identify further research perspectives, in connection with several fields of research on AMT.

As far as instructional design is concerned, the results of this experiment confirm the positive results reported by Roh and Lee (2017) in the case of finite limits. Although the improvement of teaching is not the only goal of research in mathematics education, it is rewarding to see that the collective effort of the community of researchers has produced a coherent body of knowledge allowing for fine-grained and efficient task design. In the preliminary analysis of the engineering, we laid emphasis on the results of research literature bearing either on the specific mathematical content (limits), or on general frameworks for the introduction and definition of advanced mathematical concepts. This case-study complements – since it deals with infinite limits – but also strengthens the positive results of Roh and Lee (2017), in two respects. First, it took place in more constrained conditions, namely with standard classes of high school seniors: students with very little knowledge and experience of logic (beyond the distinction between ⇒ and ⇐, and occasional encounters with quantifiers); students whose experience of mathematical analysis was – until then – entirely of the calculus type, and for whom this session on the definition of the infinite limit was the first encounter with the radically different framework of analysis. Second, we designed a milieu which we thought could lead students to word and acknowledge a definition of the infinite limit, whereas in the task designs implemented in classroom conditions, the definition (whether in its standard form or not) is usually given as an element of the milieu, for students to either assess, acknowledge, exemplify or rephrase (possibly a combination of these).

These constrained conditions of this experiment have an impact on the effects that could be expected and on the tools to objectify them. From an epistemological viewpoint, testing whether or not students can demonstrate some understanding and command of the definition in the context of a proof-task is probably what makes the most sense, since the main raison d’être of definitions of advanced concepts lies in their ability to contribute to the establishment of the network of deductibly derived mathematical facts which make up a mathematical theory. This was not an option in the ordinary high school context of this experiment.

In 2016, we attempted to assess the ability of students to recognize the formal definition and display conceptual understanding of the differences between “tends to +∞” and “not bounded above”, several months after the session. The results, discussed in (Chorlay 2018), are rather positive, even though the various levels of command of formal logic hindered direct comparison among groups (two of which being groups of 1st-year university students).

Another possible way to objectify the impact on students is to study their engagement in closely related situations of definition construction. In particular, students could be asked to compare and assess other definitions of the infinite limit (Ouvrier-Buffet 2006). They could also be asked to suggest definitions for finite limits. Since the latter definition is also required to be studied in the current French curriculum, the latter task was also entrusted to students in 2016 and 2017, in sessions designed by teachers 1 and 2. Since these sessions were not designed in a research context, their analysis could shed light not only on students’ ability to use their fresh experience of defining in a neighboring context, but also on teachers’ practices.

In this paper, we opted for the standard form of validation in the framework of didactic engineering, namely the comparison between the actual implementation and the hypothesized behaviors described in the a priori analysis. In particular, our data do not provide insight into individual student learning, or the variety of cognitive styles (Pinto and Tall 2002).

As far as expected educational effects are concerned, the specific conditions of this experiment suggest another potential line of investigation. Indeed, beyond the definition of limits itself, this teaching session provided an isolated occasion for senior high school students to experience a piece of mathematics which is typical of higher-education, with an emphasis on properties rather than on formulas, on argumentation rather than on calculation, and on perfecting analysis as a coherent deductive theory rather than as a toolbox for modeling discrete or continuous phenomena. As has often been stressed, these differences create a twofold challenge for students going through the secondary-tertiary transition: not only are many tasks new and difficult to carry out, but they often do not even make sense for students who cannot identify them as legitimate forms of mathematical activity (see (Artigue et al. 2007) and (Schneider 2008) for global analyses; see (Jablonka et al. 2017) for a recent case-study). Whether or not early but very limited exposition to analysis can have a long term impact on students’ image of mathematics and help smooth out the secondary-tertiary transition is probably well-worth investigating; all the more, since in several countries (among which Spain and France), the assumption that it could seems to be at play in the official high school curricula.

From a more theoretical perspective, we would like to stress that the two parts of this paper, far from being two independent contributions – one bearing on the role of conceptual differentiation in the history and didactics of advanced mathematics, and one on the role of the teacher in a classroom mathematical discussion – should be regarded as two sides of the same coin. Indeed, the way we analyzed classroom interactions and teacher intervention was shaped by the elements gathered in the preliminary and a priori analyses.

Clearly, the forms of teacher intervention observed in this experiment match those documented in other studies on classroom discussion. For instance, from the perspective of semiotic mediation, Bartolini-Bussi and Mariotti stressed the role of the teacher in “focalizing”, in “synthesizing”, and highlighted the fact that “the teacher is responsible on how far the evolution is to be stretched or stopped.” (Bartolini Bussi and Mariotti 2008, p.778) From the same perspective, Fischbein and Mariotti (1997) also documented the fact that it is usually the role of the teacher to clarify the logical connections between properties mentioned by students; to point to consequences of a choice of definition that had escaped students’ attention; and to highlight logical inconsistencies so as to prevent that students reach a consensual but mathematically unsatisfactory solution. From a different theoretical perspective, Yackel also underlined the importance of moves which played a part in our experiment, such as “initiate a shift in the discourse so that what was previously done in action can become an explicit object of conversation” (Yackel 2002, p.242), or “(use) their argumentative support to compare and contrast two reasonable interpretations (without indicating) that either or both were correct or incorrect.” (Yackel 2002, p.430).

Several theoretical frameworks allow can help us specify observables for the analysis of teacher intervention. In this paper, we did not use the framework presented in (Stephan and Rasmussen 2002), on the basis of (Cobb and Yackel 1996), for several reasons: our theoretical background was TDS and not RME; we did not use Toulmin’s model of argumentation, but deemed that, for a defining session which involved neither modeling nor proving, Balacheff’s notion of decision was more relevant; moreover, the time-scale of this study did not enable us to study the gradual emergence of classroom practices, or the stabilization of work-routines demonstrating the internalization of new argumentative norms and conceptual contents.⁵ Rather, we aimed at demonstrating that some well-identified high-level educational goals could also be reached in constrained conditions. To this effect, we designed a teaching path in which the role of the teacher was to be – in a sense – minimal, in order to maximize the interactions among peers and with the mathematical milieu; a milieu which we had designed so that the formulation of target-definition was a likely adaptative response. In particular, the preliminary and a priori analyses sought to justify and clearly delineate the admissible range of didactic teacher intervention: imposing uniqueness at the end of phase 1; at the beginning of phase 3, focusing students’ attention on “not bounded above” and requiring a shift from the rhetorical register – in which properties are referred to by their names – to a formal or partly formal register in which properties are defined. Thus, a posteriori analysis documents the range of teacher interventions insofar as they were – or were not – responses to the challenge of mediation between the students and the milieu. Since the defining activity was rooted in a classification problem, and not in the study of a conjecture or the making of a proof, we could only use part of the theoretical tools provided by Ouvrier-Buffet. In particular, we did not retain the notion of zero-definition; nor did we provide an a priori analysis of the range of candidate-definitions which students were likely to suggest at the beginning of phase2. However, the elements we retained provided tools to study the cognitive trajectory of students in phases 2 and 3, and to ground the claim that they actually engaged in a defining activity. As far as teacher intervention is concerned, the extension of Ouvrier-Buffet’s framework with the distinction between Os and Cs on the one hand, and HOs and HCs on the other hand, helped us assess the level of adidacticity in the codidactic situation. Although this approach is close to that of Bartolini Bussi (2009) and Bartolini Bussi and Mariotti (2008), the emphasis on adidacticy distances our approach from theirs, since they occasionally value didactic teacher intervention and imitation by the students.

Finally, this experiment raises questions as to its transferability to other teaching contexts. The fact that, on all four occasions, in constrained conditions, and with little direct didactic teacher intervention, the experiments led to the expected result, testifies to the robustness of the design. However, although robustness is probably a necessary condition of transferability, it does not warrant it. In particular, our a posteriori analysis showed that the mathematical, epistemological and didactical elements synthesized in the a priori analysis form a necessary background for principled teacher guidance. This fully parallels Yackel’s conclusion: “the analyses demonstrate that teachers need to have both an in-depth understanding of students’ mathematical conceptual development and a sophisticated understanding of the mathematical concepts that underlie the instructional activities being used.” (Yackel 2002, p.423).

Appendix. Candidate-definitions written by students – or pairs of students – at the beginning of phase 2 in the 2016 experiments

The candidate-definitions are numbered for the sake of clarity. We stayed as close as we could to the original French wording and to the layout of the original texts. The candidate-definitions selected for the collective discussion are in bold print.

2016–1.

• 1. For a sequence to tend to + ∞, we need to have∀ n ∈ ℕ, u_n +1> u_n.

• 2. The sequence (u_n) tends to + ∞ if and only if for all natural numbersn, (u_n) is increasing and not bounded above.

  ∀ n ∈ ℕ  u_n +1> u_nand (u_n) not bounded above

• 3. The sequence (u_n) tends to + ∞ when it is not bounded above.

• 4. The sequence (u_n) tends to + ∞: the sequence increases while getting ever closer to + ∞ but without ever reaching it.

• 5. A sequence (u_n) which tends to + ∞ is a sequence whose terms increase so that we cannot determine the last term of this sequence.

• 6. ∀M ∈ ℝ  ∃ n ∈ ℕ  u_n > M, moreover, the sequence (u_n) has to be bounded below.

• 7. To say that a sequence tends to +∞ means that there is no upper limit to the sequence.

• 8. A limit is a real number, unreachable for a given sequence.

• 9. A sequence (u_n) tends to +∞ if it is constant in +∞, or increasing without being bounded above.

  Sometimes some sequences tend to both +∞ and -∞

• 10. $\underset{n\to \infty }{\lim }=+\infty$

  In a sequence (u_n), there exists a n such that u_n =  + ∞

• 11. A sequence is said to “tend to +∞” when it is either constant at +∞, or constantly increasing. Exception: a sequence can also tend to +∞ and -∞, then it tends to +∞.

• 12. You never reach the limit, you can just come closer to it. By taking the greatest value of n that you please, you come really closer to the limit but you never go beyond it.

• 13. A sequence (u_n) which tends to +∞ is a sequence that is increasing and not bounded above by one of its terms.

• 14. The limit of a sequence is the value beyond which it cannot go any further

• 15. A sequence which tends to +∞ is a sequence which increases more than it decreases.

• 16. This sequence has no end. It is increasing. This increasing is endless, it is infinite. You always find an ordinate greater than the preceding one.

  u_n + 1 > u_n holds all in all for sequences in general, but, for instance, for (−1)ⁿ × n it does not, it becomes u_n + 2 > u_n.

2016–2

• 1. A sequence has limit + ∞ when it’s bounded below by a real number m .

• 2. Let (u_n) be any sequence. Then the sequence tends to + ∞ when (u_n) is strictly increasing

• 3. One can say that a sequence has limit + ∞ if all the terms of the sequence belong to (a number known or unknown, n ) or ( n , a number known …), this number of terms must not be finite.

• 4. The greatest value to which the sequence tends, whether it’s increasing or decreasing, is its limit.

• 5. A sequence has limit + ∞ ⇔ it’s increasing and not bounded above

• 6. A sequence (u_n) has limit + ∞ if and only if whenntends to + ∞, (u_n) tends to a unique number close to + ∞. If (u_n) is bounded above, the limit of (u_n) is the upper bound.

• 7. A limit is a value that a given sequence will never go beyond, whatever the value of its unknown.

  A sequence with limit + ∞ is an increasing sequence which has no limit.

• 8. A sequence has limit +∞ when ∀n, u_n + 2 > u_n and the sequence is bounded above by no real number.

• 9. There exists a unique limit to a sequence such that the values of that sequence are not greater than or equal to +∞

• 10. The limit of a sequence is a maximal value towards which the sequence tends.

• 11. A sequence (u_n) has limit k if and only if u_n tends towards k.

• 12. A sequence (u_n) has limit +∞ if and only if ∀n ∈ ℕ, (u_n) is not bounded and strictly increasing.

• 13. A sequence has limit +∞ if and only if it is strictly increasing and not bounded above and u_n can increase up to infinity

• 14. A sequence (u_n) has limit +∞ if and only if ∀n ∈ ℕ, the sequence (u_n) is increasing and not bounded above.