1 Introduction

Numerous practical and theoretical fields, such as engineering, health, transportation, and insurance, depend on count models. To describe pandemonium behaviour, crop harvesting, corporate data mining, e-commerce fraud, and other difficulties, data science methodologies have been utilised (see [30, 34,35,36]). One of the most significant applications of statistics is dealing with natural events or various real-world situations and representing them in a probability function that has a particular probability distribution that fits with those events. As a result, we must be aware of these accidents and express them using a random variable (rv). Every rv can be expressed by a probability distribution function, which can be discrete, continuous, or mixed. In this article, we present a mixed count model based on the Lagrange expansion given in [20].

In modeling count data, Poisson distribution is one common model in literature. This distribution, however, has unique characteristics that make it unsuitable for the majority of count data, particularly when there are problems with overdispersion or underdispersion. The majority of count data deviates from the assumption that the Poisson distribution’s mean and variance are equal (equidispersion). Consequently, it limits the applications of this distribution, see [23, 25]. Researchers have provided mixed-Poisson distributions in modeling count datasets as a possible solution to this issue. For instance, the authors in [7] created the Poisson-transmuted exponential distribution, a new mixed-Poisson distribution by combining the Poisson distribution with the transmuted exponential distribution (PTED). The Poisson-Bilal distribution was first introduced by [3]. The author in [5] introduced the Poisson-x gamma distribution. The Poisson-generalized Lindley distribution was first developed by [4]. An extensive literature review on mixed-Poisson distributions can be found in [22]. Many researchers have recommended using generalized distributions to explain the behaviour of their problems in order to deal with situations where many non-homogeneous events and common distributions are ineffective. The generalized distributions characterized by their ability to represent homogeneous and non-homogeneous population, also it is much wider than their traditional forms, see [8, 10, 39].

The authors in [10] developed generalized Poisson distribution (GPD) by using Lagrange expansion given in [20]. In contrast to the usual Poisson distribution, which has no dispersion flexibility, the GPD must be more appropriate in many types of data with overdispersion or underdispersion. The authors in [10] demonstrated that, depending on the value of the parameter, if it is positive, zero, or negative, respectively, the variance of the GPD is larger than, equal to, or less than the mean. Additionally, they demonstrated that when parameter values increased, so did the variance and mean values, see [23, 39]. The GPD model, which generalizes the Poisson distribution, is preferred in many statistical applications. In distribution theory and numerous applications, including branching processes, queuing theory, science, ecology, biology, and genetics, the properties of the GPD and the potential to represent data with overdispersion or underdispersion as well as the data with equal dispersion make it a desirable distribution. In the theory of Lagrangian distributions, GPD also occupies the greatest space and is the most important concept, one can refer by [29].

The moment distributions arise in the context of unequal probability sampling; have great importance in reliability, biomedicine, ecology, and life-testing. The authors in [12] proposed the moment exponential distribution (MED) through assigning weight to the exponential distribution by following the idea of [14]. The MED model attained great attention due to its flexibility so various authors studied and further generalized it for more complex datasets. For example, exponentiated-MED (see [15]), generalized exponentiated-MED (see [19]), Marshall-Olkin length biased MED (see [37]). The author in [2] recently put forth the Poisson-MED (PMED) model with one parameter count. Given the need for a more flexible distribution for statistical data processing, a new three-parameter discrete probability distribution with mixed generalized Poisson and moment exponential distributions is proposed in this paper. The proposed distribution will be more suited for analyzing count datasets. After little parameterization, the GPMED is similar to the Poisson Ailamujia distribution proposed by [16]. Also, the GPMED is a generalization of the PMED.

In addition, count data containing extra zeros are prevalent in many fields, including agriculture, biology, ecology, engineering, epidemiology, sociology, etc. Examples of such data include the number of women over 80 who pass away each day ([17]), the number of fetal movements per second ([26]), the number of HIV-positive patients ([38]), and the number of ambulances call for illnesses brought on by the heat ([6]), the number of health services visits during a follow-up time ([13]). Numerous zero-inflated models, including the zero-inflated Poisson distribution (ZIPD), the zero-inflated negative binomial distribution, and many others, have been researched in the literature to explain count data with excess zeros (see [40]). Zero-inflated models are becoming more and more common in various disciplines. In this article, we also create the zero-inflated version of the GPMED and give it the name zero-inflated GPMED (ZIGPMED).

The following is how the rest of the article is sorted. The detailed description of the Lagrange expansion and MED are covered in Sect. 2. The definition and some of its special cases are discussed in Sect. 3. Some mathematical properties, and other details are presented in Sect. 4. In Sect. 5, the maximum likelihood estimation technique is defined to estimate the unknown parameters of the new distribution, and the significane of the additional parameters included in the new distribution is tested in Sect. 6. The performance of the GPMED parameters for the maximum likeliood estimation is also studied using simulation technique in the Sect. 7. A zero-inflated model with respect to the new distribution is discussed in Sect. 8. The applications and the empirical studies based on the new model concerning two real datasets are conducted in Sect. 9. Then, Sect. 10 finishes with the decisive concluding words.

2 Some Preliminaries

In this section, we provide some mathematical background on the discrete generalized Lagrangian probability distribution (DGLPD), and definition of the MED.

2.1 The Discrete Generalized Lagrangian Probability Distribution

Let g(z) and h(z) be two analytic function of z, which are successively differentiable in [-1,1] such that \(g(1)=h(1)=1\), and \(g(0)\ne {0}\). Lagrange considered the inversion of the Lagrange transformation \(u=\frac{z}{g(z)}\), and expressed it as a power series of u. The author in [20] defined the Lagrange expansion to be:

$$\begin{aligned} {} h(u)=h(0)+\sum _{x=1}^{\infty }\frac{u^{x}}{x!}\, D^{x-1}\bigg [\big (g(z)\big )^{x}h^{'}(z)\bigg ]\bigg |_{z=0}, \end{aligned}$$
(2.1)

where \(D^{r}=\frac{\partial ^{r}}{\partial {z^{r}}}\) and \(h^{'}(z)=\frac{\partial {h(z)}}{\partial {z}}\).

If every term in the series (2.1) is non-negative, the series turns into a probability generating function (pgf) in u and gives the probability mass function (pmf) of the class of DGLPD, which is as follows:

$$\begin{aligned} {} P(X=x)={\left\{ \begin{array}{ll} h(0) &{} x=0,\\ \\ \frac{D^{x-1}\left[ (g(z))^{x}h'(z)\right] |_{z=0}}{x!}&{}x=1,2,3\dots \end{array}\right. } \end{aligned}$$
(2.2)

Using the Lagrange expansion described in (2.1), The authors in [11] defined and studied the class of DGLPD. For more references on the class of DGLPD, see [9].

According to [27], it is possible to derive the DGLPDs by relaxing the requirement that \(g(1)=h(1)=1\) for creating Lagrangian probability distributions. We create the new discrete mixture distribution based on the DGLPD using this relaxation.

2.2 The Moment Exponential Distribution

A rv T follows a MED, denoted as \(X\sim MED(\alpha )\), if its probability density function (pdf) is given by

$$\begin{aligned} {} f(t)=\frac{t}{\alpha ^{2}}\,e^{-\frac{t}{\alpha }},\,\,t>0,\alpha >0. \end{aligned}$$
(2.3)

Now, the cumulative density function (cdf) of the MED is given as

$$\begin{aligned} F(t)=1-\bigg (1+\frac{t}{\alpha }\bigg )\,e^{-\frac{t}{\alpha }}, \end{aligned}$$

where \(t>0\) and \(\alpha >0\).

The rth order non-central moment (\(\mu _{r}\)) associated with the MED is given by

$$\begin{aligned} \mu _{r}=E(T^{r})=\alpha ^{r}\Gamma (r+2),\,r=1,2,\dots , \end{aligned}$$

We have employed the gamma function defined by \(\Gamma (m)=\int _{0}^{\infty }t^{m-1}e^{-t}dt\), with the relation \(\Gamma (m)=(m-1)!\) for any positive integer m.

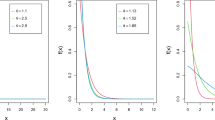
The graphical depiction of the pdf of the MED is shown in the plots in Fig. 1. To learn more about the MED, see [12].

Fig. 1
figure 1

Various shapes of pdf of the MED for different parameter values

Full size image

3 The Generalized Poisson-Moment Exponential Distribution

With the DGLPD, the following theorem from [28] is applied to create the new mixture of the MED, is given by

Theorem 3.1

Let \(g(z)>0\) and \(h(z)>0\) (for all \(z>0\)) be analytic functions such that \(g(0)\ne {0}\), \(\biggl \{D^{x-1}\left[ \left( g(z)\right) ^{x}h^{'}(z)\right] \biggr \}\bigg |_{z=0}{\ge {0}}\), and \(h(0)\ge {0}\), where \(D=\frac{\partial }{\partial {z}}\) is a derivative operator. If the series

$$\begin{aligned} h(u)=h(0)+\sum _{x=1}^{\infty }\frac{u^{x}}{x!}\biggl \{D^{x-1}\left[ \left( g(z)\right) ^{x}h^{'}(z)\right] \biggr \}\bigg |_{z=0} \end{aligned}$$

converges uniformly on any closed and bounded interval, then a rv X has a unform mixture of Lagrangian distribution with the pmf

$$\begin{aligned} {} P(X=x)={\left\{ \begin{array}{ll} \int _{0}^{1}\bigl \{\frac{h(0)}{h(t)}\bigr \}dt,&{} x=0,\\ \\ \int _{0}^{1}\biggl \{\frac{\big (\frac{t}{g(t)}\big )^{x}}{x! h(t)}\biggl \{D^{x-1}\left[ \left( g(z)\right) ^{x}h^{'}(z)\right] \biggr \}\bigg |_{z=0}\biggr \}dt,&{} x\ge {1}. \end{array}\right. } \end{aligned}$$
(3.1)

Proof

Proof is given in [28] and hence omitted. \(\square \)

Theorem 3.2

Let g(t) and h(t) satisfy the conditions in Thorem 3.1 and let f(t) be a pdf for some continuous rv T, then the pmf of X, a continuous mixture of Lagrangian distribution, is given by

$$\begin{aligned} {} P(X=x)={\left\{ \begin{array}{ll} h(0)\int _{-\infty }^{\infty }\big (\frac{f(t)}{h(t)}\big )dt,&{} x=0,\\ \\ \int _{-\infty }^{\infty }\,\biggl \{f(t)\frac{\big (\frac{t}{g(t)}\big )^{x}}{x! h(t)}\biggl \{D^{x-1}\left[ \left( g(z)\right) ^{x}h^{'}(z)\right] \biggr \}\bigg |_{z=0}\biggr \}dt,&{} x\ge {1}. \end{array}\right. } \end{aligned}$$
(3.2)

Proof

Proof is given in [28] and hence omitted. \(\square \)

Proposition 3.1

Assume that X follows the new mixture generalized Poisson-moment exponential distribution (GPMED) with \(\lambda >0\), \(0<\rho <1\) and \(\alpha >0\), the pmf of X is given by

$$\begin{aligned} {} P(x)=\frac{\lambda {\alpha ^{x}}\left( \lambda +\rho {x}\right) ^{x-1}\left( x+1\right) }{\big (1+\alpha (\lambda +\rho {x})\big )^{x+2}}, x=0,1,2,\dots \end{aligned}$$
(3.3)

This distribution is denoted as GPMED(\(\lambda ,\rho ,\alpha \)), and one can note \(X\sim {GPMED(\lambda ,\rho ,\alpha )}\) to inform that X follows the GPMED with parameters \(\lambda \), \(\rho \) and \(\alpha \).

Proof

Let \(g(z)=e^{\rho {z}}\) and \(h(z)=e^{\lambda {z}}\), where \(0<\rho <1\) and \(\lambda >0\). Under the transformation \(z=ue^{\rho {z}}\) and using the Lagrange expansion given in (2.1), we have

$$\begin{aligned} \begin{aligned} e^{\lambda {z}}&=1+\sum _{x=1}^{\infty }\,\frac{u^{x}}{x!}\,\biggl \{D^{x-1}\bigg [\left( e^{\rho {z}}\right) ^{x}\lambda \,e^{\lambda {z}}\bigg ]\biggr \}\bigg |_{z=0}\\&=1+\sum _{x=1}^{\infty }\,\frac{\lambda ~u^{x}}{x!}\,\biggl \{D^{x-1}\bigg [e^{(\lambda +\rho {x})z}\bigg ]\biggr \}\bigg |_{z=0}\\&=1+\sum _{x=1}^{\infty }\frac{\lambda }{x!}\bigg (\frac{z}{g(z)}\bigg )^{x}(\lambda +\rho {x})^{x-1}\\&=1+\sum _{x=1}^{\infty }\frac{\lambda }{x!}\bigg (\frac{z}{e^{\rho {z}}}\bigg )^{x}(\lambda +\rho {x})^{x-1}. \end{aligned} \end{aligned}$$

substituting \(z=t\), we get

$$\begin{aligned} \begin{aligned} e^{\lambda {t}}&=\sum _{x=0}^{\infty }\frac{\lambda \left( te^{-\rho t}\right) ^{x}\left( \lambda +\rho {x}\right) ^{x-1}}{x!}, \end{aligned} \end{aligned}$$

which implies

$$\begin{aligned} 1=\sum _{x=0}^{\infty }\frac{\lambda {t}\left( \lambda {t}+\rho {tx}\right) ^{x-1}\,e^{-\lambda {t}-\rho {tx}}}{x!}. \end{aligned}$$

when t = 1 the above formulation reduces to the GPD given in [10].

Therefore, by Theorem 3.1, we have a uniform mixture of the GPD as:

$$\begin{aligned} \begin{aligned} P(x)&=\int _{0}^{1}\frac{\lambda {t}\left( \lambda {t}+\rho {tx}\right) ^{x-1}\,e^{-\lambda {t}-\rho {tx}}}{x!},\\&=\frac{\lambda }{\left( \lambda +\rho {x}\right) ^{2}}\bigg [1-e^{-(\lambda +\rho {x})}\sum _{j=0}^{x}\frac{\left( \lambda +\rho {x}\right) ^{j}}{j!}\bigg ], \end{aligned} \end{aligned}$$

where \(x=0,1,2,\dots \)

Clearly, g(t) and h(t) generate a DGLPD, which satisfies the conditions given in Theorem 3.1. More generally, assuming that the conditions given in Theorem 3.1 hold, and by letting the variable t to be a continuous rv from the MED with pdf given in (2.3).

By using Theorem 3.2, the pmf of the proposed new mixture model is obtained as follows:

$$\begin{aligned} \begin{aligned} p(x)&=\int _{0}^{\infty }\bigg (\frac{t}{\alpha ^{2}} e^{-\frac{t}{\alpha }}\bigg )\frac{t^{x}e^{-\lambda {t}-\rho {tx}}}{x!}\,\lambda \left( \lambda +\rho {x}\right) ^{x-1}dt\\&=\frac{\lambda \left( \lambda +\rho {x}\right) ^{x-1}}{x!\,\alpha ^{2}}\int _{0}^{\infty }t^{x+1}\,e^{-\left( \lambda t+\rho {x}t+\frac{t}{\alpha }\right) }dt\\&=\frac{\lambda \left( \lambda +\rho {x}\right) ^{x-1}}{x!\,\alpha ^{2}}\frac{\Gamma (2+x)}{\left( \lambda +\rho {x}+\frac{1}{\alpha }\right) ^{2+x}}\\&=\frac{\lambda {\alpha ^{x}}\left( \lambda +\rho {x}\right) ^{x-1}\left( 1+x\right) }{\big (1+\alpha (\lambda +\rho {x})\big )^{x+2}}. \end{aligned} \end{aligned}$$

Hence the proof. \(\square \)

3.1 Some special cases of the GPMED are discusseed below,

  1. (a)

    Now, for \(\lambda =1\), \(\rho =0\), the pmf of the GPMED reduces to

    $$\begin{aligned} {} p(x)=\frac{\alpha ^{x}(1+x)}{(1+\alpha )^{2+x}},x=0,1,2,\dots \end{aligned}$$
    (3.4)

    The expression in Eq. (3.4) is the pmf of PMED, which was introduced by [2]. Thus, the GPMED is a special case of the PMED and hence GPMED is a generalization of the PMED.

  2. (b)

    For \(\lambda =1\), \(\rho =0\) and \(\alpha =\frac{1}{\beta }\), we obtain the pmf of Poisson Ailamujia, which was introduced by [16]. Hence the GPMED is a special case of Poisson Ailamujia distribution.

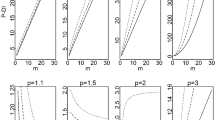
Now, the possible pmf and hazard rate function (hrf) plots for various values of the parameters of the GPMED are portrayed in Figs. 2 and 3, respectively.

Fig. 2
figure 2

Various shapes of pmf of the GPMED for different parameter values

Full size image
Fig. 3
figure 3

Various shapes of hrf of the GPMED for different parameter values

Full size image

4 Mathematical Properties

In this section, different structural properties of the GPMED have been evaluated. These include median, mode, non-central moment, etc.

4.1 Median

Let X be a rv following the GPMED. Then the median of X is defined by the smaller integer m in \(\left\{ 0,1,2,\dots \right\} \). By the definition, m is the smallest integer in \(\left\{ 0,1,2,\dots \right\} \) such that \(P(X\le {m})\ge {\frac{1}{2}}\),

$$\begin{aligned} \sum _{x=0}^{m}\biggl \{\frac{\left( \lambda +\rho {x}\right) ^{x-1}\alpha ^{x}(1+x)}{\big (1+\alpha (\lambda +\rho {x})\big )^{x+2}}\biggr \}\ge \frac{1}{2\lambda }, \end{aligned}$$
(4.1)

which is equivalent to the desired result.

4.2 Mode

Let X be a rv following the GPMED. Then, the mode of X, denoted by \(x_{m}\), exists in \(\left\{ 0,1,2,\dots \right\} \), and lies in the case:

We must find the integer \(x=x_{m}\) for which f(x) has the greatest value. That is, we aim to solve \(f(x)\ge {f(x-1)}\) and \(f(x)\ge {f(x+1)}\). First, note that f(x) can also be written as:

$$\begin{aligned} f(x)=\frac{\lambda \alpha ^{x}(\lambda +\rho {x})^{x-1}(1+x)}{(1+\alpha (\lambda +\rho {x}))^{x+2}}, \end{aligned}$$

Obviously, \(f(x)\ge {f(x-1)}\) implies that

$$\begin{aligned} {} \frac{\eta (x)}{\eta {(x-1)}}\ge \frac{1}{\alpha }, \end{aligned}$$
(4.2)

where

$$\begin{aligned} \eta (x)=\frac{(1+x)(\lambda +\rho {x})^{x-1}}{(1+\alpha (\lambda +\rho {x}))^{x+2}} \end{aligned}$$

Also, \(f(x)\ge {f(x+1)}\) implies that

$$\begin{aligned} {} \frac{\eta {(x)}}{\eta (x+1)}\ge {\alpha } \end{aligned}$$
(4.3)

By combining (4.2) and (4.3), we get (4.4).

$$\begin{aligned} {} \frac{\eta (x_{m}-1)}{\eta (x_{m})}\le {\alpha }\le {\frac{\eta (x_{m})}{\eta (x_{m}+1)}}, \end{aligned}$$
(4.4)

where

$$\begin{aligned} \eta (x_{m})=\frac{(1+x_{m})(\lambda +\rho {x_{m}})^{x_{m}-1}}{(1+\alpha (\lambda +\rho {x_{m}}))^{x_{m}+2}}. \end{aligned}$$

4.3 rth Order Non-Central Moment

The rth non-central moment \(\mu _{r}^{'}=E(X^{r})\) of the discrete variable X from the pmf given in (3.2) is:

$$\begin{aligned} {} \mu _{r}^{'}=E(X^{r})=\sum _{x=0}^{\infty }x^{r}p(x) \end{aligned}$$
(4.5)

and

$$\begin{aligned} {} E(X^{r})=\sum _{x=0}^{\infty }x^{r}\int _{-\infty }^{\infty }f(t)\frac{t^{x}}{x!\left( g(t)\right) ^{x}h(t)}\bigg [D^{x-1}\left( g(z)\right) ^{x}h^{'}(z)\bigg ]\bigg |_{z=0}dt. \end{aligned}$$
(4.6)

Then

$$\begin{aligned} {} E(X)=\int _{-\infty }^{\infty }\frac{f(t)}{h(t)}\sum _{x=0}^{\infty }x\,\frac{t^{x}}{\left( g(t)\right) ^{x}x!}\bigg [D^{x-1}\left( g(z)\right) ^{x}h^{'}(z)\bigg ]\bigg |_{z=0}dt. \end{aligned}$$
(4.7)

[20] showed that the Lagrange expansion could be written as

$$\begin{aligned} {} h(t)=h(0)+\sum _{x=1}^{\infty }\frac{\big (\frac{t}{g(t)}\big )^{x}}{x!}\bigg [D^{x-1}\left( g(z)\right) ^{x}h^{'}(z)\bigg ]\bigg |_{z=0}. \end{aligned}$$
(4.8)

Taking the first derivative of (4.8) partially with respect to t, we have

$$\begin{aligned} {} D^{1}\left[ h(t)\right] =\left( \frac{g(t)}{t}\right) \,D^{1}\left[ \frac{t}{g(t)}\right] \sum _{x=1}^{\infty }\frac{x\,\big (\frac{t}{g(t)}\big )^{x}}{x!}\bigg [D^{x-1}\left( g(z)\right) ^{x}h^{'}(z)\bigg ]\bigg |_{z=0}. \end{aligned}$$
(4.9)

which implies that

$$\begin{aligned} {} \frac{t\,D^{1}(h(t))}{g(t)D^{1}\left( \frac{t}{g(t)}\right) }=\sum _{x=1}^{\infty }\frac{x\,\big (\frac{t}{g(t)}\big )^{x}}{x!}\bigg [D^{x-1}\left( g(z)\right) ^{x}h^{'}(z)\bigg ]\bigg |_{z=0}. \end{aligned}$$
(4.10)

On using (4.10) in (4.7), we get

$$\begin{aligned} E(X)=\int _{-\infty }^{\infty }\,f(t)\,\frac{t\,D^{1}(h(t))}{h(t)g(t)D^{1}\left( \frac{t}{g(t)}\right) }dt=\int _{-\infty }^{\infty }\frac{f(t)D^{1}\log {(h(t))}}{D^{1}\log {\left( \frac{t}{g(t)}\right) }}dt. \end{aligned}$$
(4.11)

Taking the second derivative of (4.10), we get

$$\begin{aligned} D^{1}\bigg [\frac{t\,D^{1}(h(t))}{g(t)D^{1}\left( \frac{t}{g(t)}\right) }\bigg ]=\sum _{x=1}^{\infty }\frac{x^{2}\,\big (\frac{t}{g(t)}\big )^{x-1}}{x!}~D^{1}\left[ \frac{t}{g(t)}\right] \bigg [D^{x-1}\left( g(z)\right) ^{x}h^{'}(z)\bigg ]\bigg |_{z=0}. \end{aligned}$$

On multiplying both sides by \(f(t)t\left[ h(t)g(t)D^{1}\left( \frac{t}{g(t)}\right) \right] ^{-1}\), we get

$$\begin{aligned} {}{} & {} f(t)t\left[ h(t)g(t)D^{1}\left( \frac{t}{g(t)}\right) \right] ^{-1} D^{1}\bigg [\frac{t\,D^{1}(h(t))}{g(t)D^{1}\left( \frac{t}{g(t)}\right) }\bigg ]\nonumber \\{} & {} \quad =\sum _{x=1}^{\infty }\frac{x^{2}\,f(t)\big (\frac{t}{g(t)}\big )^{x}}{h(t)x!}\bigg [D^{x-1}\left( g(z)\right) ^{x}h^{'}(z)\bigg ]\bigg |_{z=0}. \end{aligned}$$
(4.12)

Therefore,

$$\begin{aligned} \begin{aligned} E(X^{2})&=\sum _{x=0}^{\infty }x^{2}p(x)\\&=\sum _{x=0}^{\infty }x^{2}\int _{-\infty }^{\infty }\frac{f(t)(\frac{t}{g(t)})^{x}}{h(t)x!}\bigg [D^{x-1}\left\{ (g(z))^{x}h'(z)\right\} \bigg ]\bigg |_{z=0}dt\\&=\int _{-\infty }^{\infty }\sum _{x=0}^{\infty }\frac{x^{2}f(t)\left( \frac{t}{g(t)}\right) ^{x}}{h(t)x!}\bigg [D^{x-1}\left\{ (g(z))^{x}h'(z)\right\} \bigg ]\bigg |_{z=0}dt\\&=\int _{-\infty }^{\infty }\frac{f(t)t}{h(t)g(t)D\left( \frac{t}{g(t)}\right) }\,D\bigg [\frac{tD\,h(t)}{D\left( \frac{t}{g(t)}\right) g(t)}\bigg ]dt\\&=\int _{-\infty }^{\infty }\frac{f(t)}{h(t)D\log \left( \frac{t}{g(t)}\right) }D\bigg [\frac{D\log h(t)}{Dlog\left( \frac{t}{g(t)}\right) }\bigg ]dt\\ \end{aligned} \end{aligned}$$

Similarely, the rth order non-central moment of X is given by,

$$\begin{aligned} {} E(X^{r})=\int _{-\infty }^{\infty }f(t)W_{r}(t)dt=E(X)W_{r}(T), \end{aligned}$$
(4.13)

where \(W_{1}(t)=D\left\{ \log {h(t)}\left[ D\log \left( \frac{t}{g(t)}\right) \right] ^{-1}\right\} ,W_{2}(t)=L(t)D\left\{ W_{1}(t)\right\} ,\)

   \(\dots ,W_{r}(t)=L(t)D\left( W_{r-1}(t)\right) \), where

$$\begin{aligned} L(t)=\left[ D\log \left( \frac{t}{g(t)}\right) \right] ^{-1}. \end{aligned}$$

4.4 Mean and Variance

Using (4.13), the mean (\(\mu _{x}\)) of the GPMED is derived as:

$$\begin{aligned} \begin{aligned} E(X)=\mu _{x}&=\int _{0}^{\infty }\frac{f(t)D^{1}\log {(h(t))}}{D^{1}\log {\left( \frac{t}{g(t)}\right) }}dt\\&=\frac{\lambda }{\alpha ^{2}}\int _{0}^{\infty }t^{2}e^{-\frac{t}{\alpha }}(1-t\rho )^{-1}dt. \end{aligned} \end{aligned}$$

Analogously, the variance (\(\sigma ^{2}_{x}\)) of the GPMED is given by

$$\begin{aligned} \begin{aligned} \sigma ^{2}_{x}&=E(X^{2})-\big (\mu _{x}\big )^{2}\\&=\int _{0}^{\infty }\frac{f(t)}{h(t)D\log \left( \frac{t}{g(t)}\right) }D\bigg [\frac{D\log h(t)}{Dlog\left( \frac{t}{g(t)}\right) }\bigg ]dt-\big (\mu _{x}\big )^{2}\\&=\frac{\lambda }{\alpha ^{2}}\int _{0}^{\infty }t^{2}e^{-(\lambda +\frac{1}{\alpha })t}(1-t\rho )^{-3}dt-\big (\mu _{x}\big )^{2}, \end{aligned} \end{aligned}$$

where \(\mu _{x}=\frac{\lambda }{\alpha ^{2}}\int _{0}^{\infty }t^{2}e^{-\frac{t}{\alpha }}(1-t\rho )^{-1}dt\).

It is important to observe that the integral part is incomplete gamma distribution and consequently the mean and variance of the GPMED do not exist as in the case of quasi-negative binomial distribution (see [29]).

5 Estimation

Here, we employ the method of maximum likelihood (ML) to estimate the GPMED’s unknown parameters.

Let \(X_1,X_2,\ldots ,X_n\) be n independently and identically distributed (iid) from the GPMED(\(\lambda ,\rho ,\alpha \)) (consequently, using the pmf from (3.3)), and \(x_1,x_2,\ldots ,x_n\) be n observations. Following that, the appropriate likelihood function is provided by

$$\begin{aligned} L = \frac{\lambda ^{n}\alpha ^{\sum _{i=1}^{n}x_{i}}\prod _{i=1}^{n}\left( \lambda +\rho {x_{i}}\right) ^{x_{i}-1}\prod _{i=1}^{n}\left( 1+x_{i}\right) }{\prod _{i=1}^{n}\big [1+\alpha \left( \lambda +\rho {x_{i}}\right) \big ]^{2+x_{i}}}. \end{aligned}$$

The log-likelihood function is given by

$$\begin{aligned} {} \begin{aligned} \mathcal {L}_{n}&=n\log {\lambda }+\sum _{i=1}^{n}\log \left( \lambda +\rho {x_{i}}\right) ^{x_{i}-1}+\sum _{i=1}^{n}x_{i}\log {\alpha }+\sum _{i=1}^{n}\log \left( 1+x_{i}\right) \\&\quad -\sum _{i=1}^{n}\log \big [1+\alpha \left( \lambda +\rho {x_{i}}\right) \big ]^{2+x_{i}}. \end{aligned} \end{aligned}$$
(5.1)

The ML estimate (MLE) of the parameter vector \({\Theta }=(\lambda , \rho ,\alpha )\), say \( \hat{\Theta }=(\hat{\lambda }, \hat{\alpha },\hat{\rho })\), is obtained by the solutions of the likelihood equations \(\frac{\partial {\mathcal {L}_{n}}}{\partial \lambda }=0\), \(\frac{\partial {\mathcal {L}_{n}}}{\partial \rho }=0\), and \(\frac{\partial {\mathcal {L}_{n}}}{\partial \alpha }=0\) with respect to \(\lambda \), \(\rho \) and \(\alpha \). With these notations, \(\hat{\lambda }\), \(\hat{\rho }\) and \(\hat{\alpha }\) are also called MLEs of \(\lambda \), \(\rho \) and \(\alpha \), respectively.

$$\begin{aligned} \frac{\partial {\mathcal {L}_{n}}}{\partial \lambda }= & {} \frac{n}{\lambda }+\sum _{i=1}^{n}\frac{\left( x_{i}-1\right) }{\left( \lambda +\rho {x_{i}}\right) }-\sum _{i=1}^{n}\frac{\left( 2+x_{i}\right) \alpha }{\big [1+\alpha \left( \lambda +\rho {x_{i}}\right) \big ]}=0\\ \frac{\partial {\mathcal {L}_{n}}}{\partial \rho }= & {} \sum _{i=1}^{n}\frac{\left( x_{1}-1\right) x_{i}}{\left( \lambda +\rho {x_{i}}\right) }-\sum _{i=1}^{n}\frac{\left( 2+x_{i}\right) \alpha x_{i}}{\big [1+\alpha \left( \lambda +\rho {x_{i}}\right) \big ]}=0 \end{aligned}$$

and

$$\begin{aligned} \frac{\partial {\mathcal {L}_{n}}}{\partial \alpha }=\frac{\sum _{i=1}^{n}x_{i}}{\alpha }-\sum _{i=1}^{n}\frac{\left( 2+x_{i}\right) \left( \lambda +\rho {x_{i}}\right) }{\big [1+\alpha \left( \lambda +\rho {x_{i}}\right) \big ]}=0. \end{aligned}$$

It is impossible to find analytical solutions to the likelihood equations. Even so, the MLEs can still be calculated numerically by maximizing the log-likelihood function provided in (5.1) using the best method enabled in the R programming language when adopting the L-BFGS-B algorithm.

6 Generalized Likelihood Ratio Test

In this section, we use the generalized likelihood ratio test (GLRT) to examine the importance of an extra parameter included in the GPMED. To learn more, see [32].

To test whether the additional parameter \(\lambda \) and \(\rho \) of the GPMED(\(\lambda ,\rho ,\alpha \)) is significant, we take over the GLRT method. Here, the null hypothesis is:

$$\begin{aligned} H_{0}:\lambda =1,\rho =0 \,\,\,\,\text {verses}\,\,\,\, H_{1}:\lambda \ne {1},\rho \ne {0}. \end{aligned}$$

In the case of the GLRT, the test statistic is given as:

$$\begin{aligned} -2\log \lambda ^{*}=2\left( \mathcal {L}_{n}(\hat{\Theta })-\mathcal {L}_{n}(\hat{\Theta }^{*})\right) , \end{aligned}$$
(6.1)

where \(\mathcal {L}_{n}(\hat{\Theta })\), with \(\hat{\Theta }\) is the MLE of \(\Theta =(\lambda ,\rho ,\alpha )\) with no restrictions and \(\hat{\Theta }^{*}\) is the MLE of \(\Theta \) under \(H_{0}\). The test statistic shown in (6.1) is asymptotically distributed as the chi-square distribution with two degree of freedom.

7 Simulation Study

To evaluate the performance of the estimates obtained using the ML estimation approach in random samples, we run a quick simulation exercise in this section. Here, we simulate a GPMED random sample using the inverse transformation method (see [33]). The following is the inverse transform algorithm for generating the GPMED rv:

  1. Step 1

    : Generate a random number from uniform U(0, 1) distribution.

  2. Step 2

    : \(i=0\), \(p=\left( 1+\lambda \alpha \right) ^{-2}\), \(F=p\).

  3. Step 3

    : If \(U<F\), set \(X=i\), and stop.

  4. Step 4

    : \(p=p\times \frac{\alpha (i+2)\,\left[ \lambda +\rho (i+1)\right] ^{i}\,\left[ 1+\alpha (\lambda +\rho {i})\right] ^{i+2}}{(i+1)\left[ \lambda +\rho {i}\right] ^{i-1}\left[ 1+\alpha \left( \lambda +\rho (i+1)\right) \right] ^{i+3}}\), \(F=F+p\), \(i=i+1\).

  5. Step 5

    : Go to Step 3.

where p is the probability that \(X=i\), and F is the probability that X is less than or equal to i.

The iteration process is repeated for \(N=1,000\) times. The specification of the parameter values is as follows:

  1. (i)

    \(\lambda =0.97, \alpha =0.5\) and \(\rho =0.01\).

  2. (ii)

    \(\lambda =0.71,\alpha =0.16,\rho =0.27\).

  3. (iii)

    \(\lambda =0.15,\alpha =0.25,\rho =0.75\).

Thus, we computed the average of the mean square error (MSE), and average absolute bias using the MLEs.

The average absolute bias of the simulated estimates equals \(\frac{1}{1000}\sum _{i=1}^{1000}|\hat{d}_{i}-d|\) and the average MSE of the simulated estimates equals \(\frac{1}{1000}\sum _{i=1}^{1000}(\hat{d}_{i}-d)^2\), in which i is the number of iterations, \(d\in \left\{ \lambda ,\rho ,\alpha \right\} \) and \(\hat{d}\) is the estimate of d.

Table 1 provides a summary of the study for the samples of sizes 50, 125, 500, and 1,000. As the sample size increases, it can be seen that the MSE in both cases of the parameter sets is in decreasing order, and the MLEs of the parameters go closer to their original parameter values, indicating the consistency property of the MLEs.

Table 1 The MLE simulation results for three parameters \(\lambda ,\alpha \), and \(\rho \)
Full size table

8 Zero-inflated GPMED

Overdispersed count data are often characterized with an excessive number of zeros and long or heavy tail properties. Common distributions used to fit data with long or heavy tail are either NBD or GPD. However, for the situation with an excessive number of zeros, these distributions may fail to adequately fit the proportion of zeros. The situation of excessive zeros often arises from the results of clustering (see [21]). For instance, in the insurance industry, excess zeros may arise when claims near the deductible are not reported to the insurer, as claim payments could be less than the increase in future premiums. In this article, we present the definition and some important properties of the zero-inflated version of the new proposed model GPMED, known as zero-inflated generalized Poisson moment exponential distribution (ZIGPMED).

Definition 8.1

Let \(\psi \) be a rv degenerate at the point zero and let X follows GPMED(\(\lambda ,\rho ,\alpha \)). Assume that \(\psi \) and X are statistically independent. Then a discrete rv Y is said to follow the zero inflated GPMED if its pmf has the following form.

$$\begin{aligned} {} \begin{aligned} f(y)&=\omega \,P(\psi =y)+(1-\omega )\,P(X=y)\\&={\left\{ \begin{array}{ll} \omega +(1-\omega )(1+\lambda {\alpha })^{-2},&{}y=0\\ \\ (1-\omega )\,\frac{\lambda \alpha ^{y}(\lambda +\rho {y})^{y-1}(y+1)}{\left[ 1+\alpha (\lambda +\rho {y})\right] ^{y+2}},&{}y=1,2,3\dots \end{array}\right. } \end{aligned} \end{aligned}$$
(8.1)

in which \(\omega \in {[0,1]}\), \(\lambda >0\), \(0<\rho <1\) and \(\alpha >0\).

Clearly, when \(\omega =0\), the ZIGPMED reduces to the GPMED(\(\lambda ,\alpha ,\rho \)) with pmf given in (8.1). Next, we present certain properties of the ZIGPMED through the following results.

By definition, the pgf of the ZIGPMED with pmf given in (8.1) is

$$\begin{aligned} \begin{aligned} \Psi (t)&=\sum _{y=0}^{\infty }t^{y}\,f(y)\\&=\omega +\frac{1-\omega }{(1+\lambda {\alpha })^{2}}+(1-\omega )\sum _{y=1}^{\infty }\frac{(y+1)\left[ t(\lambda +\rho {y})\right] ^{y}}{(\lambda +\rho {y})\left[ 1+\alpha (\lambda +\rho {y})\right] ^{y}} \end{aligned} \end{aligned}$$

The corresponding mean and variance of the ZIGPMED is as follows:

$$\begin{aligned} Mean=(1-\omega )\sum _{y=1}^{\infty }\frac{y(y+1)(\lambda +\rho {y})^{y-1}}{\left[ 1+\alpha (\lambda +\rho {y})\right] ^{y+2}} \end{aligned}$$

and

$$\begin{aligned} Variance=(1-\omega )\sum _{y=1}^{\infty }\frac{y^{2}(y+1)(\lambda +\rho {y})^{y-1}}{\left[ 1+\alpha (\lambda +\rho {y})\right] ^{y+2}}-(1-\omega )^{2}\biggl \{\sum _{y=1}^{\infty }\frac{y(y+1)(\lambda +\rho {y})^{y-1}}{\left[ 1+\alpha (\lambda +\rho {y})\right] ^{y+2}}\biggr \}^{2}. \end{aligned}$$

The likelihood function of the ZIGPMED based on n observations, say (\(x_{1},x_{2},\dots ,x_{n}\)) is:

$$\begin{aligned} {} L(\omega ,\lambda ,\alpha ,\rho )=\prod _{i=1}^{n}\biggl \{\bigg [\omega +(1-\omega )(1+\lambda \alpha )^{-2}\bigg ]+\biggl [(1-\omega )\frac{(\lambda +\rho {x_{i}})^{x_{i}-1}(x_{i}+1)}{[1+\alpha (\lambda +\rho {x_{i}})]}\biggr ]^{x_{i}+2}\biggr \}. \end{aligned}$$
(8.2)

The log-likelihood function of the equation given in (8.2) can be expressed as follows:

$$\begin{aligned} {} \begin{aligned} log\mathcal {L}(\omega , \lambda , \rho )=\mathcal {L}=\sum _{i=1}^{n}\log \biggl \{\bigg [\omega +(1-\omega )(1+\lambda \alpha )^{-2}\bigg ] +\biggl [(1-\omega )\frac{(\lambda +\rho {x_{i}})^{x_{i}-1}(x_{i}+1)}{[1+\alpha (\lambda +\rho {x_{i}})]}\biggr ]^{x_{i}+2}\biggr \}. \end{aligned} \end{aligned}$$
(8.3)

The estimates of the parameters in the non-linear equation given in (8.3) can be obtained by numerical optimization using “optim” or “nlm” functions in the R software, see [31].

9 Applications in Real Life Study

This section consists of demonstrating the empirical importance of the GPMED and ZIGPMED.

9.1 Presentation

To show the usage of the proposed model, we utilize two real life data applications in this paper: the first is the number of potato data set given in [18], which is used to compare the data modeling ability of the GPMED over some competitive distributions, and the second is the number of insurance claims data set given in [24], which is used to compare the data modeling ability of the ZIGPMED over some competitive distributions.

In order to compare our proposed distribution and other competing models given in Tables 2 and 5, respectively. We consider the negative log-likelihood (-logL), the criteria like Akaike information criterion (AIC), Bayesian information criterion (BIC) and corrected Akaike information criterion (AICc). The better distribution corresponds to lesser AIC, BIC and AICc values.

$$\begin{aligned} AIC=2k-2\,\textrm{log}L, BIC=k\textrm{log}\,n-2\,\textrm{log}L\, \hbox {and}\, AICc= AIC+\frac{2k(k+1)}{n-k-1}. \end{aligned}$$

where k is the number of parameters in the statistical model, n is the sample size and \(\textrm{log}L\) is the maximized value of the log-likelihood function under the considered model.

Furthermore, the form of the hrf of the datasets is determined using a graphical method based on Total Time on Test (TTT). If the empirical TTT plot is convex, concave, convex then concave, and concave then convex, then the form of associated hrf is decreasing, increasing, bathtub shape, upside-down bathtub shape, respectively (see [1]). We use the RStudio software for numerical evaluations of these datasets.

9.2 Number of Potato Data Set

These data are available in [18]. Table 3 shows the descriptive measures of this data, which include sample size n, minimum (min), first quartile (\(Q_{1}\)), median (Md), third quartile (\(Q_{3}\)), maximum (max), and interquartile range (IQR). The empirical index of dispersion (ID) of the data is equal to 3.4557. As a result, our model employed to describe the current data set is capable of dealing with overdispersion.

In addition, Fig. 4 shows an empirical TTT plot of the data and it reveals an decreasing hrf. To demonstrate the GPMED’s potential benefit, the distributions given in Table 2 are considered for comparison.

Fig. 4
figure 4

Total Time on Test (TTT) plot for the student enrollment data set

Full size image
Table 2 The considered competitive distributions
Full size table

According to Table 4, the GPMED’s AIC, BIC and AICc values are lower than those of the other distributions under consideration. Therefore, the proposed model is the best choice for modeling the provided data set.

Table 3 Descriptive statistics for the number of potato datasets
Full size table
Table 4 MLEs, AIC, BIC and AICc values for the potato data set
Full size table

In the case of GLRT, the calculated value based on the test statistic in (6.1) is \(2(-128.5026+134.7959)=12.5866\) (p-value \(=0.00153\)). As a result, at any level \(>0.00153\), the null hypothesis is rejected in favour of the alternative hypothesis. Hence, we conclude that the additional parameters \(\lambda \) and \(\rho \) in the GPMED is significant in the light of the test procedure outlined in Sect. 6.

9.3 Number of Insurance Claims Data Set

We consider the second data set which reports the number of claims for 9461 automobile insurance policies, see [24]. This datasets also used in [41]. The percentage of zeros in insurance policies data is 81.32. Likewise, this data indicates overdispersion problem with ID 1.3476. As a result, our model employed to describe the current data set is capable of dealing with overdispersion. Table 6 shows the descriptive measures of this data, which include n, min, \(Q_{1}\), Md, \(Q_{3}\), max, and interquartile IQR. The fitted distributions for the number of claims are shown in Table 5. It illustrates that the best fit is the ZIGPMED, followed by the ZIPD, ZINBD and finally the ZINB-SD.

In addition, Fig. 5 shows an empirical TTT plot of the data and it reveals an decreasing hrf.

Fig. 5
figure 5

Total Time on Test (TTT) plot for the number of insurance claims datasets

Full size image
Table 5 The considered competitive distributions
Full size table

According to Table 7, the ZIGPMED’s AIC, BIC and AICc values are lower than those of the other distributions under consideration. Therefore, the proposed zero-inflated model is the best choice for modeling the provided data set.

Table 6 Descriptive statistics for the potato data set
Full size table
Table 7 MLEs, AIC, BIC and AICc values for the insurance claims datasets
Full size table

10 Conclusion

In this work, the mixed count model is proposed, known as GPMED. We show that its special case is the PMED. In particular, we derive some mathematical properties of the GPMED. The estimation procedure for parameters is also implemented by the maximum likelihood method. Also, we proposed zero-inflated version of the GPMED, known as ZIGPMED. The two proposed distributions are applied to two real datasets and it is compared with some important competitive distributions. The comparison results of the minus log-likelihood, AIC, BIC and AICc values for distributions show that the best fit model is the GPMED and ZIGPMED. In conclusion, the GPMED is a flexible model that can be an alternative way to model count data with too many zeros. If the bivariate version of the GPMED is constructed, the direction of this study might change. This task needs a lot of revisions and research, which we will leave for further study.