1 Introduction

For modeling of count observations, several one-parameter discrete distributions have been proposed by combining the Poisson distribution and one-parameter lifetime distributions. Compounding a discrete with a continuous probability distribution is a useful technique for developing flexible distributions to aid in the analysis of count data. The count models are important in a variety of applied and theoretical applications, including health, transportation, insurance, engineering, etc. Data science approaches have been used to describe pandemonium behavior, crop harvesting, corporate data mining, e-commerce fraud, and other challenges [1,2,3,4]. Some discrete probability distributions are; discrete Weibull [5], discrete Lindley [6], discrete Burr-Hatke [7], discrete Rayleigh [8], Poisson Ailamujia [9], Poisson xgamma [10], exponentiated discrete Lindley [11], discrete inverted Topp-Leone distribution [12], discrete Ramous-Louzada distribution [13] discrete type-II half-logistic exponential distribution [14] and discrete power-Ailamujia distribution [15].

The moment exponential (ME) distribution was proposed by [16] by weighting the exponential distribution in accordance with Fisher's (1934) theory. The probability density function is given by

$$f\left( {x;\beta } \right) = \frac{x}{{\beta^{2} }}e^{{ - \frac{x}{\beta }}} , \,x > 0,\,\beta > 0$$

where β is the scale parameter. The ME model attained great attention due to its flexibility so various authors studied and further generalized it for more complex datasets. For example, generalized exponentiated moment exponential [17], Marshall-Olkin length biased exponential distribution [18], Kumaraswamy moment exponential distribution [19], and Weibull-Moment Exponential distribution [20] and references therein.

In this study, a new discrete probability distribution is proposed by combing Poisson and moment exponential distributions, as there is a need for a more flexible distribution for statistical data analysis. The proposed distribution has an over-dispersed nature, so this model will be more suited for analyzing over-dispersed count data sets. After little parameterization, the PMEx distribution is similar to the Poisson Ailamujia distribution proposed by [9]. We further investigate new results containing mode, moment generating function, and associated measures. We calculate its reliability characteristics including survival function, hazard function (failure rate), reversed hazard function, second failure rate, and mean residual life function. The actuarial measures are also derived. Seven different estimation methods are used to estimate the model parameter. In the end, four different datasets are used to show the flexibility of the PMEx distribution.

The rest of the study is organized as follows. The derivation of the Poisson-Moment Exponential distribution (PMExD) and the shape of its probability mass function (pmf) is presented in Sect. 2. Section 3 deals with the derivation of statistical properties. The estimation of the PMExD parameter has been discussed using the methods of maximum likelihood, maximum product spacing, Anderson darling, Cramer von-Misses, least-squares, and weighted least-squares estimation in Sect. 4. A comprehensive simulation study is also discussed in this section. In Sect. 5, the suitability of PMExD along with some competitive models has been discussed. Finally, Sect. 6 deals with the concluding remarks of the study.

2 PMEx Distribution

Definition 1

If \(Y\left| \lambda \right.\sim P\left( \lambda \right),\) where \(\lambda\) is a random variable with a parameter that follows a moment exponential distribution with parameter \(\left( \beta \right)\), the distribution that arises from marginalizing over \(\lambda\) is known as a compound of the Poisson and the moment exponential distribution. The resultant distribution is known as \(PMExD\left( {Y;\beta } \right)\). It should be emphasized that because the parent distribution is discrete, the proposed distribution will be discrete.

Theorem 1

The probability mass function (pmf) of Poisson Moment Exponential distribution, i.e. \(PMExD\left( {x;\eta } \right)\) is given by

$$P\left( {X = x} \right) = \frac{{\beta^{x} \left( {1 + x} \right)}}{{\left( {1 + \beta } \right)^{x + 2} }}, x = 0,1,2, \ldots , ;\beta > 0$$
(1)

Proof:

The pmf of a PMExD can be obtained using definition (1) as follows:

$$f\left( {x{|}\lambda } \right) = \frac{{e^{ - \lambda } \lambda^{x} }}{x!},\quad x = 0,\,1,\,2, \ldots , \& \, \lambda > 0.$$

The parameter λ follows moment exponential distribution with the probability density function (pdf)

$$m\left( {\lambda ;\beta } \right) = \frac{\lambda }{{\beta^{2} }}e^{{ - \frac{\lambda }{\beta }}} ,\, \lambda \ge 0\,\& \,\beta > 0.$$

We have

$$P\left( {X = x} \right) = \mathop \smallint \limits_{0}^{\infty } f\left( {x{|}\lambda } \right)m\left( {\lambda ;\beta } \right)d\lambda$$
$$P\left( {X = x} \right) = \mathop \smallint \limits_{0}^{\infty } \frac{{e^{ - \lambda } \lambda^{x} }}{x!}\frac{\lambda }{{\beta^{2} }}e^{{ - \frac{\lambda }{\beta }}} d\lambda$$
$$P\left( {X = x} \right) = \frac{{\beta^{x} \left( {1 + x} \right)}}{{\left( {1 + \beta } \right)^{x + 2} }};\quad x = 0,\,1,\,2, \ldots \& \, \beta > 0.$$

which is the pmf of PMExD. □

Note that for \(\alpha = \frac{1}{\beta },\) we obtain Poisson Ailmujia distribution.

Remark 1:

The first derivative of \(p\left( x \right)\) is

$$\frac{dp\left( x \right)}{{dx}} = \frac{{\beta^{x} \left( {1 + \left( {1 + x} \right)\log \left( \beta \right) - \left( {1 + x} \right)\log \left( {1 + \beta } \right)} \right)}}{{\left( {1 + \beta } \right)^{2 + x} }}$$

gives:

$$\hat{x} = \frac{{1 - \log \left( {1 + \frac{1}{\beta }} \right)}}{{\log \left( {1 + \frac{1}{\beta }} \right)}}.$$

For:

  1. 1.

    \(\beta > \frac{1}{e - 1}:\hat{x} = \frac{{1 - \log \left( {1 + \frac{1}{\beta }} \right)}}{{\log \left( {1 + \frac{1}{\beta }} \right)}}\) is a critical point which \(p\left( {\hat{x};\beta } \right)\) is maximum.

  2. 2.

    \(0 < \beta \le \frac{1}{e - 1}\), the pmf is decreasing function of x.

and the second derivative is

$$\frac{{d^{2} p\left( x \right)}}{{dx^{2} }} = \frac{{\beta^{x} \log \left( {\frac{\beta }{1 + \beta }} \right)\left( {2 + \left( {1 + x} \right)\log \left( {\frac{\beta }{1 + \beta }} \right)} \right)}}{{\left( {1 + \beta } \right)^{2 + x} }}$$

Therefore the mode of PMExD is given by:

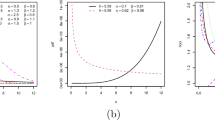
$$mode\left( X \right) = \left\{ \begin{gathered} \frac{{1 - \log \left( {1 + \frac{1}{\beta }} \right)}}{{\log \left( {1 + \frac{1}{\beta }} \right)}}\quad for\,\,\beta > \frac{1}{e - 1} \hfill \\ 0\quad \quad \quad \quad \quad \quad otherwise \hfill \\ \end{gathered} \right.$$

Figure 1 shows the plots of the PMEx distribution pmf for different β values. It is found that the probabilities can be decreasing or unimodal shaped.

Fig. 1
figure 1

probability mass function plots for PMExD

Full size image

The corresponding cumulative distribution function (cdf) is

$$F\left( {x;\beta } \right) = 1 - \frac{{\beta^{x + 1} \left( {\beta + 2 + x} \right)}}{{\left( {1 + \beta } \right)^{x + 2} }}$$
(2)

3 Mathematical Properties

3.1 Survival (Reliability) Function

The reliability function is defined as the probability of a system surveying for a certain time. The survival function of PMExD is as follows:

$$\begin{gathered} S\left( {x;\beta } \right) = P\left( {X \ge x} \right) = 1 - P\left( {X \le x - 1} \right) \hfill \\ \quad \quad \quad = \frac{{\beta^{x} \left( {1 + x + \beta } \right)}}{{\left( {1 + \beta } \right)^{x + 1} }} \hfill \\ \end{gathered}$$
(3)

3.2 Hazard Function (Failure Rate)

The hazard function of PMExD is given by

$$h\left( {x;\beta } \right) = \frac{{\left( {1 + x} \right)}}{{\left( {1 + \beta } \right)\left( {1 + x + \beta } \right)}}$$
(4)

Proposition 1:

The hazard function of PMExD is an increasing function of x.

Proof:

Using the idea of Glaser (1980) and from the pmf of PMExD.

$$\rho \left( x \right) = - \frac{{p^{\prime}\left( x \right)}}{p\left( x \right)} = - \frac{{1 + \left( {1 + x} \right)\log \left( {\frac{\beta }{1 + \beta }} \right)}}{{\left( {1 + x} \right)}}$$

It follows that

$$\rho^{\prime}\left( x \right) = \frac{1}{{\left( {1 + x} \right)^{2} }} > 0$$

As \(\rho^{\prime}\left( x \right) > 0\) the hazard function of PMExD is increasing.□

Figure 2 displays the failure rate curves of the PMEx distribution for some choices of parameter β.

Fig. 2
figure 2

Failure rate curves for PMExD

Full size image

3.3 Reversed Hazard and Second Failure Rate

The reversed hazard rate and second failure rate of PMEx distribution are given by, respectively

$$r\left( x \right) = \frac{P\left( x \right)}{{F\left( x \right)}} = \frac{{\beta^{x} \left( {1 + x} \right)}}{{\left( {1 + \beta } \right)^{x + 2} - \beta^{x + 1} \left( {2 + x + \beta } \right)}}$$
(5)

and

$$r^{*} \left( {x;\beta } \right) = \log \left( {\frac{{\left( {1 + \beta } \right)\left( {1 + x + \beta } \right)}}{{\beta \left( {2 + x + \beta } \right)}}} \right)$$
(6)

3.4 Mean Residual Life (MRL)

For a discrete random variable, the MRL function is defined as

$$MRL = \varepsilon \left( i \right) = E\left( {X - i{|}X \ge i} \right) = \frac{1}{{1 - F\left( {i - 1,\beta } \right)}} \mathop \sum \limits_{j = i + 1}^{w} \left[ {1 - F\left( {j - 1,\beta } \right)} \right]; i \in {\mathbb{N}}_{0} ,$$

where \({\mathbb{N}}_{0} = \left\{ {0, \,1,\, 2, \ldots ,\,w} \right\}\) and \(0 < w < \infty\). Let Xl be the PMExD random variable, then the MRL is defined as

$$MRL = \frac{{\left( {1 + \beta } \right)^{i + 1} }}{{\beta^{i} \left( {1 + i + \beta } \right)}} \mathop \sum \limits_{j = i + 1}^{w} \left[ {\frac{{\beta^{j} \left( {1 + j + \beta } \right)}}{{\left( {1 + \beta } \right)^{j + 1} }}} \right]$$
$$MRL = \frac{{\left( {1 + \beta } \right)^{i} }}{{\beta^{i} \left( {1 + i + \beta } \right)}}\left\{ {\frac{{\beta^{i + 1} }}{{\left( {1 + \beta } \right)^{i - 1} }} + \frac{{i \beta^{i + 1} }}{{\left( {1 + \beta } \right)^{i} }} + \frac{{ \beta^{i + 1} }}{{\left( {1 + \beta } \right)^{i - 1} }}} \right\}$$
$$MRL = \frac{{\beta \left( {2 + 2\beta + i} \right)}}{{\left( {1 + i + \beta } \right)}}$$
(7)

3.5 Moments and Associated Measures

3.5.1 Moment Generating Function

The moment generating function of the PMEx distribution can be obtained as

$$M_{x} \left( t \right) = E\left( {e^{tx} } \right) = \mathop \sum \limits_{x = 0}^{\infty } e^{tx} P\left( x \right) = \mathop \sum \limits_{x = 0}^{\infty } e^{tx} \frac{{\beta^{x} \left( {1 + x} \right)}}{{\left( {1 + \beta } \right)^{x + 2} }}$$
$$M_{x} \left( t \right) = \frac{1}{{\left( {1 + \beta } \right)}}\left[ {\frac{{\left( {1 + \beta - e^{t} \beta } \right) + e^{t} \beta }}{{\left( {1 + \beta - e^{t} \beta } \right)^{2} }}} \right]$$
$$M_{x} \left( t \right) = \frac{1}{{\left( {1 + \beta - e^{t} \beta } \right)^{2} }}$$
(8)

The first four moments are about the origin of the PMExD.

$$\mu_{1}^{^{\prime}} = 2\beta$$
$$\mu_{2}^{^{\prime}} = 2\beta \left( {1 + 3\beta } \right)$$
$$\mu_{3}^{^{\prime}} = 2\beta \left( {1 + 9\beta + 12\beta^{2} } \right)$$
$$\mu_{4}^{^{\prime}} = 2\beta \left( {1 + 21\beta + 72\beta^{2} + 60\beta^{3} } \right)$$

The moments about mean can be obtained using the following relation \(\mu_{1} = E\left( {Y - \mu_{1}^{^{\prime}} } \right)^{r}\). The first four moments about the mean for the PMExD are given by;

$$\mu = 2\beta$$
$$\mu_{2} = 2\beta \left( {1 + \beta } \right)$$
$$\mu_{3} = 2\beta \left( {1 + 3\beta + 2\beta^{2} } \right)$$
$$\mu_{4} = 2\beta \left( {1 + 13\beta + 24\beta^{2} + 12\beta^{3} } \right)$$

The dispersion index (DI) is

$$DI = \frac{Var\left( y \right)}{{Mean\left( y \right)}} = \left( {1 + \beta } \right) > 1.$$

We noted that the PMExD is overdispersed.

The coefficient of variation (CV), coefficients of skewness (CS), and coefficients of kurtosis (CK) for the PMExD are given by

$$CV = \frac{SD\left( y \right)}{{Mean\left( y \right)}} = \sqrt {\frac{1 + \beta }{{2\beta }}}$$
$$CS = \frac{{\beta \left( {2\beta^{2} + 3\beta + 1} \right)}}{{\sqrt 2 \left( {\beta \left( {1 + \beta } \right)} \right)^{3/2} }}$$
$$CK = \frac{{1 + 13\beta + 24\beta^{2} + 12\beta^{3} }}{{2\beta \left( {1 + \beta } \right)^{2} }}$$

Some moments, variance, CV, DI in terms of β are presented in Table 1.

Table 1 Moments and DI of the PXL distribution
Full size table

3.6 Actuarial Measures

In this section, two risk measure value at risk (VaR) and tail value at risk (TVaR) of the PMExD. The VaR measure is frequently used by practitioners in the field of actuarial sciences and standard financial market risk. The VaR is always supplied with a level of confidence, say p, and represents the percentage loss in portfolio value that will be equaled or exceeded only X percent of the time. Let X represents the loss random variable. The VaR of PMExD is derived as

\(P\left( {X > \tau_{p} } \right) = 1 - p,\) and then \(\tau_{p} = F^{ - 1} \left( p \right),\)where \(p\) is the solution of the equation \(\beta^{x} \left( {\beta + 2 + x} \right) = \left( {1 + \beta } \right)^{x + 2} \left( {1 - p} \right)\).

The TVaR is also known as “conditional tail expectation” or “tail conditional expectation”. It is a useful metric for calculating the expected value of a loss when an event occurs outside of a particular probability level. If X belongs to the PMExD, then the TVaR of X is

$$TVaR_{p} = E\left( {X{|}X > \tau_{p} } \right) = \frac{1}{{1 - F\left( {\tau_{p} } \right)}}\mathop \sum \limits_{{x = \tau_{p} }}^{\infty } xp\left( x \right).$$
$$TVaR_{p} = \frac{{\beta^{{\tau_{p} }} \left( {1 + \beta } \right)^{{ - 1 - \tau_{p} }} \left( {\tau_{p} + \left( {\tau_{p} } \right)^{2} + 2\beta \tau_{p} + 2\beta \left( {1 + \beta } \right)} \right)}}{{1 - F\left( {\tau_{p} } \right)}}$$
(9)

Some values of \(VaR_{p}\) and \(TVaR_{p}\) measures for PMExD are listed in Table 2.

Table 2 The risk measures (VaR and TVaR) for the PMEx distribution
Full size table

4 Parameter Estimation

In this section, seven different estimation methods are used to estimate the parameter of PMExD including maximum likelihood (MLE), maximum product spacing (MPSE), Anderson–Darling (ADE), Cramer-von misses (CVME), least-squares (OLSE), weighted least-squares (WLSE) and right tailed Anderson-Darling (RADE) method.

Let \(X_{1} ,\,X_{2} , \ldots ,\,X_{n}\) be a random sample from the PMExD and \(X_{\left( 1 \right)} < X_{\left( 2 \right)} < \ldots < X_{\left( n \right)}\) denote the corresponding order statistics. Moreover, \(x_{\left( i \right)}\) refers to the observed values of \(X_{\left( i \right)}\). In this regard, the log-likelihood function of the PMEx distribution is

$$\ell = \mathop \sum \limits_{i = 1}^{n} x_{i} \log \left( \beta \right) + \mathop \sum \limits_{i = 1}^{n} \log (1 + x_{i} ) - \mathop \sum \limits_{i = 1}^{n} \left( {2 + x_{i} } \right)\log \left( {1 + \beta } \right)$$
(10)

Then, the MLE of parameter \(\beta\) is given as follows

$$\hat{\beta }_{MLE} = \begin{array}{*{20}c} {{\text{argmax}}\left( \beta \right)} \\ \beta \\ \end{array}$$
(11)

Let us define five functions that are used to obtain the minimum distance-based estimates:

$${\text{Q}}_{AD} \left( \beta \right) = - n - \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {2_{i} - 1} \right)\left[ {\log \left( {1 - \frac{{\beta^{{{\text{x}}_{i:n} + 1}} \left( {\beta + 2 + {\text{x}}_{i:n} } \right)}}{{\left( {1 + \beta } \right)^{{{\text{x}}_{i:n} + 2}} }}} \right) + \log \left( {\frac{{\beta^{{{\text{x}}_{i:n} + 1}} \left( {\beta + 2 + {\text{x}}_{i:n} } \right)}}{{\left( {1 + \beta } \right)^{{{\text{x}}_{i:n} + 2}} }}} \right)} \right]^{2} ,$$
$${\text{Q}}_{RAD} \left( \beta \right) = \frac{n}{2} - 2\mathop \sum \limits_{i = 1}^{n} \left[ {1 - \frac{{\beta^{{{\text{x}}_{i:n} + 1}} \left( {\beta + 2 + {\text{x}}_{i:n} } \right)}}{{\left( {1 + \beta } \right)^{{{\text{x}}_{i:n} + 2}} }}} \right] - \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {2_{i} - 1} \right)\log \left[ {1 - \frac{{\beta^{{{\text{x}}_{i:n} + 1}} \left( {\beta + 2 + {\text{x}}_{i:n} } \right)}}{{\left( {1 + \beta } \right)^{{{\text{x}}_{i:n} + 2}} }}} \right],$$
$${\text{Q}}_{CVM} \left( \beta \right) = \frac{1}{12n} + \mathop \sum \limits_{i = 1}^{n} \left[ {1 - \frac{{\beta^{{{\text{x}}_{i:n} + 1}} \left( {\beta + 2 + {\text{x}}_{i:n} } \right)}}{{\left( {1 + \beta } \right)^{{{\text{x}}_{i:n} + 2}} }} - \frac{2i - 1}{{2n}}} \right]^{2} ,$$
$${\text{Q}}_{OLS} \left( \beta \right) = \mathop \sum \limits_{i = 1}^{n} \left[ {1 - \frac{{\beta^{{{\text{x}}_{i:n} + 1}} \left( {\beta + 2 + {\text{x}}_{i:n} } \right)}}{{\left( {1 + \beta } \right)^{{{\text{x}}_{i:n} + 2}} }} - \frac{i}{n + 2}} \right]^{2} ,$$

and

$${\text{Q}}_{WLS} \left( \beta \right) = \mathop \sum \limits_{i = 1}^{n} \frac{{\left( {n + 1} \right)^{2} \left( {n + 2} \right)}}{{i\left( {n - i + 1} \right)}}\left[ {1 - \frac{{\beta^{{{\text{x}}_{i:n} + 1}} \left( {\beta + 2 + {\text{x}}_{i:n} } \right)}}{{\left( {1 + \beta } \right)^{{{\text{x}}_{i:n} + 2}} }} - \frac{i}{n + 1}} \right]^{2} .$$

The ADEs, RADEs, CVMEs, OLSEs and WLSEs of the parameter \(\beta\) are given, respectively, by

$$\hat{\beta }_{ADE} = \begin{array}{*{20}c} {{\text{argmin}}\left\{ {{\text{Q}}_{AD} \left( \beta \right)} \right\}} \\ \beta \\ \end{array}$$
(12)
$$\hat{\beta }_{RADE} = \begin{array}{*{20}c} {{\text{argmin}}\left\{ {{\text{Q}}_{RAD} \left( \beta \right)} \right\}} \\ \beta \\ \end{array}$$
(13)
$$\hat{\beta }_{CVME} = \begin{array}{*{20}c} {{\text{argmin}}\left\{ {{\text{Q}}_{CVM} \left( \beta \right)} \right\}} \\ \beta \\ \end{array}$$
(14)
$$\hat{\beta }_{OLSE} = \begin{array}{*{20}c} {{\text{argmin}}\left\{ {{\text{Q}}_{OLS} \left( \beta \right)} \right\}} \\ \beta \\ \end{array}$$
(14)
$$\hat{\beta }_{WLSE} = \begin{array}{*{20}c} {{\text{argmin}}\left\{ {{\text{Q}}_{WLS} \left( \beta \right)} \right\}} \\ \beta \\ \end{array}$$
(15)

The estimators presented in Eqs. (12, 13, 14, 15, 16) can be obtained by using the optim () function in R.

The maximum product spacing is obtained using the following approach. For \(m = 1,2,3, \ldots , h + 1\), assume \(D_{m} \left( \beta \right) = F\left( {x_{\left( m \right)} |\beta } \right) - F\left( {x_{{\left( {m - 1} \right)}} |\beta } \right),\) be the uniform spacings of a random sample from the PMEx model, where \(F\left( {x_{\left( 0 \right)} |\beta } \right) = 0\), \(F\left( {x_{{\left( {h + 1} \right)}} |\beta } \right) = 1\) and \(\mathop \sum \limits_{r = 1}^{h + 1} D_{m} \left( \beta \right) = 1\). The MPSE of the parameter \(\beta\), say \(\hat{\beta }\), can be estimated by maximizing the geometric mean of the spacings

$${\text{MPSE}}\left( \beta \right) = \left[ {\mathop \prod \limits_{m = 1}^{h + 1} D_{m} \left( \beta \right)} \right]^{{\frac{1}{h + 1}}}$$
(17)

with respect to the parameter \(\beta\).

4.1 Simulation Study

This section is based on a comprehensive simulation study to compare the estimation performance of the derived estimator in the previous section. The samples are generated from PMExD with sizes n = 10, 25, 50, 100, 200, and four settings \(\left( {\beta = 0.25, \,0.5,\,1.0,\,2.0,\, 5.0} \right)\) are considered. The simulation procedure is based on 10,000 repetitions. The ABSs, MREs and MSEs are given by

$$ABSs = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left| {\hat{\beta } - \beta } \right|,$$
$$MRE = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \frac{{\left| {\hat{\beta } - \beta } \right|}}{\beta },$$

and

$$MSE = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} \left( {\hat{\beta } - \beta } \right)^{2}$$

The average estimates (AVEs), average biases (ABSs), mean relative errors (MREs), and mean square errors (MSEs) are presented in Tables 3, 4, 5, 6 and 7.

Table 3 The AVEs, ABSs, MREs, and MSEs for the parameter \(\left( {\beta = 0.25} \right)\)
Full size table
Table 4 The AVEs, ABSs, MREs, and MSEs for the parameter \(\left( {\beta = 0.50} \right)\)
Full size table
Table 5 The AVEs, ABSs, MREs, and MSEs for the parameter \(\left( {\beta = 0.25} \right)\)
Full size table
Table 6 The AVEs, ABSs, MREs, and MSEs for the parameter \(\left( {\beta = 2.0} \right)\)
Full size table
Table 7 The AVEs, ABSs, MREs, and MSEs for the parameter \(\left( {\beta = 5.0} \right)\)
Full size table

It is found that the average estimates moved closer to the true parameter values as the sample increases. Further, the ABSs and MSEs for all estimators are decreasing with an increase in sample size. Hence, the MLE demonstrates the consistency property. As a result, we conclude that the MLE performs well in predicting the DRL distribution's parameter.

5 Application

In this section, four datasets from different fields are used for application purposes. The fit of the PMExD is compared with some competitive one-parameter distributions such as discrete Rayleigh (DR), discrete Burr-Hatke (DBH), discrete Pareto (DPr), discrete inverted Topp-Leone (DITL), and Poisson. The fitted probability distributions are compared using maximized log-likelihood \(\left( l \right)\), Akaike information criterion (AIC), Bayesian information criterion (BIC), Kolmogorov–Smirnov (KS), and the Chi-square test with its corresponding P-values.

Data set I: The first data were reported in [21] and represents the failure times for a sample of 15 electronic components in an acceleration life test. The number are as follows; 1, 5, 6, 11, 12, 19, 20, 22, 23, 31, 37, 46, 54, 60 and 66. The measures, mean, variance dispersion index, skewness, and kurtosis for this data are 27.533, 431.98, 15.689, 0.5532, and 2.0616, respectively. These measures portray that the data set is over-dispersed, positive skewness, and leptokurtic behavior. The MLEs and goodness-of-fit for this dataset are listed in Table 8. The P-P plots for all fitted models are given in Fig. 3.

Table 8 The MLEs and goodness-of-fit measures of all fitted models for the first data set
Full size table
Fig. 3
figure 3

P-P plots of all fitted models for the first dataset

Full size image

From Table 8, it is obvious that the PMEx distribution gives a higher value of log-likelihood and Kolmogorov–Smirnov test. Furthermore, the proposed distribution yields a minimum value of AIC and BIC criteria. Figure 3, supports the results listed in Table 8.

Data set II: The second dataset consists of the 2003 final examination marks of 48 slow-pace students in mathematics at the Indian Institute of Technology at Kanpur (Bakouch et al. 2014). The observations are; 29, 25, 50, 15, 13, 27, 15, 18, 7, 7, 8, 19, 12, 18, 5, 21, 15, 86, 21, 15, 14, 39, 15, 14, 70, 44, 6, 23, 58, 19, 50, 23, 11, 6, 34, 18, 28, 34, 12, 37, 4, 60, 20, 23, 40, 65, 19 and 31. The mean, variance, skewness, kurtosis, and dispersion index of this data set are 25.895, 346.14, 1.3317, 4.3233, and 13.367 respectively. The parameter estimates along with model selection measures are given in Table 9. Figure 4 shows the P-P plots of all fitted models for the second data set.

Table 9 The MLEs and goodness-of-fit measures of all fitted models for the second data set
Full size table
Fig. 4
figure 4

P-P plots of all fitted models for the second dataset

Full size image

The estimates of \(\hat{\beta }\) and goodness-of-fit measures for the PMExD and other models are reported in Table 9. It is observed that the PMEx distribution is more adequate for these data than the DR, DBH, DPr, Poisson, and DITL distributions. Figure 4 also concludes these results.

Data set III: The third data set represents epileptic seizure counts reported in [22]. The parameter estimates and goodness-of-fit measures for all fitted distributions for the third data set are listed in Table 10. It is evident from the below table, the proposed distribution fits this data set quite well. Figure 5 also supports these results.

Table 10 The MLEs and goodness-of-fit measures of all fitted models for the third data set
Full size table
Fig. 5
figure 5

The estimated pmfs of the third data set

Full size image

Data set IV: The fourth data set is the biological experiment data listed in Table 11 obtained from [23] on the European corn borer. It was an experiment conducted randomly on 8 hills in 15 replications, and the experimenter counts the number of borers per hill of corn. The MLEs for all fitted models are presented in Table 11. The fitted pmfs are given in Fig. 6. It is found that the PMEx distribution provides more efficient fits than competitive distributions.

Table 11 The MLEs and goodness-of-fit measures of all fitted models for the fourth data set
Full size table
Fig. 6
figure 6

The estimated pmfs of the fourth data set

Full size image

6 Conclusion

A new one-parameter discrete distribution is proposed. The new distribution is called the Poisson moment exponential distribution (PMExD) and it is suitable for modeling over-dispersed datasets. We derived its mathematical properties, including its moments and associated measures, reliability properties, and two risk or actuarial measures. The distribution parameter is estimated using seven different estimation methods. A Monte Carlo simulation study was used to investigate the efficiency of derived estimators. The PMExD distribution was applied on four datasets from different fields and compared with DR, DBH, DPr, Poisson, and DITL distributions. The findings show that the PMEx distribution outperforms competitive distributions. Further, the Neutrosophic form of the proposed distribution for modeling of datasets with indeterminacy is under investigation.