1 Introduction

Viscocohesive–frictional particle agglomerates are commonly found in civil engineering such as clusters of cemented granular materials [1,2,3,4] and in industries such as iron-ores [5,6,7,8,9] and cohesive powder mixtures [10, 11]. The mechanical properties of such agglomerates are popularly characterized by their compressive and tensile strengths. Compressive and tensile strengths can be measured by generating the diametrical impact test or diametrical compression test of viscocohesive–frictional particle agglomerates [12, 13]. Commonly, the compressive and tensile strengths of such agglomerates reveal complex behavior due to the arbitrary natural properties of primary particles, the inclusion of the adhesives, the configurations, and the conditions of the tests [1, 14,15,16,17,18,19]. These mechanical strengths of agglomerates basically increase with increasing the size polydispersity and interparticle friction coefficient of grains, the cohesive properties of adhesives, and the loading speed as compressive or impact speed [1, 13, 15]. The compressive and tensile responses become much more complicated due to the simultaneous effects of cohesive and viscous forces between grains, in which, the viscous forces reveal both contractive and extensive effects depending on the relative displacement between grains in contact [13, 20]. Therefore, controlling both compressive and tensile strengths of such agglomerates under the action of different impact parameters above plays an important role, this controlled behavior can be expected to characterize by the unified description of both compressive and tensile strength.

In order to get a better understanding of the compressive and tensile properties of viscocohesive–frictional particle agglomerates, both experimental works and numerical simulations in different configurations and conditions have been performed over the last few decades [9, 14, 21, 22]. The difficulties of varying different real parameters related to the material properties such as particle shape and density, particle roughness, and adhesives between grains lead to the disadvantages of giving general and correct statements about both compressive and tensile responses of granular materials. Contrarily, the mechanical strength of agglomerates can be analyzed numerically by systematically varying different values of material and operational parameters. However, most of these numerical works have been performed with nearly brittle materials composed of primary particles glued via solid bonds [2, 23,24,25]. Furthermore, controlling the mechanical strength of such agglomerates still remains elusive due to without fully considering different interaction forces between grains which are well known as microscopic origins of the macroscopic properties.

Recently, the compressive and tensile strengths of viscocohesive–frictional particle agglomerates composed of particles interacted via capillary bonds, impacting on a rigid surface, were nicely controlled by using a dimensionless impact number \(I_{\textrm{n}}\) [13, 20]. \(I_{\textrm{n}}\) is defined as a ratio of the impact rate-dependent stresses (expressed as a linear combination between the inertial stress \(\sigma _\textrm{i}\) and the viscous stress \(\sigma _{\textrm{v}}\) with a weighting factor) and impact rate-independent stress (as cohesive stress \(\sigma _{\textrm{c}}\)) exerted on each particle, leading to a well description as a square root of multiply between Capillary number \(\text{ Ca }\) and the Stokes number \(\text{ St }\), \(I_{\textrm{n}} = \{\text{ Ca }(\text{ St } + \beta )\}^{1/2}\), where \(\text{ Ca } = \sigma _{\textrm{v}}/\sigma _{\textrm{c}}\), \(\text{ St } = \sigma _{\textrm{i}}/\sigma _{\textrm{v}}\), and \(\beta \) is the weighting factor. The dimensionless impact number \(I_{\textrm{n}}\) was a remarkable extension of the generalized inertial number which is used to excellently describe the rheological properties and textures of pressured-controlled simple shearing flows of viscocohesive–frictional granular materials [26]. Meanwhile, however, the compressive strength of such agglomerates at the early stage impact is well described as a quadratic function of the dimensionless impact number [20], the tensile strength is expressed as a function of the same dimensionless number with a different power [13]. This difference may be due to the gravity effect of primary particles in the impact test, leading to representation the strong difference of intensity, density, and orientation of compressive and tensile forces between grains.

In this paper, we break the above-mentioned doubt by the numerical analysis of the compressive and tensile strengths of viscocohesive–frictional particle agglomerates composed of primary particles, subjected to a diametrical compression test by means of the three-dimensional discrete element method. The numerical method is coupled with an approximate analytical expression of the cohesive forces and viscous forces between near-neighboring particles having a separation distance not exceeding the debonding distance between grains at their contacts. By systematically varying a broad range of values of the cohesive stress \(\sigma _{\textrm{c}}\), the liquid viscosity \(\eta \), and the compression speed \(v_{{0}}\) applied on the top platen of the model, the compressive and tensile strengths of agglomerates are analyzed in detail as well as the intensity, density, and orientation of the normal forces between grains at the peak stage. As we shall see, a nontrivially unified description of both compressive strength and tensile strength is introduced as the same quadratic function form of the dimensionless number, which was defined in our previous works. This unified description may be explained due to the similar representation of density, intensity, and orientation of normal compressive and tensile forces between grains.

The rest of the paper is organized as follows: we briefly introduce the numerical method in the framework of the discrete element method used in our previous works and the sample preparation in Sect. 2. The paper then analyzes the compressive and tensile strengths of viscocohesive–frictional particle agglomerates with a nontrivially unified description of these strengths by a dimensionless number in Sect. 3. In Sect. 4, the microscopic origins of the unified description of macroscopic responses of agglomerates are explored by considering the density, intensity, and orientation of all normal forces between grains. Finally, a short summary of salient results and further research directions are discussed in Sect. 5.

2 Numerical procedures

All simulations performed in this ongoing work are carried out by employing an in-house three-dimensional (3D) discrete element method (DEM) code program, named cFGd-3D++ [27], developed and applied in our previous works [13, 20, 26]. By adding the capillary cohesion law enhanced by the cohesive forces and viscous forces with the classical DEM in order to reflect the solid–liquid interactions, the code has been extensively used for simulations of unsaturated granular materials in 3D models.

Fig. 1
figure 1

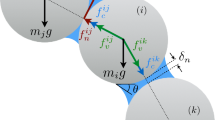
Schematic drawings representation the solid contact model of particle i in contacting with particle j in the case of without existing capillary bridge (a), and the contact model of particle i in non-contacting with particle j in the case of existing capillary bridge (b). Signorini condition for the normal contact force \(f_{\textrm{n}}\) as a function of the normal deflection \(\delta _{\textrm{n}}\) (c), Coulomb friction condition for the tangential contact force \(f_{\textrm{t}}\) as a function of the relative tangential displacement \(\delta _\textrm{t}\) (d). The cohesive force \(f_{\textrm{c}}\) as a function of \(\delta _{\textrm{n}}\) (e) and the viscous force \(f_{\textrm{v}}\) as a function of \(\delta _{\textrm{n}}\) in the case of considering a positive value of the relative normal velocity \(v_\textrm{n}\) between particles i and j (f)

Full size image

In the framework of DEM [28,29,30,31], all particles are considered as rigid grains with a requirement for the high stiffness resolution in order to integrate the interaction between particles. Various types of contact models have been used in the literature within DEM modeling [4, 32,33,34,35,36]. The choice of contact model depends on the properties of the simulated material and the behavior of interest. While cohesive or cohesive–viscous model is appropriate for modeling fine powders or wet granular materials, the use of viscocohesive–frictional models can be applied to a wider range of granular materials (from powder mixture to cemented granular materials). Toward possible applications to geomaterials, a fully viscocohesive–frictional model has been employed at the contact scale in this present paper. As presented in our previous works for the simulations of viscocohesive–frictional granular materials [13, 20, 37], each particle interacts with its near-neighboring others through the normal contact forces \(f_{\textrm{n}}\), tangential contact forces \(f_{\textrm{t}}\), normal cohesive forces \(f_{\textrm{c}}\), and normal viscous forces \(f_{\textrm{v}}\). \(f_{\textrm{n}}\) and \(f_{\textrm{t}}\) are appeared when a particle i in contacting with particle j, as shown in Fig. 1a, and are expressed as a function of the relative normal and tangential displacements, which are nicely shown in Fig. 1c, d, respectively, that are obtained based on a step-wise integration of Newton’s second law [31].

In our simulations, the liquid is in the form of capillary bonds between grains [20, 38], which are assumed to be initially homogeneously distributed and irreversibly broken in the compression process. In the case of existing capillary bond, as shown in Fig. 1b, it induces the cohesive force \(f_{\textrm{c}}\) and viscous force \(f_{\textrm{v}}\) up to the rupture distance \(d_{\textrm{r}}\) between grains. \(f_{\textrm{c}}\) is obtained by Laplace–Young equation, and its approximate solution is given by Eq. (4) in Ref. [20], this force depends on the volume of the liquid bridge, liquid–vapor surface tension, and the solid–liquid–gas contact angle \(\theta \), and shown in Fig. 1e as a function of the normal deflection \(\delta _{\textrm{n}}\). The cohesive force \(f_{\textrm{c}}\) tends to reach a maximum value when there is an overlap between grains (\(\delta _{\textrm{n}} \le 0\)). This cohesive force was discovered to be in excellent agreement with experiments on wet granular media [33]. The viscous force \(f_{\textrm{v}}\) is formulated due to the lubrication effects of liquid bridges, this force depends proportionally on the particle size, liquid viscosity, and relative normal velocity \(v_\textrm{n}\) between grains, but depends inversely proportional to the normal separation distance \(\delta _{\textrm{n}}\). Due to the extensive and contractive properties of liquid bridges and also the separation distance \(\delta _{\textrm{n}}\) between particles, \(f_{\textrm{v}}\) can be obtained by Eqs. (8), (9), and (10) in Ref. [20] and commonly plotted in Fig. 1f in our current work for the case of only considering the positive value of \(v_\textrm{n}\). These determinations of \(f_{\textrm{v}}\) are used to confirm the good agreement between numerical simulation [39] and experiment [40] on the erosion dynamics of agglomerates within the dry granular flows.

To construct the numerical model, the simulations involve three different stages: (1) building a large assembly of non-cohesive spherical particles by applying isotropic compression, (2) extracting a spherical aggregate from the particle assembly and activating the initially homogeneous distribution of capillary bonds between grains, and (3) subjecting to a diametrical compression test by applying a constant downward velocity on the top platen while immobilizing the bottom platen.

A large sample consists of nearly 70,000 spherical particles with the weak size polydispersity \(d_{{\max }} = 2 \times d_{{\min }}\), where \(d_{{\max }}\) and \(d_{{\min }}\) refer to the maximum and minimum particle diameters, respectively. This means that all particle diameters are only varied in a range between \(d_{{\min }}\) and \(d_{{\max }}\) by considering the uniform distribution of particle volume fraction, thus the number of particles in each size class depends on its particle diameters [41]. Initially, each particle is randomly placed in grid inside a cube without contacting and without considering the particle gravity. The sample is then compressed isotropically by translating six side walls with a constant moving velocity. This isotropic compression is done when reaching a dense assembly of particles in an equilibrium state. In these preparation steps, the interparticle friction coefficient is set to 0.01 in order to reach a densest packing.

A spherical probe is then applied at the center of the cuboidal sample to extract an agglomerate with its diameter increased until reaching the largest agglomerate (nearly 31,500 particles). This method allows having a large enough number of particles that belong to the computational efficiency of the current code program, leading to a reduction of the surface effects of agglomerate on its physical and mechanical properties. After extracting a spherical agglomerate, capillary bonds characterized by the capillary cohesion forces and viscous forces are activated homogeneously inside agglomerates and the friction coefficient is set to 0.4.

Fig. 2
figure 2

Snapshots representation the diametrical compression model of a viscocohesive–frictional particle agglomerate (a) and (b), the compressive forces chains distribution (c) and (d), and the tensile force chains distribution (e) and (f) at the peak stage and during the compression test

Full size image

The viscocohesive–frictional particle agglomerate is then subjected to a diametrical compression test between two rigid platens by imposing a downward compression velocity on the top platen, whereas the bottom one is immobilized, as shown in Fig. 2a, b. We ran totally 252 simulations by systematically varying the compression velocity \(v_0\) in a range [0.07, 0.7] m/s, the cohesive stress \(\sigma _{\textrm{c}}\) in a wide range [1.0, 24.0] kPa, and the liquid viscosity \(\eta \) in a range [1.0, 1000.0] mPa s in order to comprehensively investigate the compressive and tensile strengths of such agglomerate. All values of the material, operational, and systematical parameters in our simulations are listed in Table 1. The choice of values of these parameters is based on the computational efficiency of the numerical works as well as the natural properties of the raw materials and the binding liquid, e.g., the number of primary particles, the friction coefficient \(\mu \), the particle density \(\rho \), the particle stiffness k, and the cohesive and viscous stress induced by capillary bonds.

3 Macroscopic responses

3.1 Compressive and tensile strengths

Figure 2 displays the snapshots of the diametrical compression test at the beginning and during the deformation of a viscocohesive–frictional particle agglomerate under a constant downward velocity \(v_0\) applied on the top platen. At the beginning steps of the compression test, some of the primary particles at the top and bottom of agglomerate are in contact with two platens, these particles receive the compression force from the top and bottom platen, then transmit to other primary particles via the solid and capillary bridge contacts, as shown in Fig. 2a, c, e. The agglomerate then deforms, leading to an increase in the number of particles contacting with two platens as well as changing the densities, intensities, and orientations of both compressive and tensile forces, as shown in Fig. 2b, d, f. These changes tend to vary the macroscopic responses of agglomerates.

Table 1 Simulation parameters used in the compression test
Full size table

To characterize the evolution of the macroscopic properties of such agglomerates under the axial compression test, the compressive stress vs. strain (\(\sigma ^{\textrm{c}}\) vs. \(\varepsilon \)) and tensile stress vs. strain (\(\sigma ^{\textrm{t}}\) vs. \(\varepsilon \)) curves are considered. In these simulations, \(\sigma ^{\textrm{c}} = \sigma _{{zz}}\) and \(\sigma ^{\textrm{t}} = (\sigma _{{xx}} + \sigma _{{yy}})/2\) are the compressive stress and tensile stress of viscocohesive–frictional agglomerates, respectively [13, 20], where \(\sigma _{{xx}}\), \(\sigma _{{yy}}\), and \(\sigma _{{zz}}\) are components of the stress tensor of viscocohesive–frictional particle agglomerates, determined by measuring the interparticle interaction forces and the branch vectors that join the centers between near-neighboring particles in contact, as given by following expression:

$$\begin{aligned} \sigma _{{{ij}}} = \frac{1}{V_{\textrm{a}}} \sum _{k=1}^{N_{\textrm{c}}} f_{{k}}^{{ij}} \ell _{{k}}^{{ij}} = n_{\textrm{c}} \langle f_{{k}}^{{ij}} \ell _{{k}}^{{ij}} \rangle _{{k}}, \end{aligned}$$
(1)

where i and j are the x, y, and z directions, \(V_{\textrm{a}}\) is the total volume of viscocohesive–frictional particle agglomerate, \(N_{\textrm{c}}\) denotes the number of capillary bridges inside such agglomerate, \(n_{\textrm{c}} = N_{\textrm{c}}/V_{\textrm{a}}\) is the density of the capillary bonds, and \(f_{{k}}^{{ij}}\) and \(\ell _{{k}}^{{ij}}\) are the components of the force vector and the branch vector \(\ell \) of the contact k, respectively. The symbol \(\langle \dots \rangle _{{k}}\) denotes averaging over all contacts k within agglomerate [15].

The cumulative vertical strain \(\varepsilon \) is obtained by considering the ratio between the cumulative vertical displacement \(\Delta h\) and the initial diameter \(D_a\) of agglomerate, as given:

$$\begin{aligned} \varepsilon = \frac{\Delta h}{D_a}, \end{aligned}$$
(2)

where \(\Delta h = v_0 \times t\) denotes the cumulative vertical deformation of the viscocohesive–frictional particle agglomerate under the constant downward velocity \(v_0\).

Fig. 3
figure 3

a Compressive stress \(\sigma ^{\textrm{c}}\) and b tensile stress \(\sigma ^\textrm{t}\) vs. cumulative vertical strain \(\varepsilon \) for different values of the cohesion stress \(\sigma _{\textrm{c}}\) for a given value of the liquid viscosity \(\eta =1000\) mPa s and the compression velocity \(v_0 = 0.7\) m/s. (Color figure online)

Full size image

Figure 3a, b shows the evolutions of the compressive stress \(\sigma ^{\textrm{c}}\) and the tensile stress \(\sigma ^\textrm{t}\) as a function of the cumulative vertical strain \(\varepsilon \) for different values of the cohesive stress \(\sigma _{\textrm{c}}\) and the liquid viscosity \(\eta \), respectively, as a given value of the compression velocity \(v_0\). Both these stresses increase rapidly with small displacement of the top platen from the equilibrium state of agglomerate. The growth rate of these stresses increases with increasing the cohesive stress \(\sigma _{\textrm{c}}\) between grains. \(\sigma ^\textrm{c}\) and \(\sigma ^\textrm{t}\) then reach the peak before declining with the rate that also depends on the magnitude of the cohesive stress. Remarkably, the declination rate of \(\sigma ^\textrm{t}\) is higher than that of the compressive stress \(\sigma ^\textrm{c}\), this may be due to the irreversible characteristics of the capillary bonds at the core of agglomerates and the displacements of particles outside.

Fig. 4
figure 4

a Compressive stress \(\sigma ^{\textrm{c}}\) and b tensile stress \(\sigma ^\textrm{t}\) vs. cumulative vertical strain \(\varepsilon \) for different values of the liquid viscosity \(\eta \) with a given value of the cohesion stress \(\sigma _{\textrm{c}} = 12\) kPa and the compression velocity \(v_0 = 0.5\) m/s

Full size image

Similar to the cohesive stress \(\sigma _{\textrm{c}}\) of capillary bonds, the liquid viscosity also affects to the macroscopic responses of agglomerates during compression. Figure 4a, b displays the roles of the viscosity \(\eta \) of the binding liquid on the evolution of the compressive stress \(\sigma ^\textrm{c}\) and the tensile stress \(\sigma ^\textrm{t}\) as a function of the cumulative vertical strain \(\varepsilon \). It is remarkable to note that \(\sigma ^\textrm{c}\) and \(\sigma ^\textrm{t}\) increase nearly proportional to the liquid viscosity \(\eta \) due to the enhancement of contractive and extensive behavior of capillary bonds, respectively. However, the effects of \(\eta \) on the compressive response of agglomerates are larger than that on the tensile stress, as shown in the range of values of these stresses at each cumulative vertical strain.

Fig. 5
figure 5

Evolution of the compressive strength \(\sigma _{\textrm{p}}^{\textrm{c}}/\sigma _{\textrm{c}}\) (a) and tensile strength \(\sigma _{\textrm{p}}^{\textrm{t}}/\sigma _{\textrm{c}}\) (b) as a function of the compression velocity \(v_0\) for all simulations. Each symbol and color represents a group of simulations in which the liquid viscosity \(\eta \) is fixed while the cohesive stress \(\sigma _{\textrm{c}}\) and compression velocity \(v_0\) are varied, as shown in the top-left corner of the upper figure. (Color figure online)

Full size image

Besides different influences of the liquid properties characterized by the cohesive stress \(\sigma _{\textrm{c}}\) and the viscosity \(\eta \) on the compressive and tensile stresses of viscocohesive–frictional particle agglomerates under diametrical compression test, loading speed characterized by the compression velocity \(v_0\) also strongly affects the macroscopic properties of such agglomerates. In order to fully reflect the changes of the mechanical properties by systematically varying different main parameters in including the compression velocity \(v_0\), the correlation between the mechanical strength (compressive and tensile strengths) and \(v_0\) is considered. The compressive strength is obtained by normalizing the peak of the compressive stress \(\sigma _{\textrm{p}}^{\textrm{c}}\) and the reference cohesive stress \(\sigma _{\textrm{c}}\); meanwhile, the tensile strength is defined as a ratio of the peak of tensile stress \(\sigma _{\textrm{p}}^{\textrm{t}}\) and \(\sigma _{\textrm{c}}\) of capillary bonds.

Figure 5a, b shows all data points of the compressive strength \(\sigma _{\textrm{p}}^{\textrm{c}}/\sigma _{\textrm{c}}\) and the tensile strength \(\sigma _{\textrm{p}}^{\textrm{t}}/\sigma _{\textrm{c}}\) expressed as a function of the loading speed \(v_0\), respectively. The tendency of these expressions is similar and both strengths increase with increase in the compression velocity. However, it is remarkable to note that the compressive strength is much higher than that of the tensile strength for each value of \(v_0\). This can be explained due to the material properties of the grains and the adhesive behavior of the binding liquid. Meanwhile, indeed, the compressive stress is strongly contributed by both stiffness of the primary particles and the adhesives, the tensile stress is mainly controlled by the cohesive and viscous properties of capillary bridges. As these representations of the variations of the mechanical strength of agglomerates, the compressive and tensile strength of such agglomerates may be uniformly described by a dimensionless parameter that incorporates the liquid properties and the compression velocity.

3.2 Unified description of compressive and tensile strengths

As excellently reported in our previous works on the compressive strength and tensile strength of viscocohesive–frictional agglomerates impacting on a rigid surface, a dimensionless impact number was defined as the square root of the multiply between the Capillary number \(\text{ Ca }\) and the sum of Stokes number \(\text{ St }\) and a weighting factor \(\beta \), \(I_{\textrm{n}} = \sqrt{\text{ Ca } ( \text{ St } + \beta )}\), where \(\beta \) is a weighting factor that considers the contribution of the viscous effects as compared to the initial effects during the impact. This dimensionless number is a remarkable extension of the inertial number I which is clearly defined in previous works for dry granular materials [42, 43] and also an extension of the generalized inertial number \(I_{\textrm{m}}\) defined for the simple shear flows of unsaturated granular materials [26]. As a result, this dimensionless parameter allows governing the compressive strength and tensile strength of such agglomerates, but with different values of the weighting factor \(\beta \) and with different power-fitting function forms. These differences may be explained due to the gravity effects of the primary particles, leading to significant changes in densities, intensities, and orientations of the forces between grains during the impact process.

Fig. 6
figure 6

The compressive strength \(\sigma _{\textrm{p}}^{\textrm{c}}/\sigma _{\textrm{c}}\) (a, b) and tensile strength \(\sigma _{\textrm{p}}^{\textrm{t}}/\sigma _{\textrm{c}}\) (c, d) of viscocohesive–frictional particle agglomerates are expressed as a function of the dimensionless number \(I_{\textrm{n}}\) in linear–linear and log–log scales for all our simulations. The symbols and their colors represent the same values of the liquid viscosity for different values of \(\sigma _{\textrm{c}}\) and the compression velocity \(v_0\). The symbols and their colors represent the same set of simulations as shown in Fig. 5. (Color figure online)

Full size image

In this paper, we analyze the compressive and tensile strengths of viscocohesive–frictional particle agglomerates in the case of without considering the particle gravity, subjected to a diametrical compression test in order to reduce the local effects of gravity of primary particles. By using the same dimensionless number defined in our recent works, \(I_{\textrm{n}} = \sqrt{\text{ Ca } ( \text{ St } + \beta )}\) [13, 20], both compressive strength and tensile strength are expected to uniformly control by setting the same value of the weighting factor \(\beta \). Figure 6a–d excellently expresses the compressive strength \(\sigma _{\textrm{p}}^{\textrm{c}}/\sigma _{\textrm{c}}\) and the tensile strength \(\sigma _{\textrm{p}}^{\textrm{t}}/\sigma _{\textrm{c}}\) as a function of the dimensionless parameter \(I_{\textrm{n}} = \sqrt{\text{ Ca } ( \text{ St } + \beta )}\) in linear–linear and log–log scales, respectively, for all values of the principal parameters (\(\sigma _{\textrm{c}}\), \(\eta \), and \(v_0\)) by setting \(\beta = 0.075\). This value is much larger than that (\(\beta = 0.001\)) for controlling the compressive strength of agglomerates impacting on a rigid plane, implying that the viscosity of the binding liquid is much more contributed to the compressive strength in the case of without gravity than that in the case of considering the particle gravity.

More interestingly, in the case of lacking the confining stress and the particle gravity of the diametrical compression test in this ongoing work, the value \(\beta = 0.075\) set for describing both compressive strength \(\sigma _{\textrm{p}}^{\textrm{c}}/\sigma _{\textrm{c}}\) and the tensile strength \(\sigma _{\textrm{p}}^{\textrm{t}}/\sigma _{\textrm{c}}\) is exact what we obtained for excellently expressing the rheological properties of pressure-controlled shearing flows of unsaturated granular materials in the steady state [26]. This finding strongly provides evidence that the contribution of the liquid viscosity to the macroscopic properties is independent on the configurations of viscocohesive–frictional granular materials by without considering the particle gravity, the macroscopic responses can be reflected via the mechanical strength of agglomerates subjected to a diametrical compression test and the rheological properties of viscocohesive–frictional granular materials at its steady-state shearing flows.

Although the compressive strength is much higher than the tensile strength of agglomerates, as discussed above and shown in Fig. 6, the evolution tendency of these strengths is similar and all data points of \(\sigma _{\textrm{p}}^{\textrm{c}}/\sigma _{\textrm{c}}\) and \(\sigma _{\textrm{p}}^{\textrm{t}}/\sigma _{\textrm{c}}\) excellently collapse on a master curve as an increasing function of the dimensionless parameter \(I_{\textrm{n}}\) by setting \(\beta = 0.075\). At very low values of \(I_{\textrm{n}}\), in particular, the compressive strength \(\sigma _{\textrm{p}}^{\textrm{c}}/\sigma _{\textrm{c}}\) approximates 0.8, whereas the tensile strength \(\sigma _{\textrm{p}}^{\textrm{t}}/\sigma _{\textrm{c}}\) is only slightly larger than 0.4. In the range of values of \(I_{\textrm{n}}\) observed in this paper, the growth rate of \(\sigma _{\textrm{p}}^{\textrm{c}}/\sigma _{\textrm{c}}\) is nearly double as compared to \(\sigma _{\textrm{p}}^{\textrm{t}}/\sigma _{\textrm{c}}\). Remarkably, we proposed two quadratic functions that allow to well fit all data points of \(\sigma _{\textrm{p}}^{\textrm{c}}/\sigma _{\textrm{c}}\) and \(\sigma _{\textrm{p}}^{\textrm{t}}/\sigma _{\textrm{c}}\) with different pre-factors, as given following by Eqs. (3) and (4), respectively.

$$\begin{aligned}{} & {} \frac{\sigma _{\textrm{p}}^{\textrm{c}}}{\sigma _{\textrm{c}}} = A_0 + A_1 I_{\textrm{n}}^{\alpha _1} + A_2 I_{\textrm{n}}^{\alpha _2}, \end{aligned}$$
(3)
$$\begin{aligned}{} & {} \frac{\sigma _{\textrm{p}}^{\textrm{t}}}{\sigma _{\textrm{c}}} = A_3 + A_4 I_{\textrm{n}}^{\alpha _1} + A_5 I_{\textrm{n}}^{\alpha _2}, \end{aligned}$$
(4)

where \(A_0 = 0.77\), \(A_1 = 12.00\), \(A_2 = 130.00\), \(A_3 = 0.40\), \(A_4 = 6.50\), and \(A_5 = 42.00\) are the pre-factors, and the power \(\alpha _1 = 1.00\) and \(\alpha _2 = 2.00\). These two scalings represent in the increasing part of the quadratic function of the dimensionless parameter \(I_{\textrm{n}}\) which has a range that is wide enough to fully cover the quasi-static regime (determined below) of the compression test. The fitting quadratic functional form strongly confirms the nontrivially unified description of both compressive strength and tensile strength of viscocohesive–frictional particle agglomerates subjected to a diametrical compression test by the dimensionless number \(I_{\textrm{n}}\) in its certain range, leading to well understanding of the rheological properties of viscocohesive–frictional granular materials.

To provide evidence for the quasi-static regime used in our simulations, the comparison between the particle displacement induced by the compression and the mean particle diameter \(\langle d \rangle \) is considered [15]. As shown in Fig. 2a, the top platen is moved downward by applying a constant velocity \(v_0\); meanwhile, the bottom platen is immobilized. With a maximum compression velocity \(v_0 = 0.7\) m/s used in the simulations and the time step \(\Delta t = 8 \times 10^{-8}\) seconds, the displacement of a particle during one step is \(v_0 \times \Delta t \approx 5 \times 10^{-8}\) m. This equals approximately \(6 \times 10^{-5}\) times the mean particle diameter \(\langle d \rangle \), implying that a quasi-static regime of the compression test is considered in our simulations, and the above scalings strongly provide possible applications in viscocohesive-frictional granular materials in the quasi-static regime.

4 Microscopic origins

As aforementioned, the nontrivially unified description of compressive and tensile strengths of viscocohesive–frictional agglomerates expressed as a quadratic function of the dimensionless parameter \(I_{\textrm{n}}\) maybe come from the unified representation of the microscopic origins of the macroscopic properties of agglomerates in the case of without gravity subjected to a diametrical compression test. In this ongoing work, the crucial enlightenment on the microscopic properties can be characterized by the density, intensity, and orientation of the normal forces which are used to highlight the origins of the macroscopic properties. At the particle scale, the normal forces are appeared between two particles in contact and joining their centers. In viscocohesive–frictional granular materials, the normal forces between grains involve two different components: compressive and tensile forces. The compressive forces have the contractional direction, whereas the tensile forces mobilize the extensional direction between particles in contact, as shown in Fig. 2d, e, respectively. The line thickness is proportional to the intensity of the compressive and tensile forces, and the force network represents the inhomogeneous nature of granular materials in density, intensity, and directions of the forces. Meanwhile, the density and intensity of the normal forces between grains can be understandably represented by considering the probability density function (pdf) of the normal forces \(f_{\textrm{n}}\) for different values of the cohesive stress \(\sigma _{\textrm{c}}\), liquid viscosity \(\eta \), and the compression speed \(v_0\), the orientation of the normal compressive and normal tensile forces is observed via their polar representations.

Fig. 7
figure 7

Probability density function of the normal force \(f_{\textrm{n}}\) (a) and the normalization \(f_n/(\sigma _{\textrm{c}} \langle d \rangle ^2)\) (b) for different values of the cohesive stress \(\sigma _{\textrm{c}}\) between particles

Full size image

As well known in granular materials, the probability density function (pdf) of the normal forces \(f_{\textrm{n}}\) is used to specify the probability of \(f_{\textrm{n}}\) falling within a particular range of values in a given sample. In this current work, we consider all normal compressive and tensile forces formed within the viscocohesive–frictional agglomerates. Figure 7a, b displays the pdf of without and with the normalization of the normal forces \(f_{\textrm{n}}\) by the cohesive force (\(\sigma _{\textrm{c}} \langle d \rangle ^2\)) exerted on mean particle diameter \(\langle d \rangle \) for different values of the cohesive stress \(\sigma _{\textrm{c}}\) at the peak stage. As shown in Fig. 7a, both the density and intensity of the normal compressive forces \(f_n^+\) and normal tensile forces \(f_n^-\) increase with increase in the cohesive stress \(\sigma _{\textrm{c}}\) between grains. Remarkably, the intensity of the strong compressive forces is about four times higher as compared to the strong tensile forces. This finding of the normal forces may be explained as the microscopic origins for the high observations of the compressive strength as compared to the tensile strength due to the crucial contribution of the strong normal forces on the mechanical strength of granular materials [44]. By making the normalization between \(f_{\textrm{n}}\) and \(\sigma _{\textrm{c}} \langle d \rangle ^2\), there are only small differences of the density and intensity of the normal forces when using different values of the cohesive stress \(\sigma _{\textrm{c}}\).

Fig. 8
figure 8

Probability density function of the normalization between the normal force \(f_{\textrm{n}}\) and the cohesive force \(\sigma _{\textrm{c}} \langle d \rangle ^2\) for different values of the liquid viscosity \(\eta \) (a) and different values of the compression speed \(v_0\) (b)

Full size image

The liquid viscosity \(\eta \) and the compression speed \(v_0\) also affect to the normal forces network at the peak stage (see Fig. 8a, b). However, in contrast to the slight decreases of the density and intensity of the normalization \(f_n / \sigma _{\textrm{c}} \langle d \rangle ^2\) with increasing \(\sigma _{\textrm{c}}\), both the density and intensity of this normalization slightly increase with increasing \(\eta \), as shown in Fig. 8a. The slightly reverse phenomenon of the effects of \(\sigma _{\textrm{c}}\) and \(\eta \) on the normal forces network may be due to the compensating effects between the cohesion and viscosity of the binding liquid as a consequence of the contraction and extension behavior of the viscous forces.

Fig. 9
figure 9

Polar diagrams representation the orientations of the normal forces \(f_{\textrm{n}}\), normal compressive forces \(f_\textrm{n}^+\), and normal tensile forces \(f_\textrm{n}^-\) in the initial (a) and peak (b) stage of an agglomerate under a diametrical compression test. The radii of these polar plots represent the number of the forces falling within an angular interval of three degrees

Full size image

Although the density and intensity of the normal compressive and tensile forces at the peak stage basically provide evidence for the nontrivially unified description of both compressive and tensile strengths, the orientation of the normal forces should be also considered in order to get a better understanding of the force directions during the compression. Figure 9a, b presents the polar diagrams of the orientation of the normal forces for the initial and peak instants, respectively. These polar diagrams of the normal forces, compressive forces, and tensile forces are determined by considering the number of the normal forces (including touching and non-touching cases between particles) falling within an angular interval of three degrees. As shown in Fig. 9a for the initial stage, the polar diagram displays a much more homogeneous orientation of both normal compressive and tensile forces due to the equilibrium behavior of viscocohesive–frictional particle agglomerates. The orientation of the normal forces changes significantly at the peak stage (as also observed in previous similar simulations [14]), and the number of the compressive and tensile forces is much more inhomogeneous due to the external triggering of the compression loading. In particular, the compressive forces occur along the major principal compressive stress direction \(\pi /2\), whereas the tensile forces mainly concentrate on the direction \(\pi \) of the major principal tensile stress. Remarkably, the number of the normal compressive and tensile forces is similar in their principal compressive and tensile stresses, as shown in Fig. 9b. These observations strongly confirm the unified description of the compressive and tensile strengths above.

5 Conclusions

In this paper, a 3D particle dynamics algorithm together with a capillary cohesion law enhanced by the normal cohesion forces and normal viscous forces is used to analyze the macroscopic responses and the microscopic properties of viscocohesive–frictional particle agglomerates, which are subjected to a diametrical compression test by imposing a constant downward velocity on the top platen, whereas the bottom platen is immobilized. The viscocohesive–frictional particle agglomerates are composed of spherical solid grains stuck by capillary bonds that are assumed to be homogeneously distributed inside agglomerates in the initial state. In this ongoing work, a capillary bond between two particles is assumed to be irreversibly broken during the compression when the separation distance between them exceeds the rupture distance. By systematically varying a broad range of values of the cohesive stress, the liquid viscosity, and the compression velocity in the inclusion of without considering the particle gravity, the mechanical strength of agglomerates characterized by the compressive and tensile strengths is analyzed in detail with the expectation of introducing a unified description of both compressive and tensile strengths by the dimensionless parameter that is defined in our previous investigations [13, 20].

As expected, both compressive and tensile strengths of viscocohesive–frictional particle agglomerates increase with increase in the cohesive stress and viscosity of the binding liquid as well as the compression speed of the top platen. Remarkably, the paper nicely introduced the nontrivially unified description of the compressive and tensile strengths of such agglomerates as a quadratic increasing function of a dimensionless number, this number is the same as defined in our previous work but with a different value of the weighting factor, \(\beta = 0.075\), reflecting the contribution of the viscosity of the binding liquid on the macroscopic responses of viscocohesive–frictional granular materials. This value observed in the ongoing work represents the same contribution of the liquid viscosity on the rheological properties of viscocohesive–frictional granular materials in the configuration of pressure-controlled steady flowing state but with a higher contribution as compared to the mechanical strength of agglomerates in the configuration of impacting on a rigid surface as a consequence of without considering the particle gravity. The unified description of both compressive and tensile strengths can be well explained by the unified representation of the density, intensity, and orientation of the normal compressive forces and normal tensile forces, these are well known as microscopic origins of the macroscopic properties of granular materials [14, 45].

The results reported in this ongoing work on the compressive and tensile strengths of viscocohesive–frictional particle agglomerates subjected to a diametrical compression test are a remarkable extension of the rheological properties of the pressure-controlled simple shear flow model at the steady state [26]. The findings confirm that the effects of the liquid viscosity on these macroscopic properties are nearly independent of the configurations and conditions of the tests, leading to providing insights into the rheological properties of viscocohesive–frictional granular materials widely presented in civil engineering and industries.