Effect of the intermediate principal stress on the mechanical behaviour of breakable granular materials using realistic particle models

Abstract

The effect of the intermediate principal stress (relative magnitude quantified by b) on the mechanical behaviour of breakable granular materials was studied using a DEM simulation of realistic particle models. The realistic particle model obtained by 3D scanning was divided into coplanar and glued Voronoi polyhedrons to reflect particle morphology more truly and fracture. After isotropic compression, a series of true triaxial tests under various b values were conducted using cubic and isotropic specimens. The macro-behaviour showed that the peak and critical shear strength first increased to a crest and then decreased with increasing b. Particle breakage caused a decrease in dilatancy and an increase in coaxiality. Increasing b resulted in an increase in cracks oriented in the intermediate principal stress direction and more broken particles. From the particle-scale analysis, as the b value increased, both the coordination number at the peak state and the percentage of sliding contacts at the critical state decreased. Particle breakage reduced the normal and shear contact forces at the critical state.

1 Introduction

The mechanical behaviour of granular materials (e.g. sands) has been explored using triaxial tests [6, 7, 22]. For example, Yu [57] conducted a series of triaxial tests to investigate the characteristics of the critical state locus. The investigation by Yu [58] incorporated particle breakage to interpret the mechanical behaviour of coarse sands in the triaxial test. In these tests, the loading is axisymmetric and inconsistent with those encountered in the field. A more generalised three-dimensional stress state exists in the field [20]. A dimensionless parameter b is proposed to study the influence of the intermediate principal stress σ₂, expressed as follows:

$$b = {{\left( {\sigma_{2} - \sigma_{3} } \right)} \mathord{\left/ {\vphantom {{\left( {\sigma_{2} - \sigma_{3} } \right)} {\left( {\sigma_{1} - \sigma_{3} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\sigma_{1} - \sigma_{3} } \right)}}$$

(1)

This parameter indicates the relative magnitude of σ₂ with respect to the major principal stress σ₁ and minor principal stress σ₃. In the three-dimensional stress state, hollow cylinder torsion tests [25] and true triaxial compression tests [24] were developed to explore the mechanical behaviour of cohesionless granular materials. According to experimental data, insights into the effect of σ₂ were proven, such as the stress–strain response, strength evolution, and shear band. However, it should also be noted that most previous studies have ambiguous results. For example, beyond a certain b value, the shear strength of granular materials increases monotonically, remains unchanged, or decreases slightly [26, 34, 53]. It is speculated that this scattering can be attributed to a variety of factors, such as the initial density, test method, testing apparatus, and materials. More importantly, owing to the inherent dispersion and heterogeneity of granular materials, it is difficult to track the evolution of particle breakage using existing test equipment in true triaxial tests [23, 33]. Hence, particle breakage is usually ignored in true triaxial tests. This certainly hampers the understanding of the effect of σ₂ on particle breakage.

The aforementioned inherent defects with the experimental approach can be easily avoided by using the discrete element method (DEM), which can generate specimens with no bias in the initial fabric. Thus, the DEM has become a powerful tool to study the mechanical behaviour of granular materials under complex stress paths. For example, Ng [38] conducted true triaxial numerical tests with ellipsoid rigid particles and found the relationship between b and shear strength. Jafarzadeh et al. [20] investigated the effect of sample preparation on anisotropic deviatoric response using true triaxial tests without considering particle breakage. Mahmud et al. [34] explored the effect of b on the macro–micro-response of granular materials composed of spherical rigid particles. Additionally, Cao et al. [5] investigated the effect of b on binary granular mixtures using rigid coarse particles with real shape and rigid fine particles with spherical shape. Obviously, these studies often ignore the influence of particle breakage and only assume that the particles are rigid bodies. As investigated by others [9, 31], particle breakage can greatly affect the macro–micro-mechanical behaviours of granular materials, which cannot be ignored. As the DEM improved, particle breakage was introduced [29]. Generally, two main methods were used to address particle breakage in the DEM. One method named the replacement method (RM) replaces the parent particle with several small child particles when a certain crushing criterion is reached [5]. Based on the RM, Zhou et al. [67] analysed the macro–micro-response of breakable particles. Nevertheless, the RM has some defects. For example, parent and child particles can only be spherical. In addition, the crushing criterion and pattern are controversial [68]. The other method is the bonding cell method (BCM), which can model complex-shaped particles. This method has been extensively used in studies related to particle breakage [9, 17, 59].

Balls are often used as cells to fill the interior of particles [54, 63]. For example, Liu et al. [28] used this method to examine the effect of intermediate principal stress on particle breakage. However, volume is not conserved during particle crushing. In addition, the accuracy of reproducing complex-shaped particles with balls is limited, or a large number of balls are required at high computational costs. The irregularity of particles and debris is difficult to reflect in the RM or BCM in which balls are used as child particles or cells, respectively. To offset these shortcomings, balls are replaced by tetrahedrons [37, 51] or Voronoi polyhedrons [17]. It is simple to divide arbitrarily complex particles into collections of tetrahedrons. As pointed out in [12, 30], compared with tetrahedral cells, Voronoi polyhedrons are more consistent with the composition of like-rock materials (e.g. marble) and give a more realistic representation of the fracture path. Therefore, a BCM using Voronoi polyhedrons as cells is adopted in this study. To simplify, most studies use sphere or simple polyhedrons to simulate breakable particles in the DEM [17, 31]. Even the most recent work [9] only uses the convex hulls of real particles. Note that convexity affects the mechanical behaviour of granular materials [3, 42]. Additionally, convexity of particles may also affect particle breakage. Thus, it is not rigorous to ignore the convexity of particles when studying particle breakage in the DEM. As Raisianzadeh et al. [46] stated, a natural evolution of DEM is to accurately replicate the particle breakage of real granular materials. Therefore, building a realistic particle model composed of Voronoi polyhedrons becomes a key problem to simulate particle breakage in the DEM. Few published studies have used realistic particle models to study the effect of σ₂ on the macro–micro-mechanical behaviour of breakable granular materials.

In view of the above research status, realistic particle models composed of Voronoi polyhedrons are adopted in this study to study the effect of intermediate principal stress on the mechanical behaviour of breakable granular materials via a 3D DEM system. This work is arranged as follows. First, a numerical simulation is briefly presented. Then, the macroscopic mechanical behaviour, microscopic mechanical behaviour, and particle breakage characteristics are examined. Finally, some main conclusions of the work are obtained. In addition, assemblies composed of unbreakable realistic particle models are also investigated in a parallel study to highlight the effects of particle breakage on the macro–micro-mechanical behaviours.

2 Numerical simulation process

2.1 Breakable particle models with realistic shapes

In this study, numerical true triaxial tests are carried out using the DEM program PFC3D [18]. Thirty pieces of rubble of similar size (d≈20 mm) were randomly selected from a quarry and numbered 1 ~ 30. The morphology of the particle was obtained by scanning selected rubble with a three-dimensional white-light scanner named Wiiboox Reeyee. The scan file for each particle was saved in STL format. The scan images of the 30 particles are shown in Fig. 1. Each particle model is composed of millions of triangular meshes.

Fig. 1

Scan images of 30 differently shaped rubble particles

Since a particle surface obtained by scanning consists of millions of triangular meshes, the modelling and computing efficiency will be greatly reduced. Thus, the spherical harmonic (SH) analysis proposed in previous studies [10, 65] was used to reconstruct the particle surfaces. Herein, the SH theory and mathematical analysis are briefly introduced. As expressed in Eq. (2), the major purpose of SH analysis is to extend the polar radius of the particle profile from a standard sphere and calculate the related SH coefficients:

$$r\left( {\theta ,\phi } \right) = \sum\limits_{n = 0}^{N} {\sum\limits_{m = - n}^{n} {a_{{\text{n}}}^{{\text{m}}} Y_{{\text{n}}}^{{\text{m}}} \left( {\theta ,\phi } \right)} }$$

(2)

where $r\left( {\theta ,\phi } \right)$ is the polar radius from the particle centre to the corresponding spherical coordinates;$\theta \in \left[ {0,\pi } \right]$ and $\phi \in \left[ {0,2\pi } \right]$ are the zenith angle and azimuth angle in spherical coordinate system, respectively. $Y_{{\text{n}}}^{{\text{m}}} \left( {\theta ,\phi } \right)$ is the SH series obtained by Eq. (3); $a_{{\text{n}}}^{{\text{m}}}$ is the SH coefficient corresponding to $Y_{{\text{n}}}^{{\text{m}}} \left( {\theta ,\phi } \right)$, and the total number of one set of ${a}_{\mathrm{n}}^{\mathrm{m}}$ is (n + 1)².

$$Y_{{\text{n}}}^{{\text{m}}} \left( {\theta ,\phi } \right) = \sqrt {\frac{{\left( {2n + 1} \right)\left( {n - \left| m \right|} \right)!}}{{4\pi \left( {n + \left| m \right|} \right)!}}} p_{{\text{n}}}^{{\text{m}}} \left( {\cos \theta } \right)e^{im\phi }$$

(3)

where ${p}_{\mathrm{n}}^{\mathrm{m}}(x)$ is the associated Legendre function; m and n are the degree and order of ${p}_{\mathrm{n}}^{\mathrm{m}}\left(x\right),$ respectively.

As pointed out by Fu et al. [10], the advantage of SH analysis is that it reconstructs a smooth and continuous surface mesh that is suitable for DEM modelling, as shown in Fig. 2. Clearly, the precision of the reconstructed particle is related to SH degree n. The larger the n value is, the more accurate the reconstructed particles are. Zhou and Wang [64] have proven that SH analysis is sufficient to represent the small-scale morphological characteristics of particles when n ≥ 15. In addition, the number of triangular meshes also affects the accuracy of the reconstructed particles. Zhao and Wang [61] stated that the overall shape of a particle will be reflected when the number of triangular meshes is greater than 1280. Zhou et al. [66] found that the mesh size dependency on particle crushing behaviour can be eliminated when the number of triangular meshes is greater than 1280. Therefore, to reconstruct the particle surfaces accurately in this study, the SH degree n and the number of triangular meshes were set to 15 and 1536, respectively.

Fig. 2

Development of the SH-reconstructed particle surface of a typical particle compared with its corresponding scan image

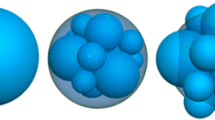
Current packages (e.g. Neper [45] and PFC3D [18]) only support the Voronoi subdivision of simple convex polyhedrons. In this part, an improved subdivision method was developed to divide particle models with complex shapes. The specific process is shown in Fig. 3. First, based on the radius enlargement method, balls of equal size were filled into the particle contour, as shown in Fig. 3a. The number of balls corresponds to the number of divided Voronoi polyhedrons. Then, taking the centres of these balls as the coordinates of seeds, Voronoi polyhedrons were generated in the smallest cuboid that can encapsulate the particle contour, as shown in Fig. 3b. After that, the intersection of each polyhedron and the particle contour was obtained, as shown in Fig. 3c. Note that the intersection may be non-convex due to the particle profile, which is unfavourable to DEM simulation. Hence, using the command “convhull” in MATLAB, the convex hull per intersection was obtained as a cell, as shown in Fig. 3c. Similarly, the above steps were performed for all Voronoi polyhedrons. Last, as shown in Fig. 3d, the aggregate formed by splicing all the cells together is the breakable particle model. One notable feature of the model is that the cells are coplanar with each other, so there is no gap in the model. Evidently, the precision of the particle model is controlled with a single continuously variable parameter, i.e. the number of cells. Garcia et al. [11] believed that when the number of cells in a Voronoi model is more than 75, the particle strength does not depend on the number of cells. Therefore, to balance the reconstruction precision and computational costs, the number of cells was set to 100. In addition, to facilitate the subsequent simulations, the equivalent diameter d $\left( {d = 2 \times \sqrt[3]{{3V_{p} /\left( {4\pi } \right)}}} \right)$ of all particle models is set to 20 mm, where V_p is the particle volume.

Fig. 3

Process of Voronoi subdivision for a realistic particle model

These cells were stuck together using the linear parallel bond model LPBM (an intrinsic constitutive model in PFC3D). This model determines the mechanical behaviour of a finite-sized grain of cement-like material deposited between two glued cells. Thus, it is widely used in research on particle breakage [9, 28]. For completeness, the LPBM mechanism was briefly introduced below.

As illustrated in Fig. 4, LPBM contains two interfaces. One is an infinitesimal, linear elastic (no-tension), and frictional interface that carries a force. The other is a linear elastic bond interface with a specific size. The former is equivalent to the linear elastic model. The latter is called parallel bond. Parallel bonds can transmit both force and moment between glued cells. If the tensile strength limit is exceeded, then the bond breaks in tension; if the shear strength limit is exceeded, then the bond breaks in shear.

Fig. 4

Behaviour and rheological components of the linear parallel bond model with inactive dashpots [18]

2.2 Simulation parameter calibration

In this study, the 30 particles selected were first subjected to a uniaxial compression test according to the numbering sequence, and the corresponding strength values σ were calculated according to Eq. (4) [19]:

$$\sigma =\frac{F}{\hbox{d}^{2}}$$

(4)

where F is the maximum force recorded on the top platen. Previous experiments [27, 52] have demonstrated that the breakage strength σ of particles of equal size conforms to a Weibull distribution, as expressed in Eq. (5):

$$\ln \left[ {\ln \left( {{1 \mathord{\left/ {\vphantom {1 {P_{{\text{s}}} }}} \right. \kern-\nulldelimiterspace} {P_{{\text{s}}} }}} \right)} \right] = m\ln \left( {{\sigma \mathord{\left/ {\vphantom {\sigma {\sigma_{0} }}} \right. \kern-\nulldelimiterspace} {\sigma_{0} }}} \right)$$

(5)

where σ₀ is the characteristic breakage strength in which 1/e (37%) of the samples survive; m is the Weibull modulus, which quantifies the scatter of the strength values; and P_s can be calculated as follows:

$$P_{{\text{s}}} = 1 - {i \mathord{\left/ {\vphantom {i {\left( {N + 1} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {N + 1} \right)}}$$

(6)

where i is the rank position of a particle when the particles are sorted in increasing order of breakage strength and N is the total number of particles (N = 30 in this study). McDowell and Harireche [36] deleted 0–25% of cells to realize a Weibull distribution in the DEM. When more cells (e.g. 20%) are deleted, a particle will show “porous” characteristics, which is not consistent with a real particle. A uniaxial compression numerical test corresponding to the experiment was also conducted in the order of numbering. By adjusting the micro strength parameters (i.e. cohesive and tensile strength), the simulated and tested crushing strengths are basically consistent, as shown in Fig. 5. In its inset, it is obvious that the fragmentation mode in the physical test is almost consistent with the simulation. Furthermore, Fig. 6 shows the experimental and numerical breakage strength values of all the particles. In the inset of Fig. 6, the overlapping data come from the same particle. It is just one from the simulation (red circle) and one from the experiment (black square). Clearly, the simulation data match well with the test data. The breakage strength presents a significant Weibull distribution (R² = 0.98).

Fig. 5

Stress–displacement curves in the experimental and simulated tests for particle No. 11. The inset shows the result of particle breakage

Fig. 6

Survival distribution of the single breakage strengths in experiments and numerical simulations; the inset shows the Weibull modulus and characteristic stress

A simple linear displacement–force contact law was adopted to model the particle–particle and particle–wall interactions. The normal contact stiffness k_n of the particles varies according to $k_{{\text{n}}} = \pi E_{{\text{c}}} r_{{{\text{min}}}} /\left( {r_{{\text{a}}} + r_{{\text{b}}} } \right)$, where E_c is the contact effective modulus, r_a and r_b represent the radii of the cells in contact, and r_min is the smaller value of r_a and r_b. The ratio k_n/k_s (where k_s denotes the shear contact stiffness) for realistic granular materials is in the range of 1.0 < k_n/k_s < 1.5, as shown by Goldenberg and Goldhirsch [13]. Hence, k_n/k_s = 4/3 was used in this study. All microscale parameters used in the DEM simulation are listed in Table 1.

Table 1 Microscale parameters used in the DEM simulation

2.3 Isotropic and true triaxial compression

Using the 30 scanned particle models as templates, 1200 non-contacting particles with random orientations were initially generated within a cube, as shown in Fig. 7a. The cube was modelled using six rigid walls. Gong et al. [14] and Nie et al. [40] tested assemblies with different particle numbers (1331–20,000) and believed that this range had a slight effect on the shear behaviour of granular materials. Thus, the particle number used in this study is acceptable. Temporarily, the gravitational acceleration and the friction coefficient between particle–particle and particle–wall contacts were set to zero to avoid force gradients and obtain isotropically dense assemblies. The micro-strength value is temporarily increased by 1000 times to prevent particle breakage during isotropic compression. The walls compressed the isotropic particles at a low velocity. The desired confining pressure σ_c (σ_c = 200 kPa) was obtained by using a servo-control mechanism. When the stress tolerance was less than 0.1% and the ratio of the average static unbalanced force to the average contact force was less than 0.5‰, the assemblies were considered to be in equilibrium. To eliminate specimen size effects and minimise stress non-uniformities inside the test assembly, the ratio of specimen size to maximum particle size should be greater than 5 [21]. In this study, the ratio was approximately 10, as shown in Fig. 7b. Note that all specimens have the same relative density after isotropic compression because the initial friction coefficient was set to zero, as outlined by Rothenburg and Bathurst [47] and Azema and Radjai [1].

Fig. 7

Isometric view of the isotropic compression: a initial state,b final assembly. l0, w0 and h0 are the initial length, width and height, respectively, of the assembly after isotropic compression.c Cubic element with the principal stresses and reference axis

After isotropic compression, the friction coefficient between particles was adjusted to 0.5, and the micro-strength inside the particles returned to the actual values. The relation between the directions of the three principal stresses and axes is shown in Fig. 7c. During the true triaxial tests, the major principal stress σ₁ was changed by shifting the top wall at a constant velocity, while the minor principal stress σ₃ was kept at 200 kPa by the servo-control mechanism. The intermediate principal stress σ₂ was varied with σ₁ by the servo-control mechanism. Meanwhile, the b value remained constant. In this study, the b values are 0.0, 0.2, 0.4, 0.6, 0.8 and 1.0. To ensure quasi-static shearing, the shear ratio had to be sufficiently slow so that the kinetic energy generated during shearing was negligible. This can be quantified by an inertia parameter I_m, as follows:

$$I_{{\text{m}}} = \dot{\varepsilon }d\sqrt {{\rho \mathord{\left/ {\vphantom {\rho {p^{^{\prime}} }}} \right. \kern-\nulldelimiterspace} {p^{^{\prime}} }}}$$

(7)

where $\dot{\varepsilon }$ is the shear strain rate, d is the maximum particle diameter, ρ is the particle density, and p' is the average stress. Due to the computational expense, the I_m value was less than 1.6 × 10^–3 throughout the simulations, which was less than the threshold (2.5 × 10^–3) recommended by Perez et al. [44]. Note that to highlight the particle breakage, the same true triaxial tests were also simulated for unbreakable granular materials with various b values.

3 Macroscopic mechanical behaviour

3.1 Macroscopic parameters

The macroscale stress tensor for the microscale quantities of the contact forces and contact vectors is as follows [2]:

$$\sigma_{{{\text{ij}}}} = \frac{1}{V}\sum\limits_{{c \in N_{{\text{c}}} }} {f_{{\text{i}}}^{{\text{c}}} } l_{{\text{j}}}^{{\text{c}}}$$

(8)

where V is the volume of the assembly; $f_{{\text{i}}}^{{\text{c}}}$ is the ith component of the contact force at contact c within the assembly; $l_{{\text{j}}}^{{\text{c}}}$ is the jth component of the contact vector at contact c; and N_c is the total number of contacts. For true triaxial stress, the effective mean stress (p') and deviatoric stress (q) can be defined as follows:

$$p^{\prime} = (\sigma_{1} + \sigma_{2} + \sigma_{3} )/3$$

(9)

$$q = \sqrt {3 \cdot J_{2} }$$

(10)

where J₂ is the second invariant of the stress deviatoric tensor. For true triaxial tests, the internal friction angle φ, which represents the shear strength of a granular material, can be calculated as follows:

$$\sin \varphi = \frac{{\sigma_{1} - \sigma_{3} }}{{\sigma_{1} + \sigma_{3} }} = \frac{{\left( {{q \mathord{\left/ {\vphantom {q {p^{\prime}}}} \right. \kern-\nulldelimiterspace} {p^{\prime}}}} \right) \cdot 1/\left( {1 - b + b^{2} } \right)^{0.5} }}{{2 + \left( {{q \mathord{\left/ {\vphantom {q {p^{\prime}}}} \right. \kern-\nulldelimiterspace} {p^{\prime}}}} \right) \cdot ({1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3} - 2b/3)/(1 - b + b^{2} )^{0.5} }}$$

(11)

The axial strain ε₁, lateral strains ε₂ and ε₃, volumetric strain ε_v, and deviatoric strain ε_d are given by:

$$\varepsilon_{1} = {{\left( {h_{0} - h} \right)} \mathord{\left/ {\vphantom {{\left( {h_{0} - h} \right)} {h_{0} }}} \right. \kern-\nulldelimiterspace} {h_{0} }}$$

(12)

$$\varepsilon_{2} = {{\left( {w_{0} - w} \right)} \mathord{\left/ {\vphantom {{\left( {w_{0} - w} \right)} {w_{0} }}} \right. \kern-\nulldelimiterspace} {w_{0} }}$$

(13)

$$\varepsilon_{3} = {{\left( {l_{0} - l} \right)} \mathord{\left/ {\vphantom {{\left( {l_{0} - l} \right)} {l_{0} }}} \right. \kern-\nulldelimiterspace} {l_{0} }}$$

(14)

$$\varepsilon_{{\text{V}}} = {{\left( {V - V_{0} } \right)} \mathord{\left/ {\vphantom {{\left( {V - V_{0} } \right)} V}} \right. \kern-\nulldelimiterspace} V}_{0}$$

(15)

$$\varepsilon_{{\text{d}}} = \frac{\sqrt 2 }{3}\sqrt {\left( {\varepsilon_{1} - \varepsilon_{2} } \right)^{2} + \left( {\varepsilon_{2} - \varepsilon_{3} } \right)^{2} + \left( {\varepsilon_{3} - \varepsilon_{1} } \right)^{2} }$$

(16)

where h₀, w₀, and l₀ are the dimensions of the specimen before shear and h, w, and l are the dimensions of the specimen at a given deformation state. V and V₀ are the volume of the specimen at the initial and shear states, respectively. The dilatancy angle ψ in true triaxial loading is defined as follows:

$$\sin \psi = \frac{{{{{\text{d}}\varepsilon {}_{{\text{V}}}} \mathord{\left/ {\vphantom {{{\text{d}}\varepsilon {}_{{\text{V}}}} {{\text{d}}\varepsilon {}_{{1}}}}} \right. \kern-\nulldelimiterspace} {{\text{d}}\varepsilon {}_{{1}}}}}}{{2 + {{{\text{d}}\varepsilon {}_{{\text{V}}}} \mathord{\left/ {\vphantom {{{\text{d}}\varepsilon {}_{{\text{V}}}} {{\text{d}}\varepsilon {}_{{1}}}}} \right. \kern-\nulldelimiterspace} {{\text{d}}\varepsilon {}_{{1}}}}}}$$

(17)

3.2 Shear strength

In this study, the true triaxial test was completed until the axial strain ε₁ equalled 40%. For such a large deformation, typical critical conditions, i.e. constant stress ratio and constant volumetric strain, are basically obtained. Figure 8 shows the stress ratio–axial strain relationship for unbreakable and breakable particles. As observed, in the two series of tests, the stress ratio evolved in a manner similar to dense cohesion-less granular materials. At a small strain state (ε₁ ≤ 0.5%), owing to the dense packing fraction of the initial specimens and the slight deviation of σ₂ from σ₃, q/p' rises rapidly and is not sensitive to the b value. After that, q/p' continues to rise until it peaks. Meanwhile, continuous compression will inevitably lead to an increase in σ₁. To keep the constant b value, σ₂ changes greatly. Therefore, the influence of the b value on q/p' gradually appears. After the peak, q/p' gradually decreases, eventually reaching a relatively constant plateau, i.e. the critical (residual) state. Except for a small ε₁ state, the effect of the b value on q/p' is approximately stable. Specifically, q/p' generally decreases with an increase in the b value, whether the particles are broken or not. A similar observation was also obtained by Cao et al. [6], in which rigid particles were used. Clearly, the introduction of particle breakage has an impact on q/p'_.

Fig. 8

Stress ratio–axial strain response for a unbreakable and b breakable particles

The peak internal friction angle φ_p and critical internal friction angle φ_c were obtained according to Eq. (11), as shown in Fig. 9. Note that the φ_c value is the mean value of φ at the critical state (i.e. ε₁ ∈ [30%, 40%]). For unbreakable particles, φ_p first increases to the peak with increasing b value. When b is unity, φ_p decreases slightly. A similar trend was also expressed in previous studies [6, 24, 34, 38]. In addition, φ_c as a whole appears to rise first and then decline. For breakable particles, as the b value increases, the trends of φ_p and φ_c are similar to those of unbreakable particles. In addition, regardless of whether particles are breakable, the minimum φ_p occurs when b = 0.0, implying that φ_p derived from conventional triaxial tests (i.e. b = 0.0) is conservative. Compared with φ of unbreakable particles, particle breakage resulted in a significant drop in φ_p and hardly affected φ_c, which is consistent with previous research [9] in which particle breakage mainly affects φ_p instead of φ_c. Previous studies [55, 56] also found that under otherwise similar conditions, the critical shear strength is a constant independent of grading, but, for a given grading, the critical shear strength is highly dependent on particle shape. In this study, due to Voronoi subdivision, the shapes of debris and original particles are highly irregular, and the particle breakage mainly leads to the change of grading. Therefore, the critical shear strength of breakable particles is almost the same as that of unbreakable particles.

Fig. 9

Variation in the peak and critical internal friction angle versus the b value for unbreakable and breakable particles

The gap (∆φ_p) of φ_p between unbreakable particles and breakable particles was also investigated, as shown in the inset. Interestingly, as the b value increases, the ∆φ_p value increases monotonically linearly. Considering the promoting effect of particle breakage on φ_p decline, variations in ∆φ_p are presumed to be related to different degrees of particle breakage under various b values. According to the trend of ∆φ_p, the relationship of φ_p between the unbreakable particles and breakable particles can be expressed as Eq. (18):

$$\varphi_{{\text{p}}}^{^{\prime}} = \varphi_{{\text{p}}} - (k_{{\text{s}}} b + c)$$

(18)

where ${\varphi }_{\mathrm{p}}^{^{\prime}}$ and $\varphi_{{\text{p}}}$ are the peak shear strength with and without particle breakage, k_s and c is the linear fitting parameters. Based on the published papers [9, 59], the c value is related to the confining pressure of the triaxial test. Under the same stress level, the properties of particles (e.g. breakage strength, particle shape, particle size) may lead to different crushing reactions [8, 9, 58]. Therefore, k_s value is not constant. Specifically, under the same stress level, the more easily broken granular materials, the more obvious the peak strength decline, and the greater the k_s value.

The shear strength derived from the DEM was compared with four typical empirical failure criteria that were developed from experimental data for real soils. The four models involved are as follows:

Lade model [24, 26]:

$$\frac{{\left( {\sigma_{1} + \sigma_{2} + \sigma_{3} } \right)^{3} }}{{\sigma_{1} \sigma_{2} \sigma_{3} }} - 27{ = }\eta_{1}$$

(19)

Ogawa model [43]:

$$\frac{{\sigma_{1} \sigma_{2} + \sigma_{1} \sigma_{3} + \sigma_{2} \sigma_{3} }}{{\left( {\sigma_{1} + \sigma_{2} + \sigma_{3} } \right)^{2} }} + \gamma \frac{{3\sigma_{1} \sigma_{2} \sigma_{3} - \left( {\sigma_{1} \sigma_{2} + \sigma_{1} \sigma_{3} + \sigma_{2} \sigma_{3} } \right)\left( {\sigma_{1} + \sigma_{2} + \sigma_{3} } \right)}}{{3\left( {\sigma_{1} + \sigma_{2} + \sigma_{3} } \right)^{3} }} = \eta_{2}$$

(20)

Matsuoka–Nakai model [35]:

$$\frac{{\left( {\sigma_{1} - \sigma_{3} } \right)^{2} }}{{\sigma_{1} \sigma_{3} }} + \frac{{\left( {\sigma_{1} - \sigma_{2} } \right)^{2} }}{{\sigma_{1} \sigma_{2} }} + \frac{{\left( {\sigma_{2} - \sigma_{3} } \right)^{2} }}{{\sigma_{2} \sigma_{3} }}{ = }\eta_{3}$$

(21)

Satake model [49]:

$$\left( {\frac{{\sigma_{1} - \sigma_{3} }}{{\sigma_{1} + \sigma_{3} }}} \right)^{2} + \left( {\frac{{\sigma_{1} - \sigma_{2} }}{{\sigma_{1} + \sigma_{2} }}} \right)^{2} + \left( {\frac{{\sigma_{2} - \sigma_{3} }}{{\sigma_{2} + \sigma_{3} }}} \right)^{2} { = }\eta_{4}$$

(22)

In previous studies [16, 38], spherical and ellipsoidal rigid particles are used for true triaxial simulation tests to evaluate the optimal failure criterion. This part further investigates the applicability of the four failure criteria in the case of realistic particle shape and breakage properties. Figure 10 displays the comparison between the empirical results derived from the four models and the measured data in this study. At the peak state, the Matsuoka and Satake models have identical predictions, and they do not fit well with the measured φ_p. In contrast, the Lade and Ogawa models give a better fit, especially the Ogawa model. The insets also show that almost all data derived from the Ogawa model fall in the range ± 2%. In the critical state, it is more complicated than that in the peak state. All predicted results from the four models seem to be roughly close to the measured results from the simulation. However, it is difficult to pick out the optimal failure model intuitively. To quantify the deviation, the error ε ($= {{\left| {\varphi_{\bmod } - \varphi_{{{\text{DEM}}}} } \right|} \mathord{\left/ {\vphantom {{\left| {\varphi_{\bmod } - \varphi_{{{\text{DEM}}}} } \right|} {\varphi_{{{\text{DEM}}}} }}} \right. \kern-\nulldelimiterspace} {\varphi_{{{\text{DEM}}}} }} \times 100\%$) of the friction angle was adopted, where φ_mod and φ_DEM represent the friction angles obtained from the failure model and DEM simulation, respectively. The results are listed in Table 2, where < ε > is the mean value of all data. Although, the prediction accuracy of the Matsuoka and Satake models for φ_c is better than that for φ_p. The best fit model is still the Ogawa model, even if it is not as accurate as it would be at the peak state. Additionally, the results in Table 2 further verify that the Ogawa model gives the best fit compared with the other models for φ_p, regardless of whether particle breakage is considered. On the whole, these four models can be ranked as Ogawa model > Lade model > Matsuoka model = Satake model. Similar observations have been provided by Ng [38], although he adopted ellipsoidal and rigid particles rather than breakable particles with realistic shapes.

Fig. 10

Evaluation of different failure criteria. a φp for breakable particles; b φp for unbreakable particles; c φc for breakable particles; d φc for unbreakable particles. Insets represent the performance of different failure criteria at the peak and critical states for breakable and unbreakable particles

Table 2 Average error < ε > between the predicted friction angle and measured friction angle

3.3 Dilatancy response

The relationships between the volumetric strain ɛ_V and axial strain for breakable and unbreakable particles are plotted in Fig. 11. At small ε₁ (ε₁≈2%), the volume contracts, and the contractions gradually increase with increasing b value. As shear continues, the dilatancy of the specimens increases with increasing b value. As shown in the inset, the maximum dilatancy angle ψ_max generally increases monotonically with increasing b value. In addition, ψ_max increases by 20° for unbreakable particles, while this value increases by only 8.8° for breakable particles. The reason is that debris produced by particle breakage fills the voids between large particles, which tends to cause volume compression. Thus, when particle breakage is considered, the value of ψ_max is obviously smaller than that of unbreakable particles. Additionally, the gap of ψ_max between unbreakable and breakable particles gradually widens as the b value increases. This is because a larger b value will lead to more serious particle breakage, as investigated in [28]. In the critical state, ε_V of unbreakable particles first decreases and then increases with increasing b, as observed by Cao et al. [6]. In contrast, as b increases, the critical ε_V of breakable particles first decreases and then does not increase but remains basically unchanged. Previous studies [9, 28] have shown the promoting effect of b on particle breakage which causes a decrease in the critical ε_V. Thus, the different behaviour of critical ε_V is presumably related to the fact that a larger b causes greater particle breakage.

Fig. 11

Evolution of the volumetric strain versus the axial strain for a unbreakable and b breakable particles

Considering the effect of ψ_max and φ_p, the stress–dilatancy relationship proposed by Rowe [48] was simplified by Bolton [4], which is expressed as follows:

$$\varphi_{{\text{p}}} = k\psi_{\max } + \varphi_{{\text{c}}}$$

(23)

where k is a line-fitting parameter. Figure 12 exhibits the stress–dilatancy relationship of breakable and unbreakable particles. It is clear that for true triaxial tests, the assemblies satisfy the relationships expressed in Eq. (23), whether the particles are broken or not. A comparison between Figs. 9 and 11 shows that the variation in ψ_max is more obvious than φ when particle breakage is considered. Specifically, compared with unbreakable cases, φ_p-φ_c decreased significantly less than ψ_max of breakable particles. In addition, Eq. (23) can be converted to: $k = {{\left( {\varphi_{{\text{p}}} - \varphi_{{\text{c}}} } \right)} \mathord{\left/ {\vphantom {{\left( {\varphi_{{\text{p}}} - \varphi_{{\text{c}}} } \right)} {\psi_{\max } }}} \right. \kern-\nulldelimiterspace} {\psi_{\max } }}$. Therefore, the k value of breakable particles is obviously larger than that of unbreakable particles.

Fig. 12

Stress–dilatancy relationship of breakable and unbreakable particles considering different b values

Figure 13 displays the evolutions of lateral strains (ε₂, ε₃) and deviatoric strain ε_d with respect to the axial strain ε₁. Generally, ε₁ and b have similar effects on breakable and unbreakable particles. Specifically, for small b, ε₂ decreases with increasing ε₁ and is negative, implying expansion in the σ₂ direction. When b = 0.4, ε₂ remains constant at 0. When b ≥ 0.6, ε₂ increases with increasing ε₁ and is positive, implying compression in the σ₂ direction. Due to the change in σ₂ from small to large, ε₂ increases with increasing b. That is, the assembly gradually turns from expansion to compression in the σ₂ direction. In Fig. 13b, increases in ε₁ and b cause a decrease in ε₃, meaning that both continuous shear and larger b lead to larger expansion in the σ₃ direction. In Fig. 13c, ε_d increases with increasing ε₁ and b. Note that the lateral strains of breakable particles are generally slightly lower than those of unbreakable particles. That is, under the same conditions, breakable assemblies tend to be denser in the σ₂ and σ₃ directions than unbreakable assemblies, which is in agreement with the variation in ε_V (shown in Fig. 11) and previous studies [9, 32]. A coefficient (A_c) [60, 67] was used to characterise the coaxiality of the contacts and stresses, which was defined as follows:

$$A_{{\text{c}}} = \frac{{tr\left( {\alpha_{{{\text{ij}}}}^{^{\prime}} \beta_{{{\text{ij}}}}^{^{\prime}} } \right)}}{{\sqrt {\alpha_{{{\text{ij}}}}^{^{\prime}} \alpha_{{{\text{ij}}}}^{^{\prime}} } \sqrt {\beta_{{{\text{ij}}}}^{^{\prime}} \beta_{{{\text{ij}}}}^{^{\prime}} } }}$$

(24)

where $\alpha_{{{\text{ij}}}}^{^{\prime}}$ and $\beta_{{{\text{ij}}}}^{^{\prime}}$ are the deviatoric tensors of $\alpha_{{{\text{ij}}}}$ and $\beta_{{{\text{ij}}}}$, respectively. $\alpha_{{{\text{ij}}}}$ and $\beta_{{{\text{ij}}}}$ can be defined as follows:

$$\alpha_{{{\text{ij}}}} = \left[ {\begin{array}{*{20}c} {{\text{d}}\varepsilon_{1} } & {} & {} \\ {} & {{\text{d}}\varepsilon_{2} } & {} \\ {} & {} & {{\text{d}}\varepsilon_{3} } \\ \end{array} } \right]$$

(25a)

$$\beta_{{{\text{ij}}}} = \left[ {\begin{array}{*{20}c} {\sigma_{1} } & {} & {} \\ {} & {\sigma_{2} } & {} \\ {} & {} & {\sigma_{3} } \\ \end{array} } \right]$$

(25b)

where dε₁, dε₂ and dε₃ are the strain increments corresponding to ε₁, ε₂ and ε₃, respectively. Figure 14 shows the relationships between the coaxiality coefficient and b at the peak and critical states. Whether particles are breakable or not, at b = 0.0 and 1.0, A_c≈1.0, implying that the strain increases and stresses are roughly coaxial, which is consistent with the observation in [6]. Similarly, Huang et al. [16] also stated that coaxiality in the $\pi$ plane occurs under b = 0.0 and 1.0 conditions. For two series of tests, A_c at the critical and peak states first decreases and then increases with increasing b, meaning that coaxiality first weakens and then strengthens. The weakening effect is more obvious at the critical state than at the peak state. Comparing the difference in A_c between breakable and unbreakable particles shows that particle breakage enhances coaxiality in both the peak and critical states.

Fig. 13

Evolution of the lateral strain a–b versus the deviatoric strainc versus the axial strain considering various b values

Fig. 14

Relationship between the coaxiality parameter and the b value at the peak and critical states

4 Particle breakage characteristics

To evaluate the effect of intermediate principal stress on particle breakage, the distribution of crack orientation, relative breakage and breakage pattern were investigated.

4.1 Crack orientation

In the simulations, once the bond between two touching cells was broken, a crack was generated at the location of the centre of the two bonding planes. The dip direction of the crack was perpendicular to the bonding planes. The rose diagrams of crack orientation under ε₁ = 40% for b = 0.0, 0.4 and 1.0 are plotted in Fig. 15. The anisotropy of crack orientation is roughly the same in the X–Z plane, owing to the same vertical strain and constant σ₃. Additionally, in the X–Z plane, the crack distribution exhibits a dumbbell shape, indicating that particles primarily split along the vertical direction. This is related to the fact that the major principal stress σ₁ is remarkably larger than the minor principal stress σ₃, resulting in the strong contact force being mainly distributed vertically. Similar observations have also been recorded in conventional triaxial tests [9]. In the lateral direction, with increasing b, the crack orientation changes from circular to elliptical with the major axis in the Y direction. In other words, with increasing b, particles change from equal breakage probability in various horizontal directions to easier breakage along the σ₂ direction. This is because the relative magnitude of σ₂ with respect to σ₃ varies with increasing b. As b increases, σ₂ increases from being equal to σ₃ at first (b = 0.0) to being greater than σ₃, leading to a larger contact force forming along the σ₂ direction than along the σ₃ direction. It also shows that a larger b value leads to more anisotropy of crack orientation in the X–Y plane.

Fig. 15

Rose diagrams of the crack direction at ε1 = 40% for b = 0.0, 0.4 and 1.0

4.2 Evolution of particle breakage

Relative breakage (B_r) [15] is adopted in this report to quantitatively define the degree of particle breakage and is expressed as follows:

$$B_{{\text{r}}} = {{B_{{\text{t}}} } \mathord{\left/ {\vphantom {{B_{{\text{t}}} } {B_{{\text{p}}} }}} \right. \kern-\nulldelimiterspace} {B_{{\text{p}}} }}$$

(26)

where B_p is the crushing potential, i.e. the area between the initial grading and the final particle size d_u (d_u = 0.074 mm), and B_t is the total breakage, i.e. the area between the initial grading, current grading and d_u. Figure 16 depicts the evolution of B_r with respect to b under various shearing states. As shown, both the shear strain and b value can promote particle breakage, which does not seem innovative. In previous studies, the promoting effect of shear strain [9, 59] and b value [28] was also demonstrated. Interestingly, taking b = 0.6 as the watershed, the rate of increase in B_r decreases first and then increases with increasing b. This trend is more obvious at a larger shear strain state and is not in agreement with the observation by Liu et al. [28]. They stated that the rate of increase in B_r will decrease with the increase in b. This may be related to the shear state. In their study [28], shearing stops when ε₁ = 15%, which is far less than ε₁ (i.e. ε₁ = 40%) in the current study. For a large shear stage (e.g. ε₁ = 30%) and large b value, σ₁ and σ₂ are significantly greater than σ₃, which is not reflected in the small shear strain. The combined effect of larger σ₁ and σ₂ causes greater particle breakage. Therefore, at larger ε₁ and larger b (≥ 0.6), the rate of increase in B_r increased instead. Figure 17 visualises the fragment distribution for various b values at ε₁ = 40%, where the greyer a particle is, the larger its size, and the bluer a particle is, the smaller its size. Clearly, with increasing b, the blue area in the assembly becomes more obvious, meaning that the number of fragments increases. Figure 17 can further intuitively reflect the promoting effect of the intermediate principal stress on particle breakage. Additionally, Fig. 16 demonstrates that increasing ∆φ_p (shown in Fig. 9) corresponds to larger particle breakage.

Fig. 16

Evolution of the relative breakage Br versus the b value considering various shearing states

Fig. 17

Fragment distribution considering different b values at ε1 = 40%

The evolutions of the particle size distribution curves with different b values during shear are plotted in Fig. 18. As observed, at different b values and loading stages, the size of the large-diameter particles remains nearly, as outlined by Nguyen et al. [39]. The reason is that even under the large deformation state of the assembly, many particles are broken, while others remain intact, as shown in Fig. 17. At the same shear stage, with the increasing b value, the increase in particle breakage leads to the increase in debris, as shown in Fig. 17. Hence, the grading curve moves upwards obviously, meaning that the proportion of fine particles increases. In addition, comparing different shear states, it is found that for the same b value, continuous loading leads to continuous breakage, resulting in the increase in the proportion of debris and the upward movement of the grading curve. It can also be observed that the gap of grading curves corresponding to different b values becomes larger at the larger axial strain. It should be noted that restricted by the cell size, these grading curves drop abruptly at the particle sizes equal to 4 mm.

Fig. 18

Evolutions of the particle size distribution curves with different b values during shear: a ɛ1 = 10%; b ɛ1 = 20%; c ɛ1 = 30%; dɛ1 = 40%

4.3 Breakage pattern

The average number of fragments (N_f) is the ratio of the number of all fragments to the number of broken particles at a given state. The relationships between N_f and the b value during shearing are displayed in Fig. 19. Generally, at a given strain state, the N_f value increases linearly with increasing b, indicating that larger b values cause particles to break into more fragments. In addition, for different strain states, the fitted lines show different slopes and intercepts, as shown in the inset. Specifically, as shear continues, the slopes and intercepts of the fitted lines generally increase monotonically as a whole. This suggests that ε₁ has a similar function to b in promoting a particle to break into more fragments.

Fig. 19

Evolution of the average value of Nf versus the b value during shearing

In addition, the average main fragment percentage (P_mf), which reflects the largest fragment formed by a broken particle, can be obtained at a specific state as follows:

$$P_{{{\text{mf}}}} = \frac{1}{{N_{{{\text{bp}}}} }}\sum\limits_{i = 1}^{{N_{{{\text{bp}}}} }} {\left( {{{V_{\max } } \mathord{\left/ {\vphantom {{V_{\max } } {V_{{\text{p}}} }}} \right. \kern-\nulldelimiterspace} {V_{{\text{p}}} }}} \right)} \times 100{\text{\% }}$$

(27)

where N_bp is the total number of broken particles and V_max is the maximum volume of all fragments produced by a broken particle. The changes in P_mf versus axial strain for different b values are plotted in Fig. 20. When b = 0.0 (i.e. a conventional triaxial test), P_mf fluctuates slightly at approximately 75% during shearing, meaning that ε₁ has a slight effect on P_mf. As the b value increases, the effect of ε₁ on P_mf gradually appears. Specifically, continuous shear will gradually reduce the volume of the largest fragment. Additionally, at a given strain state, especially a large deformation, the P_mf value generally declines with increasing b.

Fig. 20

Average value of Pmf –axial strain responses for different b values during shearing

5 Microscopic mechanical behaviour

To explore the effect of b on the mechanical response at the particle scale, various microscopic behaviours, including the coordination number (CN), sliding contact, contact force and contact anisotropy, were investigated.

5.1 Coordination number

The CN is an important parameter for quantifying the internal structure characteristics of granular materials. The traditional definition is the mean number of particles touching any specific particle. Numerically, the mean CN can be calculated as ${\text{CN}} = \frac{1}{{N_{{\text{p}}} }}\sum\nolimits_{i = 1}^{{N_{{\text{p}}} }} {N_{{\text{i}}}^{{\text{c}}} }$, where ${N}_{\mathrm{i}}^{\mathrm{c}}$ is the number of particles in contact with the ith particle and N_p denotes the number of particles. Figure 21 displays the evolution of the mean CN values versus ε₁ under different b values for breakable and unbreakable particles. For unbreakable particles, the mean CN value first declines exponentially and then remains at a low plateau. In addition, the evolution of CN is independent of the b value, as confirmed in previous studies [34, 50]. When particle breakage is considered, the mean CN value shows a declining trend from fast to slow. Furthermore, under large ε₁, the rate of decline in the mean CN value gradually slows down as the b value increases. Even at a high b value (e.g. b = 1.0), it is basically zero. As seen in Fig. 21a, the b value has little effect on the CN at a large shear strain. In contrast, the CN at the peak state is obviously affected by the b value. Specifically, the average CN value decreases with increasing b value. Fang et al. [9] observed that, accompanied by particle breakage, the proportion of “floating” particles (CN ≤ 2) increases, resulting in the declining trend of the CN at the peak state. As demonstrated in our previous work [9], at a large strain state, particle breakage causes the volume to shrink. Accordingly, denser assemblies increase the probability of contact between particles, leading to a decrease in the proportion of “floating” particles. Moreover, the shrinkage phenomenon is more obvious in the case of larger particle breakage. Thus, the rate of decline in the mean CN value gradually slows down with increasing b value.

Fig. 21

Evolution of the mean coordination number (CN) versus the axial strain ε1 for breakable a and unbreakable b particles

5.2 Sliding contact

Coulomb’s friction law is used to determine the occurrence of sliding contact. The sliding ratio S_c is defined as $S_{{\text{c}}} = \left| {f_{{\text{s}}} } \right|/\left( {\mu f_{{\text{n}}} } \right)$, where f_s and f_n are the shear and normal contact forces, respectively, and μ is the friction coefficient between particles. When S_c ≥ 1.0, sliding contact is considered to occur. The percentage of sliding contacts SCP is expressed as SCP = N_sc/N_c × 100%, where N_sc is the number of sliding contacts and N_c represents the number of contacts within the particle system. The variation in the SCP at the critical state with the b value for unbreakable and breakable particles is shown in Fig. 22. For unbreakable particles, the SCP showed a trend of first declining and then stabilising with increasing b. This seems to contradict the observation of Mahmud et al. [34], in which the SCP only shows little divergence for variations in b value at a large shear state. This trend is presumed to be due to the increase in the mean confining pressure under a larger b value, which makes it harder for the particles to slide. For breakable particles, the trend of the SCP is basically the same as that of unbreakable particles, but it is numerically smaller. A similar effect of particle breakage on the SCP was also observed in [9]. A reasonable explanation is that unbreakable particles rearrange through sliding contact. However, for potential breakable particles (i.e. the applied stress is greater than their strength), the particles tend to break rather than slide, which leads to a lower SCP.

Fig. 22

Variation in the SCP at the critical state versus the b value for breakable and unbreakable particles

5.3 Contact force

In particle systems, external loads are transferred by the contact between particles, which forms a contact force. The contact force is regarded as an important factor affecting the mechanical behaviour of granular materials [8, 62]. Figure 23 depicts the evolution of the mean contact force at the critical state with respect to b. Clearly, for two series of tests, the normal force f_n is greater than the shear force f_s, as observed in [8, 41]. In addition, for unbreakable particles, both the normal f_n and shear forces f_s increase with increasing b, which corresponds to a greater potential for particle breakage under larger b cases. However, when particle breakage is considered, the values of f_n and f_s are significantly less than those of unbreakable particles. Moreover, the gap in the contact force between unbreakable and breakable particles increases with increasing b. One reason is that the particle breakage increased at higher b values, and a number of stress concentrations induced by interlocking were removed, decreasing the number of particles with high stresses in the breakable assemblies. This is also related to the fact that a greater force per contact was produced between the larger particles. Therefore, additional new contacts formed between fragments during breakage have lower contact forces, owing to the smaller size of fragments. The above phenomena are positively correlated with particle breakage. Coincidentally, particle breakage increases with increasing b value, as shown in Fig. 16.

Fig. 23

Evolution of the mean normal and shear contact forces at the critical state versus the b value for breakable and unbreakable particles

6 Conclusions

In this paper, the effect of the b value on the mechanical behaviour of breakable granular materials with realistic particle models was studied via DEM simulation. To truly reflect the particle fractures and irregular debris, particle models obtained by 3D scanning were subdivided into coplanar and bonded Voronoi polyhedrons to simulate breakable particles. After isotropic compression, a cubic specimen composed of 1200 particles was prepared. Then, all specimens were subjected to shear by true triaxial compression tests under various b values (b = 0.0, 0.2, 0.4, 0.6, 0.8 and 1.0). The macroscopic behaviour, particle breakage characteristics and microscopic behaviour were investigated using these simulations. The main findings are summarised as follows.

Whether or not the assemblies are breakable, the peak φ_p and critical φ_c shear strength first increase to a crest and then decrease with increasing b. The φ_p of breakable particles is lower than that of unbreakable particles, and the gap in φ_p between breakable and unbreakable particles increases linearly with increasing b. The Ogawa model is better at predicting shear strength than other empirical failure models. Compared with unbreakable particles, particle breakage causes a decline in dilatancy and an increase in coaxiality. For breakable particles, a linear relationship between the maximum dilatancy angle ψ_max and φ_p-φ_c is satisfied. The slope of the linear relationship is larger than that of unbreakable particles.

The b value has little effect on the distribution of crack orientation in the X–Z plane. In contrast, in the horizontal direction, the larger b value causes a crack to concentrate in the intermediate principal stress direction. The degree of particle breakage increases with increasing b. At a large shear strain, as b increases, the rate of increase in particle breakage first decreases and then increases. Under a larger b value, particles tend to break into more fragments, and accordingly, the maximum in these fragments produced by one broken particle was smaller.

b mainly affects the coordination number at the peak state. That is, the peak CN declines with increasing b. The percentage of sliding contacts SCP at the critical state decreased first and then remained roughly constant as the b value increased. Due to the breakage of particles that should slide, the SCP of breakable particles is lower than that of unbreakable particles. For breakable particles, the normal f_n and shear f_s contact forces are less than those of unbreakable particles. The greater the value of b is, the greater the gap between them.