The roles of the reversibility and irreversibility of capillary bonds on the impact dynamics of agglomerates

Abstract

Wet agglomerates such as iron-ores, tablets, and aggregates are omnipresent in multi–field industries. However, our understanding of the impact dynamics of these materials is limited. Recently, Vo et al. reported the mechanical strength and deposition height of impact agglomerates which are well described by the Capillary–Stokes inertial number by considering the physical assumption of the irreversible breakage of capillary bonds between particles in the pendular regime (Vo et al. in Comput Particle Mech). Here, we provide a comprehensive comparison of the roles of the reversible and irreversible characteristics of capillary bridges on the agglomerate strength, deposition behavior, and energy consumption of agglomerates impacting a rigid surface. We reveal that the roles of both characteristics of capillary bonds strongly expressed via the differences of the mechanical strength, deposition behavior, and energy absorption of wet agglomerates. In particular, the mechanical strength of agglomerates of the reversible case is slightly higher than that of the irreversible one due to having small agglomerates’ deformation and the small number of loosing capillary bonds, and the larger differences of the final–deposition height and energy consumption of such agglomerates between the reversible and irreversible cases are due to the formation/reformation of capillary bonds and dry interactions. Interestingly, by systematically varying a broad range of values of controlled parameters such as the liquid viscosity, the liquid–vapor surface tension, and the impact speed of such agglomerates, the strength, deposition height, and energy consumption for both reversible and irreversible cases nicely collapse on concave master curves with the same function forms of the cohesive inertial number. The function form of the agglomerate strength represents a non–general(ized) $\mu (I)$ rheology due to the strong domination of the cohesive stress as compared to gravity (or confining stress). These results provide evidence of important applications for the handling of cohesive granular materials in industries.

1 Introduction

Agglomerates composed of fine solid particles with the interstitial liquid are the common case of unsaturated granular materials [45]. Wet agglomerates are not only omnipresent in nature in the terms of soil aggregates and clumps of powders but also in industrial applications such as iron–ores in steel making, tablets in pharmaceutical, and aggregates in cemented materials [7, 11, 22, 33, 34, 42]. By mixing the raw materials with an amount of the liquid in the industrial processes and the drainage or the condensation from the liquid vapor in the nature, the primary grains stick together via the liquid clusters, leading to the formation of the agglomerates [33, 63]. For the small amount of the liquid volume, the liquid clusters are in the form of binary bridges, called pendular regime, connected to two particles [28, 35, 38, 61]. Each liquid bridge induces the capillary attraction force and viscous force, these forces tend to increase the strength as well as improve the physical properties of agglomerate [48, 57]. Under the action of the external loads from sintering, mixing, delivering, or flowing, such agglomerates can change their mechanical strength, shape, and morphology not only depending on the natural properties of liquid bridges but also the transport and redistribution of the binding liquid [10, 24, 25, 53, 56], and the rate and shape of reaching the final deposition stage depends on the energy dissipation and absorption of agglomerates [3, 21, 32, 50, 62].

Indeed, the physical and mechanical properties of such agglomerates strongly depend on the existence and transport of the liquid [30, 44]. As the flows of wet granular materials occurred under the actions mentioned above, the capillary bonds between near–neighboring particles govern the strength and physical properties of agglomerates [57]. In particular, the capillary bridges between two particles can be broken when its separation distance exceeded the rupture gap, the liquid is then shared to two primary particles proportional to their sizes [57, 59]. Theoretically, these capillary bonds can be re–formed (reversible capillary bonds) during the movements of primary particles [54]. However, the capillary bridges may also not be re–formed (irreversible capillary bonds) as a consequence of the diffusion or evaporation of the binding liquid [44, 57]. Furthermore, as a small amount of the binding liquid, the liquid is also mainly adsorbed into the rough surface of primary particles, this leads to the difficult formation of the capillary bonds when the two particles meet [58]. Therefore, it is necessary to get a profound understanding of the physical and mechanical properties of such agglomerates by considering both reversible and irreversible capillary contacts in numerical simulations. In the case of the agglomerates impacting a rigid surface investigated in this current work, the mechanical and physical properties of granules are characterized by the average vertical strength and the deposition height [25, 57], respectively.

In cohesive granular materials, the irreversible capillary bonds are mainly considered in the compression test of agglomerates [4, 57] or its erosion dynamics in different flow configurations [27, 55], whereas the reversible capillary contacts between primary particles are modeled for the steady–state flows [5, 26, 40, 43, 54, 60]. The combination of the inertial number I and the cohesion number $\xi$ can be used to well behave the strength of agglomerates and the rheological properties of such flows [4, 8], where I is defined as a ratio of the relaxation time $\langle d \rangle (\rho /\sigma _n)^{1/2}$ and the flow time ${{\dot{\gamma }}}^{-1}$ [6, 13, 18, 23], $\langle d \rangle$ denotes the mean particle diameter, $\rho$ is the particle density, and $\sigma _n$ is defined as the confining pressure, and $\xi$ is a cohesion number defined as a ratio of the cohesion stress $\sigma _c = \pi \gamma _s/\langle d \rangle$ and $\sigma _n$, where $\gamma _s$ denotes the liquid–vapor surface tension. Similarly, by considering the reversible liquid–viscous bonds between spherical particles, the rheological properties of the simple shear flows can also be scaled by a non–dimensional parameter that incorporating the inertial number I and the Stokes number $\text{ St }$ [54], where $\text{ St }$ is defined as a ratio of the inertial stress $\sigma _i = \rho \langle d \rangle ^2 {{\dot{\gamma }}}^2$ obtained by the collective movements of particles and the viscous stress $\sigma _v = \eta {{\dot{\gamma }}}$, where $\eta$ is the liquid viscosity [2, 9, 51, 54]. More complicatedly, when both cohesive and viscous effects of the reversible binding liquid come into play with the inertial, frictional, and elastic effects of raw materials, the rheology of these steady–state flows can also behave as a general dimensionless number combining I, $\xi$, and $\text{ St }$ [60]. These examples lead to raise the question that whether the strength, the deposition height, and the energy consumption of agglomerates impacting a flat surface can be also well described as a function of the same or entirely different dimensionless parameter as compared to previous observations for both reversible and irreversible cases of liquid bridges? What are the roles of the reversible and irreversible capillary contacts in the mechanical and physical properties of such agglomerates? These questions will be well addressed in this paper.

In this paper, we address the above–interesting questions by analyzing the strength, deposition height, and energy consumption of a single agglomerate impacts on a rigid plane under considering both reversible and irreversible capillary bonds between near–neighboring particles. The agglomerate is modeled by composing primary spherical particles with the inclusion of the visco–cohesive liquid binding. By systematically varying a broad range of values of the liquid viscosity, the surface tension of liquid, and the impact condition of the agglomerate, the average vertical strength, deposition height, and energy consumption of such impact agglomerate change proportionally to these controlled parameters expressed via two dimensionless numbers. Remarkably, these measurements of the reversible case are higher than that of the irreversible one, and as we shall see, these mechanical and physical properties can be non–trivially scaled by the same non–dimensional parameter that represents the different description as compared to previous investigations.

In the following, we first briefly introduce the discrete element method in Section 2. We then show the impact test of a single agglomerate in Section 3. In Section 4, we measure the strength of such agglomerate by quantifying its average vertical stress and its deposition height and the energy consumption. We introduce the scaling properties of such agglomerate in Section 6 for both reversible and irreversible capillary bonds. Finally, in Section 7, we conclude with a salient summary of the remarkable results and its further research directions.

2 Methodology

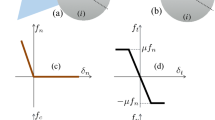
In the discrete element method (DEM) [12, 20, 37, 49], the primary particles are simulated as rigid bodies. In order to compute the particle interactions, a large repulsive stiffness of particles and a high time resolution are required. Each particle interacts with its near–neighboring particles via the contact forces including the normal and tangential contact forces [29, 37]. These forces between particles are proportional to the relative displacements between them, and the particle movements are determined by the step–wise computation via the Newton’s second law. In cohesive granular materials, the equation of motion of a rigid body i with its radius $R_i$ is obtained by integrating all forces exerted on particles including the normal contact forces $f_n$, the frictional forces $f_t$, the normal cohesive forces $f_c$, the normal viscous forces $f_v$, and the gravitational forces [1]. Although, the visco–cohesive bonds in the pendular regime can have a small contribution to the tangential forces in each particle interaction, the tangential cohesive forces and tangential viscous forces are neglected to simplify the numerical models in this current work.

The equations of motion of particle i are given by the following expressions:

$$\begin{aligned} m_i \frac{\text{ d}^2 {\mathbf {r}}_i}{\text{ d }t^2}= & {} \sum [(f_n^{ij} + f_c^{ij} + f_v^{ij}){\mathbf {n}}^{ij} + (f_c^{ik} + f_v^{ik}){\mathbf {n}}^{ik}+ \nonumber \\&f_t^{ij} {\mathbf {t}}^{ij}] + m_i {\mathbf {g}}, \\ {\mathbf {I}}_i \frac{\text{ d } \mathbf {\omega }_i}{\text{ d }t}= & {} \sum f_t^{ij} {\mathbf {c}}^{ij} \times {\mathbf {t}}^{ij}, \nonumber \end{aligned}$$

(1)

where particle i is in contacting with the particle j and non–contacting with near–neighboring particle k, as shown in Figure 1. $\omega _i$ is the angular velocity vector of the particle i, $\mathbf {g}$ denotes the gravitational acceleration vector, and $m_i$, ${\mathbf {I}}_i$, and ${\mathbf {r}}_i$ are the mass, inertia matrix, and position of particle i, respectively. ${\mathbf {n}}^{ij}$ (${\mathbf {n}}^{ik}$) is the normal unit vector between particle i and particle j (k), and pointing from particle j (k) to particle i. ${\mathbf {t}}^{ij}$ denotes the tangential unit vector when particle i in contacting with particle j, and having the direction opposite to the relative tangential movement. ${\mathbf {c}}^{ij}$ denotes the unit vector that pointing from the particle center i to the contact point with its neighboring particle j. In these simulations, we employed a velocity–Verlet time–stepping scheme for assimilation of the equations of motion of all particles [1, 16, 37].

Fig. 1

Schematic drawing representation two different cases of capillary bridges: contacting between particles i and j and non–contacting between particles i and k

The normal contact force $f_n$ involves two different components:

$$\begin{aligned} \displaystyle {f_n = f_n^e + f_n^d} \ . \end{aligned}$$

(2)

The normal elastic force $f_n^e=k_n \delta _n$ is a linear function of the normal elastic deflection $\delta _n$ at the contact point, where $k_n$ is the normal stiffness, and the damping force $f_n^d= \gamma _n {\dot{\delta }}_n$ is proportional to the relative normal velocity ${\dot{\delta }}_n$, where $\gamma _n$ is the normal viscous damping parameter. These contact forces occur only when there is the overlap between particles ($\delta _n < 0$).

The tangential force $f_t$ is the sum of an elastic force $f_t^e = k_t \delta _t$ and a damping force $f_t^d = \gamma _t {\dot{\delta }}_t$, where $k_t$ is the tangential stiffness, $\gamma _t$ denotes the tangential damping parameter, and $\delta _t$ and ${\dot{\delta }}_t$ are the tangential movement and the tangential velocity, respectively. The frictional force is the minimum value between $(k_t\delta _t + \gamma _t {\dot{\delta }}_t)$ and $(\mu (f_n + f_v + f_v))$ according to the Coulomb friction law [15, 29, 37, 46]:

$$\begin{aligned} f_t = -\!\min \left\{ (k_t\delta _t + \gamma _t {\dot{\delta }}_t), \mu (f_n + f_c + f_v) \right\} \end{aligned}$$

(3)

In the “pendular” regime, the liquid is in the form of capillary bridges [14, 28, 38, 47]. The formation of these capillary bridges may be a consequence of the mixing of rigid grains with the interstitial liquid, drainage of the liquid streamline in granular packing, or the condensation of the liquid vapor in nature [22]. Simplistically, our numerical simulations account for the cohesive forces and viscous forces of the capillary bonds up to the rupture distance with the liquid bridges assumed to be distributed homogeneously inside agglomerates in the initial state [57, 58]. During the rapid impact of wet particle agglomerates on a rigid plane, a capillary bond can be broken, and this capillary bridge can be or not be re–formed depending on the liquid volume and the surface roughness of particles as well as the recovering of the liquid volume on the particle rough surface.

In the case of existing the capillary bridges between primary particles, the cohesive force $f_c$ depends on the volume $V_b$ of the capillary bridge, surface tension $\gamma _s$ of the liquid and solid–liquid–gas contact angle $\theta$ which assumed to be zero due to the fully covering of the liquid on the particle surface, implying that this contact angle is independent of the liquid properties. This cohesive force is obtained from the Laplace-Young equation, and approximate solution of this equation is given by the following expression [31, 39]:

$$ f_{c} = \left\{ {\begin{array}{*{20}l} { - \kappa R,} \hfill & {{\text{for}}\;\delta _{n} < 0} \hfill \\ { - \kappa \text{Re} ^{{{{ - \delta _{n} } \mathord{\left/ {\vphantom {{ - \delta _{n} } \lambda }} \right. \kern-\nulldelimiterspace} \lambda }}} ,} \hfill & {{\text{for}}\;0 \le \delta _{n} \le d_{{rupt}} ,} \hfill \\ {0,} \hfill & {{\text{for}}\;\delta _{n} > d_{{rupt}} ,} \hfill \\ \end{array} } \right. $$

(4)

where $R = \sqrt{R_i R_j}$ is the geometrical mean radius of two particles radii $R_i$ and $R_j$ and the capillary force pre–factor $\kappa$ is

$$\begin{aligned} \kappa = 2\pi \gamma _s \cos \theta . \end{aligned}$$

(5)

This cohesion force was found to provide an excellent agreement with experimental data on the cohesion of wet granular materials [39]. The debonding distance $d_{rupt}$ is given by [28]

$$\begin{aligned} \displaystyle {d_{rupt} = \left( 1+\frac{\theta }{2}\right) V_b^{1/3} } \ . \end{aligned}$$

(6)

The characteristic length $\lambda$ in equation (4) is given by

$$\begin{aligned} \lambda = c\ h(r)\ \left( \frac{V_b}{R'}\right) ^{1/2}, \end{aligned}$$

(7)

where $R'= 2R_iR_j/(R_i+R_j)$ denotes the harmonic mean radius, $r\!=\!\max \{ R_i/R_j ; R_j/R_i\}$ is the size ratio between two primary particles, $h(r) = r^{-1/2}$, and $c \simeq 0.9$ [36, 38, 39].

The normal viscous force $f_v$ due to the lubrication effect of liquid bridges between two smooth spherical particles is given by [19, 27, 58,59,60]

$$\begin{aligned} f_v = \frac{3}{2} \pi R^2 \eta \frac{{v_n}}{\delta _n}, \end{aligned}$$

(8)

where $\eta$ is the viscosity of capillary bridges and $v_n$ is the relative normal velocity obtained by taking the derivative of $\delta _n$, this velocity is a positive value when the separation distance $\delta _n$ is decreasing. This computation implies that the liquid viscous force tends to diverges when the gap $\delta _n$ tends to zero. We define here a characteristic length $\delta _{n0}$ reflecting the depth of the particle roughness. The liquid viscous force is given following:

$$\begin{aligned} f_v = \frac{3}{2} \pi R^2 \eta \frac{{v_n}}{\delta _n+\delta _{n0}} \; \; \; \; \text{ for } \; \; \delta _n > 0. \end{aligned}$$

(9)

When occurring the overlap ($\delta _n <0$) between two spherical particles, the liquid viscous force reaches the largest value, and given by:

$$\begin{aligned} f_v = \frac{3}{2} \pi R^2 \eta \frac{{v_n}}{\delta _{n0}} \; \; \; \; \text{ for } \; \; \delta _n \le 0. \end{aligned}$$

(10)

Thus, the viscous force $f_v$ is as a function of the gap $\delta _n$ up to the debonding distance $d_{rupt}$ between two particles for a given value of the relative normal velocity for different values of the liquid viscosity. In all simulations investigated in this current work, we set $\delta _{n0} = 5.10^{-4} d_{min}$, where $d_{min}$ is the smallest diameter of primary particle. This value leads to the prevention of the divergence of the liquid viscous forces.

3 Impact of agglomerate

To get a comprehensive understanding of the roles of reversible and irreversible capillary bonds on macroscopic properties of wet granular materials, the impact test of a single agglomerate is performed. The macroscopic properties of such agglomerate are characterized by its mechanical strength, energy consumption, and deposition height. After constructing a spherical agglomerate composed of 31,500 wet primary particles in a cuboidal sample of 65,000 particles with a size ratio $d_{max}/d_{min}=2$, where $d_{max}$ and $d_{min}$ are the largest and smallest particle diameter [52], the impact test is generated by releasing such agglomerate from a height that equals to a half of its radius, measured from the lowest point of agglomerate, and setting an initial falling velocity $v_0$ for all primary particles. For all particles, gravity is set to g = 9.81 m/s$^2$, and the coefficient of friction between primary spherical particles is set to 0.5. After activating the initial velocity for all spherical particles, the agglomerate is falling down, tending to interact with the rigid plane. Due to consideration the particle gravity in the impact process, the early–impact velocity $v_{i}$ is different as compared to the initial falling velocity $v_0$ of agglomerate, this differential level depends on the value of $v_0$. Upon the impact, the average vertical stress of agglomerate changes and it tends to reach the plateau at the peak and deposition stages. The values of the agglomerate strength and the deposition height as well as the rate of reaching the deposition strongly depend on the both reversible and irreversible capillary bonds and the values of controlled parameters such as the liquid viscosity $\eta$, the liquid–vapor surface tension $\gamma _s$, and the initial falling velocity $v_0$. Furthermore, the deposition behavior is due to the energy absorption of such agglomerates. In this current work, 468 numerical computations were performed by systematically varying a broad range of values of three controlled parameters ($\eta$, $\gamma _s$, and $v_0$) for two assumptions of the capillary bonds (reversible and irreversible). All systematic and material parameters and their values are given in Table 1.

Table 1 Different values of key parameters used in numerical simulations

Fig. 2

A schematic diagram showing the reversible and irreversible cases of the capillary bonds between primary particles during the impact test

The different values of the key parameters are chosen based on the numerical efficiency. The choice of the normal and tangential stiffnesses of particles is based on the elastic defection that is set below 0.01 after considering both cohesive and viscous forces. This means that two particles in solid contact with the presence of the capillary bridge can be overlapped under the action of the cohesive forces and external forces induced by surrounding particles. In this case, we neglected the effects of fluid pressure induced by changing the capillary shape between two particles in contact due to the overlapping between them.

Fig. 3

Snapshots of a wet agglomerate falling down with an initial falling velocity $v_0$ and initial diameter $D_0$ to impact a rigid plane (a), the velocity profile of agglomerate (b) for the reversible (left) and irreversible (right) cases during the impact process, and the final deposition stage (c) for a given value of the cohesive stress ($\sigma _c = 16.2$kPa) and the initial falling velocity ($v_0 = 4.0$m/s) for the cases of considering the reversible (left) and irreversible (right) capillary contacts

We first clarify the physical assumptions of the reversible and irreversible breakage of capillary bridges between grains used in this current work. Figure 2 shows both reversible and irreversible cases of capillary bonds during the impact test. Particle 1 is in contact with particle 2 with the presence of the capillary bond, meanwhile, the liquid is covered on the surface of particle 3 in the initial state. The liquid bridge between particles 1 and 2 is broken as a consequence of the separation distance exceeding their rupture gap. In all our simulations, the rupture distance is assumed to be characterized for the volume of the liquid bridge between two particles in contact. After breaking, this liquid bridge is assumed to be shared to particles 1 and 2 depending on their sizes. Then, the capillary bonds between particle 1 and particle 2 (or particle 2 and particle 3) can be reformed (or formed) or can not be reformed (or formed), respectively, depending on the particle properties and diffusion of the liquid during the test. These characteristics represent the reversibility and irreversibility of capillary bridges between near–neighboring particles. In this current work, both these reversible and irreversible contacts are considered.

Figure 3 displays the normal impact process of a single wet agglomerate on a rigid surface by considering both reversibility and irreversibility of capillary bridges for a given value of the cohesive stress $\sigma _c$ and the initial falling velocity $v_0$. Upon the impact, the agglomerate deforms as a consequence of having the relative movements between primary particles, tending to break some of the initial capillary bonds. These capillary bridges can be reformed or non–reformed depending on the discrete nature of the raw materials and the liquid. For the irreversible case of capillary bonds, the particles’ velocity are much higher than those of the reversible case of capillary bridges at each specific impact time, as shown in Fig. 3b, this can be explained due to the consumption of the impact energy that is not only dissipated through the frictional contacts between particles but also via the visco–cohesive capillary bonds [32, 62]. The agglomerate then reaches the final deposition stage as a consequence of fully loosing the impact energy, as shown in Fig. 3c, reflected via the final deposition height $D_{stop}$. In contrast to the particles’ velocity, the deposition height of agglomerate for the irreversible case of the capillary contacts is smaller than that of the reversible case of the capillary bonds.

In order to clearly highlight the roles of the reversibility and irreversibility of capillary bridges between primary particles, the macroscopic properties are analyzed. In our simulations, the mechanical property of the single wet agglomerate impacting a rigid plane is characterized by the average vertical stress $\sigma _{zz}$, measured by considering z–components of the force vectors that combining all normal forces (with and without capillary bridges) and tangential forces activating between primary particles and the branch vectors joining two particle centers, as particularly expressed following:

$$\begin{aligned} \sigma _{\mathrm {{zz}}} = \frac{1}{V_{\mathrm {agg}}} \sum _{k=1}^{N_{\mathrm {c}}} f_{\mathrm {{z}}}^k \ell _{\mathrm {z}}^k, \end{aligned}$$

(11)

where $V_{\mathrm {agg}}$ denotes the current volume of the agglomerate, $N_{\mathrm {c}}$ is the number of contacts (with and without capillary bonds) in current computational step, $f_{\mathrm {z}}^k$ and $l_{\mathrm {z}}^k$ are the z–components of the force and branch vector of contact k, respectively.

Fig. 4

Evolution of average vertical stress $\sigma _{zz}$ as a function of impact time for three different values of the cohesive stress $\sigma _c$ between primary particles for the reversible (solid lines) and irreversible (dashed lines) cases of the capillary bonds with a given value of the liquid viscosity $\eta = 1000$mPa.s and the initial falling velocity $v_0 = 5.0$m/s

Figure 4 displays the evolution of $\sigma _{zz}$ of single wet particles agglomerate impacting a rigid surface over the impact time for three different values of the cohesive stress $\sigma _c$ for both reversible and irreversible capillary bonds with a given value of $\eta = 1000.0$ mPa.s and $v_0 = 5.0$ m/s. It is interesting to see that $\sigma _{zz}$ is very slightly greater than zero in the equilibrium state before occurring the collision with the surface, the average vertical stress then rises immediately and fluctuates in a range in the peak stage, the noise of this stress in the peak stage depends on the liquid properties and impact conditions of the test. The peak data of each simulation are obtained by averaging the stress in the peak stage, as plotted via their standard deviation in Fig. 7. This peak stress for the irreversible case of capillary bridges is slightly lower than that of the reversible case as a consequence of having the small number of capillary bonds broken at this early–stage impact. $\sigma _{zz}$ then declines smoothly with the rate that increases with increasing $\sigma _c$ at the post–impact stages. Interestingly, it is easy to distinguish the stress properties of agglomerate before reaching the final deposition stages. Meanwhile, the average vertical stress of the reversible case of the binding liquid drops suddenly due to representation of the rapid absorption of the impact energy, this stress for the irreversible one declines exponentially as a function of the impact time. As a result, the agglomerate with the reversible capillary contacts reaches the final deposition stage much faster than the case of irreversible contacts of wet primary particles.

Fig. 5

The normalized agglomerate height $D_z/D_0$ as a function of the impact time for three different values of the cohesive stress $\sigma _c$ between primary particles with a given value of the liquid viscosity $\eta = 1000$mPa.s and the initial falling speed $v_0 = 5.0$m/s. The solid lines are presented for the reversible capillary contacts whereas the dashed lines are shown for the irreversible case

Fig. 6

Evolution of the height $D_z$ normalized by the initial diameter of agglomerate $D_0$ as a function of the impact time t for the cases of the reversible capillary contacts (solid lines) and the irreversible capillary bonds (dashed lines) with two different values of the liquid viscosity $\eta$ (mPa.s) and the initial falling velocity $v_0$ (m/s) with a given value of the cohesive stress $\sigma _c = 34.0$kPa

The rate of reaching the final deposition stage of impact agglomerate is also an interesting feature representing the different responses of agglomerate between the reversible and irreversible cases, this interesting point is expressed via the evolution of the height $D_z$ of agglomerate in the normal impact test, where $D_z$ is defined as the distance in the vertical direction between the free surface of the lowest and highest particles. Figure 5 shows the normalized height $D_z/D_0$ of agglomerate as a function of the impact time for three different values of $\sigma _c$ for two cases of the capillary bridges, where $D_0$ is the initial diameter of the agglomerate. $D_z$ of agglomerate decreases rapidly, then reaches the final deposition height $D_{stop}$. The value considering the disparity of $D_{stop}$ between the irreversible and reversible capillary bonds declines with increasing the cohesive stress $\sigma _c$. Due to the contraction properties of the visco–cohesive liquid bridges between near–neighboring particles [54], the effects of the viscosity of liquid bridges on the deposition behavior of agglomerate are similar to the liquid–vapor surface tension $\gamma _s$ and inverse to the impact speed of agglomerate, as shown in Fig. 6. Indeed, the agglomerates of the reversible case reach the final deposition stage with the height that is higher than that of the irreversible one, and this deposition height increases with increasing the viscosity of the liquid whereas it declines with the increasing of the impact speed as a consequence of weakening the contraction and strengthening the extension.

4 Macroscopic properties of impact agglomerates

To elucidate comprehensively the roles of the reversibility and irreversibility of capillary bridges on the macroscopic properties of agglomerate impacting a rigid plane, the mechanical strength, deposition height, and the energy consumption are considered in different stages of the impact process. Meanwhile, the mechanical strength is measured as average vertical stress at the peak stages, the deposition height and the energy consumption are quantified in the final deposition stage and a specific time after the agglomerate colliding on the rigid surface, respectively.

Fig. 7

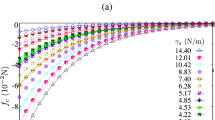
Evolution of the normalized peak stress $\sigma _p/\sigma _c$ of wet agglomerate as a function of the cohesive stress $\sigma _c$ for two different values of the liquid viscosity $\eta$ (mPa.s) and the initial falling velocity $v_0$ (m/s). The filled symbols are presented for the case of the reversible capillary contacts, whereas the open symbols correspond to the irreversible case of the capillary bonds. The error bars represent their standard deviation in each simulation. Each error bar symbol represents the result for different values of the cohesive stress $\sigma _c$ (kPa) with a given value of the liquid viscosity $\eta$ (mPa.s) and the initial velocity $v_0$ (m/s)

Figure 7 shows the normalized vertical peak stress $\sigma _p/\sigma _c$ of agglomerate at its early–stage impact as a function of the cohesive stress $\sigma _c$ for two different values of the liquid viscosity $\eta$ and the initial falling velocity $v_0$ for both reversible and irreversible formation of the capillary bridges between spherical particles. As expected for high values of the cohesive stress and a small value of the initial falling velocity, corresponding to strong agglomerates and slow impact energy, respectively, there is almost no difference of $\sigma _p/\sigma _c$ between the reversibility and irreversibility of capillary bonds. In particular, this normalized vertical stress is very small and almost constant with $v_0 = 1.0$m/s for a whole range of values of the cohesive stress considered in this current work (see Table 1). These similar characteristics of $\sigma _p/\sigma _c$ are also observed for agglomerates with the cohesive stress $\sigma _c > 30.0$ kPa and the rapid impact of agglomerate, although the agglomerate strength of these cases is slightly higher than that of the case of slow impact speed. It is also interesting to see that this strength then shows the difference between the reversible and irreversible cases of the capillary bonds, in particular, this difference increases with decreasing the cohesive stress $\sigma _c$ between primary particles and decreasing the liquid viscosity $\eta$ of the binding liquid for high value of the initial falling velocity $v_0$. Simultaneously, in all cases of the liquid properties and the impact conditions, the mechanical strength of the agglomerate of the irreversible case is always lower than that of the reversible case of the capillary bridges as a consequence of loosing the capillary contacts.

As presented in previous section, the final deposition stage of impact agglomerate is obtained after passing the peak stage of the impact test. In contrast to the mechanical strength of agglomerate in the early–stage impact, the reversibility and irreversibility of the capillary bonds represent the significant effects on the deposition behavior of agglomerate due to the formation/reformation and the breakage of capillary contacts, respectively. Figure 8 shows the normalized height of agglomerates at the final deposition stage as a function of the cohesive stress $\sigma _c$ for two different values of the liquid viscosity $\eta$ and two different values of the initial falling velocity $v_0$. We can see that $D_{stop}/D_0$ increases exponentially with different curves depending on the reversible and irreversible characteristics of capillary bridges for all values of the liquid properties and the impact conditions. In particular, $D_{stop}/D_0$ of the reversible case is much higher than that of the irreversible one as a consequence of the formation/reformation of the reversible capillary bonds and the loosing of the irreversible capillary contacts, leading to different absorptions of the impact energy, especially for rapid impact test. The roles of reversibility and irreversibility of capillary bonds continue strongly representing with lower impact speed for weak agglomerates. Nevertheless, we obtained the similar deposition behavior of agglomerates for both reversible and irreversible capillary bridges for strong cohesion between primary particles and the slow impact velocity, this can be explained due to the rapid absorption of the impact energy after colliding the rigid plane.

Fig. 8

The normalized deposition height $D_{stop}/D_0$ of wet agglomerate as a function of the cohesive stress $\sigma _c$ for two different values of the liquid viscosity $\eta$ and the initial falling velocity $v_0$. The filled symbols are presented for the case of reversible capillary contacts, whereas the open symbols correspond to the irreversible case of the capillary bonds. Each symbol represents the result for different values of the cohesive stress $\sigma _c$ with a given value of the liquid viscosity $\eta$ (mPa.s) and the initial falling velocity $v_0$ (m/s)

Fig. 9

The energy consumption $\varDelta E$ of wet agglomerate after colliding the rigid plane $8 \times 10^{-3}$ sec. as a function of the cohesive stress $\sigma _c$ for two different values of the liquid viscosity $\eta$ and the initial falling velocity $v_0$. The filled symbols are presented for the case of reversible capillary contacts, whereas the open symbols correspond to the irreversible case of the capillary bonds. Each symbol represents the result for different values of the cohesive stress $\sigma _c$ with a given value of the liquid viscosity $\eta$ and the initial velocity $v_0$

Indeed, the deposition behavior of the agglomerates impacting a rigid plane strongly depends on the energy consumption during the test. Thus, it is necessary to measure the energy absorption in a period of the impact time for different values of the liquid properties and the impact conditions. In this current work, in order to simplify the measurement of energy consumption $\varDelta E$, it is calculated as the difference of the sum ($E = E_{pi} + E_i$) of potential energy $E_{pi}$ and kinetic energy $E_i$ obtained just before occurring the collision with the rigid surface and their sum ($E_{pc} + E_c$) at the current stage. In our simulations, the initial falling velocity $v_0$ of agglomerates is set in a broad range of values [0.3,5.0] m/s. Thus, in order to unify the measurement of kinetic energy before reaching the final deposition stage of agglomerates, the energy consumption $\varDelta E$ is quantified after $8 \times 10^{-3}$ seconds as compared to the time occurring the collision between agglomerates and the plane.

Figure 9 displays the energy consumption of agglomerates as a function of the cohesive stress $\sigma _c$ for two different values of the liquid viscosity $\eta$ and the initial falling velocity $v_0$ for both reversible and irreversible cases of the capillary bonds. Similar to the height of agglomerates at the final deposition stage, the energy consumption $\varDelta E$ increases with increasing the cohesive stress $\sigma _c$, this is due to the significant absorption of kinetic energy in the cohesive contacts between primary particles. Indeed, due to the formation/reformation of the capillary bridges during the impact test, the energy consumption of the reversible case is higher than that of the irreversible case of the binding liquid as a consequence of loosing such contacts. Furthermore, the energy consumption increases with increasing the falling velocity and the liquid viscosity, and the cohesive stress, but the effects of $v_0$ and $\sigma _c$ are much more significant than $\eta$.

5 Microscopic origins of macroscopic responses

As discussed previously, the effects in different degrees of the reversibility and irreversibility of capillary bridges on the macroscopic properties of agglomerates in different stages may be due to the formation/reformation of the capillary bonds in the reversible case and the irreversible breakage of capillary bridges in the irreversible one. In this section, crucial enlightenment on the microscopic origins of the macroscopic responses observed above is brought by considering the number of capillary contacts in different stages for a thin layer of agglomerates in order to improve the visibility. As reported in previous observations about the contributions of the wet coordination number on the shear strength of granular materials [6, 26, 54], in this ongoing work, the distribution and reversible/irreversible degrees of capillary bridges may explain for the slight difference of mechanical strength at the early–impact stage, and larger different observations of energy consumption and deposition behavior of agglomerates for both cases of capillary bridges.

Fig. 10

Snapshots representation the instants of the forces between primary particles during the impact process for a given value of the cohesive stress $\sigma _c = 16.2$ kPa and the initial falling velocity $v_0 = 1.0$ m/s. (a) and (c) show the sequences of the cohesive forces of the reversible and irreversible cases of capillary bonds, respectively. (b) and (d) represent the cohesive forces of the capillary contacts formed/reformed during the test of the reversible case and the contact forces of the irreversible case of capillary bridges. The line is the normal force joining two near–neighboring particles, and the line thickness is proportional to the magnitude of the normal forces

Figure 10 shows the instantaneous snapshots of the normal forces between primary particles arranged in a thin section during the impact test with a given value of the liquid viscosity $\eta$, the cohesive stress $\sigma _c$, and the slow initial falling velocity $v_0$ for both reversible and irreversible cases of the capillary contacts. The normal forces with capillary bonds are distributed homogeneously within agglomerates in the initial state. The forces distribution seems similarly at the early–stage impact between the reversible and irreversible cases of the capillary bridges as a consequence of the small deformation of the agglomerates. This similarity of reversible and irreversible cases is not only presented via the total capillary forces, as shown in Fig. 10a–1, a–2 and c–1, c–2, respectively, but also the formed/reformed capillary forces of the reversible case (Figure 10 (b–1, b–2)) and the formed/reformed dry forces of the irreversible case (Fig. 10(d–1, d–2)). These are reliable evidence to explain for the slight difference of agglomerate strength with $\sigma _c = 16.2$ kPa and $v_0 = 1.0$ m/s (as shown in Fig. 7).

Fig. 11

Snapshots representation the instants of the forces between primary particles during the impact process for a given value of the cohesive stress $\sigma _c = 16.2$kPa and the initial falling velocity $v_0 = 4.0$m/s. (a) and (c) show the sequences of the cohesive forces of the reversible and irreversible cases of capillary bonds, respectively. (b) and (d) represent the cohesive forces of the capillary contacts formed/reformed during the test of the reversible case and the contact forces of the irreversible case of the capillary bridges. The line is the normal force joining two near–neighboring particles, and the line thickness is proportional to the magnitude of the normal forces

After undergoing the peak stage, the number of loss capillary contacts increases, leading to the increase of the number of formed/reformed capillary bonds of the reversible cases and the number of dry contacts of the irreversible one. These identifications are reflected via the two next snapshots of rows (b–3, b–4) and (d–3, d–4) in Fig. 10. However, the density and intensity of the formed/reformed forces of the reversible case are higher than the formed/reformed contact forces of the irreversible case. Thus, the slight difference of $D_{stop}/D_0$ and $\varDelta E$ between the reversible and irreversible cases can be explained due to the formation/reformation of capillary bonds between primary particles.

For a much larger initial falling velocity ($v_0 = 4.0$m/s, for example), the density of the normal forces for the reversible cases is significantly higher than that of the irreversible one during the test. Indeed, Fig. 11 shows the distribution of normal forces for both reversible and irreversible capillary contacts with a given value of the cohesive stress $\sigma _c = 16.2$kPa, liquid viscosity $\eta = 1000$mPa.s. In contrast to the case exhibited in Fig. 10, the difference of the forces distribution in the two first snapshots of the early-stage impact for the reversible (a–1 and a–2) and irreversible (c–1 and c–2) cases becomes clearer, leading to the increase of the agglomerate strength $\sigma _p/\sigma _c$ for the reversible case as compared to the irreversible one.

The large difference of the deposition behavior and the slight difference of the energy consumption in a period of time considered in this work depend on the large disparity of the normal capillary forces between reversible and irreversible cases. The difference of the normal capillary forces between these cases is significantly presented via the density and direction of the forces after passing the peak stage. Meanwhile, the forces for the reversible case are dense and the strong forces mainly showed in the vertical direction (Fig. 11a), the forces for the irreversible case are loose and almost broken just above the plane. By applying a large initial falling velocity, three last snapshots (Fig. 11b–3, b–4, and b–5) represent the significant increase of the formed/reformed capillary bonds for the reversible case, whereas the number of formed/reformed dry contacts for the irreversible case is still low (Fig. 11d–3, d–4, and d–5).

Fig. 12

The bond coordination number Z a and the lost capillary contacts ($Z_{lost}$ b as a function of the cohesive stress $\sigma _c$ for two different values of the liquid viscosity $\eta$ and two different values of the initial falling velocity $v_0$. The filled symbols are presented for the case of reversible capillary contacts, whereas the open symbols correspond to the irreversible case of the capillary bonds. Each symbol represents the result for different values of the cohesive stress $\sigma _c$ with a given value of the liquid viscosity $\eta$ and the initial velocity $v_0$

To more clearly highlight the roles of microscopic properties on the macroscopic responses of agglomerates, wet coordination number Z and the number of lost capillary contacts $Z_{lost}$ are measured. Figure 12 shows the average number of capillary contacts Z and the average number of lost capillary contacts $Z_{lost}$ as a function of the cohesive stress $\sigma _c$ for two different values of the liquid viscosity and initial falling velocity. We can see that for each value of the cohesive stress $\sigma _c$, Z of the reversible case (filled symbols) is higher than that of the irreversible case of capillary bonds (open symbols), and the differential degrees of Z between reversible and irreversible cases strongly depend on the liquid properties and the falling conditions of agglomerates. More interestingly, meanwhile, Z of the reversible case is expressed as a concave curve function of $\sigma _c$ due to the decrease of the formed/reformed capillary bridges when increasing $\sigma _c$, Z of the irreversible case is shown as a convex curve. In contrast to Z, the average number of lost capillary bridges $Z_{lost}$ increases as a convex curve by increasing $\sigma _c$.

6 Scaling behavior of macroscopic properties

As discussed above, it is interesting to see that all variations of the normalized vertical strength $\sigma _p/\sigma _c$ in the early–stage impact, the normalized height $D_{stop}/D_0$ at the final–stage deposition, and the energy consumption $\varDelta E$ of agglomerate in a time span after impacting for both reversible and irreversible cases of capillary bridges have similar tendencies and mainly come from the strong effects of the impact conditions and the cohesive effects of liquid bridges. Based on previous observations [8, 51, 52, 54, 59, 60], the results obtained in this current work lead to raising the questions that whether all the data points of $\sigma _p/\sigma _c$, $D_{stop}/D_0$, and $\varDelta E$ can collapse on a master curve as a function of a dimensionless scaling parameter for both cases of the capillary bonds considered in our simulations? and how do the roles of the reversibility and irreversibility of capillary contacts on these scalings? Before going to address these two questions, we should first define a scaling parameter as a dimensionless number.

In unsaturated granular materials, due to the same properties of the cohesive stress $\sigma _c$ and the confining stress $\sigma _n$ as well as the viscous stress $\sigma _v$ and the inertial stress $\sigma _i$, the inertial number $I = (\sigma _i/\sigma _n)^{1/2}$ of noncohesive granular materials can be replaced by the modified inertial number $I_m$ as a result of considering the stress additivity exerted on each particle [60]:

$$\begin{aligned} I_m = \bigg ( \frac{\sigma _i + a \times \sigma _v}{\sigma _n + b \times \sigma _c}\bigg )^{1/2} \end{aligned}$$

(12)

where a and b are the pre–factors. In this current work, the confining stress $\sigma _n$ is absent. This leads to re-express Eq. 12 by considering two different dimensionless numbers: the Capillary number $\text{ Ca } = \sigma _v/\sigma _c$ and the Stokes number $\text{ St } = \sigma _i/\sigma _v$ [52, 60], implying

$$\begin{aligned} I_m=\{ \text{ Ca }(a + \text{ St}) \} ^{1/2}. \end{aligned}$$

(13)

By setting $a \approx 10^{-3}$, all the data points of the normalized strength of wet agglomerates in the early-stage impact nearly collapse well on a master curve as a function of $I_m$ (not shown here). As compared to a broad range of large values of the Stokes number $\text{ St }$ that is obtained in our simulations ($\text{ St } = [3.0 \times 10^{-1}, 200.0]$), however, it is possible to completely neglect the effect of the viscous stress in Eq. 12. Thus, the modified inertial number $I_m$ in Eq. 13 can be replaced by the cohesive inertial number $I_c$, as given by the following expression:

$$\begin{aligned} I_m=(\text{ Ca } \times \text{ St})^{1/2}=\bigg ( \frac{\sigma _i}{\sigma _c}\bigg )^{1/2}={\dot{\gamma }} \langle d \rangle \bigg ( \frac{\rho }{\sigma _c}\bigg )^{1/2} \equiv I_c \end{aligned}$$

(14)

where ${{\dot{\gamma }}}$ is the impact rate of agglomerate, defined as a ratio of the early-stage impact velocity $v_i$ and the initial diameter of agglomerate $D_0$. $\langle d \rangle$ and $\rho$ denote the mean particle diameter and particle density, respectively.

Fig. 13

Normalized strength $\sigma _p/\sigma _c$ of wet agglomerates as a function of the cohesive inertial number $I_c = \sqrt{\sigma _i/\sigma _c}$ with the case of representation the absence of the confining pressure for the linear–linear (a) and log–linear (b) scales. The data points and the dark–green solid line are the scaling corresponding to the case of reversible capillary bonds, meanwhile the red dashed line is the scaling for the case of irreversible breaking of the capillary contacts. Both these lines are the analytical expression of Eq. 15 with different values of pre–factors

Surprisingly, Fig. 13 shows all data points of the agglomerate strength $\sigma _p/\sigma _c$ nicely collapse on two concave master curves in linear–linear and semi–log scales, corresponding to the reversible and irreversible capillary bonds, as a function of the cohesive inertial number $I_c$. The results obtained in this current work strongly provide evidence for the unified description of the agglomerate strength by a dimensionless scaling parameter combining the impact rate and cohesive stress of materials. Remarkably, all the data points of the normalized strength of a single wet agglomerate impacting a rigid surface can be fitted by a functional form by choosing different pre–factors corresponding to the roles of the reversibility and irreversibility of capillary bonds. In which, the scaling line for the reversible case (solid line) is above the irreversible one (dashed line), especially for high values of the cohesive inertial number $I_c$. The common function form can be expressed following:

$$\begin{aligned} \frac{\sigma _p}{\sigma _c}(I_c) = a_i I_c^2 + b_i I_c + c_i, \end{aligned}$$

(15)

where $a_i \equiv a_r = 125.0$, $b_i \equiv b_r = 7.5$, and $c_i \equiv c_r = 0.21$ are the pre–factors for the reversible case; and $a_i \equiv a_{ir} = 95.0$, $b_i \equiv b_{ir} = 8.1$, and $c_i \equiv c_{ir} = 0.17$ are the pre–factors for the case considering the irreversible breaking of the capillary bonds. It is interesting to note that, for small values of the cohesive inertial number ($I_c < 0.07$), there is no difference of vertical strength of impact agglomerate between the reversible and irreversible considerations of capillary bridges. In this range of values of $I_c$, indeed, the impact energy is small, this tends to break a small number of capillary bonds at the peak stress stage of agglomerate. For higher values of $I_c$, corresponding to large values of the initial falling velocity and low cohesion between grains, it starts opening the gap between two cases of the binding liquid. This gap almost increases proportionally to the cohesive inertial number $I_c$. The physical argument behind the same scaling of agglomerate strength observed for small $I_c$ and larger difference for higher $I_c$ between reversible and irreversible cases of capillary bonds can be explained due to the formation/reformation degree of capillary bridges and dry interactions, as shown in Figs. 10b,d and 11b,d, respectively.

The Eq. (15) proposed for the scaling of mechanical strength in this current work is quite different as compared to the generalized $\mu (I)$ rheology in steady–state flows of dry and wet granular materials [13, 17, 18, 23, 41, 43, 54, 60]. Indeed, meanwhile, the agglomerate strength observed in this work is expressed as a concave curve function of the cohesive inertial number $I_c$ (as shown in Figure 13a), the shear stress ratio $\mu$ of the steady–state flows is described as a convex curve function of the inertial number I ($\mu (I) = \mu _0 + (\mu _{\infty } - \mu _0)/(1+(1 + I_0/I))$, where $\mu _0$ and I are the shear stress ratio and inertial number of the flows in the quasi–static state, and $\mu _{\infty }$ denotes the shear stress ratio in the infinity of such flows. This difference may be explained due to the strong domination of the cohesive stress as compared to the gravity (confining stress) in the impact test of wet agglomerates, leading to the local quantity of the cohesive inertial number ($I_c = \sqrt{\sigma _i/\sigma _c}$), whereas the inertial number I or $I_m$ is defined in global one.

Fig. 14

Normalized the height $D_{stop}/D_0$ at the final deposition stage of wet agglomerates as a function of the modified inertial number $I_c = \sqrt{\sigma _i/\sigma _c}$ with the case of representation the absence of the confining pressure for the linear–linear (a) and log–linear (b) scales. All the data points and the dark–green solid line correspond to the scaling for the reversible capillary contacts, the red dashed line is the scaling corresponding to the case of irreversible breaking of the capillary contacts. These lines are the analytical expression in Eq. 16. The symbols and their colors are the same as those in Fig. 13 with different values of pre–factors

The above scaling of mechanical properties of impact agglomerate characterized by the agglomerate strength $\sigma _p/\sigma _c$ represents the good combination of the inertial stress and cohesive stress for both reversible and irreversible capillary bridges. Although $I_c$ nicely describes the normalized peak stress of the impact agglomerate, it is also essential to check its deposition behavior which represents the mobilization of primary particles during post–impact process due to the effects of the reversible and irreversible capillary bonds. As expected, the normalized final deposition height of wet agglomerate could be described as a function of the same cohesive inertial number $I_c$. Figure 14 displays all the data points of $D_{stop}/D_0$ collapse well on two master curves as a function of $I_c$ for the reversible and irreversible breaking of capillary contacts. As such, the cohesive inertial number $I_c$ provides a unique dimensionless parameter that controls not only for the agglomerate strength but also the final-vertical deposition height of agglomerates. These scalings obtained in this current work are consistent with the fact that the height at the final–stage deposition of agglomerate decreases with increasing the impact rate or decreasing the liquid–vapor surface tension.

As presented for the mechanical response of such impact agglomerate, $D_{stop}/D_0$ is also nicely fitted for both reversible and irreversible capillary contacts by using a functional form

$$\begin{aligned} \frac{D_{stop}}{D_0}(I_c) = \frac{1}{1 + \alpha _i I_c^{\beta }}, \end{aligned}$$

(16)

where $\alpha _i \equiv \alpha _r = 33.20$ and $\alpha _i \equiv \alpha _{ir} = 60.20$ are the pre–factors for the reversible and irreversible cases of the capillary bonds, respectively, and $\beta = 1.61$ is the power of the cohesive inertial number.

Fig. 15

Normalized energy consumption $\varDelta E$ of agglomerates after colliding the rigid plane $8 \times 10^{-3}$ seconds. All the data points are plotted for the reversible case of capillary contacts. The dark–green line is the scaling corresponding to the reversible case, meanwhile the red dashed line is for the irreversible one. Both these lines are the power–law fitting form of Eq. 17 with different values of pre–factors

In order to get a better understanding of the deposition behavior of agglomerates of the impact test, the energy consumption of such agglomerates is also expected to describe as a function of the same cohesive inertial number $I_c$. Interestingly, by normalizing the normalized energy consumption ($\varDelta E/E$) by the normalized impact velocity ($v_i/v_p$), all these data points collapse well on a master curve, where $v_i$ is the early-stage impact velocity, $v_p$ denotes the free–fall velocity of particle with mean diameter. Indeed, Fig. 15 shows the normalized energy consumption nicely expresses as a function of the cohesive inertial number $I_c$ for both reversible and irreversible cases of the capillary bonds. All the data points of the energy consumption for the reversible case of capillary bridges are nicely fitted by the solid line, whereas the dashed line represents for scaling of the irreversible one (all the data points for the irreversible case are absent here for improving the visibility). Both these lines are plotted by the same function form:

$$\begin{aligned} \frac{\varDelta E}{E}/\frac{v_i}{v_p}(I_c) = \chi _i I_c^{\zeta }, \end{aligned}$$

(17)

where $\chi _i \equiv \chi _r = 1.20 \times 10^{-3}$ and $\chi _i \equiv \chi _{ir} = 0.80 \times 10^{-3}$ are the pre–factors for the reversible and irreversible cases of capillary bridges, respectively, and $\zeta = -0.75$ is the power of the cohesive inertial number $I_c$. As contrast to the scaling of the final–stage deposition height of agglomerates observed above, the scaling line for the reversible case is much higher than that for the irreversible one, especially for small values of the cohesive inertial number $I_c$, corresponding to the slow impact velocity and strong agglomerates. For concerning the larger values of $I_c$, implying rapid impact test for weak agglomerates, the differential degree of the energy consumption between reversible and irreversible cases of capillary bridges decreases significantly, tending to loosing the energy absorption in both cases, as discussed in Sect. 5. Thus, the final–stage deposition height $D_{stop}$ of agglomerates impacting a flat surface can be explained due to the energy consumption during the impact process. A high value of $D_{stop}$ may be due to the rapid consumption of the impact energy that may have the origins from the absorption of the kinetic energy into the cohesive contacts.

7 Conclusions

In this paper, we study the roles of the reversible and irreversible breaking of the capillary bonds between primary particles on the mechanical strength, deposition behavior, and energy consumption of a single wet particle agglomerate, subjected to the impact test on a rigid surface by means of discrete element simulations. Each primary particle was defined as a rigid grain and interacts with its others under considering both solid contacts and visco–cohesive liquid contacts. In our simulations, the solid particles are assumed to be homogeneously distributed by particle volume fraction. The initial homogeneous distribution of the capillary bridges can be broken, then reformed or non–reformed during the movements of particles. We also varied systematically a broad desired range value of three different controlled parameters: the impact rate and two characteristics of the liquid bridges: the viscosity and the surface tension, with the expectation that the mechanical and physical properties of such agglomerate can be described by a dimensionless number obtained from these controlled parameters for both cases of the capillary bonds.

We showed that the mechanical strength, the final deposition height, and the energy consumption of agglomerate represent different behavior depending on the liquid properties and the impact conditions for both reversible and irreversible cases of capillary bridges. Interestingly, by introducing the cohesive inertial number (as an inertial number of dry granular materials), all the macroscopic properties of agglomerates are nicely described by power-law function forms. Remarkably, the scaling of the mechanical strength in the early-stage impact of agglomerates represents a slight difference between the reversible and irreversible cases of capillary contacts, whereas the significant differences of the final-stage deposition height and energy consumption in a specific time span are observed between the reversibility and irreversibility of capillary bonds. All these different degrees of macroscopic properties have microscopic origins that are characterized by the formation/reformation of capillary contacts and the average number of wet and loss–wet capillary bonds. Furthermore, due to the strong domination of the cohesive stress as compared to the gravity (as confining stress) in the impact test, the scaling of mechanical strength of agglomerates is quite different from the generalized $\mu (I)$ rheology of the steady–state flows of dry and wet granular materials. Indeed, the agglomerate strength is proposed as a concave curve function of the cohesive inertial number, whereas the shear–stress ratio of the general flows is expressed as a convex curve function of the inertial number [23, 43, 60].

The results reported in this current work may provide a better understanding of the roles of the reversible and irreversible breaking of the binding liquid on the dynamic behavior of wet granular materials. The liquid bonds can be reformed after breaking due to the total recovery of the liquid on the particle surface, as considered in previous investigations [60]. However, the capillary bridges may be also not reformed for small amount of the binding liquid in granular materials as a consequence of diffusing and evaporating or filling on the particle rough surface [52]. These results can be extended for the granulation process, where both reversible and irreversible capillary bridges should be considered. Another extension is the free surface gravity–driven flows of wet granular materials on inclined plane where the particle gravity plays an important role in the flow rheology and microstructure as compared to the cohesive and viscous stresses exert on particles. A diametrical compression test of wet particle agglomerates without considering the gravity effect may be also an interesting configuration in order to investigate the effects of the reversibility and irreversibility of capillary bonds as well as comparing to the generalized $\mu (I)$ rheology.