Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

It is already well-known from pure fluid problems on fixed meshes, that the second order ordinary Crank-Nicolson scheme suffers from instabilities, particularly for long-term computations [7]. Optimal error estimates Crank-Nicolson scheme.

The normally unconditionally stable Crank-Nicolson scheme is restricted by the condition

$$k \leq c{h}^{2/3},$$
(1)

where k and h denote the time-step size and the mesh-size parameter, respectively. However, the scheme can be stabilized by moving the θ-parameter (using a One-Step-θ scheme, see, e.g., [14]) slightly to the implicit side, leading to the shifted Crank-Nicolson scheme [10, 12]. On the other hand, several authors detected numerical instabilities on moving domains for higher order time-stepping schemes caused by the ALE convection term [2, 4, 5, 9].

Specifically, the ALE convection term is a numerical artifact that only appears on moving domains [4, 5, 11]. However, the relevance in numerical computations is not yet completely understand. The stability is closely related to the verification of the Geometric Conservation Law (GCL) [2, 4, 5, 9]. Moreover, they proved that the GCL condition does not degrade the accuracy of the numerical schemes. In this study, the previously mentioned results are combined with estimates for structural interactions. Finally, some second-order time-stepping schemes are compared within a numerical study.

2 The Equations

For the fluid, we consider a time-dependent domain \(\varOmega _{f}(t) \subset {R}^{d}\), d = 2, with the boundary \(\varGamma = \varGamma _{\text{ in}} \cup \varGamma _{\text{ wall}} \cup \varGamma _{\text{ out}} \cup \varGamma _{i}\). The boundary part Γ i denotes later the interface between the fluid subsystem and the structural system. Moreover, we denote by I = (0, T] the time interval. The unknowns are the fluid velocity \(v_{f} : \varOmega _{f} \times {R}^{+} \rightarrow {R}^{d}\), and the fluid pressure \(p_{f} : \varOmega _{f} \times {R}^{+} \rightarrow R\). Then, the Navier-Stokes equations of an incompressible, isothermal fluid read:

$$\begin{array}{rcl} \rho _{f}\hat{\partial }_{t}v_{f} + \rho _{f}(v_{f} - w) \cdot \nabla v_{f} -\text{ div}\sigma _{f}& = 0\quad \text{ in }\varOmega _{f}(t) \times I,& \\ \text{ div}v_{f}& = 0\quad \text{ in }\varOmega _{f}(t) \times I,&\end{array}$$
(2)

where w denotes the fluid domain velocity, which is defined by \(v_{f} = w = \partial \hat{u}_{s}\) on Γ i . The fluid Cauchy stress tensor reads

$$\sigma _{f} := -p_{f}I + \mu _{f}(\nabla v_{f} + \nabla v_{f}^{T}).$$

The (dynamic) viscosity is denoted by \(\mu _{f} := \rho _{f}\nu _{f}\) in which ρ f and ν f denote density and the (kinematic) viscosity, respectively. We notice that the term \(\hat{\partial }_{t}v_{f}\) denotes the ALE time derivative [6].

The structure problem is defined in a fixed domain \(\widehat{\varOmega }_{s}\) with the boundary \(\widehat{\varGamma }_{ \text{ s,fixed}} \cup \widehat{\varGamma }_{i}\). The structure is fixed on \(\widehat{\varGamma }_{\text{ s,fixed}}\) using homogenous Dirichlet conditions. The physical unknown is the structure displacement \(\hat{u}_{s} :\widehat{ \varOmega }_{s} \times {R}^{+} \rightarrow {R}^{3}\). The governing equations for the structural subsystem in a mixed formulation read ([15]):

$$\begin{array}{rcl} \hat{\rho }_{s}\partial _{t}\hat{v}_{s} -\widehat{\text{ div}}(\widehat{F}\widehat{\sigma }_{s}(\hat{u}_{s})) + \gamma _{w}\hat{v}_{s} - \gamma _{s}\widehat{\text{ div}}(\hat{\varepsilon }(\hat{v}_{s}))& =& \hat{\rho }_{s}\hat{f}_{s}\quad \text{ in }\widehat{\varOmega }_{s},\,t \in I, \\ \hat{\rho }_{s}(\partial _{t}\hat{u}_{s} -\hat{v}_{s})& =& 0\quad \text{ in }\widehat{\varOmega }_{s},\,t \in I, \\ \hat{u}_{s} = 0,\quad \hat{v}_{s} = \partial _{t}\hat{u}_{s}& =& 0\quad \text{ on }\widehat{\varGamma }_{s,\text{ in,out,wall}} = \widehat{\varGamma }_{\text{ fixed}}.\end{array}$$
(3)

The structural stress tensor (namely the Saint Venant Kirchhoff material - STVK), \(\widehat{\varSigma }_{s}\), is defined as

$$\begin{array}{rcl} \widehat{\varSigma }_{s}& =& (\lambda _{s}(\text{ tr}\widehat{E})\hat{I} + 2\mu _{s}\widehat{E}),\quad \widehat{E} = {2}^{-1}({\widehat{F}}^{T}\widehat{F} -\hat{I}), \\ \quad \widehat{F}& =& \hat{I} + \widehat{\nabla }\hat{u}_{s},\quad \hat{\epsilon }(\hat{v}_{s}) = {2}^{-1}(\widehat{\nabla }\hat{v}_{ s} + \widehat{\nabla }\hat{v}_{s}^{T}), \\ \end{array}$$

in which \(\hat{I}\) denotes the identity tensor. The elastic structure is characterized by the Lamé coefficients μ s , λ s .

3 Stability of the Time-Discretized ALE Fluid Problem and the FSI Problem

In this section, a slight modification of the classical Crank-Nicolson scheme (i.e., it is a Gauss-Legendre implicit second-order Runge-Kutta method) is considered [5]. We work with an ALE map \(\hat{\mathcal{A}}\) which is defined from the previous time step t n − 1 to the the present time step t n . Thus, the reference configuration at time step t n is denoted by \({\varOmega }^{n}\). Moreover, \({v}^{n} \in {\varOmega }^{n}\) is used as an approximation to \(v(t_{n})\), which is transported from \({\varOmega }^{n}\) to any other configuration Ω l (for \(l\neq n\)) through the ALE map ([11]):

$$\hat{\mathcal{A}}_{n,l} = \hat{\mathcal{A}}_{l} \circ \hat{\mathcal{A}}_{n}^{-1}.$$

For the sake of notation, we omit the explicit representation of the ALE map when we work with the value v n in a domain Ω l with n ≠ l, i.e.,

$$\int_{\varOmega _{l}}{v}^{n}\mathrm{d}x := \int_{\varOmega _{l}}{v}^{n} \circ \hat{\mathcal{A}}_{ n,l}\mathrm{d}x,\quad \text{ and }\quad \vert \vert {v}^{n}\vert \vert _{{ \varOmega }^{l}} := \vert \vert {v}^{n} \circ \hat{\mathcal{A}}_{ n,l}\vert \vert _{{\varOmega }^{l}},$$

which we use frequently in the following.

To get a stability result for the time-discretized Crank-Nicolson scheme on moving domains, we use the methodology used in [4, 5, 11]. It holds:

Proposition 1.

For the time-discretized solution of ALE fluid problems with the help of the Crank-Nicolson scheme holds:

$$\begin{array}{rcl} & & \rho _{f}\vert \vert v_{f}^{n+1}\vert \vert _{ \varOmega _{f}^{n+1}}^{2} + k\mu _{ f}\vert \vert D(v_{f}^{n+1} + v_{ f}^{n})\vert \vert _{ \varOmega _{f}^{n+1}}^{2} + \frac{k} {4}\rho _{f} \int_{\varOmega _{f}^{n+1}}\nabla \cdot {w}^{n+\frac{1} {2} }\,\vert v_{f}^{n+1} + v_{f}^{n}{\vert }^{2}\mathrm{x} \\ & & \quad = \rho _{f}\vert \vert v_{f}^{n}\vert \vert _{ \varOmega _{f}^{n+1}}^{2}.\end{array}$$

For \(\nabla \cdot w\,>\,0\) for all \(x\,\in \,\varOmega _{f}\) and for all \(t\,\in \,I\) (a uniform contraction of the mesh), the Crank-Nicolson scheme is unconditionally stable. Otherwise, the ALE convection term causes instabilities that restricts the choice of the time step size [5, 11].Therefore, the convection term is estimated as follows:

$$\begin{array}{rcl} \frac{k\rho _{f}} {4} \int_{\varOmega _{f}^{n+1}}\nabla \cdot {w}^{n+1}\,\vert v_{ f}^{n+1} + v_{ f}^{n}{\vert }^{2}\mathrm{d}x \leq k\varDelta _{ w}\,{\bigl (\vert \vert v_{f}^{n+1}\vert \vert _{ \varOmega _{f}^{n+1}}^{2} + \vert \vert v_{ f}^{n}\vert \vert _{ \varOmega _{f}^{n+1}}^{2}\bigr )},& & \\ \end{array}$$

in which the Young inequality is used to estimate the right-hand-side term. Specifically, it holds:

$$k \leq \varDelta _{w}^{-1},\quad \text{ with }\quad \varDelta _{ w} := \frac{\rho _{f}} {2} \vert \vert \nabla \cdot {w}^{n+1}\vert \vert _{{ L}^{\infty }(\varOmega _{f}^{n+1})}.$$

Proof.

For the proof, we refer the reader to [15].

Combining this result with the restriction (1), which was analyzed by Rannacher et al. [7, 12], provides us

Proposition 2.

Using the ordinary (i.e., unstabilized) Crank-Nicolson scheme leads to the following time step condition for pure fluid problems on moving domains:

$$k \leq \min \left \{c{h}^{2/3},\varDelta _{ w}^{-1}\right \}.$$
(4)

Using the shifted Crank-Nicolson scheme [12],the first condition in (4)can be removed, such that \(k \leq {k}^{{_\ast}}\) , with some constant \({k}^{{_\ast}}\) that only depends on the problem.

It seems that the time step restriction \(k \leq \varDelta _{w}^{-1}\) induced by the mesh movement seems to be of lower order and it has less influence than the first condition \(k \leq c{h}^{2/3}\). In fact, Formaggia and Nobile [5], p. 4098, state that they found no example of blow-up caused by the ALE convection term for linear advection-diffusion equations. This might be due to the fact that the ALE convection term is only defined on a lower-dimensional manifold and not over the whole domain.

We utilize the previous results to analyze the monolithically coupled fluid-structure interaction system. First, we recall the coupling conditions that are required for an implicit solution algorithm:

$$\begin{array}{rcl} \hat{u}_{f}^{n+1}& =& \hat{u}_{ s}^{n+1}\quad \text{ on }\widehat{\varGamma }_{ i},\qquad {\hat{w}}^{n+1} = \frac{1} {k}(\hat{u}_{f}^{n+1} -\hat{u}_{ f}^{n})\quad \text{ in }\widehat{\varOmega }_{ f}, \\ {2}^{-1}(v_{ f}^{n+1} + v_{ f}^{n})& =& w_{ f}^{n+1}\quad \text{ on }\varGamma _{ i},\qquad \hat{u}_{s}^{n+1} = 0\quad \text{ on }\widehat{\varGamma }_{ s,D}. \end{array}$$
(5)

Using the Crank-Nicolson scheme for temporal discretization, the second relation in (5), can be further developed into

$${ \hat{w}}^{n+1} = {k}^{-1}(\hat{u}_{ f}^{n+1} -\hat{u}_{ f}^{n}) = {2}^{-1}(\hat{v}_{ f}^{n+1} + \hat{v}_{ f}^{n}).$$
(6)

Fernández and Gerbeau [3] proved a result using the backward Euler scheme to discretize the fluid. The structure is discretized with a second-order mid-point rule. In our study, both systems are time-discretized with the same time-stepping scheme. We emphasize, that fluid flows on moving meshes with a Crank-Nicolson time discretization only serve for a conditioned stability (see Proposition 1). Consequently, we cannot expect a better result for the overall problem.

To derive the next proposition, we use a Crank-Nicolson discretization for the fluid with the stability result proven in Proposition 1. The coupling term on the interface Γ i reads:

$$\sigma _{f}(v_{f}^{n+1} + v_{ f}^{n})n_{ f} + \widehat{F}\widehat{\varSigma }(\hat{u}_{s}^{n+1} + \hat{u}_{ s}^{n})\hat{n}_{ s} + \gamma _{s}\hat{\epsilon }(\hat{v}_{s}^{n+1} + \hat{v}_{ s}^{n})\hat{n}_{ s} = 0.$$
(7)

Proposition 3.

Let the fluid-structure interaction problem be coupled via an implicit solution algorithm and let both subproblems be time-discretized with the second order Crank-Nicolson scheme. The coupled problem is assumed to be isolated, i.e., \(v_{f}^{n+1} = 0\) on \(\partial \varOmega _{f} \setminus \varGamma _{i}\) and \(\widehat{F}\widehat{\Sigma }(\hat{u}_{s}^{n+1})\hat{n}_{s} = 0\) on \(\partial \widehat{\varOmega }_{s} \setminus \widehat{\varGamma }_{i}\) . Further, in the case of strong damping \(\gamma _{w} > 0\) , let \(\hat{\varepsilon }(\hat{v}_{s}^{n+1})\hat{n}_{s} = 0\) on \(\partial \widehat{\varOmega }_{s} \setminus \widehat{\varGamma }_{i}\) . Then,

$$\begin{array}{rcl} & & \rho _{f}\vert \vert v_{f}^{n+1}\vert \vert _{ \varOmega _{f}^{n+1}}^{2} + \hat{\rho }_{ s}\vert \vert \hat{v}_{s}^{n+1}\vert \vert _{\widehat{ \varOmega }_{s}}^{2} + \int_{\widehat{\varOmega }_{s}}W{\bigl (\widehat{F}(\hat{u}_{s}^{n+1})\bigr )}\mathrm{d}x + k\mu _{ f}\vert \vert D(v_{f}^{n+1} + v_{ f}^{n})\vert \vert _{ \varOmega _{f}^{n+1}}^{2} \\ & & \quad + \frac{k\rho _{f}} {4} \int_{\varOmega _{f}^{n+1}}\nabla \cdot {w}^{n+1}\vert v_{ f}^{n+1} + v_{ f}^{n}{\vert }^{2}{{\rm d}x} + \frac{k\gamma _{w}} {2} \vert \vert \hat{v}_{s}^{n+1}\vert \vert _{\widehat{ \varOmega }_{s}}^{2} + \frac{k\gamma _{s}} {2} \vert \vert \hat{\epsilon }(\hat{v}_{s}^{n+1})\vert \vert _{ E}^{2} \\ & & \leq \, \rho _{f}\vert \vert v_{f}^{n}\vert \vert _{ \varOmega _{f}^{n+1}}^{2} + \rho _{ s}\vert \vert \hat{v}_{s}^{n}\vert \vert _{\widehat{ \varOmega }_{s}}^{2} + \int_{\widehat{\varOmega }_{s}}W(\widehat{F}(\hat{u}_{s}^{n})){{\rm d}x} + \frac{k\gamma _{w}} {2} \vert \vert \hat{v}_{s}^{n}\vert \vert _{\widehat{ \varOmega }_{s}}^{2} + \frac{k\gamma _{s}} {2} \vert \vert \hat{\varepsilon }(\hat{v}_{s}^{n})\vert \vert _{ E}^{2}.\end{array}$$

Proof.

For the proof, we refer to [15].

Comparing Propositions 1 and 3, we notice that global stability of solutions depends only on the uncertainty of the ALE convection term. We draw the following conclusion from our previous findings:

Hypothesis 1 (Stable long-term computations of FSI problems). 

Numerically stable long-term computations of fluid-structure interaction can be computed by (at least) strictly A-stable time-stepping schemes (such as the shifted Crank-Nicolson scheme and the Fractional-Step-θ scheme) provided that the time step k is restricted by

$$k \leq \varDelta _{w}^{-1},$$

as shown in Proposition  2.

3.1 Discretization of the ALE Convection Term

In this section, we discuss possible temporal discretizations of the ALE convection term. From Eq. (2), we extract

$$\begin{array}{rcl} (v_{f} - w) \cdot \nabla v_{f} = v_{f} \cdot \nabla v_{f} - w \cdot \nabla v_{f}\quad \text{ in }\varOmega _{f}.& & \\ \end{array}$$

In detail, the One-Step-θ discretization yields (θ = 0. 5 or \(\theta = 0.5 + k\)):

$$\begin{array}{rcl} & & \theta v_{f} \cdot \nabla v_{f} + (1 - \theta )v_{f}^{n-1} \cdot \nabla v_{ f}^{n-1} - {k}^{-1}(u_{ f} - u_{f}^{n-1}) \cdot \nabla v_{ f},\quad [\mathrm{Sec}\ CN(v)] \\ & & \theta v_{f} \cdot \nabla v_{f} + (1 - \theta )v_{f}^{n-1} \cdot \nabla v_{ f}^{n-1} - \theta w \cdot \nabla v_{ f} - (1 - \theta ){w}^{n-1} \cdot \nabla v_{ f}^{n-1},\quad [\mathrm{Sec}\ CN(vw)] \\ & & \theta (v_{f} + v_{f}^{n-1}) \cdot \nabla \theta (v_{ f} + v_{f}^{n-1}) - \theta (w + {w}^{n-1}) \cdot \nabla \theta (v_{ f} + v_{f}^{n-1})\quad [\mathrm{Tang}\ CN(vw)].\end{array}$$

We notice that the tangential scheme is used for a stability and accuracy analysis for pure fluid problems [7]. This scheme is slightly more stable than the secant Crank-Nicolson scheme [13], which we also observed in our numerical tests (see at left of Fig. 2).

Fig. 2
figure 2

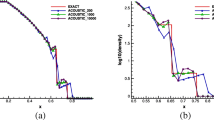
Blow-up (using the time step k = 0. 01) of the unstabilized Crank-Nicolson schemes (secant and tangent) whereas the shifted Crank-Nicolson schemes is stable throughout the whole time interval. We notice that the secant Crank-Nicolson scheme exhibits the instabilities earlier than the tangent version. The unit of the time axis is s, whereas the drag unit is \(\mathrm{{kg/m\,s}}^{2}\)

Full size image

4 Numerical Tests and Observations

In the final section, we compare all relevant second-order time-stepping schemes for solving fluid-structure interaction. For details on temporal discretization, we refer the reader to [15, 16]. Spatial discretization is based on a Galerkin finite element scheme; for details on our solution algorithm, we refer to [15, 16].

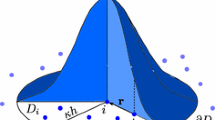
We consider the numerical benchmark test FSI 2 [1, 8]. The (qualitative) convergence with respect to space and time on three different (globally-refined) mesh levels is studied using with 1914, 7176 and 27744 degrees of freedom using the \(Q_{2}^{c}/P_{1}^{dc}\) element. Moreover, we use three different time levels with the time steps \(k\,=\,0.01,0.005\) and 0. 001. It is sufficient to study the results for the drag evaluation because we observed the same qualitative behavior for all the four quantities of interest (the x- and the y-displacement, the drag, and the lift). Specifically, the drag is computed as line integral over the cylinder and the interface of the elastic beam. The configuration is sketched in Fig. 1.

Fig. 1
figure 1

Elastic beam attached at a cylinder with circle-centerC = (0. 2, 0. 2) and radius r = 0. 05

Full size image

Boundary conditions

A parabolic inflow velocity profile is given on \(\hat{\varGamma }_{ \text{ in}}\) by

$$v_{f}(0,y) = 1.5\bar{v}\frac{4y(H - y)} {{H}^{2}} ,\quad \bar{v} = 1.0m{s}^{-1}.$$

At the outlet \(\hat{\varGamma }_{\text{ out}}\) the do-nothing outflow condition is imposed. Homogenous Dirichlet boundary conditions are prescribed on the remaining boundary parts.

Initial conditions

For the unsteady tests, a smooth increase of the velocity-profile in time is chosen:

$$v_{f}(t;0,y) = \left \{\begin{array}{@{}l@{\quad }l@{}} v_{f}(0,y)\frac{1-\cos (\frac{\pi } {2} t)} {2} \quad &\text{ if}\,\,\,t < 2.0s \\ v_{f}(0,y) \quad &\text{ otherwise}.\\ \quad \end{array} \right.$$

Parameters

We choose for our computation the following parameters. For the fluid, we use \(\mu _{f} =\mathrm{{ {m}^{2}s}}^{-1}\). The elastic structure is characterized by \(\varrho _{s}\,=\,1{0}^{4}\mathrm{{kgm}}^{-3}\), \(\nu _{s}\,=\,0.4\), \(\mu _{s}\,=\,5 {_\ast} 1{0}^{5}\mathrm{{kgm}}^{-1}\mathrm{{s}}^{-2}\). Moreover, we set \(\gamma _{w}\,=\,\gamma _{s}\,=\,0\).

Discussion of the results

We observed in our computations that there are only minor differences in the drag evaluation computed with the unstabilized Crank-Nicolson scheme using the different ALE convection term discretizations defined in the problems above. Specifically, we observed unstable behavior (blow-up) for computations over long-term intervals, as illustrated in Fig. 2. Naturally, we expected this behavior from our previous numerical analysis.

As expected, the shifted Crank-Nicolson scheme and the Fractional-Step-θ scheme showed no stability problems in long-term computations, even for the large time step k = 0. 01 (see at left of Fig. 3). This result indicates that the instabilities induced by the ALE convection term have minor consequences, and our observation is in agreement with the statement in [5]. Furthermore, all time-stepping schemes are stable over the entire time interval for a sufficiently small time step k = 0. 001; (see the bottom Fig. 3). Consequently, we were able to find a suitable bound such that the requirements of Proposition 2 are satisfied.

Fig. 3
figure 3

Left: stable solution (using the large time step k = 0. 01) computed with the shifted Crank-Nicolson and the Fractional-Step-θ scheme. Recall the blow-up of the unstabilized Crank-Nicolson scheme in this case. Right: using the smaller time step k = 0. 001 yields stable solutions for any time-stepping scheme. The unit of the time axis is s, whereas the drag unit is \(\mathrm{{kg/m\,s}}^{2}\)

Full size image