1 Introduction

With high elasticity, wear resistance and other superior properties, hyperelastic materials are widely used in aerospace, petrochemical, construction, medicine and other fields, such as seals, bushings, tires, dielectric elastomers, artificial blood vessels, muscles and so on. Hyperelastic materials are also called Green elastic materials [1], rubber and rubber-like materials are typical representations of these materials, and the constitutive relations can be characterized by their strain energy functions, during which the neo-Hookean, Mooney–Rivlin, Ogden, Rivlin–Saunders and Gent–Thomas models are the classical ones [2,3,4,5,6]. Structures composed of hyperelastic materials usually have both material and geometric nonlinearities, so the deformations and motions of related structures under external loads have always been the focus of nonlinear mechanics. The common structures usually include solid structures, structures with micro-void, plates, shells and membranes and so on. The forms of external loads mainly include constant loads and time-dependent loads.

Bifurcation and chaos are two main aspects of nonlinear dynamics, the original intention of bifurcation and chaos is to study the qualitative behaviors of the nonlinear problems which are difficult to be solved analytically, and with the help of them, many complex nonlinear problems have been investigated numerically [7,8,9,10]. Moreover, in the existing methods, the Lyapunov exponent, bifurcation diagram, and correlation dimension are commonly used to describe chaos and its different routes [11,12,13].

Under the framework of nonlinear dynamic theories, many progress has been made in the deformations and motions of hyperelastic structures under external loads. Knowles [14] analyzed the stability of an isotropic incompressible hyperelastic cylindrical shell firstly. The author derived the governing equations by using the symmetry of motion and the incompressible constraint and analyzed the free vibration of the shell, which laid the foundation for the subsequent dynamic analysis of hyperelastic structures. Wang et al. [15] derived a coupled partial differential equation describing the radial and axial motions of thermal hyperelastic cylindrical shells under the assumption of axisymmetric deformation, and analyzed the influences of internal and external boundary temperatures on the existence of bounded traveling waves, the effects of compressibility and material parameters on periodic waves, solitary waves and periodic cusp waves were also discussed in detail, and the corresponding numerical simulations were carried out. By taking radial symmetric deformation as the condition of quasi-equilibrium motion, Mihai and Alamoudi [16] derived the nonlinear differential equation describing the deformation of the hyperelastic heterogeneous spherical shell composed of neo-Hookean materials. The results showed that the oscillation amplitude and period were characterized by the probability distribution and mainly depended on the initial conditions. Zhao et al. [17] studied the nonlinear dynamic behaviors of visco-hyperelastic spherical shells under dynamic loads. Based on the Euler–Lagrange equation, the coupled integral–differential equations describing the radial symmetric motions of visco-hyperelastic spherical shells were derived. The results showed that when the viscosity coefficient of the material changed, the resonance frequency of the system also shifted, and the motions of the system appeared chaos and multi-period vibration alternating phenomenon. Zhao et al. [18] further studied the influences of dynamic loads and structural damping on the nonlinear characteristics of incompressible hyperelastic spherical shells and discussed the dynamic behaviors of periodic, quasi-periodic and chaotic motions under different load types. Based on the Euler–Lagrange equation, Firouzi and Kamil [19] obtained a generalized formula for describing the finite deformation of hyperelastic membranes under different geometric shapes and load loads. This formula considered the anisotropy of isotropic and transversely isotropic hyperelastic materials, and the effectiveness of the formula was verified by practical examples. Eriksson and Nordmark [20] studied the stability of the spherical membrane under internal pressures based on the hyperelastic theory, derived the nonlinear differential equation describing the motion of the membrane, and discussed the dependence of the dynamic behaviors on related parameters. Soares et al. [21] derived a nonlinear mathematical model describing the motions of a hyperelastic spherical membrane under internal pressures by the variational principle. Firstly, the influences of material parameters on the natural frequency of the system were discussed, and the approximate results obtained by skeleton line and harmonic balance method were compared to highlight the influence of higher order nonlinear terms of the differential equation on the dynamic responses of the structure. Then, parameter analysis was conducted on the membrane under harmonic excitation, and the important influences of damping on system resonance, attraction domain, and bifurcation diagram were revealed. Zhao et al. [22] obtained the governing equations describing the nonlinear radial symmetric motions of a hyperelastic spherical membrane under the assumption of spherical symmetric deformation. The dynamic characteristics of the system were qualitatively analyzed in detail in terms of different values of material parameters. Particularly, for given constant loads, the parameter spaces describing the bifurcation behaviors of equilibrium curves were established and the characteristics of equilibrium points were presented. For periodically perturbed loads, the quasi-periodic and chaotic behaviors were discussed for the systems with two and three equilibrium points, respectively. Zheng et al. [23] studied the radial nonlinear vibrations for a thin-walled hyperelastic cylindrical shell composed of the classical incompressible Mooney–Rivlin materials subjected to a radial harmonic excitation. Using Lagrange equation, Donnell's nonlinear shallow-shell theory and small strain assumption, the nonlinear differential governing equation of motion is obtained for the incompressible Mooney–Rivlin material thin-walled hyperelastic cylindrical shell. The chaotic behavior of the radial nonlinear vibration of a thin-walled superelastic cylindrical shell made of incompressible Mooney–Rivlin material is discussed by numerical simulation. The results demonstrate that the nonlinear dynamic responses of thin-walled hyperelastic cylindrical shell are highly sensitive to the structural parameters and external excitation. Zhang et al. [24] derived the differential governing equations of motion describing the hyperelastic cylindrical shell with the initial geometric imperfections by using the Donnell's theory, hyperelastic constitutive relations and Lagrange equation. The amplitude-frequency and force-amplitude response curves are obtained for the hyperelastic cylindrical shell by using the multiple scale method. The effect of different parameters on the linear frequencies, amplitude-frequency response curves, force-amplitude response curves and chaotic responses of the hyperelastic cylindrical shell are discussed. The results demonstrate that with the changes of the parameters, the dynamic responses of the hyperelastic cylindrical shell with the imperfections change the period to chaotic vibrations alternately. More research on the dynamic problems of hyperelastic structures can be found from the review of Alijani and Amabili [25].

In the researches of hyperelastic materials, a typical problem is that when the structure is subjected to external tensile loads, the internal will be accompanied by the formation and growth of micro-void, the penetration of adjacent micro-void and so on. How to reduce the harm brought by this defect is an issue that cannot be ignored. Gent and Lindley [26] observed the phenomenon of the cavity formation in hyperelastic materials in the experiment firstly. Ball [27] proposed a nonlinear model of the cavity formation in hyperelastic materials, studied the singular solution of nonlinear differential equation describing such materials, and pointed out that the existence of the singular solution depended on the characteristics of strain energy function. Then, Horgan and Abeyaratne [28] examined the sudden growth of pre-existing micro-void, and discussed the physical significance of model. For the sphere composed of transversely isotropic incompressible hyperelastic materials, Yuan et al. [29] studied the motions of the micro-void and made qualitative analyses of the equilibrium points of the system. They proved that the motions of the micro-void were nonlinear periodic vibrations, and the forms of the periodic motions were completely different for different material parameters. Ren et al. [30] studied the dynamic generations of cavities in incompressible hyperelastic spheres under periodic loads, and numerical simulations were carried out by using time-history curves, phase diagrams and Poincaré sections. The results indicated that there existed a critical value for the periodic load. By analyzing the relationship between the average load and the critical value in detail, some problems such as whether there were cavities generated were discussed. Yuan and Zhang [31] investigated the generation and motion of the micro-void in the hyperelastic sphere composed of transversely isotropic Valanis-Landel materials under constant and periodic stepped loads. When the sphere was subjected to constant loads, they proved that once the loads exceed the critical value, the micro-void generated in the sphere, and the motion of micro-void presented periodic oscillation. The conditions for the periodic oscillation of micro-void under periodic stepped loads were also provided.

So far, many researches have been achieved on the nonlinear dynamics of hyperelastic spherical structures, while most of them focused on fully integrable Hamiltonian systems, and only a few researches examined the nonlinear dynamic responses of nearly integrable Hamiltonian systems under periodic disturbance loads. In recent years, Zhao et al. [17, 18, 22] have discussed the influence of nonlinear damping forces in depth for hyperelastic spherical structures, mainly studying the chaotic behaviors of spherical shells and spherical membranes under dynamic loading. Particularly, Gent [26], Ball [27] and Horgan [28] have done a lot of pioneering works on micro-void structures for incompressible hyperelastic spheres. Based on this research, Yuan [29, 31] and Ren [30] et al. further expanded the study on the nonlinear dynamics of micro-void in hyperelastic spheres. On the one hand, their achievements focused on the analysis of the formation and growth of micro-void and the phenomenon of breakage with the increase in applied load and focused on the oscillation form of micro-void and the stability judgment of micro-void motion. On the other hand, it is mainly the stress discontinuity and stress concentration during the formation of micro-void. At present, there is no literature that systematically analyzes the complex dynamic phenomena of periodic perturbation loads and structural damping on the micro-void motion in incompressible hyperelastic spheres.

In this paper, the dynamic behavior of an incompressible hyperelastic sphere with a central micro-void is investigated, where the sphere is composed of a class of radial transversely isotropic Gent–Thomas materials and subjected to periodic perturbation loads and structural damping. The structure damping is introduced into the micro-void structure for the first time by the energy variational principle, and the chaos threshold of the perturbation parameter \(\tilde{\eta }_{cr} = 0.3947\) is determined by Melnikov method with numerical method. The chaotic characteristics in the sense of Smale horseshoe are analyzed in detail by using the Poincaré sections, and the bifurcation characteristics of micro-void motion are analyzed in detail by the bifurcation diagram. The results show that, under the combined load of periodic perturbation loads and structural damping, the micro-void motion goes through a process from periodic to chaotic and then to periodic, and the amplitude of periodic response shows a hopping phenomenon. In particular, the first time the system enters chaos from period and the first time it returns to period are characterized by period-doubled bifurcation and inverse period-doubled bifurcation, respectively. The research contents in this paper are of great significance to complement and perfect the complex dynamic behaviors of micro-void.

The structure of this paper is organized as follows. Firstly, a mathematical model describing the radial symmetric motions of the micro-void is derived based on the variational principle. Secondly, the nonlinear dynamic behaviors of the micro-void under constant loads and structural damping are analyzed, respectively. Then, the threshold of chaotic motion is derived using the Melnikov method and numerical calculations, and the bifurcation characteristics of micro-void are discussed. Furthermore, the chaotic characteristics of the micro-void under the periodic perturbation loads and structural damping are analyzed in detail. Finally, the conclusions are given.

2 Formulation of the problem

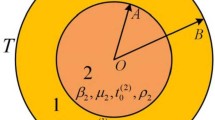
Assume that the sphere of radius \(A\) is composed of an incompressible hyperelastic material, and that a micro-void of radius \(\varepsilon\) is at its center. When the external surface of the sphere is subjected to sudden periodic loads, the radial symmetric motions of the micro-void are investigated.

The initial configuration of the sphere is denoted by

$$ \begin{aligned}{{\varvec{\Omega}}}_{ \, 0} = &\left\{ (R, \, \Theta , \, \Phi ): \, \varepsilon \le R < A, \,\right.\\ &\left.\qquad 0 < \Theta \le 2\pi , \, 0 \le \Phi \le \pi \right\}.\end{aligned} $$
(1)

According to the assumption of spherical symmetric deformation, the current configuration of the sphere is given by

$$ \begin{aligned}{{\varvec{\Omega}}} = &\left\{ (r, \, \theta , \, \phi ): \, r = r(R, \, t) > 0, \, \varepsilon < R < A,\right.\\ &\left.\, r(\varepsilon , \, t) \ge 0, \, \theta = \Theta , \, \phi = \Phi \right\}.\end{aligned} $$
(2)

The deformation gradient tensor used to describe the mapping relationship between two configurations is \({\mathbf{F}} = {\text{diag}}\left\{ {\partial r/\partial R, \, r/R, \, r/R} \right\}\), where \(\lambda_{1} = \partial r/\partial R\), \(\lambda_{2} = \lambda_{3} = r/R\) are called the radial and circumferential principal stretches, respectively.

In the initial configuration, there is no deformation, and the sphere is stationary; then, the initial conditions are as follows

$$ r(R, \, 0) = R, \, \dot{r}(R, \, 0) = 0. $$
(3)

The hyperelastic material in this paper is the radial transversely isotropic incompressible Gent–Thomas model [32], and the specific form of the strain energy function is as follows

$$ \begin{aligned}W =&\, \frac{{\mu_{1} }}{2}[(\lambda_{1}^{2} + \lambda_{2}^{2} + \lambda_{3}^{2} - 3) + \alpha \ln (\lambda_{1}^{2} \lambda_{2}^{2} \\ &+ \lambda_{2}^{2} \lambda_{3}^{2} + \lambda_{1}^{2} \lambda_{3}^{2} - 2) + \beta (\lambda_{1}^{2} - 1)^{2} ],\end{aligned} $$
(4)

where \(\mu_{1} > 0, \, \mu_{2} \ge 0\) are shear moduli of the material and \(\alpha = {{\mu_{2} } \mathord{\left/ {\vphantom {{\mu_{2} } {\mu_{1} }}} \right. \kern-0pt} {\mu_{1} }}\). \(\beta \ge 0\) is a material parameter that reflects the degree of anisotropy, it simplified as an isotropic Gent–Thomas material model for \(\beta = 0\).

For incompressible materials, it requires that \(\lambda_{1} \lambda_{2} \lambda_{3} = 1\), i.e., \({{\partial r(R, \, t)} \mathord{\left/ {\vphantom {{\partial r(R, \, t)} {\partial R = {{R^{2} } \mathord{\left/ {\vphantom {{R^{2} } {r^{2} (R, \, t)}}} \right. \kern-0pt} {r^{2} (R, \, t)}}}}} \right. \kern-0pt} {\partial R = {{R^{2} } \mathord{\left/ {\vphantom {{R^{2} } {r^{2} (R, \, t)}}} \right. \kern-0pt} {r^{2} (R, \, t)}}}}\). Integrating \(R\) on both sides of the above equation, we have

$$ r = r(R, \, t) = [R^{3} + r_{1}^{3} (t) - \varepsilon^{3} ]^{1/3} , \, t \ge 0, $$
(5)

where \(r_{1} (t) = r_{1} (\varepsilon ,t) \ge 0\) is an undetermined function, represents the radius of the micro-void in the current configuration. It is easy to see that Eq. (5) can describe the radial symmetric motion of the sphere completely.

Then, the initial condition (3) reduces to

$$ r_{1} (0) = \varepsilon , \, \dot{r}_{1} (0) = 0. $$
(6)

Let \(\kappa = {r \mathord{\left/ {\vphantom {r R}} \right. \kern-0pt} R}\), the strain energy function can be expressed as follows

$$\begin{aligned} W(\kappa ) = &\frac{{\mu_{1} }}{2}[(2\kappa^{2} + \kappa^{ - 4} - 3) \\ &+ \alpha \ln (2\kappa^{ - 2} + \kappa^{4} - 2) + \beta (\kappa^{ - 4} - 1)^{2} ].\end{aligned} $$
(7)

Particularly, the potential energy of the structure is \(\prod = \int_{{{{\varvec{\Omega}}}_{ \, 0} }} {W(\kappa ){\text{d}}V}\). Substituting Eq. (7) into the potential energy, we have

$$ \begin{aligned}\prod = & 4\pi \int_{\varepsilon }^{A} \frac{{\mu_{1} }}{2}[(2\kappa^{2} + \kappa^{ - 4} - 3) + \alpha \ln (2\kappa^{ - 2} \\ &+ \kappa^{4} - 2) + \beta (\kappa^{ - 4} - 1)^{2} ]R^{2} {\text{d}}R .\end{aligned} $$
(8)

The kinetic energy of the structure is \(K = \int_{{{\varvec{\Omega}}}} \frac{1}{2} \rho \dot{r}^{2} (R, \, t){\text{d}}V\). Substituting \(\dot{r} = r^{ - 2} r_{1}^{2} \dot{r}_{1}\) into the above equation, it can be expressed in the following form

$$ \begin{aligned} K =&\, \int_{{{\varvec{\Omega}}}} \frac{1}{2} \rho r^{ - 4} r_{1}^{4} \dot{r}_{1}^{2} {\text{d}}V \\ =& 2\rho \pi r_{1}^{4} \dot{r}_{1}^{2} [r_{1}^{ - 1} - (r_{1}^{3} + A^{3} - \varepsilon^{3} )^{ - 1/3} ],\end{aligned} $$
(9)

where \(\rho\) is the material density.

In nonlinear dynamics, damping is not only a fundamental physical quantity in structural dynamic analysis, but also reflects the energy dissipation mechanism during structural oscillation. In this paper, the non-conserved damping is introduced through the Rayleigh’s dissipation function [33]

$$ W_{R} = \frac{1}{2}(c_{1} \dot{r}_{1}^{2} + c_{2} \dot{\theta }^{2} + c_{3} \dot{\phi }^{2} ), $$
(10)

where \(c_{1}\) is the damping ratio at the radial direction, and \(c_{2}\) and \(c_{3}\) are the damping ratios at the circumferential direction, whose specific values are determined by relevant experiments. In this paper, only the radial symmetric motion is considered, so it satisfies \(c_{2} = c_{3} = 0\).

Assume that the outer surface of the structure is subjected to radial dynamic loads with the following form

$$ p(t) = p_{0} + \eta \sin \omega t, $$
(11)

where \(\omega\) is the excitation frequency, \(p_{0}\) is the constant loads, and \(\eta\) is the excitation amplitude.

Then, the work done by the radial loads is given by

$$ W_{v} = \int_{A}^{{r_{2} }} {4\pi p(t)A^{2} {\text{d}}r = } 4\pi p(t)A^{2} (r_{2} - A), $$
(12)

where \(r_{2} = r(A, \, t) = [r_{1}^{3} (t) + A^{3} - \varepsilon^{3} ]^{1/3}\).

The generalized force \({\varvec{Q}}\) is obtained by differentiation of the Rayleigh’s dissipation function \(W_{R}\) and the work \(W_{v}\),

$$ {\varvec{Q}} = - \frac{{\partial W_{R} }}{{\partial \dot{r}_{1} }} + \frac{{\partial W_{v} }}{{\partial r_{1} }} = - c_{1} \dot{r}_{1} + 4\pi p(t)A^{2} r_{2}^{ - 2} r_{1}^{2} . $$
(13)

The variational principle requires that

$$ \frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{\partial (K - \prod )}{{\partial \dot{r}_{1} }}} \right) - \frac{\partial (K - \prod )}{{\partial r_{1} }} = {\varvec{Q}}. $$
(14)

Substituting Eqs. (8)–(13) into (14), the governing equation describing the radial symmetric motion of micro-void is given as follows

$$ \begin{aligned} &4\pi \rho r_{1}^{4} \left[ {r_{1}^{ - 1} - (r_{1}^{3} + \delta^{3} A^{3} )^{ - 1/3} } \right]\ddot{r}_{1} + 2\pi \rho r_{1}^{2}\\ &\quad \left[ {3 - 4r_{1} (r_{1}^{3} + \delta^{3} A^{3} )^{ - 1/3} + r_{1}^{4} (r_{1}^{3} + \delta^{3} A^{3} )^{ - 4/3} } \right]\dot{r}_{1}^{2} \hfill \\ &\quad+ c_{1} \dot{r}_{1} + 4\pi \int_{\varepsilon }^{A} {\frac{\partial W(\kappa )}{{\partial r_{1} }}} R^{2} {\text{d}}R \\ &\quad- 4\pi p(t)A^{2} (r_{1}^{3} + \delta^{3} A^{3} )^{ - 2/3} r_{1}^{2} = 0. \hfill \\ \end{aligned} $$
(15)

For convenience, the following dimensionless transformations are introduced

$$ \begin{aligned} &x = \frac{{r_{1} }}{A}, \, \delta = \frac{{(A^{3} - \varepsilon^{3} )^{1/3} }}{A}, \, \tau = \frac{t}{{\sqrt {\rho A^{2} /\mu_{1} } }}, \\ &\tilde{\omega } = \omega \sqrt {\rho A^{2} /\mu_{1} } , \, P(\tau ) = \frac{p(t)}{{\mu_{1} }}, \hfill \\ & P = \frac{{p_{0} }}{{\mu_{1} }}, \, \tilde{\eta } = \frac{\eta }{{\mu_{1} }}, \, \tilde{c}_{1} = \frac{{c_{1} }}{{4\pi A^{2} \sqrt {\rho \mu_{1} } }}, \, \hat{W}(\kappa ) = \frac{W(\kappa )}{{\mu_{1} }}, \hfill \\ \end{aligned} $$
(16)

where \(\tilde{\omega }\) is the dimensionless excitation frequency, and \(\delta\) is the dimensionless structure parameter.

According to notations of Eq. (16), the governing Eq. (15) turns into

$$\begin{aligned}& F(x, \, \delta )\ddot{x} + G(x, \, \delta )\dot{x}^{2} + \frac{{\tilde{c}_{1} }}{{x^{2} }}\dot{x}\\ &\quad + H(x, \, \delta , \, P, \, \tilde{\eta }, \, \tilde{\omega }) = 0,\end{aligned} $$
(17)

where \(F(x, \, \delta ) = x - \frac{{x^{2} }}{{(x^{3} + \delta^{3} )^{1/3} }}\), \(G(x, \, \delta ) = \frac{{x^{4} }}{{2(x^{3} + \delta^{3} )^{4/3} }} - \frac{2x}{{(x^{3} + \delta^{3} )^{1/3} }} + \frac{3}{2}\),

$$\begin{aligned}& H(x, \, \delta , \, P, \, \tilde{\eta }, \, \tilde{\omega }) = - P(\tau )(x^{3} + \delta^{3} )^{ - 2/3} \, + \int_{{(x^{3} /(1 - \delta^{3} ))^{1/3} }}^{{(x^{3} + \delta^{3} )^{1/3} }} \\ &\quad{\frac{{2\kappa \!- \!2\kappa^{ - 5} \!+\! {{2\alpha (\kappa^{3} \!-\! \kappa^{ - 3} )} \mathord{\left/ {\vphantom {{2\alpha (\kappa^{3} - \kappa^{ - 3} )} {(2\kappa^{ - 2} + \kappa^{4} - 2)}}} \right. \kern-0pt} {(2\kappa^{ - 2} \!+\! \kappa^{4} \!-\! 2)}} \!+\! 4\beta \kappa^{ - 5} (1 - \kappa^{ - 4} )}}{{1 \!-\! \kappa^{3} }}} {\text{d}}\kappa .\end{aligned} $$
(18)

In addition, the initial condition (6) becomes

$$ x(0) = (1 - \delta^{3} )^{1/3} , \, \dot{x}(0) = 0. $$
(19)

So far, the mathematical model is established for the nonlinear dynamic responses of the micro-void at the center of the hyperelastic sphere subjected to periodically perturbed loads and structural damping, and the sphere is composed of the radial transversely isotropic incompressible Gent–Thomas materials. It should be pointed out that the structural damping \(\frac{{\tilde{c}_{1} }}{{x^{2} }}\dot{x}\) will enrich the nonlinear dynamic responses of the micro-void.

3 Dynamic responses of micro-void under constant loads

When \(\tilde{\eta } = 0\), the micro-void is subjected to constant loads, i.e., \(P(\tau ) = P\). Firstly, the periodic oscillation of the micro-void under constant loads without structural damping is discussed. Then, by analyzing the equilibrium point curves and potential wells of the system, the influences of constant loads and structural parameters on the bifurcation of micro-void are discussed in detail.

Let \(\dot{x} = y\), Eq. (17) is reduced to the following system of equations, i.e.,

$$ \left( \begin{gathered} {\dot{x}} \hfill \\ {\dot{y}} \hfill \\ \end{gathered} \right) = \left( \begin{gathered} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \, y \hfill \\ \frac{{ - G(x, \, \delta )y^{2} - {{\tilde{c}_{1} y} \mathord{\left/ {\vphantom {{\tilde{c}_{1} y} {x^{2} }}} \right. \kern-0pt} {x^{2} }} - H(x, \, \delta , \, P, \, 0, \, \tilde{\omega })}}{F(x, \, \delta )} \hfill \\ \end{gathered} \right). $$
(20)

In Eq. (20), let \(\dot{x} = 0, \, \dot{y} = 0\), if the system has a solution \((x_{i} , \, 0)\), then, \((x_{i} , \, 0)\) must be the equilibrium point of the system. It is clear that the number of solutions of Eq. (17) corresponds to the number of equilibrium points of the system (20), and the equilibrium points can be determined by the following equation

$$ \begin{aligned}P =& (x^{3} + \delta^{3} )^{2/3} \int_{{(x^{3} /(1 - \delta^{3} ))^{1/3} }}^{{(x^{3} + \delta^{3} )^{1/3} }} {\frac{{2\kappa - 2\kappa^{ - 5} + {{2\alpha (\kappa^{3} - \kappa^{ - 3} )} \mathord{\left/ {\vphantom {{2\alpha (\kappa^{3} - \kappa^{ - 3} )} {(2\kappa^{ - 2} + \kappa^{4} - 2)}}} \right. \kern-0pt} {(2\kappa^{ - 2} + \kappa^{4} - 2)}} + 4\beta \kappa^{ - 5} (1 - \kappa^{ - 4} )}}{{1 - \kappa^{3} }}} {\text{d}}\kappa .\end{aligned} $$
(21)

When other parameters are given, there exists a critical value \(\beta_{0}\) for the material parameter \(\beta\), the system only has one equilibrium point for \(0 < \beta < \beta_{0}\). There are two critical loads \(P_{t1}\) and \(P_{t2}\); the system will have a secondary turning bifurcation for \(\beta_{0} < \beta\). (i) The system also has only one equilibrium point for \(P < P_{t1}\) or \(P > P_{t2}\). (ii) The system has three equilibrium points for \(P_{t1} < P < P_{t2}\), as shown in Fig. 1a. Similarly, material parameter \(\alpha\) and structural parameter \(\delta\) also have critical values \(\alpha_{0}\) and \(\delta_{0}\), respectively, and the impacts on the number of equilibrium points are shown in Fig. 1b, c.

Fig. 1
figure 1

Equilibrium point curves of the system

Full size image

3.1 Constant loads without damping

When there is no structural damping, i.e., \(\tilde{c}_{1} = 0\), qualitative analysis of the equilibrium points is performed by the first integral of the system, where \(\delta = 0.999,\alpha = 1.2,\beta = 1,P = 3.85,C_{0} = - 0.00613\).

It can be derived that the first integral is given by

$$ \begin{aligned}&\frac{1}{2}x^{2} F(x, \, \delta )\dot{x}^{2} + P\left[ {1 - (x^{3} + \delta^{3} )^{1/3} } \right] \\ &\qquad + \int_{{(1 - \delta^{3} )^{1/3} }}^{x} {z^{2} } \int_{{(z^{3} /(1 - \delta^{3} ))^{1/3} }}^{{(z^{3} + \delta^{3} )^{1/3} }} {\frac{{\hat{W}^{\prime}(\kappa )}}{{1 - \kappa^{3} }}} {\text{d}}\kappa {\text{d}}z = C,\end{aligned} $$
(22)

where \(C\) is an integral constant.

Under the given initial condition, the micro-void performs periodic motions and the period is as follows

$$ T = 2\int_{{(1 - \delta^{3} )^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}}} }}^{{x_{\max } }} {\left( {\frac{{x^{2} F(x, \, \delta )}}{{2\left[ {C - P[1 - (x^{3} + \delta^{3} )^{1/3} ] - \int_{{(1 - \delta^{3} )^{1/3} }}^{x} {z^{2} } \int_{{(z^{3} /(1 - \delta^{3} ))^{1/3} }}^{{(z^{3} + \delta^{3} )^{1/3} }} {\frac{{\hat{W}^{\prime}(\kappa )}}{{1 - \kappa^{3} }}} {\text{d}}\kappa {\text{d}}z} \right]}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} {\text{d}}x, $$
(23)

where \(x_{\max }\) is the maximum radius of the micro-void.

Figure 2 shows the potential wells and the contour lines of the system. The types of equilibrium points can be discussed by analyzing the potential wells, and then, the periodic motions of micro-void around different potential wells also can be analyzed.

Fig. 2
figure 2

Potential wells and contour lines of the system

Full size image

It can be seen from Fig. 2 that different energy constants \(C\) correspond to different orbits of micro-void. As shown in Fig. 2a, b, there are three critical values of \(C\), i.e., \(C_{1} = - 0.15495, \, C_{2} = - 0.00753, \, C_{0} = - 0.00613\), which cause the periodic motions of micro-void around different potential wells. There is no equilibrium point in the system for \(C < C_{1}\). The system has one equilibrium point \((x_{1} ,0)\) for \(C_{1} < C < C_{2}\), which is a center, in this case, the motions of micro-void are periodical around the single potential well. The system has two equilibrium points \((x_{2} ,0), \, (x_{3} ,0)\) for \(C_{2} \le C < C_{0}\), which are both centers; the motions of micro-void are periodical around either of the potential wells. The system has three equilibrium points \((x_{4} ,0), \, (x_{5} ,0), \, (x_{6} ,0), \, (x_{4} < x_{5} < x_{6} )\) for \(C \ge C_{0}\), where \((x_{4} ,0)\) and \((x_{6} ,0)\) are centers, \((x_{5} ,0)\) is a saddle point, the motions of micro-void are periodical around the double potential wells. Figure 2c, d shows the variations of the phase trajectory curves with loads. It can be found that there exists a critical load \(P = P_{c2}\), which causes significant changes of structural stiffness.

3.2 Constant loads with damping

When there exists structural damping, i.e., \(\tilde{c}_{1} \ne 0\), the domain of attraction, vector field and the convergence of phase orbit of the system are mainly discussed.

Figure 3 shows the influence of the structural damping on the domain of attractions of the system. Under the action of damping, it can be seen from the vector field that the system has two focuses and one saddle point, where the black curve represents the homoclinic orbit of the system, and the red and blue curves represent the phase orbit curves at different initial values. For \(\tilde{c}_{1} = 0.0001\), the phase orbits do not converge to the focus of the system. When \(\tilde{c}_{1}\) increases, the phase orbits converge to the focus of the system, as shown in Fig. 3b–d. Specifically, for \(\tilde{c}_{1} = 0.1\) and \(\tilde{c}_{1} = 0.5\), even if the initial values are at the left of the saddle point, the phase orbits converge to the right focus, but if the damping is large enough, such as \(\tilde{c}_{1} = 5\), if the initial value is at the left of the saddle point, the phase orbit converges to the left focus of the system. On the other hand, under the action of the structural damping, the energy dissipation generated by the system will affect the convergence speed of the system, and the greater the damping, the faster the convergence speed. The influence also leads to changes of the shape and size of the attraction domain, and it is obvious that the attraction domain of the right focus is much larger than that of the left focus.

Fig. 3
figure 3

Attraction domains of the system with different damping coefficients

Full size image

4 Dynamic responses of micro-void under periodic loads

4.1 Quasi-periodic motion of micro-void

When \(\tilde{\eta } > 0\), the micro-void is subjected to periodic perturbation loads, i.e., \(P(\tau ) = P + \tilde{\eta }\sin \tilde{\omega }\tau\), the system is a nearly integrable Hamiltonian system. By giving the initial value \(x_{0} = [1.65, \, 0]\) and parameters \(\delta = 0.999, \, \alpha = 1.2, \, \beta = 1, \, P = 3.85, \, \tilde{\omega } = 1\), the dynamic behaviors near the center of the system are analyzed by the time response curves, the phase orbits and the Poincaré sections.

4.1.1 Periodic loads without damping

When there is no structural damping, i.e., \(\tilde{c}_{1} = 0\), the influences of different perturbation parameters on the quasi-periodic behaviors of micro-void near the center are discussed in detail.

The time response curves and Poincaré sections of the system with different perturbation parameters are shown in Fig. 4. For \(\tilde{\eta } = 0\), the time response curve is periodical, and the system performs periodic motions, as shown in Fig. 4a. For \(\tilde{\eta } = 0.01 > 0\), the time response curve presents perturbation and is no longer periodical, with the increase in \(\tilde{\eta }\), the perturbation increases further, as shown in Fig. 4b, c. For \(\tilde{\eta } = 0.1\), the Poincaré section is a closed curve, as shown in Fig. 4d, therefore, it can be determined that the micro-void performs the quasi-periodic motion near the center.

Fig. 4
figure 4

Time response curves and Poincaré sections near the center under different perturbation parameters

Full size image

4.1.2 Periodic loads with damping

Next, we will discuss that the system is subjected to the structural damping, i.e., \(\tilde{c}_{1} > 0\), the mainly analysis focuses on the dynamic behaviors of micro-void near the center under different perturbation parameters and structural damping.

For \(\tilde{\eta } = 0.1\), Fig. 5 shows the time response curves, phase orbits, and Poincaré sections near the center under different damping coefficients. The time response curves of the system are non-periodic, and the amplitude gradually decreases for \(\tilde{c}_{1} = 0.001\), but are periodic for \(\tilde{c}_{1} = 0.1\). It can be seen from phase orbit curves and Poincaré sections that in a periodic excitation system with damping, there exists a critical value \(\tilde{c}_{1cr}\) of the damping, the micro-void still presents quasi-periodic motion near the center for \(\tilde{c}_{1} < \tilde{c}_{1cr}\), while the motion of micro-void changes from a quasi-periodic state to a periodic state for \(\tilde{c}_{1} > \tilde{c}_{1cr}\). It is worth noting that the orbit converges to a stable fixed point during the quasi-periodic motion of the micro-void.

Fig. 5
figure 5

a, b Time response curves, c, d phase orbits, and e, f Poincaré sections under different damping

Full size image

4.2 Chaotic motion of micro-void

In this part, firstly, the chaotic behaviors of the system under periodic perturbation loads are analyzed, and then, the more complex nonlinear dynamic phenomena of the micro-void under periodic perturbation loads and structural damping are discussed.

4.2.1 Periodic loads without damping

When there is no structural damping, the influence of the perturbation parameters on the chaotic motions of the micro-void near the saddle point is discussed by time response curves and Poincaré sections. As shown in Fig. 6, the time response curve of the system is obviously non-periodic for \(\tilde{\eta } = 0.01\), while \(\tilde{\eta }\) increases, the disturbance of the system is further strengthened; the phase orbit curves have similar behavior, as shown in Fig. 6c,d.

Fig. 6
figure 6

a, b Time response curves and c, d phase orbit curves near the saddle point under different perturbation parameters

Full size image

Figure 7 shows the Poincaré sections when the perturbation parameters are different. The projections of the phase orbit of the system on the Poincaré section are irregular scattered points near the homoclinic orbit with \(\tilde{\eta } = 0.001\), as shown in Fig. 7a, when the perturbation parameters increase, the projection area increases significantly, indicates that when the perturbation parameters increase, the irregularity of the nonlinear motions of the micro-void is further strengthened, as shown in Fig. 7b–d.

Fig. 7
figure 7

Poincaré sections near the saddle point under different perturbation parameters

Full size image

4.2.2 Periodic loads with damping

When consider the effect of the structural damping, firstly, Melnikov method is used to deduce the chaos in the sense of smale horseshoe in the motion of the micro-void. Secondly, bifurcation diagrams are used to analyze the bifurcation characteristics of the micro-void in detail. Finally, the chaotic attractor is discussed.


Melnikov method:

The implicit expression for the homoclinic orbit \((x_{1} , \, x_{2} )\) is given by

$$ C = \frac{1}{2}x_{1}^{2} F(x_{1} {, }\delta )x_{2}^{2} + \int_{{(1 - \delta^{3} )^{1/3} }}^{{x_{1} }} {z^{2} \int_{{(z^{3} /(1 - \delta^{3} ))^{1/3} }}^{{(z^{3} + \delta^{3} )^{1/3} }} {\frac{{\hat{W}^{\prime}(\kappa )}}{{1 - \kappa^{3} }}} {\text{d}}\kappa } {\text{d}}z + P[1 - (x_{1}^{3} + \delta^{3} )^{1/3} ]. $$
(24)

Then, the expression of \(x_{2}\) is

$$ x_{2} = \pm \sqrt {2x_{1}^{ - 2} F^{ - 1} (x_{1} , \, \delta )\left[ {C - \int_{{(1 - \delta^{3} )^{1/3} }}^{{x_{1} }} {z^{2} \int_{{(z^{3} /(1 - \delta^{3} ))^{1/3} }}^{{(z^{3} + \delta^{3} )^{1/3} }} {\frac{{\hat{W}^{\prime}(\kappa )}}{{1 - \kappa^{3} }}} {\text{d}}\kappa } {\text{d}}z - P[1 - (x_{1}^{3} + \delta^{3} )^{1/3} ]} \right]} . $$
(25)

Let \(\tau = 0\), we have \(x_{2} = 0\), the intersection of homoclinic orbit and horizontal axis, denoted by \(x_{0}\), satisfies that

$$ \int_{{(1 - \delta^{3} )^{1/3} }}^{{x_{0} }} {z^{2} \int_{{(z^{3} /(1 - \delta^{3} ))^{1/3} }}^{{(z^{3} + \delta^{3} )^{1/3} }} {\frac{{\hat{W}^{\prime}(\kappa )}}{{1 - \kappa^{3} }}} {\text{d}}\kappa } {\text{d}}z + P[1 - (x_{0}^{3} + \delta^{3} )^{1/3} ] = C. $$
(26)

Integrating Eq. (26) with respect to \(x_{1}\) leads to that

$$ \tau = \int_{{x_{0} }}^{{x_{1} }} {\frac{{{\text{d}}x}}{{ \pm \sqrt {2x^{ - 2} F^{ - 1} (x, \, \delta )\left[ {C - \int_{{(1 - \delta^{3} )^{1/3} }}^{x} {z^{2} \int_{{(z^{3} /(1 - \delta^{3} ))^{1/3} }}^{{(z^{3} + \delta^{3} )^{1/3} }} {\frac{{\hat{W}^{\prime}(\kappa )}}{{1 - \kappa^{3} }}} {\text{d}}\kappa } {\text{d}}z - P[1 - (x^{3} + \delta^{3} )^{1/3} ]} \right]} }}} = \tau (x_{1} ). $$
(27)

The system under the periodic perturbation loads and structural damping is reduced to

$$ \dot{\user2{x}} = {\varvec{f}}({\varvec{x}}) + \tilde{\varepsilon }{\varvec{g}}({\varvec{x}},\tau ), $$
(28)

where.

\({\varvec{x}} = \left( {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ \end{array} } \right), \, {\varvec{f}}({\varvec{x}}) = \left( {\begin{array}{*{20}c} {f_{1} } \\ {f_{2} } \\ \end{array} } \right)\), \(0 < \tilde{\varepsilon } \ll 1\), \({\varvec{g}}({\varvec{x}}, \, \tau ) = \left( {\begin{array}{*{20}c} 0 \\ {\frac{{\tilde{\varepsilon }\tilde{\eta }(x_{1}^{3} + \delta^{3} )^{ - 2/3} \sin (\tilde{\omega }\tau ) - \tilde{\varepsilon }\tilde{c}_{1} x_{1}^{ - 2} x_{2} }}{{F(x_{1} , \, \delta )}}} \\ \end{array} } \right)\),and

$$ \left\{ \begin{gathered} f_{1} = x_{2} \hfill \\ f_{2} = \frac{{P(x_{1}^{3} + \delta^{3} )^{ - 2/3} - [G(x_{1} , \, \delta )x_{2}^{2} + \int_{{(x_{1}^{3} /(1 - \delta^{3} ))^{1/3} }}^{{(x_{1}^{3} + \delta^{3} )^{1/3} }} {\frac{{\hat{W}^{\prime}(\kappa )}}{{1 - \kappa^{3} }}} {\text{d}}\kappa ]}}{{F(x_{1} , \, \delta )}} \hfill \\ \end{gathered} \right., $$
$$ {\mathbf{D}}{\varvec{f}} = \left( {\begin{array}{*{20}c} 0 & 1 \\ {\frac{{\partial f_{2} }}{{\partial x_{1} }}} & {\frac{{ - 2x_{2} G(x_{1} , \, \delta )}}{{F(x_{1} , \, \delta )}}} \\ \end{array} } \right),\;{\text{tr(}}{\mathbf{D}}{\varvec{f}}{)} = \frac{{ - 2x_{2} G(x_{1} , \, \delta )}}{{F(x_{1} , \, \delta )}}, $$
$$\begin{aligned} &{\varvec{f}}({\varvec{x}}_{0} ) \wedge {\varvec{g}}({\varvec{x}}_{0} , \, \tau + \tau_{0} ) \\ &\quad= \frac{{x_{2} [\tilde{\varepsilon }\tilde{\eta }(x_{1}^{3} + \delta^{3} )^{ - 2/3} \sin \left( {\tilde{\omega }(\tau + \tau_{0} )} \right) - \tilde{\varepsilon }\tilde{c}_{1} x_{1}^{ - 2} x_{2} ]}}{{F(x_{1} , \, \delta )}}.\end{aligned} $$

Note: in the above expression, “\(\wedge\)” denotes the exterior product.

Using the above variable substitution, Eq. (27) satisfies that

$$ e(\tau ) = \int_{0}^{\tau } {{\text{tr(}}{\mathbf{D}}{\varvec{f}}{\text{)d}}\tau } = - 2\int_{{x_{0} }}^{{x_{1} }} {\frac{{G(x_{1} , \, \delta )}}{{F(x_{1} , \, \delta )}}{\text{d}}x_{1} } = e(x_{1} ). $$
(29)

Then, we have

$$ \begin{aligned} &{\varvec{f}}({\varvec{x}}_{0} ) \wedge {\varvec{g}}({\varvec{x}}_{0} , \, \tau + \tau_{0} ) \hfill \\ &\quad= \frac{{\tilde{\eta }x_{2} (x_{1}^{3} + \delta^{3} )^{ - 2/3} \sin \left( {\tilde{\omega }\tau (x_{1} )} \right)}}{{F(x_{1} , \, \delta )}}\cos (\tilde{\omega }\tau_{0} ) \\ &\qquad+ \frac{{\tilde{\eta }x_{2} (x_{1}^{3} + \delta^{3} )^{ - 2/3} \cos \left( {\omega \tau (x_{1} )} \right)}}{{F(x_{1} , \, \delta )}}\sin (\tilde{\omega }\tau_{0} )\\ &\qquad - \frac{{\tilde{c}_{1} x_{1}^{ - 2} x_{2}^{2} }}{{F(x_{1} , \, \delta )}}. \hfill \\ \end{aligned} $$
(30)

The Melnikov function of the system is given by

$$ \begin{aligned} &M(\tau_{0} ) = \int_{ - \infty }^{\infty } {{\varvec{f}}({\varvec{x}}_{0} ) \wedge {\varvec{g}}{(}{\varvec{x}}_{0} , \, \tau + \tau_{0} {\text{)exp}}\left( { - \int_{0}^{\tau } {{\text{tr(}}{\mathbf{D}}{\varvec{f}}{\text{)d}}t} } \right){\text{d}}\tau } \\ &\quad= \tilde{\eta }\cos (\tilde{\omega }\tau_{0} )\int_{ - \infty }^{\infty } {\frac{{x_{2} (x_{1}^{3} + \delta^{3} )^{ - 2/3} \sin \left( {\tilde{\omega }\tau (x_{1} )} \right)}}{{F(x_{1} , \, \delta )}}{\text{exp}}\left( { - e(x_{1} )} \right){\text{d}}\tau } \\ &\qquad + \tilde{\eta }\sin (\tilde{\omega }\tau_{0} )\int_{ - \infty }^{\infty } \frac{{x_{2} (x_{1}^{3} + \delta^{3} )^{ - 2/3} \cos \left( {\omega \tau (x_{1} )} \right)}}{{F(x_{1} , \, \delta )}}\\ &\qquad{\text{exp}}\left( { - e(x_{1} )} \right){\text{d}}\tau - \tilde{c}_{1} \int_{ - \infty }^{\infty } {\frac{{x_{1}^{ - 2} x_{2}^{2} }}{{F(x_{1} , \, \delta )}}{\text{exp}}\left( { - e(x_{1} )} \right){\text{d}}\tau } \\ &\qquad\doteq \tilde{\eta }\cos (\tilde{\omega }\tau_{0} )J_{1} + \tilde{\eta }\sin (\tilde{\omega }\tau_{0} )J_{2} - \tilde{c}_{1} J_{3}\\ &\qquad = \tilde{\eta }\sqrt {J_{1}^{2} + J_{2}^{2} } \sin [\tilde{\omega }\tau_{0} + \arctan ({{J_{1} } \mathord{\left/ {\vphantom {{J_{1} } {J_{2} }}} \right. \kern-0pt} {J_{2} }})] - \tilde{c}_{1} J_{3} \, . \\ \end{aligned} $$
(31)

Therefore, the condition that function \(M(\tau_{0} )\) has zero points is

$$ \left| {\tilde{\eta }} \right| > \frac{{\tilde{c}_{1} J_{3} }}{{\sqrt {J_{1}^{2} + J_{2}^{2} } }}. $$
(32)

Equation (32) is a necessary condition for the emergence of chaos in the motions of the micro-void. At this time, the stable manifold and the unstable manifold of the system appear cross homoclinic points on the Poincaré sections, i.e., system (17) has chaos in the sense of smale horseshoe. Particularly, when \(\tilde{\omega } = 1, \, \tilde{c}_{1} = 0.01\), the threshold value of chaos is calculated numerically as \(\tilde{\eta }_{cr} = 0.3947\).

4.2.3 Numerical simulation

In this section, numerical simulations of the chaotic motions are given. Firstly, the bifurcation characteristics of micro-void under different damping are discussed using the bifurcation diagrams of the system. Secondly, the chaotic motions of micro-void in the sense of smale horseshoe are also examined.

Figure 8 shows the bifurcation diagrams of system velocity with load \(P\). When damping coefficient is \(\tilde{c}_{1} = 0.001\), as the load \(P\) increases, the response of the system presents a process from periodic to chaotic motion, as shown in Fig. 8a, and the chaotic region decreases obviously with the increase in \(\tilde{c}_{1}\), as shown in Fig. 8b. Specifically, when \(\tilde{c}_{1} = 0.1\), the response of the system completely becomes periodic motion, and the amplitude of the periodic response presents a jumping phenomenon, as shown in Fig. 8c.

Fig. 8
figure 8

Bifurcation diagrams of system velocity \(\dot{x}\) with load \(P\)

Full size image

Figure 9 shows the bifurcation diagrams of system velocity with perturbation parameters \(\tilde{\eta }\). The response of the system presents a large area of chaotic phenomena with \(\tilde{c}_{1} = 0\), as shown in Fig. 9a. For \(\tilde{c}_{1} = 0.001\), the response of the system appears a periodic state. For \(\tilde{c}_{1} = 0.01\), the response of the system presents from periodic to chaotic and then to periodic alternately; moreover, the amplitude of periodic response also has a jumping phenomenon, and the amplitude of chaotic motion is significantly higher than that of periodic motion. Specifically, the system performs the period-2 motion from period-1 motion through a nonlinear dynamic characteristic of period-doubling bifurcation for \(\tilde{\eta } = 0.392\). When \(\tilde{\eta } = 0.394\), the system performs period-4 motion again through the period-doubling bifurcation, and then, the frequency band of bifurcation becomes narrower and narrower, and it performs chaotic motion through the period-doubling bifurcation. When \(\tilde{\eta } = 0.397\), the system performs an inverse period-doubling bifurcation for the first time, the system presents from a chaotic state to a period-4 motion, as shown in Fig. 9c, d.

Fig. 9
figure 9

Bifurcation diagrams of system velocity \(\dot{x}\) with perturbation parameter \(\tilde{\eta }\)

Full size image

It can be seen from the bifurcation characteristics of the micro-void that, the minimum excitation amplitude \(\tilde{\eta }\) for the system to generate chaos also increases with the increase in structural damping \(\tilde{c}_{1}\). This is because the energy dissipated by the system increases with the increase in damping and then, the minimum excitation amplitude required for chaos in the system increases, i.e., increasing damping can reduce the non-periodic motion region of the system, which can inhibit the chaotic motion of the micro-void to some extent.

When the other parameters are fixed, the perturbation parameter is \(\tilde{\eta } = 0.3955 > \tilde{\eta }_{cr}\). Figure 10 shows the Poincaré sections of the system under different structural damping. As \(\tilde{c}_{1} = 0.001\), a large number of irregularly scattered points appear in the Poincaré section, and the system performs the chaotic motion, as shown in Fig. 10a. As \(\tilde{c}_{1} = 0.01\), the Poincaré section performs a certain hierarchical structure and has the characteristics of horseshoe chaos, as shown in Fig. 10b.

Fig. 10
figure 10

Poincaré sections of the system with different structural damping coefficients

Full size image

Figures 11 and 12 show the phase orbits and Poincaré sections of the periodic motion of the micro-void under different perturbation parameters and structural damping, respectively. It can be seen that although the motions of the micro-void both present periodic forms, the phase orbits of their motions are very different, the micro-void moves periodically around the single potential well of the system in Fig. 11, moves periodically around the double potential wells in Fig. 12, which means that the periodic motion of the micro-void changes from single well motion to double wells motion with the changes of perturbation parameters and structural damping.

Fig. 11
figure 11

Phase orbit and Poincaré section of the system for \(\tilde{\eta } = 0.35, \, \tilde{c}_{1} = 0.01\)

Full size image
Fig. 12
figure 12

Phase orbit and Poincaré section of the system for \(\tilde{\eta } = 0.3955, \, \tilde{c}_{1} = 0.1\)

Full size image

Figure 13 shows the Poincaré sections of the system for different excitation frequencies. It can be found that with the changes of the excitation frequencies, the Poincaré sections produce fractal structures and become strange attractors. The existence of the strange attractors shows that under the periodic perturbation loads and structural damping, even though the motion of the micro-void is irregular and unpredictable, the motion region is still certain.

Fig. 13
figure 13

Poincaré sections of the system for different excitation frequencies

Full size image

5 Conclusions

In this paper, the effects of periodic perturbation load and structural damping on the nonlinear dynamic behaviors of the micro-void at the center of a sphere are examined, where the sphere is composed of a class of radial transversely isotropic incompressible Gent–Thomas material. The second-order nonlinear ordinary differential equation describing the radial symmetric motion of the micro-void is derived by the variational principle. Through qualitative analysis of solutions, the main conclusions are as follows:

  1. (1)

    For the constant loads without damping, the bifurcation behaviors of the micro-void are discussed, the influences of relevant parameters on the number of equilibrium points are given, and the periodic motions of the micro-void around different potential wells are analyzed in detail. For the constant loads with damping, the influences of structural damping on the attraction domains are mainly analyzed. The results show that the phase orbits of the system converge to different focuses under different damping, and the greater the damping is, the faster the system converges. The existence of damping also leads to changes of the shape and size of attraction domain, in which the right focus attraction domain is much larger than that of the left focus.

  2. (2)

    For the periodic loads without damping, the quasi-periodic motions of the micro-void near the center and the chaotic motions near the saddle point are discussed, and the influences of perturbation parameters on the chaotic motions are analyzed. For the periodic loads with damping, the periodic and quasi-periodic motions of the micro-void near the center are discussed. Near the saddle point of the system, firstly, the chaos threshold is obtained by the Melnikov method. Secondly, the bifurcation characteristics of the micro-void are analyzed by the bifurcation diagrams. The results show that, the response of the system presents from periodic to chaotic and then to periodic alternately, and the chaotic region is reduced obviously; moreover, the amplitude of periodic response also has a jumping phenomenon, and the amplitudes of chaotic motions are significantly higher than these of periodic motions. Finally, the Poincaré sections of the system have fractal features with the changes of the excitation frequencies, and it is found that the strange attractors are generated during the movements of the micro-void.

  3. (3)

    By analyzing the dynamic response characteristics of the system with and without damping, the influence of structural damping on the response amplitude has been discovered. Specifically, it has been found that structural damping can significantly constrain the amplitude range of micro-void vibration response and stabilize the response, thereby enhancing the structure service performance and safety.