Bifurcation dynamics of complex period-1 motions to chaos in an electromagnetically tuned duffing oscillator

Abstract

In this paper, bifurcation dynamics of periodic motions in the electromagnetically tuned Duffing oscillator are studied through symmetric period-1 to asymmetric period-2 motions. On the bifurcation routes, there exist one branch of symmetric period-1 motions and 4 branches of asymmetric period-1 motions, one branch of the four asymmetric period-1 motion branches with asymmetric period-2 motion to chaos is obtained. The corresponding stability and bifurcations of periodic motions are determined. The frequency-amplitude characteristics for bifurcation routes of such periodi-1 motions to chaos are presented. Numerical illustrations are presented for complex symmetric period-1 motions, asymmetric period-1 to period-2 motions. For low frequency, the complex period-1 motions are obtained, and for the high frequency, the simple period-1 motions are observed. The asymmetric period-1 motions from the symmetric period-1 motion are obtained through the saddle-node bifurcation, and the asymmetric period-2 motions from the asymmetric period-1 motions are obtained from the saddle-node bifurcation. The study of periodic motions can help design the vibration reduction and energy harvesting system.

1 Introduction

The tuned mass damper (TMD) [1] has been considered as a classic dynamic vibration absorber, and it is one of the most effective devices for energy dissipation and vibration reduction [2] from the recent study. Thus, researchers have introduced various methods to study the dynamical behaviors of TMD and to optimize the parameters of such systems.

For the tuned mass damper, in 1981, Kaynia et al. [3] studied a one-degree-freedom probabilistic model with and without TMD, and found was that the damping coefficient effects most on the response ration. In 2005, Krenk [4] studied the damping of a tuned mass damper through dynamic amplification analysis. In 2009, Alexander and Schilder [5] used a numerical method to study the periodic response of a nonlinear tuned mass damper (NTMD) in a two degree-of-freedom system. For energy harvesting, electromagnetic resonant shunt damper has been used to convert mechanical energy to electrical energy [6]. In 2017, Luo et al. [7] proposed an electromagnetic resonant shunt tuned mass damper inerter for the wind induced vibration control and energy harvesting.

On the other hand, studies of periodic motions in nonlinear systems have a much longer history. In 1788, Lagrange [8] used the method of averaging to study a three-body problem. In 1899, Poincare [9] introduced the perturbation method to determine the periodic motions of celestial bodies. In 1920, van der Pol [10] applied the method of averaging for the periodic motions of an oscillator circuit. In 1935, Krylov and Bogoliubov [11] extended the method of averaging to nonlinear vibration systems. In 1964, Hayashi [12] used the perturbation methods, averaging method and harmonic balance method to discuss nonlinear oscillations and subharmonic periodic motions were presented. In 1969, Barkham and Soudack [13] extended the Krylov–Bogoliubov method for the approximated solutions of a second-order nonlinear autonomous differential equations. In 1987, Garcia-Margallo and Bejarano [14] determined the approximated solutions of nonlinear oscillations through a harmonic balance method. In 1990, Coppola and Rand [15] presented the approximation of limit cycles via the averaging method with elliptic functions.

The traditional analytical methods cannot give accurate solutions of periodic motions. The unstable periodic motions are very difficult to be obtained. To resolve such issues, in 2012, Luo [16] proposed a generalized harmonic balance method for accurate analytical solutions of periodic motions and chaos (also see, Luo [17,18,19]). Luo and Huang [20] applied such a method to a Duffing oscillator and obtained the accurate analytical solutions of periodic motions. However, the generalized harmonic balance method is very difficult to be applied for periodic motions in dynamical systems with nonpolynomial vector fields. In 2015, Luo [21] developed a semi-analytical implicit mapping method for periodic motions in nonlinear dynamic system. In 2016, Luo and Guo [22] applied such a method for periodic motions in a periodically forced pendulum. Luo and Xing [23] presented the periodic motions in a twin-well, Duffing oscillator with time-delay displacement feedback and discussed the possibility of infinite bifurcation trees in such a nonlinear oscillator. Luo and Xu [24] applied such implicit mapping method for a coupled van der Pol Duffing oscillator and found a series of periodic motions. In 2019, Luo and Guo [25] determined the periodic motions in a periodically forced and damped double pendulum system using the implicit mapping method. In 2021, Guo and Luo [26] initially presented the symmetric and asymmetric periodic motions in the electromagnetically tuned Duffing oscillator.

However, the complex period-1 motions for such a system were not discussed. Especially the complex periodic motions in the low-frequency range cannot be obtained through the traditional analysis. For the energy harvesting and vibration reduction of an oscillator, dynamical behaviors for the low excitation frequency play an important role. Such behaviors cannot easily be obtained by the traditional perturbation methods. The bifurcation routes for symmetric period-1 motion to chaos were not determined analytically. Herein, the complex periodic motion for low frequency range will be discussed and the bifurcation routes of periodic motions to chaos will be obtained. Frequency-amplitude analysis of periodic motions on the bifurcation routes will be completed, and stable period-1 and period-2 motions in such an oscillator will be illustrated for motion complexity illustrations.

2 Periodic motions

Consider an electromagnetically tuned Duffing oscillator with a main mass $m_{s}$, a linear spring $k_{s}$, a nonlinear spring $k_{sn}$, and a damper $d_{s}$, as shown in Fig. 1. There is an electromagnetic tuned mass damper with mass $m_{t}$, a linear spring $k_{t}$, a nonlinear spring $k_{tn}$, and a damper $d_{t}$. An inerter $b$ is grounded on one side and connected to the tuned mass damper on the other side with an electric circuit of resistance $R$, inductance $L$, and capacitance $C$. An electromagnetic transducer is also grounded on one side and connected to the tuned mass damper on the other side. $k_{v}$ and $k_{f}$ are the voltage and force constants of the transducer.

Fig. 1

A schematic of an electromagnetically tuned Duffing oscillator

From the physical laws, the electromagnetically tuned Duffing oscillator is described by

$$ \begin{aligned} & m_{s} \ddot{x}_{s} + d_{s} \dot{x}_{s} - d_{t} (\dot{x}_{t} - \dot{x}_{s} ) + k_{s} x_{s} + k_{{sn}} x_{s}^{3} \\ &\quad - k_{t} (x_{t} - x_{s} )- k_{{tn}} (x_{t} - x_{s} )^{3} = F\sin (\Omega t), \\ & (m_{t} + b)\ddot{x}_{t} \hfill \, + d_{t} (\dot{x}_{t} - \dot{x}_{s} ) + k_{t} (x_{t} - x_{s} ) + k_{{tn}} (x_{t} - x_{s} )^{3} \\ & \quad + k_{f} I = 0, \\ & - k_{v} \dot{x}_{t} + RI + L\dot{I} + \frac{1}{C}\int {Idt} = 0. \\ \end{aligned} $$

(1)

For convenience, the physical quantities become mathematical quantity and variables herein. Assume

$$ \begin{gathered} x_{1} = x_{s} ,\,x_{2} = x_{t} ,\,x_{3} = I,\,m_{1} = m_{s} ,m_{2} = m_{t} \hfill \\ k_{1} = k_{s} ,\,k_{2} = k_{sn} ,\,k_{3} = k_{t} ,\,k_{4} = k_{tn} , \hfill \\ \,k_{5} = k_{v} = k_{f} ,\,d_{1} = d_{s} ,\,d_{2} = d_{t} . \hfill \\ \end{gathered} $$

(2)

Equation (1) becomes

$$ \begin{aligned} \dot{x}_{1} =\,& y_{1} , \hfill \\ \dot{x}_{2} =\,& y_{2} , \hfill \\ \dot{x}_{3} =\,& y_{3} , \hfill \\ \dot{y}_{1} = \,&\tfrac{1}{{m_{1} }}[ - d_{1} y_{1} + d_{2} (y_{2} - y_{1} ) - k_{1} x_{1} - k_{2} x_{1}^{3}\\ & + k_{3} (x_{2} - x_{1} ) + k_{4} (x_{2} - x_{1} )^{3} + F\sin \Omega t], \hfill \\ \dot{y}_{2} =& \tfrac{1}{{m_{2} + b}}[ - d_{2} (y_{2} - y_{1} ) - k_{3} (x_{2} - x_{1} )\\ & - k_{4} (x_{2} - x_{1} )^{3} - k_{5} x_{3} ], \hfill \\ \dot{y}_{3} =& \tfrac{1}{LC}(k_{5} C\dot{y}_{2} - RCy_{3} - x_{3} ). \hfill \\ \end{aligned} $$

(3)

For a period-m motion discretized into (mN + 1) nodes during m-periods, consider a mapping $P_{k}$ for a time interval of $t \in (t_{k - 1} ,t_{k} )$ as

$$ \begin{gathered} P_{k} :({\mathbf{x}}_{k - 1} ,\;{\mathbf{y}}_{k - 1} ) \to ({\mathbf{x}}_{k} ,\;{\mathbf{y}}_{k} ),\, \\ (k = 1,2, \ldots ,mN) \\ \end{gathered} $$

(4)

where ${\mathbf{x}}_{k} = (x_{1,k} ,x_{2,k} ,x_{3,k} )^{{\text{T}}}$ and ${\mathbf{y}}_{k} = (y_{1,k} ,y_{2,k} ,y_{3,k} )^{{\text{T}}}$

For the period-m motion, the total mapping is defined as $P = P_{mN} \circ P_{mN - 1} \circ \cdots \circ P_{2} \circ P_{1}$ with

$$ \begin{gathered} P:({\mathbf{x}}_{0} ,\;{\mathbf{y}}_{0} ) \to ({\mathbf{x}}_{mN} ,\;{\mathbf{y}}_{mN} ),{\text{ i}}{\text{.e}}{.,} \hfill \\ ({\mathbf{x}}_{mN} ,\;{\mathbf{y}}_{mN} ) = P({\mathbf{x}}_{0} ,\;{\mathbf{y}}_{0} ). \hfill \\ \end{gathered} $$

(5)

A set of discrete points $({\mathbf{x}}_{k}^{*} ,{\mathbf{y}}_{k}^{*} ),$$(k = 1,2, \cdots ,mN)$ on the period-m motion is obtained by

$$ \begin{gathered} \left. \begin{gathered} ({\mathbf{x}}_{k}^{*} ,{\mathbf{y}}_{k}^{*} ) = P_{k} ({\mathbf{x}}_{k - 1}^{*} ,{\mathbf{y}}_{k - 1}^{*} ),{\text{i.e.}}, \hfill \\ {\mathbf{g}}_{k} ({\mathbf{x}}_{k - 1}^{*} ,{\mathbf{y}}_{k - 1}^{*} ,{\mathbf{x}}_{k}^{*} ,{\mathbf{y}}_{k}^{*} ,{\mathbf{p}}) = {\mathbf{0}},\, \hfill \\ \end{gathered} \right\}(k = 1,2, \cdots ,mN), \hfill \\ ({\mathbf{x}}_{0}^{*} ,\;{\mathbf{y}}_{0}^{*} ) = ({\mathbf{x}}_{mN}^{*} \;,{\mathbf{y}}_{mN}^{*} ) \hfill \\ \end{gathered} $$

(6)

where ${\mathbf{g}}_{k} = (g_{1,k} ,g_{2,k} , \ldots ,g_{6,k} )^{{\text{T}}} .$.

The corresponding algebraic equations are

$$ \begin{aligned} g_{1,k} =\,& x_{1,k} - x_{1,k - 1} - \tfrac{h}{2}(y_{1,k} + y_{1,k - 1} ), \\ g_{2,k} =\, &x_{2,k} - x_{2,k - 1} - \tfrac{h}{2}(y_{2,k} + y_{2,k - 1} ), \\ g_{3,k} =\,& x_{3,k} - x_{3,k - 1} - \tfrac{h}{2}(y_{3,k} + y_{3,k - 1} ), \\ g_{4,k} =\,& y_{1,k} - y_{1,k - 1} - \tfrac{h}{{m_{1} }} \, \{ - \tfrac{1}{2}d_{1} (y_{1,k} + y_{1,k - 1} )\\& + d_{2} [\tfrac{1}{2}(y_{2,k} + y_{2,k - 1} ) - \tfrac{1}{2}(y_{1,k} + y_{1,k - 1} )] \\ &- \tfrac{1}{2}k_{1}(x_{1,k} + x_{1,k - 1} )\\ & - k_{2} [\tfrac{1}{2}(x_{1,k}+ x_{1,k - 1} )]^{3} + F\sin \Omega (t_{k - 1} + \tfrac{h}{2}) \\ &+ k_{3} [\tfrac{1}{2}(x_{2,k} + x_{2,k - 1} ) - \tfrac{1}{2}(x_{1,k} + x_{1,k - 1} )]\\ & + k_{4} [\tfrac{1}{2}(x_{2,k} + x_{2,k - 1} ) - \tfrac{1}{2}(x_{1,k} + x_{1,k - 1} )]^{3} \} , \\ g_{5,k} =\,& y_{2,k} - y_{2,k - 1} - \tfrac{h}{{m_{2} + b}}\{ - d_{2} [\tfrac{1}{2}(y_{2,k} + y_{2,k - 1} ) \\ &- \tfrac{1}{2}(y_{1,k} + y_{1,k - 1} )] - \tfrac{1}{2} k_{5} (x_{3,k} + x_{3,k - 1} ) \\ &- k_{3} [\tfrac{1}{2}(x_{2,k} + x_{2,k - 1} ) - \tfrac{1}{2}(x_{1,k} + x_{1,k - 1} )]\\ & - k_{4} [\tfrac{1}{2}(x_{2,k} + x_{2,k} ) - \tfrac{1}{2}(x_{1,k} + x_{1,k - 1} )]^{3} \} , \\ g_{6,k} =\,& y_{3,k} - y_{3,k - 1} - \tfrac{h}{LC} \, [\tfrac{1}{2}k_{5} C (y_{2,k} - y_{2,k - 1} ) \\ & - \tfrac{1}{2} RC (y_{3,k} + y_{3,k - 1} ) - \tfrac{1}{2}(x_{3,k} + x_{3,k - 1} )]. \\ \end{aligned}$$

(7)

For ${\mathbf{z}}_{k} = ({\mathbf{x}}_{k} ,{\mathbf{y}}_{k} )^{{\text{T}}}$, from the mapping structure in Eq. (6), the variational equation is

$$ \Delta {\mathbf{z}}_{mN} = DP\Delta {\mathbf{z}}_{0} = DP_{mN} \cdot DP_{mN - 1} \cdots DP_{k} \cdots DP_{1} \Delta {\mathbf{z}}_{0} $$

(8)

and

$$ \Delta {\mathbf{z}}_{k} = DP_{k} \Delta {\mathbf{z}}_{k - 1} { (}k = 1,2, \cdots ,mN) $$

(9)

where

$$ \begin{aligned}DP_{k} =\,& \left[ {\frac{{\partial {\mathbf{z}}_{k} }}{{\partial {\mathbf{z}}_{k - 1} }}} \right]_{{({\mathbf{z}}_{k}^{*} ,{\mathbf{z}}_{k - 1}^{*} )}}\\ =& - \left[ {\frac{{\partial {\mathbf{g}}_{k} }}{{\partial {\mathbf{z}}_{k} }}} \right]^{ - 1} \cdot \left[ {\frac{{\partial {\mathbf{g}}_{k} }}{{\partial {\mathbf{z}}_{k - 1} }}} \right]_{{({\mathbf{z}}_{k}^{*} ,{\mathbf{z}}_{k - 1}^{*} )}} ;\end{aligned} $$

(10)

which is from the variational equation of mapping $P_{k}$, i.e.,

$$ \frac{{\partial {\mathbf{g}}_{k} }}{{\partial {\mathbf{z}}_{k - 1} }}\left| {_{{({\mathbf{z}}_{k}^{*} ,{\mathbf{z}}_{k - 1}^{*} )}} } \right. + \frac{{\partial {\mathbf{g}}_{k} }}{{\partial {\mathbf{z}}_{k} }}\left| {_{{({\mathbf{z}}_{k}^{*} ,{\mathbf{z}}_{k - 1}^{*} )}} } \right.\frac{{\partial {\mathbf{z}}_{k} }}{{\partial {\mathbf{z}}_{k - 1} }}\left| {_{{({\mathbf{z}}_{k}^{*} ,{\mathbf{z}}_{k - 1}^{*} )}} } \right. = {\mathbf{0}}. $$

(11)

The components of $DP_{k}$ matrix are listed in Appendix. The eigenvalue of $DP$ matrix is computed by

$$ {|}DP - \lambda {\mathbf{I}}_{6 \times 6} {|} = 0. $$

(12)

The stability and bifurcation conditions for periodic motions are given as follows.

• (i) If $|\lambda_{i} {|} < 1$ ($\,i = 1,2, \cdots ,6$), the approximate periodic solution is stable.

• (ii) If $|\lambda_{i} {|} > 1$ ($\,i \in \{ 1,2, \cdots ,6\}$), the approximate periodic solution is unstable.

• (iii) The boundaries between stable and unstable periodic motions with higher order singularity give bifurcations.

The bifurcation conditions of periodic motion are presented as follows.

• (i) If $\lambda_{i} = 1$ and $|\lambda_{j} {|} < 1$($\,i,j \in \{ 1,2, \cdots ,6\} ,j \ne i$), the saddle-node bifurcation (SN) occurs.

• (ii) If $\lambda_{i} = - 1$ and $|\lambda_{j} {|} < 1$($\,i,j \in \{ 1,2, \cdots ,6\} ,j \ne i$), the period-doubling bifurcation (PD) occurs.

• (iii) If $|\lambda_{i,j}| = 1$ with $\lambda_{i} = \overline{\lambda }_{j}$ and $|\lambda_{l} {|} < 1$ ($\,i,j,l \in \{ 1,2, \cdots ,6\} ,j,i \ne l$), the Neimark bifurcation (NB) occurs.

3 Bifurcation routes of period-1 motion to chaos

Consider a set of parameters for the Duffing oscillator system as

$$ \begin{gathered} m_{1} = 8.46,m_{2} = 0.66,k_{1} = 7.12,k_{2} = 1, \hfill \\ k_{3} = 0.821,k_{4} = 0.1,k_{5} = 0.15,d_{1} = 0.4,d_{2} = 0.2, \hfill \\ L = 1.17,R = 0.1,C = 1.02,b = 0.33,F = 200. \hfill \\ \end{gathered} $$

(13)

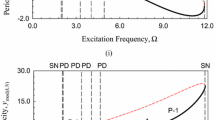
The periodic nodes ${\mathbf{x}}_{i,\bmod (k,N)}$ and ${\mathbf{y}}_{i,\bmod (k,N)}$ ($i = 1,2,3$ and $\bmod (k,N) = 0$) varying with excitation frequency in an electromagnetically tuned Duffing oscillator are presented. The stable and unstable periodic motions are colored in solid and dash curves, respectively. The acronym ‘SN’ is for saddle-node bifurcation, ‘S’ is for symmetric motion and ‘A’ is for asymmetric motion. The global views for periodic motions in the frequency range of $\Omega \in (0,10)$ are presented in Fig. 2. Period-1 motions for the frequency range of $\Omega > 10$ are with simple bifurcation trees. Displacement and velocity nodes for the Duffing oscillator are presented in Fig. 2(i) and (ii). Displacement and velocity nodes for the tuned mass damper oscillator are presented in Fig. 2(iii) and (iv). The turned damper oscillator possess larger vibration motions than the Duffing oscillator. The current and current change rate are presented in Fig. 2(v) and (vi). The large stable asymmetric period-1 motion occurs at $\Omega \approx 7.75$, and the large unstable symmetric period-1 motion occurs at $\Omega \approx 8.5$. For the low frequency, the motions amplitude should be smaller, but the periodic motions become more complex, and the period-1 motion to chaos occurs in the low frequency range. Thus, the zoomed version will be presented in Figs. 3 and 4 partially without abundant illustrations.

Fig. 2

A global view of discrete nodes of periodic motions ($\bmod (k,N) = 0$) varying with excitation frequency ($\Omega \in (0,10)$): i displacement $x_{1,\bmod (k,N)}$; ii velocity $y_{1,\bmod (k,N)}$, iii displacement $x_{2,\bmod (k,N)}$, iv velocity $y_{2,\bmod (k,N)}$, v current $x_{3,\bmod (k,N)}$; vi current change $y_{3,\bmod (k,N)}$. ($m_{1} = 8.46,$$m_{2} = 0.66,\,\,$$k_{1} = 7.12,\,$$\,k_{2} = 1,\,$$k_{3} = 0.821,$$k_{4} = 0.1,\,$$k_{5} = 0.15,\,$$d_{1} = 0.4,\,$$d_{2} = 0.2,\,$$L = 1.17,$$R = 0.1,$$\,C = 1.02,$$b = 0.33,$$F = 200$

Fig. 3

A zoomed view of discrete nodes of periodic motions ($\bmod (k,N) = 0$) varying with excitation frequency (zoom-1, $\Omega \in (0.15,0.30)$ ): i displacement $x_{1,\bmod (k,N)}$; ii velocity $y_{1,\bmod (k,N)}$, iii displacement $x_{2,\bmod (k,N)}$, iv velocity $y_{2,\bmod (k,N)}$, v current $x_{3,\bmod (k,N)}$; vi current change $y_{3,\bmod (k,N)}$. ($m_{1} = 8.46,$$m_{2} = 0.66,\,\,$$k_{1} = 7.12,\,$$\,k_{2} = 1,\,$$k_{3} = 0.821,$$k_{4} = 0.1,\,$$k_{5} = 0.15,\,$$d_{1} = 0.4,\,$$d_{2} = 0.2,\,$$L = 1.17,$$R = 0.1,$$\,C = 1.02,$$b = 0.33,$$F = 200$)

Fig. 4

A zoomed view of discrete nodes of periodic motions ($\bmod (k,N) = 0$) varying with excitation frequency (zoom-2, $\Omega \in (0.73,0.76)$): i displacement $x_{1,\bmod (k,N)}$; ii velocity $y_{1,\bmod (k,N)}$, iii displacement $x_{2,\bmod (k,N)}$, iv velocity $y_{2,\bmod (k,N)}$, v current $x_{3,\bmod (k,N)}$; vi current change $y_{3,\bmod (k,N)}$. ($m_{1} = 8.46,$$m_{2} = 0.66,\,\,$$k_{1} = 7.12,\,$$\,k_{2} = 1,\,$$k_{3} = 0.821,$$k_{4} = 0.1,\,$$k_{5} = 0.15,\,$$d_{1} = 0.4,\,$$d_{2} = 0.2,\,$$L = 1.17,$$R = 0.1,$$\,C = 1.02,$$b = 0.33,$$F = 200$)

The main branch of periodic motions is for symmetric period-1 motions in interval $\Omega \in (0,10.0)$, as shown in Fig. 2. There are four branches of asymmetric period-1 motions in frequency intervals of $\Omega \in (0.655,0.743)$, $\Omega \in (0.796,0.821)$, $\Omega \in (0.774,0.82)$ and $\Omega \in (0.998,7.676)$. There is also one branch for asymmetric period-2 motions in frequency interval $\Omega \in (0.554,0.737)$. Two zoomed views of discrete nodes in the frequency intervals of $\Omega \in (0.15,0.30)$ and $\Omega \in (0.73,0.76)$ are shown in Figs. 3 and 4. The acronyms ‘NB’ is for Neimark bifurcation and acronyms ‘PD’ is for period-doubling bifurcation. The stable and unstable period-1 motions are clearly presented for low frequency range, and the corresponding bifurcation points are labelled. In Fig. 3, the period-1 motion for the low frequency is presented. In Fig. 4, the bifurcation routes of symmetric period-1 motion to period-2 motions are presented. The saddle-node bifurcation is a symmetry break for the symmetric to asymmetric period-1 motion. The period-doubling bifurcation is observed for the asymmetric period-1 to period-2 motion. The period-doubling bifurcation of the period-2 motion is for the asymmetric period-4 motion, and the Neimark bifurcation of the symmetric period-1 motion is observed for the quasi-periodic motions. The detailed bifurcation points for symmetric period-1 to period-2 motions are tabulated in Table 1.

Table 1 Stability and bifurcations of period-1 and period-2 motions($m_{1} = 8.46,$$m_{2} = 0.66,\,\,$$k_{1} = 7.12,\,$$\,k_{2} = 1,\,$$k_{3} = 0.821,$$k_{4} = 0.1,\,$$k_{5} = 0.15,\,$$d_{1} = 0.4,\,$$d_{2} = 0.2,\,$$L = 1.17,$$R = 0.1,$$\,C = 1.02,$$b = 0.33,$$F = 200$)

4 Frequency-amplitude characteristics

From the semi-analytical prediction, discrete nodes of periodic motions are obtained through the implicit mapping. Then these discrete nodes are used for discrete Fourier analysis. Consider the node point of period-m motions as ${\mathbf{x}}_{k} = (x_{1,k} ,x_{2,k} ,x_{3,k} )^{{\text{T}}}$ for $k = 0,1,2, \cdots ,mN$. The approximate expression for a period-m motion is determined by the finite Fourier series as

$$ {\mathbf{x}}(t) = {\mathbf{a}}_{0} + \sum\limits_{k = 1}^{mN} {{\mathbf{b}}_{k/m} \cos (k\Omega t) + {\mathbf{c}}_{k/m} \sin (k\Omega t)} . $$

(14)

where

$$ \begin{aligned} & {\mathbf{a}}_{0} =\, (a_{1,0} ,a_{2,0} ,a_{3,0} )^{{\text{T}}} , \\ & {\mathbf{b}}_{k/m} =\, (b_{1,k/m} ,b_{2,k/m} ,b_{3,k/m} )^{{\text{T}}} , \\ & {\mathbf{c}}_{k/m} =\, (c_{1,k/m} ,c_{2,k/m} ,c_{3,k/m} )^{{\text{T}}} . \\ \end{aligned} $$

(15)

The coefficients ${\mathbf{a}}_{0}$, ${\mathbf{b}}_{k/m}$ and ${\mathbf{c}}_{k/m}$ are achieved by

$$ \begin{aligned} &{\mathbf{a}}_{0} = \frac{1}{mN}\sum\limits_{j = 0}^{mN - 1} {{\mathbf{x}}_{j} } , \\ & {\mathbf{b}}_{k/m} = \frac{2}{mN}\sum\limits_{j = 0}^{mN - 1} {{\mathbf{x}}_{j} \cos (k\frac{2\pi j}{{mN}})} , \\ & {\mathbf{c}}_{k/m} = \frac{2}{mN}\sum\limits_{j = 0}^{mN - 1} {{\mathbf{x}}_{j} \sin (k\frac{2\pi j}{{mN}})} , \\ & \qquad \quad \,(k = 1,2, \ldots mN/2). \\ \end{aligned} $$

(16)

Then harmonic amplitudes and phases for a period-1 motion can be expressed by

$$ \begin{aligned} A_{i,k/m} =& \sqrt {(b_{i,k/m} )^{2} + (c_{i,k/m} )^{2} } ,\\ \varphi_{i,k/m} = &\arctan \frac{{c_{i,k/m} }}{{b_{i,k/m} }}\, \qquad (i = 1,2,3). \\ \end{aligned} $$

(17)

Based on the Fourier series expression of the period-m motions, the frequency-amplitude characteristics of period-1 and period-2 motion can be obtained.

For the periodic motions, we have

$$ \begin{gathered} x_{1} = a_{1,0} + \sum\limits_{k = 1}^{\infty } {A_{1,k} \cos (k\Omega t + \varphi_{1,k} )} , \\ x_{2} = a_{2,0} + \sum\limits_{k = 1}^{\infty } {A_{2,k} \cos (k\Omega t + \varphi_{2,k} )} , \\ x_{3} = a_{3,0} + \sum\limits_{k = 1}^{\infty } {A_{3,k} \cos (k\Omega t + \varphi_{3,k} )} . \\ \end{gathered} $$

(18)

The derivatives of the displacements ($x_{1} ,x_{2} ,x_{3}$) with the respect to time gives

$$ \begin{gathered} y_{2} = \dot{x}_{2} = - \sum\limits_{k = 1}^{\infty } {(k\Omega )A_{2,k} \sin (k\Omega t + \varphi_{2,k} )} , \\ \dot{y}_{2} = \ddot{x}_{2} = - \sum\limits_{k = 1}^{\infty } {(k\Omega )^{2} A_{2,k} \cos (k\Omega t + \varphi_{2,k} )} ; \\ y_{3} = \dot{x}_{3} = - \sum\limits_{k = 1}^{\infty } {(k\Omega )A_{3,k} \sin (k\Omega t + \varphi_{3,k} )} , \\ \dot{y}_{3} = \ddot{x}_{3} = - \sum\limits_{k = 1}^{\infty } {(k\Omega )^{2} A_{3,k} \cos (k\Omega t + \varphi_{3,k} )} . \\ \end{gathered} $$

(19)

Submission of Eqs.(18) and (19) to the differential equation of

$$ \dot{y}_{3} = \tfrac{1}{LC}(k_{5} C\dot{y}_{2} - RCy_{3} - x_{3} ) $$

(20)

gives

$$ \begin{aligned}& - \sum\limits_{k = 1}^{\infty } {(k\Omega )^{2} A_{3,k} \cos (k\Omega t + \varphi_{3,k} )} \\&\quad= - \sum\limits_{k = 1}^{\infty } {\tfrac{1}{L}k_{5} (k\Omega )^{2} A_{2,k} \sin (k\Omega t + \varphi_{2,k} )} \\ &\qquad+ \sum\limits_{k = 1}^{\infty } {\tfrac{R}{L}(k\Omega )A_{3,k} \sin (k\Omega t + \varphi_{2,k} )} \\ &\qquad - \tfrac{1}{LC}[a_{3,0} + \sum\limits_{k = 1}^{\infty } {A_{3,k} \cos (k\Omega t + \varphi_{3,k} )}] . \\ \end{aligned} $$

(21)

Thus,

$$ a_{3,0} = 0. $$

(22)

The frequency-amplitude characteristics of displacement $x_{1}$, displacement $x_{2}$ and current $x_{3}$ are obtained through the finite Fourier series. Harmonic amplitudes of $A_{i,0} ,$ and $A_{i,k/2} ,\,\,$ ($i = 1,2,3;$$k = 1,2, \cdots ,4,6,8,157,158$) are presented in Figs. 5–7 respectively, and the local zoomed views are also presented. The stable and unstable periodic motions are colored in solid and dash curves. The acronyms ‘S’ and ‘A’ are for the symmetric and asymmetric motions. The acronyms ‘SN’, ‘NB’ and ‘PD’ are for saddle-node, Neimark and period-doubling bifurcations, respectively.

Fig. 5

Frequency-amplitude characteristics of displacement $x_{1}$: i, ii $A_{1,0}$; iii $A_{1,1/2}$; iv–vi $A_{1,1}$; vii $A_{1,3/2}$; viii, ix $A_{1,2}$; x–xii $A_{1,3}$; xiii–xiv $A_{1,4}$; xv $A_{1,157/2}$; xvi $A_{1,79}$; ($m_{1} = 8.46,\,m_{2} = 0.66,\,k_{1} = 7.12,\,\,$$k_{2} = 1,\,k_{3} = 0.821,\,k_{4} = 0.1,\,k_{5} = 0.15,\,d_{1} = 0.4,\,d_{2} = 0.2,\,L = 1.17,\,R = 0.1,\,\,$$\,C = 1.02,b = 0.33,F = 200.$)

Fig. 6

Frequency-amplitude characteristics of displacement $x_{2}$: i, ii $A_{2,0}$; iii $A_{2,1/2}$; iv–vi $A_{2,1}$; vii $A_{2,3/2}$; viii, ix $A_{2,2}$; x–xii $A_{2,3}$; xiii–xiv $A_{2,4}$; xv $A_{2,157/2}$; xvi $A_{2,79}$; ($m_{1} = 8.46,$$m_{2} = 0.66,\,\,$$k_{1} = 7.12,\,$$\,k_{2} = 1,\,$$k_{3} = 0.821,$$k_{4} = 0.1,\,$$k_{5} = 0.15,\,$$d_{1} = 0.4,\,$$d_{2} = 0.2,\,$$L = 1.17,$$R = 0.1,$$\,C = 1.02,$$b = 0.33,$$F = 200$)

Fig. 7

Frequency-amplitude characteristics of current $x_{3}$: i $A_{3,1/2}$; ii–iv $A_{3,1}$; v $A_{3,3/2}$; vi–vii $A_{3,2}$; viii–x $A_{3,3}$; xi–xii $A_{3,4}$; xiii $A_{3,157/2}$; xiv $A_{3,79}$. ($m_{1} = 8.46,$$m_{2} = 0.66,\,\,$$k_{1} = 7.12,\,$$\,k_{2} = 1,\,$$k_{3} = 0.821,$$k_{4} = 0.1,\,$$k_{5} = 0.15,\,$$d_{1} = 0.4,\,$$d_{2} = 0.2,\,$$L = 1.17,$$R = 0.1,$$\,C = 1.02,$$b = 0.33,$$F = 200$)

The harmonic frequency-amplitude curves of displacement $x_{1}$ are shown in Fig. 5. The global view of the constant term is presented in Fig. 5(i). The quantity level of the constant term is about $A_{1,0} \sim 1.6.$ $A_{1,0} \approx 1.31$ is at $\Omega \approx 1.11$. The zoomed view of the constant term is given in Fig. 5(ii). The frequency-amplitudes for the bifurcation of period-1 to period-2 motion are clearly presented. For period-2 motion, the harmonic amplitude of $A_{1,1/2}$ is presented in Fig. 5(iii). For period-1 motion, $A_{1,1/2} = 0$. The appearance of period-2 motion is the saddle-node bifurcation, which is equivalent to the period-doubling bifurcation of period-1 motion. The primary harmonic amplitude versus excitation frequency is presented in Fig. 5(iv). For the symmetric period-1 motion, the frequency-amplitude characteristics is alike the untuned Duffing oscillator. However, in the range of the low frequency, the corresponding primary harmonic amplitudes are presented in Fig. 5(v) and (vi). The bifurcation tree from symmetric period-1 to asymmetric period-2 motion is presented through the primary harmonic frequency-amplitude curves. The harmonic amplitude of $A_{1,3/2}$ is presented In Fig. 5(vii) for period-2 motion. The harmonic amplitude contribution on the stable period-2 motion is quite small comparted to the unstable period-2 motions. The quantity level of harmonic amplitude $A_{1,1/2}$ is a little bit larger than $A_{1,3/2}$. The harmonic amplitude $A_{1,2}$ for the asymmetric period-1 and period-2 motions are presented in Fig. 5(viii) and (ix). For the low-frequency range, the harmonic amplitudes are enlarged for a better illustration, and the bifurcation trees are clearly observed. The subharmonic frequency-amplitude curves for $A_{1,3}$ are presented in Fig. 5(x)–(xii). For the low frequency range, the corresponding harmonic amplitudes $A_{1,3}$ are presented in Fig. 5(xi) and (xii). Compared to the primary harmonic amplitude, the quantity level of the harmonic amplitude $A_{1,3}$ does not drop too much, which implies such harmonic terms will significantly contribute on period-1 and period-2 motions. The peak values of are $A_{1,1} \approx 31.3$ at $\Omega \approx 8.58$ and $A_{1,3} \approx 5.28$ at $\Omega \approx 0.76$. The harmonic amplitude $A_{1,4}$ for the asymmetric period-1 and period-2 motions are presented in Fig. 5(xiii) and (xiv). For the low-frequency range, the quantity level of harmonic amplitude $A_{1,4}$ are the same level as the high-frequency. The harmonic amplitude contribution on the stable period-2 motion is quite small comparted to the unstable period-2 motions. The saddle-node bifurcation at $\Omega \approx 1.15$ has $A_{1,2} \approx 4.26$. At $\Omega \approx 7.68$, there is a saddle-node bifurcation. For harmonic term $A_{1,4}$, peak value is $A_{1,4} \approx 1.14$ at $\Omega \approx 1.15$. The saddle-node bifurcation points $\Omega \approx 7.68$ still has another peak with lower value. Without abundant illustrations, the harmonic amplitude $A_{1,157/2}$ is presented in Fig. 5(xv) with the quantity level of $A_{1,157/2} \sim 10^{ - 12}$. The harmonic amplitude $A_{1,79}$ is presented in Fig. 5 (xvi) for the low frequency range from $A_{1,79} \in (10^{ - 14} ,10^{0} )$. For $\Omega > 0.9$, the quantity level of harmonic amplitude $A_{1,79}$ is already less than $A_{2,79} < 10^{ - 14}$.

The harmonic frequency-amplitude curves for displacement $x_{2}$ are shown in Fig. 6. The similar layout of illustrations is given. The constant term for displacement $x_{2}$ is presented in Fig. 6(i) and the zoomed version for the low frequency range is presented in Fig. 6(ii). The centers of periodic motion off the corresponding local origins are different. The harmonic amplitude of $A_{2,1/2}$ for period-2 motion is presented in Fig. 6(iii). The primary harmonic amplitude versus excitation frequency is presented in Fig. 6(iv). The primary harmonic amplitudes for the tuned mass damper are much higher than the Duffing oscillator. However, for the low frequency range, the harmonic frequency-amplitude curves for the tuned mass damper with the Duffing oscillators are kind of similarity, and the quantity levels of the harmonic amplitudes are almost same, as shown in Fig. 6(v) and (vi). The harmonic amplitude of $A_{2,3/2}$ for the period-2 motion is presented in Fig. 6(vii). The quantity levels of harmonic amplitudes $A_{2,1/2}$ is almost same as $A_{2,3/2}$. The harmonic amplitude $A_{2,2}$ for the asymmetric period-1 and period-2 motions are presented in Fig. 6(viii) and (ix). The quantity level of the harmonic amplitude $A_{2,2}$ is much higher than the harmonic amplitude $A_{1,2}$. The harmonic frequency-amplitude curves for $A_{2,3}$ are presented in Fig. 6(x)–(xii). For the low frequency range, the corresponding harmonic amplitudes $A_{2,3}$ are presented in Fig. 6(xi) and (xii), which are almost like the harmonic amplitude $A_{1,3}$. Compared to the primary harmonic amplitude, the quantity level of the harmonic amplitude $A_{2,3}$ drop dramatically for the high frequency range, but for the low-frequency range, such harmonic terms will significantly contribute on period-1 and period-2 motions compared to the primary harmonic term. The peak values of are $A_{2,1} \approx 71.8$ at $\Omega \approx 8.58$ and $A_{2,3} \approx 14.1$ at $\Omega \approx 0.76$. The harmonic amplitude $A_{2,4}$ for the asymmetric period-1 and period-2 motions are presented in Fig. 6(xiii) and (xiv). For the low-frequency range, the quantity level of harmonic amplitude $A_{2,4}$ are the same level as the high-frequency. The peak value of $A_{2,2} \approx 14.7$ at $\Omega \approx 2.87$ is a saddle-node bifurcation. Another peak exists at $\Omega \approx 7.68$. For the peak value, $A_{2,4} \approx 3.03$ at $\Omega \approx 0.81$. Without abundant illustrations, the harmonic amplitude $A_{2,157/2}$ is presented in Fig. 6(xv) with the quantity level of $A_{2,157/2} \sim 10^{ - 12}$. The harmonic amplitude $A_{2,79}$ is presented in Fig. 6(xvi) for the low frequency range from $A_{2,79} \in (10^{ - 14} ,10^{0} )$. For $\Omega > 0.9$, the quantity level of harmonic amplitude $A_{2,79}$ is already less than $A_{2,79} < 10^{ - 14}$.

The harmonic frequency-amplitude curves for current $x_{3}$ are shown in Fig. 7. Constant terms of $x_{3}$ for all the motions are zero,$A_{3,0} = 0$. The harmonic amplitude of $A_{3,1/2}$ for period-2 motion is presented in Fig. 7(i). The primary harmonic amplitude $A_{3,1}$ for the current is presented in Fig. 7(ii). For the low frequency range, the harmonic frequency-amplitude curves are zoomed in Fig. 7(iii) and (iv). The harmonic amplitude of $A_{3,3/2}$ for the period-2 motion is presented in Fig. 7(v). The quantity levels of harmonic amplitudes $A_{3,3/2}$ is much higher than $A_{3,1/2}$. The harmonic amplitude $A_{3,2}$ for the asymmetric period-1 and period-2 motions are presented in Fig. 7(vi) and (vii). The harmonic frequency-amplitude curves for the current $A_{3,3}$ are presented in Fig. 7(viii)-(x). For the low frequency range, the corresponding harmonic amplitudes $A_{3,3}$ are presented in Fig. 7(ix) and (x). Compared to the primary harmonic amplitude, the quantity level of the harmonic amplitude $A_{3,3}$ drop dramatically for the high frequency range, but for the low-frequency range, the harmonic amplitude $A_{3,3}$ has the same quantity level of the primary harmonic amplitude $A_{3,1}$. The peak values of are $A_{3,1} \approx 9.28$ at $\Omega \approx 8.58$ and $A_{3,3} \approx 2.46$ at $\Omega \approx 0.29$. The harmonic amplitude $A_{3,4}$ for the asymmetric period-1 and period-2 motions are presented in Fig. 7(xi) and (xii). For the low-frequency range, the quantity level of harmonic amplitude $A_{3,4}$ are little bit higher than the high-frequency. The peak value of $A_{3,4} \approx 0.42$ at $\Omega \approx 0.81$ is also a saddle-node bifurcation. The peak at $\Omega \approx 7.68$ is another saddle-node bifurcation. The peak value of $A_{3,4} \approx 0.42$ at $\Omega \approx 0.81$. Similarly, without abundant illustrations, the harmonic amplitude $A_{3,157/2}$ is presented in Fig. 7(xiii) with the quantity level of $A_{3,157/2} \sim 10^{ - 13}$. The harmonic amplitude $A_{3,79}$ is presented in Fig. 7(xiv) for the low frequency range from $A_{3,79} \in (10^{ - 14} ,10^{ - 3} )$. For $\Omega > 0.9$, the quantity level of harmonic amplitude $A_{3,79}$ is already less than $A_{3,79} < 10^{ - 14}$.

5 Numerical illustrations

Numerical illustrations of stable symmetric period-1 to period-2 motions are carried out through a numerical integration method. The initial conditions of numerical illustrations are obtained from the semi-analytical predictions. Phase trajectories and harmonic amplitudes and harmonic phases of the corresponding periodic motions are presented. In the following plots, the circular symbols and solid curves are for analytical and numerical results, respectively. The blue symbol is for initial condition and labeled with acronyms “I.C”. For asymmetric motions, the paired asymmetric periodic motions are depicted in black and red curves.

In Fig. 8, Two stable symmetric period-1 motions are presented for $\Omega \approx 5.0$ and $\Omega \approx 0.83$. The trajectories for two oscillators and the circuit of symmetric period-1 motion at $\Omega \approx 5.0$ are shown in Fig. 8 (i)–(iii). The initial conditions are $(x_{10} ,y_{10} ) \approx ( - 0.0149, - 4.9287),$ $(x_{20} ,y_{20} ) \approx (0.0434,0.1721),$ and $(x_{30} ,y_{30} ) \approx (5.83 \times 10^{ - 3} ,0.022)$. Such a symmetric periodic motion is very simple. The trajectories of symmetric period-1 motion for the two sub-oscillators and the circuit at $\Omega \approx 0.83$ are presented in Fig. 8 (iv)–(vi). The initial conditions are $(x_{10} ,y_{10} ) \approx ( - 0.8896,1.7029),$ $(x_{20} ,y_{20} ) \approx ( - 1.3020, - 21.5140)$ and $(x_{30} ,y_{30} ) \approx (1.9807,$ $- 6.2005)$. The symmetric period-1 motion becomes more complex compared to the high frequency. The numerical and analytical results match very well.

Fig. 8

Symmetric stable period-1 motions: i–iii phase trajectories $(x_{i} ,y_{i} ),\,(i = 1,2,3)$ at $\Omega \approx 5.0$ with initial conditions $(x_{10} ,y_{10} ) \approx ( - 0.0149, - 4.9287)$, $(x_{20} ,y_{20} ) \approx (0.0434,0.1721)$ and $(x_{30} ,y_{30} ) \approx (5.83 \times 10^{ - 3} ,0.022)$; iv–vi phase trajectories $(x_{i} ,y_{i} ),\,(i = 1,2,3)$ at $\Omega \approx 0.83$ with initial conditions $(x_{10} ,y_{10} ) \approx ( - 0.8896,1.7029)$, $(x_{20} ,y_{20} ) \approx ( - 1.3020, - 21.5140)$ and $(x_{30} ,y_{30} ) \approx (1.9807, - 6.2005)$. ($m_{1} = 8.46,$$m_{2} = 0.66,\,\,$$k_{1} = 7.12,\,$$\,k_{2} = 1,\,$$k_{3} = 0.821,$$k_{4} = 0.1,\,$$k_{5} = 0.15,\,$$d_{1} = 0.4,\,$$d_{2} = 0.2,\,$$L = 1.17,$$R = 0.1,$$\,C = 1.02,$$b = 0.33,$$F = 200$)

From the semi-analytical solutions, phase trajectories and harmonic amplitude spectrums of stable periodic motions for symmetric period-1 to asymmetric period-2 motions are presented in Fig. 9–11 for $\Omega \approx 0.75,0.74,0.737.$

Fig. 9

Symmetric stable period-1 motions at $\Omega \approx 0.75$: i–iii phase trajectories $(x_{i} ,y_{i} ),\,(i = 1,2,3)$ with initial conditions $(x_{10} ,y_{10} ) \approx ( - 3.722,6.324)$, $(x_{20} ,y_{20} ) \approx ( - 14.887,23.162)$ and $(x_{30} ,y_{30} ) \approx ( - 13945,1.910)$; iv–vi harmonic amplitudes spectrums $A_{i,k} ,\,(i = 1,2,3)$. ($m_{1} = 8.46,$$m_{2} = 0.66,\,\,$$k_{1} = 7.12,\,$$\,k_{2} = 1,\,$$k_{3} = 0.821,$$k_{4} = 0.1,\,$$k_{5} = 0.15,\,$$d_{1} = 0.4,\,$$d_{2} = 0.2,\,$$L = 1.17,$$R = 0.1,$$\,C = 1.02,$$b = 0.33,$$F = 200$)

Fig. 10

Asymmetric stable period-1 motions at $\Omega \approx 0.74$: i–iii phase trajectories $(x_{i} ,y_{i} ),\,(i = 1,2,3)$ with initial conditions $(x_{10}^{b} ,y_{10}^{b} ) \approx ( - 1.328,6.112)$, $(x_{20}^{b} ,y_{20}^{b} ) \approx ( - 11.485,19.964)$, $(x_{30}^{b} ,y_{30}^{b} ) \approx ( - 1.452,1.321)$ and $(x_{10}^{r} ,y_{10}^{r} ) \approx ( - 2.770,4.046)$, $(x_{20}^{r} ,y_{20}^{r} ) \approx ( - 9.458,29.966)$, $(x_{30}^{r} ,y_{30}^{r} ) \approx ( - 1.190,2.716)$; iv–vi harmonic amplitudes spectrums $A_{i,k} ,\,(i = 1,2,3)$. ($m_{1} = 8.46,\,m_{2} = 0.66,\,k_{1} = 7.12,\,\,k_{2} = 1,\,\,k_{3} = 0.821,\,k_{4} = 0.1,\,k_{5} = 0.15,$$d_{1} = 0.4,\,d_{2} = 0.2,\,L = 1.17,\,R = 0.1,\,\,C = 1.02,b = 0.33,F = 200$)

Fig. 11

Asymmetric stable period-2 motions at $\Omega \approx 0.737$: i–iii phase trajectories $(x_{i} ,y_{i} ),\,(i = 1,2,3)$ with initial conditions $(x_{10}^{b} ,y_{10}^{b} ) \approx ( - 0.986,6.331)$, $(x_{20}^{b} ,y_{20}^{b} ) \approx ( - 11.002,18.122)$, $(x_{30}^{b} ,y_{30}^{b} ) \approx ( - 1.401,1.051)$ and $(x_{10}^{r} ,y_{10}^{r} ) \approx ( - 2.933,3.934)$, $(x_{20}^{r} ,y_{20}^{r} ) \approx ( - 8.364,29.311)$,$(x_{30}^{r} ,y_{30}^{r} ) \approx ( - 1.049,2.661)$; iv–vi harmonic amplitudes spectrums $A_{i,k/2} ,\,(i = 1,2,3)$. ($m_{1} = 8.46,$$m_{2} = 0.66,\,\,$$k_{1} = 7.12,\,$$\,k_{2} = 1,\,$$k_{3} = 0.821,$$k_{4} = 0.1,\,$$k_{5} = 0.15,\,$$d_{1} = 0.4,\,$$d_{2} = 0.2,\,$$L = 1.17,$$R = 0.1,$$\,C = 1.02,$$b = 0.33,$$F = 200$)

In Fig. 9, phase trajectories and harmonic amplitude spectrums of a stable symmetric period-1 motion at $\Omega \approx 0.75$ are presented. The initial condition is $(x_{1} ,y_{1} ) \approx ( - 3.722,6.324)$, $(x_{2} ,y_{2} ) \approx ( - 14.887,23.162)$ and $(x_{3} ,y_{3} ) \approx ( - 13945,1.910)$. The phase trajectory has one small cycle on the left and right sides with a large cycle. The trajectory symmetry is clearly observed, and the two same small cycles are asymmetric. The even harmonic terms are all zero for symmetric motions. For the Duffing oscillator, the main harmonic amplitudes of displacement $x_{1}$ are $A_{1,1} \approx 4.3801$, $A_{1,3} \approx 4.6846$, $A_{1,5} \approx 1.3695$, $A_{1,7} \approx 0.6622$, $A_{1,9} \approx 0.1337$, $A_{1,11} \approx 0.1278$, $A_{1,13} \approx 0.0409$ and $A_{1,k} \in (10^{ - 14} ,10^{ - 4} )$ for $k = 27,28, \cdots ,79$ with $A_{1,79} \sim 10^{ - 14} .$ For The tuned mass damper, the main harmonic amplitudes of displacement $x_{2}$ are $A_{2,1} \approx 5.3583$, $A_{2,3} \approx 11.2622$, $A_{2,5} \approx 3.8725$, $A_{2,7} \approx 0.4840$, $A_{2,9} \approx 0.0708$, $A_{2,11} \approx 0.2866$, $A_{2,13} \approx 0.2191$ and $A_{2,k} \in (10^{ - 14} ,10^{ - 4} )$ for $k = 35,36,37, \cdots ,79$ with $A_{2,79} \sim 10^{ - 14} .$ For the circuit, the main harmonic amplitudes of the current $x_{3}$ are $A_{3,1} \approx 1.3664$, $A_{3,3} \approx 1.7285$, $A_{3,5} \approx 0.5278$, $A_{3,7} \approx 0.0640$ and $A_{3,k} \in (10^{ - 14} ,10^{ - 4} )$ for $k = 29,30, \cdots ,79$ with $A_{3,79} \sim 10^{ - 14} .$ Such a symmetric period-1 motion need 39 terms to keep the accuracy of $\varepsilon \approx 10^{ - 14}$.

From the bifurcation analysis, $\Omega < \Omega_{cr} \approx 0.743$, the symmetric period-1 motion becomes asymmetric period-1 motions. Thus, phase trajectories and harmonic amplitude spectrums of the paired asymmetric stable period-1 motion are presented in Fig. 10 for $\Omega \approx 0.74$ through black and red curves. The initial conditions of the paired asymmetric period-1 motions are $(x_{10}^{b} ,y_{10}^{b} ) \approx ( - 1.328,6.112)$, $(x_{20}^{b} ,y_{20}^{b} ) \approx ( - 11.485,19.964)$, $(x_{30}^{b} ,y_{30}^{b} ) \approx ( - 1.452,1.321)$ and $(x_{10}^{r} ,y_{10}^{r} ) \approx ( - 2.770,4.046)$, $(x_{20}^{r} ,y_{20}^{r} ) \approx ( - 9.458,29.966)$, $(x_{30}^{r} ,y_{30}^{r} ) \approx ( - 1.190,2.716)$. The symmetry of the two paired asymmetric period-1 motions is clearly observed. The small cycles on the right and left side are different. For the Duffing oscillator, the constant terms are with $a_{1,0}^{b} = - a_{1,0}^{r} \approx 0.2668$, the main harmonic amplitudes of displacement $x_{1}$ are $A_{1,1} \approx 5.3177$, $A_{1,2} \approx 0.1614$, $A_{1,3} \approx 3.3982$, $A_{1,4} \approx 0.4642$, $A_{1,5} \approx 1.5411$, $A_{1,6} \approx 0.0447$, $A_{1,7} \approx 0.3889$ and $A_{1,k} \in (10^{ - 14} ,10^{ - 1} )$ for $k = 8,9, \cdots ,80$ with $A_{1,80} \sim 10^{ - 14}$. For the tuned mass damper, the constant terms satisfy $a_{2,0}^{B} = - a_{2,0}^{R} \approx 0.1437$, the main harmonic amplitudes of displacement $x_{2}$ are $A_{2,1} \approx 6.1996$, $A_{2,2} \approx 0.5160$, $A_{2,3} \approx 9.4792$, $A_{2,4} \approx 1.8232$, $A_{2,5} \approx 2.8184$, $A_{2,6} \approx 0.4664$, $A_{2,7} \approx 0.2322$, $A_{2,8} \approx 0.0762$ and $A_{2,k} \in (10^{ - 14} ,10^{ - 2} )$ for $k = 9,10, \cdots ,80$ with $A_{2,80} \sim 10^{ - 14}$. For current $x_{3}$, the constant terms are $a_{3,0}^{B} = - a_{3,0}^{R} = 0$. The main harmonic amplitudes are $A_{3,1} \approx 1.4647$, $A_{3,2} \approx 0.1067$, $A_{3,3} \approx 1.4626$, $A_{3,4} \approx 0.2583$, $A_{3,5} \approx 0.3848$, $A_{3,6} \approx 0.0624$, $A_{3,7} \approx 0.0307$ and $A_{3,k} \in (10^{ - 14} ,10^{ - 4} )$ for $k = 8,9, \cdots ,80$ with $A_{2,80} \sim 10^{ - 14}$. For asymmetric period-1 motion, the harmonic amplitudes for even harmonic terms are non-zero., which cause the asymmetry of the paired asymmetric period-1 motions.

For $\Omega < \Omega_{cr} \approx 0.7377$, the asymmetric period-2 motion exists. In Fig. 11, phase trajectories and harmonic amplitude spectrums of the paired asymmetric stable period-2 motions are presented for $\Omega \approx 0.737$. The initial conditions of two paired asymmetric period-2 motions are $(x_{10}^{b} ,y_{10}^{b} ) \approx ( - 0.986,6.332)$, $(x_{20}^{b} ,y_{20}^{b} ) \approx ( - 11.002,18.122)$, $(x_{30}^{b} ,y_{30}^{b} ) \approx ( - 1.401,1.051)$ and $(x_{10}^{r} ,y_{10}^{r} ) \approx ( - 2.933,3.934)$, $(x_{20}^{r} ,y_{20}^{r} ) \approx ( - 8.364,29.311)$, $(x_{30}^{r} ,y_{30}^{r} ) \approx ( - 1.049,2.661)$. The phase trajectories of the asymmetric period-2 motions double the trajectories of asymmetric period-1 motions. The skew symmetry of the two asymmetric period-2 motions is observed. For the Duffing oscillator, the constant terms $a_{1,0}^{B} = - a_{1,0}^{R} \approx 0.3233$, the main harmonic amplitudes of displacement $x_{1}$ for the asymmetric period-2 motion are $A_{1,1/2} \approx 0.0422$, $A_{1,1} \approx 5.4295$, $A_{1,3/2} \approx 1.112 \times 10^{ - 3}$, $A_{1,2} \approx 0.2118$, $A_{1,5/2} \approx 0.0119$, $A_{1,3} \approx 3.2224$, $A_{1,7/2} \approx 0.0171$, $A_{1,4} \approx 0.5704$ and $A_{1,k/2} \in (10^{ - 14} ,10^{ - 4} )$ for $k = 9,10, \cdots ,160$ with $A_{1,80} \sim 10^{ - 14}$. For the tuned mass damper, the constant term is with $a_{2,0}^{b} = - a_{2,0}^{r} \approx 0.1437$, the main harmonic amplitudes of displacement $x_{2}$ are $A_{2,1/2} \approx 0.0371$, $A_{2,1} \approx 6.3313$, $A_{2,3/2} \approx 0.0923$, $A_{2,2} \approx 0.6588$, $A_{2,5/2} \approx 0.0549$, $A_{2,3} \approx 9.2262$, $A_{2,7/2} \approx 0.0913$, $A_{2,4} \approx 2.1362$ and $A_{2,k/2} \in (10^{ - 14} ,10^{0} )$ for $k = 9,10, \cdots ,160$ with $A_{2,80} \sim 10^{ - 14}$. For 60 harmonic terms, an approximate solution has the accuracy of $A_{2,30} \sim 10^{ - 4}$. For current $x_{3}$, the constant terms are zero, i.e.,$a_{3,0}^{b} = - a_{3,0}^{r} = 0$. The main harmonic amplitudes are $A_{3,1/2} \approx 9.1805 \times 10^{ - 4}$, $A_{3,1} \approx 1.4627$, $A_{3,3/2} \approx 0.0365$, $A_{3,2} \approx 0.1369$, $A_{3,5/2} \approx 9.3275 \times 10^{ - 3}$, $A_{3,3} \approx 1.4260$, $A_{3,7/2} \approx 0.0134$, $A_{3,4} \approx 0.3029$ and $A_{3,k/2} \in (10^{ - 14} ,10^{ - 1} )$ for $k = 8,9, \cdots ,160$ with $A_{1,80} \sim 10^{ - 14}$. With 48 harmonic terms, an approximate solution has the accuracy of $A_{3,24} \sim 10^{ - 4}$.

6 Conclusions

In this paper, bifurcation routes of periodic motions in an electromagnetic tuned Duffing oscillator were studied through the implicit mapping method. On the bifurcation routes, there exist one branch of symmetric period-1 motions and 4 branches of asymmetric period-1 motions, one branch of the four asymmetric period-1 motion branches with asymmetric period-2 motion to chaos was obtained. The frequency-amplitude characteristics of symmetric period-1 to asymmetric period-2 motions were obtained through the finite Fourier series analysis. The simple and complex periodic motions were illustrated for different frequencies. The symmetric period-1 to asymmetric period-2 motions on the bifurcation tree were also illustrated from the semi-analytical results. For low frequency, periodic motions need more harmonic terms to give accurate approximate solutions. Peak values of current also occur in the low frequency range, which means higher energy harvesting and vibration reduction efficiency.

Appendix

The components of DP matrix in Eq. (10) are given as follows.

$$ \begin{aligned} \frac{{\partial g_{1,k} }}{{\partial x_{1,k} }} =& 1,\,\frac{{\partial g_{1,k} }}{{\partial x_{2,k} }} = 0,\,\frac{{\partial g_{1,k} }}{{\partial x_{3,k} }} = 0,\\ \frac{{\partial g_{1,k} }}{{\partial y_{1,k} }} =& - \frac{h}{2}, \frac{{\partial g_{1,k} }}{{\partial y_{2,k} }} = 0,\,\frac{{\partial g_{1,k} }}{{\partial y_{3,k} }} = 0; \hfill \\ \frac{{\partial g_{2,k} }}{{\partial x_{1,k} }} =& 0,\,\frac{{\partial g_{2,k} }}{{\partial x_{2,k} }} = 1,\,\frac{{\partial g_{2,k} }}{{\partial x_{3,k} }} = 0,\\ \frac{{\partial g_{2,k} }}{{\partial y_{1,k} }} =& 0,\,\frac{{\partial g_{2,k} }}{{\partial y_{2,k} }} = - \frac{h}{2},\,\frac{{\partial g_{2,k} }}{{\partial y_{3,k} }} = 0; \hfill \\ \frac{{\partial g_{3,k} }}{{\partial x_{1,k} }} =& 0,\,\frac{{\partial g_{3,k} }}{{\partial x_{2,k} }} = 0,\,\frac{{\partial g_{3,k} }}{{\partial x_{3,k} }} = 1,\\ \frac{{\partial g_{3,k} }}{{\partial y_{1,k} }} =& 0,\,\frac{{\partial g_{3,k} }}{{\partial y_{2,k} }} = 0,\,\frac{{\partial g_{3,k} }}{{\partial y_{3,k} }} = - \frac{h}{2}; \hfill \\ \frac{{\partial g_{4,k} }}{{\partial x_{1,k} }} =& \tfrac{h}{{2m_{1} }}\{ k_{1} + 3k_{2} [\tfrac{1}{2}(x_{1,k} + x_{1,k - 1} )]^{2} + k_{3} \\ &+ 3k_{4} [\tfrac{1}{2}(x_{2,k} + x_{2,k - 1} ) - \tfrac{1}{2}(x_{1,k} + x_{1,k - 1} )]^{2} \} ; \hfill \\ \frac{{\partial g_{4,k} }}{{\partial x_{2,k} }} =& - \tfrac{h}{{2m_{1} }}\{ k_{3} + 3k_{4} [\tfrac{1}{2}(x_{2,k} + x_{2,k - 1} )\\ & - \tfrac{1}{2}(x_{1,k} + x_{1,k - 1} )]^{2} \} ; \hfill \\ \frac{{\partial g_{4,k} }}{{\partial x_{3,k} }} =& 0,\,\frac{{\partial g_{4,k} }}{{\partial y_{1,k} }} = 1 + \tfrac{h}{{2m_{1} }}(d_{1} + d_{2} ),\\ \frac{{\partial g_{4,k} }}{{\partial y_{2,k} }} = &- \tfrac{{hd_{2} }}{{2m_{1} }},\,\frac{{\partial g_{4,k} }}{{\partial y_{3,k} }} = 0; \hfill \\ \frac{{\partial g_{5,k} }}{{\partial x_{1,k} }} = &- \tfrac{h}{{2(m_{2} + b)}}\{ k_{3} + 3k_{4} [\tfrac{1}{2}(x_{2,k} + x_{2,k - 1} ) \\ &- \tfrac{1}{2}(x_{1,k} + x_{1,k - 1} )]^{2} \} \hfill \\ \frac{{\partial g_{5,k} }}{{\partial x_{2,k} }} =& \tfrac{h}{{2(m_{2} + b)}}\{ k_{3} + 3k_{4} [\tfrac{1}{2}(x_{2,k} + x_{2,k - 1} ) \\ &- \tfrac{1}{2}(x_{1,k} + x_{1,k - 1} )]^{2} \} ; \hfill \\ \frac{{\partial g_{5,k} }}{{\partial x_{3,k} }} =& \tfrac{{hk_{5} }}{{2(m_{2} + b)}},\,\frac{{\partial g_{5,k} }}{{\partial y_{1,k} }} = - \tfrac{{hd_{2} }}{{2(m_{2} + b)}},\\ \frac{{\partial g_{5,k} }}{{\partial y_{2,k} }} = & 1 + \tfrac{{hd_{2} }}{{2(m_{2} + b)}},\,\frac{{\partial g_{5,k} }}{{\partial y_{3,k} }} = 0; \hfill \\ \frac{{\partial g_{6,k} }}{{\partial x_{1,k} }} = & 0,\,\frac{{\partial g_{6,k} }}{{\partial x_{2,k} }} = 0,\,\frac{{\partial g_{6,k} }}{{\partial x_{3,k} }} = \tfrac{h}{2LC},\,\frac{{\partial g_{6,k} }}{{\partial y_{1,k} }} = 0,\\ \frac{{\partial g_{6,k} }}{{\partial y_{2,k} }} =& - \tfrac{{hk_{5} }}{2L},\,\frac{{\partial g_{6,k} }}{{\partial y_{3,k} }} = 1 + \tfrac{hR}{{2L}}; \hfill \\ \end{aligned} $$

(23)

and

$$ \begin{aligned} \frac{{\partial g_{1,k} }}{{\partial x_{1,k - 1} }} =& - 1,\,\frac{{\partial g_{1,k} }}{{\partial x_{2,k - 1} }} = 0,\,\frac{{\partial g_{1,k} }}{{\partial x_{3,k - 1} }} = 0,\\ \frac{{\partial g_{1,k} }}{{\partial y_{1,k - 1} }} = &- \frac{h}{2},\,\frac{{\partial g_{1,k} }}{{\partial y_{2,k - 1} }} = 0,\,\frac{{\partial g_{1,k} }}{{\partial y_{3,k - 1} }} = 0; \\ \frac{{\partial g_{2,k} }}{{\partial x_{1,k - 1} }} =\,& 0,\,\frac{{\partial g_{2,k} }}{{\partial x_{2,k - 1} }} = - 1,\,\frac{{\partial g_{2,k} }}{{\partial x_{3,k - 1} }} =\, 0,\\ \frac{{\partial g_{2,k} }}{{\partial y_{1,k - 1} }} =\,& 0,\,\frac{{\partial g_{2,k} }}{{\partial y_{2,k - 1} }} = - \frac{h}{2},\,\frac{{\partial g_{2,k} }}{{\partial y_{3,k - 1} }} =\, 0; \\ \frac{{\partial g_{3,k} }}{{\partial x_{1,k - 1} }} =\,& 0,\,\frac{{\partial g_{3,k} }}{{\partial x_{2,k - 1} }} =\, 0,\,\frac{{\partial g_{3,k} }}{{\partial x_{3,k - 1} }} = - 1,\\ \frac{{\partial g_{3,k} }}{{\partial y_{1,k - 1} }} =\,& 0,\,\frac{{\partial g_{3,k} }}{{\partial y_{2,k - 1} }} =\, 0,\,\frac{{\partial g_{3,k} }}{{\partial y_{3,k - 1} }} = - \frac{h}{2}; \\ \frac{{\partial g_{4,k} }}{{\partial x_{1,k - 1} }} =& \tfrac{h}{{2m_{1} }}\{ k_{1} + 3k_{2} [\tfrac{1}{2}(x_{1,k} + x_{1,k - 1} )]^{2} + k_{3} \\ &+ 3k_{4} [\tfrac{1}{2}(x_{2,k} + x_{2,k - 1} ) - \tfrac{1}{2}(x_{1,k} + x_{1,k - 1} )]^{2} \} , \\ \frac{{\partial g_{4,k} }}{{\partial x_{2,k - 1} }} =& - \tfrac{h}{{2m_{1} }}\{ k_{3} + 3k_{4} [\tfrac{1}{2}(x_{2,k} + x_{2,k - 1} )\\ & - \tfrac{1}{2}(x_{1,k} + x_{1,k - 1} )]^{2} \} , \\ \frac{{\partial g_{4,k} }}{{\partial x_{3,k - 1} }} =\,& 0,\,\frac{{\partial g_{4,k} }}{{\partial y_{1,k - 1} }} = - 1 + \tfrac{h}{{2m_{1} }}(d_{1} + d_{2} ),\\ \frac{{\partial g_{4,k} }}{{\partial y_{2,k - 1} }} =& - \tfrac{{hd_{2} }}{{2m_{1} }},\,\frac{{\partial g_{4,k} }}{{\partial y_{3,k - 1} }} =\, 0; \\ \frac{{\partial g_{5,k} }}{{\partial x_{1,k - 1} }} = &- \tfrac{h}{{2(m_{2} + b)}}\{ k_{3} + 3k_{4} [\tfrac{1}{2}(x_{2,k} + x_{2,k - 1} ) \\ &- \tfrac{1}{2}(x_{1,k} + x_{1,k - 1} )]^{2} \} ; \\ \frac{{\partial g_{5,k} }}{{\partial x_{2,k - 1} }} =& \tfrac{h}{{2(m_{2} + b)}}\{ k_{3} + 3k_{4} [\tfrac{1}{2}(x_{2,k} + x_{2,k - 1} ) \\ &- \tfrac{1}{2}(x_{1,k} + x_{1,k - 1} )]^{2} \} ; \\ \frac{{\partial g_{5,k} }}{{\partial x_{3,k - 1} }} =& \tfrac{{hk_{5} }}{{2(m_{2} + b)}},\,\frac{{\partial g_{5,k} }}{{\partial y_{1,k - 1} }} = - \tfrac{{hd_{2} }}{{2(m_{2} + b)}},\\ \frac{{\partial g_{5,k} }}{{\partial y_{2,k - 1} }} =& - 1 + \tfrac{{hd_{2} }}{{2(m_{2} + b)}},\,\frac{{\partial g_{5,k} }}{{\partial y_{3,k - 1} }} =\, 0; \\ \frac{{\partial g_{6,k} }}{{\partial x_{1,k - 1} }} =\,& 0,\,\frac{{\partial g_{6,k} }}{{\partial x_{2,k - 1} }} =\, 0,\,\frac{{\partial g_{6,k} }}{{\partial x_{3,k - 1} }} = \tfrac{h}{2LC},\\ \frac{{\partial g_{6,k} }}{{\partial y_{1,k - 1} }} =& 0,\,\frac{{\partial g_{6,k} }}{{\partial y_{2,k - 1} }} = \tfrac{{hk_{5} }}{2L},\,\frac{{\partial g_{6,k} }}{{\partial y_{3,k} }} = - 1 + \tfrac{hR}{{2L}}. \\ \end{aligned} $$

(24)