Dynamics behavior of a novel infectious disease model considering population mobility on complex network

Abstract

To describe the impact of population mobility between different cities on the spread of infectious disease, a new infectious disease complex dynamical model is proposed. Moreover, we obtain the basic regeneration number of the model based on applied spectral analysis. And the disease-free equilibrium points and local equilibrium points of the model are discussed, and it is found that two kind equilibrium points are globally asymptotically stable. In addition, the final scale of the presented model is analyzed and an expression for the final scale is obtained. Furthermore, we analyze the impact of population mobility on the spread of infectious diseases via numerical simulations. Our results reveal that the increase of population mobility between two cities leads to more intense disease transmission. Finally, the influence of media effects on the spread of infectious diseases is investigated. It is shown that the spread of diseases is suppressed because of the increase of individual's self-isolation rate. Therefore, controlling the population mobility is an effective initiative to curb outbreaks of infectious diseases throughout the network. These results can provide a theoretical basis for preventing and controlling the spreading of infectious diseases.

1 Introduction

Infectious diseases are transmitted by pathogenic (micro) organisms. The spread of infectious diseases is both covert and sudden. Infectious diseases have always caused great harm to human health and caused great losses to social and economic development. The global outbreak of influenza in 1918 [1, 2], with a death toll of 20 million, the outbreak of SARS virus [3, 4] in 2003, and the global outbreak of COVID-19 [5, 6] in 2019 all posed a great threat to human health. In the last few decades, the study of complex networks has gradually become a hot issue in the field of complexity disciplines. Scholars have made significant contributions to the study in these areas such as transportation, social [7,8,9], financial [10,11,12] and biological [13, 14] networks. As research into complex networks have continued, the spreading of computer viruses in computer networks, contagious diseases in social networks can have an effect on the development of human society [15]. Therefore, the behavior of transmission dynamics on complex networks has become one of the research directions of great interest.

The dynamics propagation on complex network has achieved some very important studies in recent decades [16,17,18,19,20,21,22,23]. Due to the complex topology of the network, the relationships between individuals can be accurately depicted. Study on the transmission of infectious diseases on complex networks mostly focuses on static networks [24,25,26]. Static networks are effective tools for studying short-term infectious diseases [27], but for some infectious diseases with a long duration, population mobility factors are likely to change the topological structure of the network [28,29,30]. Hence, studying the spread of infectious diseases on complex dynamic networks is of great significance. Jin et al. designed an infectious disease model that incorporates population statistics into complex network theory to study the impact of population statistics on population distribution [31]. Pan et al. established the community structure of the SIS epidemic model and discussed the impact of population statistics on disease transmission [32]. Also, authors proposed an infectious diseases model that considers the demographic characteristics on a complex network. They study the spread of the dynamic of two different infectious diseases [33]. Therefore, it is very meaningful to study the impact of population mobility on complex network.

In recent years, researchers have increasingly considered the impact of population mobility on the spread of diseases. For example, Ref. [34]. proposed a spatiotemporal model that estimates the causal effect of changes in community mobility (intervention) on infection rates. Researchers used mobile phone data to describe the connectivity among areas and study the impact of this connectivity on the spread of COVID-19 during the second wave of the pandemic in 2020 [35]. Authors mutually compared time series of covid-19-related data and mobility data across Belgium’s 43 arrondissements. They concluded that there is a strong correlation between physical movement of people and viral spread in the early stage of the sars-cov-2 epidemic in Belgium, though its strength weakens as the virus spreads [36]. Ref. [37] investigated the bi-directional relationship between human mobility and COVID-19 spread across U.S. counties during the early phase of the pandemic when infection rates were stabilizing and activity-travel behavior reflected a fairly steady return to normal following the drastic changes observed during the pandemic’s initial shock. Authors studied the interaction between disease transmission and disease related awareness transmission, and then proposed a new coupled disease transmission model on a two-layer multiple network [38, 39]. Subrata Ghosh proposed a deterministic compartmental model of infectious disease that considers the test kits as an important ingredient for the suppression and mitigation of epidemics. Furthermore, they consider heterogeneous networks to study the impact of long and short-distance human migration among the patches [40].

However, these existing works are inadequate in fully describing the realistic roles of the population mobility on complex network. In real life, the population mobility plays crucial role in the spreading of infectious disease. Most importantly, individuals typically move not only on single-layer networks, but also on more complex multi-layer networks. According to the above considerations, this paper focuses on studying the impact of population mobility on disease transmission on a two-layer network.

The paper is organized as follows. In Sect. 2, an infectious disease model is presented that takes into account population movements between two cities. Section 3 investigates the basic regeneration number and the global stability of the model using the next-generation matrix scheme. Section 4 verifies the theoretical results through numerical simulation. Finally, Sect. 5 summarizes the study.

2 Model formulation

As is well known, the spread of infectious diseases between two cities due to floating populations become more complex. In the following, let $N_{i,k} \left( t \right)$, $S_{i,k} \left( t \right),S_{{q_{i,k} }} \left( t \right),E_{i,k} \left( t \right),I_{i,k} \left( t \right),Q_{i,k} \left( t \right),R_{i,k} \left( t \right)$ denote the number of individuals whose states are $N$, $S,S_{q} ,E,I,Q,R$ of degree $k$ in city $i$ at time $t$.

And the total human population size is denoted as $\left( N \right)$, and the total population $N$ is divided into six subclasses: people who are easily infected are called susceptible people $\left( S \right)$, susceptible individuals have a sense of self-isolation, and those who adopt self-isolation measures are referred to as self-quarantine susceptible $\left( {S_{q} } \right)$, infected individuals in the incubation period are called exposed $\left( E \right)$, people who are infected with the virus and have symptoms are called infected individuals $\left( I \right)$, exposed and infected individuals separated from uninfected individuals are referred to as quarantined $\left( Q \right)$, the group of patients including exposed, infected and quarantined have undergone treatment and rehabilitation are called recovered $\left( R \right)$.

For the total human population, we suppose that $N_{i,k} \left( t \right) = S_{i,k} \left( t \right) + S_{{q_{i,k} }} \left( t \right) + E_{i,k} \left( t \right) + I_{i,k} \left( t \right) + Q_{i,k} \left( t \right) + R_{i,k} \left( t \right)$.

First, some assumptions and symbols are given by

• (1) It is assumed that there are no independent individuals. That is to say, an individual must contact with people. And an individual can be associated with $m$ individuals at most. That is $k \in \left\{ {1, \cdots m} \right\},i \in \left\{ {1,2} \right\}.$ An individual only contact with a maximum of m individuals.

• (2) We assume the following equation holds:

  $$\begin{aligned} \sum\limits_{k = 1}^{m} {S_{i,k} \left( t \right)} &= S_{i} \left( t \right),\sum\limits_{k = 1}^{m} {S_{{q_{i,k} }} \left( t \right) = S_{{q_{i} }} \left( t \right),\sum\limits_{k = 1}^{m} {E_{i,k} \left( t \right)} }\\ & = E_{i} \left( t \right),\sum\limits_{k = 1}^{m} {I_{i,k} \left( t \right) = I_{i} \left( t \right),}\end{aligned} $$
  $$ \begin{aligned}&\sum\limits_{k = 1}^{m} {Q_{i,k} \left( t \right) = Q_{i} \left( t \right)} ,\\ &\sum\limits_{k = 1}^{m} {R_{i,k} \left( t \right)} = R_{i} \left( t \right),\sum\limits_{k = 1}^{m} {N_{i,k} \left( t \right) = N_{i} } \left( t \right). \end{aligned}$$

  These equations represent the sum of individuals with different degrees as all individuals in city $i$.

• (3) Suppose that all newborns are susceptible. And newborns enter the city $i$ with a probability of $\delta_{i,k}$.The number of newborn individual in city $i$ is $A_{i}$ at each step time.

• (4) The network’s nodes do not have multiple edges and self-loop. This implies that we consider the contact number between different individuals is single. In addition, any individual cannot be infected unless interconnecting other individuals.

• (5) The probability of a susceptible individual will be infected by exposed in city $i$ is $\lambda_{i}$. The probability of a susceptible individual will be infected by infectious in city $i$ is $\beta_{i}$. And the natural mortality rate of $d_{1}$, the mortality rate due to disease is $d_{2}$. We assume that $q$ stands for self-isolation rate,$q_{1}$ represents the probability that the self-quarantined individuals will be released from isolation. We define $\xi_{i}$ as the rate of population movement from city $i$ to another one. Let $\gamma_{i}^{1}$ represents the recovery rate of quarantined individuals, let $\gamma_{i}^{2}$ represents the recovery rate of infectious. And,$\alpha_{i}^{1}$ and $\alpha_{i}^{2}$ represent the isolation rate of exposed individuals and the isolation rate of infectious, respectively. Furthermore, the conversion rate from the exposed to infectious is $\varepsilon_{i}$ in city $i$. The number of individuals contacted in city $i$ due to population mobility is $\omega_{i}$.

• (6) The proportion of individuals whose degree is $k$ in city $i$ can be defined as $p_{i,k} = N_{i,k} /N_{i}$.The probability of randomly selecting an edge connecting to an infective neighbor is given by

  $$ \theta_{i} \left( t \right) = \left( {\sum\limits_{k = 1}^{m} {kp_{i,k} I_{i,k} \left( t \right)/N_{i,k} \left( t \right)} } \right)/\left\langle {k_{i} } \right\rangle = \left( {\sum\limits_{k = 1}^{m} {kI_{i,k} \left( t \right)} } \right)/\left( {\sum\limits_{k = 1}^{m} {kN_{i,k} \left( t \right)} } \right) $$

  (1)

  And $\left\langle {k_{i} } \right\rangle = \sum\limits_{k = 1}^{m} {kp_{i,k} ,i = 1,2.}$

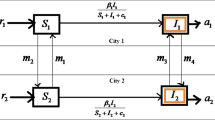
Figure 1 shows the propagation mechanism of the epidemic. The blue and green boxes represent city 1 and city 2, respectively. City 1 and city 2 contain different individuals that are connected through human contacts. The blue and green lines represent the individual’s states that change in different cities due to population mobility. The parameters are marked next to the line bar, what are the paths they represent for a group to transition from one state to another (Table 1).

Fig. 1

The propagation mechanism of the two-city model with population mobility

Table 1 Explanation of main symbols

Based on the above assumptions and mechanism of transmission, the infectious disease model taking into account the population mobility is established as follows

$$ \left\{ \begin{gathered} S_{i,k}^{\prime } = \delta_{i,k} A_{i} + q_{1} S_{{q_{i,k} }} - \left( {q + d_{1} } \right)S_{i,k} - \left( {\beta_{i} + \lambda_{i} } \right)k\left( {1 - \xi_{i} } \right)\theta_{i} \left( t \right)S_{i,k} - \omega_{i} k\xi_{i} \left( {\lambda_{{i{\prime} }} + \beta_{{i{\prime} }} } \right)\left( {\frac{{I_{{i{\prime} }} + E_{{i{\prime} }} }}{{N_{{i{\prime} }} }}} \right)S_{i,k} \hfill \\ S_{{q_{i,k} }}^{\prime } = qS_{i,k} - d_{1} S_{{q_{i,k} }} - q_{1} S_{{q_{i,k} }} \hfill \\ E_{i,k}^{\prime } = \left( {\beta_{i} + \lambda_{i} } \right)k\theta_{i} \left( t \right)\left( {1 - \xi_{i} } \right)S_{i,k} + \omega_{i} k\xi_{i} \left( {\lambda_{{i{\prime} }} + \beta_{{i{\prime} }} } \right)\left( {\frac{{I_{{i{\prime} }} + E_{{i{\prime} }} }}{{N_{{i{\prime} }} }}} \right)S_{i,k} - \left( {d_{1} + \varepsilon_{i} + \alpha_{i}^{1} } \right)E_{i,k} \hfill \\ I_{i,k}^{\prime } = \varepsilon_{i} E_{i,k} - \left( {d_{1} + d_{2} + \gamma_{i}^{2} + \alpha_{i}^{2} } \right)I_{i,k} \hfill \\ Q_{i,k}^{\prime } = \alpha_{i}^{1} E_{i,k} + \alpha_{i}^{2} I_{i,k} - \left( {d_{1} + d_{2} + \gamma_{i}^{1} } \right)Q_{i,k} \hfill \\ R_{i,k}^{\prime } = \gamma_{i}^{1} Q_{i,k} + \gamma_{i}^{2} I_{i,k} - d_{1} R_{i,k} \hfill \\ \end{gathered} \right. $$

(2)

In the model (2),$\delta_{i,k} A_{i}$ shows the number of newborn individuals in city $i$ that have a degree of $k$ as they are connected to $k$ existing individuals.$q_{1} S_{{q_{i,k} }}$ denotes that self-isolated individuals become susceptible person.$\left( {q + d_{1} } \right)S_{i,k}$ means natural death or self-isolation of susceptible individuals.$\left( {\beta_{i} + \lambda_{i} } \right)k\left( {1 - \xi_{i} } \right)\theta_{i} \left( t \right)S_{i,k}$ describes the susceptible individuals does not move across cities, but contacts the latent and sick people in city $i$.

$\omega_{i} k\xi_{i} \left( {\lambda_{{i{\prime} }} + \beta_{{i{\prime} }} } \right)\left( {\frac{{I_{{i{\prime} }} + E_{{i{\prime} }} }}{{N_{{i{\prime} }} }}} \right)S_{i,k}$ indicates that susceptible individuals are infected as latent people because of population movements, contact with lurkers and infected people in another city.

3 Dynamical analysis

In this section, we carry out a theoretical analysis on the basic regeneration number and the stability of the equilibrium point of the proposed model (2).

3.1 The basic regeneration number

From hypothesis, we have $N^{\prime}_{i,k} = \delta_{i,k} A_{i} - d_{1} N_{i,k} - d_{2} \left( {I_{i,k} + Q_{i,k} } \right).$

Theorem 3.1

The model (2) has solutions in the invariant region.

$$ \Omega = \left\{ {\left( \begin{gathered} S_{1,1} ,S_{{q_{1,1} }} E_{1,1} ,I_{1,1} ,Q_{1,1} ,R_{1,1} LS_{1.m} ,S_{{q_{1,m} }} ,E_{1,m} ,I_{1,m} ,Q_{1m} ,R_{1,m} , \hfill \\ S_{2,1} ,S_{{q_{2,1} }} ,E_{2,1} ,I_{2,1} ,Q_{2,1} ,R_{2,1} LS_{2,m} ,S_{{q_{2,m} }} ,E_{2,m} ,I_{2,m} ,Q_{2,m} ,R_{2,m} \hfill \\ \end{gathered} \right) \in R^{12n} ,N_{i,k} \left( t \right) \le \frac{{\delta_{i,k} A_{i} }}{{d_{1} }}} \right\} $$

(3)

Proof

We have

$$ N^{\prime}_{i,k} = \delta_{i,k} A_{i} - d_{1} N_{i,k} - d_{2} \left( {I_{i,k} + Q_{i,k} } \right) $$

(4)

$$ N^{\prime}_{i,k} \le \delta_{i,k} A_{i} - d_{1} N_{i,k} , $$

then

$$ N_{i,k} \left( t \right) \le \frac{{\delta_{i,k} A_{i} }}{{d_{1} }} + \left( {N_{i,k} \left( 0 \right) - \frac{{\delta_{i,k} A_{i} }}{{d_{1} }}} \right)e^{{ - d_{1} t}} ,\quad \forall t > 0. $$

(5)

Now, we let $N_{i,k} \left( 0 \right) \le \frac{{\delta_{i,k} A_{i} }}{{d_{1} }}.$

In the end, the following equation can be obtained

$$ 0 \le N_{i,k} \left( t \right) \le \frac{{\delta_{i,k} A_{i} }}{{d_{1} }}. $$

(6)

Thus, the region $\Omega$ is positively invariant and attracting for the Eq. (2).

According to the model (2), the disease-free equilibrium point of the model is

$$\begin{aligned} E_{0} &= \left( S_{1,1}^{0} ,S_{{q_{1,1} }}^{0} ,0,0,0,0, \cdots ,S_{1,m}^{0} ,S_{{q_{1,m} }}^{0} ,0,0,0,0,\right.\\ &\quad \left. S_{2,1}^{0} ,S_{{q_{2,1} }}^{0} ,0,0,0,0, \cdots ,S_{2,m}^{0} ,S_{{q_{2,m} }}^{0} ,0,0,0,0 \right).\end{aligned} $$

Next, we discuss the basic regeneration number of the model.

$R_{0}$ is defined as the average number of secondary cases caused by an infected individual during his infectivity period when he is introduced to a population of susceptible individuals without intervention.

In general, the next generation matrix method is used to calculate $R_{0}$. The input matrix ${\varvec{F}}_{{\varvec{1}}}$ and the output matrix ${\varvec{V}}_{{\varvec{1}}}$ are given below, respectively.

$$ {\varvec{F}}_{{\varvec{1}}} = \left( \begin{gathered} \left( {\beta_{i} + \lambda_{i} } \right)k\left( {1 - \xi_{i} } \right)\theta_{i} S_{i,k} + \left( {\beta_{{i^{\prime}}} + \lambda_{{i^{\prime } }} } \right)\left( {\frac{{I_{{i^{\prime}}} + E_{{i^{\prime } }} }}{{N_{{i^{\prime } }} }}} \right)k\xi_{i} \omega_{i} S_{i,k} \\ 0 \\ 0 \\ \end{gathered} \right). $$

$$ {\varvec{V}}_{{\varvec{1}}} = \left( \begin{gathered} \left( {d_{1} + \varepsilon_{i} + \alpha_{i}^{1} } \right)E_{i,k} \\ \left( {d_{1} + d_{2} + \gamma_{i}^{2} + \alpha_{i}^{2} } \right)I_{i,k} - \varepsilon_{i} E_{i,k} \\ \left( {d_{1} + d_{2} } \right)Q_{i.k} + \gamma_{i}^{1} Q_{i,k} - \alpha_{i}^{1} E_{i,k} - \alpha_{i}^{2} I_{i,k} \\ \end{gathered} \right). $$

The partial derivative of the input matrix and output matrix at the disease-free equilibrium point are as follows:

$$ \user2{F = }\left( {\begin{array}{*{20}c} {{\varvec{F}}_{{{\varvec{11}}}} } & {{\varvec{F}}_{{{\varvec{12}}}} } & {\varvec{0}} \\ {\varvec{0}} & {\varvec{0}} & {\varvec{0}} \\ {\varvec{0}} & {\varvec{0}} & {\varvec{0}} \\ \end{array} } \right). $$

$$ \begin{aligned} & {\varvec{F}}_{{{\varvec{11}}}} = \left( {\begin{array}{*{20}c} 0 & \cdots & 0 & {m_{11} } & \cdots & {m_{11} } \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & {m_{1m} } & \cdots & {m_{1m} } \\ {m_{21} } & \cdots & {m_{21} } & 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ {m_{2m} } & \cdots & {m_{2m} } & 0 & \cdots & 0 \\ \end{array} } \right),\\ & {\varvec{F}}_{{{\varvec{12}}}} = \left( {\begin{array}{*{20}c} {f_{11} } & \cdots & 0 & {m_{11} } & \cdots & {m_{11} } \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ {f_{1m} } & \cdots & {f_{1m} } & {m_{1m} } & \cdots & {m_{1m} } \\ {m_{21} } & \cdots & {m_{21} } & {f_{21} } & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ {m_{2m} } & \cdots & {m_{2m} } & {f_{2m} } & \cdots & {f_{2m} } \\ \end{array} } \right).\end{aligned} $$

where $m_{1l} = \left( {\beta_{2} + \lambda_{2} } \right)k\xi_{1} \frac{{\omega_{1} }}{{N_{2} }}S_{1,l}^{0} ,m_{2l} = \left( {\beta_{1} + \lambda_{1} } \right)k\xi_{2} \frac{{\omega_{2} }}{{N_{1} }}S_{2,l}^{0} ,\quad l = 1 \cdots m.$

$$ f_{1l} = \left( {\beta_{1} + \lambda_{1} } \right)\left( {1 - \xi_{1} } \right)kl\frac{{S_{1,l}^{0} }}{{N_{1,l} }},f_{2l} = \left( {\beta_{2} + \lambda_{2} } \right)\left( {1 - \xi_{2} } \right)kl\frac{{S_{2,l}^{0} }}{{N_{2,l} }},l = 1 \cdots m. $$

$$ \user2{V = }\left( {\begin{array}{*{20}c} {{\varvec{V}}_{11} } & {\varvec{0}} & {\varvec{0}} \\ {{\varvec{V}}_{21} } & {{\varvec{V}}_{22} } & {\varvec{0}} \\ {{\varvec{V}}_{31} } & {{\varvec{V}}_{32} } & {{\varvec{V}}_{33} } \\ \end{array} } \right). $$

$$ \begin{aligned}&{\varvec{V}}_{11} = \left( {\begin{array}{*{20}c} {\eta_{1} } & \cdots & 0 & 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & {\eta_{1} } & 0 & \cdots & 0 \\ 0 & \cdots & 0 & {\eta_{2} } & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & 0 & \cdots & {\eta_{2} } \\ \end{array} } \right)\\&{\varvec{V}}_{21} = \left( {\begin{array}{*{20}c} { - \varepsilon_{1} } & \cdots & 0 & 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & { - \varepsilon_{1} } & 0 & \cdots & 0 \\ 0 & \cdots & 0 & { - \varepsilon_{2} } & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & 0 & \cdots & { - \varepsilon_{2} } \\ \end{array} } \right),\\&{\varvec{V}}_{32} = \left( {\begin{array}{*{20}c} { - \alpha_{1}^{2} } & \cdots & 0 & 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & { - \alpha_{1}^{2} } & 0 & \cdots & 0 \\ 0 & \cdots & 0 & { - \alpha_{2}^{2} } & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & 0 & \cdots & { - \alpha_{2}^{2} } \\ \end{array} } \right).\end{aligned} $$

$$ \begin{aligned}&{\varvec{V}}_{22} = \left( {\begin{array}{*{20}c} {\mu_{1} } & \cdots & 0 & 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & {\mu_{1} } & 0 & \cdots & 0 \\ 0 & \cdots & 0 & {\mu_{2} } & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & 0 & \cdots & {\mu_{2} } \\ \end{array} } \right),\\&{\varvec{V}}_{31} = \left( {\begin{array}{*{20}c} { - \alpha_{1}^{1} } & \cdots & 0 & 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & { - \alpha_{1}^{1} } & 0 & \cdots & 0 \\ 0 & \cdots & 0 & { - \alpha_{2}^{1} } & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & 0 & \cdots & { - \alpha_{2}^{1} } \\ \end{array} } \right),\\&{\varvec{V}}_{33} = \left( {\begin{array}{*{20}c} {\sigma_{1} } & \cdots & 0 & 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & {\sigma_{1} } & 0 & \cdots & 0 \\ 0 & \cdots & 0 & {\sigma_{2} } & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & 0 & \cdots & {\sigma_{2} } \\ \end{array} } \right). \end{aligned}$$

where $\eta_{1} = d_{1} + \varepsilon_{1} + \alpha_{1}^{1} ,\eta_{2} = d_{1} + \varepsilon_{2} + \alpha_{2}^{1}$_,$\sigma_{1} = \gamma_{1}^{1} + d_{1} + d_{2} ,\sigma_{2} = \gamma_{2}^{1} + d_{1} + d_{2} .$

$$ \mu_{1} = d_{1} + d_{2} + \gamma_{1}^{2} + \alpha_{1}^{2} ,\mu_{2} = d_{1} + d_{2} + \gamma_{2}^{2} + \alpha_{2}^{2} . $$

Based on the above calculation, it can be concluded that.

$$ R_{0} = \rho \left( {{\varvec{FV}}^{ - 1} } \right). $$

(7)

Let the right term of model (2) be 0, and we get the local equilibrium point.

$$\begin{aligned} E^{*} & = \left( S_{1,k}^{*} ,S_{{q_{1,k} }}^{*} ,E_{1,k}^{*} ,I_{1,k}^{*} ,Q_{1,k}^{*} ,R_{1,k}^{*} ,S_{2,k}^{*} ,S_{{q_{2,k} }}^{*} ,\right.\\ & \quad \left. E_{2,k}^{*} ,I_{2,k}^{*} ,Q_{2,k}^{*} ,R_{2,k}^{*} \right),\end{aligned} $$

wherein,

$$ S_{i,k}^{*} = {{N_{{i{\prime} }} \left( {d_{1} + q_{1} } \right)\delta_{i.k} A_{i} } \mathord{\left/ {\vphantom {{N_{{i{\prime} }} \left( {d_{1} + q_{1} } \right)\delta_{i.k} A_{i} } \tau }} \right. \kern-0pt} \tau },\;S_{{q_{i,k} }}^{*} = {{qN_{{i{\prime} }} \delta_{i.k} A_{i} } \mathord{\left/ {\vphantom {{qN_{{i{\prime} }} \delta_{i.k} A_{i} } \tau }} \right. \kern-0pt} \tau }. $$

$$ E_{i,k}^{*} = {{N_{{i{\prime} }} \delta_{i.k} A_{i} \left[ {\left( {d_{1} + q_{1} } \right)\left( {\delta_{i,k} A_{i} - d_{1} } \right) - d_{1} q} \right]} \mathord{\left/ {\vphantom {{N_{{i{\prime} }} \delta_{i.k} A_{i} \left[ {\left( {d_{1} + q_{1} } \right)\left( {\delta_{i,k} A_{i} - d_{1} } \right) - d_{1} q} \right]} {\tau \left( {d_{1} + \varepsilon_{i} + \alpha_{i}^{1} } \right)}}} \right. \kern-0pt} {\tau \left( {d_{1} + \varepsilon_{i} + \alpha_{i}^{1} } \right)}}. $$

$$ I_{i,k}^{*} = {{\varepsilon_{i} N_{{i{\prime} }} \delta_{i.k} A_{i} \left[ {\left( {d_{1} + q_{1} } \right)\left( {\delta_{i,k} A_{i} - d_{1} } \right) - d_{1} q} \right]} \mathord{\left/ {\vphantom {{\varepsilon_{i} N_{{i{\prime} }} \delta_{i.k} A_{i} \left[ {\left( {d_{1} + q_{1} } \right)\left( {\delta_{i,k} A_{i} - d_{1} } \right) - d_{1} q} \right]} {\tau \tau_{1} }}} \right. \kern-0pt} {\tau \tau_{1} }}. $$

$$ Q_{i,k}^{*} = {{\varphi \left[ {\tau_{3} \left( {N_{{i{\prime} }} \alpha_{i}^{1} \delta_{i.k} A_{i} } \right) + \alpha_{i}^{2} N_{{i{\prime} }} \delta_{i,k} A_{i} } \right]} \mathord{\left/ {\vphantom {{\varphi \left[ {\tau_{3} \left( {N_{{i{\prime} }} \alpha_{i}^{1} \delta_{i.k} A_{i} } \right) + \alpha_{i}^{2} N_{{i{\prime} }} \delta_{i,k} A_{i} } \right]} {\tau \tau_{2} }}} \right. \kern-0pt} {\tau \tau_{2} }}. $$

$$ R_{i,k}^{*} = {{\varphi \left[ {\gamma_{i}^{1} \tau_{3} \left( {N_{{i{\prime} }} \alpha_{i}^{1} \delta_{i.k} A_{i} } \right) + \gamma_{i}^{1} \alpha_{i}^{2} N_{{i{\prime} }} \delta_{i,k} A_{i} + \varphi_{1} } \right]} \mathord{\left/ {\vphantom {{\varphi \left[ {\gamma_{i}^{1} \tau_{3} \left( {N_{{i{\prime} }} \alpha_{i}^{1} \delta_{i.k} A_{i} } \right) + \gamma_{i}^{1} \alpha_{i}^{2} N_{{i{\prime} }} \delta_{i,k} A_{i} + \varphi_{1} } \right]} {\tau \tau_{2} d_{1} }}} \right. \kern-0pt} {\tau \tau_{2} d_{1} }}.. $$

where $\varphi_{1} = \gamma_{i}^{2} \left( {d_{1} + d_{2} + \gamma_{i}^{1} } \right)$,$\varphi = \left[ {\left( {d_{1} + q_{1} } \right)\left( {\delta_{i,k} A_{i} - d_{1} } \right) - d_{1} q} \right]$.

$$ \tau = N_{{i^{\prime}}} d_{1} \left( {d_{1} + q_{1} + q} \right) + N_{{i^{\prime}}} \left( {\beta_{i} + \lambda_{i} } \right)k\left( {1 - \xi_{i} } \right)\theta_{i}^{*} + \omega_{i} \left( {\beta_{{i^{\prime}}} + \lambda_{{i^{\prime}}} } \right)\xi_{i} k\left( {I_{{i^{\prime}}} + E_{{i^{\prime}}} } \right). $$

$$ \tau_{1} = \left( {d_{1} + d_{2} + \gamma_{i}^{2} + \alpha_{i}^{2} } \right)\left( {d_{1} + \varepsilon_{i} + \alpha_{i}^{1} } \right).\;\tau_{2} = \left( {d_{1} + d_{2} + \gamma_{i}^{2} + \alpha_{i}^{2} } \right)\left( {d_{1} + \varepsilon_{i} + \alpha_{i}^{1} } \right)\left( {d_{1} + d_{2} + \gamma_{i}^{1} } \right).\;\tau_{3} = \left( {d_{1} + d_{2} + \gamma_{i}^{2} + \alpha_{i}^{2} } \right). $$

where $\theta_{i}^{*} = \left( {\sum\limits_{k = 1}^{m} {kI_{i,k}^{*} } } \right)/\left( {\sum\limits_{k = 1}^{m} {kN_{i,k}^{*} } } \right)$.

3.2 The stability of equilibrium

In this section, we analyze the stability analysis on the two equilibrium points of the model and obtained the following two conclusions. According to Theorem 2 in reference [41], we can obtain the following lemma,

Lemma 3.1

For model (2), the disease-free equilibrium $E_{0}$ is locally asymptomatically stable in $\Omega$ when $R_{0} < 1$, but unstable if $R_{0} > 1$, where $R_{0}$ is defined by next generation matrix method.

Firstly, the stability of the disease-free equilibrium point at $R_{0} < 1$ has been demonstrated and we obtained the result of Theorem 3.2.

Theorem 3.2

For system (2), if $R_{0} < 1$, the disease-free equilibrium $E_{0}$ is globally asymptomatically stable in $\Omega$.

Then, we derive a proof of the stability of local equilibrium points when $R_{0} > 1$ and we obtained the result of Theorem 3.3.

Theorem 3.3

If $R_{0} > 1$,the endemic equilibrium $E^{*}$ is globally asymptomatically stable in $\Omega$ for model (2).

Please, refer to “Appendix A” for details on the stability analysis.

3.3 Final sizes

This subsection is devoted to the calculation of final size of model. It is well known that the final size can be used to describe the degree of transmission of infectious diseases. Usually, we analyze the final number of susceptible individuals because it is determined how many people will have contracted the disease at the end of the epidemic. Here, we neglect birth and death, and then model (2) can be described as

$$ \left\{ \begin{gathered} S^{\prime}_{i,k} = q_{1} S_{{q_{i,k} }} - qS_{i,k} - \left( {\beta_{i} + \lambda_{i} } \right)k\left( {1 - \xi_{i} } \right)\theta_{i} \left( t \right)S_{i,k} - \omega_{i} k\xi_{i} \left( {\lambda_{{i{\prime} }} + \beta_{{i{\prime} }} } \right)\left( {\frac{{I_{{i{\prime} }} + E_{{i{\prime} }} }}{{N_{{i{\prime} }} }}} \right)S_{i,k} \hfill \\ S^{\prime}_{{q_{i,k} }} = qS_{i,k} - q_{1} S_{{q_{i,k} }} \hfill \\ E^{\prime}_{i,k} = \left( {\beta_{i} + \lambda_{i} } \right)k\theta_{i} \left( t \right)\left( {1 - \xi_{i} } \right)S_{i,k} + \omega_{i} k\xi_{i} \left( {\lambda_{{i{\prime} }} + \beta_{{i{\prime} }} } \right)\left( {\frac{{I_{{i{\prime} }} + E_{{i{\prime} }} }}{{N_{{i{\prime} }} }}} \right)S_{i,k} - \left( {\varepsilon_{i} + \alpha_{i}^{1} } \right)E_{i,k} \hfill \\ I^{\prime}_{i,k} = \varepsilon_{i} E_{i,k} - \left( {\gamma_{i}^{2} + \alpha_{i}^{2} } \right)I_{i,k} \hfill \\ Q^{\prime}_{i,k} = \alpha_{i}^{1} E_{i,k} + \alpha_{i}^{2} I_{i,k} - \gamma_{i}^{1} Q_{i,k} \hfill \\ R^{\prime}_{i,k} = \gamma_{i}^{1} Q_{i,k} + \gamma_{i}^{2} I_{i,k} \hfill \\ \end{gathered} \right. $$

(8)

Then, add the first and second equations in model (8) to obtain the density of all susceptible individuals $\left( {\frac{{dS_{a} }}{dt}} \right)$.

Wherein $S_{a} = S_{i,k} + S_{{q_{i,k} }}$.

Without loss of generality, let $\overline{\omega } = \int\limits_{0}^{\infty } {\omega \left( t \right)dt}$.

For model (8), diseases will eventually die out. So we have $I_{i,k} \left( \infty \right) = 0,E_{i,k} \left( \infty \right) = 0,Q_{i,k} \left( \infty \right) = 0$.

Add the first and third equations in model (8)

$$ E^{\prime}_{i,k} + S^{\prime}_{a} = - \left( {\varepsilon_{i} + \alpha_{i}^{1} } \right)E_{i,k} . $$

(9)

Integrate from 0 to infinity on both sides of the Eq. (9)

$$ E_{i,k} \left( 0 \right) - E_{i,k} \left( \infty \right) + S_{a} \left( 0 \right) - S_{a} \left( \infty \right) = \left( {\varepsilon_{i} + \alpha_{i}^{1} } \right)\overline{E}_{i,k} . $$

(10)

According to Eqs. (8) and (9), Eq. (10) can be rewritten as

$$ \overline{E}_{i,k} = \frac{{E_{i,k} \left( 0 \right) + S_{a} \left( 0 \right) - S_{a} \left( \infty \right)}}{{\left( {\varepsilon_{i} + \alpha_{i}^{1} } \right)}}. $$

(11)

Similarly,

$$ \int\limits_{0}^{\infty } {\left( {S^{\prime}_{a} + E^{\prime}_{i,k} + I^{\prime}_{i,k} } \right){\text{d}}t} = - \alpha_{i}^{1} \overline{E}_{i,k} - \left( {\gamma_{i}^{2} + \alpha_{i}^{2} } \right)\overline{I}_{i,k} . $$

(12)

Integrate from 0 to infinity on both sides of the Eq. (12)

$$ S_{a} \left( 0 \right) - S_{a} \left( \infty \right) + E_{i,k} \left( 0 \right) + I_{i,k} \left( 0 \right) = \alpha_{i}^{1} \overline{E}_{i,k} + \left( {\gamma_{i}^{2} + \alpha_{i}^{2} } \right)\overline{I}_{i,k} . $$

(13)

$$ \overline{I}_{i,k} = \frac{{\varepsilon_{i} \left[ {S_{a} \left( 0 \right) - S_{a} \left( \infty \right) + E_{i,k} \left( 0 \right)} \right]}}{{\left( {\gamma_{i}^{2} + \alpha_{i}^{2} } \right)\left( {\varepsilon_{i} + \alpha_{i}^{1} } \right)}} + \frac{{I_{i,k} \left( 0 \right)}}{{\gamma_{i}^{2} + \alpha_{i}^{2} }}. $$

(14)

Similarly, Add the fourth and fifth equations in model (8)

$$ I^{\prime}_{i,k} + Q^{\prime}_{i,k} = \left( {\varepsilon_{i} + \alpha_{i}^{1} } \right)E_{i,k} - \gamma_{i}^{1} Q_{i,k} - \gamma_{i}^{2} I_{i,k} . $$

(15)

Integrate both sides of the Eq. (15) from 0 to $\infty$,

$$I_{i,k} \left( 0 \right) + Q_{i,k} \left( 0 \right) = - \left( {\varepsilon_{i} + \alpha_{i}^{1} } \right)\overline{E}_{i,k} + \gamma_{i}^{1} \overline{Q}_{i,k} + \gamma_{i}^{2} \overline{I}_{i,k} .$$

Substitute Eqs. (11) and (14) into (16):

$$ \begin{aligned}\overline{Q}_{i,k} & = \frac{{Q_{i,k} \left( 0 \right)}}{{\gamma_{i}^{1} }} + \frac{{\alpha_{i}^{2} I_{i,k} \left( 0 \right)}}{{\gamma_{i}^{1} \left( {\gamma_{i}^{2} + \alpha_{i}^{2} } \right)}} + \frac{{\gamma_{i}^{2} \alpha_{i}^{1} + \alpha_{i}^{2} \varepsilon_{i} + \alpha_{i}^{2} \alpha_{i}^{1} }}{{\gamma_{i}^{1} \left( {\gamma_{i}^{2} + \alpha_{i}^{2} } \right)\left( {\varepsilon_{i} + \alpha_{i}^{1} } \right)}}\\ &\quad\left[ {S_{a} \left( 0 \right) - S_{a} \left( \infty \right) + E_{i,k} \left( 0 \right)} \right].\end{aligned} $$

(17)

Integrate the first equation in model (8) from 0 to $t$.

$$ \ln \frac{{S_{a} \left( 0 \right)}}{{S_{a} \left( t \right)}} = \left( {\beta_{i} + \lambda_{i} } \right)\left( {1 - \xi_{i} } \right)\frac{k}{{\left\langle {k_{i} } \right\rangle }}\sum {kp\left( k \right)} \frac{{\int\limits_{0}^{t} {I_{i,k} {\text{d}}t} }}{{N_{i.k} }} + \omega_{i} \xi_{i} \left( {\lambda_{{i^{\prime}}} + \beta_{{i^{\prime}}} } \right)\frac{k}{{N_{{i^{\prime}}} }}\int\limits_{0}^{t} {\left( {I_{{i^{\prime}}} + E_{{i^{\prime}}} } \right)} {\text{d}}t. $$

(18)

When $t \to \infty$_, we can obtain the relationship formula for the final scale.

$$ \ln \frac{{S_{a} \left( 0 \right)}}{{S_{a} \left( \infty \right)}} = \left( {\beta_{i} + \lambda_{i} } \right)\left( {1 - \xi_{i} } \right)\frac{k}{{\left\langle {k_{i} } \right\rangle }}\sum {kp\left( k \right)} \frac{{\overline{I}_{i,k} }}{{N_{i.k} }} + \omega_{i} \xi_{i} \left( {\lambda_{{i^{\prime}}} + \beta_{{i^{\prime}}} } \right)\frac{k}{{N_{{i^{\prime}}} }}\left( {\sum\limits_{k} {\overline{I}_{{i^{\prime},k}} + \overline{E}_{{i^{\prime},k}} } } \right). $$

(19)

4 Numerical simulations

In this section, we investigate the influence of basic reproduction number on the spread of infectious diseases and the influence of parameters related to population flow on the spread of infectious diseases.

Figure 2 shows the variation of all individual density of $S,S_{q} ,E,I,Q,R$ at $R_{0} < 1$ over time, the black dashed line represents the changing trends of different subcategories in city 1, while the red line represents the changing trends of different subcategories in city 2. It can be seen from Fig. 2, when $R_{0} < 1$, the density of individuals such as $E,I$ and $Q$ gradually stabilizes towards 0 over time, at this point, the disease gradually disappears after the outbreak. Figure 3 shows the variation of all individual density of $S,S_{q} ,E,I,Q,R$ at $R_{0} < 1$ over time. Also, Fig. 3 shows when $R_{0} > 1$, the density of infected persons tends to a certain stable value. At this point, infectious diseases become endemic and always exist.

Fig. 2

Changes in individual density over time

Fig. 3

Changes in individual density over time

Figure 4 indicates the relationship between $I_{1} \left( t \right)$ and population mobility rate. In Fig. 4, different lines represent different population mobility rates, which mainly reveal the relationship between population mobility rates $\xi$ and infected individuals $I_{1} \left( t \right)$ in city 1. It is found that when the population mobility rate increased, the speed of disease outbreak accelerated, and the number of patients increased significantly. This behavior exacerbates the outbreak of diseases and also increases the number of infected individuals.

Fig. 4

The relationship between $I_{1} \left( t \right)$ and population mobility rate

In Fig. 5, different lines represent different values of the number of contacts. From Fig. 5, we can see that the lines with larger values of contacts which have larger peak values and the earliest time to reach the peak value. And the vertical axis represents the infected individuals in city 1. From the perspective of disease transmission, when a disease spreads between two cities due to population mobility, the more people encounter during individual mobility, the greater risk of encountering infected individuals and contracting the virus.

Fig. 5

The relationship between $I_{1} \left( t \right)$ and contact population

Figure 6 shows the relationship between self-isolation rate $\left( q \right)$ and infected individual $I_{1} \left( t \right)$ in city 1, different lines represent different values of self-isolation rate. From Fig. 6, we can observe that the higher of the self-isolation rate $\left( q \right)$ is, the slower of the speed of disease outbreak is, and the number of patients is significantly reduced. In fact, when diseases spread, people will develop a sense of self isolation and take some self- isolation measures, such as working from home, wearing masks, reducing going out, and so on. The result of this approach is a decrease in population mobility, which can reduce the chance of exposure to the virus and control the spread of diseases. In particular, we notice that the media effect plays positive role on curbing the spreading of infectious diseases. That is, the media calls on people to take self-protection measures or reflect on the trajectories of nearby infected individuals, thereby increasing individual self-isolation rates. This measure can greatly avoid the probability of individual infection.

Fig. 6

The relationship between $I_{1} \left( t \right)$ and self-isolation rate

To better characterize the model behavior with respect to its main parameters, we have also discussed the relationship between the basic regeneration number and the population movement rate in two cities.

The relationship between $R_{0}$ and two population mobility rates is depicted in Fig. 7a. While Fig. 7b can be obtained from a top-down three-dimensional graph. The color bar in the figure indicates that as the color changes from blue to red, the corresponding $R_{0}$ value also increases. We observe an increase of population mobility in both cities as the basic regeneration number $R_{0}$ increases. In fact, if the flow of population between cities is reduced, the basic number of regenerations can be controlled and the spread of diseases can be effectively suppressed.

Fig. 7

The relationship between $R_{0}$ and $\xi$

The relationship between $R_{0}$ and the number of contact $\omega$ in two cities is shown in Fig. 8. Figure 8a presents the change of $R_{0}$ with $\omega_{1}$ and $\omega_{2}$ in the form of a three-dimensional graph, Fig. 8b is observed from the perspective of a top-down 3D view. It is found that as the number of effective contacts increases in both cities, the basic regeneration number $R_{0}$ gradually increases. This is of great significance for the spread of diseases in real life. If the number of effective contacts between cities is reduced, the basic number of regenerations can be controlled and the spread of diseases can be effectively suppressed.

Fig. 8

The relationship between $R_{0}$ and $\omega$

The blue line in Fig. 9 represents $I_{1} \left( t \right)$ with different degrees, while the green line represents $I_{2} \left( t \right)$ with different degrees. Figure 9 depicts the changes of $I_{1} (t)$(blue curve) and $I_{2} (t)$(green curve) as the degree of the initial node increases. We can observe that as the degree increases,$I(t)$ also increases. The higher the degree of the initial node, the more neighbors it has. When infectious diseases spread, the transmission rate of infected nodes also increases. In other words, an increase in the number of neighboring nodes of a node results in an increase in the density of infected individuals.

Fig. 9

The relationship between degree and $I(t)$

In what follows, we intend to analyze the relationship between the infection balance states of nodes and the degree of nodes. Besides, the NW small world network and BA scale-free network were used in numerical simulation, and Fig. 10 gives the trend of the infection equilibrium state curve and the trend of degree curve.

Fig. 10

The correlation between the node degree and its infected equilibrium state

As shown in Fig. 10a, the node with large degree has large infected equilibrium state. However, Fig. 10b indicates that the relevance is a little weaker for the BA scale-free network. As a consequence, the node with higher degree is easier to be infected.

These numerical results imply that population mobility between cities has a significant impact on disease transmission. If we want to quickly curb the spread of the disease, we need to control population mobility, such as policies such as school closures, to isolate the spread of the disease from the outside world.

5 Conclusions

This paper proposed an improved infectious disease model, taking into account the factors of population mobility and self-isolation in two cities. Furthermore, the dynamic analysis of the model, including the basic regeneration number and the stability of the equilibrium point, have been theoretically derived. In addition, we analyzed the final scale of the presented model and obtained the according expression. Furthermore, the impact of population mobility on the spread of infectious diseases is investigated via numerical simulations. Our results show that people are more susceptible to infection when the rate of population movement within cities increases. When the rate of population movement between the two cities increases, the rate of infection of susceptible individuals accelerates, and the rate of spread of infectious diseases increases rapidly. Meanwhile, if the media effect is greater, it means that the number of self-isolated individuals will increase, which can slow down the spread of infectious diseases.

Appendix A: Specific derivation of stability analysis

Stability plays a crucial role in the dynamic analysis of infectious disease models. The following content is the theoretical derivation of stability analysis. Let's first derive the global stability of the disease-free equilibrium point at $R_{0} < 1$.

Firstly, the disease-free equilibrium $E_{0}$ of system (2) is $\left( {S_{i,k}^{0} ,S_{{q_{i,k} }}^{0} ,0,0,0} \right)$.

Where

$$ S_{i,k}^{0} = \frac{{\delta_{i,k} A_{i} \left( {d_{1} + q_{1} } \right)}}{{d_{1} + q_{1} - qq_{1} }} $$

(A1)

$$S_{{q_{{i,k}} }}^{0} = \frac{{q\delta _{{i,k}} A_{i} }}{{d_{1} + q_{1} - qq_{1} }}.$$

(A2)

System (2) is rewritten in the form.

$$ \left\{ \begin{gathered} \frac{{{\text{d}}X}}{{{\text{d}}t}} = F\left( {X,Z} \right) \hfill \\ \frac{{{\text{d}}Z}}{{{\text{d}}t}} = G\left( {X,Z} \right) \hfill \\ \end{gathered} \right.. $$

(A3)

Where $X = \left( {S_{i,k} \left( t \right),S_{{q_{i,k} }} \left( t \right)} \right)^{\prime }$$Z = \left( {E_{i,k} \left( t \right),I_{i,k} \left( t \right),Q_{i,k} \left( t \right)} \right)^{\prime }$.

$$ \begin{aligned} F\left( {X,Z} \right) & = \left( \begin{gathered} \delta_{i,k} A_{i} + q_{1} S_{{q_{i,k} }} - \left( {q + d_{1} } \right)S_{i,k} - \left( {\beta_{i} + \lambda_{i} } \right)k\left( {1 - \xi_{i} } \right)\theta_{i} S_{i,k} - \omega_{i} k\xi_{i} \left( {\beta_{{i{\prime} }} + \lambda_{{i{\prime} }} } \right)\left( {\frac{{I_{{i{\prime} }} + E_{{i{\prime} }} }}{{N_{{i{\prime} }} }}} \right)S_{i,k} \\ qS_{i,k} - d_{1} S_{{q_{i,k} }} - q_{1} S_{{q_{i,k} }} \\ \end{gathered} \right). \\ G\left( {X,Z} \right) & = \left( \begin{gathered} \theta_{i} \left( {\beta_{i} + \lambda_{i} } \right)k\left( {1 - \xi_{i} } \right)S_{i,k} + \left( {\beta_{{i{\prime} }} + \lambda_{{i{\prime} }} } \right)\left( {\frac{{I_{{i{\prime} }} + E_{{i{\prime} }} }}{{N_{{i{\prime} }} }}} \right)k\omega_{i} \xi_{i} S_{i,k} - \left( {d_{1} + \varepsilon_{i} + \alpha_{i}^{1} } \right)E_{i,k} \\ \varepsilon_{i} E_{i,k} - \left( {d_{1} + d_{2} + \gamma_{i}^{2} + \alpha_{i}^{2} } \right)I_{i,k} \\ \alpha_{i}^{1} E_{i,k} + \alpha_{i}^{2} I_{i.k} - \gamma_{i}^{1} Q_{i,k} - \left( {d_{1} + d_{2} } \right)Q_{i,k} \\ \end{gathered} \right). \\ \end{aligned} $$

$U_{0} = \left( {X_{0} ,0} \right) = \left( {S_{i,k}^{0} ,S_{{q_{i,k} }}^{0} ,0,0,0} \right)$ denotes the disease-free equilibrium of system.

Then, we have the following two conditions:

$\left( {H_{1} } \right)$ For $\frac{dX}{{dt}} = F\left( {X,0} \right) = \left( \begin{gathered} \delta_{i,k} A_{i} + q_{1} S_{{q_{i,k} }} - \left( {q + d_{1} } \right)S_{i,k} \hfill \\ qS_{i,k} - d_{1} S_{{q_{i,k} }} - q_{1} S_{{q_{i,k} }} \hfill \\ \end{gathered} \right)$,$x_{0} = \left( {S_{i,k}^{0} ,S_{{q_{i,k} }}^{0} ,0,0,0} \right)$ is a globally asymptomatically stable equilibrium of $\frac{dx}{{dt}} = F\left( {x,0} \right)$. Hence,$U_{0}$ is globally asymptomatically stable.

$$ \left( {H_{2} } \right)\;G\left( {X,Z} \right) = {\varvec{A}}Z - \tilde{G}\left( {X,Z} \right). $$

$$ \user2{A = }\left( {\begin{array}{*{20}c} {{\varvec{A}}_{11} } & {{\varvec{A}}_{12} } & {\varvec{0}} \\ {{\varvec{A}}_{21} } & {{\varvec{A}}_{22} } & {\varvec{0}} \\ {{\varvec{A}}_{31} } & {{\varvec{A}}_{32} } & {{\varvec{A}}_{33} } \\ \end{array} } \right). $$

$$ {\varvec{A}}_{11} = \left( {\begin{array}{*{20}c} { - \eta_{1} } & \cdots & 0 & {\rho_{11} } & \cdots & {\rho_{11} } \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & { - \eta_{1} } & {\rho_{1m} } & \cdots & {\rho_{1m} } \\ {\rho_{21} } & \cdots & {\rho_{21} } & { - \eta_{2} } & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ {\rho_{2m} } & \cdots & {\rho_{2m} } & 0 & \cdots & { - \eta_{2} } \\ \end{array} } \right),\;{\varvec{A}}_{12} = \left( {\begin{array}{*{20}c} {f_{11} } & \cdots & 0 & {\rho_{11} } & \cdots & {\rho_{11} } \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ {f_{1m} } & \cdots & {f_{1m} } & {\rho_{1m} } & \cdots & {\rho_{1m} } \\ {\rho_{21} } & \cdots & {\rho_{21} } & {f_{21} } & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ {\rho_{2m} } & \cdots & {\rho_{2m} } & {f_{2m} } & \cdots & {f_{2m} } \\ \end{array} } \right) $$

And ${\varvec{A}}_{21} \user2{ = - V}_{21}$, ${\mathbf{A}}_{22} {\mathbf{ = }} - {\mathbf{V}}_{22}$, ${\varvec{A}}_{31} \user2{ = } - {\varvec{V}}_{31}$, ${\varvec{A}}_{32} \user2{ = } - {\varvec{V}}_{32}$, ${\varvec{A}}_{33} \user2{ = } - {\varvec{V}}_{33}$.

Where $\rho_{1l} = \left( {\beta_{2} + \lambda_{2} } \right)k\xi_{2} \omega_{2} \frac{{S_{1,l}^{0} }}{{N_{2} }},\rho_{2l} = \left( {\beta_{1} + \lambda_{1} } \right)k\xi_{1} \omega_{1} \frac{{S_{2,l}^{0} }}{{N_{1} }},l = 1 \cdots m.$

Note that ${\varvec{A}}$ is an Metzler matrix,$\user2{ - A}$ is an M-matrix, and all eigenvalues with respect to ${\varvec{A}}$ have negative real parts when $R_{0} < 1$.We derive that $Z\left( t \right)$ is globally asymptomatically stable, which means.

$$ \mathop {\lim }\limits_{t \to \infty } Z\left( t \right) = 0, $$

$$ \mathop {\lim }\limits_{t \to \infty } \left( {X\left( t \right),Z\left( t \right)} \right) = \left( {x_{0} ,0} \right) = U_{0} . $$

Then, the disease-free equilibrium $E_{0}$ is globally asymptomatically stable when $R_{0} < 1$.

Next, we discuss the global stability of the local equilibrium point at $R_{0} { > }1$.

Proof

Consider the following Lyapunov function candidate

$$ \begin{gathered} L = \left( {S_{i,k} - S_{i,k}^{*} - S_{i,k}^{*} \ln \frac{{S_{i,k} }}{{S_{i,k}^{*} }}} \right) + h_{1} \left( {S_{{q_{i,k} }} - S_{{q_{i,k} }}^{*} - S_{{q_{i,k} }}^{*} \ln \frac{{S_{{q_{i,k} }} }}{{S_{{q_{i,k} }}^{*} }}} \right) \\ \quad + h_{2} \left( {E_{i,k} - E_{i,k}^{*} - E_{i,k}^{*} \ln \frac{{E_{i,k} }}{{E_{i,k}^{*} }}} \right) \hfill \\ \quad + h_{3} \left( {I_{i,k} - I_{i,k}^{*} - I_{i,k}^{*} \ln \frac{{I_{i,k} }}{{I_{i,k}^{*} }}} \right) + h_{4} \left( {Q_{i,k} - Q_{i,k}^{*} - Q_{i,k}^{*} \ln \frac{{Q_{i,k} }}{{Q_{i,k}^{*} }}} \right). \hfill \\ \end{gathered} $$

(A4)

where $h_{1} ,h_{2} ,h_{3} ,h_{4}$ and $h_{5}$ are positive constants to be determined later. Differentiating the function with respect to time yields.

$$ L^{\prime} = (1 - \frac{{S_{i,k}^{*} }}{{S_{i,k} }})S^{\prime}_{i,k} + h_{1} (1 - \frac{{S_{{q_{i,k} }}^{*} }}{{S_{{q_{i,k} }} }})S^{\prime}_{{q_{i,k} }} + h_{2} (1 - \frac{{E_{i,k}^{*} }}{{E_{i,k} }})E^{\prime}_{i,k} + h_{3} (1 - \frac{{I_{i,k}^{*} }}{{I_{i,k} }})I^{\prime}_{i,k} + h_{4} (1 - \frac{{Q_{i,k}^{*} }}{{Q_{i,k} }})Q^{\prime}_{i,k} . $$

(A5)

Substituting system (A5) into the above formula and sorted out:

$$ \begin{aligned} L^{\prime} & = \left( {1 - \frac{1}{{x_{1} }}} \right)\left( {\delta_{i,k} A_{i} + q_{1} S_{{q_{i,k} }} } \right) + \left( {1 - x_{1} } \right)S_{i,k}^{*} \left[ {\left( {q + d_{1} } \right) + \left( {\beta_{i} + \lambda_{i} } \right)k\left( {1 - \xi_{i} } \right)\theta_{i} + \omega_{i} k\xi_{i} \left( {\beta_{{i^{\prime}}} + \lambda_{{i^{\prime}}} } \right)\left( {\frac{{I_{{i^{\prime}}} + E_{{i^{\prime}}} }}{{N_{{i^{\prime}}} }}} \right)} \right] \\ & \quad + h_{1} qS_{i,k}^{*} \left( {x_{1} - \frac{{x_{1} }}{{x_{2} }}} \right) + \left( {1 - x_{2} } \right)h_{1} \left( {d_{1} + q_{1} } \right)S_{{q_{i,k} }}^{*} + \left( {1 - x_{3} } \right)h_{2} E_{i,k}^{*} \left( {d_{1} + \varepsilon_{i} + \alpha_{i}^{1} } \right) \\ & \quad + \left( {x_{1} - \frac{{x_{1} }}{{x_{3} }}} \right)h_{2} S_{i,k}^{*} \left[ {\left( {\beta_{i} + \lambda_{i} } \right)k\left( {1 - \xi_{i} } \right)\theta_{i} + \omega_{i} k\xi_{i} \left( {\beta_{{i^{\prime}}} + \lambda_{{i^{\prime}}} } \right)\left( {\frac{{I_{{i^{\prime}}} + E_{{i^{\prime}}} }}{{N_{{i^{\prime}}} }}} \right)} \right] + \left( {1 - x_{4} } \right)h_{3} I_{i,k}^{*} \left( {d_{1} + d_{2} + \gamma_{i}^{2} + \alpha_{i}^{2} } \right) \\ & \quad + \left( {x_{3} - \frac{{x_{3} }}{{x_{4} }}} \right)h_{3} \varepsilon_{i} E_{i,k}^{*} + \left( {1 - x_{5} } \right)h_{4} Q_{i,k}^{*} \left( {d_{1} + d_{2} + \gamma_{i}^{1} } \right) + \left( {x_{3} - \frac{{x_{3} }}{{x_{5} }}} \right)h_{4} \alpha_{i}^{1} E_{i,k}^{*} + \left( {x_{4} - \frac{{x_{4} }}{{x_{5} }}} \right)h_{4} \alpha_{i}^{2} I_{i,k}^{*} . \\ \end{aligned} $$

(A6)

where $x_{1} = \frac{{S_{i,k} }}{{S_{i,k}^{*} }},x_{2} = \frac{{S_{{q_{i,k} }} }}{{S_{{q_{i,k} }}^{*} }},x_{3} = \frac{{E_{i,k} }}{{E_{i,k}^{*} }},x_{4} = \frac{{I_{i,k} }}{{I_{i,k}^{*} }},x_{5} = \frac{{Q_{i,k} }}{{Q_{i,k}^{*} }}$.

The above formula can be simplified

$$ \begin{aligned} L^{\prime} & = \delta_{i,k} A_{i} + q_{1} S_{{q_{i,k} }} + S_{i,k}^{*} \left[ {\left( {q + d_{1} } \right) + \left( {\beta_{i} + \lambda_{i} } \right)k\left( {1 - \xi_{i} } \right)\theta_{i} + \omega_{i} k\xi_{i} \left( {\beta_{{i^{\prime}}} + \lambda_{{i^{\prime}}} } \right)\left( {\frac{{I_{{i^{\prime}}} + E_{{i^{\prime}}} }}{{N_{{i^{\prime}}} }}} \right)} \right] \\ & \quad + h_{1} \left( {d_{1} + q_{1} } \right)S_{{q_{i,k} }}^{*} + h_{2} E_{i,k}^{*} \left( {d_{1} + \varepsilon_{i} + \alpha_{i}^{1} } \right) + h_{3} I_{i,k}^{*} \left( {d_{1} + d_{2} + \gamma_{i}^{2} + \alpha_{i}^{2} } \right) + h_{4} Q_{i,k}^{*} \left( {d_{1} + d_{2} + \gamma_{i}^{1} } \right) \\ & \quad - \left( {\delta_{i,k} A_{i} + q_{1} S_{{q_{i,k} }} } \right)\frac{1}{{x_{1} }} + \left[ {h_{1} q - \left( {q + d_{1} } \right) + \left( {\beta_{i} + \lambda_{i} } \right)k\left( {1 - \xi_{i} } \right)\theta_{i} + \omega_{i} k\xi_{i} \left( {\beta_{{i^{\prime}}} + \lambda_{{i^{\prime}}} } \right)\left( {\frac{{I_{{i^{\prime}}} + E_{{i^{\prime}}} }}{{N_{{i^{\prime}}} }}} \right)} \right]x_{1} S_{i,k}^{*} \\ & \quad + h_{2} S_{i,k}^{*} \left[ {\left( {\beta_{i} + \lambda_{i} } \right)k\left( {1 - \xi_{i} } \right)\theta_{i} + \omega_{i} k\xi_{i} \left( {\beta_{{i^{\prime}}} + \lambda_{{i^{\prime}}} } \right)\left( {\frac{{I_{{i^{\prime}}} + E_{{i^{\prime}}} }}{{N_{{i^{\prime}}} }}} \right)} \right] - x_{2} h_{1} \left( {d_{1} + q_{1} } \right)S_{{q_{i,k} }}^{*} \\ & \quad + x_{3} E_{i,k}^{*} \left[ {h_{3} \varepsilon_{i} + h_{4} \alpha_{i}^{1} - h_{2} \left( {d_{1} + \varepsilon_{i} + \alpha_{i}^{1} } \right)} \right] + x_{4} I_{i,k}^{*} \left[ {h_{4} \alpha_{i}^{2} - h_{3} \left( {d_{1} + d_{2} + \gamma_{i}^{2} + \alpha_{i}^{2} } \right)} \right] \\ & \quad - x_{5} Q_{i,k}^{*} \left[ {\left( {d_{1} + d_{2} + \gamma_{i}^{1} } \right)} \right] - \frac{{x_{1} }}{{x_{2} }}h_{1} qS_{i,k}^{*} - \frac{{x_{1} }}{{x_{3} }}S_{i,k}^{*} h_{2} \left[ {\left( {\beta_{i} + \lambda_{i} } \right)k\left( {1 - \xi_{i} } \right)\theta_{i} + \omega_{i} k\xi_{i} \left( {\beta_{{i^{\prime}}} + \lambda_{{i^{\prime}}} } \right)\left( {\frac{{I_{{i^{\prime}}} + E_{{i^{\prime}}} }}{{N_{{i^{\prime}}} }}} \right)} \right] \\ & \quad - \frac{{x_{3} }}{{x_{4} }}h_{3} \varepsilon_{i} E_{i,k}^{*} - \frac{{x_{3} }}{{x_{5} }}h_{4} \alpha_{i}^{1} E_{i,k}^{*} - \frac{{x_{4} }}{{x_{5} }}h_{4} \alpha_{i}^{2} I_{i,k}^{*} . \\ \end{aligned} $$

(A7)

Considering $h_{3} = 1$, by setting the coefficients of $x_{2} ,x_{3} ,x_{4} ,x_{5}$ to 0 and solving for $h_{1} ,h_{2} ,h_{4}$ yields.

$h_{1} = {{\left[ {\left( {q + d_{1} } \right) + a} \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {q + d_{1} } \right) + a} \right]} q}} \right. \kern-0pt} q}.$$h_{2} = {{\left[ {\alpha_{i}^{2} \varepsilon_{i} + \alpha_{i}^{1} \left( {d_{1} + d_{2} + \alpha_{i}^{2} + \gamma_{i}^{2} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {\alpha_{i}^{2} \varepsilon_{i} + \alpha_{i}^{1} \left( {d_{1} + d_{2} + \alpha_{i}^{2} + \gamma_{i}^{2} } \right)} \right]} {\left[ {\alpha_{i}^{2} \left( {d_{1} + \varepsilon_{i} + \alpha_{i}^{1} } \right)} \right]}}} \right. \kern-0pt} {\left[ {\alpha_{i}^{2} \left( {d_{1} + \varepsilon_{i} + \alpha_{i}^{1} } \right)} \right]}}$.$h_{4} = {{\left[ {\left( {d_{1} + d_{2} + \alpha_{i}^{2} + \gamma_{i}^{2} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {d_{1} + d_{2} + \alpha_{i}^{2} + \gamma_{i}^{2} } \right)} \right]} {\alpha_{i}^{2} }}} \right. \kern-0pt} {\alpha_{i}^{2} }}.$$a = \left( {\beta_{i} + \lambda_{i} } \right)k\left( {1 - \xi_{i} } \right)\theta_{i} + \left( {\beta_{{i^{\prime}}} + \lambda_{{i^{\prime}}} } \right)\left( {\frac{{I_{{i^{\prime}}} + E_{{i^{\prime}}} }}{{N_{{i^{\prime}}} }}} \right)k\xi_{i} \omega_{i}$.

Using the arithmetic–geometric means inequality, it is found that $L$ is less or equal to zero with equality only if $x_{1} = 1,x_{2} = 1,x_{3} = 1,x_{4} = 1,x_{5} = 1$. By LaSalle’s invariance principle, we know the largest invariant set in $\Omega$ is reduced to the endemic equilibrium $E^{*}$, and the largest invariant set contained in

$$ \left\{ {\left( {S_{i,k} ,S_{{q_{i,k} }} ,E_{i,k} ,Q_{i,k} ,I_{i,k} ,R_{i,k} } \right) \in \Omega |L^{\prime} = 0} \right\} $$

(A8)

Then, we conclude that the endemic equilibrium is globally asymptotically stable in $\Omega$.