1 Introduction

One of the essential topics in control engineering is the mathematical modeling of complex systems (Fortuna et al. 2012). The majority of practical system designs are complex from a research standpoint. This often leads to high computational demands for analysis purposes. Because the original model is too complex to apply, reduction or approximation approaches based on mathematical or physical factors are employed to create a simpler model than the original and can be utilized for analysis. The topic of MOR is very significant for engineers and scientists working in various engineering domains, especially those working in the field of process control (Gutman et al. 1982). MOR approaches are essential in the design of controllers for complicated, numerically demanding processes in control engineering. Low-order controllers will be used, with lower hardware requirements for the designer. Many publications have addressed the method of obtaining ROM in recent years (Kumar and Sikander 2022; Kumar and Ezhilarasi 2023; Sikander and Prasad 2017; Sambariya and Arvind 2016; Chand 2014; Smamash 1981; Chen et al. 1979, 1980a; Krishnamurthy and Seshadri 1978; Chen and Shieh 1968).

MOR methods approximate low-order transfer functions whose unknown coefficients are determined by various factors. Padé-type approximations (Bultheel and Van Barel 1986), Continued fraction expansion (CFE) methods (Rathore et al. 1979), MOR using the Routh stability criterion (Krishnamurthy and Seshadri 1978), MOR based on the Routh table criterion (Pal 1979), MOR using stability equations (Lucas 1985), and mixed approximation methods (Sikander and Prasad 2015a) are the frequency domain MOR techniques.

Several recent studies have looked at model order reduction in detail. Recently (Prajapati and Prasad 2020) developed a mixed method that combines two conventional techniques to obtain the reduced-order models. Sikander and Thakur (2018) proposed a modified cuckoo search algorithm (MCS) for finding the reduced model of the complex system. Ghosh and Senroy (2013) developed a balanced truncation method for MOR, Sikander and Prasad (2015b) suggested a basic MOR technique based on improved Hermite normal form. Desai and Prasad (2013) has developed a new reduced-order method for LTI structures based on Routh approximation (RA). Erol and Eksin (2006) proposed a Big Bang-Big Crunch (BB-BC) optimization for MOR in 2006. In this reduction approach, the coefficients of denominator polynomials are calculated using Routh Approximation to maintain stability, and the reduced order of numerator is evaluated with the BB-BC algorithm. Other literature that discussed the MOR concepts could be found in Biradar et al. (2016), Sikander and Prasad (2015a), Prajapati and Prasad (2023), Duddeti (2023). The optimization approach is not recent in the new era of machine engineering. Different researchers working in the field of model order reduction have taken different cost functions, such as minimizing the integral square of impulse response error (Walton et al. 2011), minimizing integral error, minimizing weighted time integral error (Eitelberg 1981), or minimizing \(L_1\) and \(L_2\) norm (El-Attar and Vidyasagar 1978) for finding the reduced model using The transfer function thus constructed with each table’s second The transfer function thus constructed with each table’s second and third rows is given by optimization techniques. Nature-inspired optimization methods have been commonly employed to create the reduced-order model of complex systems. Goldberg (1989) proposed a genetic algorithm (GA), which is the most common algorithm inspired by the concept of biology, and Kennedy and Eberhart (1995) proposed particle swarm optimization (PSO). In addition, researchers in the other literature have proposed various mixed approaches for reduced-order modeling. In these mixed processes, the idea is to retain the reduced system’s stability. The stability-preserving method of MOR always leads to a stable reduced model polynomial (Parmar et al. 2007; Sikander and Prasad 2015a; Vishwakarma and Prasad 2009). Sikander and Prasad (2015b) suggested a combination of stability equation and optimization approach to find the reduced model. The stability equation approach was used to derive the denominator coefficients, and then PSO was used to calculate the numerator polynomial of the simplified model.

The motivation behind this paper stems from the need to provide researchers and practitioners with a comprehensive understanding of MOR methods, particularly in the context of high-dimensional complex systems. Reviewing the existing literature, this study aims to consolidate and summarize the fundamental theories, limitations, and practical aspects of conventional MOR methods discussed above.

Moreover, the paper conducts a comparative analysis of different MOR strategies using six test systems. By evaluating the step response and frequency response generated by these methods, the study aims to assess their efficacy in reducing system complexity while preserving the system’s dynamic behavior. The integral square error criterion is utilized as an objective measure to quantify the accuracy of the reduction procedures.

Finally, the paper proposes a novel system abatement method based on Atomic Orbital Search optimization to enhance the existing MOR techniques. This new approach leverages optimization algorithms to obtain reduced-order models for large-scale linear time-invariant (LTI) systems. Additionally, the proposed method offers insights into designing controllers based on the reduced order models, thus enabling practical applications in real-world scenarios.

The remaining sections of this paper are structured as follows. Section 2 provides an in-depth overview of various model order reduction (MOR) techniques applicable to reducing the order of large-scale linear time-invariant (LTI) systems. These techniques encompass Factor division, Pade Approximation, Stability Equation, Differentiation, and Routh Approximation methods. In Sect. 4, the proposed methodology is presented. This methodology entails constructing a reduced-order transfer function that approximates the original system transfer function, utilizing the Atomic Orbital Search optimization algorithm. To showcase the efficacy of the proposed methodology, Sect. 5 offers a numerical illustration featuring diverse test systems, employing the MOR techniques described in Sects. 2 and 4. The numerical results indicate that the proposed method significantly reduces the computational time required to simulate large-scale LTI systems while maintaining the accuracy of the results to a considerable degree. Lastly, Sect. 6 concludes the paper by summarizing the key findings derived from the review and underscoring the importance of MOR techniques in mitigating the computational complexity associated with large-scale LTI systems. Additionally, the section presents potential directions for future research in this area.

2 Model order reduction techniques

2.1 Factor division method

In this method, dominant poles are retained, and the numerator of G(s) 1 is divided by the factor \((s+d_n)\) and given in 2.

$$\begin{aligned} G(s)=\frac{c_{0}+c_{1} s+c_{2} s^{2}+\cdots +c_{n-1} s^{n-1}}{\left( s+b_{1}\right) \left( s+b_{2}\right) \cdots \left( s+b_{n}\right) } \end{aligned}$$
(1)

where \(b_{i}>0(i=1,2,3, \ldots , n)\) are considered as real valued variables for simplicity \(b_{1} \le b_{2} \le b_{3} \le \cdots \le b_{n}\).

$$\begin{aligned} G_{n-1}(s)=\frac{d_{0}+d_{1} s+d_{2} s^{2}+\cdots +d_{n-2} s^{n-2}}{\left( s+b_{1}\right) \left( s+b_{2}\right) \cdots \left( s+b_{n-1}\right) } \end{aligned}$$
(2)

where

$$\begin{aligned} d_{0}=c_{0} / b_{n} \end{aligned}$$

and

$$\begin{aligned}{} & {} d_{i}=\left( c_{i}-d_{i-1}\right) / b_{n}\\{} & {} i=1,2, \ldots , n-2 \end{aligned}$$

The unknown coefficients of the numerator polynomial of the ROM \(G_{k}(s)\) are obtained by the power series expansion of the following expression about \(s=0\)

$$\begin{aligned} \frac{b_{0}+b_{1} s+\cdots +b_{n-1} s^{n-1}}{e_{0}+e_{1} s +\cdots +e_{n-k} s^{n-k}} \end{aligned}$$

The transfer function of ROM is then given by 3

$$\begin{aligned} G_{k}(s)=\frac{\alpha _{0}+\alpha _{1} s+\cdots +\alpha _{k-1} s^{k-1}}{\left( s+b_{1}\right) \left( s+b_{2}\right) \cdots \left( s+b_{k}\right) } \end{aligned}$$
(3)

2.2 Pade approximation method

In this MOR method, higher order polynomial (4) is first expanded about \(s=0\) using power series expansion. Unknown coefficients of ROM are calculated by equating the coefficients of obtained power series expansion given (5).

A generalized higher-order system is given in transfer function form as

$$\begin{aligned} G(s) =\frac{c_{0}+c_{1} s+c_{2} s^{2}+\ldots +b_{n-1} s^{n-1}}{b_{n} +e_{1} s+b_{2} s^{2}+\ldots +b_{n} s^{n}} \end{aligned}$$
(4)

Power series of (4) about \(s=0\) is

$$\begin{aligned} G(s)=e_{0}+e_{1} s+e_{2} s^{2}+\ldots \end{aligned}$$
(5)

Since the original higher-order system is asymptotically stable, the \(b_{i}\) is proportional to the system’s time moments (Shamash 1975).

Assume it needs a reduced \(G_R(s)\) model of the order k that maintains the pole at, say, \(s=-s_{1}\).

Let

$$\begin{aligned} G_R(s)=\frac{p_{0}+p_{1} s+p_{2} s^{2}+\ldots +p_{k-1} s^{k-1}}{q_{0}+q_{1} s+q_{2} s^{2}+\ldots +q_{k-1} s^{k-1}+s^{k}} \end{aligned}$$
(6)

To simplify the notation, The orders of the numerator of \(G_R(s)\) and G(s) have been taken as one less than the denominators. Then for \(G_R(s)\) to be a Pade approximant of G(s) (7).

$$\begin{aligned} \left. \begin{array}{l} p_{0}=q_{0} e_{0} \\ p_{1}=q_{0} e_{1}+q_{1} e_{0} \\ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\ 0=q_{0} e_{2 k-2}+q_{1} e_{2 k-1}+\ldots +e_{k-1} \\ 0=q_{0} e_{2 k-1}+q_{1} e_{2 k-2}+\ldots +e_{k} \end{array}\right\} \end{aligned}$$
(7)

To retain the k poles of the reduced order model, R(s) can then be written as

$$\begin{aligned} R(s)&=\frac{p_{0}+p_{1} s+\ldots +p_{k-1} s^{k-1}}{\left( s+s_{1}\right) \left( s+\delta p_{2}\right) \ldots \left( s+s_{k}\right) } \nonumber \\&=\frac{p_{0}+p_{1} s+\ldots +p_{k-1} s^{k-1}}{q_{0}+q_{1} s+\ldots +q_{k-1} s^{k-1}+s^{k}} \end{aligned}$$
(8)

where the \(q_{i}(i=0,1, \ldots , k-1)\). \(p_i\) can be determined from the first k equations from the (7).

Mathematical computation of this method is straightforward, and it provides the consent between the steady state of the output and the model of the polynomial inputs belonging to a particular class of the form \(\sum \alpha p_{i} t^{i}\). Pade approximations have the major drawback of making the reduced-order system unstable even if the higher-order system is stable.

2.3 Stability equation method

In this reduction technique, using the numerator and denominator polynomial of the original system, an equation is formed that is known as the stability equation. After forming the stability equation, only dominant poles and zeros are retained, and non-dominant poles and zeros are discarded.

Steps for finding ROM using the Stability equation method are given below:

Step 1.:

Consider original higher order system

$$\begin{aligned} F(s)&=\frac{b_{0}+b_{1} s+b_{2} s^{2}+\ldots +b_{n-1} s^{n-1}}{a_{0}+a_{1} s+a_{2} s^{2}+\ldots +a_{n} s^{n}} \nonumber \\&=\frac{F_{N}(s)}{F_{D}(s)} \end{aligned}$$
(9)

Generally, order of \(F_{D}(s)\) is higher than \(F_{N}(s)\). The stability equation is written in the following form by discarding the non-dominant poles of \(\left( p_{i}\right)\) and zeros \(\left( z_{i}\right)\). The results are given as

$$\begin{aligned} F_{D e}^{\prime }(s)-\left( \prod _{i=(k / 2)+1}^{n / 2} z_{i}^{2}\right) \cdot \left[ \prod _{i=1}^{k / 2} \left( s^{2} \mid z_{i}^{2}\right) \right] \end{aligned}$$
(10)

and

$$\begin{aligned} F_{D o}^{\prime }(s)=s \cdot \left( \prod _{i=(k+1) / 2}^{(n-1) / 2} p_{i}^{2}\right) \cdot \left[ \prod _{i=1}^{(k-1) / 2} \left( s^{2}+p_{i}^{2}\right) \right] \end{aligned}$$
(11)

where k is the required order of the reduced model. The denominator of the reduced order is obtained as

$$\begin{aligned} F_{D}^{\prime }(s)&=F_{D e}^{\prime }(s)+F_{D o}^{\prime }(s) \nonumber \\&=\sum _{j=0}^{k} e_{i} s^{i} \end{aligned}$$
(12)
Step 2.:

In this original step system given in Eq. (9) is expanded about \(s=0\) using the power series expansion method

$$\begin{aligned} F(s)=c_{0}+c_{1} s+c_{2} s^{2}+\ldots \end{aligned}$$
(13)

where

$$\begin{aligned} c_{0}&=b_{0} / a_{0} \nonumber \\ c_{i}&=\frac{1}{a_{0}}\left( b_{i}-\sum _{j=1}^{i} a_{i} c_{i-1}\right) \quad i>0 \end{aligned}$$
(14)

with

$$\begin{aligned} b_i = 0 \quad for i \ge n-1 \end{aligned}$$
(15)
Step 3.:

The ROM obtained by this method is given by \(F_{k}(s),\) of order k.

$$\begin{aligned} F_{k}(s)=\frac{p_{0}+d_{1} s+p_{2} s^{2}+\ldots +p_{k-1} s^{k-1}}{q_{0}+e_{1} s+q_{2} s^{2}+\ldots +q_{k} s^{k}} \end{aligned}$$
(16)

The key benefit of this strategy is that it keeps the original higher-order system stable. The major downside of this strategy is that it compromises the correlations between the original and reduced models to maintain structural stability.

2.4 Differentiation method

The reciprocal of the numerator and denominator is computed first in this MOR method. Then obtained reciprocal is differentiated accordingly to obtain the coefficients of the ROM. Steps to be followed to find the reduced order using the differentiation method:

Step 1.:

Obtain the unknown coefficients of \(k_{th}\) order of denominator polynomial using (17)

$$\begin{aligned} D_{n-k}(s)=D_n (s) - \frac{s}{n} D^\prime _n (s) \end{aligned}$$
(17)

where n and k are the order of denominators of the original and reduced system, respectively.

Now reciprocal polynomial is differentiated \(n-k\) times, and again reciprocal of the differentiated polynomial is calculated to obtain the final denominator polynomial of the ROM.

$$\begin{aligned} d(s) = e_0 + e_1 s + e_2 s^2 + \cdots + e_k s^k \end{aligned}$$
(18)
Step 2.:

Unknown coefficients of numerator polynomial of \(k_{th}\) order is obtained using (19)

$$\begin{aligned} N_{n-k}(s)=N_n (s) - \frac{s}{n} N^\prime _n (s) \end{aligned}$$
(19)

Now differentiate the reciprocal polynomial equation of numerator \(n-k\) times and then reciprocate back to find the unknown numerator polynomial of ROM as

$$\begin{aligned} n(s) = d_0 + d_1 s + d_2 s^2 + \cdots + d_k s^{k-1} \end{aligned}$$
(20)

By putting the n(s) and d(s) polynomial, reduced order transfer function is then constructed as

$$\begin{aligned} G_R (s) = \frac{n(s)}{d(s)} \end{aligned}$$
(21)

The significant advantage of this method is that it is mathematically simple and can be applied to any system, like unstable, minimum phase, or non-minimum phase systems.

3 Key limitations of transfer function based model order reduction method

  1. (1)

    Frequency Domain Approximation: Transfer function-based model reduction methods primarily focus on approximating a system’s behavior in the frequency domain. However, they might struggle to accurately represent transient behaviors and time-domain characteristics.

  2. (2)

    Neglect of Dynamics: Transfer function-based reduction techniques often emphasize the dominant poles and zeros, leading to the neglect of higher-order dynamics that could be critical in capturing system behaviors such as resonances, overshoots, and settling times.

  3. (3)

    Limited Representation of Distributed Systems: Transfer function-based approaches are more suitable for lumped-parameter systems. These methods can struggle to capture spatial variations and distributed effects when dealing with distributed parameter systems, like those found in some physical processes.

  4. (4)

    Parametric Sensitivity Issues: Model reduction methods that rely on transfer functions might be sensitive to variations in system parameters. Changes in system parameters can result in significant deviations from the original system behavior, limiting the predictive accuracy of the reduced model.

  5. (5)

    Nonlinear Systems Approximation: Transfer function-based techniques are designed for linear systems. When applied to nonlinear systems, these methods lose accuracy due to the inherent complexity of nonlinear interactions and the inability to accurately linearize the dynamics.

  6. (6)

    Frequency Range Limitations: Transfer function-based reduction is often most accurate around the dominant poles and zeros in a limited frequency range. The reduced model might fail to accurately capture system behaviors and resonances outside this range.

  7. (7)

    Loss of Unmodeled Dynamics: Certain system characteristics might be overlooked during model reduction, leading to the loss of important dynamics not captured by the dominant transfer functions.

  8. (8)

    Poor Representation of Coupled Systems: Transfer function-based approaches might struggle to accurately capture the interactions and coupling effects between different subsystems, which are crucial in complex interdependencies.

  9. (9)

    Uncertainty and Robustness: Transfer function-based model reduction might not provide robust representations in the presence of uncertainties or parameter variations, limiting their applicability in scenarios where robustness is crucial.

  10. (10)

    Difficulty with Multi-Input Multi-Output (MIMO) Systems: Handling MIMO systems with transfer function-based reduction methods can be complex, as accurately capturing cross-couplings and interactions between inputs and outputs is challenging.

4 Proposed methodology based on atomic orbital search optimization

Following steps to be followed to find the optimal values of the FOPID controller

Step 1::

Based on the mathematical relation given in (22), the initial positions of the electrons within the electron cloud are determined.

$$\begin{aligned} x_i^j(0)&=x_{i, \min }^j+{\text {rand}} . \left( x_{i, \max }^j-x_{i, \min }^j\right) \nonumber \\&\quad \left\{ \begin{array}{l} i=1,2 \ldots , m \\ j=1,2, \ldots , d \end{array}\right. \end{aligned}$$
(22)

where, \(x_i^j (0)\) is the starting position of a solution candidate, with \(x_{i,\min }^j\) and \(x_{i,\max }^j\) being the lower and upper limits, respectively, for the \(j_{th}\) decision variable of the \(i_{th}\) solution candidate. The term rand refers to a random number that is uniformly distributed and falls within the range of [0, 1].

Fig. 1
figure 1

Flowchart of AOS

Full size image

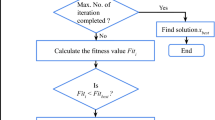
The flowchart of AOS for finding the optimal values of the FOPID controller is given in Fig. 1.

Step 2::

Calculate the binding state \(BS^k\) and energy \(BE^k\) of the \(k_{th}\) layer by using the following relations

$$\begin{aligned}&B S^k=\frac{\sum _{i=1}^p X_i^k}{p},\left\{ \begin{array}{l} i=1,2, \ldots , p \\ j=1,2, \ldots , n \end{array}\right. \nonumber \\&B E^k=\frac{\sum _{i=1}^p E_i^k}{p}, \left\{ \begin{array}{l} i=1,2, \ldots , p \\ j=1,2, \ldots , n \end{array}\right. \end{aligned}$$
(23)

where, \(X_i^k\) and \(E_i^k\) represent the location and objective value of the \(i{th}\) solution possibility in the \(k{th}\) stage, with m being the total number of potential solutions in the search area.

By minimizing the ISE value as an objective function given in Eq. (24), optimization helps in determining the reduced-order model \(G_r(s)\) from the \(n{th}\) order complex plant \(G_n(s)\):

$$\begin{aligned} \text {ISE}=\int _{0}^{t} \left[ y_{n}(t)-y_{r}(t)\right] ^{2} \textrm{dt} \end{aligned}$$
(24)

Other performance indices such as integral time multiplied by squared error (ITSE), integral of absolute error (IAE), and integral of time multiplied by absolute error (ITAE) given in Eqs. (25)–(27) are also computed to compare the closeness of the obtained reduced-order model.

$$\begin{aligned} ITSE&=\int _{0}^{t} t \left[ y_{n}(t)-y_{r}(t)\right] ^{2} \textrm{dt} \end{aligned}$$
(25)
$$\begin{aligned} IAE&= \int _{0}^{t} \mid y_{n}(t) - y_{r}(t) \mid \textrm{dt} \end{aligned}$$
(26)
$$\begin{aligned} ITAE&=\int _{0}^{t} t\mid y_{n}(t)-y_{r}(t) \mid \textrm{dt} \end{aligned}$$
(27)

where, \(y_{n}(t)\) and \(y_{r}(t)\) are the step response of original and reduced-order model and t is the simulation time.

Parameters of AOS for obtaining the optimal values of the FOPID controller are given in Table 1.

Table 1 AOS parameters
Full size table

5 Numerical illustrations

Example 1

In this example, a 9th order system is taken from Tiwari and Kaur (2017).

$$\begin{aligned} G_{9}(s)&=\frac{s^{4}+35 s^{3}+291 s^{2}}{s^{9}+9 s^{8} +66 s^{7}+294 s^{6}+1029 s^{5}+2541 s^{4}} \\&\quad \frac{+1093 s+1700}{+4684 s^{3}+5856 s^{2}+4620 s+1700} \end{aligned}$$

ROM obtained using different techniques are given in the form of coefficients of numerator and numerator and tabulated in 2. \(3{rd}\) order ROM is obtained for Example 1. The step response plot of the original and third-order systems obtained using different techniques is shown in Fig.  2. From Fig 2, it is visible that the reduced order system obtained by Philip & Pal is a close approximation to the original system. Also, Philip & Pal’s ROM gives the lowest settling time value, integral square error, and integral absolute error. A graphical representation of parameters like integral square error (ISE) and integral absolute error (IAE) for different techniques is shown in Fig. 4. Table 2 compares various performance metrics, including peak value, settling time, ISE, ITSE, IAE, and ITAE. These metrics offer insights into different aspects of system behavior and allow for evaluating and contrasting their respective characteristics.

Fig. 2
figure 2

Step response of Example 1

Full size image
Fig. 3
figure 3

Bode plot of Example 1

Full size image
Fig. 4
figure 4

Bar chart representation of performance indices for Example 1

Full size image
Table 2 Qualitative comparison for Example 1
Full size table

Example 2

An 8th order system is taken from the Krishnamurthy and Seshadri (1978) for finding the ROM of 5th order.

$$\begin{aligned} G_{8}(s)&= \frac{35 s^{7}+1086 s^{6}+13285 s^{5} +82402 s^{4}}{s^{8}+33 s^{7}+437 s^{6}+3017 s^{5}+11870 s^{4}} \\&\quad \frac{+278376 s^{3}+511812 s^{2}+482964 s+194480}{+27470 s^{3}+37492 s^{2}+28880 s+9600} \end{aligned}$$

The numerator and denominator coefficients of \(5{th}\) order ROM obtained by different techniques, for Example 2. is given in Table 4. \(5{th}\) order ROM is obtained for Example 2. The step response plot of the original system and \(5{th}\) order system obtained using different techniques is shown in Fig.  5. From Fig. 5, it is visible that the reduced order system obtained by the mixed method of Routh approximation and Pade approximation is close to the original system. Also, ROM obtained by the mixed method of Routh approximation and Pade approximation gives the lowest value of settling time, integral square error, and integral absolute error. A graphical representation of parameters like integral square error (ISE) and integral absolute error (IAE) for different techniques is shown in Fig.  7. Table 3 compares various performance metrics, including peak value, settling time, ISE, ITSE, IAE, and ITAE. These metrics offer insights into different aspects of system behavior and allow for evaluating and contrasting their respective characteristics.

Fig. 5
figure 5

Step response Example 2

Full size image
Fig. 6
figure 6

Bode plot Example 2

Full size image
Fig. 7
figure 7

Bar chart representation of performance indices for Example 2

Full size image
Table 3 Qualitative comparison for Example 2
Full size table

Example 3

An \(8{th}\) order system is taken from the Krishnamurthy and Seshadri (1978) for finding the ROM of \(2{nd}\) order.

$$\begin{aligned} G_{8}(s)&= \frac{18s^7+514s^6+5982s^5+36380s^4}{s^8+36s^7+546s^6+4536s^5+22449s^4} \\&\quad \frac{+122664s^3+222088s^2+185760s+40320}{+67284s^3 +118124s^2+109584s+40320} \end{aligned}$$

The numerator and denominator coefficients of \(5{th}\) order ROM obtained by different techniques, for Example 3. is given in Table 4. \(2{nd}\) order ROM is obtained for Example 3. The step response plot of the original system and \(5{th}\) order system obtained using different techniques is shown in Fig.  5. From Fig. 5, it is visible that the reduced order system obtained by the mixed method of Routh approximation and Pade approximation is close to the original system. Also, ROM obtained by the mixed method of Routh approximation and Pade approximation gives the lowest value of settling time, integral square error, and integral absolute error. A graphical representation of parameters like integral square error (ISE) and integral absolute error (IAE) for different techniques is shown in Fig.  10. Table 4 compares various performance metrics, including peak value, settling time, ISE, ITSE, IAE, and ITAE. These metrics offer insights into different aspects of system behavior and allow for evaluating and contrasting their respective characteristics.

Fig. 8
figure 8

Step response Example 3

Full size image
Fig. 9
figure 9

Bode plot Example 3

Full size image
Fig. 10
figure 10

Bar chart representation of performance indices for Example 3

Full size image
Table 4 Qualitative comparison for Example 3
Full size table

Example 4

In this example a \(5{th}\) order is considered from Prajapati and Prasad (2019, 2020), whose transfer function is given below

$$\begin{aligned} G_{5}(s)=\frac{s^4 + 7s^3 + 42s^2 + 142^s + 156}{s^5 + 25s^4 + 258s^3 + 930s^2 + 1441s + 745} \end{aligned}$$

ROM by proposed technique (AOS) given in Sect. 4 is

$$\begin{aligned} R_{2}(s)=\frac{0.1929s + 0.0047}{s^2 + 0.9257s + 0.0249} \end{aligned}$$

ROM obtained using the Balance Truncation and Routh Approximation (Prajapati and Prasad 2020) in 2019 is as follows.

$$\begin{aligned} R_{2}(s)=\frac{0.1922s + 0.002387}{s^2 + 0.9295s + 0.0114} \end{aligned}$$

ROM obtained using the Stability equation and Pade Approximation (Chen et al. 1980a) is as follows.

$$\begin{aligned} R_{2}(s)=\frac{142.0174s + 156}{909.5238s^2 + 1441s + 745} \end{aligned}$$
Table 5 Performance comparison for Example 4
Full size table
Fig. 11
figure 11

Step response for Example 4

Full size image
Fig. 12
figure 12

Bode plot for Example 4

Full size image
Fig. 13
figure 13

Iteration Graph for Example 4

Full size image

The step response of a ROM obtained using the suggested AOS method is compared with other previously published research and shown in Fig. 11. The bode plot of the original system and the ROM generated by the recommended AOS approach are presented in Fig. 12. The suggested AOS technique’s step response and bode plot of the reduced system are also compared with Prajapati and Prasad (2020), Chen et al. (1979, 1980a, b). The convergence graph of Example 4 is shown in 13. Table 5 presents a numerical data comparison of time response parameters and error indices. Using the suggested method, the ISE value calculated is \(1.35 \times 10^{-4}\), which is smaller than the recently developed reduced-order by the mixed method of Balance truncation and Routh approximation (Prajapati and Prasad 2020). Various metrics demonstrate the proposed AOS method’s effectiveness, including settling time, peak value, and performance indices such as ITAE, IAE, and ITSE. These measures are employed to assess and highlight the efficacy of the AOS approach.

Example 5

In this example, a \(3{rd}\) order system of power system model is considered from Kumar and Sikander (2020), Saxena and Hote (2013), Kumar and Sikander (2021), whose transfer function is given below

$$\begin{aligned} G_{3}(s)=\frac{250}{s^3 + 15.88s^2 + 42.46s + 106.2} \end{aligned}$$

ROM by proposed technique (AOS) given in section 4 is

$$\begin{aligned} R_{2}(s)=\frac{0.000573 s+0.2487}{s^{3}+1.4330 s^{2}+0.9959 s+0.2487} \end{aligned}$$

ROM obtained using Balance Truncation and Routh Approximation (Prajapati and Prasad 2020) in 2019 is as follows.

$$\begin{aligned} R_{2}(s)=\frac{-1.268s + 17.25}{s^2 + 2.391s + 7.327} \end{aligned}$$

ROM obtained using the Routh Hurwitz method (Krishnamurthy and Seshadri 1978) is as follows.

$$\begin{aligned} R_{2}(s)=\frac{250}{15.88s^2 + 35.772s + 106.2} \end{aligned}$$
Fig. 14
figure 14

Step response for Example 5

Full size image
Fig. 15
figure 15

Bode plot for Example 5

Full size image
Fig. 16
figure 16

Iteration Graph for Example 5

Full size image
Table 6 Performance comparison for Example 5
Full size table

The step response of a ROM obtained using the suggested AOS method is compared with other previously published research and shown in Fig. 14. The bode plot of the original system and the ROM generated by the recommended AOS approach are presented in Fig. 15. The suggested AOS technique’s step response and bode plot of the reduced system are also compared with Prajapati and Prasad (2020), Krishnamurthy and Seshadri (1978), Sikander and Prasad (2015a). The convergence graph of example 5 is shown in 16. Table 6 presents a numerical data comparison of time response parameters and error indices. Using the suggested method, the ISE value calculated is \(7.8 \times 10^{-4}\), smaller than the recently developed reduced-order system using the MCS algorithm (Sikander and Thakur 2018). Various metrics demonstrate the proposed AOS method’s effectiveness, including settling time, peak value, and performance indices such as ITAE, IAE, and ITSE. These measures are employed to assess and highlight the efficacy of the AOS approach.

Example 6

In this example, a \(6{th}\) order system is considered to design a PID controller using the proposed technique’s reduced model.

$$\begin{aligned} G_{8}(s)&= \frac{2 s^{5}+3 s^{4}+16 s^{3}}{2 s^{6} +33.6 s^{5}+155.94 s^{4}+209.5 s^{3}} \\&\quad \frac{+20 s^{2}+8 s+1}{+102.42 s^{2}+18.3 s+1} \end{aligned}$$

ROM obtained by the proposed technique is

$$\begin{aligned} \frac{0.0177 s+0.1686}{0.0177 s^{2}+1.7594 s+0.1686} \end{aligned}$$

ROM obtained by Prajapati et al. (2020) is

$$\begin{aligned} \frac{ 5.934s + 1}{101 s^{2}+16.23 s+1} \end{aligned}$$

ROM obtained by Routh Stability (Krishnamurthy and Seshadri 1978) is

$$\begin{aligned} \frac{7.106s+1}{87.38s^{2}+15.94 s+1} \end{aligned}$$

ROM obtained by Stability equation method (Chen et al. 1979) is

$$\begin{aligned} \frac{8s+1}{101s^{2}+18.3 s+1} \end{aligned}$$
Fig. 17
figure 17

Step plot for Example 6

Full size image
Table 7 Comparison of time domain parameters for Example 6
Full size table

The step plot for the original and ROM obtained by the proposed method is shown in Fig. 17. It is evident from the step plot that the ROM obtained by the proposed method is a very close approximation of the original system given in Example 4. This work considers this example for designing the PID controller using the ROM obtained by the proposed method. PID controller using the ROM is designed using the proposed optimization algorithm. By minimizing the ISE values, the proposed method finds the optimal parameters of the PID controller as \(K_p = 99.9967, K_i=25.1755, K_d=29.9144, N=194.8570\). Figure 18 shows the step plot of the closed-loop system with PID controller in a unity feedback configuration. It is evident from Fig. 18 that the controller’s dynamics almost match when the same controller is used in the higher-order original system. The closed-loop step plot of the original system with the suggested controller developed utilizing the ROM system damped out relatively quickly compared to the controller proposed by other authors, as shown in Fig. 18. Table 7 shows the time response parameters and ISE values. It is evident from Table 7 that the settling time, rise time, peak time, and peak overshoot values of the closed-loop system with the proposed controller are lower than the recently developed controller. Also, the ISE value calculated for the proposed system is 0.0276, the lowest among the other proposed controllers (Prajapati et al. 2020; Krishnamurthy and Seshadri 1978; Langholz and Feinmesser 1978; Chen et al. 1979).

Fig. 18
figure 18

Closed loop response with PID controller for Example 6

Full size image

6 Conclusions

This study addresses the challenges of analyzing complex practical systems by comprehensively reviewing the model order reduction (MOR) technique. The research has focused on high-dimensional complex systems, exploring conventional MOR methods’ fundamental theories and limitations. Among the various MOR methods, the Pade approximation (PA) method has emerged as a widely studied and practical approach for retaining the crucial dynamics of such systems.

Furthermore, this study proposes a novel system abatement method based on Atomic Orbital Search (AOS) optimization. This method offers a promising approach for obtaining ROMs of large-scale linear time-invariant (LTI) systems and designing controllers based on the obtained reduced-order model. The accuracy of the reduced order system has been quantitatively compared using parameters such as the integral square error (ISE) and integral absolute error (IAE). The findings of this study provide valuable insights for researchers and practitioners in model order reduction, particularly those working with high-dimensional complex systems. This study is a comprehensive resource for understanding MOR’s core principles, limitations, and practical implications in the context of high-dimensional complex systems.