1 Introduction

Flexible manipulators, providing high productivity and energy efficiency, are regularly advantaged than their rigid analogs. Allowing high speed maneuvering and low energy consumption, they are systematically introduced in innovative industrial applications [1]. However, either their modeling approaches or control strategies, that have been the subject of numerous research papers [2], are far from those used for traditional heavy and rigid structures [3].

A flexible manipulator position tracking must consider its elastic nature, so highly accurate and computational power effective dynamic models are compulsory while deriving a high-precision driving algorithm [4, 5]. The rigid body motion is well modeled using the energetic approaches such as the Lagrange formulation and the Newton–Euler formulation [1, 2, 6], but errors are induced when the potential energy, stored as a deflection at the robot's links, joints or drives, is neglected [3]. When considering their flexible nature, reliable flexible manipulators models result, very often, in continuous partial differential equations with infinite degrees of freedom, so they obligate very high memory usage and inconvenient computational effort. Hence, discretized models are more suitable and are far more employed. Reducing the system degrees of freedom to a finite number is usually achievable via Finite Element Method (FEM) or Assumed Mode Method (AMM) [4]. When the assumed modes method is used, the number of modes to be considered should be reduced to simplify the model simulation, yet the disregarding of higher modes should be wisely sustained to reach the targeted precision [7].

Many research papers have been focusing on flexible manipulator control, and numerous strategies have been used. Essentially, there are two main categories of control schemes when dealing with flexible manipulator active vibration control: feedforward and feedback control. The first idea focuses on the control input filtering/adaptation to anticipate the vibration while tracking the reference rigid body position. Examples of these techniques are the input shaping technique [8, 9] and the trajectory planning [10]. Relatively to this approach, one immediate drawback to mention is the lack of robustness. The feedback control strategies, on the other hand, depend on the system states/outputs to control the vibration in a closed loop framework. Some of these control strategies are based on the linear quadratic regulator [11], adaptive control [12], state decoupling and/or sliding-mode control [13, 14] and fuzzy logic control [15]. As the control signal is a closed loop state-based function, a state observer is very often necessary to this end, and many strategies have been used to dress this issue such as sliding mode observers/differentiators [16,17,18] and extended/unscented Kalman filtering [19, 20].

In this paper, a robust Adaptive Model-based Predictive Controller (AMPC) based on an auxiliary Super-Twisting Integral Sliding Mode Control (STISMC) is proposed. The main objective of the control strategy is to actively damp the flexible manipulator with a feasible control signal in the presence of bounded and matched uncertainties and/or external disturbance. The nominal plant model is derived in Sect. 2. It is a very accurate, yet a nonlinear one. The equations of motion are explicitly deduced using the Hamilton principle, and the elastic displacement is approximated using the assumed modes method. The modeling process allows for several modes of vibration contribution, yet we restrict the proposed model to the first and more significant first one. The underactuated system is formulated in the state space form to simplify the controller description. In the third section, the AMPC algorithm is briefly summarized. State variables required for the behavior prediction are supposed to be available through adequate sensors, so the observer formulation is beyond the scope of this paper. In Sect. 4, the proposed STISMC is introduced, the sliding surface is defined, and the control algorithm is summarized. In Sect. 5, the simulation results are illustrated to assess the controller performances. Different prediction horizons are examined to provide the best possible tuning, and several indicators are then evaluated to appraise the results. Concluding remarks are given in the last section.

2 The One-link flexible manipulator dynamic model

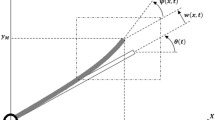
The dynamic model of the flexible one-link manipulator, used for simulation and control algorithm assessment, is detailed in this section. The manipulator, illustrated in Fig. 1, is assumed to be an Euler–Bernoulli clamped-free beam acting on the horizontal plane. The clamped end is rigidly attached to the shaft of an electric servomotor, and the dynamic is fully described by the angular position \(\theta (t)\), the elastic displacement \(w(x,t)\) and the transverse section rotation \(\psi (x,t)\).

Fig. 1
figure 1

Flexible manipulator geometry and coordinates

Full size image

According to the Euler–Bernoulli theory, the shear deformation of the beam is neglected [6], and:

$$\psi \left(r,t\right)=\frac{\partial w\left(r,t\right)}{\partial r}$$
(1)

Hamilton’s principle [6] is used to derive the system equations:

$${\int }_{{t}_{0}}^{{t}_{f}}\left(\delta T-\delta P+\delta W\right)dt=0$$
(2)

\(\mathrm{T}\) and \(\mathrm{P}\) are, respectively, the kinetic and potential energies of the system, while \(\mathrm{W}\) is the work done by external forces. The position \(\left({x}_{M},{y}_{M}\right)\) of a point at a distance \(r\) from the motor shaft, with coordinates \((x,y)\) before deformation, is described in the inertial system \(\left(X,Y\right)\) by (3).

$$\left\{\begin{array}{c}{x}_{M}=rcos\left(\theta \left(t\right)\right)-w\left(r,t\right)\mathit{sin}\left(\theta \left(t\right)\right)-rsin\left(\theta \left(t\right)+\psi \left(r,t\right)\right)\\ {y}_{M}=rsin\left(\theta \left(t\right)\right)+w\left(r,t\right)\mathit{cos}\left(\theta \left(t\right)\right)-rcos\left(\theta \left(t\right)+\psi \left(r,t\right)\right)\end{array}\right.$$
(3)

Let \({\mathrm{I}}_{\mathrm{H}}\) be the motor and hub total inertia, the kinetic energy of the system is then [21]:

$$T=\frac{1}{2} {I}_{H}{\dot{\theta }}^{2}+\frac{1}{2} {\int }_{0}^{L}\rho A\left[{\left(r\dot{\theta }+\dot{V}\right)}^{2}+{\left(V\dot{\theta }\right)}^{2}\right]dr+\frac{1}{2} {\int }_{0}^{L}\rho I{\left(\dot{\theta }+\dot{\psi }\right)}^{2}dr$$
(4)

where \(\uprho ,\mathrm{ A}\) and \(\mathrm{I}\) are respectively the mass density of the beam, its cross-section area and its moment of inertia.

According to the Euler–Bernoulli assumption, and neglecting the gravity effect, the potential energy of the flexible manipulator is only due to its bending rigidity \(EI\). It is given by [6]:

$$P=\frac{1}{2}{\int }_{0}^{L}EI{\left(\frac{{\partial }^{2}w\left(r,t\right)}{\partial {r}^{2}}\right)}^{2}dr$$
(5)

If the mechanical torque applied by the servomotor is \(\tau \left(t\right)\), then the work done by external forces is:

$$\delta W=\tau \delta \theta $$
(6)

The elastic displacement \(w(t)\) is approximated using the assumed modes method:

$$w\left(r,t\right)=\sum_{i=1}^{N}{q}_{i}\left(t\right){\varphi }_{i}\left(r\right)=q\left(t\right)\varphi \left(r\right)$$
(7)

where \({q}_{i}\left(t\right)\) and \({\varphi }_{i}\left(r\right)\) are the \({i}^{th}\) modal coordinate and its respective mode of vibration. \(N\) is the number of assumed modes that we restrict in this study to the first dominant one.

The Hamilton’s principle results on the following equations:

$$\left(EI{\int }_{0}^{L}\frac{{\partial }^{4}\varphi \left(r\right)}{\partial {r}^{4}}dr\right)q\left(t\right)+\rho A\frac{{L}^{2}}{2}\ddot{\theta }\left(t\right)+\left(\left(\rho A{\int }_{0}^{L}\varphi \left(r\right)dr\right)-\left(\rho I{\int }_{0}^{L}\frac{{\partial }^{2}\varphi \left(r\right)}{\partial {r}^{2}}dr\right)\right)\ddot{q}\left(t\right)-\left(\left(\rho A{\int }_{0}^{L}\varphi \left(r\right)dr\right)q\left(t\right)\right){\dot{\theta }(t)}^{2}=0$$
(8)

And

$$\begin{aligned}&\left(\left(\rho A{\int }_{0}^{L}r\varphi \left(r\right)dr\right)+\left(\rho I{\int }_{0}^{L}\frac{\partial \varphi \left(r\right)}{\partial r}dr\right)\right)\ddot{q}\left(t\right)\\ &+\left[\left(\rho A{\int }_{0}^{L}{\varphi }^{2}\left(r\right)dr\right){q\left(t\right)}^{2}\right]\ddot{\theta }\left(t\right)\\ &+\left({I}_{H}+\rho A\frac{{L}^{3}}{3}+\rho IL\right)\ddot{\theta }\left(t\right)\\ &+\left({I}_{H}+\rho A\frac{{L}^{3}}{3}+\rho IL\right)\ddot{\theta }\left(t\right)\\ &+ 2\left[\left(\rho A{\int }_{0}^{L}{\varphi }^{2}\left(r\right)dr\right)q\left(t\right)\dot{q}\left(t\right)\right]\dot{\theta }\left(t\right)=\tau (t)\end{aligned}$$
(9)

Rearranging those equations, we obtain the following general form:

$$M\left(q\right)\left(\begin{array}{c}\ddot{\theta }\\ \ddot{q}\end{array}\right)+h\left(\dot{\theta }, q, \dot{q}\right)+K\left(\begin{array}{c}\theta \\ q\end{array}\right)=u\left(t\right)$$
(10)

where \(M\left(q\right)\) and \(K\) are respectively the mass and the stiffness matrices. The vector \(h(q,\dot{q})\) regroups the nonlinear centrifugal and Coriolis terms, and \(u\left(t\right)={[\begin{array}{cc}\tau (t)& 0\end{array}]}^{T}\) is the vector of external forces. Explicit matrices formulations are given in the appendix.

To higher the accuracy of the model, the motor viscous friction coefficient \({\alpha }_{m}\) and the beam structural damping are considered via a modal damping matrix \({H}_{d}\) as [22]:

$${H}_{d}=\left[\begin{array}{cc}{\alpha }_{m}& 0\\ 0& 2\xi {m}_{22}\omega \end{array}\right]$$
(11)

where \(\omega \) is the first assumed mode natural frequency, and \(\xi \) its respective modal damping coefficient. Coefficient \({ m}_{22}\) is the corresponding element of the mass matrix \(M(q)\).

Considering the damping matrix, the mathematical model of the system is then given by:

$$M\left(q\right)\left(\begin{array}{c}\ddot{\theta }\\ \ddot{q}\end{array}\right)+{H}_{d}\left(\begin{array}{c}\dot{\theta }\\ \dot{q}\end{array}\right)+h\left(\dot{\theta }, q, \dot{q}\right)+K\left(\begin{array}{c}\theta \\ q\end{array}\right)=\left(\begin{array}{c}\tau (t)\\ 0\end{array}\right)$$
(12)

To accommodate the controller formulation, the system equations are formulated in the state space form with the state vector given by:

$$x={\left[\begin{array}{cc}\begin{array}{cc}\theta & q\end{array}& \begin{array}{cc}\dot{\theta }& \dot{q}\end{array}\end{array}\right]}^{T}$$
(13)

So, the model is finally given by:

$$\dot{x}=f\left(x\right)+g\left(x\right)\tau \left(t\right) $$
(14)

With:

$$f= \left[\begin{array}{c}\dot{\theta }\\ {\dot{q}}_{1}\\ -{M\left(q\right)}^{-1}\left({H}_{d}\left(\begin{array}{c}\dot{\theta }\\ \dot{q}\end{array}\right)+h\left(\dot{\theta }, q, \dot{q}\right)+K\left(\begin{array}{c}\theta \\ q\end{array}\right)\right)\end{array}\right]$$
(15)

And:

$$g\left(x\right)= \left[\begin{array}{c}0\\ 0\\ {M\left(q\right)}^{-1}\left[\begin{array}{c}1\\ 0\end{array}\right]\end{array}\right]$$
(16)

3 The adaptive model predictive controller principle

For the MPC algorithm, several structures exist and have proven to be profitable for numerous applications [23]. Its main concept as well as detailed design has been subject of numerous textbooks and research papers, and the authors may suggest [24] for interested readers.

The MPC algorithm based on a linear nominal model is summarized in Fig. 2.

Fig. 2
figure 2

Basic MPC principle

Full size image

The control signal optimizer uses a nominal process model to predict the future system outputs over a prediction horizon of \({N}_{p}\) samples. Based on the references and actual outputs, projected desired trajectories are designed, at each time step, and compared to predicted outputs to calculate future errors. The control signal optimizer then adjusts the next \({N}_{c}\) samples of the control signal, so a cost function \(J\) formulated in terms of future predicted errors and control signal changes, is minimized. It is worth mentioning that when the process model and state/control signal constraints are linear, and \(J\) is quadratic, the control signal may be formulated offline in a state feedback framework. The algorithm is then referred to as linear time invariant MPC, and it results in a convex optimization problem where a global optimum for the process exists.

For a discrete, linear, time invariant system:

$$\left\{\begin{array}{c}x\left(k+1\right)=Ax\left(k\right)+Bu(k)\\ y\left(k\right)=Cx\left(k\right) \end{array}\right.$$
(17)

An augmented state vector is defined:

$${x}_{a}\left(k\right)=\left(\genfrac{}{}{0pt}{}{\Delta x\left(k\right)}{y\left(k\right)}\right)=\left(\genfrac{}{}{0pt}{}{x\left(k+1\right)-x\left(k\right)}{y\left(k\right)}\right)$$
(18)

Then, Eqs. (17) and (18) are rearranged to obtain:

$${x}_{a}\left(k+1\right)={\left[\genfrac{}{}{0pt}{}{\Delta x\left(k+1\right)}{y\left(k+1\right)}\right]}_{\left(n+m\right)\times 1}$$
$$={\left[\begin{array}{cc}A& {0}_{n\times m}\\ CA& {I}_{m\times m}\end{array}\right]}_{\left(n+m\right)\times \left(n+m\right)}{\left[\genfrac{}{}{0pt}{}{\Delta x\left(k\right)}{y\left(k\right)}\right]}_{\left(n+m\right)\times 1}+{\left[\genfrac{}{}{0pt}{}{B}{CB}\right]}_{\left(n+m\right)\times 1}\Delta u\left(k\right)={A}_{a}{x}_{a}\left(k\right)+{B}_{a}\Delta u\left(k\right)$$
(19)

Matrices \({A}_{a}, {B}_{a}\) and \({C}_{a}\) define the augmented state model and are used to optimize the control signal. For the prediction of state and outputs over an optimization window of \({N}_{p}\) samples, let the future \({N}_{c}\) control samples trajectory be denoted as:

$$ \Delta U = [\Delta u(k),\Delta u(k + 1),...\Delta u(k + N_{c} - 1)]^{T} $$
(20)

With the setpoint vector defined in Eq. (21), the cost function that is to be minimized is given by Eq. (22):

$${S}_{p}={\left[\begin{array}{ccc}\begin{array}{cc}1& 1\end{array}& \dots & 1\end{array}\right]}_{1\times {N}_{p}}r\left(k\right)=\overline{{S }_{p}}r\left(k\right)$$
(21)
$$J={\left({S}_{p}-{Y}_{p}\right)}^{T}Q\left({S}_{p}-{Y}_{p}\right)+{\Delta U}^{T}R\Delta U$$
(22)

where \(Q\) and \(R\) are symmetric semidefinite weighting matrices.

The control signal that minimizes the cost function is calculated assuming that:

$$ \frac{\partial J}{{\partial \Delta U}} = 0 = - 2\phi^{T} Q(S_{p} - Fx(k_{i} )) + 2(\phi^{T} \phi + R)\Delta U $$
(23)

With:

$$F={\left[\begin{array}{ccc}{C}_{a}{A}_{a}& {C}_{a}{A}_{a}^{2}& {C}_{a}{A}_{a}^{3}\end{array} \begin{array}{cc}\dots & {C}_{a}{A}_{a}^{{N}_{p}}\end{array}\right]}^{T}$$
(24)

And

$$\Phi =\left[\begin{array}{ccccc}{C}_{a}{B}_{a}& 0& 0& \dots & 0\\ {C}_{a}{A}_{a}{B}_{a}& {C}_{a}{B}_{a}& 0& \dots & 0\\ {C}_{a}{A}_{a}^{2}{B}_{a}& {C}_{a}{A}_{a}{B}_{a}& {C}_{a}{B}_{a}& \dots & 0\\ \dots & \dots & \dots & \dots & \dots \\ \dots & \dots & \dots & \dots & \dots \\ {C}_{a}{A}_{a}^{{N}_{p}-1}{B}_{a}& {C}_{a}{A}_{a}^{{N}_{p}-2}{B}_{a}& {C}_{a}{A}_{a}^{{N}_{p}-3}{B}_{a}& \dots & {C}_{a}{A}_{a}^{{N}_{p}-{N}_{c}}{B}_{a}\end{array}\right]$$
(25)

Finally, at time sample \(k\), the feedback incremental control within the framework of predictive control is given by:

$$ \Delta u(k) = \begin{array}{*{20}c} {\left[ {[\begin{array}{*{20}l} 1 \hfill & 0 \hfill & 0 \hfill & {...} \hfill & 0 \hfill \\ \end{array} } \right]_{{1 \times N_{c} }} (\phi^{T} \phi + R)^{ - 1} \phi^{T} Q\overline{S}_{p} ]r(k)} \\ { - \left[ {[\begin{array}{*{20}l} 1 \hfill & 0 \hfill & 0 \hfill & {...} \hfill & 0 \hfill \\ \end{array} } \right]_{{1 \times N_{c} }} (\phi^{T} \phi + R)^{ - 1} \phi^{T} QF]x(k_{i} )} \\ \end{array}={K}_{r}r\left(k\right)- {K}_{x}x\left({k}_{i}\right)$$
(26)

When dealing with a nonlinear model, the AMPC algorithm is a possible solution. The process model is linearized at each time step around the actual state and control signal. The problem is still a convex optimization one, except that the process model is time-variant, reason why it should be adapted iteratively.

4 Integral super twisting sliding mode control

The nominal plant has been used for the AMPC predictions in the earlier section, and an auxiliary integral sliding mode controller is proposed, in this section, to tackle uncertainties and external disturbance that may affect the flexible manipulator. The integral sliding mode control (ISMC) maintains the order of the compensated system’s dynamics and can be systematically combined to the AMPC algorithm. Nevertheless, conventional ISMC always causes inadmissible chattering over the control input, so a super twisting integral sliding mode controller is suggested in this study.

The nominal model for the one-link flexible manipulator is given by Eqs. (14), (15) and (16) derived in Sect. 2. Uncertainties on the system parameters and external disturbance are introduced in this section as follows:

$$\dot{x}=\left(f\left(x\right)+\Delta f\left(x\right)\right)+\left(g\left(x\right)+\Delta g\left(x\right)\right)\tau \left(t\right)+d\left(x,t\right)={\dot{x}}_{nom}+\Delta f\left(x\right)+\Delta g\left(x\right)\tau \left(t\right)+d\left(x,t\right)$$
(27)

where \({\dot{x}}_{nom}\) is the nominal part of the system used for the AMPC controller development. \(\Delta f\left(x\right)\) and \(\Delta g\left(x\right)\) are the lumped uncertainties of the system, and \(d\left(x,t\right)\) is a bounded external disturbance.

In this work, we assume that system uncertainties as well as external disturbance are satisfying the matching condition, so we may write:

$$\Delta f\left(x\right)+\Delta g\left(x\right)\tau \left(t\right)+d\left(x,t\right)=g\left(x\right)v\left(x,u,t\right)$$
(28)

We also assume that the upper bound of the equivalent disturbance \(\left({v}_{m}=\mathrm{sup}\left|v(t)\right|\right)\) is known.

The proposed control scheme aims to control the system using both the AMPC control \({u}_{nom}\), based on the nominal plant derived in the earlier section, while ensuring the robustness of the control law using the ISMC control \({u}_{ISM}\). The control signal is then given by:

$$u={u}_{nom}+{u}_{ISM}$$
(29)

The integral sliding surface is defined as [25]:

$$s=F\left(x-{x}_{0}-{\int }_{0}^{t}{\dot{x}}_{nom} dt\right)$$
(30)

\(F\) is a design vector parameter such that \(Fg(x)\) is non singular.

Now, we have:

$$\begin{aligned}\dot{s}&=F\left(\dot{x}-{\dot{x}}_{nom}\right)\\ &=F\Bigg(f\left(x\right)+g\left(x\right)\left({u}_{nom}+{u}_{ISM}\right)+g\left(x\right)v\left(x,u,t\right)-f\left(x\right) \\ &\quad -g\left(x\right){u}_{nom}\Bigg) =F\left(g\left(x\right){u}_{ISM}+g\left(x\right)v\left(x,u,t\right)\right)\end{aligned}$$
(31)

The auxiliary sliding mode should start from the very beginning without any reaching phase, and the conventional ISM control is derived based on the \(k\)-reachability condition given by \(s\dot{s}<k\left|s\right|\) [26].

Let the ISM control signal be:

$${u}_{ISM}=-{v}_{m}-{\left(Fg\left(x\right)\right)}^{-1}ksign\left(s\right)$$
(32)

Then, using the Lyapunov candidate function \(V=\frac{1}{2}{s}^{2}\), we have:

$$\frac{dV}{dt}=s\dot{s}$$
$$\qquad\,\,=F\left(g\left(x\right){u}_{ISM}+g\left(x\right)v\left(x,u,t\right)\right)s$$
$$\begin{aligned}\qquad\,\,&=F\Bigg(g\left(x\right)\left(-{v}_{m}-{\left(Fg\left(x\right)\right)}^{-1}ksign\left(s\right) \right)\\ &\qquad +g\left(x\right)v\left(x,u,t\right)\Bigg)s\end{aligned}$$
$$\begin{aligned}\qquad &<F\left(g\left(x\right)\left(-{v}_{m}-{\left(Fg\left(x\right)\right)}^{-1}ksign\left(s\right) \right)+g\left(x\right){v}_{m}\right)s\\ \qquad &= -k\left|s\right|\end{aligned}$$
(33)

The use of the sign function \(\left(sign\left(s\right)\right)\) will cause the chattering to be dominant in the control input given by (32). To prevent this, we propose in this study the use of the supertwisting algorithm [27] to ensure the robustness of the control strategy, while eliminating the chattering. Hence,

$$\left\{\begin{array}{ll}{u}_{ISM}=-\lambda \sqrt{\left|s\right|}sign\left(s\right)+z\\ \dot{z}=-\alpha sign\left(s\right)\end{array}\right.$$
(34)

And the modified control signal is finally given by:

$$\left\{\begin{array}{ll}{u}_{ISM}=\left(-\lambda \sqrt{\left|s\right|}sign\left(s\right)+z\right){\left(Fg\left(x\right)\right)}^{-1}\\ \dot{z}=-\alpha sign\left(s\right) \end{array}\right.$$
(35)

5 Simulations results

The performance of the AMPC controller, regarding the tracking of the flexible manipulator rigid body position (\(\theta \left(t\right)\)) along with vibration (\(q\left(t\right)\)) minimizing, is first analyzed. The nominal model is used for the optimization of the control signal over the prediction horizon. Then, the effectiveness of the proposed ISMC to tackle the uncertainties affecting the system while maintaining the control signal free of chattering is assessed.

The explicit expression of different matrices used for the system modeling are given in the appendix, and Table 1 shows the beam and the DC motor parameters used for the numerical simulation.

Table 1 Numerical parameters of the system
Full size table

The AMPC algorithm was implemented in Matlab environment, and the model simplifying as well as the Jacobians derivation was carried out using the Matlab Symbolic Math Toolbox. Small time steps for numerical integration have been required due to the nonlinearities of the nominal plant. The step time has been set to \(0.001\mathrm{ s}\).

The AMPC controller effectiveness is stated for different prediction horizons. The parameters for the controller tuning are set as reported in Table 2, and the setpoints are set to \({\theta }_{ref}=\pi /2 rad\) and \({q}_{ref}=0\).

Table 2 AMPC tuning parameters when only \({\varvec{\theta}}\left({\varvec{t}}\right)\) is predicted
Full size table

In Figs. 3, 4 and 5, are illustrated the angular position, modal coordinate and control signal respectively, with predictions on the pair \(\theta \left(t\right)\) and \(q\left(t\right)\) over different prediction horizons.

Fig. 3
figure 3

Angular position \(\theta \left(t\right)\) for different prediction horizons

Full size image
Fig. 4
figure 4

Modal coordinate \(q\left(t\right)\) for different prediction horizons

Full size image
Fig. 5
figure 5

Nominal control signal for different prediction horizons

Full size image

Smaller prediction horizon results in an unsatisfactory rigid body response. The angular position response has an important overshoot, and a very large settling time. Thus, it is inferred that, although a larger prediction horizon leads to a larger calculation time, and may require sophisticated material resources, it produces much better output responses.

In Table 3, a summary of output performances is outlined. For the rigid body component \(\theta \left(t\right),\) the overshoot \(d\mathrm{\%}\) and the settling time for \(5\mathrm{\%}\) tolerance band are inspected, while the maximum absolute value and root mean squared error (cf. Equation (35) with \({T}_{s}\) the sampling time and \({N}_{S}\) the number of samples) are appraised for the modal coordinate \(q\left(t\right)\). The control signal incremental weighting matrix is a scalar set to 10.

Table 3 Summary of the output performances for different AMPC prediction horizons
Full size table
$$RMSE\left(q\left(t\right)\right)=\sqrt{\frac{1}{{N}_{s}}\sum_{k=0}^{{N}_{s}-1}{\left(q(k{T}_{s})\right)}^{2}}$$
(35)

According to the results in Table 3, the prediction horizon has a great impact on the rigid body position angular. A smaller prediction horizon (e.g. \({N}_{p}=100\)) leads to undesirable overshoot \(\left(23.97\mathrm{\%}\right)\) and very slow dynamic \(\left({tr}_{5\mathrm{\%}}\gg 10s\right)\). However, the maximum absolute value of the modal coordinate is clearly lowered \(\left(0.0086\right)\). The best performance agreement is met when \({N}_{p}=2000\) and \(Q=\left[\begin{array}{cc}10& 0\\ 0& 5000\end{array}\right]\).This configuration results in a rigid body dynamic with no overshoot, a settling time of \(2.2189s\), a maximum absolute value of the modal coordinate equal to \(0.0342\) and the best modal coordinate RMSE that is equal to \(0.0081\).

To assess the effectiveness of the super twisting ISMC, a sine wave disturbance has been added to the nominal control signal:

$$v\left(t\right)=0.4\mathrm{sin}\left(2\pi t\right)$$
(36)

For the controller, parameters \(\alpha \) and \(\lambda \) has been set to \(5\) and \(2\) respectively. The vector parameter \(F\) has been set to \(\left[\begin{array}{cc}\begin{array}{cc}0& 0\end{array}& \begin{array}{cc}1& 1\end{array}\end{array}\right]\).

In Fig. 6, are illustrated the nominal torque \({u}_{nom}\left(t\right)\) and the disturbed one \({u}_{nom}\left(t\right)+v\left(t\right)\). The nominal torque is optimized via the AMPC controller for the best agreement of performance found earlier.

Fig. 6
figure 6

Optimal nominal control and disturbed control

Full size image

As illustrated in Fig. 7, the super twisting integral sliding mode control \({u}_{ISM}\left(t\right)\) is slightly the opposite of the bounded disturbance and is quasi chattering free. Thus, the effect of the equivalent disturbance on the system is tackled from the very beginning, and the robustness of the optimal control law is guaranteed. The perfect matching of nominal and disturbed angular position \(\theta \left(t\right)\) and modal coordinate \(q(t)\), illustrated in Figs. 8 and 9 respectively, demonstrates the effectiveness of the proposed control scheme.

Fig. 7
figure 7

ISMC control and equivalent disturbance

Full size image
Fig. 8
figure 8

Nominal and disturbed angular positions \(\theta \left(t\right)\)

Full size image
Fig. 9
figure 9

Nominal and disturbed modal coordinates \(q\left(t\right)\)

Full size image

6 Conclusions

Adaptive Model Predictive Control has been used to track the rigid body position of a one-link flexible manipulator regarding its residual vibration minimizing. The control scheme has been associated to a STISMC to guarantee its robustness in the presence of bounded system uncertainties and/or external disturbance.

The STISMC has demonstrated that the output of the system subject to a time variable disturbance is the same as the output of the nominal one. Furthermore, the control signal provided by the controller is chattering free, so it is practical for an experimental setup.

The control strategy offered the best performance tradeoff when the prediction horizon is of \(2000\) samples, and the weighting matrix \(Q\) is \(\left[\begin{array}{cc}10& 0\\ 0& 5000\end{array}\right]\). Simulation results showed that the rigid body dynamic is with no overshoot and that the settling time of \((2.2189s)\) is very satisfying. Also, the maximum absolute value of the modal coordinate has been lowered to \(0.0342\) and the modal coordinate RMSE to \(0.0081\).

The illustration of the control torque, required for the best performance agreement, made clear its possible implementation in an experimental context if compared to other control strategies commonly used for active vibration control.