Keywords

1 Introduction

With the advancement of technology, many manual works are replaced by robots in the field of medicine, industries, military, aerospace and so on [1, 2]. In the field of robotics, many anthropomorphic manipulators are assigned to carry and move objects in specialised sectors [3]. For faster operational speed and lesser energy consumption, many rigid and bulky manipulators are replaced by flexible manipulators [4]. In recent decades, flexible manipulators have acquired and received much attention in modelling the dynamics and its control for completing the task faster [5, 6]. Many control methods are exploited to deal with payload variation and modelling uncertainties [7]. Some problems are solved for controlling payload variations at the free end [8]. Moreover, control of tip position of a flexible manipulator using an adaptive model predictive approach is done in [9]. Some control approaches are reported for controlling a two-link flexible manipulator (TLFM) like backstepping [10], SMC techniques [11, 12], fuzzy logic control [13], etc. However, many challenges like high non-linearity, uncertainties and elastic deformations are hardly overcome [14].

Reference [15] discussed the control problems by applying singular perturbation and applied to flexible manipulators. In [16], it is shown that the frequencies of the elastic deflections are much more higher than the rigid counterparts and hence a flexible manipulator system can be divided into two parts. A slow subsystem and a fast subsystem. References [17, 18] adopted computed torque method for controlling the slow subsystem and pole placement for controlling the fast subsystem. Variable structure control is used for the slow subsystem and Lyapunov based control, virtual force control are designed for the fast subsystem in [19, 20], respectively. However, the choice of the controller parameters in the above reported papers are user dependent. Hence, there is a wider scope to improve this issue where the control parameters are computed through a process which is feasible and optimal.

Fig. 1.
figure 1

Schematic diagram of a planar two-link flexible manipulator.

Full size image

In this chapter, we propose a robust control technique which includes Linear Matrix Inequality (LMI) with Sliding Mode Control (SMC) for the slow subsystem and LMI with state feedback strategy for the fast subsystem. The simulation results are shown where the desired trajectories are tracked and deflections are suppressed properly.

The rest of the paper is organised as follows: Sect. 2 describes the mathematical modelling of a two-link flexible manipulator. Model decomposition by singular perturbation is given in Sect. 3. Designing of a controller, and results and discussion are given in Sects. 4 and 5, respectively. Finally, Sect. 6 describes the conclusions of this paper.

2 Mathematical Modelling of a Two-Link Flexible Manipulator

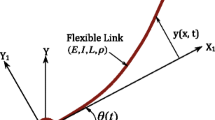
Considering a TLFM is rotated in a horizontal plane by two motors, let \((X_{0},Y_{0})\) represents the generalised coordinate frame in Fig. 1. \((X_{i},Y_{i})\) be the inertial frame and \((\hat{X}_{i},\hat{Y}_{i})\) be the moving frame associated with the \(i^{th}\) link of the rigid body. A payload of mass \(M_{p}\) is attached at the tip of the manipulator. \(\theta _{i}\) is the joint angle made by each \(i^{th}\) link. The total displacement made by the flexible manipulator is given as

$$\begin{aligned} y_{i}=\theta _{i}l_{i}+u_{i} \end{aligned}$$
(1)

where \(u_{i}\) is the elastic deflection. \(l_{i}\) is the length of \(i^{th}\) link. The elastic deflection is given as

$$\begin{aligned} u_{i}(x,t)=\sum _{j=1}^{n}\eta _{ij}(t)\xi _{ij}(x) \end{aligned}$$
(2)

where \(\eta _{ij}(t)\) is the \(j^{th}\) modes and \(\xi _{ij}(x)\) is the \(j^{th}\) mode shape of the \(i^{th}\) link. Thus, the generalised Lagrangian co-ordinate can be given as \(q=[\theta ^{T}_{i},\eta ^{T}_{ij}(t)]\). The dynamic equation of a TLFM based on Lagrange’s assumed modes method [21] can be written as

$$\begin{aligned} N(\theta _{ij},\eta _{ij})\left( \begin{array}{c} \ddot{\theta }_{i} \\ \ddot{\eta }_{ij} \\ \end{array} \right) +h(\theta ,\dot{\theta },\eta _{ij},\dot{\eta }_{ij})+K\left( \begin{array}{c} \theta _{i} \\ \eta _{ij} \\ \end{array} \right) +D\left( \begin{array}{c} \dot{\theta }_{i} \\ \dot{\eta }_{ij} \\ \end{array} \right) =\left( \begin{array}{c} I \\ 0 \\ \end{array} \right) \tau \end{aligned}$$
(3)

which can be further simplified as

$$\begin{aligned} N(q)\ddot{q}+h(q,\dot{q})+Kq+D\dot{q}=\left( \begin{array}{c} I \\ 0 \\ \end{array} \right) \tau \end{aligned}$$
(4)

where \(q=[\theta _{1},\theta _{2},\eta _{11},\eta _{12},\eta _{21},\eta _{22}]^{T}=[\theta ^{T}~\eta ^{T}]^{T}\), N(q) is the inertia matrix, \(h(q,\dot{q})\) is the centrifugal and coriolis force, K is the positive definite stiffness matrix, D is the positive definite damping matrix and \(\tau \) is the joint torque. All the matrices are of approximate dimensions and two modes are considered here.

3 Model Decomposition by Singular Perturbation

Considering only the first two modes of a link of a TLFM, the dynamic model can be written as

$$\begin{aligned} N\left( \begin{array}{c} \ddot{\theta } \\ \ddot{\eta } \\ \end{array} \right) +\left( \begin{array}{c} h_{s}(\theta ,\dot{\theta },\eta ,\dot{\eta }) \\ h_{f}(\theta ,\dot{\theta },\eta ,\dot{\eta }) \\ \end{array} \right) +\left( \begin{array}{c} D_{1}\dot{\theta } \\ D_{2}\dot{\eta } \\ \end{array} \right) +\left( \begin{array}{c} K_{1}\theta \\ K_{2}\eta \\ \end{array} \right) =\left( \begin{array}{c} I \\ 0 \\ \end{array} \right) \tau \end{aligned}$$
(5)

where \(\theta =[\theta _{1}~\theta _{2}]^{T}\) is the joint angle, \(\eta =[\eta ^{T}_{1}~\eta ^{T}_{2}]^{T}\), \(\eta _{i}=[\eta _{i1}~\eta _{i2}]^{T}\) is the modes of the \(i^{th}\) link and \(i=1,2\). The mass matrix is a positive definite and its inverse is written as

$$\begin{aligned} N^{-1}=B=\left( \begin{array}{cc} B_{11} &{} B_{12}\\ B_{21} &{} B_{22}\\ \end{array} \right) =\left( \begin{array}{cc} M_{s} &{} M_{sf}^{T}\\ M_{sf} &{} M_{f}\\ \end{array} \right) ^{-1} \end{aligned}$$
(6)

where \(M_{s}=(B_{11}-B_{12}B_{22}^{-1}B_{21})^{-1}\), \(B_{11}\in R^{2X2}\), \(B_{12}\in R^{2X4}\), \(B_{21}\in R^{4X2}\), \(B_{22}\in R^{4X4}\) and \(K_{1}=0\). We can rewrite (5) as

$$\begin{aligned} \ddot{\theta }=-B_{11}(D_{1}\dot{\theta }+h_{s}+K_{1}\theta )-B_{12}(D_{2}\dot{\eta }+h_{f}+K_{2}\eta )+B_{11}\tau \end{aligned}$$
(7)
$$\begin{aligned} \ddot{\eta }_{ij}=-B_{21}(D_{1}\dot{\theta }+h_{s}+K_{1}\theta )-B_{22}(D_{2}\dot{\eta }+h_{f}+K_{2}\eta )+B_{21}\tau \end{aligned}$$
(8)

For a singular perturbation, we define a new state variables \(\eta =\epsilon \delta \) and \(K_{s}=\epsilon K_{2}\) and \(\epsilon \) is the perturbation parameter. \(\frac{1}{\epsilon }\) is the smallest value of the stiffness constant matrix K. The singularly perturbed model of a TLFM, given in (7) and (8), can be described as

$$\begin{aligned} \ddot{\theta }=-B_{11}(D_{1}\dot{\theta }+h_{s})-B_{12}(D_{2}\epsilon \dot{\delta }+h_{f}+K_{s}\delta )+B_{11}\tau \end{aligned}$$
(9)
$$\begin{aligned} \ddot{\eta }=-B_{21}(D_{1}\dot{\theta }+h_{s})-B_{22}(D_{2}\epsilon \dot{\delta }+h_{f}+K_{s}\delta )+B_{21}\tau \end{aligned}$$
(10)

With the composite control strategy, the total torque can be divided as

$$\begin{aligned} \tau =\tau _{s}+\tau _{f} \end{aligned}$$
(11)

where \(\tau _{s}\) and \(\tau _{f}\) are the torques for the slow and fast subsystems, respectively.

For identifying the slow subsystem, we set \(\epsilon =0\) in (10) and is obtained as

$$\begin{aligned} \bar{\delta }=-K_{s}^{-1}\bar{B}_{22}^{-1}(\bar{B}_{21}\bar{D}_{1}\dot{\bar{\theta }}+\bar{B}_{21}\bar{h}_{s}+\bar{B}_{22}\bar{h}_{f}-\bar{B}_{21}\tau _{s}) \end{aligned}$$
(12)

where overbar indicates the value of the variable when \(\epsilon =0\).

Applying two-time scale perturbation technique, the slow and the fast subsystems can be obtained. The slow subsystem is described as

$$\begin{aligned} \ddot{\bar{\theta }}=(\bar{B}_{11}-\bar{B}_{12}\bar{B}_{22}^{-1}\bar{B}_{21})(-\bar{D}_{1}\dot{\bar{\theta }}-\bar{h}_{s}+\tau _{s}) \end{aligned}$$
(13)

Using (6), the slow subsystem can be written as

$$\begin{aligned} \ddot{\bar{\theta }}=\bar{M}_{s}^{-1}(-\bar{D}_{1}\dot{\bar{\theta }}-\bar{h}_{s}+\tau _{s}) \end{aligned}$$
(14)

In order to derive a boundary layer correction, a fast time scale, \(\gamma =\frac{t}{\sqrt{\epsilon }}\) and boundary layer correction terms \(x_{1}=\delta - \bar{\delta }\) and \(x_{2}=\sqrt{\epsilon }\delta \) is defined.

The fast subsystem is described as

$$\begin{aligned} \dot{x}_{f}=A_{f}x_{f}+B_{f}\tau _{f} \end{aligned}$$
(15)

where \(A_{f}=\left( \begin{array}{cc} 0 &{} I \\ -\bar{B}_{22}K_{s} &{} 0 \\ \end{array} \right) \); \(B_{f}=\left( \begin{array}{c} 0 \\ \bar{B}_{21} \\ \end{array} \right) \); \(x_{f}=\left( \begin{array}{c} x_{1} \\ x_{2} \\ \end{array} \right) \)

which corresponds to the linear system parameters of the slow subsystem.

4 Designing of Controller

The dynamics of the slow subsystem of a TLFM, given in (14) can be written in state space form as

$$\begin{aligned} \dot{w}=A(w)w+B(w)u+d(t) \end{aligned}$$
(16)

where \(w=[\bar{\theta }^{T}~\dot{\bar{\theta }}^{T}]=[w_{1}^{T}~w_{2}^{T}]^{T}\), \(w_{1}=\bar{\theta }\), \(w_{2}=\dot{\bar{\theta }}\), \(u=\tau _{s}\), \(d=[0^{T}~d_{l}^{T}]^{T}\in R^{4X1}\).

$$\begin{aligned} A(w)=\left( \begin{array}{cc} 0 &{} I \\ 0 &{} -M_{s}^{-1}D_{1} \\ \end{array} \right) , B(w)=\left( \begin{array}{c} 0 \\ -M_{s}^{-1} \\ \end{array} \right) \end{aligned}$$
(17)

Here, the system matrix A(w) and input matrix B(w) are written as

$$\begin{aligned} A(w)=\left( \begin{array}{cc} A_{11} &{} A_{12} \\ A_{21} &{} A_{22} \\ \end{array} \right) , B(w)=\left( \begin{array}{c} 0 \\ B_{2} \\ \end{array} \right) \end{aligned}$$
(18)

where \(A_{11}=0_{2X2}\), \(A_{12}=I_{2X2}\), \(A_{21}=0_{2X2}\), \(A_{22}=-M_{s}^{-1}D_{1}\in R^{2X2}\), \(B_{2}= -M_{s}^{-1}\in R^{2X2}\).

Now, the state space model of (16) can be written as

$$\begin{aligned} \dot{w}_{1}=A_{11}w_{1}+A_{12}w_{2} \end{aligned}$$
(19)
$$\begin{aligned} \dot{w}_{2}=A_{21}w_{1}+A_{22}w_{2}+B_{2}u+d_{l} \end{aligned}$$
(20)

where \(d_{l}\) is the matched uncertainties and is bounded as \(|d_{l}(t)|=|\dot{d}_{l}(t)|\le l_{l}\)

4.1 LMI Based SMC for Slow Subsystem

Here, a normal SMC using LMI is designed for the trajectory tracking of the slow subsystem of a TLFM. Consider the \(w_{di}\in R^{2X1}\) be the desired trajectories, then trajectories tracking error dynamics is defined as

$$\begin{aligned} {\left\{ \begin{array}{ll} e_{1}=w_{1}-w_{d1}\\ e_{2}=w_{2}-w_{d2} \end{array}\right. } \end{aligned}$$
(21)

where \(w_{d1}=[\theta _{1d}~\theta _{2d}]^{T}, w_{d2}=[\dot{\theta }_{1d}~\dot{\theta }_{2d}]^{T}\).

Assumption 1

Consider the \(w_{di}\) is consistent with the plant system matrix. Let the dynamics of the desired trajectories \(w_{di}\) is continuous and is excited by \(u_{w}\). It is described as:

$$\begin{aligned} \dot{w}_{d1}=A_{11} w_{d1}+A_{12} w_{d2} \end{aligned}$$
(22)
$$\begin{aligned} \dot{w}_{d2}=A_{21} w_{d1}+A_{22} w_{d2}+u_{w} \end{aligned}$$
(23)

Now, the normal sliding surface is defined as

$$\begin{aligned} s(e)=e_{2}+\lambda e_{1} \end{aligned}$$
(24)

where \(\lambda >0\) is the constant matrix which is determined here using LMI toolbox.

The necessary condition for the existence of sliding surface is \(s(e)=0\), the equivalent sliding mode dynamics is described as

$$\begin{aligned} e_{2}=-\lambda e_{1} \end{aligned}$$
(25)

Using (18), (19), (22) and (23), the equivalent sliding mode dynamics for \(e_{1}\) is described as

$$\begin{aligned} \dot{e}_{1}=(A_{11}-A_{12}\lambda )e_{1} \end{aligned}$$
(26)

Theorem 1

Suppose, there exist matrices \(\beta ,X,Y>0\) with appropriate dimensions and satisfy the following LMI:

$$\begin{aligned} Q=\left( \begin{array}{cc} A_{11}X-A_{12}Y+XA_{11}^{T}-Y^{T}A_{12}^{T} &{} X \\ X &{} -\alpha \\ \end{array} \right) < 0 \end{aligned}$$
(27)

Then, the error dynamics (26) is asymptotically stable. The value of \(\lambda \) can be obtained as \(\lambda =YX^{-1}\).

Proof

Considering a Lyapunov function candidate as

$$\begin{aligned} {\left\{ \begin{array}{ll} V_{1}(e_{1})=e^{T}_{1}Re_{1} \dot{V}_{1}(e_{1})=e_{1}^{T}R\dot{e}_{1}+\dot{e}_{1}^{T}Re_{1} \end{array}\right. } \end{aligned}$$
(28)

where R is positive definite matrix. Using (26), (28) can be written as

$$\begin{aligned} \dot{V}_{1}(e_{1})=e_{1}^{T}[R(A_{11}-A_{12}\lambda )+(A_{11}-A_{12}\lambda )^{T}R]e_{1} \end{aligned}$$
(29)

Suppose the following inequality holds

$$\begin{aligned} R(A_{11}-A_{12}\lambda )+(A_{11}-A_{12}\lambda )^{T}R\le -\alpha ^{-1} \end{aligned}$$
(30)

then

$$\begin{aligned} \begin{aligned} \dot{V}_{1}&\le e_{1}^{T}(-\alpha ^{-1})e_{1}\\&\le -(\mu _{min}(\alpha ^{-1}))\Vert e_{1}\Vert ^{2} \end{aligned} \end{aligned}$$
(31)

where \(\mu _{min}\) is the minimum eigenvalue of \(\alpha ^{-1}\). The Lyapunov function (31) can be simplified as

$$\begin{aligned} \dot{V}_{1}\le -\gamma V_{1}(e_{1}) \end{aligned}$$
(32)

where \(\gamma =(\mu _{min}(\alpha ^{-1})/\mu _{max}(R))\). Since \(\alpha \) is the positive definite matrix, the quantity \(\gamma \) is the positive scalar. Now, consider \(X=R^{-1}\)and pre multiplying and post multiplying X in (30) we get

$$\begin{aligned} A_{11}X-A_{12}\lambda X+XA_{11}^{T}-A_{12}^{T}(\lambda X)^{T}\le -X\alpha X^{-1} \end{aligned}$$
(33)

Considering \(Y=\lambda X\) in (33) and using Shur complement [22], the LMI in (28) is satisfied. Thus, the equivalent sliding mode error dynamics (26) is asymptotically stable if the LMI (27) is feasible.

The existence of the manipulator dynamics (16) on the sliding surface (34) is achieved using the following Theorem 2.

Theorem 2

Consider, the sliding surface defined in (24) and suppose the value of \(\lambda \) is determined using LMI in (27), and if the control torque input for the slow subsystem of TLFM dynamics (16) is defined as

$$\begin{aligned} \tau _{s}=M_{s}P_{s}+h_{s}+D_{1}\dot{\bar{\theta }}-\rho tanh(s) \end{aligned}$$
(34)

where \(P_{s}=-c_{s}e_{2}+\ddot{z}_{d}\), tanh is the tan hyperbolic function and \(\rho \) is the positive gain. Then, the trajectories of the flexible manipulator dynamics converge to the sliding surface (24) in finite time and remain on it.

Proof

Consider another Lyapunov function candidate as

$$\begin{aligned} V_{2}(s)=\frac{1}{2}ss^{T} \end{aligned}$$
(35)

Taking the derivative (35) and using (24), it can be written as

$$\begin{aligned} \dot{V}_{2}(s)=-\frac{\eta }{\sqrt{2}}\le -\eta V_{3}^{\frac{1}{2}} \end{aligned}$$
(36)

where \(\eta >0\) and \(\rho = \lambda l_{l}+\frac{\eta }{\sqrt{2}}\). Hence, the joint trajectories of the flexible manipulator (3) follow the desired trajectories using the control input torque proposed in (34).

4.2 LMI Based State Feedback Controller (SFC) for Fast Subsystem

Here, in this section an LMI based state feedback controller (SFC) is designed for regulating the fast subsystem dynamics of the TLFM to zero. Suppose the matrices \(A_{f}\) and \(B_{f}\) in (15) are controllable then a suitable state feedback based controller can be designed as below.

$$\begin{aligned} \tau _{f}=-kx_{f} \end{aligned}$$
(37)

where \(k\in R^{2X8}\) is the positive definite matrix and its value is determined using the feasible solution of a LMI obtained from Theorem 3.

Theorem 3

Suppose there exist matrices \(P,S>0\) with appropriate dimensions and following LMI is satisfied:

$$\begin{aligned} {\left\{ \begin{array}{ll} P>0\\ A_{f}P-B_{f}S+PA_{f}^{T}-S^{T}B_{f}^{T}<0 \end{array}\right. } \end{aligned}$$
(38)

Then, the fast subsystem is asymptotically stable along the equilibrium trajectory \(\bar{x}\) defined in (12). The value of k in (37) can be obtained as \(k=SP^{-1}\).

Proof

Suppose there exist a positive definite matrix P which satisfies the following inequality

$$\begin{aligned} A_{c}P+PA_{c}^{T}<0 \end{aligned}$$
(39)

where \(A_{c}=(A_{f}-B_{f}k)\) is the closed loop state matrix of (15). The inequality (38) can be written as

$$\begin{aligned} (A_{f}-B_{f}k)P+P(A_{f}-B_{f}k)^{T}<0 \end{aligned}$$
(40)

Now, consider a positive definite matrix S which is described as \(S=kP\), then (40) can be modified as

$$\begin{aligned} A_{f}P-B_{f}S+PA_{f}^{T}-S^{T}B_{f}^{T} \end{aligned}$$
(41)

Thus, using (41), the LMI in (38) can be obtained. In (41) two matrices P and S are unknown whose value can be obtained from the feasible solution of LMI defined in (38). The gain of the SFC input k can be obtained as \(k=SP^{-1}\).

Fig. 2.
figure 2

Joint trajectory tracking: (a) Link-1 and (b) Link-2.

Full size image

5 Results and Discussion

Fig. 3.
figure 3

Modes of the respective link: (a) Mode-1 of the link-1 (b) Mode-2 of the link-1 (c) Mode-1 of the link-2 (d) Mode-2 of the link-2.

Full size image
Fig. 4.
figure 4

Tip deflection of the links: (a) Link-1 (b) Link-2.

Full size image
Fig. 5.
figure 5

Sliding surfaces of the slow subsystem: (a) Link-1 (b) Link-2.

Full size image
Fig. 6.
figure 6

Required torque of the slow subsystem: (a) Link-1 (b) Link-2.

Full size image
Fig. 7.
figure 7

Required torque of the fast subsystem: (a) Link-1 (b) Link-2.

Full size image
Fig. 8.
figure 8

Composite control torque inputs of the flexible manipulator: (a) Link-1 (b) Link-2.

Full size image

The proposed control technique with singular perturbation modelling method is validated on a TLFM. The parameters of the manipulator are given in Table 1. All the simulations are solved using ode-45 solver in MATLAB-14a simulation environment with fixed step size of 0.001. The desired trajectories for both the joints are considered as:

$$\begin{aligned} \theta _{1d}=\frac{\pi }{4}-\frac{7}{6}e^{-\frac{3}{2}t}+\frac{7}{19}e^{-2t} \end{aligned}$$
(42)
$$\begin{aligned} \theta _{2d}=\frac{\pi }{6}-\frac{7}{5}e^{-\frac{3}{2}t}+\frac{7}{11}e^{-2t} \end{aligned}$$
(43)
Table 1. The parameters of the physical system of TLFM.
Full size table

The initial conditions for simulating the manipulator dynamics are given as \(q=(0.05,0,0,0,0,0,0,0)^{T}\). The external disturbance d(t) added to the manipulator is \(d(t)=[0.1 sin(\pi q)~sin(\pi \dot{q})]^{T}\). The value of different constants obtained from the LMI is given below:

$$\begin{aligned} \lambda =\left( \begin{array}{cc} 11.8095 &{} 0 \\ 0 &{} 11.8095 \\ \end{array} \right) \end{aligned}$$
$$\begin{aligned} k=\left( \begin{array}{cccccccc} -0.164 &{} 14.081 &{} 30.513 &{} 49.255 &{} 3.045 &{} -0.405 &{} 0.222 &{} -4.960 \\ 0.166 &{} -2.133 &{} -4.816 &{} -10.295 &{} -0.505 &{} -0.565 &{} -0.277 &{} 0.713 \\ \end{array} \right) \end{aligned}$$

The other constants used for simulating SMC of the slow subsystem are \(\rho _{1}=10\), \(\rho _{2}=10\). These parameter values are chosen by trial and error to maintain a good tracking performance and low control input. Figure 2 shows the joint trajectory tracking of links. It is seen that manipulator track the desired trajectories properly within a small time of \(2\,s\) for both the links. The obtained two modes of each link are shown in Fig. 3. The tip deflection in Fig. 4 is the combination of the modes with its mode shapes. It is seen in Fig. 4 that the tip deflection of the first link and the second link is suppressed within 0.05mm and 0.005mm, respectively. The proposed sliding surfaces for the slow subsystem are shown in Fig. 5. Figures 6 and 7 show the proposed control inputs for the slow subsystem dynamics and fast subsystem dynamics, respectively. The composite control inputs which is the combination of slow and fast subsystems control inputs are shown in Fig. 8. It is apparent from the Fig. 8 that the maximum torque requirement for the first link and second link are in bound of \([-35,10]\)Nm and \([-15,1]\)Nm, respectively.

6 Conclusions

The dynamics of a TLFM is obtained using assumed modes method and separated into slow and fast subsystems describing the rigid and flexible dynamics using singular perturbation technique in this chapter. A composite control for tracking the desired trajectories and tip deflection suppression is proposed for a two-link flexible manipulator. A linear matrix inequality based sliding mode control is designed for tracking the control problem of slow subsystem in order to remove the uncertainties due to nonlinear structure. In addition, a linear matrix inequality based state feedback control is designed for regulating the control problem of fast subsystem. The effectiveness of the proposed control technique is validated in simulation environment in the presence of an external disturbance. Simulation results reflect that the objectives of the chapter are successfully achieved.