Stability and bifurcations investigation of an axially functionally graded beam coupled to a geometrically nonlinear absorber

Abstract

In this paper, the forced vibration behavior of an axially functionally graded (AFG) cantilever-based beam is explored while a lightweight geometrically nonlinear absorber is connected to it. It is shown that the attachment can control the unwanted vibrations and prevent the structure from failure, especially in the resonance situation. The particular configuration of the absorber produces a stiffness with a negative linear and a cubic nonlinear term. The equations of motion of the system are solved both analytically (complexification-averaging method) and numerically. According to the results, in order to reach the best efficiency of the absorber, the best place for attaching it is the free-end of the cantilever beam. The saddle-node bifurcation occurs only for small amounts of the absorber damping. Besides, the interval of the saddle-node bifurcation would grow with reducing the elasticity modulus gradient and damping. Moreover, the strongly modulated response (SMR) region would be increased by rising the elasticity modulus gradient and reducing the density gradient. Hence, the performance of the absorber has the same relation as SMR region to the elasticity modulus gradient and density gradient. Furthermore, the frequency range for the existence of the SMR is apparent when considering the energy and entropy diagrams.

1 Introduction

In the current modern era with an increasing demand for higher technologies, it seems that new advanced materials can be a major revision to classic homogeneous ones, and common homogeneous materials can no longer meet the requisite of the industry in many cases. The functionally graded materials (FGM) are one of these new advanced materials that have been extensively used in energy transmissions, biomedical engineering, electronic devices, and optics due to their special features [1]. Thus, static and dynamic analysis of these materials is important and should be investigated. Some researchers have been worked on the linear and nonlinear vibrational analysis of FGM based systems [2,3,4,5]. Calim [6] studied about free and forced vibrations of axially functionally graded (AFG) beams on two-parameter viscoelastic foundation based on Timoshenko beam theory. In these kinds of beams, material properties changed through the axis and he found that there is a relation and consistency with findings of the literature. Šalinić et al. [7] considered vibration analysis of axially functionally graded non-uniform rods and beams. They also examined the effects of masses and springs connected at the ends of beams and rods on their natural frequencies. For the first time, Attia et al. [8] investigated the size-dependent free vibration of functionally graded viscoelastic (FGV) Nano-beams and studied the simultaneous effects of the microstructure rotation and surface energy. The results implied the relation of small size, surface energy, and viscosity behavior on the free vibration response of the Nano-beam. Shooshtari et al. [9] presented multiple time scale solutions to discuss the influences of material property distribution and the type of free end support on the nonlinear dynamic behavior of cantilevered FGM beams. Şimşek et al. [10] investigated non-linear free vibration of a size-dependent FGM beam, which its material properties change along the thickness continuously, according to simple power-law form. This study was based on the nonlocal strain gradient theory and the Euler–Bernoulli beam theory. They also discussed the Effects of vibration amplitude, strain gradient length scale, nonlocal parameters and various material compositions on the nonlinear frequency ratio (ratio of nonlinear frequency to linear frequency). Rahmani et al. [11] investigated the size-dependent effects in functionally graded material (FGM) Timoshenko beam. They studied the effects of the gradient index, length scale parameter and length-to-thickness ratio on the vibration of FGM nanobeams. They understood from the results that these parameters are necessary in the study of the free vibration. More researches on the vibrations of the FGM beams can be found in refs. [12,13,14,15,16,17,18,19].

Vibration control of FGM structures is an important issue owing to the dynamic instabilities and possibility of damage due to large amplitude vibration in these systems. Although lots of researchers have been worked on vibration control of FGM structures, most of these studies have used active control methods to eliminate unwanted vibration [20,21,22]. These methods have complexity in design and implementing and need equipment and maintenance. In comparison to active control methods, passive methods do not require any special equipment and they are very simple to use [23]. Nonlinear energy sink (NES) is a dynamic system which is a compound of a low mass, damper and a nonlinear stiffness that can passively adjust its oscillation frequency to the natural frequency of the system and decrease its vibration domain. In such a system, the vibrational energy can be transferred from the primary system to the nonlinear attachment. The NES can run from low frequencies to high frequencies and substantially give energy to the system [24, 25]. Many researches have been worked on vibration reduction of beams by nonlinear energy sinks as follows; Ding and Chen [26] provided an inclusive review of Designs, analysis, and applications on Nonlinear Energy Sinks.Zhang et al. [27], investigated a new multifunctional lattice sandwich structure involving a lattice sandwich beam, a NES and a giant magnetostrictive material. They have done a comparative analysis of related parameters such as spring stiffness, NES mass and damping coefficient. More extensive studies on NES can be found in Refs. [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43].

Some researchers have worked on increasing the performance of nonlinear energy sinks for reducing the oscillatory energy of the primary system, for instance, Gendelman et al. [44] concluded that using multiple NESs could absorb more energy from the primary system. Zhang et al. [45] suggested an enhanced NES which was NES with an inerter. Zhang et al. [46] presented a novel nonlinear energy sink in which the mass in the traditional NES was substituted with an inerter. AL-Shudeifat et al. [47] modified an NES by adding a negative linear part to that. This modified nonlinear energy sink (MNES) had a better performance than other existing NESs implied in the literature. They mentioned that approximately 99% of the impact of shock energy has been rapidly transmitted and is localized by the modified NES. Yang et al. [48] presented a targeted energy transfer made to reduce the vibrations of a tube containing fluid using a modified nonlinear energy sink. They compared the performance of the enhanced and classical NESs. They found that the enhanced NES can absorb vibration energy with a faster rate, achieving simultaneous small threshold, higher energy dissipation efficiency, and higher robustness in comparison to classic NES.

To the best of authors’ knowledge, the effectiveness of the nonlinear passive absorbers in vibration control of functionally graded beams has not been studied. This paper investigates the nonlinear dynamics, stability, and forced vibration of an axially functionally graded (AFG) cantilever beam attached to a geometrically nonlinear absorber. It is assumed that the density and the elastic modulus of the beam vary linearly in the axial direction. The absorber consists of two linear springs, a linear damper and a lightweight mass which has been introduced and studied in Refs. [47, 48]. The effect of the external force and design parameters on the behavior of the system and the absorber efficiency are studied. The beam is modeled using Euler–Bernoulli theory, and it is considered that a harmonic force is applied to the whole beam. In the context of vibration control, the occurrence of the Strongly Modulated Response (SMR) is crucial for the system in the resonance situation. In the presence of this desirable response, the TET would perfectly occur, which results an abrupt reduction in the oscillation amplitude of the main system. The absorber is placed at several points of the AFG beam with the aim of identifying the most efficient location. In addition, the existence of the saddle-node and Hopf bifurcations are examined for several absorber damping, external force magnitude and frequency. The nonlinear dynamic behavior of the coupled system is investigated through the frequency response, phase portraits, time history, frequency spectrum diagrams, energy, entropy, and Poincare maps for various elasticity modulus and density. According to the results, one can comprehensively simulate the control of vibration of AFG cantilever beams utilizing a geometrically nonlinear absorber under harmonic excitation.

2 Mathematical modeling

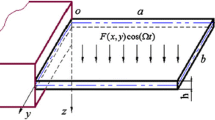
Figure 1 depicts an AFG cantilever beam and the geometrically nonlinear absorber. Owing to the fact that periodical forces are utterly prevalent in several industries, the system of the current study is subjected to an external sinusoidal excitation. With the presumption that the length to cross-section area ratio is significantly large, the Euler–Bernoulli beam theory holds rational.

Fig. 1

A schematic view of a cantilever AFG beam and the absorber

The arrangement in Fig. 1 (right side) has been utilized for understanding the basically nonlinear stiffness dependent on the mathematical nonlinearity got by the transverse linear springs when they are not elongated or compressed at their vertical position. Thus, the subsequent basically nonlinear oscillator has no linear stiffness segments. The nonlinear geometry of the linear springs of the absorber produces nonlinear and negative linear stiffness [45]. K is the stiffness of springs. Here, it is considered that the linear springs are under pressure when they are in a horizontal situation, where some potential energy is stockpiled. Based on the Ref. [47], the force of the springs will be as bellow:

$$ F_{{net}} \approx - 2K(w - v - z_{c} )\left[ {1 - \frac{1}{{\sqrt {L_{0} + (w - v - z_{c} )^{2} } }}} \right] \approx K_{l} (w - v - z_{c} ) - K_{{nl}} (w - v - z_{c} )^{3} $$

(1)

where, $K_{{nl}} = \frac{K}{{\gamma ^{3} L^{2} }},\,\,K_{l} = 2K\left( {\frac{1}{\gamma } - 1} \right),\,\,\gamma = \frac{{L_{0} }}{L}$.

The coupled equations of motion of the AFG beam and the absorber induced by a harmonic force are obtained as follows:

$$ \begin{aligned} \frac{{\partial ^{2} }}{{\partial x^{2} }}\left( {E(x)I\frac{{\partial ^{2} w(x,t)}}{{\partial x^{2} }}} \right) & + M(x)\frac{{\partial ^{2} w(x,t)}}{{\partial t^{2} }} + c_{p} \frac{{\partial w(x,t)}}{{\partial t}} \\ & - K_{l} \left( {w(x,t) - v(t) - z_{c} (t)} \right)\delta (x - d) \\ & + K_{{nl}} \left( {w(x,t) - v(t) - z_{c} (t)} \right)^{3} \delta (x - d) + C\left( {\frac{{\partial w(x,t)}}{{\partial t}} - \frac{{\partial v(t)}}{{\partial t}}} \right)\delta (x - d) \\ & = F_{0} \cos (\omega _{0} t) \\ \end{aligned} $$

(2a)

$$ \begin{aligned} m\frac{{\partial ^{2} v(t)}}{{\partial t^{2} }} & + K_{l} \left( {w(x,t) - v(t) - z_{c} (t)} \right)\delta (x - d) \\ & - K_{{nl}} \left( {w(x,t) - v(t) - z_{c} (t)} \right)^{3} \delta (x - d) + C\left( {\frac{{\partial w(x,t)}}{{\partial t}} - \frac{{\partial v(t)}}{{\partial t}}} \right)\delta (x - d) \\ & = 0 \\ \end{aligned} $$

(2b)

Here, w(x,t) and v(t) are the lateral displacement of the beam and the absorber, respectively. I and M are respectively the moment of inertia and the mass per unit length of the beam. m and C are the mass and damping of the absorber. In this article, the elastic modulus (E) and density (ρ) would alter linearly along the beam. They are introduced as

$$ \begin{gathered} E(x) = E_{0} f_{1} (x) \hfill \\ \rho (x) = \rho _{0} f_{2} (x) \hfill \\ \end{gathered} $$

(3)

where,

$$ \begin{gathered} f_{1} (x) = 1 + \frac{x}{L}(\alpha _{E} - 1),\;\alpha _{E} = \frac{{E_{L} }}{{E_{0} }} \hfill \\ f_{2} (x) = 1 + \frac{x}{L}(\alpha _{R} - 1),\;\alpha _{R} = \frac{{\rho _{L} }}{{\rho _{0} }} \hfill \\ \end{gathered} $$

(4)

In Eq. (4), α_E and α_R are respectively the elastic modulus and density gradient. It is cogent that if they are equal to one, the AFG beam will be uniform.

Substituting Eqs. (3) and (4) into Eq. (2) yield the following system equations:

$$ \begin{gathered} E_{0} {\text{If}}_{1} (x)w_{{xxxx}} + 2E_{0} {\text{If}}_{{1x}} (x)w_{{xxx}} + E_{0} {\text{If}}_{{1x}} (x)w_{{xx}} + \rho _{0} {\text{Af}}_{2} (x)w_{{tt}} + c_{p} w_{t} \hfill \\ + K_{{{\text{nl}}}} (w - v - z_{c} )^{3} \delta (x - d) - K_{l} (w - v - z_{c} )\delta (x - d) + C(w_{t} - v_{t} )\delta (x - d) = F_{0} \cos (\omega _{0} t) \hfill \\ {\text{mv}}_{{{\text{tt}}}} - K_{{{\text{nl}}}} (w - v - z_{c} )^{3} \delta (x - d) + K_{l} (w - v - z_{c} )\delta (x - d) - C(w_{t} - v_{t} )\delta (x - d) = 0 \hfill \\ \end{gathered} $$

(5)

To achieve the dimensionless form of Eq. (2), the following variables are introduced:

$$ \begin{gathered} \bar{x} = \frac{x}{L},\,\,\bar{w} = \frac{w}{L},\,\,\bar{v} = \frac{v}{L},\,\,\bar{z}_{c} = \frac{{z_{c} }}{L},\,\,\tau = \frac{t}{T},\,\,\Omega = T\omega _{0} , \hfill \\ \varepsilon = \frac{m}{{\rho _{0} A}},\,\,T = \frac{{L^{2} }}{{\lambda _{1} ^{2} }}\sqrt {\frac{{\rho _{0} A}}{{E_{0} I}}} ,\,\,\alpha _{C} = \frac{{CL^{2} }}{{m\lambda _{1} ^{2} \sqrt {\rho _{0} AE_{0} I} }},\,\,\beta = \frac{{\rho _{0} AK_{{nl}} L^{5} }}{{m\lambda _{1} ^{4} E_{0} I}}, \hfill \\ \bar{c}_{P} = \frac{{c_{P} L^{2} \sqrt {\rho _{0} A} }}{{m\lambda _{1} ^{2} \sqrt {E_{0} I} }},\,\,\bar{F} = \frac{{F_{0} L^{3} \rho _{0} A}}{{m\lambda _{1} ^{4} E_{0} I}} \hfill \\ \end{gathered} $$

(6)

By replacing the aforementioned parameters into Eq. (5), the dimensionless equations are acquired as bellow:

$$ \begin{gathered} f_{1} \bar{w}_{{xxxx}} + 2Lf_{{1x}} \bar{w}_{{xxx}} + L^{2} f_{{2xx}} \bar{w}_{{xx}} + f_{2} \bar{w}_{{tt}} + \varepsilon \bar{c}_{p} \bar{w}_{t} + \varepsilon \beta (\bar{w} - \bar{v} - \bar{z}_{c} )^{3} \delta (\bar{x} - \bar{d}) + \hfill \\ \varepsilon 2\gamma ^{3} \left(\frac{1}{\gamma } - 1\right)\beta \left(\bar{w} - \bar{v} - \bar{z}_{c} \right)\delta (\bar{x} - \bar{d}) + \varepsilon \alpha _{c} (\bar{w}_{t} - \bar{v}_{t} )\delta (\bar{x} - \bar{d}) = \varepsilon \bar{F}\cos (\Omega \tau ) \hfill \\ \end{gathered} $$

(7a)

$$ \begin{gathered} \varepsilon \bar{v}_{{tt}} - \varepsilon \beta (\bar{w} - \bar{v} - \bar{z}_{c} )^{3} \delta (\bar{x} - \bar{d}) - \hfill \\ \varepsilon 2\gamma ^{3} \left(\frac{1}{\gamma } - 1\right)\beta (\bar{w} - \bar{v} - \bar{z}_{c} )\delta (\bar{x} - \bar{d}) - \varepsilon \alpha _{c} (\bar{w}_{t} - \bar{v}_{t} )\delta (\bar{x} - \bar{d}) = 0 \hfill \\ \end{gathered} $$

(7b)

In order to discretize system Eq. (7) through an infinite set of ordinary differential equations, the standard Galerkin method is applied. Therefore, the displacement is expanded as

$$ \bar{w}(\bar{x},\tau ) = \sum\limits_{{r = 1}}^{N} {\Phi _{r} (\bar{x})q_{r} (\tau )} $$

(8)

where $\Phi _{r} (\bar{x})$ are the mode functions for the AFG beam [31]. The vibrational mode of the un-damped clamped-free beam is $\phi _{r} (x) = \cosh (\sqrt {\lambda _{r} } x) - \cos (\sqrt {\lambda _{r} } x) - \sigma _{r} [\sinh (\sqrt {\lambda _{r} } x) - \sin (\sqrt {\lambda _{r} } x)]$. where λ_r is the rth nondimensional natural frequency of the AFG beam. $q_{r} (\tau )$ are the generalized time-varying coordinates. By substituting Eq. (8) into Eq. (7), equations of the system take the following form:

$$ \begin{gathered} m_{{rs}} \ddot{q}_{r} + k_{{rs}} q_{r} + \varepsilon \bar{c}p_{{rs}} \dot{q}_{r} + \varepsilon \beta \phi _{d} (q_{r} (t)\phi _{d} - \bar{v}(t) - \bar{z}_{c} )^{3} + \hfill \\ \varepsilon \beta (2\gamma ^{3} )\left(\frac{1}{\gamma } - 1\right)\phi _{d} (q_{r} (t)\phi _{d} - \bar{v}(t) - \bar{z}_{c} ) + \varepsilon \bar{\alpha }_{c} \phi _{d} (\dot{q}_{r} (t)\phi _{d} - \dot{\bar{v}}(t)) = F\varepsilon \cos (\Omega \tau ) \hfill \\ \end{gathered} $$

(9.a)

$$ \begin{gathered} \varepsilon \ddot{\bar{v}} - \varepsilon \beta \phi (q_{r} (t)\phi _{d} - \bar{v}(t) - \bar{z}_{c} )^{3} - \hfill \\ \varepsilon \beta (2\gamma ^{3} )\left(\frac{1}{\gamma } - 1\right)(q_{r} (t)\phi _{d} - \bar{v}(t) - \bar{z}_{c} ) - \varepsilon \bar{\alpha }_{c} (\dot{q}_{r} (t)\phi _{d} - \dot{\bar{v}}(t)) = 0 \hfill \\ \end{gathered} $$

(9.b)

For the sake of simplification, the following transformation is considered:

$$ \bar{q}_{r} (\tau ) = \phi _{d} q_{r} (\tau ) $$

(10)

Using this simplification, the equations of the system can be written as

$$ \begin{gathered} \frac{{m_{{rs}} \ddot{\bar{q}}_{r} }}{{\phi _{d} ^{2} }} + \frac{{k_{{rs}} \bar{q}_{r} }}{{\phi _{d} ^{2} }} + \frac{{\varepsilon \bar{c}p_{{rs}} }}{{\phi _{d} }}\dot{\bar{q}}_{r} + \varepsilon \beta (\bar{q}_{r} (t) - \bar{v}(t) - \bar{z}_{c} )^{3} + \hfill \\ \varepsilon \beta (2\gamma ^{3} )\left (\frac{1}{\gamma } - 1\right)(\bar{q}_{r} (t) - \bar{v}(t) - \bar{z}_{c} ) + \varepsilon \bar{\alpha }_{c} (\dot{\bar{q}}_{r} (t) - \dot{\bar{v}}(t)) = \frac{{F\varepsilon }}{{\phi _{d} }}\cos (\Omega \tau ) \hfill \\ \end{gathered} $$

(11a)

$$ \begin{gathered} \varepsilon \ddot{\bar{v}} - \varepsilon \beta (\bar{q}_{r} (t) - \bar{v}(t) - \bar{z}_{c} )^{3} - \hfill \\ \varepsilon \beta (2\gamma ^{3} )\left(\frac{1}{\gamma } - 1\right)(\bar{q}_{r} (t) - \bar{v}(t) - \bar{z}_{c} ) - \varepsilon \bar{\alpha }_{c} (\dot{\bar{q}}_{r} (t) - \dot{\bar{v}}(t)) = 0 \hfill \\ \end{gathered} $$

(11b)

where,

$$ \begin{gathered} m_{{rs}} = \int\limits_{0}^{1} {f_{2} (\bar{x})} \phi _{r} (\bar{x})\phi _{s} (\bar{x})d\bar{x} \hfill \\ k_{{rs}} = \int\limits_{0}^{1} {\left\{ {f_{1} (\bar{x})\phi _{r} ^{{\prime \prime \prime \prime }} (\bar{x})\phi _{s} (\bar{x}) + 2Lf_{1} ^{\prime } (\bar{x})\phi _{r} ^{{\prime \prime \prime }} (\bar{x})\phi _{s} (\bar{x}) + L^{2} f_{1} ^{{\prime \prime }} (\bar{x})\phi _{r} ^{{\prime \prime }} (\bar{x})\phi _{s} (\bar{x})} \right\}d\bar{x}} \hfill \\ \bar{c}p_{{rs}} = \int\limits_{0}^{1} {c_{p} \phi _{r} (\bar{x})\phi _{s} (\bar{x})d\bar{x}} ,F = \bar{F}\int\limits_{0}^{1} {\phi _{s} (\bar{x})d\bar{x}} \hfill \\ \end{gathered} $$

(12)

3 Analytical solution

The Complexification-averaging technique (CX-A) has been utilized to analytically calculate the response of the coupled system comprising the AFG beam and the absorber. This method was firstly employed by Manevitch [49] for a systematic investigation of nonlinear oscillators with nonlinear asymmetric characteristics. It is founded on the complex illustration of the dynamic equations of the system. In this approach, the slow and fast varying terms of motion are disentangled from each other. The fast-varying term is associated with the natural frequency of the system, while the slow-varying part is connected to the amplitude of the oscillation of the beam and the absorber.

Due to the fact that the ratio of the mass of the absorber to the beam is considerably minor, the influence of the absorber on the natural frequency of the system is insignificant and can be ignored. Now, the following variable changes are applied to the system for evaluating the absorption effectiveness and relative displacement of the system.

$$ \begin{gathered} v(t) = \bar{q}(t) + \varepsilon \bar{v}(t) \hfill \\ w(t) = \bar{q}(t) - \bar{v}(t) \hfill \\ \end{gathered} $$

(13)

In the CX-A method, the solution is attained in a series of responses that embrace dominant frequencies in the system. Here, for both the displacement of the beam and the absorber, a dominant motion, which consist of movement with the natural frequency of the system, is considered.

$$ \begin{gathered} \psi _{1} = v_{t} (t) + i\Omega v(t) \hfill \\ \psi _{2} = w_{t} (t) + i\Omega w(t) \hfill \\ \end{gathered} $$

(14)

where $i = \sqrt { - 1}$

$$ \psi _{j} = \phi _{j} e^{{i\Omega \tau }} \;j = 1,2 $$

(15)

Substituting Eqs. (13–15) into Eq. (11), averaging over the fast time scale $\tau$, and including only terms with $e^{{i\Omega \tau }}$, results in the following equation that denotes the slow time scale of the system behavior:

$$ \frac{{d\phi _{1} (\tau )}}{{d\tau }} + h_{1} \phi _{2} (\tau ) + h_{2} \phi _{2} (\tau )\left| {\phi _{2} (\tau )} \right|^{2} + h_{3} F = 0 $$

(16a)

$$ \frac{{d\phi _{2} (\tau )}}{{d\tau }} + h_{4} \phi _{2} (\tau ) + h_{5} \phi _{2} (\tau )\left| {\phi _{2} (\tau )} \right|^{2} + h_{6} F = 0 $$

(16b)

The coefficients of the above equation are presented as parameters of $h_{i}$ for simplification. The first stage for analyzing the steady-state solutions of Eq. (16a,b) is to find the stationary points of the system. For this sake, $\frac{{d\phi _{1} }}{{d\tau }}$ and $\frac{{d\phi _{2} }}{{d\tau }}$ are set equal to zero, and the value of the resulting $\phi _{{20}}$ is set equal to the value of the function $\phi _{2} (\tau )$. It should be noted that $\phi _{1} (\tau )$ is achieved from Eq. 16a and is substituted into Eq. 16b.

By examining the variations of $\left| {\varphi _{{20}} } \right|^{2}$, the absorption effectiveness is found. In the condition that the large values of $\left| {\varphi _{{20}} } \right|^{2}$ and small values of $\left| {\varphi _{{10}} } \right|^{2}$ are on the same side, the absorbing proficiency is proper.

Assuming that $\left| {\varphi _{{20}} } \right|^{2} = Z$ in Eq. (14), the characteristic equation are obtained as bellow:

$$ a_{1} Z^{3} + a_{2} Z^{2} + a_{3} Z^{1} + a_{4} = 0 $$

(17)

The system in Eq. (17) has one or three roots, so it is predictable that there will be a series of bifurcations in the system. In order to gain the position of the saddle-node, in addition to satisfying the above condition, its derivative must be equal to zero.

Hopf bifurcation may take place in an area in which the slow response of the system is turning dynamic from the static mode, and the system has complex fixed points lacking the real part; In fact, the system is unstable in that state. In order to find the Hopf bifurcation, small perturbations around the equilibrium point is induced in the system.

$$ \begin{gathered} \phi _{1} (\tau ) = \phi _{{10}} + \delta _{1} \hfill \\ \phi _{2} (\tau ) = \phi _{{20}} + \delta _{2} \hfill \\ \end{gathered} $$

(18)

Substituting Eq. (18) into Eq. (16a, b) and disregarding the nonlinear parts, the following equations that indicate the dynamic behavior of the system around the equilibrium positions are achieved as:

$$ \begin{gathered} \delta _{{1t}} = \alpha _{1} \delta _{1} + \alpha _{2} \delta _{1}^{*} + \alpha _{3} \delta _{2} + \alpha _{4} \delta _{2}^{*} \hfill \\ \delta _{{2t}} = b_{1} \delta _{1} + b_{2} \delta _{1}^{*} + b_{3} \delta _{2} + b_{4} \delta _{2}^{*} \hfill \\ \end{gathered} $$

(19)

In the above relations, the sign (*) connotes the conjugate state. By writing Eq. (19) into a matrix form, the polynomial characteristic equation can be written as follows:

$$ \xi ^{4} + \eta _{1} \xi ^{3} + \eta _{2} \xi ^{2} + \eta _{3} \xi + \eta _{4} = 0 $$

(20)

The Hopf bifurcation may occur in the system if Eq. (20) has a pair of complex roots with a zero real part. In this scenario, roots take the following form:

$$ \xi = \pm \hat{\Omega }i $$

(21)

Here, $\hat{\Omega }$ is the characteristic frequency of the periodic courses of the system gained by bifurcation of the stationary points.

Now, by substituting Eq.(20) into Eq.(21), and splitting real and imaginary terms of the result, the characteristic frequency of the system is realized as:

$$ \hat{\Omega } = \frac{{\eta _{3} }}{{\eta _{1} }} $$

(22)

By substituting Eq. (22) into Eq. (20), the required condition for the existence of Hopf bifurcation is acquired. By considering $Z = \left| {\phi _{{20}} } \right|^{2}$ the simplified equation can be presented as

$$ Z^{4} + \zeta _{1} Z^{3} + \zeta _{2} Z^{2} + \zeta _{3} Z + \zeta _{4} = 0 $$

(23)

The computational flow chart for simplification and better understanding of the methodology is shown in Fig. 2.

Fig. 2

The computational flow charts

For the sake of validation of the results of the present work, Fig. 3a and b are provided. The first figure indicates that the amplitude response of the system when the beam is approximated based on different number of modes are significantly close to each other. In fact, although there is a slight difference between them, the deviation is totally negligible since the overall behavior of the system is the same for different cases. Therefore, in light of the fact that this paper aims to investigate the general behavior of an AFG beam coupled with a nonlinear absorber in various situations, one-mode approximation would be sufficient. For anaslytical methodology verification, the parameters of the studied system have been selected in such a way that the system simulates the behavior of the two degrees of freedom system examined in Ref. [50]. Figure 3b displays the periodic solution and the interval of Hopf bifurcation in the response of the system. As can be seen, there is a good agreement between the results.

Fig. 3

a The frequency response of the system based on different Galerkin approximations. b The amplitude response of the present work and Ref. [50]

4 Results

In this part, the influence of elasticity modulus gradient, density gradient, position of the absorber, and the geometry of that on the incidence of the saddle-node bifurcation, Hopf bifurcation, and SMR in the coupled system are numerically (The numerical algorithm utilized in this article is Runge–Kutta) and analytically examined.

In this study, the parameter γ takes the value of 0.96, so it realizes a cubic essentially nonlinear energy sink with a negative linear stiffness. Additionally, σ is the detuning parameter.

4.1 The effect of the absorber position

One of the main concerns in vibration control of structures is to find the optimum position of the absorber on the primary system. To address this issue, the saddle-node and Hopf bifurcations of the system will be studied for a number of values for the parameter d in Figs. 4 and 5.

Fig. 4

The saddle-node bifurcation region when a d = 0.4, b d = 0.6, and c d = 0.99

Fig. 5

The Hopf bifurcation region when a d = 0.4, b d = 0.6, and c d = 0.99

Based on the figure, the saddle-node bifurcation region is condensed by putting the absorber at the free end of the beam. It can also be observed that by growing the damping of the absorber, the system requests more amplitude of the excitation force for the incidence of the saddle-node and Hopf bifurcation. The excitation necessary for the occurrence of the saddle-node and Hopf bifurcation shows that as the absorber gets closer to the clamped end of the beam, the system calls for a larger excitation force for the existence of the saddle-node and Hopf bifurcation in light of the low amplitude vibration. Thus, the free-end of a cantilever beam is the finest location for attaching the absorber.

To better understand and demonstrate the best position for the absorber installation, the kinetic energy of the primary system at different absorber positions is investigated. The percentage of kinetic energy reduction of the system using the concept of root mean square (RMS) is shown in Fig. 6. This graph shows the percentage reduction in RMS for two different values of σ. As can be seen, as the absorber approaches the end of the beam, a greater percentage of the energy of the initial system is reduced, and for the two σ values, the end of the beam is the best place to install the absorber. This diagram can also be drawn to examine the best location for the absorber to be installed for beams with different modulus elasticity and density gradients.

Fig. 6

The percentage reduction of the RMS in various values of σ

Figure 7 shows the percentage reduction in RMS for different values of α_E and α_R. According to the diagram related to α_E, it will be seen that by increasing the amount of α_E, although the amount of RMS has decreased at the end of the beam, the end of the beam will be still the best place to install the absorber. Another diagram shows that for α_R values smaller than one, the end of the beam will not be the best place to install the absorber. While for α_R values greater than one, the end of the beam is still the best place for the absorbent.

Fig. 7

The percentage reduction of the RMS in various values of α_E (left) and α_R (right)

4.2 The effect of α _E on the absorber performance

The primary goal of the present study is to examine the necessary condition for the incidence of the bifurcations in the nonlinear dynamic behavior of the system for various elasticity modulus and density variations. The area of these bifurcations are explored in Fig. 8. It displays the existence of the saddle-node bifurcation by variations in modulus of the elasticity of the beam, damping of the NES, and external force amplitude. According to the figure, the saddle-node bifurcation only happens for minuscule amounts of NES damping, and the interval of the occurrence of the saddle-node bifurcation is diminished as the damping and elasticity modulus grow.

Fig. 8

The saddle-node bifurcation region of the system for varying α_E, α_C, and F

The dynamical behaviors of the coupled system are studied for several values of elasticity modulus α_E (0.1, 0.25, 0.5 and 1) in Fig. 9. The figure illustrations that the district of the Hopf bifurcation is dissimilar for each α_E. The essential amplitude of the excitation force for the occurrence of the Hopf bifurcation is swelling by increasing α_E.

Fig. 9

The area of the occurrence of the Hopf bifurcation with α_R = 1, σ = -2 and various α_E

It is noted that in cases with more than one periodic response, there is an uncertainty in defining the specific bifurcation responses. In order to resolve the uncertainty, pairs of branching diagrams for some values of σ are presented. Additionally, diagrams of the branch sections by fixing the damping value and detuning parameter for different values of α_E and α_R are obtained. For further understanding, the bifurcations and the steady-state amplitude of the periodic motion are depicted as a function of the excitation amplitude in Fig. 10 for several values of α_E. Since each value of F is not related to a specific $\left| {\phi _{{20}} } \right|$ for at a certain interval, there is jumping phenomenon in the system. So, before the curve comes in the Hopf bifurcation region, there is no (SMR) in the response of the system. This is numerically presented for one of the curves displayed in Fig. 10 (α_E = 0.5 ) in Fig. 11. It is also interpreted from Fig. 10 that the amplitude of the system would be enhanced by increasing the amount of α_E . Additionally, by escalating the value of α_E the range of the occurrence of Hopf bifurcation before jumping becomes smaller, and with the increase of α_E, this phenomenon disappears completely. In the case of the jump phenomenon, it also happens that with the increase of α_E, the interval of the jump phenomenon is becoming smaller.

Fig. 10

The amplitude response of the system for various α_E with α_C = 0.2, and σ = -2(dash line: Saddle-node bifurcation and black line: Hopf bifurcation)

Fig. 11

The time history and phase plane diagrams with α_C = 0.2, F = 0.4

For larger values of F, the system response is in the form of a signal that denotes the highest performance of the absorber. This is illustrated numerically in Fig. 12. Based on Fig. 10, one can define the range of the excitation force in which the SMR would take place for each α_E . It is cogent that for lower α_E, the periodic response would happen for lower excitation forces. Conversely, for higher α_E , the system calls for more external force to enter the SMR area. Besides, the SMR area grows by increasing α_E .

Fig. 12

The time history and phase plane diagrams with α_C = 0.2, F = 1, α_E = 0.5

By enhancing the magnitude of the external force, the response of the system would leave the SMR area and convert to a weakly periodic motion, which is presented numerically for three values of F in Fig. 13.

Fig. 13

The time history and phase plane diagrams with α_E = 0.5 for: a F = 1.4, b F = 2.2 and c F = 3

One can also compare the amplitude response of the AFG beam when it is attached to the absorber to that without the absorber to study the effect of the absorber on the behavior of the system (Fig. 14). As shown, the system has an unstable response and its amplitude is increasing before it is connected to the absorber. While, the presence of the absorber leads to a periodic response with a small range of instability. In Fact, the absorber can significantly reduce the amplitude of the system.

Fig. 14

The amplitude response of the AFG system with and without absorber when α_E = 2 α_C = 0.2, and σ =  − 2 (Red dash line: Saddle-node bifurcation and green dash line: Hopf bifurcation)

In order to explore the influence of the elasticity modulus on the system response for diverse excitation frequencies, the frequency response of the system with different values of α_E are illustrated in Fig. 15. According to Fig. 15a, the system has a higher amplitude for larger values of α_E. The figure also depict the occurrence of two phenomena of Hopf and Saddle-node bifurcations in the system. The bifurcation of the saddle in the system is directly related to the value of α_E and is eliminated by increasing this parameter. Hopf bifurcation occurs for different values of σ, which is decreased with increasing the value of α_E. The system possesses two kinds of responses for each value of α_E. It entails a low amplitude periodic motion and undesirable branches of high amplitude periodic motions (Fig. 15b). As it is revealed in the figure, the upper part of these branches contains stable periodic responses with great amplitude, while, lower sections have unstable periodic responses. As demonstrated, this response is affected by the value of α_E. In other words increasing it can eliminate this kind of response.

Fig. 15

The frequency response of the system for various values of α_E with α_c = 0.2, F = 0.4 (dash line: Saddle node bifurcation and black line: Hopf bifurcation)

Similar to Fig. 14, one can depict the frequency response of the AFG beam in two conditions: with and without absorber, to investigate the impact of the absorber on the response of the system (Fig. 16). According to the figure, near the resonance condition (σ =  − 2), the amplitude of the system rises to very large values that can damage the system when it is not connected to the absorber. Whereas, the absorber can considerably mitigate the vibration amplitude of the system and prevent it from failure.

Fig. 16

The frequency responses of the system with and without absorber. (Red dash line: Saddle-node bifurcation and green dash line: Hopf bifurcation)$\sigma = - 2$

Figure 17 demonstrates the behavior of the system for high amplitude periodic motions. These responses are prompted by the geometrical nonlinearity of the attachment. It is mentioned that a periodic response would take place in the vicinity of the natural frequency of the system.

Fig. 17

The time history and Poincare diagrams of the system with α_E = 0.5, α_C = 0.2, F = 0.8, σ = 6

Moreover, it is witnessed that the system’s amplitude response is directly associated with the elasticity modulus as well as the effectiveness of the absorber. Thus, one can claim that for greater values of $\left| {\varphi _{{20}} } \right|$, the entire energy of the system is confined to the absorber proving that the absorber can act as a nonlinear energy sink.

According to Ref. [49], the mixture of essential nonlinearity and strong mass asymmetry leads to a probability of response regimes qualitatively deviated from steady-state and WMR standing in the proclivity of averaged flow equations when of 1:1 resonance exist. These responses are referred to as “strongly modulated response” (SMR). Now, it is time to find the frequency range for the presence of the SMR via feature extraction methods. To this end, the energy and entropy of the time response signal of the system are shown in Fig. 18 for several values of α_E.

Fig. 18

The detuning parameter-energy diagram (left) and the detuning parameter-entropy diagram (right) of Time-history signal for various values of α_E

The formulas utilized for calculating the energy and entropy of the time response is defined as follows.

$$ \begin{gathered} Energy = \sum\limits_{{n = 1}}^{N} {(x(n))^{2} } \hfill \\ Entropy = \sum\limits_{{n = 1}}^{N} {(x(n) \cdot \log \left(\frac{1}{{x(n)}})\right)^{2} } \hfill \\ \end{gathered} $$

(24)

As lucidly revealed in the figure, a range with high values of energy and entropy is detected in the response of the system. In each side of this region there is an abrupt reduction in the value of energy and entropy. Proving this region is numerically scrutinized, one can discern the SMR in the behavior of the system. Figures 19 and 20 numerically explore the response of the system in borders of high energy and entropy region. The figures confirm that a little alteration in σ can change the response of the system from SMR to the weakly modulated or periodic response and vice versa.

Fig. 19

The creation of SMR by changing the value of σ

Fig. 20

The disappearance of SMR by changing the value of σ

Now, one can determine the intervals of the SMR for different values of α_E = 0.1, 0.25, 0.5, 1, and 2, as − 4.52 < σ < 3.79, − 4.41 < σ < 3.69 − 4.29 < σ < 3.55 , − 4.11 < σ < 3.20, and − 3.84 < σ < 2.54 respectively. The outcomes indicate that by increasing the value of the detuning parameter, the SMR will happen for smaller values of α_E . Plus, the period of the occurrence of the SMR would be condensed by increasing in value of α_E.

4.3 The effect of α _R on the absorber performance

The performance of the absorber in vibration mitigation of the AFG beam with several values of α_R is studied likewise to the former part. At the beginning, the prerequisite situation for the occurrence of the saddle-node bifurcation was investigated as α_R and damping of the NES varies (Fig. 21). As can be observed, by increasing the value of α_R , the parallel amplitude of the external force which is essential for the incidence of this bifurcation is amplified. Nonetheless, by enlarging in the damping value of the NES, the bifurcation will vanish.

Fig. 21

The Saddle-node bifurcation region of the system for varying α_R, α_C, and F

In the next phase, the behavior of the system for the existence of the Hopf bifurcation is explored for various density. First of all, the Hopf bifurcation area in the damping and external force amplitude space is depicted for several density α_R (0.5, 1, 1.5 and 2) in Fig. 22. The figure shows that the district of the Hopf bifurcation is different for each α_R. Conversely, in spite of Fig. 21, the Hopf bifurcation region is compacted by rising α_R.

Fig. 22

The area of the occurrence of the Hopf bifurcation with α_E = 1 and various α_R

In order to further study the bifurcations, the steady-state amplitude of the periodic motion is demonstrated as a function of the excitation amplitude in Fig. 23 for several values of α_R. It is evident that each value of F matches to a particular $\left| {\phi _{{20}} } \right|$ in smaller value of α_R. Therefore, there is no jumping phenomenon, whereas by increasing α_R the jumping phenomenon would occur, and the saddle-node bifurcation appears in the dynamic behavior of the system. As displayed, the range of the occurrence of Hopf bifurcation is enhanced as α_R grows. One can argue that before the curve go into the Hopf bifurcation area, there is no (SMR) in the response of the system. This is presented numerically for one of the curves of Fig. 23 (α_R = 0.5 ) in Fig. 24. Moreover, Fig. 23 indicates that the amplitude of the system would be enhanced by reducing the amount of α_R.

Fig. 23

The amplitude response of the system for several α_R with α_E = 1, σ =  − 2, and α_C = 0.2 (dash line: Saddle node bifurcation and black line: Hopf bifurcation)

Fig. 24

The time history and phase plane diagrams with F = 0.5, α_C = 0.2, α_E = 1, and α_R = 0.5

For greater values of F, the system response is in the form of a signal that represents the high efficiency of the absorber. This is presented numerically in Fig. 25a. By further growing the magnitude of the external force, the response of the system would depart the SMR region and converts to weakly periodic motion, which is depicted numerically in Fig. 25b–c.

Fig. 25

The variation of the time history and phase plane diagrams of the system by changing the amplitude of the external force with α_C = 0.2, α_E = 1, and α_R = 0.5

The frequency response of the system for several values of α_R is displayed in Fig. 26 by fixing α_E and F. It is perceived that by reducing the amount of α_R , the performance of the absorber near the natural frequency of the system is enriched. By increasing the excitation frequency in the classic beam, which is marked in pink, at first the system response alters in a small interval from the periodic solution to the Hopf bifurcation. Then it go into a volatile section and the jump phenomenon ensues. Nevertheless, for smaller amounts of α_R , the Hopf bifurcation does not take place in this range of sigma. It can also be observed from the frequency response curves that for positive sigma values, there is a Hopf branch that its interval for the classical beam and larger values of α_R are maximum. In addition, there are three responses in the behavior of the system for classic a beam, but for the AFG beam, by diminishing the value of α_R , the system's unstable response has shifted around natural frequencies (Fig. 26b).

Fig. 26

The frequency response of the system for several α_R with α_E = 1, α_C = 0.2 and F = 0.4 (dash line: Saddle node bifurcation and black line: Hopf bifurcation)

According to the preceding part, the frequency range for the happening of the SMR can be examined by extracting features such as the energy or entropy from the time response of the system. Figure 27 shows the energy and entropy of the system as a function of the detuning parameter for different values of α_R. Using this plot, one can conclude the range of this event by the sudden change in the amount of energy or entropy.

Fig. 27

The detuning parameter-energy diagram (left) and the detuning parameter-entropy diagram (right) of Time-history signal for various value of α_R

According to Fig. 28, for a certain range of σ, the procedure of developing and vanishing of the strongly modulated response is presented for the AFG beam (α_R = 0.5 ) marked with green in Fig. 27. As illustrated in the Fig. 28, a SMR is occur in the system response for α_R = 0.5 in the range of −7.69 < σ < 2.37 . Likewise, the sigma interval for the existence of the SMR in different values of α_R = 1, 1.5, and 2 will be −5.50 < σ < 4.50, -4.33 < σ < 3.90, and −3.55 < σ < 1.34 , respectively. Now it is apparent that the SMR has happened earlier by decreasing α_R .

Fig. 28

The process of occurring and disappearing of the SMR by changing σ with α_E = 1 and α_R = 0.5

5 Conclusion

In this article, the nonlinear dynamic behavior of a coupled system comprising an AFG beam with a geometrically nonlinear absorber was explored by means of both numerical and analytical method. The AFG beam was under periodic excitation. The absorber involved two linear springs configured in a particular formation which could provide a negative linear and a cubic nonlinear stiffness. The mechanical properties of the AFG beam along the length were reflected in the equations of motion on the basis of the linear distributions of the elastic modulus and density. The required situation for the incidence of the Hopf bifurcation, saddle-node bifurcation, and strongly modulated response were examined. The effect of the location, gradient of the density and elasticity modulus of the AFG beam, and the magnitude of the external force on the system’s response were investigated. In what follows, the main outcomes of this research is presented:

The saddle-node bifurcation was impeded for higher excitation frequencies when the absorber was attached to the free-end of the beam. Additionally, it was detected that by rising the damping of the absorber, the saddle-node and Hopf bifurcations took place for greater excitation magnitude. Studying the impact of the elastic modulus and density on the saddle-node bifurcation indicated that the domain of the amplitude of the excitation force escalates with increasing the density, and it would be reduced by intensifying the elastic modulus. Moreover, it was illustrated that the efficiency of the absorber in vibration dissipation would be augmented by increasing the elastic modulus and reducing the density, especially when the beam was induced near its fundamental natural frequency. Furthermore, when the density was raised, the Hopf bifurcation happened for a lower excitation force.