Stability and bifurcation of a cantilever functionally graded material plate subjected to the transversal excitation

Abstract

The stability and bifurcation behaviors for a cantilever functionally graded materials rectangular plate subjected to the transversal excitation in thermal environment are studied by means of combination of analytical and numerical methods. The resonant case considered here is 1:1 internal resonances and 1/2 subharmonic resonance. Four types of degenerated equilibrium points are studied in detail, which are characterized by a double zero and two negative eigenvalues, a double zero and a pair of pure imaginary eigenvalues, a simple zero and a pair of pure imaginary eigenvalues as well as two pairs of pure imaginary eigenvalues in non-resonant case, respectively. For each case, the stability regions of the initial equilibrium solution and the critical bifurcation curves are obtained, which may lead to static bifurcation and Hopf bifurcation. The numerical solutions obtained by using fourth-order Runge-Kutta method agree with the analytic predictions.

1 Introduction

Functionally graded materials(FGMs) are extremely excellent materials. They have received increasing attention in both research community and industry due to their excellent thermo mechanical properties. FGMs have been widely used in thermal, structural, optical and electronic materials. With the development of advanced techniques, Functionally graded materials may be fabricated into various structures including beam, plate and shell [1].

Cantilever plates are commonly used in a large number of structures such as solar panels, solar sails of satellites and aircraft rotary wings and their nonlinear dynamic analysis is of great importance in safety design. Liew [2] utilized the Rayleigh-Ritz method to study the vibration of symmetrically composite laminated cantilever trapezoidal thin plates. Based on the von Karman’s nonlinear geometry plate theory and using the methods of multiple scales and finite difference, Nejad and Nazari [3] investigated the nonlinear vibrations of an isotropic cantilever plate with viscoelastic laminate and analyzed the stability and chaotic behaviors. Young and Chen [4] employed a finite element formulation and multiple scales method to obtain the nonlinear response amplitudes of a cantilever skew plate under aerodynamic pressure and in-plane force. Ciancio and Rossit [5] discussed the vibration behavior of a cantilever rectangular anisotropic plate when a concentrated mass is rigidly attached to its center point. Li [6] studied the behavior of shear-wall type buildings through a cantilevered beam analogy. Yu [7] utilized the method of superposition to obtain an analytical solution for free and forced vibrations of cantilever plates carrying point masses. However, Studies on the bifurcation and dynamic behavior of cantilever Functionally graded material plates are quite limited in number. Hao et al. [8] studied the complicated nonlinear dynamics of a FGM cantilever rectangular plate subjected to the transverse excitation in thermal environment. Zhang [9] studied the nonlinear dynamic responses and chaotic motions of a composite laminated cantilever rectangular plate under the in-plane and moment excitations. In recent years,the studies on the dynamics of functionally graded material plates [10–12] are also helpful to understand the nonlinear dynamics of cantilever functionally graded materials rectangular plates. Liew et al. [13, 14] investigated dynamic behaviors of carbon nanotube-reinforced functionally graded cylindrical panels under axial compression. Yaghoobi et al. [15] presents an analytical investigation on the buckling analysis of symmetric sandwich plates with functionally graded material face sheets resting on an elastic foundation based on the first-order shear deformation plate theory. Zhang et al. [16] studied the chaotic vibrations of an orthotropic FGM rectangular plate, in which the heat conduction and temperature-dependent material properties were also taken into account. Recently, the meshless methods [17–19] has been used to analyze the stability of functionally graded material plates. It is efficient to determine the boundary conditions of bifurcations.

The objective of this paper is to investigate the local dynamic behaviors of a functionally graded material cantilever rectangular plate subjected to the transverse excitation in thermal environment. The resonant case considered here is 1:1 internal resonance and 1/2 subharmonic resonance. Both analytical and numerical approaches are employed to consider the bifurcation and stability of this system. Four types of degenerated equilibrium points are studied in detail, which are characterized by a double zero and two negative eigenvalues, a double zero and a pair of pure imaginary eigenvalues, a simple zero and a pair of pure imaginary eigenvalues as well as two pairs of pure imaginary eigenvalues, respectively. The stability regions of the initial equilibrium solution and the critical bifurcation curves are obtained in terms of the system parameters. All numerical results agree with the analytic predictions.

This paper is organized as follows: in Sect. 2, the averaged equations of transverse motion of the cantilever FGM plate are given and the stability conditions of initial equilibrium solution are obtained explicitly. Section 3 is devoted to the studies on the dynamical behaviors of the system in the vicinity of the critical points: a double zero and two negative eigenvalues; a double zero and a pair of pure eigenvalues; a simple zero and a pair of pure imaginary eigenvalues as well as two pairs of pure imaginary eigenvalues. Finally, some conclusions are drawn in Sect. 4.

2 Formulation of the problem

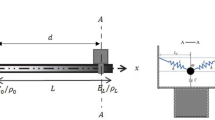
The paper focuses on the stability and bifurcation behaviors of a cantilever functionally graded material rectangular plate under a combined action of a transverse excitation and temperature field. The model is shown in Fig. 1.

Fig. 1

A cantilever functionally graded material plate and the coordinate system

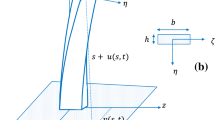
The cantilever FGM rectangular plate $(a\times b\times h)$ is subjected to a temperature field and a transversal excitation $F(x,y)cos( \varOmega t)$. The plate is defined in the Cartesian coordinate $Oxyz$ where $(x,y)$ are the coordinates of a point in the mid-plane $(z = 0)$ of the plate and $z$ is perpendicular to the mid-plane and points downwards. Let $(u,v,w)$ and $(u_{0},v_{0},w_{0})$ represent the displacements of an arbitrary point and a point in the mid-plane of the FGM rectangular plate in the $x$, $y$ and $z$ directions.

The dimensionless governing differential equations of transverse motion for the cantilever FGM rectangular plate were derived in [8]

$$\begin{aligned} \ddot{w_{1}}+&(g_{10}+\beta _{11}N^{T})w_{1} +\mu _{1}\dot{w_{1}}+g_{11}w_{1}w_{2}+g_{12}w_{1}^{2}\nonumber \\&+g_{13}w_{2}^{2}+g_{14}w_{2}w_{1}^{2}+g_{15}w_{1}w_{2}^{2} +g_{16}w_{1}^{3}\nonumber \\&+g_{17}w_{2}^{3}+(g_{18}+\beta _{12}N^{T})w_{2}=f_{1}cos(\varOmega t), \end{aligned}$$

(1a)

$$\begin{aligned} \ddot{w_{2}}+&(g_{20}+\beta _{21}N^{T})w_{2}+\mu _{2}\dot{w_{2}} +g_{21}w_{1}w_{2}+g_{22}w_{1}^{2}\nonumber \\&+g_{23}w_{2}^{2}+g_{24}w_{2}w_{1}^{2}+g_{25}w_{1}w_{2}^{2} +g_{26}w_{1}^{3}\nonumber \\&+g_{27}w_{2}^{3}+(g_{28}+\beta _{22}N^{T})w_{1}=f_{2}cos(\varOmega t), \end{aligned}$$

(1b)

where $w_{1}$ and $w_{2}$ are amplitudes of normal modes, $\mu _{1}$ and $\mu _{2}$ are two combined parameters, including damping parameters, $N^{T}$ are the thermal stress resultant, $f_{1}$ and $f_{2}$ are the magnitudes of the forcing excitation, respectively. All other constants are not listed herein for brevity due to their lengthy expressions.

This paper considers the case of 1:1 internal resonance and 1/2 subharmonic resonance for the cantilever FGM rectangular plate. In such a case we have the resonant relation

$$\begin{aligned} \omega _{1}^{2}=\frac{\varOmega }{2}+\epsilon ^{2}\sigma _{1}, \quad \omega _{2}^{2} =\frac{\varOmega }{2}+\epsilon ^{2}\sigma _{2}, \end{aligned}$$

(2)

where $\epsilon$ is a small perturbation parameter, $\omega _{1}=g_{10}+\beta _{11}N^{T}$ and $\omega _{2}=g_{20}+\beta _{21}N^{T}$ are the first order and second order linear frequencies, $\sigma _{1}$ and $\sigma _{2}$ are two detuning parameters.

Introducing the scale transformations and the temporal rescaling, the approximate solutions $w_{1}(t)$ and $w_{2}(t)$ of (1) were sought in the form of a power series of small perturbation parameter[8]

$$\begin{aligned} w_{1}(t)=\,&\epsilon ^{\delta }\psi _{0}(\tau ,\epsilon ) +\epsilon \psi _{1}(\tau ,\epsilon )e^{-i\frac{\varOmega }{2}t} +\epsilon ^{2}\psi _{2}(\tau ,\epsilon )e^{-i\varOmega t} \nonumber \\&+\epsilon ^{3}\psi _{3}(\tau ,\epsilon )e^{-i\frac{3\varOmega }{2}t} +\epsilon ^{2}\psi _{2}(\tau ,\epsilon )e^{-i2\varOmega t}+cc, \end{aligned}$$

(3a)

$$\begin{aligned} w_{2}(t)=\,&\epsilon ^{\delta }\phi _{0}(\tau ,\epsilon ) +\epsilon \phi _{1}(\tau ,\epsilon )e^{-i\frac{\varOmega }{2}t} +\epsilon ^{2}\phi _{2}(\tau ,\epsilon )e^{-i\varOmega t} \nonumber \\&+\epsilon ^{3}\phi _{3}(\tau ,\epsilon )e^{-i\frac{3\varOmega }{2}t} +\epsilon ^{2}\phi _{2}(\tau ,\epsilon )e^{-i2\varOmega t}+cc. \end{aligned}$$

(3b)

Using the asymptotic perturbation method, the differential equation for the evolution of the complex amplitudes $\psi _{1}$ and $\phi _{1}$ were obtained in [8]

$$\begin{aligned} \dot{\psi _{1}}&= \left(\frac{1}{2}\mu _{1}-\sigma _{1}i \right)\psi _{1}-\frac{(g_{18} +\beta _{12}N^{T})}{\varOmega }\phi _{1}i +\frac{2f_{1}g_{11}}{3\varOmega ^{3}}\phi _{1}^{*}i \nonumber \\&\quad +\frac{4g_{13}f_{2}}{3\varOmega ^{3}}\phi _{1}^{*}i + \left(\frac{2f_{2}g_{11}}{3\varOmega ^{3}}+\frac{4f_{1}g_{12}}{3\varOmega ^{3}}\right) \psi _{1}^{*}i\nonumber \\&\quad -\frac{8g_{13}g_{22}}{3\varOmega ^{3}}\psi _{1}^{2}\phi _{1}^{*} -\frac{g_{15}}{\varOmega }\psi _{1}^{*}\phi _{1}^{2}i -\frac{2g_{15}}{\varOmega }\phi _{1}\phi _{1}^{*}\psi _{1}i\nonumber \\&\quad + \left(\frac{12g_{11}^{2}}{3\varOmega ^{3}}-\frac{4g_{11}g_{23}}{3\varOmega ^{3}} +\frac{24g_{13}g_{21}}{3\varOmega ^{3}} -\frac{8g_{12}g_{13}}{3\varOmega ^{3}}\right)\psi _{1}^{*}\phi _{1}^{2}i\nonumber \\&\quad + \left(\frac{20g_{11}g_{12}}{3\varOmega ^{3}}+\frac{4g_{11}g_{21}}{\varOmega ^{3}} -\frac{8g_{13}g_{22}}{3\varOmega ^{3}} -\frac{g_{14}}{\varOmega }\right)\phi _{1}^{*}\psi _{1}^{2}i\nonumber \\&\quad + \left(\frac{40g_{12}^{2}}{3\varOmega ^{3}}+\frac{20g_{11}g_{22}}{3\varOmega ^{3}} -\frac{3g_{16}}{\varOmega }\right)\psi _{1}^{*}\psi _{1}^{2}i\nonumber \\&\quad + \left(\frac{20g_{11}g_{13}}{3\varOmega ^{3}}+\frac{40g_{13}g_{23}}{3\varOmega ^{3}} -\frac{3g_{17}}{\varOmega }\right)\phi _{1}^{*}\phi _{1}^{2}i\nonumber \\&\quad + \left(\frac{48g_{13}g_{22}}{3\varOmega ^{3}}+\frac{40g_{11}g_{12}}{3\varOmega ^{3}} +\frac{8g_{11}g_{21}}{3\varOmega ^{3}} -\frac{2g_{14}}{\varOmega }\right)\psi _{1}^{*}\psi _{1}\phi _{1}i\nonumber \\&\quad + \left(\frac{8g_{11}^{2}}{3\varOmega ^{3}}+\frac{24g_{11}g_{23}}{3\varOmega ^{3}} +\frac{48g_{12}g_{13}}{3\varOmega ^{3}}+\frac{16g_{13}g_{21}}{3\varOmega ^{3}}\right) \phi _{1}\phi _{1}^{*}\psi _{1}i, \end{aligned}$$

(4a)

$$\begin{aligned} \dot{\phi _{1}}&= \left(-\frac{1}{2}\mu _{2}-\sigma _{2}i \right)\phi _{1}-\frac{(g_{28} + \beta _{22}N^{T})}{\varOmega }\psi _{1}i+\frac{2f_{1}g_{21}}{3\varOmega ^{3}} \phi _{1}^{*}i\nonumber \\&\quad +\frac{4g_{23}f_{2}}{3\varOmega ^{3}}\phi _{1}^{*}i + \left(\frac{2f_{2}g_{21}}{3\varOmega ^{3}} + \frac{4g_{22}f_{1}}{3\varOmega ^{3}}\right)\psi _{1}^{*}i\nonumber \\&\quad -\frac{8g_{23}g_{22}}{3\varOmega ^{3}}\psi _{1}^{2}\phi _{1}^{*}i -\frac{2g_{24}}{\varOmega }\psi _{1}^{*}\psi _{1}\phi _{1}i\nonumber \\&\quad + \left(\frac{4g_{21}g_{11}}{\varOmega ^{3}}-\frac{8g_{22}g_{13}}{3\varOmega ^{3}} +\frac{20g_{23}g_{21}}{3\varOmega ^{3}}-\frac{g_{25}}{\varOmega }\right) \psi _{1}^{*}\phi _{1}^{2}i\nonumber \\&\quad + \left(\frac{4g_{21}^{2}}{\varOmega ^{3}}+\frac{4g_{12}g_{21}}{3\varOmega ^{3}} +\frac{8g_{11}g_{22}}{3\varOmega ^{3}} -\frac{g_{24}}{\varOmega }\right)\phi _{1}^{*}\psi _{1}^{2}i\nonumber \\&\quad + \left(\frac{40g_{22}g_{12}}{3\varOmega ^{3}}+\frac{20g_{21}g_{22}}{3\varOmega ^{3}} -\frac{3g_{26}}{\varOmega }\right)\psi _{1}^{*}\psi _{1}^{2}i\nonumber \\&\quad + \left(\frac{20g_{21}g_{13}}{3\varOmega ^{3}}+\frac{40g_{23}^{2}}{3\varOmega ^{3}} -\frac{3g_{27}}{\varOmega }\right)\phi _{1}^{*}\phi _{1}^{2}i\nonumber \\&\quad + \left(\frac{16g_{23}g_{22}}{\varOmega ^{3}}+\frac{8g_{21}g_{22}}{\varOmega ^{3}} +\frac{16g_{11}g_{22}}{3\varOmega ^{3}}\right)\psi _{1}^{*}\psi _{1}\phi _{1}i\nonumber \\&\quad + \left(\frac{40g_{21}g_{23}}{3\varOmega ^{3}}+\frac{8g_{11}g_{21}}{3\varOmega ^{3}} +\frac{16g_{22}g_{13}}{\varOmega ^{3}}-\frac{2g_{25}}{\varOmega }\right)\phi _{1} \phi _{1}^{*}\psi _{1}i. \end{aligned}$$

(4b)

In order to transform (4) into the Cartesian form, let

$$\begin{aligned} \psi _{1}=x_{1}+ix_{2}, \quad \phi _{1}=x_{3}+ix_{4}. \end{aligned}$$

(5)

Substituting (5) into (4), the averaged equations in the Cartesian form were obtained as follows [8]

$$\begin{aligned} \dot{x_{1}}=&-\frac{1}{2}\mu _{1}\,x_{1}+(\sigma _{1}+\alpha )x_{2}+(\gamma _{1} +k_{1})\,x_{4}+Nf_{1}, \end{aligned}$$

(6a)

$$\begin{aligned} \dot{x_{2}}=&(-\sigma _{1}+\alpha )\,x_{1}-\frac{1}{2}\mu _{1}x_{2}+(\gamma _{1} -k_{1})\,x_{3}+Nf_{2}, \end{aligned}$$

(6b)

$$\begin{aligned} \dot{x_{3}}=&(\gamma _{2}+k_{2})\,x_{2}-\frac{1}{2}\mu _{2}x_{3}+(\sigma _{2} +\beta )\,x_{4}+Nf_{3}, \end{aligned}$$

(6c)

$$\begin{aligned} \dot{x_{4}}=&(\gamma _{2}-k_{2})\,x_{1}+(-\sigma _{2}+\beta )x_{3} -\frac{1}{2}\mu _{2}\,x_{4}+Nf_{4}, \end{aligned}$$

(6d)

where $\alpha =a_{01}f_{1}+a_{02}f_{2}$, $\beta =b_{01}f_{1}+b_{02}f_{2}$, $\gamma _{1}=a_{02}f_{1}+a_{03}f_{2}$, $\gamma _{2}=b_{03}f_{1}+b_{01}f_{2}$, $k_{1}=a_{04}, k_{2}=b_{04}$. The nonlinear functions $Nf_{i}(i=1,2,3,4)$ and all coefficients are presented in “Appendix”.

The Jacobian matrix of (6) evaluated at the initial equilibrium solution $(x_{1},x_{2},x_{3},x_{4})=(0,0,0,0)$ is as follows

$$\begin{aligned} J=\left[ \begin{array}{cccc} -\frac{1}{2}\mu _{1}&{}\sigma _{1}+\alpha &{}0&{}\gamma _{1}+k_{1}\\ -\sigma _{1}+\alpha &{}-\frac{1}{2}\mu _{1}&{}\gamma _{1}-k_{1}&{}0\\ 0&{}\gamma _{2}+k_{2}&{}-\frac{1}{2}\mu _{2}&{}\sigma _{2}+\beta \\ \gamma _{2}-k_{2}&{}0&{}-\sigma _{2}+\beta &{}-\frac{1}{2}\mu _{2}\\ \end{array}\right] \end{aligned}$$

(7)

The characteristic polynomial is

$$\begin{aligned} f(\lambda )=\lambda ^{4}+b_{1}\lambda ^{3}+b_{2}\lambda ^{2}+b_{3}\lambda +b_{4}, \end{aligned}$$

(8)

where

$$\begin{aligned} b_{1}&= \mu _{1}+\mu _{2},\\ b_{2}&= \frac{1}{4}\mu _{2}^{2}+\,\mu _{1}\mu _{2}+\sigma _{1}^{2}-\alpha ^{2} +\frac{1}{4}\mu _{1}^{2}+\sigma _{2}^{2}-\beta ^{2}\\&\quad -2\gamma _{1}\gamma _{2}+2k_{1}k_{2},\\ b_{3}&= \sigma _{2}^{2}\mu _{1}+\frac{1}{4}\mu _{2}^{2}\mu _{1} +\sigma _{1}^{2}\mu _{2}-\alpha ^{2}\mu _{2}+\frac{1}{4}\mu _{1}^{2}\mu _{2}\\& \quad-\gamma _{1}\gamma _{2}\mu _{1} -\gamma _{1}\gamma _{2}\mu _{2}+k_{1}k_{2}\mu _{1}+k_{1}k_{2}\mu _{2},\\ b_{4}&= \sigma _{1}^{2}\sigma _{2}^{2}-\sigma _{2}^{2}\alpha ^{2} +\frac{1}{4}\sigma _{2}^{2}\mu _{1}^{2}+\frac{1}{4}\mu _{2}^{2}\sigma _{1}^{2} -\frac{1}{4}\mu _{2}^{2}\alpha ^{2}-\frac{1}{4}\mu _{1}^{2}\beta ^{2}\\&\quad -2\gamma _{1}\gamma _{2}\alpha \beta +2\gamma _{2}k_{1}\sigma _{2}\alpha +2\gamma _{2}k_{1}\sigma _{1}\beta +2\gamma _{1}k_{2}\sigma _{1}\beta \\&\quad -2k_{1}k_{2}\sigma _{1}\sigma _{2}+2\gamma _{1}k_{2}\sigma _{2}\alpha -2k_{1}k_{2}\alpha \beta -\frac{1}{2}\gamma _{1}\gamma _{2}\mu _{1}\mu _{2}\\&\quad +\frac{1}{2}k_{1}k_{2}\mu _{1}\mu _{2}+\alpha ^{2}\beta ^{2} -2\gamma _{1}\gamma _{2}\sigma _{1}\sigma _{2} -\sigma _{1}^{2}\beta ^{2}+\gamma _{1}^{2}\gamma _{2}^{2}\\&\quad -k_{1}^{2}\gamma _{2}^{2}-k_{2}^{2}\gamma _{1}^{2} +k_{1}^{2}k_{2}^{2}+\frac{1}{16}\mu _{1}^{2}\mu _{2}^{2}.\\ \end{aligned}$$

By the Routh-Hurwitz criterion, the equilibrium solution $(x_{1},x_{2},x_{3},x_{4})=(0,0,0,0)$ is stable, if the following conditions are satisfied

$$\begin{aligned} b_{1}>0, \quad b_{1}b_{2}-b_{3}>0,b_{4}>0, \quad b_{3}(b_{1}b_{2}-b_{3})-b_{1}^{2}b_{4}>0. \end{aligned}$$

(9)

Conditions (9) implies that all the eigenvalues of the Jacobian matrix (7) have negative real parts. When conditions (9) are not satisfied, the initial equilibrium solution is unstable, and bifurcations may occur. In the next section, the detailed analysis will be given when condition (9) are violated.

3 Stability and bifurcation behaviors

In this section, the stability and bifurcation analysis on the parameters $\mu _{1}$ and $\mu _{2}$ will be investigated, which can be divided into four parts.

3.1 Double zero and two negative eigenvalues

Taking parameters as follows:

$\mu _{1}=2,\mu _{2}=2,\sigma _{1}=1,\sigma _{2}=1,\alpha =0,\beta =0, \gamma _{1}=1,\gamma _{2}=2,k_{1}=k_{2}=0,a_{05}=a_{06}=a_{07}=a_{08}= a_{09}=a_{10}=a_{11}=a_{12}=a_{13}=a_{14}=1,b_{05}=b_{06}=b_{07} =b_{08}=b_{09}=b_{10}=b_{11}=b_{12}=b_{13}=b_{14}=1$, which implies that $b_{1}=b_{2}=4$, $b_{3}=b_{4}=0$, then the Jacobian matrix (7) has the eigenvalues $\lambda _{1,2}=0,\lambda _{3,4}=-2$.

Let us consider $\mu _{1}$ and $\mu _{2}$ as the perturbation parameters. Using the parameter transformation $\mu _{1}=2+\xi _{1}, \mu _{2}=2+\xi _{2}$, and the state variable transformation

$$\begin{aligned} \left[ \begin{array}{cccc} x_{1}\\ x_{2}\\ x_{3}\\ x_{4}\\ \end{array}\right] =\left[ \begin{array}{cccc} \frac{1}{2}&{}\frac{1}{2}&{}-\frac{1}{2}&{}\frac{1}{2}\\ -\frac{1}{2}&{}\frac{1}{2}&{}-\frac{1}{2}&{}-\frac{1}{2}\\ 0&{}1&{}0&{}1\\ 1&{}0&{}1&{}0\\ \end{array}\right] \left[ \begin{array}{cccc} z_{1}\\ z_{2}\\ z_{3}\\ z_{4}\\ \end{array}\right] , \end{aligned}$$

(10)

one may transform (6) into a new system as follows

$$\begin{aligned} \dot{z_{1}}=&-\frac{1}{4}(\xi _{1}+\xi _{2})z_{1}-\frac{1}{4}(\xi _{1} -\xi _{2})z_{2}+\frac{1}{4}(\xi _{1}-\xi _{2})z_{3}\nonumber \\&-\frac{1}{4}(\xi _{1}-\xi _{2})z_{4}+Ng_{1}, \end{aligned}$$

(11a)

$$\begin{aligned} \dot{z_{2}}=&\frac{1}{4}(\xi _{1}-\xi _{2})z_{1}-\frac{1}{4}(\xi _{1} +\xi _{2})z_{2}+\frac{1}{4}(\xi _{1}-\xi _{2})z_{3}\nonumber \\&+\frac{1}{4}(\xi _{1}-\xi _{2})z_{4}+Ng_{2}, \end{aligned}$$

(11b)

$$\begin{aligned} \dot{z_{3}}=&-2z_{3}+\frac{1}{4}(\xi _{1}-\xi _{2})z_{1}+\frac{1}{4}(\xi _{1} -\xi _{2})z_{2}\nonumber \\&-\frac{1}{4}(\xi _{1}+\xi _{2})z_{3}+\frac{1}{4}(\xi _{1}-\xi _{2})z_{4} +Ng_{3}, \end{aligned}$$

(11c)

$$\begin{aligned} \dot{z_{4}}=&-2z_{4}-\frac{1}{4}(\xi _{1}-\xi _{2})z_{1}+\frac{1}{4}(\xi _{1} -\xi _{2})z_{2}\nonumber \\&-\frac{1}{4}(\xi _{1}-\xi _{2})z_{3}-\frac{1}{4}(\xi _{1}+\xi _{2})z_{4}+Ng_{4}, \end{aligned}$$

(11d)

where the nonlinear functions $Ng_{i}(i=1,\ldots ,4)$ are exhibited in the “Appendix”.

The Jacobian matrix of (11) evaluated at the initial equilibrium solution $(z_{1},z_{2},z_{3},z_{4})=(0,0,0,0)$ at critical point $\xi _{1c}=\xi _{2c}=0$ is the following canonical form

$$\begin{aligned} J_{(z_{i}=0)}=\left[ \begin{array}{cccc} 0&{}0&{}0&{}0\\ 0&{}0&{}0&{}0\\ 0&{}0&{}-2&{}0\\ 0&{}0&{}0&{}-2\\ \end{array}\right] \end{aligned}$$

The local dynamic behaviors of system (11) are characterized by the critical variables $z_{1}$ and $z_{2}$. Further more, the bifurcation solutions for the noncritical variables $z_{3}$ and $z_{4}$ may be determined from system (11) up to leading orders terms as

$$\begin{aligned} z_{3}=&\frac{1}{8}(\xi _{1}-\xi _{2})z_{1}+\frac{1}{8}(\xi _{1}-\xi _{2})z_{2} -\frac{5}{16}z_{1}^{3}-\frac{13}{16}z_{2}^{3}\nonumber \\&-\frac{11}{16}z_{2}^{2}z_{1}-\frac{11}{16}z_{1}^{2}z_{2}, \end{aligned}$$

(12a)

$$\begin{aligned} z_{4}=&-\frac{1}{8}(\xi _{1}-\xi _{2})z_{1}+\frac{1}{8}(\xi _{1}-\xi _{2})z_{2} +\frac{9}{16}z_{1}^{3}+\frac{31}{16}z_{2}^{3}\nonumber \\&+\frac{23}{16}z_{2}^{2}z_{1}+\frac{25}{16}z_{1}^{2}z_{2}. \end{aligned}$$

(12b)

In order to study the bifurcation and stable properties of system (11) in the vicinity of the critical point, one only need to analyze the following two-dimensional system

$$\begin{aligned} \dot{z_{1}}=&\left[ -\frac{1}{4}(\xi _{1}+\xi _{2})+\frac{1}{16}(\xi _{1} -\xi _{2})^{2}\right] z_{1}-\frac{1}{4}(\xi _{1}-\xi _{2})z_{2}\nonumber \\&+\frac{1}{8}z_{1}^{3}-\frac{5}{8}z_{2}^{3} -\frac{3}{8}z_{1}^{2}z_{2}-\frac{1}{8}z_{2}^{2}z_{1}, \end{aligned}$$

(13a)

$$\begin{aligned} \dot{z_{2}}=&\frac{1}{4}(\xi _{1}-\xi _{2})z_{1}+\left[ -\frac{1}{4}(\xi _{1} +\xi _{2})+\frac{1}{16}(\xi _{1}-\xi _{2})^{2}\right] z_{2}\nonumber \\&-\frac{3}{8}z_{1}^{3}-\frac{23}{8}z_{2}^{3} -\frac{17}{8}z_{1}^{2}z_{2}-\frac{13}{8}z_{2}^{2}z_{1}. \end{aligned}$$

(13b)

To find the stability conditions of the initial equilibrium solution $(z_{1},z_{2})=(0,0)$, one may evaluate the Jacobian matrix of (13) at $(z_{1},z_{2})=(0,0)$ and obtain

$$\begin{aligned} J_{(z_{i}=0)}=\left[ \begin{array}{cc} a_{11}&{}a_{12}\\ a_{21}&{}a_{21}\\ \end{array}\right] \end{aligned}$$

(14)

where

$$\begin{aligned} a_{11}&= -\frac{1}{4}(\xi _{1}+\xi _{2})+\frac{1}{16}(\xi _{1}-\xi _{2})^{2},\\ a_{12}&= -\frac{1}{4}(\xi _{1}-\xi _{2}),\\ a_{21}&= \frac{1}{4}(\xi _{1}-\xi _{2}),\\ a_{22}&= -\frac{1}{4}(\xi _{1}+\xi _{2})+\frac{1}{16}(\xi _{1}-\xi _{2})^{2}.\\ \end{aligned}$$

The characteristic polynomial is

$$\begin{aligned} f(\lambda )&= \lambda ^{2}+\left[ \frac{1}{2}(\xi _{1}+\xi _{2}) -\frac{1}{8}(\xi _{1}-\xi _{2})^{2}\right] \lambda \nonumber \\&\quad +\left[ -\frac{1}{4}(\xi _{1}+\xi _{2})+\frac{1}{16}(\xi _{1} -\xi _{2})^{2}\right] ^{2}\nonumber \\&\quad +\frac{1}{16}(\xi _{1}-\xi _{2})^{2}. \end{aligned}$$

(15)

The stability conditions for the initial equilibrium solution $(z_{1},z_{2})=(0,0)$ are

$$\begin{aligned} \frac{1}{2}(\xi _{1}+\xi _{2})-\frac{1}{8}(\xi _{1}-\xi _{2})^{2}>0, \end{aligned}$$

(16)

and

$$\begin{aligned} \left[ -\frac{1}{4}(\xi _{1}+\xi _{2})+\frac{1}{16}(\xi _{1}-\xi _{2})^{2}\right] ^{2}+\frac{1}{16}(\xi _{1}-\xi _{2})^{2}>0. \end{aligned}$$

(17)

It is easy to see that $\left[ -\frac{1}{4}(\xi _{1}+\xi _{2})+\frac{1}{16}(\xi _{1}-\xi _{2})^{2}\right] ^{2}+\frac{1}{16}(\xi _{1}-\xi _{2})^{2}>0$ unless $(\xi _{1},\xi _{2})=(0,0)$ , so if $\frac{1}{2}(\xi _{1}+\xi _{2})-\frac{1}{8}(\xi _{1}-\xi _{2})^{2}>0$, the initial equilibrium solution is stable. Then a critical bifurcation curve is obtained

$$\begin{aligned} L_{1}:\frac{1}{2}(\xi _{1}+\xi _{2})-\frac{1}{8}(\xi _{1}-\xi _{2})^{2}=0. \end{aligned}$$

(18)

From (15), we can obtain the eigenvalues of the Jacobian matrix (14) at the initial equilibrium solution $(z_{1},z_{2},z_{3},z_{4})=(0,0,$ $0,0)$ as follows

$$\begin{aligned} \lambda _{1,2}=-\frac{1}{4}(\xi _{1}+\xi _{2})+\frac{1}{16}(\xi _{1} -\xi _{2})^{2}\pm \frac{1}{4}(\xi _{1}-\xi _{2})i. \end{aligned}$$

Let

$$\begin{aligned} a=Re(\lambda _{1,2})&= -\frac{1}{4}(\xi _{1}+\xi _{2})+\frac{1}{16}(\xi _{1} -\xi _{2})^{2},\\ b=Im(\lambda _{1,2})&= \frac{1}{4}(\xi _{1}-\xi _{2}), \end{aligned}$$

it is easy to see that $a=0,b>0$, and $\frac{da}{d\xi _{1}}\ne 0$, when $(\xi _{1},\xi _{2})\in L_{1}$ and $(\xi _{1},\xi _{2})\ne 0$ or $(\frac{3}{2},-\frac{1}{2})$. By Hopf bifurcation theorem, along $L_{1}$, Hopf bifurcation may occur. The bifurcation diagram is shown as Fig. 2. We can observe that the critical curves $L_{1}$ separate $\xi _{1}-\xi _{2}$ plane into two kinds of areas (I and II). The initial equilibrium solution $(x_{1},x_{2},x_{3},x_{4})=(0,0,0,0)$ is stable while $(\xi _{1},\xi _{2})$ belongs to area I( the stable region for E.S. — the initial equilibrium solution). When $(\xi _{1},\xi _{2})$ crosses $L_{1}$ and goes into area II, the initial equilibrium solution becomes unstable.

Fig. 2

Transition curves for the case of a double zero and two negative eigenvalues

Here the numerical results have been obtained by fourth-order Runge-Kutta method performed on the basis of the differential equation (6). Choosing parameter values of $\xi _{1}$ and $\xi _{2}$ from the region II (the blank area), any numerical solution starting from an arbitrary initial point$((x_{1},x_{2},x_{3},x_{4})\ne (0,0,0,0))$ diverges to infinity, initiating that the initial equilibrium solution is unstable, as predicted by the analytic study. When the parameter value is chosen from the region I (the shadow area), such as, $(\xi _{1},\xi _{2})=(0.2,0.2)$, a numerical solution starting from an initial point $(x_{1},x_{2},x_{3},x_{4})=(0.01,0,0,0.02)$ is obtained, which converges to the origin, implying that the initial equilibrium solution is stable. This is shown in Fig. 3, where the phase trajectories are projected onto the $x_{1}-x_{2}$ and $x_{3}-x_{4}$ plane. It should be noted that since the study is focused on the local dynamic behaviors of the cantilever FGM plate in the vicinity of a critical point, so the parameter $(\xi _{1},\xi _{2})$ should be chosen near the critical point $(\xi _{1},\xi _{2})=(0,0)$.

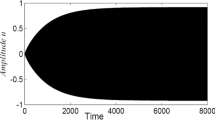
When $(\xi _{1},\xi _{2})=(0.2,-0.1664)\in L_{1}$, the trajectory starting from an initial point $(x_{1},x_{2},x_{3},x_{4})=(-0.001,0.001,0.002,0)$ yields a stable limit cycle shown in Fig. 4.

Fig. 3

Trajectory projection starting from $(x_{1},x_{2},x_{3},x_{4})=(0.01,0,0,0.02)$ converges to the E.S. when $(\xi _{1},\xi _{2})=(0.2,0.2)$, a the phase portrait on plane $(x_{1},x_{2})$; b the phase portrait on plane $(x_{3},x_{4})$

Fig. 4

Trajectory projection starting from $(x_{1},x_{2},x_{3},x_{4})=(-0.001,0.001,0.002,0)$ when $(\xi _{1},\xi _{2})=(0.2,-0.1664)$, a the phase portrait on plane $(x_{1},x_{2})$; b the phase portrait on plane $(x_{3},x_{4})$

3.2 Double zero and a pair of pure imaginary eigenvalues

Choosing the following parameter values: $\mu _{1}=0,\mu _{2}=0,\sigma _{1}=\frac{1}{2},\sigma _{2}=\frac{3}{4}, \alpha =\frac{1}{2},\beta =\frac{3}{4},\gamma _{1}=0,\gamma _{2}=1,k_{1}=1,k_{2} =\frac{1}{2}, a_{05}=a_{06}=a_{07}=a_{08}= a_{09}=a_{10}=a_{11}=a_{12}=a_{13}=a_{14}=1,b_{05}=b_{06}=b_{07}=b_{08} =b_{09}=b_{10}=b_{11}=b_{12}=b_{13}=b_{14}=1$, which implies that $b_{2}=1$, $b_{1}=b_{3}=b_{4}=0$, then the Jacobian matrix (7) has the eigenvalues $\lambda _{1,2}=0,\lambda _{3,4}=\pm i$.

Choosing $\mu _{1}$ and $\mu _{2}$ as perturbation parameters, and using the parameter transformation $\mu _{1}=\xi _{1}, \mu _{2}=\xi _{2}$. The characteristic polynomial (8) of the Jacobian matrix (7) becomes

$$\begin{aligned} \tilde{f}(\lambda )=\lambda ^{4}+\tilde{b}_{1}\lambda ^{3} +\tilde{b}_{2}\lambda ^{2}+\tilde{b}_{3}\lambda +\tilde{b}_{4}, \end{aligned}$$

(19)

where

$$\begin{aligned} \tilde{b}_{1}&= \xi _{1}+\xi _{2},\\ \tilde{b}_{2}&= \frac{1}{4}\xi _{1}^{2}+\frac{1}{4}\xi _{2}^{2} +\xi _{1}\xi _{2}+1,\\ \tilde{b}_{3}&= \frac{1}{4}\xi _{1}\xi _{2}^{2}+\frac{1}{4}\xi _{2}\xi _{1}^{2} +\frac{1}{2}\xi _{1}+\frac{1}{2}\xi _{2},\\ \tilde{b}_{4}&= \frac{1}{16}\xi _{2}^{2}\xi _{1}^{2}+\frac{1}{4}\xi _{1}\xi _{2}. \end{aligned}$$

The stability conditions for the initial equilibrium solution $(x_{1},x_{2},x_{3},x_{4})=(0,0,0,0)$ are

$$\begin{aligned} \varDelta _{1}&= \tilde{b}_{1}>0,\ i.e.\; \xi _{1}+\xi _{2}>0,\\ \varDelta _{2}&= \tilde{b}_{1}\tilde{b}_{2}-\tilde{b}_{3}>0,\\&\quad i.e.\;(\xi _{1}+\xi _{2})(\xi _{1}^{2}+\xi _{2}^{2}+3\xi _{1}\xi _{2}+2)>0,\\ \varDelta _{3}&= \tilde{b}_{3}(\tilde{b}_{1}\tilde{b}_{2}-\tilde{b}_{3}) -\tilde{b}_{1}^{2}\tilde{b}_{4},\\&\quad i.e.\;(\xi _{1}+\xi _{2})^{2}(\xi _{2}^{2}+\xi _{1}\xi _{2}+2)(\xi _{1}^{2} +\xi _{1}\xi _{2}+2)>0. \end{aligned}$$

From the three inequalities above, one may get the following three transition curves

$$\begin{aligned}&L_{2}:\xi _{1}+\xi _{2}=0, \end{aligned}$$

(20)

$$\begin{aligned}&L_{3}:\xi _{1}^{2}+\xi _{2}^{2}+3\xi _{1}\xi _{2}+2=0, \end{aligned}$$

(21)

$$\begin{aligned}&L_{4}:(\xi _{2}^{2}+\xi _{1}\xi _{2}+2)(\xi _{1}^{2}+\xi _{1}\xi _{2}+2)=0. \end{aligned}$$

(22)

Then, the transition curves are shown as Fig.5.

Fig. 5

Transition curves for the case of double zero and a pair of pure imaginary eigenvalues

When $\xi _{1}+\xi _{2}>0$, $\xi _{1}^{2}+\xi _{2}^{2}+3\xi _{1}\xi _{2}+2>0$, and $(\xi _{2}^{2}+\xi _{1}\xi _{2}+2)(\xi _{1}^{2}+\xi _{1}\xi _{2}+2)>0$ are all satisfied, the initial equilibrium solution is stable. By the Fig. 5, we can observe that the critical curves $L_{2}$, $L_{3}$, $L_{4}$ separate $\xi _{1}-\xi _{2}$ plane into two kinds of areas (I and II). When $(\xi _{1},\xi _{2})$ belongs to region I, the initial equilibrium solution is stable, and when $(\xi _{1},\xi _{2})$ belongs to region II, the initial equilibrium solution of the system is unstable.

Similar to the case in the Sect. 3.1, different parameters are chosen to confirm the analytical results obtained in this section. When the parameter is chosen as $(\xi _{1},\xi _{2})=(0.4,0.4)$, which is located in the region I, numerical results show that a trajectory starting from $(x_{1},x_{2},x_{3},x_{4})=(0.1,-0.1,0.2,-0.2)$ converges to the origin, implying that the initial equilibrium solution is stable. The phase trajectories are projected onto the $x_{1}-x_{2}$ and $x_{3}-x_{4}$ sub-spaces as shown in Fig. 6.

Fig. 6

Trajectory projection starting from $(x_{1},x_{2},x_{3},x_{4})=(0.1,-0.1,0.2,-0.2)$ converges to the E.S. when $(\xi _{1},\xi _{2})=(0.4,0.4)$, a the phase portrait on plane $(x_{1},x_{2})$; b the phase portrait on plane $(x_{3},x_{4})$

3.3 A simple zero and a pair of pure imaginary eigenvalues

Choosing the following parameter values: $\mu _{1}=2,\mu _{2}=0,\sigma _{1}=0,\sigma _{2}=1,\alpha =1,\beta =0, \gamma _{1}=k_{1}=1,\gamma _{2}=k_{2}=0,a_{05}=a_{06}=a_{07}=a_{08}=a_{09}= a_{10}=a_{11}=a_{12}=a_{13}=a_{14}=1,b_{05}=b_{06}=b_{07}=b_{08}=b_{09} =b_{10}=b_{11}=b_{12}=b_{13}=b_{14}=1$, which implies that $b_{2}=1,b_{1}=b_{3}=2,b_{4}=0$, and the Jacobian matrix (7) has the eigenvalues $\lambda _{1}=0,\lambda _{2,3}=\pm i,\lambda _{4}=-2$.

Using the parameter transformation $\mu _{1}=2+\xi _{1}, \mu _{2}=\xi _{2}$, and the subsequent state variable transformation

$$\begin{aligned} \left[ \begin{array}{cccc} x_{1}\\ x_{2}\\ x_{3}\\ x_{4}\\ \end{array}\right] =\left[ \begin{array}{cccc} 1&{}\frac{6}{5}&{}\frac{2}{5}&{}-1\\ 1&{}\frac{4}{5}&{}-\frac{2}{5}&{}1\\ 0&{}1&{}0&{}0\\ 0&{}0&{}1&{}0\\ \end{array}\right] \left[ \begin{array}{cccc} z_{1}\\ z_{2}\\ z_{3}\\ z_{4}\\ \end{array}\right] \end{aligned}$$

(23)

into (6) yields

$$\begin{aligned} \dot{z_{1}}=&-\frac{1}{2}\xi _{1}z_{1}+\frac{1}{2} (-\xi _{1}+\xi _{2})z_{3}+Nh_{1}, \end{aligned}$$

(24a)

$$\begin{aligned} \dot{z_{2}} = &z_{3}-\frac{1}{2}\xi _{2}z_{2}+Nh_{2}, \end{aligned}$$

(24b)

$$\begin{aligned} \dot{z_{3}}=&-z_{2}-\frac{1}{2}\xi _{2}z_{3}+Nh_{3}, \end{aligned}$$

(24c)

$$\begin{aligned} \dot{z_{4}}=&-2z_{4}+\frac{1}{10}(\xi _{1}-\xi _{2})z_{2} +\frac{1}{5}(\xi _{1}-\xi _{2})z_{3}\nonumber \\&-\frac{1}{2}\xi _{1}z_{4}+Nh_{4}, \end{aligned}$$

(24d)

where the nonlinear functions $Nh_{i}(i=1,\ldots ,4)$ are exhibited in the “Appendix”.

The Jacobian matrix of (24) evaluated at the initial equilibrium solution $(z_{1},z_{2},z_{3},z_{4})=(0,0,0,0)$ at critical point $\xi _{1c}=\xi _{2c}=0$ is the following canonical form

$$\begin{aligned} J_{(z_{i}=0)}=\left[ \begin{array}{cccc} 0&{}0&{}0&{}0\\ 0&{}0&{}1&{}0\\ 0&{}-1&{}0&{}0\\ 0&{}0&{}0&{}-2\\ \end{array}\right] . \end{aligned}$$

(25)

The dynamical behaviors of this system in the vicinity of the critical point is determined by the critical variables $z_{1},z_{2},z_{3}$. Referred to paper [20], introducing a nearly identity non-linear transform $z_{i}=y_{i}+g_{i}(y_{j})$ (which are omitted, since they are not significant in the following analysis) and a cylindrical coordinate transform

$$\begin{aligned} z_{1}=y, \quad z_{2}=r\cos \theta, \quad z_{3}=r\sin \theta, \quad z_{4}=z_{4}, \end{aligned}$$

(26)

yields the normal form of (24) in the cylindrical co-ordinate system as follows

$$\begin{aligned} \dot{y}=y \left(-\frac{1}{2}\xi _{1}-\frac{57}{10}r^{2}-2y^{2}\right), \end{aligned}$$

(27a)

$$\begin{aligned} \dot{r}=r \left(-\frac{1}{2}\xi _{2}+\frac{87}{100}r^{2}+\frac{12}{5}y^{2}\right), \end{aligned}$$

(27b)

and

$$\begin{aligned} \dot{\theta }=1+\frac{177}{50}r^{2}+\frac{24}{5}y^{2}. \end{aligned}$$

(28)

The steady state solutions and their stability conditions can be found from Eq. (27), while Eq. (28) determines the frequency of possible periodic solutions. Letting $\dot{y}=0$, $\dot{r}=0$ in Eq. (27) leads to the following steady state solutions:

The initial equilibrium solution (E.S.)

$$\begin{aligned} y=r=0. \end{aligned}$$

(29)

The static bifurcation solution (S.B.)

$$\begin{aligned} \left\{ \begin{aligned} y^{2}&=-\frac{\xi _{1}}{4},\\ r&=0. \end{aligned} \right. \end{aligned}$$

(30)

The Hopf bifurcation solution (H.B.)

$$\begin{aligned} \left\{ \begin{aligned} y&=0,\\ r^{2}&= \frac{50}{87}\xi _{2}. \end{aligned} \right. \end{aligned}$$

(31)

The secondary Hopf bifurcation or the second static bifurcation solution (2nd H.B. or 2nd S.B.)

$$\begin{aligned} \left\{ \begin{aligned} y^{2}&=\frac{29}{398} \left(\frac{1}{2}\xi _{1}+\frac{95}{29}\xi _{2}\right),\\ r^{2}&=-\frac{100}{597} \left(\frac{3}{5}\xi _{1}+\frac{1}{2}\xi _{2}\right). \end{aligned} \right. \end{aligned}$$

(32)

Here, the notation 2nd H.B. denotes a dynamic bifurcation from the S.B. solution (i.e., from a non-zero equilibrium to a periodic solution), while the notation 2nd S.B. represents a static bifurcation from the H.B. solution (i.e., a periodic solution having a static shift). These two bifurcation solutions actually belong to the same family of limit cycles described by Eq. (32).

The stability conditions can be determined from the Jacobian matrix of Eq. (27), given by

$$\begin{aligned} J=\left[ \begin{array}{cc} -\frac{1}{2}\xi _{1}-\frac{57}{10}r^{2}-6y^{2}&{}-\frac{57}{5}yr\\ \frac{24}{5}yr&{}-\frac{1}{2}\xi _{2}+\frac{261}{100}r^{2}+\frac{12}{5}y^{2}\\ \end{array}\right] . \end{aligned}$$

(33)

Evaluating the Jacobian matrix (33) on the E.S. (29) shows that if the conditions

$$\begin{aligned} \xi _{1}>0 \quad and \quad \xi _{2}>0 \end{aligned}$$

(34)

are satisfied, then the E.S. is stable. The region defined by equation (34) in the parameter space is shown in Fig. 7. Two critical lines which define the stability boundaries of the E.S. can be obtained from conditions (34), one of them is

$$\begin{aligned} L_{5}:\xi _{1}=0 \, (\xi _{2}>0), \end{aligned}$$

(35)

from which non-trivial equilibrium solutions (S.B.) described by Eq. (30) bifurcate from the initial equilibrium solution (29). The other critical line is defined by

$$\begin{aligned} L_{6}:\xi _{2}=0 \, (\xi _{1}>0), \end{aligned}$$

(36)

along which the H.B. solution (31) may occur.

To find the stability condition of the S.B. solution (30), evaluate the Jacobian (33) on the S.B. solution (30) to obtain

$$\begin{aligned} J_{S.B.}=\left[ \begin{array}{cc} \xi _{1}&{}0\\ 0&{}-\frac{3}{5}\xi _{1}-\frac{1}{2}\xi _{2}\\ \end{array}\right] ,\end{aligned}$$

(37)

which implies that the S.B. solution is stable if

$$\begin{aligned} \xi _{1}<0 \quad and \quad \frac{3}{5}\xi _{1}+\frac{1}{2}\xi _{2}>0. \end{aligned}$$

(38)

The stability boundaries defined by conditions (38) include the critical line $L_{5}$ and another critical line

$$\begin{aligned} L_{7}: \frac{3}{5}\xi _{1}+\frac{1}{2}\xi _{2}=0 (\xi _{1}<0). \end{aligned}$$

(39)

Thus, the S.B. solution (30) is stable in the region bounded by the critical lines $L_{5}$ and $L_{7}$(see Fig.7).

Next, the stability of the H.B. solution (31) is found by evaluating the Jacobian (33) on Eq. (31) to yield

$$\begin{aligned} J_{H.B.}=\left[ \begin{array}{cc} -\frac{1}{2}\xi _{1}-\frac{95}{29}\xi _{2}&{}0\\ 0&{}\xi _{2}\\ \end{array}\right] ,\end{aligned}$$

(40)

which, in turn, shows when

$$\begin{aligned} \frac{1}{2}\xi _{1}+\frac{95}{29}\xi _{2}>0 \quad and \quad \xi _{2}<0, \end{aligned}$$

(41)

the H.B. solution is stable, and the frequency of the periodic solution (31) is given by

$$\begin{aligned} \omega _{1}=1+\frac{59}{19}\xi _{2}. \end{aligned}$$

(42)

The second inequality of Eq. (41) is not satisfied since the H.B. solution emerges when $\xi _{2}>0$, so the H.B. solution is unstable. Therefore the limit cycles expressed by Eq. (32) cannot bifurcate from the H.B. solution along

$$\begin{aligned} L_{8}:\frac{1}{2}\xi _{1}+\frac{95}{29}\xi _{2}=0(\xi _{2}<0). \end{aligned}$$

(43)

and only bifurcate from the S.B. solution along $L_{7}$.

When the parameter values are varied such that the critical boundary $L_{7}$ is intersected, the S.B. solution becomes unstable and bifurcates into a family of limit cycles (the 2nd H.B.solution). The solution of the family is given by Eq. (32). The frequency of the family of limit cycles is given by

$$\begin{aligned} \omega _{2}=1-\frac{36}{199}\xi _{1}+\frac{169}{199}\xi _{2}. \end{aligned}$$

(44)

To investigate the stability of this family of limit cycles, evaluate the Jacobian matrix (33) on Eq. (32) to obtain

$$\begin{aligned} J_{2nd H.B.}=\left[ \begin{array}{cc} -4y^{2}&{}-\frac{57}{5}yr\\ \frac{24}{5}yr&{}\frac{87}{50}r^{2}\\ \end{array}\right] .\end{aligned}$$

(45)

Then the stability conditions are found from the trace and determinant of the Jacobian as

$$\begin{aligned} Tr&= -\frac{1}{198005}(63481\xi _{1}+217905\xi _{2})<0, \end{aligned}$$

(46)

$$\begin{aligned} Det&= \frac{1194}{25}y^{2}r^{2}. \end{aligned}$$

(47)

It is easy to see that the condition (47) is automatically satisfied as long as the H.B. (II) solution exists. Therefore there exists stable H.B.(II) solution when $\frac{1}{2}\xi _{1}+\frac{95}{29}\xi _{2}>0$, $\frac{3}{5}\xi _{1}+\frac{1}{2}\xi _{2}<0$ and $63481\xi _{1}+217905\xi _{2}>0$. The transition curves which define the stability boundaries of the H.B.(II) solution are $L_{7}$ and

$$\begin{aligned} L_{9}:63481\xi _{1}+217905\xi _{2}=0 \left(\frac{3}{5}\xi _{1}+\frac{1}{2}\xi _{2}<0 \right). \end{aligned}$$

(48)

From previous analysis, we get the only possible sequence of bifurcations as follows: first, the static bifurcation solution (30) bifurcates from the initial equilibrium solution (29) along the transition curve $L_{5}$, then, as the parameters cross the transition curve $L_{7}$, the static bifurcation solution loses its stability and bifurcates into a family of limit cycle. Finally, the H.B.(II) solution loses its stability and bifurcates into a two-dimensional torus along the transition curve $L_{9}$. The bifurcation critical lines and bifurcation solutions are shown in Fig.7.

Fig. 7

Transition curves for the case of a simple zero and a pair of pure imaginary eigenvalues

Now choosing different parameter values from the different regions in Fig. 7 to confirm the previous analytical results. When the parameter values are chosen as $(\xi _{1},\xi _{2})=(0.1,0.2)$, which is located in the region bounded by the critical lines $L_{5}$ and $L_{6}$, numerical results show that the trajectory starting from a point near the origin converges to the origin asymptotically. An example is shown in Fig. 8, in which the initial condition is $(x_{1},x_{2},x_{3},x_{4})=(-0.1,0,0.02,0.2)$.

When the parameter values are chosen as $(\xi _{1},\xi _{2})=(-0.02,0.06)$, which is located in the region bounded by the critical lines $L_{5}$ and $L_{7}$, numerical results show that the trajectory starting from a point near the origin converges to the static bifurcation solutions. An example is shown in Fig. 9, in which the initial condition is $(x_{1},x_{2},x_{3},x_{4})=(-0.2,-0.03,0,-0.02)$. It is interesting to note that the trajectory first converges to the dark area and then moves to the non-trivial equilibrium point.

When the parameter values are chosen as $(\xi _{1},\xi _{2})=(0.02,-0.0031)$, which is located in the region bounded by the critical lines $L_{7}$ and $L_{9}$, the trajectory starting from an initial point $(x_{1},x_{2},x_{3},x_{4})=(-0.1,0,0.02,0.2)$ yields a stable limit cycles shown in Fig. 10.

Fig. 8

Trajectory projection starting from $(x_{1},x_{2},x_{3},x_{4})=(-0.1,0,0.02,0.2)$ converges to the E.S. when $(\xi _{1},\xi _{2})=(0.1,0.2)$, a the phase portrait on plane $(x_{1},x_{2})$; b the phase portrait on plane $(x_{3},x_{4})$

Fig. 9

Trajectory projection starting from $(x_{1},x_{2},x_{3},x_{4})=(-0.2,-0.03,0,-0.02)$ converges to the B.S. when $(\xi _{1},\xi _{2})=(-0.02,0.06)$, a the phase portrait on plane $(x_{1},x_{2})$; b the phase portrait on plane $(x_{3},x_{4})$

Fig. 10

Trajectory projection starting from $(x_{1},x_{2},x_{3},x_{4})=(-0.1,0,0.02,0.2)$ converges to the 2nd H.B. when $(\xi _{1},\xi _{2})=(0.02,-0.0031)$, a the phase portrait on plane $(x_{1},x_{2})$; b the phase portrait on plane $(x_{3},x_{4})$

3.4 Two pairs of pure imaginary eigenvalues

Choosing the following parameter values: $\mu _{1}=0,\mu _{2}=0,\sigma _{1}=-1,\sigma _{2}=-2, \alpha =0,\beta =0,\gamma _{1}=-1,k_{1}=0,\gamma _{2}=0,k_{2}=0, a_{05}=a_{06}=a_{07}=a_{08}= a_{09}=a_{10}=a_{11}=a_{12}=a_{13}=a_{14}=1,b_{05} =b_{06}=b_{07}=b_{08}=b_{09}=b_{10}=b_{11}=b_{12}=b_{13}=b_{14}=1$, which implies that $b_{1}=b_{3}=0,b_{2}=3,b_{4}=1$, and the Jacobian matrix (7) has the eigenvalues $\lambda _{1,2}=\pm \frac{\sqrt{5}-1}{2}i,\lambda _{3,4}=\pm \frac{\sqrt{5}+1}{2}i$.

Using the parameter transformation $\mu _{1}=\xi _{1}, \mu _{2}=\xi _{2}$, and the state variable transformation

$$\begin{aligned} \left[ \begin{array}{cccc} x_{1}\\ x_{2}\\ x_{3}\\ x_{4}\\ \end{array}\right] =\left[ \begin{array}{cccc} 0&{}\frac{3+\sqrt{5}}{2}&{}0&{}\frac{3-\sqrt{5}}{2}\\ \frac{3+\sqrt{5}}{2}&{}0&{}\frac{3-\sqrt{5}}{2}&{}0\\ 0&{}-1&{}0&{}-1\\ 1&{}0&{}1&{}0\\ \end{array}\right] \left[ \begin{array}{cccc} z_{1}\\ z_{2}\\ z_{3}\\ z_{4}\\ \end{array}\right] \end{aligned}$$

(49)

one can get

$$\begin{aligned} \dot{z_{1}}&= \frac{\sqrt{5}-1}{2}z_{2}+\left[ \left( -\frac{1}{4} -\frac{3\sqrt{5}}{20}\right) \xi _{1}+\left( -\frac{1}{4} +\frac{3\sqrt{5}}{20}\right) \xi _{2}\right] z_{1}\nonumber \\&\quad +\left[ \left( \frac{1}{4}-\frac{3\sqrt{5}}{20}\right) \xi _{1}+\left( -\frac{1}{4}+\frac{3\sqrt{5}}{20}\right) \xi _{2}\right] z_{3}+NJ_{1}, \end{aligned}$$

(50a)

$$\begin{aligned} \dot{z_{2}}&= \frac{1-\sqrt{5}}{2}z_{1}+\left[ \left( -\frac{1}{4}-\frac{3\sqrt{5}}{20}\right) \xi _{2}+\left( -\frac{1}{4}+ \frac{3\sqrt{5}}{20}\right) \xi _{2}\right] z_{2}\nonumber \\&\quad +\left[ \left( \frac{1}{4}-\frac{3\sqrt{5}}{20}\right) \xi _{1}+\left( -\frac{1}{4}+\frac{3\sqrt{5}}{20}\right) \xi _{2}\right] z_{4}+NJ_{2}, \end{aligned}$$

(50b)

$$\begin{aligned} \dot{z_{3}}&= \frac{-1-\sqrt{5}}{2}z_{4}+\left[ \left( \frac{1}{4}+\frac{3 \sqrt{5}}{20}\right) \xi _{1}+\left( -\frac{1}{4} -\frac{3\sqrt{5}}{20}\right) \xi _{2}\right] z_{1}\nonumber \\&\quad +\left[ \left( -\frac{1}{4}+\frac{3\sqrt{5}}{20}\right) \xi _{1}+\left( -\frac{1}{4}-\frac{3\sqrt{5}}{20}\right) \xi _{2}\right] z_{3}+NJ_{3},\nonumber \\ \end{aligned}$$

(50c)

$$\begin{aligned} \dot{z_{4}}&= \frac{1+\sqrt{5}}{2}z_{3}+\left[ \left( \frac{1}{4} +\frac{3\sqrt{5}}{20}\right) \xi _{1}+\left( -\frac{1}{4} -\frac{3\sqrt{5}}{20}\right) \xi _{2}\right] z_{2}\nonumber \\&\quad +\left[ \left( -\frac{1}{4}+\frac{3\sqrt{5}}{20}\right) \xi _{1} +\left( -\frac{1}{4}-\frac{3\sqrt{5}}{20}\right) \xi _{2}\right] z_{4}+NJ_{4}, \end{aligned}$$

(50d)

where the nonlinear functions $NJ_{i}(i=1,\ldots ,4)$ are exhibited in the “Appendix”.

With the aid of normal form theory and the method of computer algebra, we get the normal form of (50) in polar coordinate system as follows

$$\begin{aligned} \dot{r_{1}}=r_{1}\left[ \left( -\frac{1}{4}-\frac{3\sqrt{5}}{20}\right) \xi _{1}+\left( -\frac{1}{4}+\frac{3\sqrt{5}}{20}\right) \xi _{2}\right] , \end{aligned}$$

(51a)

$$\begin{aligned} \dot{r_{2}}=r_{2}\left[ \left( -\frac{1}{4}+\frac{3\sqrt{5}}{20}\right) \xi _{1}+\left( -\frac{1}{4}-\frac{3\sqrt{5}}{20}\right) \xi _{2}\right] , \end{aligned}$$

(51b)

and

$$\begin{aligned} \dot{\theta _{1}}=\frac{\sqrt{5}}{2}-\frac{1}{2}-\frac{1}{20}\left[ (85+51\sqrt{5})r_{1}^{2}+(-120+72\sqrt{5})r_{2}^{2}\right] , \end{aligned}$$

(52a)

$$\begin{aligned} \dot{\theta _{2}}=\frac{\sqrt{5}}{2}+\frac{1}{2}+\frac{1}{20}\left[ (120+72 \sqrt{5})r_{1}^{2}+(-85+51\sqrt{5})r_{2}^{2}\right] . \end{aligned}$$

(52b)

On the base of (51), by setting $\dot{r_{1}}=\dot{r_{2}}=0$, the steady state solutions are obtained. In this case, it is easy to show that (51) has one solution $(r_{1},r_{2})=(0,0)$. The Jacobian matrix of (51) at the initial equilibrium solution is as follows

$$\begin{aligned} J=\left[ \begin{array}{cc} c_{11}&{}0\\ 0&{}c_{22}\\ \end{array}\right] \end{aligned}$$

(53)

where

$$\begin{aligned} c_{11}=\left( -\frac{1}{4}-\frac{3\sqrt{5}}{20}\right) \xi _{1} +\left( -\frac{1}{4}+\frac{3\sqrt{5}}{20}\right) \xi _{2},\\ c_{22}=\left( -\frac{1}{4}+\frac{3\sqrt{5}}{20}\right) \xi _{1} +\left( -\frac{1}{4}-\frac{3\sqrt{5}}{20}\right) \xi _{2}.\\ \end{aligned}$$

The stability conditions for the initial equilibrium solution are $\left( -\frac{1}{4}-\frac{3\sqrt{5}}{20}\right) \xi _{1}+\left( -\frac{1}{4}+\frac{3\sqrt{5}}{20}\right) \xi _{2}<0$ and $\left( -\frac{1}{4}+\frac{3\sqrt{5}}{20}\right) \xi _{1}+\left( -\frac{1}{4}-\frac{3\sqrt{5}}{20}\right) \xi _{2}<0$, or the initial equilibrium solution is unstable. So the transition curves which define the stable boundaries of the initial equilibrium solution are

$$\begin{aligned} L_{10}: \left( -\frac{1}{4}-\frac{3\sqrt{5}}{20}\right) \xi _{1} +\left( -\frac{1}{4}+\frac{3\sqrt{5}}{20}\right) \xi _{2}=0, \end{aligned}$$

(54)

and

$$\begin{aligned} L_{11}: \left( -\frac{1}{4}+\frac{3\sqrt{5}}{20}\right) \xi _{1} +\left( -\frac{1}{4}-\frac{3\sqrt{5}}{20}\right) \xi _{2}=0. \end{aligned}$$

(55)

The transition curves are illustrated in Fig. 11.

Fig. 11

Transition curves for the case of two pairs of pure imaginary eigenvalues

The numerical computation is performed on the base of the original differential equations (6). When the parameter is chosen as $(\xi _{1},\xi _{2})=(0.2,0.2)$, which is located in the region bounded by the critical lines $L_{10}$ and $L_{11}$, numerical results show that the trajectory starting from initial point $(x_{1},x_{2},x_{3},x_{4})=(0.06,0,-0.02,0)$ converges to the region, implying that the initial equilibrium solution is stable. The phase trajectories are projected onto the $x_{1}-x_{2}$ and $x_{3}-x_{4}$ sub-spaces as shown in Fig. 12.

Fig. 12

Trajectory projection starting from $(x_{1},x_{2},x_{3},x_{4})=(0.06,0,-0.02,0)$ converges to the E.S. when $(\xi _{1},\xi _{2})=(0.2,0.2)$, a the phase portrait on plane $(x_{1},x_{2})$; b the phase portrait on plane $(x_{3},x_{4})$

4 Conclusions

In this work, the stability and dynamical behaviors of a cantilever functionally graded material rectangular plate subjected to the transversal excitation in thermal environment are studied in the case of 1:1 internal resonances and 1/2 subharmonic resonance. Four types of degenerated equilibrium point are investigated in detail. The stable conditions, stable regions and critical bifurcation curves for the steady state solutions are presented explicitly in terms of the system parameters. Numerical computations have been performed and shown for each of the bifurcation cases. All numerical solutions agree with the analytical predictions, at least qualitatively.

5 Appendix

The coefficients of (6) are

$$\begin{aligned} a_{01}&= \frac{4g_{12}}{3\varOmega ^{3}}, \quad a_{02}=\frac{2g_{11}}{3\varOmega ^{3}}, \quad a_{03}=\frac{4g_{13}}{3\varOmega ^{3}}, a_{04}=\frac{g_{18}+\beta _{12}N^{T}}{\varOmega }, \quad a_{05}&= \frac{3g_{16}}{\varOmega }-\frac{20g_{11}g_{22}}{\varOmega ^{3}} -\frac{40g_{12}^{2}}{3\varOmega ^{3}}, \\ a_{06}&= \frac{g_{14}}{\varOmega }-\frac{56g_{13}g_{22}}{3\varOmega ^{3}} -\frac{20g_{11}g_{12}}{3\varOmega ^{3}}+\frac{4g_{11}g_{21}}{3\varOmega ^{3}},\\ a_{07}&= \frac{2g_{14}}{\varOmega }+\frac{16g_{13}g_{22}}{3\varOmega ^{3}} -\frac{40g_{11}g_{12}}{3\varOmega ^{3}}-\frac{8g_{11}g_{21}}{3\varOmega ^{3}},\\ a_{08}&= \frac{2g_{15}}{\varOmega }-\frac{16g_{13}g_{21}}{\varOmega ^{3}} -\frac{8g_{11}^{2}}{3\varOmega ^{3}}+\frac{8g_{11}g_{23}}{3\varOmega ^{3}} +\frac{16g_{11}g_{13}}{3\varOmega ^{3}},\\ a_{09}&= \frac{3g_{16}}{\varOmega }-\frac{20g_{11}g_{22}}{3\varOmega ^{3}} -\frac{40g_{12}^{2}}{3\varOmega ^{3}},\\ a_{10}&= \frac{3g_{14}}{\varOmega }-\frac{40g_{13}g_{22}}{3\varOmega ^{3}} -\frac{20g_{11}g_{21}}{3\varOmega ^{3}}-\frac{20g_{11}g_{12}}{3\varOmega ^{3}},\\ a_{11}&= \frac{g_{15}}{\varOmega }+\frac{8g_{13}g_{21}}{3\varOmega ^{3}} -\frac{4g_{11}^{2}}{3\varOmega ^{3}}-\frac{56g_{12}g_{13}}{3\varOmega ^{3}} -\frac{28g_{11}g_{23}}{3\varOmega ^{3}},\\ a_{12}&= \frac{3g_{15}}{\varOmega }-\frac{40g_{13}g_{21}}{\varOmega ^{3}} -\frac{20g_{11}^{2}}{3\varOmega ^{3}}-\frac{40g_{12}g_{13}}{3\varOmega ^{3}} -\frac{20g_{11}g_{23}}{3\varOmega ^{3}}, \\ a_{13}&= \frac{3g_{17}}{\varOmega }-\frac{20g_{13}g_{11}}{3\varOmega ^{3}} -\frac{40g_{13}g_{23}}{3\varOmega ^{3}},\\ a_{14}&= \frac{3g_{17}}{\varOmega }+\frac{40g_{13}g_{23}}{3\varOmega ^{3}} -\frac{20g_{11}g_{13}}{3\varOmega ^{3}},\\ b_{01}&= \frac{2g_{21}}{3\varOmega ^{3}}, b_{02}=\frac{4g_{23}}{3\varOmega ^{3}}, b_{03}=\frac{4g_{22}}{3\varOmega ^{3}}, b_{04}=\frac{g_{28} +\beta _{22}N^{T}}{\varOmega }, \\ b_{05}&= \frac{3g_{26}}{\varOmega }-\frac{20g_{21}g_{22}}{3\varOmega ^{3}} -\frac{40g_{12}g_{22}}{3\varOmega ^{3}},\\ b_{06}&= \frac{g_{24}}{\varOmega }+\frac{8g_{11}g_{22}}{3\varOmega ^{3}} +\frac{4g_{21}^{2}}{3\varOmega ^{3}}-\frac{56g_{23}g_{22}}{3\varOmega ^{3}} -\frac{28g_{12}g_{21}}{3\varOmega ^{3}},\\ b_{07}&= \frac{2g_{24}}{\varOmega }+\frac{16g_{23}g_{22}}{3\varOmega ^{3}} -\frac{8g_{21}^{2}}{\varOmega ^{3}}+\frac{8g_{11}g_{21}}{3\varOmega ^{3}} -\frac{16g_{11}g_{22}}{\varOmega ^{3}},\\ b_{08}&= \frac{2g_{25}}{\varOmega }-\frac{40g_{23}g_{21}}{\varOmega ^{3}} +\frac{16g_{13}g_{22}}{3\varOmega ^{3}} -\frac{8g_{11}g_{21}}{3\varOmega ^{3}}, \\ b_{09}&= \frac{3g_{26}}{\varOmega }-\frac{20g_{21}g_{22}}{3\varOmega ^{3}} -\frac{40g_{12}^{2}}{3\varOmega ^{3}},\\ b_{10}&= \frac{3g_{24}}{\varOmega }-\frac{40g_{23}g_{22}}{3\varOmega ^{3}} -\frac{40g_{11}g_{22}}{3\varOmega ^{3}}-\frac{20g_{21}g_{12}}{3\varOmega ^{3}} -\frac{20g_{21}^{2}}{3\varOmega ^{3}},\\ \end{aligned}$$

$$\begin{aligned} b_{11}&= \frac{g_{25}}{\varOmega }-\frac{20g_{23}g_{21}}{3\varOmega ^{3}} +\frac{4g_{11}g_{21}}{3\varOmega ^{3}}-\frac{40g_{22}g_{13}}{3\varOmega ^{3}},\\ b_{12}&= \frac{3g_{25}}{\varOmega }-\frac{20g_{23}g_{21}}{\varOmega ^{3}} -\frac{20g_{11}g_{21}}{3\varOmega ^{3}}-\frac{40g_{22}g_{13}}{3\varOmega ^{3}},\\ b_{13}&= \frac{3g_{27}}{\varOmega }-\frac{20g_{13}g_{21}}{3\varOmega ^{3}} -\frac{40g_{23}^{2}}{3\varOmega ^{3}},\\ b_{14}&= \frac{3g_{27}}{\varOmega }-\frac{20g_{13}g_{21}}{3\varOmega ^{3}} -\frac{40g_{23}^{2}}{3\varOmega ^{3}}.\\ \end{aligned}$$

The nonlinear functions $Nf_{i}(i\,=\,1,2,3,4)$ in (6) are

$$\begin{aligned} Nf_{1}&= a_{05}x_{1}^{2}x_{2}+a_{06}x_{1}^{2}x_{4}+a_{07} x_{1}x_{2}x_{3}+a_{08}x_{1}x_{3}x_{4}\\&\quad +a_{09}x_{2}^{3}+a_{10}x_{2}^{2}x_{4}+a_{11}x_{2}x_{3}^{2} +a_{12}x_{2}x_{4}^{2}\\&\quad +a_{13}x_{3}^{2}x_{4}+a_{14}x_{4}^{3},\\ Nf_{2}&= -a_{05}x_{1}^{3}-a_{10}x_{1}^{2}x_{3}-a_{05}x_{1}x_{2}^{2} -a_{07}x_{1}x_{2}x_{4}\\&\quad -a_{12}x_{1}x_{3}^{2}-a_{11}x_{1}x_{4}^{2}-a_{06}x_{2}^{2}x_{3} -a_{08}x_{2}x_{3}x_{4}\\&\quad -a_{13}x_{3}x_{4}^{2}-a_{14}x_{3}^{3},\\ Nf_{3}&= b_{05}x_{1}^{2}x_{2}+b_{06}x_{1}^{2}x_{4}+b_{07}x_{1}x_{2}x_{3} +b_{08}x_{1}x_{3}x_{4}\\&\quad +b_{09}x_{2}^{3}+b_{10}x_{2}^{2}x_{4}+b_{11}x_{2}x_{3}^{2} +b_{12}x_{2}x_{4}^{2}\\&\quad +b_{13}x_{3}^{2}x_{4}+b_{14}x_{4}^{3},\\ Nf_{4}&= -b_{05}x_{1}^{3}-b_{10}x_{1}^{2}x_{3}-b_{05}x_{1}x_{2}^{2} -b_{07}x_{1}x_{2}x_{4}\\&\quad -b_{12}x_{1}x_{3}^{2}-b_{11}x_{1}x_{4}^{2}-b_{06}x_{2}^{2} x_{3}-b_{08}x_{2}x_{3}x_{4}\\&\quad -b_{13}x_{3}x_{4}^{2}-b_{14}x_{3}^{3}. \end{aligned}$$

The nonlinear functions $Ng_{i}(i\,=\,1,2,3,4)$ in (11) are

$$\begin{aligned} Ng_{1}&= -\frac{1}{4}z_{1}z_{2}z_{4}-\frac{3}{4}z_{1}z_{3}z_{4} -\frac{1}{4}z_{1}z_{2}z_{3}+\frac{9}{4}z_{2}z_{3}z_{4}\\&\quad -\frac{3}{8}z_{1}^{2}z_{2}-\frac{7}{8}z_{1}^{2}z_{4} -\frac{5}{8}z_{4}^{2}z_{1}-\frac{19}{8}z_{2}^{2}z_{4} +\frac{7}{8}z_{2}^{2}z_{3}\\&\quad -\frac{7}{8}z_{3}^{2}z_{2}-\frac{11}{8}z_{3}^{2}z_{4} -\frac{23}{8}z_{4}^{2}z_{2}-\frac{1}{8}z_{2}^{2}z_{1} +\frac{11}{8}z_{4}^{2}z_{3}\\&\quad +\frac{7}{8}z_{1}^{2}z_{3}+\frac{7}{8}z_{3}^{2}z_{1} -\frac{5}{8}z_{2}^{3}-\frac{13}{8}z_{4}^{3}+\frac{1}{8}z_{1}^{3} +\frac{5}{8}z_{3}^{3},\\ Ng_{2}&= -\frac{11}{4}z_{1}z_{2}z_{4}-\frac{7}{4}z_{1}z_{3}z_{4} -\frac{5}{4}z_{1}z_{2}z_{3}+\frac{19}{4}z_{2}z_{3}z_{4}\\&\quad -\frac{17}{8}z_{1}^{2}z_{2}-\frac{21}{8}z_{1}^{2}z_{4} -\frac{17}{8}z_{4}^{2}z_{1}-\frac{61}{8}z_{2}^{2}z_{4} +\frac{19}{8}z_{2}^{2}z_{3}\\&\quad -\frac{21}{8}z_{3}^{2}z_{2}-\frac{25}{8}z_{3}^{2}z_{4} -\frac{65}{8}z_{4}^{2}z_{2}-\frac{13}{8}z_{2}^{2}z_{1} +\frac{23}{8}z_{4}^{2}z_{3}\\&\quad +\frac{7}{8}z_{1}^{2}z_{3}+\frac{7}{8}z_{3}^{2}z_{1} -\frac{23}{8}z_{2}^{3}-\frac{31}{8}z_{4}^{3}-\frac{3}{8}z_{1}^{3} +\frac{9}{8}z_{3}^{3},\\ Ng_{3}&= -\frac{9}{4}z_{1}z_{2}z_{4}-\frac{1}{4}z_{1}z_{3}z_{4} -\frac{3}{4}z_{1}z_{2}z_{3}+\frac{1}{4}z_{2}z_{3}z_{4}\\&\quad -\frac{11}{8}z_{1}^{2}z_{2}-\frac{7}{8}z_{1}^{2}z_{4} -\frac{7}{8}z_{4}^{2}z_{1}-\frac{23}{8}z_{2}^{2}z_{4}+\frac{5}{8}z_{2}^{2} z_{3}\\&\quad -\frac{7}{8}z_{3}^{2}z_{2}-\frac{3}{8}z_{3}^{2}z_{4} -\frac{19}{8}z_{4}^{2}z_{2}-\frac{11}{8}z_{2}^{2}z_{1} +\frac{1}{8}z_{4}^{2}z_{3}\\&\quad -\frac{7}{8}z_{1}^{2}z_{3}-\frac{7}{8}z_{3}^{2}z_{1} -\frac{13}{8}z_{2}^{3}-\frac{5}{8}z_{4}^{3}-\frac{5}{8}z_{1}^{3} -\frac{1}{8}z_{3}^{3},\\ Ng_{4}&= \frac{19}{4}z_{1}z_{2}z_{4}+\frac{5}{4}z_{1}z_{3}z_{4}+\frac{7}{4} z_{1}z_{2}z_{3}-\frac{11}{4}z_{2}z_{3}z_{4}\\&\quad +\frac{25}{8}z_{1}^{2}z_{2}+\frac{21}{8}z_{1}^{2}z_{4}+\frac{19}{8}z_ {4}^{2}z_{1}+\frac{65}{8}z_{2}^{2}z_{4}-\frac{17}{8}z_{2}^{2}z_{3}\\&\quad +\frac{21}{8}z_{3}^{2}z_{2}+\frac{17}{8}z_{3}^{2}z_{4} +\frac{61}{8}z_{4}^{2}z_{2}+\frac{23}{8}z_{2}^{2}z_{1}-\frac{13}{8}z_ {4}^{2}z_{3}\\&\quad +\frac{7}{8}z_{1}^{2}z_{3}+\frac{7}{8}z_{3}^{2}z_{1}+\frac{31}{8} z_{2}^{3} +\frac{23}{8}z_{4}^{3}+\frac{9}{8}z_{1}^{3}-\frac{3}{8}z_{3}^{3}.\\ \end{aligned}$$

The nonlinear functions $Nh_{i}(i=1,2,3,4)$ in (24) are

$$\begin{aligned} Nh_{1}&= \frac{4}{5}z_{1}z_{2}z_{4}+\frac{8}{5}z_{1}z_{3}z_{4}-\frac{108}{25} z_{1}z_{2}z_{3}+\frac{11}{5}z_{2}z_{3}z_{4}\\&\quad -\frac{171}{50}z_{2}^{2}z_{3}-\frac{99}{50}z_{3}^{2}z_{2}-\frac{3}{2} z_{1}^{2}z_{3}+\frac{2}{5}z_{3}^{2}z_{4}-\frac{1}{2}z_{4}^{2}z_{3}\\&\quad -\frac{15}{2}z_{1}^{2}z_{2}-\frac{252}{25}z_{2}^{2}z_{1}-\frac{33}{25} z_{3}^{2}z_{1}-2z_{4}^{2}z_{1}\\&\quad +z_{2}^{2}z_{4}-\frac{5}{2}z_{4}^{2}z_{2}-2z_{1}^{3}+\frac{51}{10}z_ {2}^{3}-\frac{29}{50}z_{3}^{3},\\ Nh_{2}&= \frac{16}{5}z_{1}z_{2}z_{4}-\frac{8}{5}z_{1}z_{3}z_{4}+\frac{93}{25} z_{1}z_{2}z_{3}-\frac{41}{25}z_{2}z_{3}z_{4}\\&\quad +\frac{393}{125}z_{2}^{2}z_{3}+\frac{186}{125}z_{3}^{2}z_{2} +\frac{6}{5}z_{1}^{2}z_{3}+\frac{9}{25}z_{3}^{2}z_{4}\\&\quad -\frac{2}{5}z_{4}^{2}z_{3}+\frac{33}{5}z_{1}^{2}z_{2}+\frac{207}{25} z_{2}^{2}z_{1}+\frac{33}{25}z_{3}^{2}z_{1}\\&\quad +2z_{4}^{2}z_{1}+\frac{71}{25}z_{2}^{2}z_{4}-\frac{1}{5}z_{4}^{2} z_{2}+2z_{1}^{2}z_{4}+2z_{1}^{3}\\&\quad +\frac{428}{125}z_{2}^{3}+\frac{99}{125}z_{3}^{3}+2z_{4}^{3},\\ Nh_{3}&= \frac{24}{5}z_{1}z_{2}z_{4}+\frac{8}{5}z_{1}z_{3}z_{4}-\frac{123}{25} z_{1}z_{2}z_{3}+\frac{69}{25}z_{2}z_{3}z_{4}\\&\quad -\frac{462}{125}z_{2}^{2}z_{3} -\frac{309}{125}z_{3}^{2}z_{2}-\frac{9}{5}z_{1}^{2}z_{3}+\frac{29}{25}z_{3} ^{2}z_{4}-\frac{7}{5}z_{4}^{2}z_{3}\\&\quad -\frac{42}{5}z_{1}^{2}z_{2}-\frac{297}{25}z_{2}^{2}z_{1} -\frac{33}{25}z_{3}^{2}z_{1}-2z_{4}^{2}z_{1}+\frac{121}{25}z_{2}^{2}z_{4}\\&\quad -\frac{26}{5}z_{4}^{2}z_{2}+2z_{1}^{2}z_{4}-2z_{1}^{3} -\frac{847}{125}z_{2}^{3}-\frac{46}{125}z_{3}^{3}+2z_{4}^{3},\\ Nh_{4}&= \frac{84}{25}z_{1}z_{2}z_{4}+\frac{48}{25}z_{1}z_{3}z_{4}-\frac{693}{125}z_{1}z_{2}z_{3}+\frac{372}{125}z_{2}z_{3}z_{4}\\&\quad -\frac{5337}{1250}z_{2}^{2}z_{3}-\frac{3339}{1250}z_{3}^{2}z_{2} -\frac{99}{50}z_{1}^{2}z_{3}+\frac{117}{125}z_{3}^{2}z_{4}\\&\quad -\frac{57}{50}z_{4}^{2}z_{3}-\frac{477}{50}z_{1}^{2}z_{2}-\frac{1647}{125}z_{2}^{2}z_{1}-\frac{198}{125}z_{3}^{2}z_{1}\\&\quad -\frac{12}{5}z_{4}^{2}z_{1}+\frac{438}{125}z_{2}^{2}z_{4}-\frac{231}{50}z_{4}^{2}z_{2}+\frac{6}{5}z_{1}^{2}z_{4}\\&\quad -\frac{12}{5}z_{1}^{3}-\frac{8907}{1250}z_{2}^{3}-\frac{711}{1250} z_{3}^{3}+\frac{6}{5}z_{4}^{3}.\\ \end{aligned}$$

The nonlinear functions $NJ_{i}(i=1,2,3,4)$ in (50) are

$$\begin{aligned} NJ_{1}&= \frac{21\sqrt{5}}{10}z_{1}z_{3}z_{4}-\frac{7}{2}z_{1}z_{2}z_{3} -\frac{7\sqrt{5}}{5}z_{2}z_{3}z_{4} -\frac{6\sqrt{5}}{5}z_{3}^{2}z_{2}\\&\quad -\frac{14\sqrt{5}}{5}z_{3}^{2}z_{4}+\frac{1}{2}z_{2}z_{4}^{2}+2z_{2} z_{3}^{2}-\frac{6\sqrt{5}}{5}z_{1}^{2}z_{2}-2z_{1}^{2}z_{2}\\&\quad -6z_{3}^{2}z_{4}+\frac{4\sqrt{5}}{5}z_{1}^{2}z_{4}-\frac{\sqrt{5}}{5} z_{2}^{2}z_{4}+\frac{3\sqrt{5}}{10}z_{4}^{2}z_{2}\\&\quad -\frac{3}{2}z_{2}^{3}-\frac{9\sqrt{5}}{10}z_{2}^{3}-\frac{9}{2}z_{4} ^{3}+\frac{21\sqrt{5}}{10}z_{4}^{3}\\ NJ_{2}&= \sqrt{5}z_{1}z_{2}z_{4}+\frac{3\sqrt{5}}{2}z_{2}z_{3}z_{4}-\frac{5}{2} z_{2}z_{3}z_{4}+2\sqrt{5}z_{2}^{2}z_{3}\\&\quad +3\sqrt{5}z_{4}^{2}z_{1}+\frac{15}{2}z_{1}^{3}+3\sqrt{5}z_{2}^{2} z_{1}+\frac{21\sqrt{5}}{2}z_{3}^{2}z_{1}\\&\quad +7\sqrt{5}z_{1}^{2}z_{3}+5z_{2}^{2}z_{1}-5z_{4}^{2}z_{1}-15z_{4}^ {2}z_{3}\frac{35}{2}z_{3}^{2}z_{1}\\&\quad -+\frac{9\sqrt{5}}{2}z_{1}^{3}+\frac{21\sqrt{5}}{2}z_{3}^{3} -\frac{45}{2}z_{3}^{3}+7\sqrt{5}z_{4}^{2}z_{3},\\ NJ_{3}&= -\frac{21\sqrt{5}}{10}z_{1}z_{2}z_{3}+\frac{7\sqrt{5}}{4}z_{1}z_{3} z_{4}-\frac{7}{2}z_{1}z_{2}z_{3} +\frac{6\sqrt{5}}{5}z_{3}^{2}z_{4}\\&\quad +\frac{\sqrt{5}}{5}z_{4}^{2}z_{2}-\frac{3\sqrt{5}}{10}z_{2}^{2}z_ {4}-\frac{4\sqrt{5}}{5}z_{3}^{2}z_{2}-\frac{14\sqrt{5}}{5}z_{1}^{2}z_{2}\\&\quad +\frac{6\sqrt{5}}{5}z_{1}^{2}z_{4}-\frac{1}{2}z_{2}^{2}z_{4}-6z_{1}^ {2}z_{2}+2z_{1}^{2}z_{4}-2z_{3}^{2}z_{4}\\&\quad -\frac{9}{2}z_{2}^{3}-\frac{3}{2}z_{4}^{3}+\frac{21\sqrt{5}}{10}z_{2}^{3}+\frac{9\sqrt{5}}{10}z_{4}^{3},\\ NJ_{4}&= -\frac{3\sqrt{5}}{2}z_{1}z_{2}z_{4}-\sqrt{5}z_{2}z_{3}z_{4} -\frac{5}{2}z_{1}z_{2}z_{4} -3\sqrt{5}z_{2}^{2}z_{3}\\&\quad -2\sqrt{5}z_{4}^{2}z_{1}3\sqrt{5}z_{4}^{2}z_{3}-7\sqrt{5}z_{2}^{2} z_{1}-7\sqrt{5}z_{3}^{2}z_{1}\\&\quad -\frac{21\sqrt{5}}{2}z_{1}^{2}z_{3}-15z_{2}^{2}z_{1}-5z_{2}^{2}z_{3} +5z_{4}^{2}z_{3}-\frac{35}{2}z_{1}^{2}z_{3}\\&\quad -\frac{21\sqrt{5}}{2}z_{1}^{3}-\frac{9\sqrt{5}}{2}z_{3}^{3}+\frac{15}{2}z_{3}^{3}-\frac{45}{2}z_{1}^{3}.\\ \end{aligned}$$