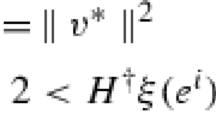1 Introduction

Recently, the “networked control systems” (NCSs) is an evolving research field in control system community in which many subsystems are connected via a communication network. NCSs has a wide range of application, for instance, electrical power grids, smart transportation, distributed control systems (DCS), remote surgery, oil and gas pipelines, wastewater collection and water distribution systems, supervisory control and data acquisition (SCADA), smart home, and industrial control systems (ICS) [1,2,3,4,5,6,7]. Time-delay is occurs in NCS owing to the finite capability of data processing and information communication among numerous subsystems. The presence of time-delay not just reduces the system performance but moreover affect the closed-loop system stability, even makes the closed-loop system unstable [8,9,10,11].

Three types of model predictive control (MPC), centralized, decentralized and distributed schemes are widely used to control large-scale distributed control systems [12]. However, in many application, the MPC may not be desirable due to the computational burden, lack of flexibility, and high maintenance cost. Designing controller without including the nonlinear behavior of actuator may cause inaccuracy, performance degradation, loss of control, and even instability, when the control action crosses the actuator maximum or minimum bounds [9, 13, 14]. Actuator saturation nonlinearity exists in all physical systems. Because physical actuators such as electric motors, airplane elevators, airplane flaperon, hydraulic and valves in process industry cannot convey infinite energy signal. The conventional controller may perform well under normal operation, but when actuator saturates, then the behavior of closed-loop system changes significantly [14]. Similarly, the presence of time-delay is pretty common in chemical processes, industrial plants, power plants, robots, pneumatic structures, distributed network control systems, and hydraulic transmission lines. The presence of time-delay in a plant generally has undesirable effects such as performance degradation, oscillations, lag, and instability [11, 12]. Throughout the past eras, the study of the time-delay plant has acquired abundant research consideration from the control system community [15,16,17,18,19,20,21,22]. The study of the stability criteria of the time-delay system can be grouped into three types, delay-independent [15,16,17,18], delay-dependent [19,20,21,22], and delay-range-dependent [11, 12]. Delay-independent stability criteria are more conservative because it does not contain the information of time-delay and can be applicable to the plant with infinite delay. Delay-dependent stability criteria include the information of time-delay. In contrast, delay-independent and delay-dependent stability criteria, delay-range-independent stability criteria time-delay diverge in a range and are least conservative amongst all [12]. Maintaining the stability of network time-delay system with state delay and input saturation is a challenging problem to control engineers.

This paper proposed state feedback controller synthesis for nonlinear time-delay distributed control systems with input saturation nonlinearity, time-varying coupling delay, and external disturbances. The nonlinear time-delay distributed control system individual state vector is without any time-delay and the states approaches from other subsystems has transportation time-delay. By applying a Lipschitz condition, global and local sector bounded condition, and Lyapunov–Krasovskii function, LMI-based conditions are provided to synthesize global and local state feedback tracking controller, which ensure the \( L_{2} \) stability of the overall closed-loop system. Simulation results are provided to demonstrate the effectiveness of the proposed global and local state feedback controller schemes.

The rest of this paper is planned as follows. Nonlinear time-delay distributed control system is introduced in Sect. 2. Sections 3 and 4 presents the global and local controller synthesis for nonlinear time-delay distributed control systems, respectively. Section 5 provides simulation results. Finally, the conclusion is presented in Sect. 6.

Notation

This article used standard notations. The \( L_{2} \) gain from \( d_{p} (t) \) to \( z_{p} (t) \) is represent by \( \sup_{{\left\| {d_{p} (t)} \right\|_{2} \ne 0}} \left( {{{\left\| {z_{p} (t)} \right\|_{2} } \mathord{\left/ {\vphantom {{\left\| {z_{p} (t)} \right\|_{2} } {\left\| {d_{p} (t)} \right\|_{2} }}} \right. \kern-0pt} {\left\| {d_{p} (t)} \right\|_{2} }}} \right) < \gamma \). \( \left\| {z_{p} (t)} \right\|_{2} \) and \( \left\| {z_{p} (t)} \right\| \) indicates the \( L_{2} \) and Euclidian norm of vector \( z_{p} (t) \), respectively. \( S > 0 \) and \( S \ge 0 \) denote that symmetric matrix \( S \) is positive-definite and positive semi-definite. Block diagonal matrix is represented by \( diag\{ x_{1} ,x_{2} , \ldots x_{n} \} \). The dead zone and saturation nonlinearity are represented by \( \text{N}_{sat} (u(t)) \) and \( \zeta_{z} (u(t)) \) respectively.

2 System description

Consider a class of two nonlinear time-delay distributed control systems with dynamic nonlinearity, input saturation, and external disturbances, represented by

$$ \begin{aligned} \dot{x}_{p1} (t) & = A_{p11} x_{p1} (t) + f(t,x_{p1} ) + A_{p12} x_{p2} (t - \tau ) \\ & \quad+ B_{u1} \text{N}_{sat} (u_{1} (t)) + B_{w1} d_{p1} (t) \\ z_{p1} (t) & = C_{p11} x_{p1} (t) + C_{p12} x_{p2} (t - \tau ) \\ & \quad+ D_{u1} \text{N}_{sat} (u_{1} (t)) + D_{w1} d_{p1} (t) \\ \dot{x}_{p2} (t) & = A_{p21} x_{p2} (t) + f(t,x_{p2} ) + A_{p22} x_{p1} (t - \tau )\\ & \quad + B_{u2} \text{N}_{sat} (u_{2} (t)) + B_{w2} d_{p2} (t) \\ z_{p2} (t) & = C_{p21} x_{p2} (t) + C_{p22} x_{p1} (t - \tau ) \\ & \quad+ D_{u2} \text{N}_{sat} (u_{2} (t)) + D_{w2} d_{p2} (t) \\ x_{p1} (t) & = \theta_{1} (t),\,t \in \left[ {\begin{array}{*{20}c} { - \tau_{2} } & 0 \\ \end{array} } \right], \\ x_{p2} (t) & = \theta_{2} (t),\,t \in \left[ {\begin{array}{*{20}c} { - \tau_{2} } & 0 \\ \end{array} } \right], \\ \end{aligned} $$
(1)

where \( x_{p1} (t) \in R^{n} \) is state of the first plant, \( x_{p2} (t) \in R^{n} \) is the state of the second plant, \( u_{1} (t) \in R^{m} \) denotes the control input to the first system, and \( u_{2} (t) \in R^{m} \) represents the control input to the second system. \( \text{N}_{sat} (u_{1} (t)) \in R^{m} \) and \( \text{N}_{sat} (u_{2} (t)) \in R^{m} \) denotes the saturated control input to the first and second system, respectively. \( z_{p1} (t) \in R^{p} \) and \( z_{p2} (t) \in R^{p} \) are the systems outputs. \( d_{p1} (t) \in R^{n} \) and \( d_{p2} (t) \in R^{p} \) represents the exogenous disturbances to the first and second system, respectively. \( \tau \) indicates the transportation time-delay in the states approaching from other subsystems. \( f(t,x_{p1} ) \) and \( f(t,x_{p2} ) \) denotes the nonlinear dynamics. The saturation \( \text{N}_{sat} (u_{k} (t)) \) and dead-zone \( \zeta_{z} (u_{k} (t)) \) nonlinearity are define as

$$\begin{aligned} \text{N}_{sat} (u_{k} (t)) &= [\text{N}_{sat1} (u_{k1} (t)),\text{N}_{sat2} (u_{k2} (t)), \ldots ,\\ & \quad\times\text{N}_{satm} (u_{km} (t))]^{T} \end{aligned}$$
(2)
$$ \zeta_{z} (u_{k} (t)) = [\zeta_{z1} (u_{k1} (t)),\zeta_{z2} (u_{k2} (t)), \ldots ,\zeta_{zm} (u_{km} (t))]^{T} $$
(3)

where, \( \text{N}_{sati} (u_{ki} (t)) = sign(u_{ki} (t)) \times \hbox{min} \{ \left| {u_{ki} (t)} \right|,\bar{v}_{k(i)} (t)\} , \, \bar{v}_{k(i)} (t) > 0,\forall \, k \in \{ 1,2.\} ,\quad i \in \{ 1, \ldots ,m\} \), \( \zeta_{zi} (u_{ki} (t)) = sign(u_{ki} (t)),\hbox{max} \{ 0,\left| {u_{ki} (t)} \right| - \bar{v}_{k(i)} (t)\} ,\bar{v}_{k(i)} (t) > 0,\forall \, k \in \{ 1,2.\} ,\quad i \in \{ 1, \ldots ,m\} \), \( \bar{v}_{(i)} \) is the i’th saturation bound. The saturation and dead-zone functions belong to the \( Sector\left[ {0,I} \right] \) and are interrelated by the subsequent relations

$$ \text{N}_{sat} (u_{1} (t)) = - \zeta_{z} (u_{1} (t)) + u_{1} (t). $$
(4)
$$ \text{N}_{sat} (u_{2} (t)) = - \zeta_{z} (u_{2} (t)) + u_{2} (t). $$
(5)

By employing Eqs. (4) and (5) the nonlinear time-delay distributed control systems (1) can be rewrite as

$$ \begin{aligned} \dot{x}_{p1} (t) & = A_{p11} x_{p1} (t) + f(t,x_{p1} ) + A_{p12} x_{p2} (t - \tau ) \\& \quad - B_{u1} \zeta_{z} (u_{1} (t)) + B_{u1} u_{1} (t)) + B_{w1} d_{p1} (t) \\ z_{p1} (t) & = C_{p11} x_{p1} (t) + C_{p12} x_{p2} (t - \tau ) + D_{u1} \text{N}_{sat} (u_{1} (t))\\& \quad + D_{w1} d_{p1} (t) \\ \dot{x}_{p2} (t) & = A_{p21} x_{p2} (t) + f(t,x_{p2} ) + A_{p22} x_{p1} (t - \tau ) \\& \quad - B_{u1} \zeta_{z} (u_{2} (t)) + B_{u2} u_{2} (t)) + B_{w2} d_{p2} (t) \\ z_{p2} (t) & = C_{p21} x_{p2} (t) + C_{p22} x_{p1} (t - \tau ) \\& \quad + D_{u2} \text{N}_{sat} (u_{2} (t)) + D_{w2} d_{p2} (t) \\ \end{aligned} $$
(6)

Consider the following state feedback tracking controller, given by

$$ \begin{aligned} u_{1} (t) & = K_{11} x_{p1} (t) + K_{12} x_{p2} (t - \tau ) \\ u_{2} (t) & = K_{21} x_{p2} (t) + K_{22} x_{p1} (t - \tau ) \\ \end{aligned} $$
(7)

where, \( K_{11} \), \( K_{12} \), \( K_{21} \) and \( K_{22} \) are the controller gain matrices of appropriate dimension. The complete closed-loop control system is attained by nonlinear time-delay distributed control systems (6) and state feedback tracking controller (7) is represented as

$$ \begin{aligned} \dot{x}_{p1} (t) & = \tilde{A}_{p11} x_{p1} (t) + \tilde{A}_{p12} x_{p2} (t - \tau ) + f_{1} (t,x_{p1} )\\& \quad - B_{u1} \zeta_{z} (u_{1} (t)) + B_{d1} d_{p1} (t) \\ z_{p1} (t) & = \tilde{C}_{p11} x_{p1} (t) + \tilde{C}_{p12} x_{p2} (t - \tau ) \\& \quad - D_{u1} \zeta_{z} (u_{1} (t)) + D_{d1} d_{p1} (t) \\ \dot{x}_{p2} (t) & = \tilde{A}_{p21} x_{p2} (t) + \tilde{A}_{p22} x_{p1} (t - \tau ) + f_{2} (t,x_{p2} )\\& \quad - B_{u2} \zeta_{z} (u_{2} (t)) + B_{d2} d_{p2} (t) \\ z_{p2} (t) & = \tilde{C}_{p21} x_{p2} (t) + \tilde{C}_{p22} x_{p1} (t - \tau ) \\& \quad - D_{u2} \zeta_{z} (u_{2} (t)) + D_{d2} d_{p2} (t) \\ \end{aligned} $$
(8)
$$ \begin{aligned} \tilde{A}_{p11} & = (A_{p11} + B_{u1} K_{11} ), \, \tilde{A}_{p12} = (A_{p12} + B_{u1} K_{12} ) \\ \tilde{C}_{p11} & = (C_{p11} + D_{u1} K_{11} ), \, \tilde{C}_{p12} = (C_{p12} + D_{u1} K_{12} ) \\ \tilde{C}_{p21} & = (C_{p21} + D_{u2} K_{21} ), \, \tilde{C}_{p22} = (C_{p22} + D_{u2} K_{22} ) \\ \tilde{A}_{p21} & = (A_{p21} + B_{u2} K_{21} ), \, \tilde{A}_{p22} = (A_{p22} + B_{u2} K_{22} ) \\ \end{aligned} $$
(9)

In order to design the global and local state feedback tracking controller for nonlinear time-delay distributed control systems we make the following assumptions.

Assumption 1

The mappings \( \varGamma_{1} :d_{p1} (t) \to z_{p1} (t) \) and \( \varGamma_{2} :d_{p2} (t) \to z_{p2} (t) \) for all real vectors \( d_{p1} (t),z_{p1} (t) \in {R}^{n} \) and \( d_{p2} (t),z_{p2} (t) \in {R}^{n} \) satisfies

$$ \left\| {z_{p1} (t)} \right\| \le \gamma_{1} \left\| {d_{p1} (t)} \right\| $$
(10)
$$ \left\| {z_{p2} (t)} \right\| \le \gamma_{2} \left\| {d_{p2} (t)} \right\| $$
(11)

Assumption 2

The nonlinear functions \( f(t,x_{p1} ) \) and \( f(t,x_{p2} ) \) for all real vectors \( x(t),\bar{x}(t) \in {R}^{n} \) fulfills

$$ \left\| {f_{1} (t,x_{p1} ) - f_{1} (t,\bar{x}_{p1} )} \right\| \le \left\| {\kappa_{f1} (x_{p1} (t) - \bar{x}_{p1} (t))} \right\| , $$
(12)
$$ \left\| {f_{2} (t,x_{p2} ) - f_{2} (t,\bar{x}_{p2} )} \right\| \le \left\| {\kappa_{f2} (x_{p2} (t) - \bar{x}_{p2} (t))} \right\| , $$
(13)

where, \( \kappa_{f1} \) and \( \kappa_{f2} \) are suitable dimensions Lipschitz constant matrices.

3 Global controller design for distributed control system

In this subsection LMI-based global condition are derived to design controller for nonlinear time-delay distributed systems. For diagonal matrices \( W_{1} \in R^{m \times m} \) and \( W_{2} \in R^{m \times m} \), the dead-zone nonlinearity satisfies global sector bounded condition (see [9, 13] and references therein)

$$ \zeta_{z} (u_{1} (t))^{T} W_{1} [u_{1} (t) - \zeta_{z} (u_{1} (t))] \ge 0 $$
(14)
$$ \zeta_{z} (u_{2} (t))^{T} W_{2} [u_{2} (t) - \zeta_{z} (u_{2} (t))] \ge 0 $$
(15)

Theorem 1

Consider the overall closed-loop nonlinear time-delay distributed control system attained by nonlinear time-delay distributed control systems (6) and state feedback tracking controller (7) satisfying assumptions A1 and A2. Presume there exist symmetric matrices\( Q_{1} \in R^{n \times n} \), \( Q_{2} \in R^{n \times n} \), \( P_{1} \in R^{n \times n} \), and\( P_{2} \in R^{n \times n} \), and symmetric diagonal matrices\( W_{1} \in R^{m \times m} \)and\( W_{2} \in R^{m \times m} \), than the nonlinear time-delay distributed control systems under input saturation nonlinearity is globally asymptotically stable, and the\( L_{2} \)gain from\( d_{p1} (t) \)to\( z_{p1} (t) \)and from\( d_{p2} (t) \)to\( z_{p1} (t) \)are less then\( \gamma_{1} \)and\( \gamma_{1} \)respectively if\( d_{p1} (t) \ne 0 \)and\( d_{p2} (t) \ne 0 \), independent of delay if the following LMI are satisfied:

$$ \varPsi = \left[ {\begin{array}{*{20}c} {\varPsi_{1} } & {\varPsi_{2} } \\ * & {\varPsi_{3} } \\ \end{array} } \right] < 0 $$
(16)
$$ \varPsi_{1} = \left[ {\begin{array}{*{20}c} {\varPsi_{11} } & 0 & 0 & {A_{p12} X_{2} + B_{u1} S_{12} } & I & 0 \\ * & {\varPsi_{22} } & {A_{p22} X_{1} + B_{u2} S_{22} } & 0 & 0 & I \\ * & * & { - (1 - \dot{\tau })Z_{1} } & 0 & 0 & 0 \\ * & * & * & { - (1 - \dot{\tau })Z_{2} } & 0 & 0 \\ * & * & * & * & { - I} & 0 \\ * & * & * & * & * & { - I} \\ \end{array} } \right] $$
$$ \varPsi_{2} = \left[ {\begin{array}{*{20}c} {\varUpsilon_{11} } & {\varUpsilon_{12} } \\ \end{array} } \right] $$
$$ \varUpsilon_{11} = \left[ {\begin{array}{*{20}c} { - B_{u1} U_{1} + S_{11}^{T} } & 0 & {B_{d1} } & 0 \\ 0 & { - B_{u2} U_{2} + S_{21}^{T} } & 0 & {B_{d2} } \\ 0 & {S_{22}^{T} } & 0 & 0 \\ {S_{12}^{T} } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right] $$
$$ \varUpsilon_{12} = \left[ {\begin{array}{*{20}c} {X_{1} \kappa_{f1}^{T} } & 0 & {X_{1} C_{p11}^{T} + S_{11}^{T} D_{u1} } & 0 \\ 0 & {X_{2} \kappa_{f2}^{T} } & 0 & {X_{2} C_{p21}^{T} + S_{21}^{T} D_{u2} } \\ 0 & 0 & 0 & {X_{1} C_{p22}^{T} + S_{22}^{T} D_{u1} } \\ 0 & 0 & {X_{2} C_{p12}^{T} + S_{12}^{T} D_{u1} } & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right] $$
$$ \varPsi_{3} = \left[ {\begin{array}{*{20}c} { - 2U_{1} } & 0 & 0 & 0 & 0 & 0 & { - U_{1} D_{u1}^{T} } & 0 \\ * & { - 2U_{2} } & 0 & 0 & 0 & 0 & 0 & { - U_{2} D_{u2}^{T} } \\ * & * & { - I\gamma_{1} } & 0 & 0 & 0 & {D_{d1}^{T} } & 0 \\ * & * & * & { - I\gamma_{2} } & 0 & 0 & 0 & {D_{d2}^{T} } \\ * & * & * & * & { - I} & 0 & 0 & 0 \\ * & * & * & * & * & { - I} & 0 & 0 \\ * & * & * & * & * & * & { - \gamma_{2} } & 0 \\ * & * & * & * & * & * & * & { - \gamma_{2} } \\ \end{array} } \right] $$

where, \( \varPsi_{11} = X_{1} A_{p11}^{T} + S_{11}^{T} B_{u1}^{T} + A_{p11} X_{1} + B_{u1} S_{11} + Z_{1} \),\( \varPsi_{22} = X_{2} A_{p21}^{T} + S_{21}^{T} B_{u2}^{T} + A_{p21} X_{2} + B_{u2} S_{21} + Z_{2} \) Moreover, the controller gain matrices can be obtain from \( K_{11} = S_{11} P_{1} \), \( K_{12} = S_{12} P_{2} \), \( K_{21} = S_{21} P_{2} \), \( K_{22} = S_{22} P_{1} \).

Proof

Consider the subsequent Lyapunov–Krasovskii functional for symmetric positive definite matrices \( Q_{1} \in R^{n \times n} \), \( Q_{2} \in R^{n \times n} \), \( P_{1} \in R^{n \times n} \) and \( P_{2} \in R^{n \times n} \) given as

$$ \begin{aligned} V(x_{p1} ,x_{p2} ,t) & = x_{p1}^{T} (t)P_{1} x_{p1} (t) + x_{p2}^{T} (t)P_{2} x_{p2} (t) \\& \quad + \int\limits_{t - \tau }^{t} {x_{p1}^{T} (\alpha )Q_{1} x_{p1} (\alpha )} d\alpha \\ & \quad+ \int\limits_{t - \tau }^{t} {x_{p2}^{T} (\alpha )Q_{2} x_{p2} (\alpha )} d\alpha \\ \end{aligned} $$
(17)

The derivative of \( V(x_{p1} ,x_{p2} ,t) \) along the closed-loop distributed control systems (1) and using (10)–(14) and (15) yields

$$ \begin{aligned}& \dot{V}(x_{{p1}} ,x_{{p2}} ,t) \le x_{{p1}}^{T} (t)\tilde{A}_{{p11}}^{T} P_{1} x_{{p1}} (t) \\ &\quad \quad + x_{{p2}}^{T} (t - \tau )\tilde{A}_{{p12}}^{T} P_{1} x_{{p1}} (t) + \,f_{1}^{T} (t,x_{{p1}} )P_{1} x_{{p1}} (t)\\ &\quad \quad - \zeta _{z}^{T} (u_{1} (t))B_{{_{{u1}} }}^{T} P_{1} x_{{p1}} (t) \\ &\quad \quad + \,d_{{p1}}^{T} (t)B_{{_{{d1}} }}^{T} P_{1} x_{{p1}} (t) + x_{{p1}}^{T} (t)P_{1} \tilde{A}_{{p11}} x_{{p1}} (t) \\ &\quad \quad + \,x_{{p1}}^{T} (t)P_{1} \tilde{A}_{{p12}} x_{{p2}} (t - \tau ) + x_{{p1}}^{T} (t)P_{1} f_{1} (t,x_{{p1}} ) \\ &\quad \quad - \,x_{{p1}}^{T} (t)P_{1} B_{{u1}} \zeta _{z} (u_{1} (t)) + \,x_{{p1}}^{T} (t)P_{1} B_{{d1}} d_{{p1}} (t) \\ &\quad \quad + \,x_{{p2}}^{T} (t)\tilde{A}_{{p21}}^{T} P_{2} x_{{p2}} (t) + x_{{p1}}^{T} (t - \tau )\tilde{A}_{{p22}}^{T} P_{2} x_{{p2}} (t) \\ &\quad \quad + \,f_{2}^{T} (t,x_{{p2}} )P_{2} x_{{p2}} (t) - \zeta _{z}^{T} (u_{2} (t))B_{{_{{u2}} }}^{T} P_{2} x_{{p2}} (t) \\ &\quad \quad + \,d_{{p2}}^{T} (t)B_{{_{{d2}} }}^{T} P_{2} x_{{p2}} (t) + \,x_{{p2}}^{T} (t)P_{2} \tilde{A}_{{p21}} x_{{p2}} (t) \\ &\quad \quad + \,x_{{p2}}^{T} (t)P_{2} \tilde{A}_{{p22}} x_{{p1}} (t - \tau ) + x_{{p2}}^{T} (t)P_{2} f_{2} (t,x_{{p2}} ) \\ &\quad \quad - \,x_{{p2}}^{T} (t)P_{2} B_{{u2}} \zeta _{z} (u_{2} (t)) + x_{{p2}}^{T} (t)P_{2} B_{{d2}} d_{{p2}} (t) \\ &\quad \quad + \,x_{{p1}}^{T} (t)Q_{1} x_{{p1}} (t) \\ &\quad \quad + \,x_{{p2}}^{T} (t)Q_{2} x_{{p2}} (t) \\ &\quad \quad + \,x_{{p1}}^{T} (t - \tau )(1 - \dot{\tau })Q_{1} x_{{p1}} (t - \tau ) + x_{{p2}}^{T} (t - \tau )(1 - \dot{\tau }) \\ &\quad\quad \times \,Q_{2} x_{{p2}} (t - \tau ) + \zeta _{z}^{T} (u_{1} (t))W_{1} K_{{11}} x_{{p1}} (t) \\ &\quad \quad + \,\zeta _{z}^{T} (u_{1} (t))W_{1} K_{{12}} x_{{p2}} (t - \tau ) - \zeta _{z}^{T} (u_{1} (t))W_{1} \zeta _{z} (u_{1} (t)) \\ &\quad \quad + \,x_{{p1}}^{T} (t)K_{{11}}^{T} W_{1} \zeta _{z} (u_{1} (t)) + x_{{p2}}^{T} (t - \tau )K_{{12}}^{T} W_{1} \zeta _{z} (u_{1} (t)) \\ &\quad \quad - \,\zeta _{z}^{T} (u_{1} (t))W_{1} \zeta _{z} (u_{1} (t)) + \zeta _{z}^{T} (u_{2} (t))W_{2} K_{{21}} x_{{p2}} (t) \\ &\quad \quad + \,\zeta _{z}^{T} (u_{2} (t))W_{2} K_{{22}} x_{{p1}} (t - \tau ) - \zeta _{z}^{T} (u_{2} (t))W_{2} \zeta _{z} (u_{2} (t)) \\ &\quad \quad + \,x_{{p2}}^{T} (t)K_{{21}}^{T} W_{2} \zeta _{z} (u_{2} (t)) + x_{{p1}}^{T} (t - \tau )K_{{22}}^{T} W_{2} \zeta _{z} (u_{2} (t)) \\ &\quad \quad - \,\zeta _{z}^{T} (u_{2} (t))W_{2} \zeta _{z} (u_{2} (t)) + x_{{p1}}^{T} (t)\kappa _{{f1}}^{T} \kappa _{{f1}} x_{{p1}} (t) \\ &\quad \quad - \,f_{1} (t,x_{{p1}} )f_{1}^{T} (t,x_{{p1}} ) + x_{{p2}}^{T} (t)\kappa _{{f2}}^{T} \\ &\quad\quad \times \,\kappa _{{f2}} x_{{p2}} (t) - f_{2} (t,x_{{p2}} )f_{2}^{T} (t,x_{{p2}} ) \\ &\quad \quad + x_{{p1}}^{T} (t)\tilde{C}_{{p11}}^{T} \gamma _{1}^{{ - 1}} \tilde{C}_{{p11}} x_{{p1}} (t) + x_{{p1}}^{T} (t)\tilde{C}_{{p11}}^{T} \gamma _{1}^{{ - 1}} \\ & \quad\quad \times \,\tilde{C}_{{p12}} x_{{p2}} (t - \tau ) - x_{{p1}}^{T} (t)\tilde{C}_{{p11}}^{T} \gamma _{1}^{{ - 1}} D_{{u1}} \zeta _{z} (u_{1} (t)) \\ & \quad\quad + x_{{p1}}^{T} (t)\tilde{C}_{{p11}}^{T} \gamma _{1}^{{ - 1}} D_{{d1}} d_{{p1}} (t)\\ &\quad \quad + x_{{p2}}^{T} (t - \tau )\tilde{C}_{{p12}}^{T} \gamma _{1}^{{ - 1}} \tilde{C}_{{p11}} x_{{p1}} (t) \\ &\quad \quad + x_{{p2}}^{T} (t - \tau )\tilde{C}_{{p12}}^{T} \gamma _{1}^{{ - 1}} \tilde{C}_{{p12}} x_{{p2}} (t - \tau ) - x_{{p2}}^{T} (t - \tau ) \\ &\quad \quad \times \,\tilde{C}_{{p12}}^{T} \gamma _{1}^{{ - 1}} D_{{u1}} \zeta _{z} (u_{1} (t)) \\ &\quad \quad + x_{{p2}}^{T} (t - \tau )\tilde{C}_{{p12}}^{T} \gamma _{1}^{{ - 1}} D_{{d1}} d_{{p1}} (t) \\ &\quad \quad - \zeta _{z}^{T} (u_{1} (t))D_{{u1}}^{T} \gamma _{1}^{{ - 1}} \tilde{C}_{{p11}} x_{{p1}} (t)\\ &\quad \quad - \,\zeta _{z}^{T} (u_{1} (t))D_{{u1}}^{T} \gamma _{1}^{{ - 1}} \tilde{C}_{{p12}} x_{{p2}} (t - \tau ) \\ &\quad \quad - \,\zeta _{z}^{T} (u_{1} (t))D_{{u1}}^{T} \gamma _{1}^{{ - 1}} \tilde{C}_{{p12}} x_{{p2}} (t - \tau ) \\ &\quad \quad + \zeta _{z}^{T} (u_{1} (t))D_{{u1}}^{T} \gamma _{1}^{{ - 1}} D_{{u1}} \zeta _{z} (u_{1} (t)) \\ &\quad \quad - \zeta _{z}^{T} (u_{1} (t)) \times D_{{u1}}^{T} \gamma _{1}^{{ - 1}} D_{{d1}} d_{{p1}} (t) \\ &\quad \quad + d_{{p1}} (t)D_{{d1}}^{T} \gamma _{1}^{{ - 1}} \tilde{C}_{{p11}} x_{{p1}} (t) \\ &\quad \quad \times \,D_{{u1}}^{T} \gamma _{1}^{{ - 1}} D_{{d1}} d_{{p1}} (t) \\ &\quad \quad + d_{{p1}} (t)D_{{d1}}^{T} \gamma _{1}^{{ - 1}} \tilde{C}_{{p11}} x_{{p1}} (t) \\ &\quad \quad + d_{{p1}} (t)D_{{d1}}^{T} \gamma _{1}^{{ - 1}} \tilde{C}_{{p12}} x_{{p2}} (t - \tau ) \\ &\quad \quad - d_{{p1}} (t)D_{{d1}}^{T} \gamma _{1}^{{ - 1}} D_{{u1}} \zeta _{z} (u_{1} (t)) \\ &\quad \quad - \,d_{{p1}} (t)D_{{d1}}^{T} \gamma _{1}^{{ - 1}} D_{{u1}} \zeta _{z} (u_{1} (t)) \\ &\quad \quad + d_{{p1}} (t)D_{{d1}}^{T} \gamma _{1}^{{ - 1}} D_{{d1}} d_{{p1}} (t) \\ &\quad \quad - \,\gamma _{1} d_{{p1}}^{T} (t)d_{{p1}} (t) \\ &\quad \quad + x_{{p2}}^{T} (t)\tilde{C}_{{p21}}^{T} \gamma _{2}^{{ - 1}} \tilde{C}_{{p21}} x_{{p2}} (t) \\ &\quad \quad + \,x_{{p2}}^{T} (t)\tilde{C}_{{p21}}^{T} \gamma _{2}^{{ - 1}} \tilde{C}_{{p22}} x_{{p1}} (t - \tau ) \\ &\quad \quad - x_{{p2}}^{T} (t)\tilde{C}_{{p21}}^{T} \gamma _{2}^{{ - 1}} \\ &\quad \quad \times \,D_{{u2}} \zeta _{z} (u_{2} (t)) + x_{{p2}}^{T} (t)\tilde{C}_{{p21}}^{T} \gamma _{2}^{{ - 1}} D_{{d2}} d_{{p2}} (t) \\ &\quad \quad + \,x_{{p1}}^{T} (t - \tau )\tilde{C}_{{p22}}^{T} \gamma _{2}^{{ - 1}} \tilde{C}_{{p21}} x_{{p2}} (t) \\ &\quad \quad + x_{{p1}}^{T} (t - \tau )\tilde{C}_{{p22}}^{T} \gamma _{2}^{{ - 1}} \tilde{C}_{{p22}} x_{{p1}} (t - \tau ) \\ &\quad \quad + x_{{p1}}^{T} (t - \tau )\tilde{C}_{{p22}}^{T} \gamma _{2}^{{ - 1}} \tilde{C}_{{p22}} x_{{p1}} (t - \tau ) \\ &\quad \quad - x_{{p1}}^{T} (t - \tau )\tilde{C}_{{p22}}^{T} \gamma _{2}^{{ - 1}} D_{{u2}} \zeta _{z} (u_{2} (t)) \\ &\quad \quad + x_{{p1}}^{T} (t - \tau ) \times \tilde{C}_{{p22}}^{T} \gamma _{2}^{{ - 1}} D_{{d2}} d_{{p2}} (t) \\ &\quad \quad - \zeta _{z}^{T} (u_{2} (t))D_{{u2}}^{T} \gamma _{2}^{{ - 1}} \tilde{C}_{{p21}} x_{{p2}} (t)\\ &\quad \quad - \zeta _{z}^{T} (u_{2} (t))D_{{u2}}^{T} \gamma _{2}^{{ - 1}} \tilde{C}_{{p22}} \\ &\quad \quad \times x_{{p1}} (t - \tau ) + \zeta _{z}^{T} (u_{2} (t))D_{{u2}}^{T} \gamma _{2}^{{ - 1}} D_{{u2}} \zeta _{z} (u_{2} (t)) \\ &\quad \quad - \zeta _{z}^{T} (u_{2} (t))D_{{u2}}^{T} \gamma _{2}^{{ - 1}} D_{{d2}} d_{{p2}} (t) \\ &\quad \quad + d_{{p2}} (t)D_{{d2}}^{T} \gamma _{2}^{{ - 1}} \tilde{C}_{{p21}} x_{{p2}} (t) \\ &\quad \quad + d_{{p2}} (t)D_{{d2}}^{T} \gamma _{2}^{{ - 1}} \tilde{C}_{{p22}} x_{{p1}} (t - \tau ) \\ &\quad \quad - d_{{p2}} (t)D_{{d2}}^{T} \gamma _{2}^{{ - 1}} \\ &\quad \quad \times \,D_{{u2}} \zeta _{z} (u_{2} (t)) + d_{{p2}} (t)D_{{d2}}^{T} \gamma _{2}^{{ - 1}} D_{{d2}} d_{{p2}} (t) \\ &\quad \quad - \gamma _{2} d_{{p2}}^{T} (t)d_{{p2}} (t) \le 0 \\ \end{aligned} $$
(18)

The inequality (18) can be written as

$$ \dot{V}(x_{p1} ,x_{p2} ,t) \le \chi_{p}^{T} (t)\bar{\varPsi }\chi_{p} (t) \le 0, $$
(19)

where,

$$ \begin{aligned} \chi_{p} (t) = [\begin{array}{*{20}c} {x_{p1}^{T} (t)} & {x_{p2}^{T} (t)} & {x_{p1}^{T} (t - \tau )} & {x_{p2}^{T} (t - \tau )} & {f_{1}^{T} (t,x_{p1} )} \\ \end{array} \\ \begin{array}{*{20}c} {f_{2}^{T} (t,x_{p2} )} & {\zeta_{z}^{T} (u_{1} (t))} & {\zeta_{z}^{T} (u_{2} (t))} & {d_{p1} (t)} & {d_{p1} (t)} \\ \end{array} ], \\ \end{aligned} $$
(20)
$$ \begin{aligned} & \bar{\Psi } \\ & \quad = \left[ {\begin{array}{*{20}c} {\bar{\Psi }_{{11}} } & 0 & 0 & {\bar{\Psi }_{{14}} } & {P_{1} } & 0 & {\bar{\Psi }_{{17}} } & 0 & {\bar{\Psi }_{{19}} } & 0 \\ * & {\bar{\Psi }_{{22}} } & {\bar{\Psi }_{{23}} } & 0 & 0 & {P_{2} } & 0 & {\bar{\Psi }_{{28}} } & 0 & {\bar{\Psi }_{{210}} } \\ * & * & {\bar{\Psi }_{{33}} } & 0 & 0 & 0 & 0 & {\bar{\Psi }_{{38}} } & 0 & {\bar{\Psi }_{{310}} } \\ * & * & * & {\bar{\Psi }_{{44}} } & 0 & 0 & {\bar{\Psi }_{{47}} } & 0 & {\bar{\Psi }_{{49}} } & 0 \\ * & * & * & * & { - I} & 0 & 0 & 0 & 0 & 0 \\ * & * & * & * & * & { - I} & 0 & 0 & 0 & 0 \\ * & * & * & * & * & * & {\bar{\Psi }_{{77}} } & 0 & {D_{{u1}}^{T} \gamma _{1}^{{ - 1}} D_{{d1}} } & 0 \\ * & * & * & * & * & * & * & {\bar{\Psi }_{{88}} } & 0 & {D_{{u1}}^{T} \gamma _{1}^{{ - 1}} D_{{d2}} } \\ * & * & * & * & * & * & * & * & { - \gamma _{1}^{{ - 1}} I} & 0 \\ * & * & * & * & * & * & * & * & * & { - \gamma _{2}^{{ - 1}} I} \\ \end{array} } \right], \\ \end{aligned}$$
(21)
$$ \begin{aligned} \bar{\varPsi }_{11} & = \tilde{A}_{p11}^{T} P_{1} + P_{1} \tilde{A}_{p11} + Q_{1} + \kappa_{f1}^{T} \kappa_{f1} + \tilde{C}_{p11}^{T} \gamma_{1}^{ - 1} \tilde{C}_{p11} , \\ \bar{\varPsi }_{14} & = P_{1} \tilde{A}_{p12} + \tilde{C}_{p11}^{T} \gamma_{1}^{ - 1} \tilde{C}_{p12} , \\ \bar{\varPsi }_{17} & = - P_{1} B_{u1} + K_{11}^{T} W_{1} - \tilde{C}_{p11}^{T} \gamma_{1}^{ - 1} D_{u1} , \\ \bar{\varPsi }_{19} & = P_{1} B_{d1} + \tilde{C}_{p11}^{T} \gamma_{1}^{ - 1} D_{d1} , \\ \end{aligned} $$
$$ \begin{aligned} \bar{\varPsi }_{22} & = \tilde{A}_{p21}^{T} P_{2} \tilde{A}_{p21} + Q_{2} + \kappa_{f2}^{T} \kappa_{f2} + \tilde{C}_{p21}^{T} \gamma_{2}^{ - 1} \tilde{C}_{p21} , \\ \bar{\varPsi }_{23} & = P_{2} \tilde{A}_{p22} + \tilde{C}_{p21}^{T} \gamma_{2}^{ - 1} \tilde{C}_{p22} , \\ \end{aligned} $$
$$ \begin{aligned} \bar{\varPsi }_{28} & = - P_{2} B_{u2} + K_{21}^{T} W_{2} - \tilde{C}_{p21}^{T} \gamma_{2}^{ - 1} D_{u2} , \\ \bar{\varPsi }_{210} & = P_{2} B_{d2} + \tilde{C}_{p21}^{T} \gamma_{2}^{ - 1} D_{d2} , \\ \end{aligned} $$
$$ \begin{aligned} \bar{\varPsi }_{33} & = - (1 - \dot{\tau })Q_{1} + \tilde{C}_{p22}^{T} \gamma_{2}^{ - 1} \tilde{C}_{p22} , \\ \bar{\varPsi }_{38} & = K_{22}^{T} W_{2} - \tilde{C}_{p22}^{T} \gamma_{2}^{ - 1} D_{u2} , \\ \bar{\varPsi }_{310} & = \tilde{C}_{p22}^{T} \gamma_{2}^{ - 1} D_{d2} , \\ \end{aligned} $$
$$ \begin{aligned} \bar{\varPsi }_{44} & = - (1 - \dot{\tau })Q_{2} + \tilde{C}_{p12}^{T} \gamma_{1}^{ - 1} \tilde{C}_{p12} , \\ \bar{\varPsi }_{47} & = K_{12}^{T} W_{1} - \tilde{C}_{p12}^{T} \gamma_{1}^{ - 1} D_{u1} , \\ \bar{\varPsi }_{49} & = \tilde{C}_{p12}^{T} \gamma_{1}^{ - 1} D_{d1} , \\ \end{aligned} $$
$$ \begin{aligned} \bar{\varPsi }_{77} & = - 2W_{1} + D_{u1}^{T} \gamma_{1}^{ - 1} D_{u1} , \\ \bar{\varPsi }_{88} & = - 2W_{2} + D_{u2}^{T} \gamma_{2}^{ - 1} D_{u2} . \\ \end{aligned} $$
(22)

By employing the Schur complement Lemma [23 and references therein] to matrix inequality (21) and then using congruence transformation by using \( diag\left\{ {\varXi_{1} ,\varXi_{1} ,\varXi_{2} ,\varXi_{3} ,\varXi_{2} ,\varXi_{2} ,\varXi_{2} } \right\} \) to the resultant matrix inequality, (where \( \varXi_{1} = diag\left\{ {P_{1} ,P_{2} } \right\} \), \( \varXi_{2} = diag\left\{ {I,I} \right\} \) and \( \varXi_{3} = diag\left\{ {W_{1} ,W_{2} } \right\} \),) and using change of variables \( P_{1}^{ - 1} = X_{1} \), \( P_{2}^{ - 1} = X_{2} \), \( K_{11} P_{1}^{ - 1} = S_{11} \), \( P_{1}^{ - 1} Q_{1} P_{1}^{ - 1} = Z_{1} \), \( K_{12} P_{2}^{ - 1} = S_{12} \), \( K_{21} P_{2}^{ - 1} = S_{21} \), \( P_{2}^{ - 1} Q_{2} P_{2}^{ - 1} = Z_{2} \), \( K_{22} P_{1}^{ - 1} = S_{22} \), \( W_{1}^{ - 1} = U_{1} \) and \( W_{2}^{ - 1} = U_{2} \), we attained the LMI (16). Further, (18) implies that

$$ \begin{aligned} & \dot{V}(x_{p1} ,x_{p2} ,t) + \gamma_{1}^{ - 1} z_{p1}^{T} (t)z_{p1} (t) - \gamma_{1} d_{p1}^{T} (t)d_{p1} (t) \\ &\quad + \gamma_{2}^{ - 1} z_{p2}^{T} (t)z_{p2} (t) - \gamma_{2} d_{p2}^{T} (t)d_{p2} (t) < 0. \\ \end{aligned} $$
(23)

Integrating (23) from \( 0 \) to \( t > 0 \) yields

$$ \begin{aligned} & V(x_{p1} ,x_{p2} ,t) - \dot{V}(x_{p1} ,x_{p2} ,0) + \gamma_{1}^{ - 1}\\& \quad \times \int\limits_{0}^{t} {z_{p1}^{T} (t)z_{p1} (t)} dt - \gamma_{1} \int\limits_{0}^{t} {d_{p1}^{T} (t)d_{p1} (t)} dt \\ & + \gamma_{2}^{ - 1} \int\limits_{0}^{t} {z_{p2}^{T} (t)z_{p2} (t)} dt - \gamma_{2} \int\limits_{0}^{t} {d_{p2}^{T} (t)d_{p2} (t)} dt < 0 \\ \end{aligned} $$
(24)

Under zeros initial condition \( x_{awc} (0) = 0 \) we can infers that \( V(x_{p1} ,x_{p2} ,0) = 0 \)\( V(x_{p1} ,x_{p2} ,t) > 0 \). Then condition (24) implies

$$ \begin{aligned} & + \gamma_{1}^{ - 1} \int\limits_{0}^{t} {z_{p1}^{T} (t)z_{p1} (t)} dt - \gamma_{1} \int\limits_{0}^{t} {d_{p1}^{T} (t)d_{p1} (t)} dt \\ & + \gamma_{2}^{ - 1} \int\limits_{0}^{t} {z_{p2}^{T} (t)z_{p2} (t)} dt - \gamma_{2} \int\limits_{0}^{t} {d_{p2}^{T} (t)d_{p2} (t)} dt < 0, \\ \end{aligned} $$
(25)

which additionally, guarantees that \( \left\| {z_{p1} (t)} \right\| \le \gamma_{1} \left\| {d_{p1} (t)} \right\| \) and \( \left\| {z_{p2} (t)} \right\| \le \gamma_{2} \left\| {d_{p2} (t)} \right\| \). Hence, the \( L_{2} \) gains from \( d_{p1} (t) \) to \( z_{p1} (t) \) and from \( d_{p2} (t) \) to \( z_{p2} (t) \) are less than \( \gamma_{1} \) and \( \gamma_{2} \) respectively, if \( d_{p1} (t) \ne 0 \) and \( d_{p2} (t) \ne 0 \). This concludes the proof of Theorem 1. □

Remark 1

In Theorem 1 we propose a global state feedback tracking controller design which ensure the global asymptotic stability of the overall closed-loop system. While in Theorem 2, we extend the global controller technique to more general local state feedback tracking controller schemes by using an auxiliary region of attraction and local sector bounded condition. Which assurance local asymptotic stability of the overall closed-loop system.

4 Local controller design for distributed control system

Consider an auxiliary regions given as

$$ S_{1} (\bar{v}_{1} ,t) = \{ w_{1} (t) \in \Re^{m} ; - \bar{v}_{1} \le u_{1} (t) - w_{1} (t) \le \bar{v}_{1} \} , $$
(26)
$$ S_{2} (\bar{v}_{2} ,t) = \{ w_{2} (t) \in \Re^{m} ; - \bar{v}_{2} \le u_{2} (t) - w_{2} (t) \le \bar{v}_{2} \} , $$
(27)

where \( w_{1} (t) \) and \( w_{2} (t) \) are the auxiliary defined vectors and \( \bar{v}_{1} \) and \( \bar{v}_{2} \) are the limits on saturation nonlinearity. For positive definite diagonal matrices \( W_{1} \in R^{m \times m} \) and \( W_{2} \in R^{m \times m} \) the dead-zone nonlinearity fulfils the local sector bounded condition (see [9, 13] and references therein), given by

$$ \zeta_{z} (u_{1} (t))^{T} W_{1} [w_{1} (t) - \zeta_{z} (u_{1} (t))] \ge 0 $$
(28)
$$ \zeta_{z} (u_{2} (t))^{T} W_{2} [w_{2} (t) - \zeta_{z} (u_{2} (t))] \ge 0 $$
(29)

\( w_{1} (t) = u_{1} (t) + G_{11} x_{p1} (t) + G_{12} x_{p2} (t) \), \( w_{2} (t) = u_{2} (t) + G_{21} x_{p1} (t) + G_{22} x_{p2} (t) \) holds true, if (26) and (27) are fulfilled.

Theorem 2

Consider the overall closed-loop control nonlinear time-delay system attained by nonlinear time-delay distributed control systems (6), and state feedback tracking controller (7) satisfying assumptions A1, and A2. Presume there exist symmetric matrices\( Q_{1} \in R^{n \times n} \), \( Q_{2} \in R^{n \times n} \), \( P_{1} \in R^{n \times n} \), and\( P_{2} \in R^{n \times n} \), and symmetric diagonal matrices\( W_{1} \in R^{m \times m} \)and\( W_{2} \in R^{m \times m} \), than the nonlinear time-delay distributed control systems under input saturation nonlinearity is locally asymptotically stable and the\( L_{2} \)gain from\( d_{p1} (t) \)to\( z_{p1} (t) \), and from\( d_{p2} (t) \)to\( z_{p1} (t) \)are less then\( \gamma_{1} \)and\( \gamma_{1} \)respectively if\( d_{p1} (t) \ne 0 \)and\( d_{p2} (t) \ne 0 \), independent of delay if the subsequent LMIs are satisfied:

$$ \bar{\varPsi }_{1}^{*} = \left[ {\begin{array}{*{20}c} {P_{1} } & 0 & {G_{11} } \\ * & {P_{2} } & {G_{12} } \\ * & * & {\mu \bar{v}_{1(k)}^{2} } \\ \end{array} } \right] \ge 0, $$
(30)
$$ \bar{\varPsi }_{2}^{*} = \left[ {\begin{array}{*{20}c} {P_{1} } & 0 & {G_{21} } \\ * & {P_{2} } & {G_{22} } \\ * & * & {\mu \bar{v}_{2(k)}^{2} } \\ \end{array} } \right] \ge 0, $$
(31)
$$ \varPsi^{*} = \left[ {\begin{array}{*{20}c} {\varPsi_{1} } & {\varPsi_{2}^{*} } \\ * & {\varPsi_{3} } \\ \end{array} } \right] < 0 $$
(32)
$$ \varPsi_{2}^{*} = \left[ {\begin{array}{*{20}c} {\varUpsilon_{11}^{*} } & {\varUpsilon_{12} } \\ \end{array} } \right] $$
$$ \varUpsilon_{11}^{*} = \left[ {\begin{array}{*{20}c} { - B_{u1} U_{1} + S_{11}^{T} + H_{11}^{T} } & {H_{22}^{T} } & {B_{d1} } & 0 \\ {H_{12}^{T} } & { - B_{u2} U_{2} + S_{21}^{T} + H_{21}^{T} } & 0 & {B_{d2} } \\ 0 & {S_{22}^{T} } & 0 & 0 \\ {S_{12}^{T} } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right] $$

Proof

Consider the condition (24) in the proof of Theorem 1, under the assumption \( x_{awc} (0) = 0 \), \( \dot{V}(x_{p1} ,x_{p2} ,0) = 0 \)\( V(x_{p1} ,x_{p2} ,t) > 0 \) yields \( V(x_{p1} ,x_{p2} ,t) < \gamma_{1} \int\limits_{0}^{t} {d_{p1}^{T} (t)d_{p1} (t)} dt + \gamma_{2} \int\limits_{0}^{t} {d_{p2}^{T} (t)d_{p2} (t)} dt \) which further gives \( x_{p1}^{T} (t)\mu P_{1} x_{p1} (t) + x_{p2}^{T} (t)\mu P_{2} x_{p2} (t) < 1 \) where, \( \int\limits_{0}^{t} {d_{p1}^{T} (t)d_{p1} (t)} dt \le \left\| {d_{p1} (t)} \right\|_{2}^{2} \le \lambda_{1}^{ - 1} \), \( \int\limits_{0}^{t} {d_{p2}^{T} (t)d_{p2} (t)} dt \le \left\| {d_{p2} (t)} \right\|_{2}^{2} \le \lambda_{2}^{ - 1} \) and \( \mu = \left( {\gamma_{1} \lambda_{1}^{ - 1} + \gamma_{2} \lambda_{2}^{ - 1} } \right)^{ - 1} \). Consequently, the states of the closed-loop system persist bounded by \( x_{p1}^{T} (t)\mu P_{1} x_{p1} (t) + x_{p2}^{T} (t)\mu P_{2} x_{p2} (t) < 1 \) for all the time. By including the region \( x_{p1}^{T} (t)\mu P_{1} x_{p1} (t) + x_{p2}^{T} (t)\mu P_{2} x_{p2} (t) < 1 \) into \( S_{1} (\bar{v}_{1} ,t) \) and \( S_{2} (\bar{v}_{2} ,t) \), we attain the matrix inequality (30) and (31), respectively. Subsequently, the region (26) and (27) and the local sector condition (28) and (29) remain valid. The linear matrix inequality (32) is attained by using transformation \( G_{11} P_{1}^{ - 1} = H_{11} \), \( G_{12} P_{2}^{ - 1} = H_{12} \), \( G_{21} P_{2}^{ - 1} = H_{21} \), \( G_{22} P_{1}^{ - 1} = H_{22} \), (8), (10)–(13) (28) and (29) in the similar approach as for the derivation of Theorem 1. This completes the proof of Theorem 2. □

For \( d_{p1} (t) = 0 \) and \( d_{p2} (t) = 0 \) a delay-dependent stability result for designing local state feedback tracking controller for nonlinear time-delay distributed control systems (1) is attained from Theorem 2.

Corollary 1

Consider the overall closed-loop control nonlinear time-delay system formed by nonlinear time-delay distributed control systems (6) and state feedback tracking controller (7) satisfy A1 and A2. Presume there exist symmetric matrices\( Q_{1} \in R^{n \times n} \), \( Q_{2} \in R^{n \times n} \), \( P_{1} \in R^{n \times n} \)and\( P_{2} \in R^{n \times n} \), and symmetric diagonal matrices\( W_{1} \in R^{m \times m} \)and\( W_{2} \in R^{m \times m} \), than the nonlinear time-delay distributed control systems under input saturation nonlinearity is locally asymptotically stable if\( d_{p1} (t) = 0 \)and\( d_{p2} (t) = 0 \), independent of delay if LMI’s (30) and (31) along with the following LMIs are satisfied:

$$ \bar{\varPsi } = \left[ {\begin{array}{*{20}c} {\varPsi_{1} } & {\bar{\varPsi }_{2} } \\ * & {\bar{\varPsi }_{3} } \\ \end{array} } \right] < 0 $$
(33)
$$ \bar{\varPsi }_{2} = \left[ {\begin{array}{*{20}c} {\bar{\varUpsilon }_{11} } & {\varUpsilon_{12} } \\ \end{array} } \right] $$
$$ \bar{\varUpsilon }_{11} = \left[ {\begin{array}{*{20}c} { - B_{u1} U_{1} + S_{11}^{T} } & 0 \\ 0 & { - B_{u2} U_{2} + S_{21}^{T} } \\ 0 & {S_{22}^{T} } \\ {S_{12}^{T} } & 0 \\ 0 & 0 \\ 0 & 0 \\ \end{array} } \right] $$
$$ \bar{\varPsi }_{3} = \left[ {\begin{array}{*{20}c} { - 2U_{1} } & 0 & 0 & 0 & { - U_{1} D_{u1}^{T} } & 0 \\ * & { - 2U_{2} } & 0 & 0 & 0 & { - U_{2} D_{u2}^{T} } \\ * & * & { - I} & 0 & 0 & 0 \\ * & * & * & { - I} & 0 & 0 \\ * & * & * & * & { - I\gamma_{1} } & 0 \\ * & * & * & * & * & { - I\gamma_{2} } \\ \end{array} } \right] $$

Remark 2

Theorems 1 and 2 propose the global and local state feedback tracking controller schemes for nonlinear time-delay distributed control plants. The proposed outcomes can easily be reduced to the linear time-delay distributed control systems by taking \( f(t,x_{p1} ) = 0 \) and \( f(t,x_{p2} ) = 0 \). Further, the proposed can also be reduced to investigate the delay-independent stability of the nonlinear time-delay distributed control systems.

Remark 3

It is valuable to note that controller design for distributed nonlinear systems has been studied in [24]. In [24] the distributed model predictive controller design problem is investigated for multi-agent nonlinear systems. However, the transportation delays among subsystems are not considered. Similarly, in the works of [25, 26], it is presumed that the communication infrastructure run in flawless environments. However, this supposition may not be true in practical implementation, because hardware limitation induces imperfections for example time delays [27]. The stabilization problem for network control system has been studied in [28, 29], by employing delay-independent and delay-dependent techniques without considering controller windup effect. These techniques may perform well in absence of input saturation, however when the control action cross the actuator bound then it may yield objectionable closed-loop performance and even instability. In contrast, we investigate a more practical scenario by considering hardware limitation such as actuator saturation, communication delays, and time-varying disturbances. That is the states coming from other subsystems have transportation time-delay. The coupling states time-delay is presumed to be time-varying within a predefined bound and the manipulating control action is bounded.

The suggested controller design method is based on the supposition that the both the delayed and un-delayed states of a nonlinear time-delay distributed control systems are accessible. If delayed or un-delayed states of the plant are not available, then numerous observer techniques for example [30,31,32] can be employed to estimate the states of the plant. A state feedback controller design problem for nonlinear time-delay distributed control systems subjected to input saturation nonlinearity and disturbances is an interesting problem if the delayed or un-delayed states of the system are not accessible and can be considered in the further work.

5 Simulation results

The following numerical example of nonlinear time-delay distributed control systems is used to show the efficiency of the suggested state feedback tracking controller:

$$ \begin{aligned} & A_{p11} = \left[ {\begin{array}{*{20}c} { - 1} & 2 & 0 \\ 1 & { - 2} & { - 1} \\ 3 & 0 & { - 6} \\ \end{array} } \right],\;A_{p12} = \left[ {\begin{array}{*{20}c} { - 0.3} & {0.2} & 0 \\ {0.1} & { - 0.2} & { - 0.1} \\ {0.3} & 0 & { - 0.6} \\ \end{array} } \right],\;\\& \quad f(t,x_{p1} ) = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ { 5. 1\sin (x_{p1} (t))} \\ \end{array} } \right], \\ & A_{p21} = \left[ {\begin{array}{*{20}c} { - 3} & 2 & 0 \\ 1 & { - 2} & { - 1} \\ 3 & 0 & { - 6} \\ \end{array} } \right],\;A_{p22} = \left[ {\begin{array}{*{20}c} { - 0.1} & {0.2} & 0 \\ {0.1} & { - 0.2} & { - 0.1} \\ {0.3} & 0 & { - 0.6} \\ \end{array} } \right],\;\\& \quad f(t,x_{p2} ) = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {4.0\sin (x_{p2} (t))} \\ \end{array} } \right], \\ & B_{u1} = \left[ {\begin{array}{*{20}c} 1 \\ { - 1} \\ 0 \\ \end{array} } \right],\,B_{u2} = \left[ {\begin{array}{*{20}c} 1 \\ 0 \\ { - 1} \\ \end{array} } \right]. \\ \end{aligned} $$
(34)

For \( \kappa_{f1} = 5.1I \), \( \kappa_{f2} = 4.0I \), \( d = 1 \), \( \bar{v} = 1 \)\( \tau_{1} = 0 \) and \( \tau_{2} = 1.6 \) the controller parameters \( K_{11} \), \( K_{12} \), \( K_{21} \) and \( K_{22} \) are calculated using LMI (16). It is calculated to be as

$$ K_{11} = \left[ {\begin{array}{*{20}c} {0.07350} & {11.0510} & { - 2.5962} \\ \end{array} } \right] $$
(35)
$$ K_{12} = \left[ {\begin{array}{*{20}c} {0.1265} & { - 0.1980} & { - 0.0706} \\ \end{array} } \right] $$
(36)
$$ K_{21} = \left[ {\begin{array}{*{20}c} {0.2051} & { - 0.1021} & { - 0.3252} \\ \end{array} } \right] $$
(37)
$$ K_{22} = \left[ {\begin{array}{*{20}c} { - 12.6462} & { - 10.0148} & {1.9289} \\ \end{array} } \right] $$
(38)

The time-varying disturbance signals \( d_{p1} (t) \) and \( d_{p2} (t) \) are selected as

$$ d_{p1} (t) = \left[ {\begin{array}{*{20}c} {3.5\cos (120t)} & {0.2\sin (80t)} & {1.5\cos (100t)} \\ \end{array} } \right]^{T} $$
(39)
$$ d_{p1} (t) = \left[ {\begin{array}{*{20}c} {2.5\cos (120t)} & {1.2\sin (80t)} & {1.8\cos (110t)} \\ \end{array} } \right]^{T} $$
(40)

The initial values of the states of the first and second subsystems are selected as \( x_{p1} (t) = \left[ {\begin{array}{*{20}c} {3.0} & { - 2.0} & {2.0} \\ \end{array} } \right]^{T} \) and \( x_{p2} (t) = \left[ {\begin{array}{*{20}c} {1.0} & { - 2.0} & {2.0} \\ \end{array} } \right]^{T} \), respectively. Figure 1a–c show the state response of the first subsystem with and without a controller. It can be clearly seen from Fig. 1a–c that all the states of the first subsystem with the proposed controller rapidly converges to zero in the existence of input saturation and time-varying disturbances. Conversely, all states of the first subsystem without the proposed controller exhibits oscillatory response due to the dynamic nonlinearity, input saturation, and external disturbances. The control input of the first subsystem with and without a controller is shown in Fig. 1d. It can be noticed from Fig. 1d that the control input of the first subsystem with a controller is smooth and convergent. However, a control input of the first subsystem without a controller is oscillatory.

Fig. 1
figure 1

First subsystem performance with and without controller. a\( x_{p1} (t) \) state response, b\( x_{p2} (t) \) state response, c\( x_{p3} (t) \) state response, d control input

Full size image

Similarly, the evolution of the states and control input of the second subsystem with and without controller are demonstrated in Fig. 2a–d, respectively. It can be clearly seen from Fig. 2a–d that all the states and control input of the second subsystem with the proposed controller rapidly converges to zero in the presence of input saturation and time-varying disturbances. The performance of the control action is adequately satisfactory. Conversely, all states and control input of the second subsystem without the proposed controller exhibits fluctuation due to the dynamic nonlinearity, input saturation, and external disturbances.

Fig. 2
figure 2

Second subsystem performance with and without controller. a\( x_{p1} (t) \) state response, b\( x_{p2} (t) \) state response, c\( x_{p3} (t) \) state response, d control input

Full size image

The convergent behavior of nonlinear time-delay distributed control systems state trajectories for \( d_{p1} (t) = 0 \) and \( d_{p2} (t) = 0 \) with initial conditions of the states \( x_{p1} (t) = \left[ {\begin{array}{*{20}c} { - 2.0} & {2.0} & { - 1.0} \\ \end{array} } \right]^{T} \) and \( x_{p2} (t) = \left[ {\begin{array}{*{20}c} { - 0.5} & { - 1.0} & {1.5} \\ \end{array} } \right]^{T} \) are depicted in Figs. 3 and 4. Figures 3 and 4 reveal that nonlinear time-delay distributed control systems without disturbance is asymptotically stable. Hence, we observe that our proposed controller technique performs well in the presence of input saturation with and without external disturbance and yield satisfactory performance.

Fig. 3
figure 3

First subsystem states response for \( d_{p1} (t) = 0 \) and \( d_{p2} (t) = 0 \)

Full size image
Fig. 4
figure 4

Second subsystem states response for \( d_{p1} (t) = 0 \) and \( d_{p2} (t) = 0 \)

Full size image

6 Conclusions

Global and local state feedback tracking controller design for nonlinear time-delay distributed control systems subjected to input saturation nonlinearity and disturbances were proposed in this paper. The nonlinear time-delay distributed control system individual state vector is without any time-delay and the states coming from other sub-systems come with time-delay. By applying a Lipschitz condition, global and local sector bounded condition, and a Lyapunov–Krasovskii function, linear matrix inequalities (LMI)-based solution is derived to synthesis state feedback tracking controller, which ensure the \( L_{2} \) stability of the overall closed-loop system. Simulation results are provided to indicate the effectiveness of the suggested global and local state feedback tracking control methodologies.