Implementation of numerical approximations in studying vibration of functionally graded beams

Abstract

In this investigation, a brief review on three efficient computational techniques viz. Finite Element Method, Differential Quadrature Method and Rayleigh–Ritz Method along with their mathematical formulation to study free vibration of thin Functionally Graded (FG) beams subject to various classical boundary supports have been presented. The deformation of FG beam is based on the framework of classical beam theory. Three different FG beam constituents assumed in this study are Al/Al$_{2}$O$_{3}$, Al/ZrO$_2$ and SUS304/Si$_3$N$_4$, in which the first component is meant for the metal constituent and the second for ceramic constituent respectively. The material properties of FG beam are assumed to vary continuously along thickness direction in a power-law form. The objective is to outline exemplary works carried out by various researchers on the concerned problem and also to find the effect of volume fraction of FG constituents on natural frequencies. The natural frequencies of different FG beams under four sets of classical edge supports have been evaluated along with two-dimensional mode shapes after finding the convergence with reference to concerned numerical methods and validation with available literature.

1 Introduction

Functionally Graded (FG) materials are emerging advanced composites in recent decade for their thermal resistance properties, which was first discovered by a group of material scientists in Japan to withstand a huge temperature fluctuation across a very thin cross-section in a space-plane project. Major components of FG composites are metal and ceramic materials, in which the constituent properties vary spatially along thickness direction in a specific mathematical pattern. As their microstructure has not yet been revealed, the mechanics and governing equations related to homogeneous case are assumed to be true for elastic FG composites. Studying dynamics of functionally graded beam is one of the interesting problems in current era and literature related to such problems using various methods have been briefly mentioned herein.

1.1 Development of FEM

One of the recent trends on solving the titled problems is based on Finite Element Method (FEM) and its research development has been reviewed first. The method is first developed in 1956 for the analysis of aircraft structural problems. Thereafter, the finite element technique has drawn enough attention within a decade for solving a wide variety of problems in applied science and engineering and has been developed over the years [1]. As regards, Öz [2] have calculated natural frequencies of an Euler-Bernoulli beam-mass system using this approach. Two $C^0$ assumed finite element formulations of Reddy’s higher-order theory were used by Nayak et al. [3] to obtain the natural frequencies of composite and sandwich plates. Chakraborty et al. [4] proposed a new beam finite element based on the first-order shear deformation theory to study the thermoelastic behavior of functionally graded beam structures. Ribeiro [5] has applied the shooting, Newton and p-version, heirarchical finite element methods to investigate geometrically nonlinear periodic vibrations of elastic and isotropic, beams and plates. Şimşek [6] has examined vibration response of a simply-supported FG beam to a moving mass by using Euler–Bernoulli, Timoshenko and the third-order shear deformation beam theories. Alshorbagy et al. [7] have used finite element method to detect the free vibration characteristics of a functionally graded beam. Shahba et al. [8] investigated free vibration and stability analysis of axially functionally graded Timoshenko tapered beams using classical and non-classical boundary conditions through finite element approach. The bending and flexural vibration behavior of sandwich FG plates have been provided by Natarajan and Manickam [9] using QUAD-8 shear flexible element developed on higher order structural theory. Vo et al. [10] have developed a finite element model for vibration and buckling of FG sandwich beams based on refined shear deformation theory. Free vibration and stability of axially functionally graded tapered Euler–Bernoulli beams have been investigated using finite element method by Shahba and Rajasekaran [11]. Vo et al. [12] have presented static and vibration analysis of FG beams using refined shear deformation theory by using finite element formulation. A novel Timoshenko beam element based on the framework of strain gradient elasticity theory is presented in [13] for the analysis of the static bending, free vibration and buckling behaviors of Timoshenko microbeams. Very recently, Hui et al. [14] have given a family of beam higher-orders finite elements based on a hierarchical one dimensional unified formulation for a free vibration analysis of three-dimensional sandwich structures. To name a few out of recent findings, one may easily find finite element solutions of structural members in [15, 16] and also literature available therein.

1.2 Development of DQM

On the other hand, differential quadrature method (DQM) is an efficient numerical procedure, which is also taken into account in present study. The DQ method, equivalent to the conventional integral quadrature method, approximates the derivative of a function at any location by a linear combination of the functional values within a closed domain. The key procedure the DQM lies in the determination of the weighting coefficients with respect to specific order derivatives [17]. Initially, the foundation of DQM is proposed mainly by Bellman and Casti [18] and implemented in various classes of partial differential equations by reducing them to ordinary differential equations and then to finite dimensional systems. A precise idea on ways to develop DQM in various forms, numerical solution of different classes of linear and nonlinear partial differential equations, splines and efficiency of this method can be observed in [19,20,21]. Following the investigation of Bellman et al. [19], Quan and Chang [22, 23] have provided new insights in solving distributed system equations by the method of differential quadrature along with results of a series of numerical experiments. The analysis of laminated composite structures has been performed by Bert and Malik [24] using this method. After a close observation to previous studies [19, 22, 23] on DQM, Shu and Du [25] have developed Generalized Differential Quadrature (GDQ) method for implementing clamped and simply supported boundary conditions for the free vibration analysis of beams and plates. In the similar fashion, a few major changes have also been incorporated in DQM in recent decades by combining with other numerical methods. As such, a mixed Ritz-DQ method has been used in free and forced vibration of functionally graded beams and isotropic rectangular plates in [26,27,28]. In a recent work, Yas et al. [29] have investigated free vibration of Euler–Bernoulli FG beams resting on elastic foundation by means of GDQ. A general formulation of the quadrature element method is presented by Jin and Wang [30] to estimate vibration of FG beams.

Fig. 1

Power-law variation of material properties of Al/Al$_{2}$O$_{3}$ functionally graded beam

1.3 Development of RRM

In addition, it is also worth to organise the investigations performed by means of Rayleigh–Ritz method. Rayleigh’s classical book ‘Theory of Sound’ was first published in 1877. In this book, lots of examples can be found on evaluating fundamental natural frequencies of free vibration of continuum systems by assuming the mode shape and setting the maximum values of potential and kinetic energy in a cycle of motion equal to each other. This procedure is well known as Rayleigh’s Method. In 1908, Ritz laid out his famous method for determining frequencies and mode shapes, choosing multiple admissible displacement functions, and minimizing a functional involving both potential and kinetic energies. Subsequently, this technique is referred to as Rayleigh–Ritz method and has taken major attention among researchers till date. These fact on the origin of Rayleigh and Ritz methods are clearly addressed in Leissa [31]. By assuming a modification, Bhat [32] have considered the characteristic orthogonal polynomials in Rayleigh–Ritz method to estimate transverse vibration response of rotating cantilever beam with a tip mass. The natural frequencies of rectangular plates using characteristic orthogonal polynomials have also been computed in [33, 34] using Rayleigh–Ritz method. Singh and Chakraverty [35,36,37] have solved transverse vibration of elliptic and circular plates using orthogonal polynomials in Rayleigh–Ritz method satisfying different boundary conditions viz. completely-free, simply-supported and clamped respectively. Rayleigh–Ritz method is used by Abrate [38] to find vibration of some non-uniform rods and beams with one end completely fixed. Ding [39] has developed a fast converging series consisting of a set of static beam functions to study vibration characteristics of thin rectangular plates. Aydogdu and Taskin [40] have investigated free vibration of a simply supported FG beam within the framework of Euler-Bernoulli beam theory, parabolic shear deformation theory and exponential shear deformation theory. Analytical solution is proposed by Ece et al. [41] to study vibration of isotropic beam with variable cross-section. Sina et al. [42] have given an analytical solution for free vibration of functionally graded beams. Refined plate theories have been implemented by Carrera et al. [43] in finding accurate free vibration analysis of anisotropic, simply supported plates. The flapwise and chordwise bending vibration analysis of rotating pre-twisted Timoshenko beam are examined in [44] by the use of Rayleigh–Ritz method. Free vibration of the baffled circular plates with radial side cracks and in contact with water on one side is studied by Si et al. [45] based on Rayleigh–Ritz method. Moreover, Chakraverty and Pradhan [46] have given an excellent monograph on vibration of functionally graded beams and plates with various geometries (rectangular, elliptic and triangular) along with the effect of complicating environments.

In the above discussion, a brief idea on implementing three efficient numerical techniques in handling structural problems has been presented. To the best of authors’ knowledge, no investigation has covered on implementing efficient numerical solutions in studying vibration of Euler–Bernoulli FG beams (estimating six natural frequencies of three FG beams consisting of various constituents and comparison of their numerical approach) along with their recent developments. As such, present study is associated with numerical approach of finite element, differential quadrature and Rayleigh–Ritz methods towards free vibration of Euler–Bernoulli functionally graded beam. The conventional procedures followed by these methods have been discussed in detail. The material properties of FG constituents vary continuously along thickness direction in power-law form. The main objective of this investigation is to address varieties of related significant works and to analyze the effect of volume fractions of constituents on natural frequencies. New results for natural frequencies along with two-dimensional (2-D) mode shapes are incorporated after checking test of convergence and validation with previous literature.

2 Functionally graded beam

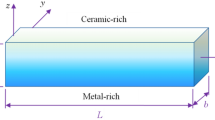
A straight FG beam of length L, width b and thickness h, having rectangular cross-section with cartesian coordinate system is considered here. In addition, the material properties of FG beam vary along the thickness direction according to power-law form as shown in Fig. 1. The power-law variation used in Sina et al. [42] is considered

$$\begin{aligned} \mathbf {P}(z) = (\mathbf {P}_{c}-\mathbf {P}_{m})\left( \frac{z}{h}+\frac{1}{2}\right) ^{\mathrm {k}} + \mathbf {P}_{m} \end{aligned}$$

(1)

where $\mathbf {P}_{c}$ and $\mathbf {P}_{m}$ denote the values of the material properties of the ceramic and metal constituents of the FG beam respectively. $\mathrm {k}$ (power-law exponent) is a non-negative variable parameter. According to this distribution, the bottom surface ($z=-\,h/2$) of FG beam is pure metal, whereas the top surface ($z=h/2$) is pure ceramic and for different values of $\mathrm {k}$ one can obtain different volume fractions of material beam as mentioned in Aydogdu and Taskin [40]. For our present formulations, the material properties viz. Young’s modulus (E) and mass density ($\rho$) are considered to vary along thickness direction except Poisson’s ratio ($\nu$) remaining as constant. In Fig. 1, FG constituents own the properties of Al (metal) and Al$_{2}$O$_{3}$ (ceramic) [42]: $E_m = 70~\text {GPa}$, $\rho _m = 2700$ kg/m$^3$, $E_c = 380~\text {GPa}$ and $\rho _c = 3800$ kg/m$^3$.

Here, classical beam theory is assumed to define the deformation of thin functionally graded beam as referred by Şimşek and Kocaturk [6], Alshorbagy et al. [7], Aydogdu and Taskin [40], Sina et al. [42] and Şimşek [47]

$$\begin{aligned} \begin{aligned}&u_{x}(x,z) = -\, z \frac{\partial w}{\partial x} \\&u_{z}(x,z) = w(x,t). \end{aligned} \end{aligned}$$

(2)

Now, Eq. (3) represent the kinematic relations with respect to displacement field of Eq. (2)

$$\begin{aligned} \begin{aligned}&\varepsilon _{xx} = -\,z\frac{\partial ^2 w}{\partial x^2} \\&\gamma _{xz} = 0 \end{aligned} \end{aligned}$$

(3)

where $\varepsilon _{xx}$ and $\gamma _{xz}$ are the normal and shear strains respectively. By assuming the material constituents of FG beam to obey the generalized Hooke’s law, the state of stresses in the beam can be written as

$$\begin{aligned} \begin{aligned}&\sigma _{xx}=Q_{11}\varepsilon _{xx} \\&\tau _{xz}=Q_{55}\gamma _{xz}. \end{aligned} \end{aligned}$$

(4)

where $\sigma _{xx}$ and $\tau _{xz}$ in Eq. (4) are the normal and the shear stresses respectively and $Q_{ij}$ are the transformed stiffness constants in the beam co-ordinate system and are defined as [48]

$$\begin{aligned} Q_{11}=\frac{E(z)}{1-\nu ^{2}},\;\; Q_{55}=\frac{E(z)}{2(1+\nu )}. \end{aligned}$$

3 Numerical formulations

First of all, the classical boundary conditions for transverse displacement (w) at the specified beam end can be introduced as provided by Öz [2]

$$\begin{aligned} \begin{aligned}&\text {Clamped (C):}~~ w = 0;~ \frac{\partial w}{\partial x} = 0 \\&\text {Simply supported (S):}~~ w = 0;~ \frac{\partial ^2 w}{\partial x^2} = 0 \\&\text {Free (F):}~~ \frac{\partial ^2 w}{\partial x^2} = 0;~ \frac{\partial ^3 w}{\partial x^3} = 0. \end{aligned} \end{aligned}$$

(5)

Further, numerical procedures of three well-known numerical techniques viz. FEM, GDQ and Rayleigh–Ritz method have been addressed to obtain the generalized eigenvalue problem for free vibration of FG beam as given below.

3.1 Finite element method

In general, the transverse displacement and rotation (slope) describe the deformed shape of the beam and these components at each end of the beam are treated as the unknown degrees of freedom. As there are four nodal displacements at the beam ends, the cubic displacement model as mentioned in Rao [1] can be defined as

$$\begin{aligned} w(x) = a_1 + a_2 x + a_3 x^2 + a_4 x^3 \end{aligned}$$

(6)

where $a_1$, $a_2$, $a_3$ and $a_4$ are the unknown coefficients and can be found by using the edge conditions. The displacement (w) and rotation ($\theta$) at $x = 0$ and L can be substituted in Eq. (6) and yield

$$\begin{aligned} \begin{Bmatrix} w_1 \\ \theta _1 \\ w_2 \\ \theta _2 \end{Bmatrix} = \begin{pmatrix} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 1 &{}\quad L &{}\quad L^2 &{}\quad L^3 \\ 0 &{}\quad 1 &{}\quad 2L &{}\quad 3L^2 \end{pmatrix} \begin{Bmatrix} a_1 \\ a_2 \\ a_3 \\ a_4 \end{Bmatrix} \end{aligned}$$

(7)

Solving Eq. (7), the shape function [N] takes the form

$$\begin{aligned}{}[N] = [N_1(x)~~~ N_2(x)~~~ N_3(x)~~~ N_4(x)] \end{aligned}$$

(8)

where

$$\begin{aligned} \begin{aligned}&N_1(x) = \frac{2x^3 - 3Lx^2 + L^3}{L^3} \\&N_2(x) = \frac{x^3 - 2Lx^2 + L^2x}{L^3} \\&N_3(x) = \frac{2x^3 - 3Lx^2}{L^3} \\&N_4(x) = \frac{x^3 - Lx^2}{L^3} \end{aligned} \end{aligned}$$

which helps to find the kinetic energy and also the connectivity matrix [B] for elastic strain energy.

$$\begin{aligned} \begin{aligned} \,[B]&= [B_1(x)~~~ B_2(x)~~~ B_3(x)~~~ B_4(x)] \\&= \left[ \frac{d^2 N_1}{d x^2}~~~ \frac{d^2 N_2}{d x^2}~~~ \frac{d^2 N_3}{d x^2}~~~ \frac{d^2 N_4}{d x^2}\right] \end{aligned} \end{aligned}$$

(9)

From Eq. (8) and (9), one may find respective element inertia and stiffness matrices as

$$\begin{aligned}{}[M_e] = \frac{\rho (z) AL}{420} \begin{pmatrix} 156 &{}\quad 22L &{}\quad 54 &{}\quad -13L \\ 22L &{}\quad 4L^2 &{}\quad 13L &{}\quad -3L^2 \\ 54 &{}\quad 13L &{}\quad 156 &{}\quad -22L \\ -13L &{}\quad -3L^2 &{}\quad -22L &{}\quad 4L^2 \end{pmatrix} \end{aligned}$$

(10)

and

$$\begin{aligned}{}[K_e] = \frac{E(z)I}{L^3} \begin{pmatrix} 12 &{}\quad 6L &{}\quad -12 &{}\quad 6L \\ 6L &{}\quad 4L^2 &{}\quad -6L &{}\quad 2L^2 \\ -12 &{}\quad -6L &{}\quad 12 &{}\quad -6L \\ 6L &{}\quad 2L^2 &{}\quad -6L &{}\quad 4L^2 \end{pmatrix} \end{aligned}$$

(11)

The formulation for local stiffness and mass matrix are clearly given in Öz [2] in case of isotropic beams. Prior to the fact that Young’s modulus in stiffness matrix and mass density in mass matrix are dependent on the thickness, there occurs a slight modification in the expression of corresponding matrices. If discretization of total length of the FG beam is considered, discretized element inertia and stiffness matrices will be combined to obtain the global inertia and stiffness matrix respectively. The equation of motion for free vibration of FG beam can be obtained from

$$\begin{aligned}{}[M]\left\{ w{''}\right\} + [K] \left\{ w\right\} = \left\{ 0\right\} \end{aligned}$$

(12)

where [K] and [M] are the global stiffness and mass matrices respectively and $\left\{ w\right\}$ is the system displacement vector. Then substituting the harmonic displacement in the form $w(x,t) = W(x) \exp (i\omega t)$ with $i = \sqrt{-1}$ and $\omega$ as natural frequency and W as amplitude of displacement, we can write Eq. (38) as

$$\begin{aligned} \left[ [K] - \varOmega ^2 [M]\right] \left\{ W\right\} = \left\{ 0\right\} \end{aligned}$$

(13)

For non-trivial solution of Eq. (13), it is assumed that the determinant of coefficient matrix must be zero and it provides

$$\begin{aligned} \det ([K] - \varOmega ^2 [M]) = 0 \end{aligned}$$

(14)

and is referred to as the generalized eigenvalue problem. Consequently, natural frequencies are to be solved by incorporating various sets of classical boundary conditions.

3.2 Differential quadrature method

Analog to the governing equation for vibration of isotropic beams given by Shu and Du [25], free vibration of Euler–Bernoulli functionally graded beam can be governed by

$$\begin{aligned} \left\{ \int _A z^2 E(z) \mathrm {d}A \right\} \frac{\partial ^4 w}{\partial x^4} + \left\{ \int _A \rho (z) \mathrm {d}A \right\} \frac{\partial ^2 w}{\partial t^2} = 0. \end{aligned}$$

(15)

The material properties E(z) and $\rho (z)$ are the Young’s moduli and mass densities of FG material constituents, which are assumed to vary along thickness direction in power-law form (as stated in Eq. 1). By considering the non-dimensional parameters are $-\frac{1}{2} \le \xi = x/L \le \frac{1}{2}$ and $-\frac{1}{2} \le \bar{z} = z/h \le \frac{1}{2}$, Eq. (15) yields

$$\begin{aligned} \frac{\widetilde{E}I}{L^4} \frac{\partial ^4 w}{\partial \xi ^4} + \widetilde{\rho } A \frac{\partial ^2 w}{\partial t^2} = 0 \end{aligned}$$

(16)

Here, $\widetilde{E} = \frac{E_m}{1-\nu ^2}\left\{ 1 + 12\left( E_r - 1\right) \left( \frac{1}{\mathrm {k}+3} - \frac{1}{\mathrm {k}+2} + \frac{1}{4\left( \mathrm {k}+1\right) } \right) \right\}$ and $\widetilde{\rho } = \rho _m \left\{ 1 + \left( \frac{\rho _r - 1}{\mathrm {k}+1}\right) \right\}$. Introducing the harmonic type displacement as $w(\xi ,t) = W(\xi ) \exp (\text {i}\omega t)$, where W(x) are the amplitude in displacement component and $\omega$ is the natural frequency. Next Eq. (16) transforms into

$$\begin{aligned} \overline{E} \frac{d^4 W}{d \xi ^4} - \varOmega ^2 \overline{\rho } W = 0 \end{aligned}$$

(17)

where $\overline{E} = \frac{1}{1-\nu ^2}\left\{ 1 + 12\left( E_r - 1\right) \left( \frac{1}{\mathrm {k}+3} - \frac{1}{\mathrm {k}+2} + \frac{1}{4\left( \mathrm {k}+1\right) } \right) \right\}$; $\overline{\rho } = \left\{ 1 + \left( \frac{\rho _r - 1}{\mathrm {k}+1}\right) \right\}$ and $\varOmega ^2 = \frac{\omega ^2 L^4 \rho _m A}{E_m I}$.

In present discussion, the power-law variations of E and $\rho$ are to be controlled by the components $E_r$ and $\rho _r$ respectively. Moreover, $\mathrm {k}$ also plays major role in evaluating both these material properties. In addition while assuming GDQ procedure, Bellman et al. [19] have assumed a sufficiently smooth function f(x) over the interval [a, b], so that its first derivative $f_{x}^{(1)}(x)$ at any grid point over [a, b] can be approximated by the following approximation

$$\begin{aligned} f_{x}^{(1)}(x_i) \cong \sum _{j = 1}^{N} c_{ij}^{(1)}f(x_j),~~~ i = 1, 2, \ldots , N \end{aligned}$$

(18)

with the coefficient matrix $(c_{ij}^{(1)})$ can be determined in various fashions. $f_{x}^{(1)}(x_i)$ finds the first order derivative of f(x) with respect to x at $x_i$. Necessarily, the key procedure in this method is to compute the weighting coefficients $c_{ij}^{(1)}$. By demanding Eq. (18) to be exact for all polynomials of degree less than or equal to $N-1$. Different approaches towards finding the weighting coefficients are mentioned below:

• 1. In first approach by Bellman et al. [19], the test functions $g_k(x) = x^{k-1};~k = 1, 2, \ldots , N$, which gives a set of linear algebraic equations

  $$\begin{aligned}&\sum _{j = 1}^{N} c_{ij}^{(1)}x_j^{k} = k x_i^{k-1},~~ i = 1, 2, \ldots , N;\\&\quad k = 0, 1, \ldots , N-1. \end{aligned}$$

  As the matrix is of Vandermonde form, this system of equations has a unique solution. But unfortunately, the concerned matrix becomes ill-conditioned and its inversion is difficult when N is very large.

• 2. On the other hand, the second approach by Bellman et al. [19] defines the test function as $g_k(x) = \frac{L_N(x)}{(x-x_k)L_N^{(1)}(x_k)};~k = 1, 2, \ldots , N$, where $L_N(x)$ is the $N{\mathrm{th}}$ order Legendre polynomial and $L_N^{(1)}(x)$ is the first order derivative of $L_N(x)$. In this approach, the necessary condition is that the coordinates of grid points should be the roots of an $N{\mathrm{th}}$ order Legendre polynomial.

• 3. To overcome such ambiguities of DQM, the generalized differential quadrature (GDQ) approach has been developed by Shu and Du [25] for the determination of weighting coefficients.

3.2.1 Weighting coefficients of first order derivative [25]

In view of the above, Shu and Du [25] has taken the benefit of two approaches of Bellman et al. [19] and approach of Quang and Cheng [22, 23] to derive the test functions in GDQ and kept no restrictions in deciding the grid points over the domain. For generality, GDQ chooses the base polynomials (or test functions) $g_k(x)$ to be the Lagrange interpolating polynomial

$$\begin{aligned} g_k(x) = \frac{M(x)}{(x-x_k)M^{(1)}(x_k)} \end{aligned}$$

(19)

where $M(x) = \prod _{j = 1}^{N} (x-x_j)$; $M^{(1)}(x) = \prod _{j = 1, j \ne k}^{N} (x_k-x_j)$ with $x_1, x_2, \ldots , x_N$ are the coordinates of the grid points and may be chosen arbitrarily. For simplicity, it is considered that

$$\begin{aligned} M(x) = N(x,x_k)(x-x_k),~k = 1, 2, \ldots , N \end{aligned}$$

with $N(x_i,x_j) = M^{(1)}(x_i) \delta _{ij}$, where $\delta _{ij}$ is the Kronecker operator. With these assumptions, Eq. (19) converts to

$$\begin{aligned} g_k(x) = \frac{N(x,x_k)}{M^{(1)}(x_k)} \end{aligned}$$

(20)

By substituting Eq. (20) into Eq. (18), we obtain

$$\begin{aligned} c_{ij}^{(1)} = \frac{N^{(1)}(x_i,x_j)}{M^{(1)}(x_j)} \end{aligned}$$

(21)

We can easily find $M^{(1)}(x_j)$ by using its concerned expression. To evaluate $N^{(1)}(x_i,x_j)$, let us differentiate M(x) successively with respect to x and we obtain the following recurrence formulation

$$\begin{aligned} M^{(m)}(x) = N^{(m)}(x,x_k) (x-x_k) + m N^{(m-1)}(x,x_k) \end{aligned}$$

(22)

where $k = 1, 2, \ldots , N$; $m = 1, 2, \ldots , N-1$; $M^{(m)}(x)$ and $N^{(m)}(x,x_k)$ are the $m^{\text {th}}$ order derivatives of M(x) and $N(x,x_k)$ respectively. The expression of $N^{(1)}(x_i,x_j)$ can be obtained from Eq. (22) as $N^{(1)}(x_i,x_j) = {\left\{ \begin{array}{ll} \frac{M^{(1)}(x_i)}{x_i - x_j};~ i \ne j \\ \frac{M^{(2)(x_i)}}{2};~ i = j \end{array}\right. }$. Substituting this expression in Eq. (21), we get

$$\begin{aligned} c_{ij}^{(1)} = {\left\{ \begin{array}{ll} \frac{M^{(1)}(x_i)}{(x_i - x_j)M^{(1)}(x_j)};~ i \ne j \\ \frac{M^{(2)(x_i)}}{2M^{(1)}(x_i)};~ i = j \end{array}\right. } \end{aligned}$$

(23)

Equation (23) is a simple expression for the computation of $c_{ij}^{(1)}$ without the restriction of choosing grid points $x_i$. Rather than evaluating $M^{(2)}(x_i)$, it is worth to mention that one set of base polynomials can be derived uniquely by linear combination of another set of base polynomials in a vector space. Moreover, $c_{ij}^{(1)}$ satisfies the relation; $\sum _{j = 1}^{N} c_{ij}^{(1)} = 0$ which may be obtained by the base polynomials $x^{k-1}$ when $k = 1$. Here, $c_{ii}^{(1)}$ can easily be determined from $c_{ij}^{(1)},~ i \ne j$.

3.2.2 Weighting coefficients of second and higher order derivatives [25]

The second and higher order derivatives of the smooth function f(x) may be written with the linear constrained relationships as follows:

$$\begin{aligned} f_{x}^{(m)}(x_i) \cong \sum _{j = 1}^{N} c_{ij}^{(m)}f(x_j),~~~ i = 1, 2, \ldots , N \end{aligned}$$

(24)

Then, the $(m-1){\mathrm{th}}$ order derivatives can be expressed as

$$\begin{aligned} f_{x}^{(m-1)}(x_i) \cong \sum _{j = 1}^{N} c_{ij}^{(m-1)}f(x_j),~~~ i = 1, 2, \ldots , N \end{aligned}$$

(25)

Now let us substitute Eq. (20) into Eqs. (24) and (25) and using Eqs. (22) and (23), a recurrence relation may be written as below:

$$\begin{aligned}&c_{ij}^{(m)} = {\left\{ \begin{array}{ll} m \left( c_{ij}^{(1)}c_{ii}^{(m-1)} - \frac{c_{ij}^{(m-1)}}{x_i - x_j} \right) ;~ i \ne j \\ \frac{M^{(m+1)}(x_i)}{(m+1)M^{(1)}(x_i)};~ i = j \end{array}\right. }\nonumber \\&\qquad \qquad \hbox {for }i,\,j = 1, 2,\ldots , N; m = 2, 3,\ldots , N-1 \end{aligned}$$

(26)

In $N-$dimensional vector space, the system of equations for $c_{ij}^{(m)}$ derived from Lagrange interpolating polynomials should also be equivalent to that derived from the base polynomials $x^{k-1},~ k = 1, 2, \ldots , N$. As discussed for the weighting coefficients of first order derivatives, the weighting coefficients of higher order derivatives also follow the equation $\sum _{j = 1}^{N} c_{ij}^{(m)} = 0$ obtained from the base polynomials $x^{k-1}$ when $k = 1$, i.e. $c_{ii}^{(m)} = \sum _{j = 1, i \ne j}^{N} c_{ij}^{(m)}$.

3.2.3 Discretization of governing equation

The non-homogeneous grid points in case of DQM are to be considered as Chebyshev–Gauss–Lobatto points in axial direction [25]. The governing equation (Eq. 17) for free vibration of FG beam can be transformed into the following expression by substituting the weighting coefficients of required derivatives,

$$\begin{aligned} \overline{E} \sum _{j = 1}^{N} c_{ij}^{(4)}W(\xi _j) - \varOmega ^2 \overline{\rho } W(\xi _i) = 0;~~~ i = 1, 2, \ldots , N \end{aligned}$$

(27)

Moreover, the classical boundary supports given in Eq. (5) may be defined as

$$\begin{aligned} \begin{aligned}&\text {Clamped (C):}~~ w_{\zeta } = 0;~ \sum _{j = 1}^{N} c_{\zeta ,j}^{(1)}W(\xi _j) = 0 \\&\text {Simply supported (S):}~~ w_{\zeta } = 0;~ \sum _{j = 1}^{N} c_{\zeta ,j}^{(2)}W(\xi _j) = 0 \\&\text {Free (F):}~~ \sum _{j = 1}^{N} c_{\zeta ,j}^{(2)}W(\xi _j) = 0;~ \sum _{j = 1}^{N} c_{\zeta ,j}^{(3)}W(\xi _j) = 0 \end{aligned}\nonumber \\ \end{aligned}$$

(28)

with $\zeta =$ 1 or N (the edges of FG beam). Now, the discretized governing equation of Eq. (27) may be modified to by using the method of modification of involved weighting coefficient matrices. We have given a simple illustration of modifying weighting coefficient matrix for clamped edge at $\xi = 0$ as mentioned below:

$$\begin{aligned} \begin{Bmatrix} w^{'}_1 \\ w^{'}_2 \\ \vdots \\ w^{'}_{N-1} \\ w^{'}_N \end{Bmatrix}&= \begin{pmatrix} c_{1,1}^{(1)} &{} c_{1,2}^{(1)} &{} \ldots &{} c_{1,N-1}^{(1)} &{} c_{1,N}^{(1)} \\ c_{2,1}^{(1)} &{} c_{2,2}^{(1)} &{} \ldots &{} c_{2,N-1}^{(1)} &{} c_{2,N}^{(1)} \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ c_{N-1,1}^{(1)} &{} c_{N-1,2}^{(1)} &{} \ldots &{} c_{N-1,N-1}^{(1)} &{} c_{N-1,N}^{(1)} \\ c_{N,1}^{(1)} &{} c_{N,2}^{(1)} &{} \ldots &{} c_{N,N-1}^{(1)} &{} c_{N,N}^{(1)} \end{pmatrix}\nonumber \\&\quad \begin{Bmatrix} w_1 \\ w_2 \\ \vdots \\ w_{N-1} \\ w_N \end{Bmatrix} = [C^{(1)}] \left\{ w_{j}\right\} \end{aligned}$$

(29)

The modification of weighting coefficient matrix involved in Eq. (29) occurs by considering $w_1 = 0$ and $w^{'}_1 = 0$ at $\xi = 0$ and takes the form

$$\begin{aligned}&\begin{Bmatrix} w^{'}_1 \\ w^{'}_2 \\ \vdots \\ w^{'}_{N-1} \\ w^{'}_N \end{Bmatrix} = \begin{pmatrix} 0 &{} 0 &{} \ldots &{} 0 &{} 0 \\ 0 &{} c_{2,2}^{(1)} &{} \ldots &{} c_{2,N-1}^{(1)} &{} c_{2,N}^{(1)} \\ \vdots &{} \vdots &{} \vdots &{} \vdots &{} \vdots \\ 0 &{} c_{N-1,2}^{(1)} &{} \ldots &{} c_{N-1,N-1}^{(1)} &{} c_{N-1,N}^{(1)} \\ 0 &{} c_{N,2}^{(1)} &{} \ldots &{} c_{N,N-1}^{(1)} &{} c_{N,N}^{(1)} \end{pmatrix}\nonumber \\&\quad \begin{Bmatrix} w_1 \\ w_2 \\ \vdots \\ w_{N-1} \\ w_N \end{Bmatrix} = [\widetilde{C}^{(1)}] \left\{ w_{j}\right\} \end{aligned}$$

(30)

In Eq. (30), $[\widetilde{C}^{(1)}]$ is the modified weighting coefficient matrix for FG beam with clamped edge at $\xi = 0$. With the usual DQ analog, the higher ($N{\mathrm{th}}$) order weighting coefficient matrix can be developed from $[\widetilde{C}^{(N)}] = [\widetilde{C}^{(N-1)}][C^{(1)}]$ by incorporating different sets of edge conditions. Further, the modified matrices are to be substituted in Eq. (27) to get the natural frequencies and mode shapes for free vibration of functionally graded beam.

3.3 Rayleigh–Ritz method

Finally, Rayleigh–Ritz method has also been implemented in present investigation. Using the constitutive relation of Eq. (4), the strain energy S and the kinetic energy T of the beam at any instant in cartesian co-ordinates may be written as

$$\begin{aligned} S= & {} \frac{1}{2}\int _{0}^{L} \!\int _A \!\left( \sigma _{xx}\varepsilon _{xx} + \tau _{xz}\gamma _{xz}\right) \mathrm {d}A \,\mathrm {d}x \end{aligned}$$

(31)

$$\begin{aligned} T= & {} \frac{1}{2}\int _{0}^{L} \!\int _A \!\rho (z)\left( \frac{\partial w}{\partial t}\right) ^{2} \mathrm {d}A \,\mathrm {d}x \end{aligned}$$

(32)

where A and $\rho$ are the area of cross-section and the mass density of the beam respectively. In Euler–Bernoulli beam theory, Eqs. (31) and (32) become

$$\begin{aligned} S= & {} \frac{1}{2}\int _{0}^{L} D_{z}w_{,xx}^{2}\,\mathrm {d}x \end{aligned}$$

(33)

$$\begin{aligned} T= & {} \frac{1}{2}\int _{0}^{L} I_{z}\left( \frac{\partial w}{\partial t}\right) ^{2}\,\mathrm {d}x \end{aligned}$$

(34)

The stiffness and inertial coefficients appearing in Eqs. (33) and (34) are defined as

$$\begin{aligned} \begin{aligned}&D_{z} = \int _{-h/2}^{h/2} \! Q_{11} z^2\,\mathrm {d}z \\&I_{z} = \int _{-h/2}^{h/2} \! \rho (z) \,\mathrm {d}z \end{aligned} \end{aligned}$$

(35)

Assuming harmonic type transverse deflection $w(x,t) = W(x)\sin {\omega t}$ with W(x) and $\omega$ as respective amplitude and natural frequency of the beam. Incorporating harmonic displacement and the non-dimensionalized length parameter $0 \le \xi = x/L \le 1$ in Eqs. (33) and (34) yield the maximum strain energy ($S_{max}$) and the maximum kinetic energy ($T_{max}$) as

$$\begin{aligned} S_{max}= & {} \frac{\overline{D}_{z}E_m}{2L^4}\int _{0}^{1} D_{z}W_{,xx}^{2}\,\mathrm {d}\xi \end{aligned}$$

(36)

$$\begin{aligned} T_{max}= & {} \frac{\omega ^2}{2}\int _{0}^{1} I_{z} W^{2}\,\mathrm {d}\xi \end{aligned}$$

(37)

Next the amplitude of vibration are expanded in terms of algebraic polynomial functions by the following series

$$\begin{aligned} W = \sum \limits _{i=1}^n c_{i}\phi _{i} \end{aligned}$$

where $c_{i}$ are the unknown constant coefficients to be determined and $\phi _{i}$ are the admissible functions, which must satisfy the essential boundary conditions and can be represented as [49]

$$\begin{aligned} \phi _{i} = fx^{i-1},\;\;\; i = 1,2,\ldots ,n. \end{aligned}$$

Here, n is the number of polynomials involved in the admissible functions and $f = x^{p}\left( x - 1\right) ^{q}$ where $p,\,q = 0,1\;\text {or}\;2$ may be expressed as per different sets of classical boundary conditions (BCs). The parameter $p =$ 0, 1 or 2 according as the side $x =~0$ is free (F), simply supported (S) or clamped (C). Similar interpretation can be given to the parameter q corresponding to the sides $x =~1$. Furthermore, Rayleigh Quotient ($\omega ^2$) can be obtained by equating $S_{max}$ and $T_{max}$. Taking partial derivative of the Rayleigh Quotient with respect to the constant coefficients involved in the admissible functions as follows

$$\begin{aligned} \frac{\partial \omega ^2}{\partial c_{i}} = 0;~~i = 1,2,\ldots ,n \end{aligned}$$

which results in the governing equation for the free vibration of FG beam in the form of generalized eigenvalue problem as mentioned below

$$\begin{aligned} \left( \mathbf {K}-\varOmega ^{2}\mathbf {M}\right) \left\{ \Delta \right\} = 0 \end{aligned}$$

(38)

where $\mathbf {K}$ and $\mathbf {M}$ are the stiffness and inertia matrices respectively and $\left\{ \Delta \right\}$ is the column vector of unknown coefficients. The eigenvalues ($\varOmega$) for the above eigenvalue problem (Eq. 38) are non-dimensional frequencies for the concerned vibration problem. The non-dimensional frequency ($\varOmega$) evaluated in all above mentioned methods takes the expression $\varOmega = \omega L^2 \sqrt{\frac{\rho _m A}{E_m I}}$. In subsequent sections, present study involves the evaluation of these frequencies after the test of convergence and validation with existing results.

Table 1 Convergence and comparison of six lowest natural frequencies of isotropic beam ($E_r = \rho _r = 1$) using finite element method

Table 2 Convergence and comparison of six lowest natural frequencies of isotropic beam ($E_r = \rho _r = 1$) using differential quadrature method

Table 3 Convergence and comparison of six lowest natural frequencies of isotropic beam ($E_r = \rho _r = 1$) using RRM

Table 4 Convergence and comparison of six lowest natural frequencies of S-S FG beam using finite element method

Table 5 Convergence and comparison of six lowest natural frequencies of S-S FG beam using differential quadrature method

Table 6 Convergence and comparison of six lowest natural frequencies of S-S FG beam using RRM

4 Convergence and validation studies

This section involves the test of convergence of natural frequencies in Tables 1, 2, 3, 4, 5 and 6 along with comparison with previously obtained results. The significant facts associated with convergence and validation studies may be summarized as given below:

• The convergence of six lowest natural frequencies of isotropic ($\mathrm {k}$ is taken as nullity) and FG beams are carried out in Tables 1, 2, 3, 4, 5 and 6 by means of the above discussed numerical techniques with reference to their corresponding parameters. The methods of finite element and differential quadrature assume such parameter to be the number of discretized elements (discretization of domain), whereas Rayleigh–Ritz method will certainly take the number of polynomials involved in transverse displacement respectively.

• The FEM is implemented in Tables 1 and 4, whereas DQM is considered in Tables 2 and 5 and RRM in Tables 3 and 6 respectively. Moreover, discretization of element domain in FEM and DQM are the non-homogeneous grids based on Gauss–Chebyshev–Lobatto points as assumed by Shu and Du [25].

• Assuming the isotropic beam $(E_r = \rho _r = 1)$, first six non-dimensional frequencies are evaluated in Tables 1, 2 and 3 using the formulation $\left( \varOmega = \omega L^2 \sqrt{\frac{\rho _m A}{E_m I}}\right)$ and are validated with Öz [2], Shu and Du [25], Abrate [38] and Ece et al. [41]. It can be observed that present results are in excellent agreement with existing literature.

• In a similar fashion, first six eigenfrequencies of FG beam with the formulation $\varOmega ^2 \left( = \omega L^2 \sqrt{\frac{\rho _m A}{E_m I}}\right)$ have been computed in Tables 4, 5 and 6 with $E_r =$0.5, 2.0 and $\mathrm {k} =$ 0, 0.1, 2.0 and constant mass density and compared with Şimşek and Kocaturk [6] and Alshorbagy et al. [7]. One can easily see a good agreement also in these computations.

• The effect of slenderness (length-to-thickness) ratio is redundant in case of Euler–Bernoulli beam as it doesn’t even occur in the formulation. As such, three lowest natural frequencies of S-S FG beam mentioned in [6, 7] have been validated in Tables 4, 5 and 6 corresponding to the largest slenderness ratio ($L/h = 100$ or very thin FG beam).

• It is interesting to note that the results found using all three numerical techniques are nearly same, but the convergence is faster in RRM with desired accuracies.

• It is also evident that natural frequencies in case of FG beam are increasing with increase in $\mathrm {k}$ for $E_r < 1$ and follow descending pattern with increase in $\mathrm {k}$ while considering $E_r > 1$.

5 Numerical results

In view of the test of convergence and validation, it is worth evaluating the first six non-dimensional frequencies of FG beams having different constituents. The three different FG beam constituents (Al/Al$_{2}$O$_{3}$, Al/ZrO$_2$ and SUS304/Si$_3$N$_4$) have been considered in Tables 7, 8, 9, 10, 11 and 12 to find their corresponding results and their material properties are reported as follows.

Al/Al$_{2}$O$_{3}$: $E_{m}$ = 70 GPa, $\rho _{m}$ = 2702 kg/m$^{3}$, $E_{c}$ = 380 GPa, $\rho _{c}$ = 3960 kg/m$^{3}$ and $\nu _m$ = $\nu _c$ = 0.3.

Al/ZrO$_2$: $E_{m}$ = 70 GPa, $\rho _{m}$ = 2700 kg/m$^{3}$, $E_{c}$ = 200 GPa, $\rho _{c}$ = 5700 kg/m$^{3}$ and $\nu _m$ = $\nu _c$ = 0.3.

SUS304/Si$_3$N$_4$: $E_{m}$ = 208 GPa, $\rho _{m}$ = 8166 kg/m$^{3}$, $E_{c}$ = 322 GPa, $\rho _{c}$ = 2370 kg/m$^{3}$ and $\nu _m$ = $\nu _c$ = 0.3.

The mathematical expression for the natural frequency in these computation is $\varOmega = \frac{\omega L^2}{h} \sqrt{\frac{\rho _m}{E_m}}$. In Tables 7, 8, 9, 10, 11 and 12, the effect of power-law indices ($\mathrm {k}$) on first six natural frequencies of different FG beams under four sets of classical edge supports have been found using all three numerical techniques. Looking into these tabulations, one may easily summarize the following facts:

• In terms of beam constituents, Al/Al$_{2}$O$_{3}$ FG beam is considered in Tables 7 and 8, Al/ZrO$_2$ constituents in Tables 9 and 10 and SUS304/Si$_3$N$_4$ is assumed in Tables 11 and 12 respectively. Prior to boundary conditions, Tables 7, 9 and 11 considers C-C and C-S edge support based FG beams, whereas Tables 8, 10 and 12 assumes the FG beam under cantilever and S-S edge conditions respectively.

• It may be observed that present results follow descending pattern with increase in power-law indices ($\mathrm {k}$) in case of Al/Al$_{2}$O$_{3}$ and SUS304/Si$_3$N$_4$ beams, whereas a few ambiguities can be seen in Al/ZrO$_2$ FG beam.

• Among all the classical edge conditions, natural frequencies in all modes of C-C FG beams are always the highest and the least in case of cantilever FG beams.

• In FEM and DQM, 20 element discretizations of domain is being taken for evaluations. On the other hand, 15 number of polynomials involved in transverse displacement have been assumed in RRM. One may easily say that RRM is more efficient than FEM and DQM in terms of convergence criterion, but the computed results at each mode are approximately close to each other.

Table 7 Effect of power-law exponents ($\mathrm {k}$) on Al/Al$_{2}$O$_{3}$ FG beam under C-C and C-S edge supports using all the assumed methods

Table 8 Effect of power-law exponents ($\mathrm {k}$) on Al/Al$_{2}$O$_{3}$ FG beam under cantilever and S-S edge supports using all the assumed methods

Table 9 Effect of power-law exponents ($\mathrm {k}$) on Al/ZrO$_2$ FG beam under C-C and C-S edge supports using all the assumed methods

Table 10 Effect of power-law exponents ($\mathrm {k}$) on Al/ZrO$_2$ FG beam under cantilever and S-S edge supports using all the assumed methods

Table 11 Effect of power-law exponents ($\mathrm {k}$) on SUS304/Si$_3$N$_4$ FG beam under C-C and C-S edge supports using all the assumed methods

Table 12 Effect of power-law exponents ($\mathrm {k}$) on SUS304/Si$_3$N$_4$ FG beam under cantilever and S-S edge supports using all the assumed methods

In particular, the eigenvectors corresponding to the natural frequencies of FG beam depicts the mode shapes of the continuous beam domain. In this part, first six two-dimensional (2-D) mode shapes associated with six lowest natural frequencies of SUS304/Si$_3$N$_4$ FG beam ($\mathrm {k} = 10$) under different boundary conditions have been demonstrated in Figs. 2, 3, 4 and 5. Moreover, Fig. 2 considers for C-C based FG beam. Similarly, Figs. 3, 4 and 5 are meant for the beam under C-S, cantilever and S-S edge conditions respectively. In view of these, one can easily depict six mode shapes for any given volume fraction of FG constituents.

Fig. 2

First six 2-D mode shapes of SUS304/Si$_3$N$_4$ C-C FG beam with $\mathrm {k} = 10$

Fig. 3

First six 2-D mode shapes of SUS304/Si$_3$N$_4$ C-S FG beam with $\mathrm {k} = 10$

Fig. 4

First six 2-D mode shapes of SUS304/Si$_3$N$_4$ cantilever FG beam with $\mathrm {k} = 10$

Fig. 5

First six 2-D mode shapes of SUS304/Si$_3$N$_4$ S-S FG beam with $\mathrm {k} = 10$

6 Concluding remarks

The present investigation is associated with free vibration of Euler–Bernoulli functionally graded beams based on finite element, differential quadrature and Rayleigh–Ritz methods. A brief review on related investigations on these methods in handling FG structural problems have also been discussed in detail. Afterwards, a detailed formulations of the given methods to solve the titled problem are clearly organized. Three different FG materials viz. Al/Al$_{2}$O$_{3}$, Al/ZrO$_2$ and SUS304/Si$_3$N$_4$ are considered to denote the beam constituents. Based on the estimated results, following significant facts may be summarized.

• Effect of slenderness (length-to-thickness) ratio is redundant in case of Euler–Bernoulli beam as it doesn’t even occur in the formulation.

• It is interesting to note that natural frequencies follow ascending pattern with increase in $\mathrm {k}$ in case of $E_r < 1$, whereas these may follow descending manner with increase in $\mathrm {k}$ while considering $E_r > 1$.

• One may observe that present results follow descending pattern with increase in power-law indices ($\mathrm {k}$) in case of Al/Al$_{2}$O$_{3}$ and SUS304/Si$_3$N$_4$ beams, whereas a few ambiguities can be seen in Al/ZrO$_2$ FG beam.

• Among all the classical edge conditions, natural frequencies in all modes of C-C FG beams are always the highest and the least in case of cantilever FG beams irrespective of the FG constituents considered.

• The convergence of natural frequencies is dependent on various factors with reference to the numerical method assumed. In FEM and DQM, the factor is discretization of beam domain, whereas it is number of polynomials involved in transverse displacement in case of RRM. On contrary, RRM is basically implemented in linear dynamical systems, whereas FEM and DQM can handle both linear and non-linear problems with efficiency. It may be observed that the computed results using three numerical techniques are nearly same, but the convergence is faster in RRM with desired accuracies.