1 Introduction

In recent years there has been considerable interest in the study of fractional order control systems. Many results have been reported for stability analysis, controller design, frequency domain analysis and time domain analysis of fractional order control systems [1–3]. However, obtaining exact or accurate time responses, such as step and impulse responses, of control systems with fractional order transfer functions is a difficult problem, since the analytical solution of the inverse Laplace transform is not possible and there is not a general method for estimating it. Generally some of the methods used for time response analysis are based on integer approximation models which replace the fractional derivative term \(s^{\alpha }, \alpha \in R\) by an approximate integer order transfer function and others are based on numerical approximation of the non-integer order operator such as the Grünwald–Letnikov (GL) approximation [4–9]. There are also some methods based on Mittag-Leffler and Gamma functions for computation of the impulse and step responses of commensurate-order systems [10, 11]. In a recent paper by the authors [12] two exact methods were given for the computation of step and impulse responses of fractional order transfer functions (FOTF). One method called the Fourier Series Method (FSM) uses the Fourier series of a low frequency square wave as the input to a FOTF to compute its step and impulse responses. The other method called the Inverse Fourier Transform Method (IFTM) is based on the inverse Fourier transform. The results obtained from these methods are exact since frequency domain data of fractional order transfer functions, which can be computed exactly, have been used.

To analyse many physical systems a closed loop with a time delay needs to be considered which was not discussed in reference [12], although some provisional results were presented in the conference paper of reference [13]. It is well known that the presence of a time delay makes the computation of time responses for systems with transfer functions more complicated, and approximate results, obtained by replacing the time delay by a Pade approximation, are often used. However, since frequency domain data for a time delay can be obtained exactly the FSM and IFTM can be used for exact step and impulse response computations of FOTF systems with time delay. These methods are presented in this paper. Thus, in this paper, we propose exact methods for the computation of step and impulse responses of a feedback control structure including a plant with time delay and a fractional order controller. The time response equations which depend on the frequency response data of the controller and plant within the closed loop control system are derived. Since the results obtained in the paper use the frequency response data such as gain and phase values at each frequency, the time response computations of the closed loop time delay system are accurate and provide useful solutions for fractional order control design.

The paper is organized as follows: in Sect. 2, an introduction to FOTF with time delay is given. The exact methods using FSM and IFTM for computation of step and impulse responses of closed loop fractional order control systems with time delay are given in Sect. 3, together with Examples to show the importance of the methods. Concluding remarks are given in Sect. 4.

2 Fractional order transfer functions with time delay

Fractional order calculus is a generalization of the ordinary differentiations by non-integer derivatives. Many mathematicians like Liouville and Riemann contributed to the field of fractional calculus. There are different definitions of fractional order operators such as Grünwald–Letnikov, Riemann–Lioville and Caputo [10]. In recent years, fractional calculus has been an important tool to be used in engineering, chemistry, physical, mechanical and other sciences [14–18] since many real systems are known to display fractional order dynamics.

A fractional order control system with input z(t), output q(t) and time delay \(\theta \) can be described by a fractional order transfer function of the form,

$$\begin{aligned} G_p (s)= & {} G(s)e^{-\theta s}\nonumber \\= & {} \frac{Q(s)}{Z(s)}e^{-\theta s}\nonumber \\= & {} \frac{b_m s^{\beta _m }+b_{m-1} s^{\beta _{m-1} }+\cdot \cdot \cdot \cdot +b_0 s^{\beta _0 }}{a_n s^{\alpha _n }+a_{n-1} s^{\alpha _{n-1} }+\cdot \cdot \cdot \cdot +a_0 s^{\alpha _0 }}e^{-\theta s} \end{aligned}$$
(1)

where \(a_i \), \(b_j \) (\(i=0,1,2,\ldots ,n\) and \(j=0,1,2,\ldots ,m)\) are real parameters and \(\alpha _i \), \(\beta _j \) are real positive numbers with \(\alpha _0 <\alpha _1 <\cdot \cdot \cdot <\alpha _n \) and \(\beta _0 <\beta _1 <\cdot \cdot \cdot <\beta _m \). Thus, a transfer function including fractional powered s terms and time delay can be called a fractional order transfer function (FOTF) with time delay. One can obtain Bode, Nyquist and Nichols diagrams of Eq. (1) replacing s by \(j\omega \) and using \((j\omega )^{\alpha }=\omega ^{\alpha }[\cos (\alpha \pi /2)+j\sin (\alpha \pi /2)]\). Therefore, the frequency response computation of FOTF or FOTF with time delay can be obtained similar to integer order transfer functions. However, for time domain computation no general analytical method is currently available, hence the FSM and IFTM introduced in the next section.

The block diagram of a closed loop fractional order control system with time delay is shown in Fig. 1.

Fig. 1
figure 1

A fractional order closed loop control system with time delay

Full size image

Here, \(L(s)=C(s)G_p (s)\) is the open loop transfer function which is in the form of Eq. (1) such as

$$\begin{aligned} L(s)= & {} C(s)G_p (s)\nonumber \\= & {} C(s)G(s)e^{-\theta s}\nonumber \\= & {} \frac{b_m s^{\beta _m }+b_{m-1} s^{\beta _{m-1} }+\cdot \cdot \cdot \cdot +b_0 s^{\beta _0 }}{a_n s^{\alpha _n }+a_{n-1} s^{\alpha _{n-1} }+\cdot \cdot \cdot \cdot +a_0 s^{\alpha _0 }}e^{-\theta s} \end{aligned}$$
(2)

Then the closed loop transfer function can be written as

$$\begin{aligned} P(s)= & {} \frac{Y(s)}{R(s)}\nonumber \\= & {} \frac{L(s)}{1+L(s)}\nonumber \\= & {} \frac{(b_m s^{\beta _m }+b_{m-1} s^{\beta _{m-1} }+\cdot \cdot \cdot \cdot +b_0 s^{\beta _0 })e^{-\theta s}}{a_n s^{\alpha _n }+a_{n-1} s^{\alpha _{n-1} }+\cdot \cdot \cdot \cdot +a_0 s^{\alpha _0 }+(b_m s^{\beta _m }+b_{m-1} s^{\beta _{m-1} }+\cdot \cdot \cdot \cdot +b_0 s^{\beta _0 })e^{-\theta s}} \end{aligned}$$
(3)

Letting

$$\begin{aligned} P(s)=\frac{Y(s)}{R(s)}=\frac{L(s)}{1+L(s)}=\frac{C(s)G_p (s)}{1+C(s)G_p (s)} \end{aligned}$$
(4)

and replacing s by \(j\omega \) in Eq. (4), one obtains

$$\begin{aligned} P(j\omega )= & {} \frac{Y(\omega )}{R(j\omega )}=\frac{C(j\omega )G_p (j\omega )}{1+C(j\omega )G_p (j\omega )}\nonumber \\= & {} \frac{(\hbox {Re}[C(j\omega )]+j\hbox {Im}[C(j\omega )])(\hbox {Re}[G_p (j\omega )]+j\hbox {Im}[G_p (j\omega )]}{1+(\hbox {Re}[C(j\omega )]+j\hbox {Im}[C(j\omega )])(\hbox {Re}[G_p (j\omega )]+j\hbox {Im}[G_p (j\omega )]}\nonumber \\= & {} \frac{U(\omega )+jV(\omega )}{Z(\omega )+jQ(\omega )} \end{aligned}$$
(5)

where

$$\begin{aligned} U(\omega )= & {} \hbox {Re}[C(j\omega )]\hbox {Re}[G_p (j\omega )] -\hbox {Im}[C(j\omega )] \hbox {Im}[G_p (j\omega )] \nonumber \\\end{aligned}$$
(6)
$$\begin{aligned} V(\omega )= & {} \hbox {Re}[C(j\omega )]\hbox {Im}[G_p (j\omega )] +\hbox {Im}[C(j\omega )]\hbox {Re}[G_p (j\omega )] \nonumber \\\end{aligned}$$
(7)
$$\begin{aligned} Z(\omega )= & {} 1+\hbox {Re}[C(j\omega )]\hbox {Re}[G_p (j\omega )]\nonumber \\&-\hbox {Im}[C(j\omega )]\hbox {Im}[G_p (j\omega )] \end{aligned}$$
(8)
$$\begin{aligned} Q(\omega )= & {} \hbox {Re}[C(j\omega )]\hbox {Im}[G_p (j\omega )]+\hbox {Im}[C(j\omega )]\hbox {Re}[G_p (j\omega )]\nonumber \\ \end{aligned}$$
(9)

and

$$\begin{aligned} \hbox {Re}[G_p (j\omega )]= & {} \hbox {Re}[G(j\omega )]\cos (\omega \theta )+\hbox {Im}[G(j\omega )]\sin (\omega \theta ) \nonumber \\\end{aligned}$$
(10)
$$\begin{aligned} \hbox {Im}[G_p (j\omega )]= & {} \hbox {Im}[G(j\omega )]\cos (\omega \theta ) -\hbox {Re}[G(j\omega )]\sin (\omega \theta ).\nonumber \\ \end{aligned}$$
(11)

Thus, \(P(j\omega )\) can be written as

$$\begin{aligned} P(j\omega )=\frac{[U(\omega )Z(\omega )+V(\omega )Q(\omega )]+j[V(\omega )Z(\omega )-U(\omega )Q(\omega )]}{Z(\omega )^{2}+Q(\omega )^{2}} \end{aligned}$$
(12)

so that the real part and imaginary parts of the closed loop transfer function \(P(j\omega )\) are

$$\begin{aligned} \hbox {Re}[P(j\omega )]= & {} \frac{[U(\omega )Z(\omega )+V(\omega )Q(\omega )]}{Z(\omega )^{2}+Q(\omega )^{2}} \end{aligned}$$
(13)
$$\begin{aligned} \hbox {Im}[P(j\omega )]= & {} \frac{[V(\omega )Z(\omega )-U(\omega )Q(\omega )]}{Z(\omega )^{2}+Q(\omega )^{2}} \end{aligned}$$
(14)

3 Step and impulse responses of closed loop fractional order time delay control systems

3.1 Fourier series method (FSM)

The method presented in [12] developed by the authors of this paper can be applied to the fractional order control system with time delay shown in Fig. 1. The Fourier series for a square wave of \(-\)1 to 1 with frequency \(\omega _s =2\pi /T\) can be written as

$$\begin{aligned} r(t)=\frac{4}{\pi }\sum _{k=1(2)}^\infty {\frac{1}{k}} \sin (k\omega _s t) \end{aligned}$$
(15)

where T is the period of the square wave. If r(t) passes through the transfer function P(s) then the output, which is the unit step response if T is sufficiently large, can be written as

$$\begin{aligned} y_s (t)\cong \frac{4}{\pi }\sum _{k=1(2)}^\infty {\frac{1}{k}} \hbox {Re}\left[ {P(jk\omega _s )} \right] \sin (k\omega _s t) \end{aligned}$$
(16)

The proof of this can be done using convolution. The following proof was given in [12] for a fractional order transfer function and it is extended here for fractional order closed loop control systems with time delay. Let \(p(t)=L^{-1}\left( {P(s)} \right) \) and using the convolution integral, the output can be written as

$$\begin{aligned} y(t)= & {} \mathop {\int }\limits _0^\infty p(\tau )r(t-\tau )d\tau \nonumber \\= & {} \mathop {\int }\limits _0^\infty {p(\tau )\left( {\frac{4}{\pi }\sum _{k=1(2)}^\infty {\frac{1}{k}} \sin (k\omega _s (t-\tau ))} \right) d\tau } \nonumber \\= & {} \frac{4}{\pi } \bigg ( \mathop {\int }\limits _0^\infty p(\tau )\sin (\omega _s (t-\tau )) d\tau \nonumber \\&+\frac{1}{3}\mathop {\int }\limits _0^\infty p(\tau )\sin (3\omega _s (t-\tau ))d\tau \nonumber \\&+\frac{1}{5}\mathop {\int }\limits _0^\infty p(\tau )\sin (5\omega _s (t-\tau ))d\tau +\cdot \cdot \cdot \cdot \cdot \bigg ) \nonumber \\= & {} \frac{4}{\pi }\left( {A_1 +A_2 +A_3 +\cdot \cdot \cdot \cdot \cdot } \right) \end{aligned}$$
(17)

If we consider the first integral

$$\begin{aligned} A_1= & {} \mathop {\int }\limits _0^\infty {p(\tau )\sin (\omega _s (t-\tau ))d \tau } \nonumber \\= & {} \frac{1}{2j}\mathop {\int }\limits _0^\infty {p(\tau )\left( e^{j\omega _s (t-\tau )}-e^{-j\omega _s (t-\tau )}\right) d\tau } \nonumber \\= & {} \frac{e^{j\omega _s t}}{2j}\mathop {\int }\limits _0^\infty {p(\tau )e^{-j\omega _s \tau }d\tau } -\frac{e^{-j\omega _s t}}{2j}\mathop {\int }\limits _0^\infty {p(\tau )e^{j\omega _s \tau }d\tau }\nonumber \\ \end{aligned}$$
(18)

from which

$$\begin{aligned} A_1= & {} \frac{e^{j\omega _s t}}{2j}P(j\omega _s )-\frac{e^{-j\omega _s t}}{2j}P(-j\omega _s ) \nonumber \\= & {} \left( {\frac{-j}{2}\cos (\omega _s t)+\frac{1}{2}\sin (\omega _s t)} \right) P( j\omega _s )\nonumber \\&+\left( {\frac{j}{2}\cos (\omega _s t)+\frac{1}{2}\sin (\omega _s t)} \right) P(-j\omega _s ) \end{aligned}$$
(19)

Since \(\hbox {Re }P(-j\omega _s )=\hbox {Re }P(j\omega _s )\) and \(\hbox {Im }P(-j\omega _s )=-\hbox {Im }P(j\omega _s )\), we can write

$$\begin{aligned} A_1 =\hbox {Re }P(j\omega _s )\sin (\omega _s t)+\hbox {Im }P(j\omega _s )\cos (\omega _s t) \end{aligned}$$
(20)

Thus, the step response can be written as

$$\begin{aligned} y_s (t)= & {} \frac{4}{\pi }\sum _{k=1(2)}^\infty \left( \frac{1}{k}\hbox {Re}\left[ P(jk\omega _s ) \right] \sin (k\omega _s t)\right. \nonumber \\&\left. +\frac{1}{k}\hbox {Im} [P(jk\omega _s )]\cos (k\omega _s t) \right) \end{aligned}$$
(21)

As \(T\rightarrow \infty \) and \(\omega _s \rightarrow 0\) the numerator of the imaginary part of \(P(jk\omega _s )\) is multiplied by \(\omega _s \) so that \(\lim _{\omega _s \rightarrow 0} \hbox {Im}[P(jk\omega _s )]=0\) and Eq. (21) becomes

$$\begin{aligned} y_s (t)\cong \frac{4}{\pi }\sum _{k=1(2)}^\infty {\frac{1}{k}\hbox {Re}\left[ {P(jk\omega _s )} \right] \sin (k\omega _s t)} \end{aligned}$$
(22)

which is the unit step response of P(s). Using Eq. (13), Eq. (22) can be written as

$$\begin{aligned} y_s (t)\cong & {} \frac{4}{\pi }\sum _{k=1(2)}^\infty {\frac{1}{k}\hbox {Re} \left[ {P(jk\omega _s )} \right] \sin (k\omega _s t)} \nonumber \\= & {} \frac{4}{\pi }\sum _{k=1(2)}^\infty \frac{1}{k}\frac{[U(k\omega _s )Z(k\omega _s )+V(k\omega _s )Q(k\omega _s )]}{[Z(k\omega _s )^{2}+Q(k\omega _s )^{2}]}\nonumber \\&\sin (k\omega _s t) \end{aligned}$$
(23)

Similarly, the impulse response, which is the derivative of the step response is given by

$$\begin{aligned} y_i (t)= & {} \frac{dy_s (t)}{dt}\nonumber \\= & {} \frac{4}{\pi }\sum _{k=1(2)}^\infty \left( \omega _s \hbox {Re}\left[ {P(jk\omega _s )} \right] \cos (k\omega _s t)\right. \nonumber \\&\left. -\omega _s \hbox {Im}[P(jk\omega _s )] \sin (k\omega _s t) \right) \nonumber \\\cong & {} \frac{4}{\pi }\sum _{k=1(2)}^\infty {\omega _s \hbox {Re} \left[ {P(jk\omega _s )} \right] \cos (k\omega _s t)} \nonumber \\= & {} \frac{4}{\pi }\sum _{k=1(2)}^\infty \omega _s \frac{[U(k\omega _s )Z(k\omega _s )+V(k\omega _s )Q(k\omega _s )]}{[Z(k\omega _s )^{2}+Q(k\omega _s )^{2}]}\nonumber \\&\cos (k\omega _s t) \end{aligned}$$
(24)

If the controller is a fractional order PID controller of the form

$$\begin{aligned} C(s)=K_p +\frac{K_i }{s^{\lambda }}+K_d s^{\mu } \end{aligned}$$
(25)

then the closed loop transfer function of the system can be written as

$$\begin{aligned} P(s)= & {} \frac{C(s)G_p (s)}{1+C(s)G_p (s)}\nonumber \\= & {} \frac{\left( K_p +\frac{K_i }{s^{\lambda }}+K_d s^{\mu }\right) G_p (s)}{1+\left( K_p +\frac{K_i }{s^{\lambda }}+K_d s^{\mu }\right) G_p (s)} \end{aligned}$$
(26)

In this equation, replacing s by \(j\omega \) and using \((j\omega )^{\lambda }=\omega ^{\lambda }[\cos (\lambda \pi /2)+j\sin (\lambda \pi /2)]\), \((j\omega )^{\mu }=\omega ^{\mu }[\cos (\mu \pi /2)+j\sin (\mu \pi /2)]\), one obtains the following equation

$$\begin{aligned} P(j\omega )= & {} \frac{\left( K_p +\frac{K_i }{(j\omega )^{\lambda }} +K_d (j\omega )^{\mu }\right) (\hbox {Re}[G_p (j\omega )] +j\hbox {Im}[G_p (j\omega )])}{1+\left( K_p +\frac{K_i }{(j\omega )^{\lambda }}+ K_d (j\omega )^{\mu }\right) (\hbox {Re}[G_p (j\omega )]+ j\hbox {Im}[G_p (j\omega )])}\nonumber \\= & {} \frac{U_{\textit{PID}} (\omega )+jV_{\textit{PID}} (\omega )}{Z_{\textit{PID}} (\omega ) +jQ_{\textit{PID}} (\omega )} \end{aligned}$$
(27)

where

$$\begin{aligned} U_{\textit{PID}} (\omega )= & {} \hbox {Re}[G_p (j\omega )] \left( K_p +K_i \cos \left( \lambda \frac{\pi }{2}\right) /\omega ^{\lambda }\right. \nonumber \\&\left. +\,K_d \omega ^{\mu }\cos \left( \mu \frac{\pi }{2}\right) \right) \nonumber \\&+\,\hbox {Im}[G_p (j\omega )]\left( K_i \sin \left( \lambda \frac{\pi }{2}\right) / \omega ^{\lambda }\right. \nonumber \\&\left. -\,K_d \omega ^{\mu }\sin \left( \mu \frac{\pi }{2}\right) \right) \end{aligned}$$
(28)
$$\begin{aligned} V_{\textit{PID}} (\omega )= & {} \hbox {Im}[G_p (j\omega )]\left( K_p +K_i \cos \left( \lambda \frac{\pi }{2}\right) /\omega ^{\lambda }\right. \nonumber \\&\left. +\,K_d \omega ^{\mu }\cos \left( \mu \frac{\pi }{2}\right) \right) \nonumber \\&+\,\hbox {Re}[G_p (j\omega )]\left( -K_i \sin \left( \lambda \frac{\pi }{2}\right) / \omega ^{\lambda }\right. \nonumber \\&\left. +\,K_d \omega ^{\mu }\sin \left( \mu \frac{\pi }{2}\right) \right) \end{aligned}$$
(29)
$$\begin{aligned} Z_{\textit{PID}} (\omega )= & {} 1+\hbox {Re}[G_p (j\omega )] \left( K_p +K_i \cos \left( \lambda \frac{\pi }{2}\right) / \omega ^{\lambda }\right. \nonumber \\&\left. +\,K_d \omega ^{\mu }\cos \left( \mu \frac{\pi }{2}\right) \right) \nonumber \\&+\,\hbox {Im}[G_p (j\omega )]\left( K_i \sin \left( \lambda \frac{\pi }{2}\right) /\omega ^{\lambda }\right. \nonumber \\&\left. -\,K_d \omega ^{\mu }\sin \left( \mu \frac{\pi }{2}\right) \right) \end{aligned}$$
(30)
$$\begin{aligned} Q_{\textit{PID}} (\omega )= & {} \hbox {Im}[G_p (j\omega )] \left( K_p +K_i \cos \left( \lambda \frac{\pi }{2}\right) / \omega ^{\lambda }\right. \nonumber \\&\left. +\,K_d \omega ^{\mu }\cos \left( \mu \frac{\pi }{2}\right) \right) \nonumber \\&+\,\hbox {Re}[G_p (j\omega )]\left( -K_i \sin \left( \lambda \frac{\pi }{2}\right) / \omega ^{\lambda }\right. \nonumber \\&\left. +\,K_d \omega ^{\mu }\sin \left( \mu \frac{\pi }{2}\right) \right) \end{aligned}$$
(31)

and \(\hbox {Re}[G_p (j\omega )]\) and \(\hbox {Im}[G_p (j\omega )]\) are given in Eqs. (10)–(11). Thus, the step and impulse responses of the closed loop system with fractional order PID controller of Eq. (25) can be written as

$$\begin{aligned} y_s (t)\cong & {} \frac{4}{\pi }\sum _{k=1(2)}^\infty \frac{1}{k}\nonumber \\&\frac{[U_{\textit{PID}} (k\omega _s )Z_{\textit{PID}} (k\omega _s )+V_{\textit{PID}} (k\omega _s )Q_{\textit{PID}} (k\omega _s )]}{[Z_{\textit{PID}} (k\omega _s )^{2}+Q_{\textit{PID}} (k\omega _s )^{2}]}\nonumber \\&\sin (k\omega _s t) \end{aligned}$$
(32)
$$\begin{aligned} y_i (t)= & {} \frac{dy_s (t)}{dt}\nonumber \\= & {} \frac{4}{\pi }\sum _{k=1(2)}^\infty \omega _s \nonumber \\&\frac{[U_{\textit{PID}} (k\omega _s )Z_{\textit{PID}} (k\omega _s )+V_{\textit{PID}} (k\omega _s )Q_{\textit{PID}} (k\omega _s )]}{[Z_{\textit{PID}} (k\omega _s )^{2}+Q_{\textit{PID}} (k\omega _s )^{2}]}\nonumber \\&\cos (k\omega _s t) \end{aligned}$$
(33)

If the controller is a fractional order lag or lead controller of the form

$$\begin{aligned} C(s)=K\frac{s^{\mu }+a}{s^{\mu }+b} \end{aligned}$$
(34)

then the closed loop transfer function can be written as

$$\begin{aligned} P(s)= & {} \frac{Y(s)}{R(s)}\nonumber \\= & {} \frac{C(s)G_p (s)}{1+C(s)G_p (s)}\nonumber \\= & {} \frac{K(s^{\mu }+a)G_p (s)}{(s^{\mu }+b)+K(s^{\mu }+a)G_p (s)}. \end{aligned}$$
(35)

Replacing s by \(j\omega \) and using \((j\omega )^{\mu }=\omega ^{\mu }[\cos (\mu \pi /2)+j\sin (\mu \pi /2)]\) then

$$\begin{aligned} P(j\omega )= & {} \frac{K((j\omega )^{\mu }+a)G_p (j\omega )}{((j\omega )^{\mu }+b)+K((j\omega )^{\mu }+a)G_p (j\omega )}\nonumber \\= & {} \frac{U_{\textit{LL}} (\omega )+jV_{\textit{LL}} (\omega )}{Z_{\textit{LL}} (\omega )+jQ_{\textit{LL}} (\omega )} \end{aligned}$$
(36)

where

$$\begin{aligned} U_{\textit{LL}} (\omega )= & {} \hbox {Re}[G_p (j\omega )]\left( K\omega ^{\mu }\cos \mu \frac{\pi }{2}+Ka\right) \nonumber \\&-\,\hbox {Im}[G_p (j\omega )]\left( K\omega ^{\mu }\sin \mu \frac{\pi }{2}\right) \end{aligned}$$
(37)
$$\begin{aligned} V_{\textit{LL}} (\omega )= & {} \hbox {Re}[G_p (j\omega )]\left( K\omega ^{\mu }\sin \mu \frac{\pi }{2}\right) \nonumber \\&+\,\hbox {Im}[G_p (j\omega )]\left( K\omega ^{\mu }\cos \mu \frac{\pi }{2}+Ka\right) \end{aligned}$$
(38)
$$\begin{aligned} Z_{\textit{LL}} (\omega )= & {} \omega ^{\mu }\cos \mu \frac{\pi }{2}+b\nonumber \\&+\,\hbox {Re}[G_p (j\omega )]\left( K\omega ^{\mu }\cos \mu \frac{\pi }{2}+Ka\right) \nonumber \\&-\,\hbox {Im}[G_p (j\omega )]\left( K\omega ^{\mu }\sin \mu \frac{\pi }{2}\right) \end{aligned}$$
(39)
$$\begin{aligned} Q_{\textit{LL}} (\omega )= & {} \omega ^{\mu }\sin \mu \frac{\pi }{2}+\hbox {Re}[G_p (j\omega )] \left( K\omega ^{\mu }\sin \mu \frac{\pi }{2}\right) \nonumber \\&+\,\hbox {Im}[G_p (j\omega )]\left( K\omega ^{\mu }\cos \mu \frac{\pi }{2}+Ka\right) \end{aligned}$$
(40)

Using these equations, the expressions for the step and impulse responses of the closed loop system from Fig. 1 with a fractional order lag or lead controller of the form of Eq. (34) are

$$\begin{aligned} y_s (t)\cong & {} \frac{4}{\pi }\sum _{k=1(2)}^\infty \frac{1}{k}\nonumber \\&\frac{[U_{\textit{LL}} (k\omega _s )Z_{\textit{LL}} (k\omega _s )+V_{\textit{LL}} (k\omega _s )Q_{\textit{LL}} (k\omega _s )]}{[Z_{\textit{LL}} (k\omega _s )^{2}+Q_{\textit{LL}} (k\omega _s )^{2}]}\nonumber \\&\sin (k\omega _s t) \end{aligned}$$
(41)
$$\begin{aligned} y_i (t)= & {} \frac{dy_s (t)}{dt}\nonumber \\= & {} \frac{4}{\pi }\sum _{k=1(2)}^\infty \omega _s \nonumber \\&\frac{[U_{\textit{LL}} (k\omega _s )Z_{\textit{LL}} (k\omega _s )+V_{\textit{LL}} (k\omega _s )Q_{\textit{LL}} (k\omega _s )]}{[Z_{\textit{LL}} (k\omega _s )^{2}+Q_{\textit{LL}} (k\omega _s )^{2}]}\nonumber \\&\cos (k\omega _s t) \end{aligned}$$
(42)
Fig. 2
figure 2

a Step responses b impulse responses

Full size image

Example 1

The aim of this example is to show the validity of the method by considering block diagram of the control system shown in Fig. 1 with integer order transfer functions for the controller and plant of

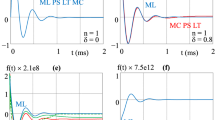
$$\begin{aligned} C(s)= & {} 0.771\left( 1+\frac{1}{16.310s}+4.077s\right) \hbox { and }\nonumber \\ G_p (s)= & {} \frac{1.2e^{-10s}}{(5s+1)(2.5s+1)} \end{aligned}$$
(43)

The step responses of the system obtained by Simulink and the FSM program are shown in Fig. 2a, where it can be seen that the results on this scale are identical. From the numerical data the error between the two plots was found to be less than \(10^{-4}\) at all the computed points. The impulse response was obtained using Matlab with a 10/10 degree Pade approximation for \(e^{-10s}\). This result together with that from the FSM are given in Fig. 2b, where it is seen that for small time values there are errors in the Matlab plot due to the Pade approximation used for the time delay in both the numerator and denominator of the closed loop transfer function.

Example 2

Consider the block diagram of the control system shown in Fig. 1 with

$$\begin{aligned} C(s)=1\hbox { and }G_p (s)=\frac{e^{-s}}{s^{0.8}} \end{aligned}$$
(44)

For this example the step responses of the closed loop control system are calculated from the FSM, Oustaloup, and Matsuda integer order approximations. Instead of replacing \(s^{0.8}\) with the equivalent integer order approximations of Outaloup and Matsuda approximation, we used \(\frac{s^{0.2}}{s}\) for the realization of the \(\frac{1}{s^{0.8}}\) in order to avoid steady state error. In order to obtain the step response of the system, the Simulink diagram of the closed loop system from Fig. 1 with \(C(s)=1\) and \(G_p (s)=\frac{s^{0.2}e^{-s}}{s}\) was set up. For \(e^{-s}\) the transport lag block of Simulink was used and for \(s^{0.2}\) the fourth and fifth order integer approximation transfer functions given in Eqs. (45) and (46), which are calculated from the Matsuda and Oustaloup methods respectively, and are given below, were used:-

$$\begin{aligned} s^{0.2}\cong & {} \frac{3.357s^{4}+161s^{3}+453.9s^{2}+95s+1}{s^{4}+95s^{3}+453.9s^{2}+161s+3.357} \end{aligned}$$
(45)
$$\begin{aligned} s^{0.2}\cong & {} \frac{2.512s^{5}+98.83s^{4}+531.7s^{3}+442.3s^{2}+56.87s+1}{s^{5}+56.87s^{4}+442.3s^{3}+531.7s^{2}+98.83s+2.512}\nonumber \\ \end{aligned}$$
(46)

The closed loop transfer function of the system for use in the FSM is

$$\begin{aligned} P(s)=\frac{L(s)}{1+L(s)}=\frac{C(s)G_p (s)}{1+C(s)G_p (s)}=\frac{e^{-s}}{s^{0.8}+e^{-s}} \end{aligned}$$
(47)

and the step response was then computed from Eq. (23). These step responses are shown in Fig. 3a where the differences between the plots can be seen more clearly on the zoomed figure. Also, the errors between the plots which use the Oustaloup and Matsuda approximations and the FSM are given in Fig. 3b where it can be concluded that the results have similar small errors. FSM is considered as the reference method in Fig. 3b.

Fig. 3
figure 3

a Step responses obtained from Matsuda 4th order, Oustaloup 5th order and FSM b Error plot between step responses obtained from Matsuda 4th order, Oustaloup 5th order and FSM

Full size image
Fig. 4
figure 4

a Step responses of \(L_{ous 5} (s)\), \(L_{ous7} (s)\) and actual system using FSM b error plots between 5th and 7th orders Oustaloup’s methods and the FSM

Full size image

Example 3

Consider Fig. 1 with

$$\begin{aligned} C(s)=1+\frac{1}{s^{0.9}}\hbox { and }G_p (s)=\frac{e^{-1.6s}}{s+2} \end{aligned}$$
(48)

then the open loop transfer function of the system is

$$\begin{aligned} L(s)=C(s)G_p (s)=\frac{s^{0.9}+1}{s^{1.9}+2s^{0.9}}e^{-1.6s} \end{aligned}$$
(49)

Here it will be shown that there is a steady state error to a step input when the fractional order derivative is replaced by an integer order approximation, and further a comparison with the Grünwald–Letnikov (GL) approximation method will be given. Oustaloup’s fifth and seventh order integer approximations for \(s^{0.9}\) are

$$\begin{aligned} s^{0.9}\cong & {} \frac{63.1s^{5}+1303s^{4}+3679s^{3}+1606s^{2}+108.4s+1}{s^{5}+108.4s^{4}+1606s^{3}+3679s^{2}+1303s+63.1} \end{aligned}$$
(50)
$$\begin{aligned} s^{0.9}\cong & {} \frac{63.1s^{7}+2470s^{6}+20450s^{5}+42940s^{4}+23750s^{3}+3462s^{2}+127.9s+1}{s^{7}+127.9s^{6}+3462s^{5}+23750s^{4}+42940s^{3}+20450s^{2}+2470s+63.1}\nonumber \\ \end{aligned}$$
(51)

Using these approximations in Eq. (49) give the two open loop transfer functions

$$\begin{aligned}&L_{ous5} (s)\nonumber \\&\quad =\frac{64.1s^{5}+1411.4s^{4}+5285s^{3}+5285s^{2}+1411.4s+64.1}{63.1s^{6}+1429.2s^{5}+6285s^{4}+8965s^{3}+3320.4s^{2}+217.8s+2}e^{-1.6s}\nonumber \\ \end{aligned}$$
(52)

and

$$\begin{aligned} L_{ous7} (s) =\frac{64.1s^{7}+2597.9s^{6}+23912s^{5}+66690s^{4}+66690s^{3}+23912s^{2}+2597.9s+64.1}{63.1s^{8}+2596.2s^{7}+25390s^{6}+83840s^{5}+109630s^{4}+50962s^{3}+7051.9s^{2}+256.8s+2}e^{-1.6s} \end{aligned}$$
(53)

The exact step response of the system obtained from FSM and the step responses of \(L_{ous5} (s)\) and \(L_{ous7} (s)\) are shown in Fig. 4a. In both cases Oustaloup’s approximations give a steady-state error equal to 0.031 (3.1 %) and increasing the approximation order further does not eliminate it. On the other hand FSM gives a steady state error of 0.004 at \(\hbox {t}=100\) s. and reduces further when t is further increased. The error plots between Oustaloup approximations and FSM are shown in Fig. 4b. The step responses of the control system with \(L_{ous 5} (s)\) and \(L_{ous7} (s)\) are obtained from Simulink using the transport lag block. If a Pade approximation is used for the time delay additional errors result.

The closed loop transfer function of the system is

$$\begin{aligned} P(s)=\frac{L(s)}{1+L(s)}=\frac{\left( s^{0.9}+1\right) e^{-1.6s}}{s^{1.9}+2s^{0.9}+(s^{0.9}+1)e^{-1.6s}} \end{aligned}$$
(54)

One can compute the step response of Eq. (54) using Grünwald–Letnikov(GL) approximation method. We used the Matlab GL program given in [2] by taking first order and second order Pade approximations for \(e^{-1.6s}\) and obtained Fig. 5. The difference between the plots can be seen more clearly on the small figure. The result from the GL method with the second order Pade approximation approach is near to that from the FSM apart from small values of time.

Fig. 5
figure 5

Step responses obtained from GL method and FSM

Full size image

Example 4

Let the control system from Fig. 1 have the following plant transfer function

$$\begin{aligned} G_p (s)=\frac{4}{s(0.4s+1)(0.1s+1)}e^{-0.6s} \end{aligned}$$
(55)

The aim is to design a lead controller of the form

$$\begin{aligned} C(s)=K\frac{s^{\mu }+a}{s^{\mu }+b} \end{aligned}$$
(56)

so that the closed loop step response satisfies the following specifications: percentage overshoot must be less than 12 %, settling time must be less than 10 s for 2 % tolerance band and rise time must be less than 2 s. Using Eq. (41), the parameters of the controller which give these specifications are computed as \(K=1.1\), \(\mu =0.88\), \(a=1\) and \(b=6\). These values are obtained by iteration from some selected initial parameters such as \(K=1\), \(\mu =1\), \(a=1\) and \(b=4\). The designed controller is

$$\begin{aligned} C(s)=1.1\frac{s^{0.88}+1}{s^{0.88}+6} \end{aligned}$$
(57)

The step response of the system is shown in Fig. 6 where it can be seen that the percentage overshoot is equal to 11.7 %, the rise time is equal to 1.84 s and the settling time is 7.76 s. Thus, with the designed controller the closed loop performance meets the required specifications.

Fig. 6
figure 6

Step response of the closed loop system with \(G_p (s)\) of Eq. (55) and C(s) of Eq. (57)

Full size image

3.2 Inverse Fourier transform method (IFTM)

It was shown in [12] that the impulse response of a fractional order transfer function can be obtained from frequency response data using the inverse Fourier transform. Here, the results given in [12] are extended for time response computation of a fractional order closed loop control system with time delay.

The impulse response, p(t), corresponding to the transfer function P(s) of Eq. (3) is given by \(p(t)=L^{-1}\left( {P(s)} \right) \) where \(L^{-1}\) denotes the inverse Laplace transform. Assuming the impulse response is that of a stable system so that \(\lim _{t\rightarrow \infty } p(t)=0\) then the Fourier transform can be evaluated. The impulse response, p(t), only exists for \(t>0\) so it will be denoted by \(p_+ (t)\) but as the range of t is from \(-\infty \) to \(\infty \) for the Fourier transform one may consider the double sided function \(p(t)=p_- (t)+p_+ (t)\), where \(p_- (t)\) exists for \(t<0\) and \(p_+ (t)\) for \(t>0\). \(p_- (t)\) may be taken as \(p_+ (-t)\) or \(-p_+ (-t)\), making the total time function either even or odd. Assuming the even case then \(P(j\omega )=\mathop {\int }\limits _{-\infty }^0 {p_- (t)} e^{-j\omega t}dt+\mathop {\int }\limits _0^\infty {p_+ (t)} e^{-j\omega t}dt=P_- (j\omega )+P_+ (j\omega )\), which can be shown to give \(P(j\omega )=2\mathop {\int }\limits _0^\infty {p_+ (t)} \cos \omega tdt\). However, our concern is with the inversion integral \(p(t)=\frac{1}{2\pi }\mathop {\int }\limits _{-\infty }^\infty {[P_+ (j\omega )+P_- (j\omega )]e^{j\omega t}d\omega } \). It can be shown that \(P_+ (j\omega )=\hbox {Re}[P(j\omega )]+j[\hbox {Im }P(j\omega )]\) where \(P(j\omega )\) is the Laplace transform of \(p_+ (t)\) or p(t), with \(s=j\omega \), since the transform is defined for \(t>0\). Further from the definition it can be seen that \(P_- (j\omega )=\hbox {Re}[P(j\omega )]-j[\hbox {Im }P(j\omega )]\), so that the integral gives

$$\begin{aligned} p(t)= & {} \frac{1}{2\pi }\mathop {\int }\limits _{-\infty }^\infty {2\hbox {Re}[P(j\omega )]e^{j\omega t}d(\omega } )\nonumber \\= & {} \frac{2}{\pi }\mathop {\int }\limits _0^\infty {\hbox {Re} [P(j\omega )]\cos (\omega t)d(\omega )} \nonumber \\= & {} \frac{2}{\pi }\mathop {\int }\limits _0^\infty {\frac{[U(\omega )Z(\omega )+V(\omega )Q(\omega )]}{[Z(\omega )^{2}+Q(\omega )^{2}]}\cos (\omega t)d(\omega )} \end{aligned}$$
(58)

Alternatively, if one assumes p(t) to be odd then \(P_- (j\omega )=-\hbox {Re}[P(j\omega )]+j[\hbox {Im }P(j\omega )]\), \(P_+ (j\omega )+P_- (j\omega )=2j\hbox {Im}[P(j\omega )]\) and

$$\begin{aligned} p(t)= & {} \frac{1}{2\pi }\mathop {\int }\limits _{-\infty }^\infty {2j \hbox {Im}[P(j\omega )]e^{j\omega t}d(\omega } )\nonumber \\= & {} -\frac{2}{\pi }\mathop {\int }\limits _0^\infty {\hbox {Im}[P(j\omega )]\sin (\omega t)d(\omega )} \nonumber \\= & {} -\frac{2}{\pi }\mathop {\int }\limits _0^\infty {\frac{[V(\omega )Z(\omega )-U(\omega )Q(\omega )]}{[Z(\omega )^{2}+Q(\omega )^{2}]}\sin (\omega t)d(\omega )}\nonumber \\ \end{aligned}$$
(59)

Thus, for the closed loop system with the fractional order PID controller, the impulse response using Eq. (25) is

$$\begin{aligned} p(t)= & {} \frac{2}{\pi }\mathop {\int }\limits _0^\infty \frac{[U_{\textit{PID}} (\omega )Z_{\textit{PID}} (\omega )+V_{\textit{PID}} (\omega )Q_{\textit{PID}} (\omega )]}{[Z_{\textit{PID}} (\omega )^{2}+Q_{\textit{PID}} (\omega )^{2}]}\nonumber \\&\cos (\omega t)d(\omega ) \end{aligned}$$
(60)

or

$$\begin{aligned} p(t)= & {} -\frac{2}{\pi }\mathop {\int }\limits _0^\infty \frac{[U_{\textit{PID}} (\omega )Z_{\textit{PID}} (\omega )-V_{\textit{PID}} (\omega )Q_{\textit{PID}} (\omega )]}{[Z_{\textit{PID}} (\omega )^{2}+Q_{\textit{PID}} (\omega )^{2}]}\nonumber \\&\sin (\omega t)d(\omega ) \end{aligned}$$
(61)

where \(U_{\textit{PID}} (\omega )\), \(V_{\textit{PID}} (\omega )\), \(Z_{\textit{PID}} (\omega )\) and \(Q_{\textit{PID}} (\omega )\) are given in Eqs. (28)–(31). Similarly, the closed loop impulse response of the time delay control system of Fig. 1 with fractional order lag or lead controller of the form of Eq. (34) is

$$\begin{aligned} p(t)= & {} \frac{2}{\pi }\mathop {\int }\limits _0^\infty \frac{[U_{\textit{LL}} (\omega )Z_{\textit{LL}} (\omega )+V_{\textit{LL}} (\omega )Q_{\textit{LL}} (\omega )]}{[Z_{\textit{LL}} (\omega )^{2}+Q_{\textit{LL}} (\omega )^{2}]}\nonumber \\&\cos (\omega t)d(\omega ) \end{aligned}$$
(62)

or

$$\begin{aligned} p(t)= & {} -\frac{2}{\pi }\mathop {\int }\limits _0^\infty \frac{[U_{\textit{LL}} (\omega )Z_{\textit{LL}} (\omega )-V_{\textit{LL}} (\omega )Q_{\textit{LL}} (\omega )]}{[Z_{\textit{LL}} (\omega )^{2}+Q_{\textit{LL}} (\omega )^{2}]}\nonumber \\&\sin (\omega t)d(\omega ) \end{aligned}$$
(63)

where \(U_{\textit{LL}} (\omega )\), \(V_{\textit{LL}} (\omega )\), \(Z_{\textit{LL}} (\omega )\) and \(Q_{\textit{LL}} (\omega )\) are given in Eqs. (37)–(40).

Fig. 7
figure 7

Step responses obtained from FSM and IFTM

Full size image

Example 5

In this example L(s) of Fig. 1 was taken as

$$\begin{aligned} L(s)= & {} C(s)G_p (s)\nonumber \\= & {} \frac{30(s^{2.15}+2s^{0.9}+0.5)}{s^{6.2}+13s^{4.84}+60s^{3.75}+150s^{3.1}+160s^{1.92}+66s^{1.12}}e^{-2s}\nonumber \\ \end{aligned}$$
(64)

Thus, the closed loop transfer function is

$$\begin{aligned} P(s)= & {} \frac{L(s)}{1+L(s)}\nonumber \\ = & {} \frac{30(s^{2.15}+2s^{0.9}+0.5)e^{-2s}}{s^{6.2}+13s^{4.84}+60s^{3.75}+150s^{3.1}+160s^{1.92}+66s^{1.12}+30(s^{2.15}+2s^{0.9}+0.5)e^{-2s}} \end{aligned}$$
(65)

The step response of P(s) using FSM and the impulse responses of \(\frac{1}{s}P(s)\) which is the step response of P(s) using IFTM are plotted in Fig. 7. From the zoomed figure given in Fig. 7, one can see there is no difference between the two plots.

4 Conclusions

In this paper, two exact methods namely FSM and IFTM have been used for the time response computation of control systems with fractional order plus time delay plant transfer functions. The FSM uses the Fourier series of a square wave with large period and the IFTM uses the inverse Fourier transform of frequency domain data. Since the frequency domain data for a fractional order control system with time delay can be obtained exactly, the step and impulse responses computed from the FSM and IFTM are very accurate. The numerical examples presented show that the results given in the paper can be very useful for the analysis and design of fractional order time delay control systems. Development of a systematic design procedure based on the FSM is the subject of future work.