1 Introduction

Pipes are indispensable accessories in various fluid-conveying occasions, such as oil exploration, gas transmission, urban water supplying, rocket propulsion, nuclear reactor cooling, etc.; therefore, the related fluid–structure coupling dynamics has attracted extensive attentions in recent years. Scholars have carried out a lot of researches on this problem and have made fruitful achievements in mechanical models, modeling theories, numerical algorithms, etc. To be specific, beam theories including Euler–Bernoulli [1, 2] or Timoshenko beams [3, 4] are commonly used to model pipes’ mechanical behavior. Typical theories such as Hamilton principle [5, 6], Newton’s second law [7], energy method [8], D’Alembert principle [9], etc., have been successfully adopted to model the governing equation with regard to pipe’s movement. Numerous methods developed from scratch or transplanted from other fields have been successfully on the problem, such as transfer matrix method (TMM) [10, 11], Galerkin’s method [12,13,14], differential quadrature method (DQM) [15, 16] and its general format (GDQM) [17], green function method (GFM) [18, 19], differential transformation method (DTM) [20], etc., as concluded by Païdoussis [21], dynamics of pipes conveying fluid has become a model dynamical problem, the experience gained in studying this problem can be radiated into other areas of applied mechanics.

Referring to relevant researching contents, it can be concluded that the investigations surrounding pipe dynamics can be divided into two branches, i.e., experimental and theoretical researches, respectively. In terms of theoretical research, the basic researching path can be summarized as follows: (i) abstracting the actual problem into mechanical model; (ii) using appropriate mathematical tools to express the mechanical model as a partial differential equation (PDE) of displacement and (iii) developing a numerical algorithm to solve the above PDE. Based on the above three steps, scholars have published a large number of significant achievements, e.g., for straight pipes, Païdoussis [22] proposed a wide spread PDE to describe its linear vibration, where he considered numerical factors affecting pipe’s transverse motion, which inspired subsequent researchers a lot. Guo et al. [23] established a linear PDE considering the flow model modification factor and figured out its exact values for different flow patterns. In 2019, aiming at a fluid-conveying pipe composed of functionally graded material, Tang and Yang [24] studied its post-buckling behavior and nonlinear vibration; in the same year, they studied the fractional dynamics when the pipes are subjected to the excitation of supporting foundation [25] and nonlinear free vibration of a fractional dynamic model for the viscoelastic pipe conveying fluid [26]. For curved pipes, Misra et al. [27, 28] established the linear equation of motion and proposed three theories, i.e., inextensible, modified inextensible and extensible theories, respectively, in 1988, their work laid a theoretical foundation for later researchers. In 2017, Zhao and Sun [29] studied the in-plane forced vibration with the consideration of added mass and damping along both axial and transverse directions according to modified inextensible theory. In 2019, Łuczko and Czerwiński [30] employed Timoshenko beam model to study flow-induced 3D motions of a curved pipe, and 2 years later, they investigated the dynamic behavior of curved pipes in the shape of circular arcs conveying fluid [31]. As a summary, it can be found that a number of research directions have gradually formed where typical ones are mainly composed of: (i) nonlinear vibration including geometric nonlinearity and motion nonlinearity, such as Zhu et al. [32] studied nonlinear nonplanar dynamics of porous functionally graded pipes conveying fluid on the basis of Euler–Bernoulli beam theory. Wang et al. [1] investigated three-dimensional dynamics of a cantilevered pipe conveying fluid with the consideration of pulsating flow velocity, where the pipe is also modeled by Euler–Bernoulli beam; (ii) dynamics of complex spatial configuration, such as Zhang et al. [8] proposed a semi-analytical method analyzing the dynamics of U-shaped, Z-shaped and regular spatial pipelines supported by multiple clamps based on Timoshenko beam theory, where the key steps are discretizing the piping system into characteristic elements and replacing connections by equivalent springs. Guo et al. [33] analyzed the vibration response of L-shaped fluid-conveying pipes subjected to base excitation and pulsation excitation concurrently by a modified transfer matrix model. Wang et al. [34] solved the flow-induced vibration of a piping system composed of a flexible pipe, and a rigid pipe is a class of hybrid flexible-rigid dynamical problem and (iii) more refined research object, such as Dou et al. [7] modeled and performed parametric studies of retaining clips on fluid-conveying pipe, where the clip is modeled as a rigid body with a certain width, which is elastically connected to the base. Cao et al. [35] proposed a hybrid energy transfer matrix method to analyze the dynamics of fluid-conveying piping system with arbitrary branches.

Threaded connection is very common seen in engineering practice, while pipes connected by threaded joint are often used to extend the conveying distance of inner fluid, which makes the application scenarios of pipes more diverse. Even though great progresses have been made with regard to fluid–structure coupling dynamics of fluid-conveying piping system as mentioned above, the theoretical research on the impact of threaded joints on the dynamic behavior of piping system is seldom mentioned to the best of authors’ knowledge, one reason is it’s rather difficult to accurately formulate the mechanical behaviors at the joint. In order to solve the problem while avoiding complex processes, a new idea modeling the whole piping system is proposed on the premise of equivalent flexural stiffness in this paper, that is, a coefficient describing the reduction of elastic modulus at the joint is introduced, besides, due to the large radial size of the joint, its rotatory inertia is also taken into account in the modeling process, then obeying the basic researching path as mentioned above, the governing equation of the whole piping system can be predictably founded as a result.

The rest of this paper is organized as follows: In Sect. 2, the mechanical model of a cantilevered fluid-conveying piping system composed of a left pipe, a right pipe and a short threaded joint is founded, and the corresponding governing equation is deduced based on the existed literatures. In Sect. 3, the characteristic equation is obtained by discretizing the above governing equation with the aid of DTM-Galerkin [36]. In Sect. 4, numerical calculations are performed, and the influences of some vital parameters on the dynamics of this piping system are studied under given conditions; in addition, appropriate discussions are made. In Sect. 5, conclusions are drawn.

2 Mechanical model and governing equation

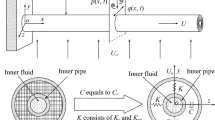
A cantilevered fluid-conveying piping system composed of a left pipe, a right pipe and a short threaded joint as Fig. 1 is considered in this paper, where the left pipe is connected to the right pipe by a joint through screw thread.

Fig. 1
figure 1

Mechanical model of the researched fluid-conveying piping system

Full size image

To promote the following investigation, some assumptions are made beforehand as follows: (i) Both the left and the right pipes are uniform and slender so that the whole piping system behaves like a Euler–Bernoulli beam although there is a short threaded joint; (ii) the internal fluid is incompressible and non-viscous so that it is modeled by plug flow and (iii) both pipes and the joint are made of the same material, and cross-section shapes are all circular; furthermore, there is no gap between pipes and the joint.

It is inevitable that the flexural stiffness at the joint will reduce due to threaded connection, then according to the principle of equivalent substitution, if the cross-section size of the joint keeps unchanged, its elastic modulus should decrease to some extent to describe the reduction of flexural stiffness as it is the product of elastic modulus and cross-section moment of inertia; therefore, the elastic modulus at the joint can be written as the product of a coefficient α (defined as regulatory factor in this paper) and Ep, i.e., \(E_{{\text{j}}} = \alpha E_{{\text{p}}}\); however, since the mass and volume have not changed, the density remains unchanged, i.e., \(\rho_{{\text{j}}} = \rho_{{\text{p}}}\). In addition, in order to describe the variation of cross-section moment of inertia and mass when it comes to the equivalent joint, two parameters are defined as follows:

$$ \lambda_{1} = \frac{{I_{{\text{j}}} }}{{I_{{\text{p}}} }} = \frac{{\left( {D_{{\text{o}}} - d_{{\text{i}}} } \right)^{4} }}{{\left( {d_{{\text{o}}} - d_{{\text{i}}} } \right)^{4} }} $$
(1)
$$ \lambda_{2} = \frac{{m_{{\text{j}}} }}{{m_{{\text{p}}} }} = \frac{{A_{{\text{j}}} }}{{A_{{\text{p}}} }} = \frac{{\left( {D_{{\text{o}}} - d_{{\text{i}}} } \right)^{2} }}{{\left( {d_{{\text{o}}} - d_{{\text{i}}} } \right)^{2} }} $$
(2)

In the following, ‘joint’ is used instead of ‘equivalent joint’ without causing ambiguity. According to Newton’s second law, the force balance equation of the piping system can be written as follows [37, 38]:

$$ \frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {R\left( x \right)\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right] = - m_{{\text{f}}} \left( {\frac{\partial }{\partial t} + U\frac{\partial }{\partial x}} \right)^{2} w - M\left( x \right)\frac{{\partial^{2} w}}{{\partial t^{2} }} + \frac{\partial }{\partial x}\left\{ {J_{{\text{j}}} \left[ {H\left( {x - L_{1} } \right) - H\left( {x - L_{2} } \right)} \right]\frac{{\partial^{3} w}}{{\partial x\partial t^{2} }}} \right\} $$
(3)

where

$$ R\left( x \right) = E_{{\text{p}}} I_{{\text{p}}} \left\{ {H\left( x \right) - H\left( {x - L} \right) - \left( {1 - \alpha \lambda_{1} } \right)\left[ {H\left( {x - L_{1} } \right) - H\left( {x - L_{2} } \right)} \right]} \right\} $$
$$ M\left( x \right) = m_{{\text{p}}} \left\{ {H\left( x \right) - H\left( {x - L} \right) - \left( {1 - \lambda_{2} } \right)\left[ {H\left( {x - L_{1} } \right) - H\left( {x - L_{2} } \right)} \right]} \right\} $$

In Eq. (3), the bending restoring force is on the left of the equal sign, and on the right of the equal sign, there are acting force from fluid, inertia forces of pipe and joint and moment of inertia of joint from the left to right, respectively.

After further manipulations, Eq. (3) can be rewritten as follows:

$$ \begin{aligned} & \frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {R\left( x \right)\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right] + m_{{\text{f}}} U^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }} + 2m_{{\text{f}}} U\frac{{\partial^{2} w}}{\partial x\partial t} + \left[ {m_{{\text{f}}} + M\left( x \right)} \right]\frac{{\partial^{2} w}}{{\partial t^{2} }} \\ & \quad - \frac{\partial }{\partial x}\left\{ {J_{{\text{j}}} \left[ {H\left( {x - L_{1} } \right) - H\left( {x - L_{2} } \right)} \right]\frac{{\partial^{3} w}}{{\partial x\partial t^{2} }}} \right\} = 0 \\ \end{aligned} $$
(4)

Boundary conditions of the current researching pipping system can be written as follows:

$$ w\left( {0,t} \right) = w^{\prime } \left( {0,t} \right) = E_{{\text{p}}} I_{{\text{p}}} w^{\prime \prime } \left( {L,t} \right) = E_{{\text{p}}} I_{{\text{p}}} w^{\prime \prime \prime } \left( {L,t} \right) = 0 $$
(5)

For simplicity, some dimensionless parameters are defined as follows:

$$ \begin{aligned} \eta & = \frac{w}{L}\quad \xi = \frac{x}{L}\quad u = UL\sqrt {\frac{{m_{{\text{f}}} }}{{E_{{\text{p}}} I_{{\text{p}}} }}} \quad \beta = \frac{{m_{{\text{f}}} }}{{m_{{\text{f}}} + m_{{\text{p}}} }} \\ \tau & = \frac{t}{{L^{2} }}\sqrt {\frac{{E_{{\text{p}}} I_{{\text{p}}} }}{{m_{{\text{f}}} + m_{{\text{p}}} }}} \quad \xi_{1} = \frac{{L_{1} }}{L}\quad \xi_{2} = \frac{{L_{2} }}{L}\quad \gamma = \frac{{J_{{\text{j}}} }}{{L^{2} \left( {m_{{\text{f}}} + m_{{\text{p}}} } \right)}} \\ \end{aligned} $$
(6)

By substituting Eq. (6) into Eq. (4), one will obtain

$$ \begin{aligned} & \frac{{\partial^{2} }}{{\partial \xi^{2} }}\left[ {r\left( \xi \right)\frac{{\partial^{2} \eta }}{{\partial \xi^{2} }}} \right] + u^{2} \frac{{\partial^{2} \eta }}{{\partial \xi^{2} }} + 2u\sqrt \beta \frac{{\partial^{2} \eta }}{\partial \xi \partial \tau } + \frac{{m_{{\text{f}}} + m\left( \xi \right)}}{{m_{{\text{f}}} + m_{{\text{p}}} }}\frac{{\partial^{2} \eta }}{{\partial \tau^{2} }} \\ & \quad - \gamma \frac{\partial }{\partial \xi }\left\{ {\left[ {H\left( {\xi - \xi_{1} } \right) - H\left( {\xi - \xi_{2} } \right)} \right]\frac{{\partial^{3} \eta }}{{\partial \xi \partial \tau^{2} }}} \right\} = 0 \\ \end{aligned} $$
(7)

where

$$ r\left( \xi \right) = H\left( \xi \right) - H\left( {\xi - 1} \right) - \left( {1 - \alpha \lambda_{1} } \right)\left[ {H\left( {\xi - \xi_{1} } \right) - H\left( {\xi - \xi_{2} } \right)} \right] $$

\(m\left( \xi \right) = m_{{\text{p}}} \left\{ {H\left( \xi \right) - H\left( {\xi - 1} \right) - } \right.\left. {\left( {1 - \lambda_{2} } \right)\left[ {H\left( {\xi - \xi_{1} } \right) - H\left( {\xi - \xi_{2} } \right)} \right]} \right\}\)

Similarly, Eq. (5) can be expressed in dimensionless form as follows:

$$ \eta \left( {0,\tau } \right) = \eta^{\prime } \left( {0,\tau } \right) = \eta^{\prime \prime } \left( {1,\tau } \right) = \eta^{\prime \prime \prime } \left( {1,\tau } \right) = 0 $$
(8)

For simplicity, dimensionless parameters are the default preferences in the next study.

3 Deduction by DTM-Galerkin

According to Galerkin’s discretization rule, solution of Eq. (7) can be expressed by

$$ \eta \left( {\xi ,\tau } \right) = \sum\limits_{n = 1}^{N} {\varphi_{n} \left( \xi \right)q_{n} \left( \tau \right)} $$
(9)

where N represents the number of superimposed items, \(\varphi_{n} (\xi )\) is the nth shape function and \(q_{n} (\tau )\) is the nth generalized coordinate.

With the introduction of Eq. (9), Eq. (7) will become

$$ \begin{aligned} & \sum\limits_{n = 1}^{N} {\left\{ {\left\{ {\frac{{{\text{d}}^{2} }}{{{\text{d}}\xi^{2} }}\left[ {r\left( \xi \right)\frac{{{\text{d}}^{2} \varphi_{n} }}{{{\text{d}}\xi^{2} }}} \right] + u^{2} \frac{{{\text{d}}^{2} \varphi_{n} }}{{{\text{d}}\xi^{2} }}} \right\}q_{n} + 2u\sqrt \beta \frac{{{\text{d}}\varphi_{n} }}{{{\text{d}}\xi }}\dot{q}_{n} } \right.} \\ & \quad + \left\{ {\left\{ {\frac{{m_{{\text{f}}} + m\left( \xi \right)}}{{m_{{\text{f}}} + m_{{\text{p}}} }}\varphi_{n} - \gamma \frac{{\text{d}}}{{{\text{d}}\xi }}\left\{ {\left[ {H\left( {\xi - \xi_{1} } \right) - H\left( {\xi - \xi_{2} } \right)} \right]\frac{{{\text{d}}\varphi_{n} }}{{{\text{d}}\xi }}} \right\}} \right\}\ddot{q}_{n} = 0} \right\} \\ \end{aligned} $$
(10)

By multiplying each shape functions \(\varphi_{m}\) \((m = 1,\;2,\;3,\; \ldots ,\;N)\) with Eq. (10), and then integrating the result with respect to ξ from 0 to 1, the result can be finally written as follows:

$$ \sum\limits_{n = 1}^{N} {\left( {K_{mn} q_{n} + G_{mn} \dot{q}_{n} + M_{mn} \ddot{q}_{n} } \right)} = 0 $$
(11)

where

\(K_{mn} = \int_{0}^{1} {\varphi_{m} \left\{ {\frac{{{\text{d}}^{2} }}{{{\text{d}}\xi^{2} }}\left[ {r\left( \xi \right)\frac{{{\text{d}}^{2} \varphi_{n} }}{{{\text{d}}\xi^{2} }}} \right] + u^{2} \frac{{{\text{d}}^{2} \varphi_{n} }}{{{\text{d}}\xi^{2} }}} \right\}{\text{d}}\xi } ,G_{mn} = 2u\sqrt \beta \int_{0}^{1} {\varphi_{m} {\text{d}}\varphi_{n} } ,\)

$$ M_{mn} = \int_{0}^{1} {\frac{{m_{{\text{f}}} + m\left( \xi \right)}}{{m_{{\text{f}}} + m_{{\text{p}}} }}\varphi_{m} \varphi_{n} {\text{d}}\xi } - \gamma \int_{0}^{1} {\varphi_{m} {\text{d}}\left\{ {\left[ {H\left( {\xi - \xi_{1} } \right) - H\left( {\xi - \xi_{2} } \right)} \right]\frac{{{\text{d}}\varphi_{n} }}{{{\text{d}}\xi }}} \right\}} $$

Eq. (11) can be rewritten in matrix form as follows:

$$ {\mathbf{Kq}} + {\mathbf{G\dot{q}}} + {\mathbf{M\ddot{q}}} = {\mathbf{0}} $$
(12)

Solution of Eq. (12) can be written as follows:

$$ {\mathbf{q}} = {\mathbf{q}}_{0} \exp \left( {{\text{i}}\omega \tau } \right) $$
(13)

where \(\omega = \Omega L^{2} \sqrt {\frac{{m_{{\text{f}}} + m_{{\text{p}}} }}{{E_{{\text{p}}} I_{{\text{p}}} }}}\) denotes the dimensionless eigenvalue, while Ω is the corresponding dimensional one.

With the introduction of Eq. (13), Eq. (12) will become

$$ \left[ {{\mathbf{K}} + {\text{i}}\omega {\mathbf{G}} - \omega^{2} {\mathbf{M}}} \right]{\mathbf{q}}_{0} = {\mathbf{0}} $$
(14)

To obtain non-trivial solution of q0, determinant of its coefficient matrix should be equal to zero, i.e.,

$$ \left| {{\mathbf{K}} + {\text{i}}\omega {\mathbf{G}} - \omega^{2} {\mathbf{M}}} \right| = 0 $$
(15)

By solving Eq. (15), the eigen values ωj \((j = 1,\;2,\;3,\; \cdots )\) with complex form will be obtained, where the real part (denoted by Re(ω)) is the dimensionless natural frequency, while the imaginary part (denoted by Im(ω)) is related to damping [21].

4 Numerical results and discussion

4.1 Physical parameters and preparations for calculation

A real piping system is considered in this section, where both pipes and the joint are all made of ordinary carbon steel, and pure water flows inside. Some specific physical parameters are listed in Table 1.

Table 1 Physical parameters of the current piping system
Full size table

With the combination of Eq. (6), the calculation result of mass ratio is \(\beta = 0.14\).

As Ref. [36] shows, DTM-Galerkin is an efficient tool in studying dynamics of a fluid‑conveying pipe; therefore, it is used directly in the current problem, where the shape functions are written as follows [39]:

$$ \varphi_{n} \left( \xi \right) = \sum\limits_{i = 0}^{{N_{0} }} {\frac{{\tilde{\omega }_{n}^{2i} }}{{\left( {4i + 2} \right)!}}\xi^{{\left( {4i + 2} \right)}} } - \frac{{\sum\nolimits_{i = 0}^{{N_{0} }} {\frac{{\tilde{\omega }_{n}^{2i} }}{{\left( {4i} \right)!}}} }}{{\sum\nolimits_{i = 0}^{{N_{0} }} {\frac{{\tilde{\omega }_{n}^{2i} }}{{\left( {4i + 1} \right)!}}} }}\sum\limits_{i = 0}^{{N_{0} }} {\frac{{\tilde{\omega }_{n}^{2i} }}{{\left( {4i + 3} \right)!}}\xi^{{\left( {4i + 3} \right)}} } $$
(16)

where \(\tilde{\omega }_{n}\) represents the nth natural frequency, and N0 denotes the iterations in DTM. In order to give consideration to calculation accuracy and efficiency simultaneously, referring to Ref. [36], N0 is taken as 60, while N is equal to 8 in the following.

4.2 Calculations of natural frequencies following flow velocity

Variations of the first four natural frequencies following flow velocity are calculated and shown in Fig. 2, where regulatory factor α, length of left pipe ξ1 and rotatory inertia of the joint γ are given beforehand, and for comparison, the case ‘uniform pipe without joint’ is also calculated.

Fig. 2
figure 2

First four natural frequencies as functions of flow velocity under given parameters

Full size image

Comparing Fig. 2a with Fig. 2b, it can be found that adding the joint slows down the speed the 1st mode decrease to zero, i.e., from \(u_{0} \simeq 6.5\) to \(u_{0} \simeq 7.2\). Combining Fig. 2b and Fig. 2c, it is obvious with the decrease in regulatory factor, the interval that the 1st mode is equal to zero shortens. The influence of rotatory inertia on natural frequency is very great as Fig. 2d shows, specifically, the 1st mode abnormally increases continuously with the increase in flow velocity compared with other three subgraphs, while the 2nd mode decreases to zero finally following the increase in flow velocity.

4.3 Researches on the stability of the piping system

As mentioned in Ref. [21], the criteria for determining the stability of a piping system from the view of numerical calculation are as follows: If \({\text{Re}} (\omega ) \ne 0\) and \({\text{Im}} (\omega ) = 0\), the pipe will flutter, while if \({\text{Re}} (\omega ) = 0\) and \({\text{Im}} (\omega ) = 0\), the divergence will appear. Based on the above principle, influences of some important parameters including regulatory factor, length of the left pipe and rotatory inertia of the joint on the piping system’s stability are studied in this subsection.

4.3.1 Regulatory factor, i.e., α

If \(\xi_{1} = 0.4\) and \(\gamma = 0\), then variations of Re(ω) and Im(ω) versus flow velocity can be worked out by the current method; thereafter, the Argand diagrams under different regulatory factors can be obtained as Fig. 3 shows, where the values adjacent to the critical flow velocities are marked by black dots combined with specific values; in addition, all flow velocity ranges are \(u \in\)[0, 10] hereafter in this paper.

Fig. 3
figure 3

Argand diagrams under different regulatory factors

Full size image

Combining all subgraphs of Fig. 3, it can be found that with the increase in regulatory factor, the critical velocities for flutter increase, meaning that if the connection stiffness of the threaded joint gets closer and closer to the pure pipe, the system will be more and more stable.

4.3.2 Length of the left pipe, i.e., ξ 1

If \(\alpha = 0.9\) and \(\gamma = 0\), then variations of Re(ω) and Im(ω) versus flow velocity can be worked out by the current method; thereafter, the Argand diagrams under different lengths of the left pipe can be obtained as Fig. 4 shows.

Fig. 4
figure 4

Argand diagrams under different lengths of the left pipe

Full size image

As Fig. 4 shows, variation of the length of the left pipe may lead to the critical velocities increase or decrease; therefore, location of the joint is worthy of being paid special attention in engineering practice.

4.3.3 Rotatory inertia of the joint, i.e., γ

It is noteworthy that rotatory inertia of the joint is not a fixed value for the radius of gyration varies with the motion of the pipe. If \(\alpha = 0.9\) and \(\xi_{1} = 0.4\), then variations of Re(ω) and Im(ω) versus flow velocity can be worked out by the current method; thereafter, the Argand diagrams under different rotatory inertias of the joint can be obtained as Fig. 5 shows.

Fig. 5
figure 5

Argand diagrams under different rotatory inertias of the joint

Full size image

As Fig. 5 shows, with the increase in rotatory inertia of the joint, all four natural frequencies decrease, but the critical velocities for flutter increase, showing that in the low-frequency range, the flow velocity can be larger, and the system can still maintain stability, which is of great significance to improve the fluid-conveying speed in the low-frequency state in engineering practice.

5 Conclusions

The dynamics of a cantilevered fluid-conveying piping system composed of two straight pipes and a short threaded joint implemented intermediately is investigated, and some important conclusions based on calculations can be drawn as follows:

  1. i.

    Increase in regulatory factor will promote the increase in critical velocities.

  2. ii.

    Variation of the length of the left pipe may lead to the critical velocities increase or decrease.

  3. iii.

    Increase in rotatory inertia of the joint will promote the decrease in natural frequencies, but increase in critical velocities.

The above conclusions have reference meaning on the experimental research about the impact of threaded joint on pipe dynamics, and the investigation can be radiated to study other connection forms in piping system.

The paper deals with the linear problems existing in fluid-conveying piping system; however, some fluid properties, such as viscosity, flow velocity, pressure, etc., may arise some nonlinearities, which will be our researching content in the future.