1 Introduction

As the simplest system characterized by fluid–structure coupling in modern industrial society, fluid-conveying pipes can be seen in various contexts, such as oil and gas transport (Cabrera-Miranda and Paik 2019), liquid fuel transmission (ElNajjar and Daneshmand 2020), solution mining (Kheiri 2020), ship and marine engineering (Zhu et al. 2019), and nuclear systems (Wu et al. 2020). Because of their wide application globally, considerable efforts were devoted to analyzing the related fluid–structure coupling dynamics in the previous century, and a series of valuable achievements have been published in authoritative journals. For example, Ibrahim studied the mechanics of fluid-conveying pipes used in nuclear power plants both theoretically (Ibrahim 2010) and practically (Ibrahim 2011), where he discussed various problems related to fluid-conveying pipes such as model type, dynamic analysis methods, and stability regimes. Dehrouyeh-Semnani et al. focused on the nonlinear dynamics of micropipes (Dehrouyeh-Semnani et al. 2017a, b) and functionally graded pipes (Dehrouyeh-Semnani et al. 2019), where they separately considered the size effect and temperature dependence of material properties for both the pipe and inner fluid. With respect to the material for manufacturing pipes, Tang et al. successively studied the dynamics of fluid-conveying pipes consisting of polymer-like material (Tang et al. 2018a), viscoelastic material (Tang et al. 2018b) or viscoelastic material under time-dependent velocity (Tang et al. 2022). They also extended the study to the nonlinear mechanics of a slender beam made of three-directional functionally graded materials (Tang et al. 2021) into fluid-conveying pipes, with consideration of piezoelectric attachments and nonlinear energy sinks (Tang et al. 2023a). Furthermore, they studied the vibration suppression problem related to fluid-conveying pipes (Tang et al. 2023b). As pointed out by Padïoussis (2008), the dynamics of pipes conveying fluid has become a model dynamical problem, and the knowledge gained can be extended to other dynamics problems across applied mechanics.

With the rapid development of natural science and computing technology, various models have been proposed based on beam theory. For example, for a straight pipe-dominant piping system, Padïoussis (2008) proposed an integrated equation to describe the linear vibration based on previous calculations, where he considered various factors affecting the pipe’s transverse motion. This inspired subsequent research efforts, and most studies referred to his work. Guo et al. (2010) established a linear vibration differential equation considering the flow model modification factor and deduced the specific value of this factor for the internal fluid flow with different models. Li and Yang (2014) presented a concise mechanical model describing the pipe’s forced vibration with consideration of different boundary conditions, and studied its steady-state displacement response in the time domain. Zhao and Liu (2023) included the “steady combined force” caused by a curved segment by integrating the Heaviside function into the governing equation of a straight pipe. They established the mathematical model of a combined straight-curved pipe as a result. For a curved pipe-dominant piping system, Misra et al. (1988a, b) established the linear vibration differential equation and proposed three theories (i.e., inextensible, modified inextensible, and extensible theories, respectively) with regard to the pipe’s centerline using finite element method (FEM) calculations and experimental validity. On this basis, Zhao and Sun (2017) developed the in-plane forced vibration model considering the influence of added mass and damping along both axial and transverse directions. Hu and Zhu (2018) established a dynamic model with the consideration of the pipe configuration and extensibility.

Dynamic problems for pipes conveying fluid have been analyzed by various approaches, among which the most commonly used is FEM. For example, Giacobbi et al. (2012) developed a fully coupled computational fluid dynamics (CFD) model and a computational structural mechanics (CFM) model in ANSYS to simulate experiments and confirm experimental results when they studied the dynamics of a cantilevered pipe aspirating fluid. Using FEM, Dunst et al. (2017) analyzed the vibration amplitudes of pipe in an ultrasonic powder transport system. By coupling the ANSYS mechanical and FLUENT finite volume solvers, Nikoo et al. (2018) developed a coupled CFD-FSI framework to carry out 3-D numerical simulations on the effectiveness of using a PIP system for VIV suppression of offshore cylindrical components. Nevertheless, there still exist limitations for FEM, including the high computing cost for changes to various system parameters (e.g., transverse and axial sizes, supporting type or cross-section shape). To overcome this drawback, many numerical methods have been developed to improve computational efficiency through improved accuracy, including the differential transformation method (DTM) (Mei 2008; Ni et al. 2011; Yalcin et al. 2009; Chen and Chen 2009), differential quadrature method (DQM) (Wang et al. 2007; Wang and Ni 2008; Ni et al. 2014a, b), transfer matrix method (TMM) (Koo and Yoo 2000; Zhao and Sun 2018; Liu and Li 2011; Wang et al. 2013), and Green’s function method (GFM) (Li and Yang 2014; Zhao and Sun 2017; Li et al. 2014; Abu-Hilal 2003, 2006). Because of the similarity in dynamic behaviors, some methods appropriate for beams can be used directly or indirectly on pipes. In this way, many valuable achievements have been realized. For example, Ni et al. (2011) employed DTM to study the natural frequency as a function of flow velocity of a straight pipe with four typical supports (i.e., cantilevered, clamped–clamped, clamped–pinned and pinned–pinned, respectively), and they also used the method to calculate some critical velocities prompting the coupling system to lose stability via different types. Wang et al. popularized DQM (Wang et al. 2007) and its generalized form (GDQM) (Wang and Ni 2008) into the fluid–structure coupling dynamics existing in fluid-conveying curved pipe with various boundary conditions and external constraints. Koo and Yoo (2000) proposed TMM based on dynamic stiffness method and continuity conditions and used it to study the dynamic characteristics of the KALIMER (Korea Advanced LIquid MEtal Reactor) intermediate heat transfer system (IHTS) hot leg piping system. Their work lays a solid foundation for further pipe-related research by TMM. This inspired Zhao and Sun (2018) to propose a new TMM based on Laplace transform (L-TMM) to study the flow-induced vibration of fluid-conveying curved pipe with elastic supports. Abu-Hilal (2003, 2006) investigated the forced vibration of the Euler–Bernoulli beam with different external conditions by GFM. Subsequently, Li and Yang (2014) used the same method to study the forced vibration of fluid-conveying straight pipe and deduced the analytical expression of steady-state displacement response in the time domain as well.

The Galerkin method is a weighted residual method, where the key point lies on the construction of shape functions. It is an efficient tool in deriving an approximate solution for differential equations, and hence has been widely used for solving dynamic problems of fluid-conveying straight pipes. For example, Guo et al. (2010) adopted the Galerkin method to calculate the stable area of a fluid-conveying straight pipe considering a flow model modification factor. Kheiri and Padïoussis (2015) analyzed the stability of a flexible pin-free cylinder in axial flow via the Galerkin method. Abdelbaki et al. successively discretized and solved the nonlinear model for a free-clamped cylinder subjected to confined axial flow (Abdelbaki et al. 2018) and the nonlinear model for a hanging tubular cantilever simultaneously subjected to internal and confined external axial flows (Abdelbaki et al. 2019) using the Galerkin method in MATLAB software. Sazesh and Shams (2019) used the Galerkin method to discretize the equation of motion of a cantilever pipe conveying fluid under distributed random excitation. Dehrouyeh-Semnani et al. employed the method to solve the nonlinear dynamics of cantilevered fluid-conveying pipes with uniform and nonuniform magnetization under an actuating parallel magnetic field (Dehrouyeh-Semnani 2022) and from macro to micro scale (Dehrouyeh-Semnani et al. 2016), respectively.

For the Galerkin method, the fundamental requirement is that shape functions must satisfy boundary conditions; thus, in the majority of published literature, as mentioned above, researchers prefer to use analytical normalized mode functions of Euler–Bernoulli straight beams [i.e., combinations of trigonometric functions (Guo et al. 2010; Kheiri and Païdoussis 2015; Abdelbaki et al. 2018, 2019; Sazesh and Shams 2019; Dehrouyeh-Semnani 2022; Dehrouyeh-Semnani et al. 2016)]. However, it is difficult to generalize when solving other fluid–structure coupling dynamic problems in the same field, i.e., its apparent combinations of trigonometric functions cannot be easily extended to solve the dynamic problems of fluid-conveying curved pipes.

The purpose of this work is to construct a new hybrid method combining DTM and Galerkin discretization, and additionally to verify the validity of this method in studying the dynamics of fluid-conveying pipes. DTM herein is used to derive the normalized mode functions, while the Galerkin technique is used to discretize the governing equation and deduce the eigenfunction as well as steady-state displacement response with the aid of normalized mode functions derived by DTM. The rest of the paper is organized as follows: Governing equations of the fluid-conveying straight pipe are deduced using the D’Alembert principle and reviewed in Sect. 2. Expressions of eigenfunction and steady-state displacement response are obtained using the Galerkin method in Sect. 3. Normalized mode functions are derived by DTM in Sect. 4, and numerical experiments are performed to verify the validity of the proposed method in Sect. 5. The method is extended to the study of dynamic problems of curved pipes as discussed in Sect. 6, and conclusions are drawn in Sect. 7.

2 A Review of the Deduction of Governing Equations Using the D’Alembert Principle

A horizontally placed straight pipe is considered. Figure 1 shows the force diagram of an element with length of dx, where \(p(x,t)\) is the distributed force along the pipe axis, Q and M represent the shearing force and bending moment at the cross-section, respectively, fI denotes the inertia force per unit length of the pipe, and ff is the force of the inner fluid acting on the pipe per unit length.

Fig. 1
figure 1

Mechanical model of the pipe element

Full size image

If w denotes lateral displacement, x and t are coordinate and time, EI represents the pipe’s flexural stiffness, mp and mf denote mass per unit length of pipe and fluid, respectively, and U is the average velocity of internal inviscid and incompressible fluid in cross-section, then according to the D’Alembert principle, equilibrium equations of force and moment (regarding the right-end point) can be written as follows:

$$\left. \begin{aligned}& p(x,\;t){\text{d}}x + Q = Q + \frac{\partial Q}{{\partial x}}{\text{d}}x + f_{\text{I}} (x,\;t){\text{d}}x + f_{\text{f}} (x,\;t){\text{d}}x \hfill \\ &M + \frac{\partial M}{{\partial x}}{\text{d}}x = M + Q{\text{d}}x + p(x,\;t){\text{d}}x \cdot \frac{{{\text{d}}x}}{2} \hfill \\ \end{aligned} \right\}$$
(1)

Substituting \(f_{{\text{I}}} (x,\;t)\) with \(m_{\text{p}} \partial^2 w/\partial t^2\) and neglecting high orders of dx will yield

$$\frac{\partial^2 M}{{\partial x^2 }} + f_{\text{f}} (x,\;t) + m_{\text{p}} \frac{\partial^2 w}{{\partial t^2 }} = p(x,\;t)$$
(2)

According to Euler–Bernoulli beam theory, M can be written as follows (Koo and Yoo 2000):

$$M = EI\frac{\partial^2 w}{{\partial x^2 }}$$
(3)

The material derivative of inner fluid can be expressed as follows (Faal and Derakhshan 2011):

$$a(x,\;t) = \left( {\frac{\partial }{\partial t} + U\frac{\partial }{\partial x}} \right)^2 w(x,\;t) = U^2 \frac{\partial^2 w}{{\partial x^2 }} + 2U\frac{\partial^2 w}{{\partial x\partial t}} + \frac{\partial^2 w}{{\partial t^2 }}$$
(4)

Then ff can be formulated as follows:

$$f_{\text{f}} (x,\;t) = m_{\text{f}} a(x,\;t) = m_{\text{f}} U^2 \frac{\partial^2 w}{{\partial x^2 }} + 2m_{\text{f}} U\frac{\partial^2 w}{{\partial x\partial t}} + m_{\text{f}} \frac{\partial^2 w}{{\partial t^2 }}$$
(5)

With the substitution of Eqs. (3) and (5) into Eq. (2), it will become

$$EI\frac{\partial^4 w}{{\partial x^4 }} + m_{\text{f}} U^2 \frac{\partial^2 w}{{\partial x^2 }} + 2m_{\text{f}} U\frac{\partial^2 w}{{\partial x\partial t}} + (m_{\text{f}} + m_{\text{p}} )\frac{\partial^2 w}{{\partial t^2 }} = p(x,\;t)$$
(6)

Some dimensionless parameters can be defined as follows:

$$\xi = \frac{x}{L}\quad \eta = \frac{w}{L}\quad \beta = \frac{{m_{\rm{f}} }}{{m_{\rm{f}} + m_{\rm{p}} }}\quad u = UL\sqrt {{\frac{{m_{\rm{f}} }}{EI}}} \quad \tau = \frac{t}{L^2 }\sqrt {{\frac{EI}{{m_{\rm{f}} + m_{\rm{p}} }}}} \quad f(\xi ,\;\tau ) = \frac{L^3 }{{EI}}p(x,\;t)$$
(7)

Considering Eq. (7), Eq. (6) can be rewritten as follows:

$$\frac{\partial^4 \eta }{{\partial \xi^4 }} + u^2 \frac{\partial^2 \eta }{{\partial \xi^2 }} + 2u\sqrt {\beta } \frac{\partial^2 \eta }{{\partial \xi \partial \tau }} + \frac{\partial^2 \eta }{{\partial \tau^2 }} = f(\xi ,\;\tau )$$
(8)

For convenience, C, P and F are used to indicate clamped, pinned and free supporting types, respectively, in the following study. For four typical kinds of pipes, their dimensionless boundary conditions can be written as follows (Ni et al. 2011):

  1. (1)

    C–F pipe

    $$\eta (0, \tau ) = \eta^{\prime}(0, \;\tau ) = \eta^{\prime \prime}(1,\; \tau ) = \eta^{\prime \prime}(1, \;\tau ) = 0$$
    (9)
  2. (2)

    C–C pipe

    $$\eta (0,\;\tau ) = \eta^{\prime}(0,\;\tau ) = \eta (1,\;\tau ) = \eta^{\prime}(1,\;\tau ) = 0$$
    (10)
  3. (3)

    C–P pipe

    $$\eta (0,\;\tau ) = \eta^{\prime}(0,\;\tau ) = \eta (1,\;\tau ) = \eta^{\prime \prime}(1,\;\tau ) = 0$$
    (11)
  4. (4)

    P–P pipe

    $$\eta (0,\;\tau ) = \eta^{\prime \prime}(0,\;\tau ) = \eta (1,\;\tau ) = \eta^{\prime \prime}(1,\;\tau ) = 0$$
    (12)

It should be noted that dimensionless parameters are usually the first choice in the following investigation unless there exists a special illustration.

3 Deduction by the Galerkin method

Using Galerkin discretization, the solution of Eq. (8) can be expressed as follows (Guo et al. 2010; Kheiri and Païdoussis 2015; Abdelbaki et al. 2018, 2019; Sazesh and Shams 2019; Dehrouyeh-Semnani 2022; Dehrouyeh-Semnani et al. 2016):

$$\eta (\xi ,\;\tau ) = \sum_{n = 1}^N {\varphi_n (\xi )q_n (\tau )}$$
(13)

where \(\varphi_n (\xi )\) denotes the nth shape function and \(q_n (\tau )\) is the nth general coordinate, and N represents the number of shape functions.

By substituting Eq. (13) into Eq. (8), it becomes

$$\sum_{n = 1}^N {(\overline{k}q_n + \overline{g}\dot{q}_n + \overline{m}\ddot{q}_n )} = f(\xi ,\;\tau )$$
(14)

where

$$\overline{k} = \frac{{{\rm{d}}^4 \varphi_n }}{{{\rm{d}}\xi^4 }} + u^2 \frac{{{\rm{d}}^2 \varphi_n }}{{{\rm{d}}\xi^2 }},\;\;\overline{g} = 2u\sqrt {\beta } \frac{{{\rm{d}}\varphi_n }}{{{\rm{d}}\xi }},\;\;\overline{m} = \varphi_n$$

By multiplying each shape function and integrating the result in \(\xi \in\)[0, 1], Eq. (14) becomes

$$\sum_{n = 1}^N {(K_{mn} q_n + G_{mn} \dot{q}_n + M_{mn} \ddot{q}_n )} = f_m ,\quad m = 1,2,3, \ldots ,N$$
(15)

where

$$\begin{array}{*{20}l} {K_{mn} = \int_0^1 {\varphi_m \left[ {\frac{{{\rm{d}}^4 \varphi_n }}{{{\rm{d}}\xi^4 }} + u^2 \frac{{{\rm{d}}^2 \varphi_n }}{{{\rm{d}}\xi^2 }}} \right]{\rm{d}}\xi } ,\;G_{mn} = 2u\sqrt {\beta } \int_0^1 {\varphi_m \frac{{{\rm{d}}\varphi_n }}{{{\rm{d}}\xi }}{\rm{d}}\xi } } \hfill \\ {M_{mn} = \int_0^1 {\varphi_m \varphi_n {\rm{d}}\xi } ,\;f_m = \int_0^1 {\varphi_m f(\xi ,\;\tau ){{\hbox{d}}}\xi } } \hfill \\ \end{array}$$

Equation (15) can be rewritten by its matrix form as follows (Zhao and Liu 2023):

$${{\varvec{K}}}_{N \times N} {{\varvec{q}}}_{N \times 1} + {{\varvec{G}}}_{N \times N} {\dot{\user2{q}}}_{N \times 1} + {{\varvec{M}}}_{N \times N} {\varvec{\ddot{q}}}{\,}_{N \times 1} = {{\varvec{f}}}_{N \times 1}$$
(16)

where the subscript denotes the order of matrix or vector.

3.1 Eigenfunction for Flow-Induced Vibration

If \({{\varvec{f}}}_{N \times 1} = {{\varvec{0}}}\), the flow-induced vibration differential equation will be obtained as follows (Zhao and Liu 2023):

$${{\varvec{K}}}_{N \times N} {{\varvec{q}}}_{N \times 1} + {{\varvec{G}}}_{N \times N} {\dot{\user2{q}}}_{N \times 1} + {{\varvec{M}}}_{N \times N} {\varvec{\ddot{q}}}{\,}_{N \times 1} = {{\varvec{0}}}$$
(17)

The solution of Eq. (17) can be expressed as follows:

$${{\varvec{q}}} = {{\varvec{q}}}_0 \exp ({\text{i}}\omega \tau )$$
(18)

where \(\omega = \Omega L^2 \sqrt {{\frac{{m_{\rm{f}} + m_{\rm{p}} }}{EI}}}\) represents the system’s characteristic variable.

With the introduction of Eq. (18) into Eq. (17), the result will be

$$\left[ {{{\varvec{K}}} + {\rm{i}}\omega {{\varvec{G}}} - \omega^2 {{\varvec{M}}}} \right]{{\varvec{q}}}_0 = {{\varvec{0}}}$$
(19)

To obtain a non-trivial solution of q0, the determinant must be equal to zero, i.e.,

$$\left| {{{\varvec{K}}} + {\rm{i}}\omega {{\varvec{G}}} - \omega^2 {{\varvec{M}}}} \right| = 0$$
(20)

Solving Eq. (20) will yield the results of eigenvalues \(\omega_i\) (\(i = 1,2,3, \ldots ,N\)). In addition, its real part ( \({\text{Re}} (\omega_i )\)) represents the ith natural frequency of the pipe, while the imaginary part ( \({\text{Im}} (\omega_i )\)) is related to the damping, with the damping ratio being \(\varsigma = - {\text{Im}} (\omega_i )/{\text{Re}} (\omega_i )\) (Païdoussis 2008).

3.2 Steady-State Displacement Response for Forced Vibration

A complex period excitation can be approximated by finite harmonic terms by using Fourier series (Zhao and Sun 2017). Hence, for a concentrated harmonic excitation normal to the pipe axis characterized by a single frequency, p(x, t) can be written in complex form as follows (Li and Yang 2014):

$$p(x,\;t) = F_0 \delta (x - A)\exp ({\rm{i}}\overline{\Omega }t)$$
(21)

where F0, A and \(\overline{\Omega }\) denote the amplitude, coordinate, and frequency of the excitation, respectively.

According to Eq. (7), the dimensionless form of Eq. (21) is

$$f(\xi ,\;\tau ) = f_0 \delta (\xi - a)\exp ({\rm{i}}\overline{\omega }\tau )$$
(22)

where

$$f_0 = \frac{L^2 }{{EI}}F_0 ,\;a = \frac{A}{L},\;\overline{\omega } = \overline{\Omega }L^2 \sqrt {{\frac{{m_{\rm{f}} + m_{\rm{p}} }}{EI}}}$$

Under this condition, the solution of Eq. (22) can be expressed as follows:

$${{\varvec{q}}} = {{\varvec{q}}}_0 {\rm{exp(i}}\overline{\omega }\tau {\rm{)}}$$
(23)

Substituting Eqs. (22)–(23) into Eq. (16) will yield

$${{\varvec{q}}}_0 = \left[ {{{\varvec{K}}} + {\rm{i}}\overline{\omega }{{\varvec{G}}} - \overline{\omega }^2 {{\varvec{M}}}} \right]^{ - 1} {{\varvec{f}}}$$
(24)

where \({{\varvec{f}}} = f_0 \left[ {\varphi_1 (a),\varphi_2 (a), \ldots ,\varphi_N (a)} \right]^{\rm{T}}\).

Thereby, with the combination of Eqs. (13), (23)–(24), the steady-state displacement response in the time domain can be written as follows:

$$\eta (\xi ,\;\tau ) = {\text{Re}} \left\{ {{\varvec{\varphi }}\left[ {{{\varvec{K}}} + {\rm{i}}\overline{\omega }{{\varvec{G}}} - \overline{\omega }^2 {{\varvec{M}}}} \right]^{ - 1} {{\varvec{f}}}} \right\}\cos (\overline{\omega }\tau ) - {\text{Im}} \left\{ {{\varvec{\varphi }}\left[ {{{\varvec{K}}} + {\rm{i}}\overline{\omega }{{\varvec{G}}} - \overline{\omega }^2 {{\varvec{M}}}} \right]^{ - 1} {{\varvec{f}}}} \right\}\sin (\overline{\omega }\tau )$$
(25)

By taking into account Sects. 3.1 and 3.2, it is clear that K, G, M and f are all directly related to shape functions. Then we can determine \(\varphi_n (\xi )\), which is the research goal in this study.

4 Normalized Mode Functions Using DTM

Detailed illustration of DTM can be seen in Ni et al. (2011); therefore, it can be used directly here. For a homogeneous Euler–Bernoulli straight beam, its equation of motion can be achieved directly by ignoring the fluid-related terms and excitation as in Eq. (8).

$$\frac{\partial^4 \eta }{{\partial \xi^4 }} + \frac{\partial^2 \eta }{{\partial \tau^2 }} = {0}$$
(26)

The solution of Eq. (26) can be expressed as follows:

$$\eta (\xi ,\;\tau ) = y(\xi )\exp ({\rm{i}}\omega \tau )$$
(27)

where \(\omega = \Omega L^2 \sqrt {{\frac{{m_{\text{p}} }}{EI}}}\) is the dimensionless characteristic variable, with mp, L, and EI having the same meanings as with the straight pipe mentioned in Eqs. (6)–(7).

Introducing Eq. (27) into Eq. (26) will yield

$$y^{\left( 4 \right)} - \omega^2 y = 0$$
(28)

Referring to Ni et al. (2011), the differential transformation of Eq. (28) can be written as follows:

$$Y(n_0 + 4) = \frac{\omega^2 }{{\prod_{j = 1}^4 {(n_0 + j)} }}Y(n_0 )$$
(29)

where n0 denotes the n0th iteration in DTM.

If a C–F pipe is taken as an example, then the differential transformation of its dimensionless boundary conditions can be written as follows:

$$\begin{aligned}Y(0) & = Y(1) = \sum_{n_0 = 0}^{N_0 } {n_0 (n_0 - 1)Y(n_0 )} \\ & = \sum_{n_0 = 0}^{N_0 } {n_0 (n_0 - 1)(n_0 - 2)Y(n_0 )} = 0 \end{aligned}$$
(30)

where N0 denotes the number of iterations.

Then, combining Eqs. (30) and (29), the recurrence relations of Y(n) can be formulated as follows:

$$\left\{ {\begin{array}{*{20}c} {Y(4m) = 0\ } \\ {Y(4m + 1) = 0} \\ \end{array} } \right.,\quad m = 0,1,2, \ldots$$
(31)
$$\left\{ {\begin{array}{*{20}c} {Y(4m + 2) = \frac{2!}{{(4m + 2)!}}\omega^{2m} Y(2)} \\ {Y(4m + 3) = \frac{3!}{{(4m + 3)!}}\omega^{2m} Y(3)} \\ \end{array} } \right.,\ \quad m = 0,1,2, \ldots$$
(32)

The final expression can be written as follows:

$${\bf{AY}} = {{\varvec{0}}}$$
(33)

where \({\bf{Y}} = \{ Y(2),\;Y(3)\}^{\rm{T}}\), and if N0 is an integer multiple of 4, we will have

$$\begin{array}{*{20}l} {A_{11} = \sum_{j = 0}^{\frac{N_0 }{4} - 1} {\frac{1}{(4j)!}\omega^{2j} } ,\quad A_{12} = 3\sum_{j = 0}^{\frac{N_0 }{4} - 1} {\frac{1}{(4j + 1)!}\omega^{2j} } } \hfill \\ {A_{21} = \sum_{j = 1}^{\frac{N_0 }{4} - 1} {\frac{1}{(4j - 1)!}\omega^{2j} } ,\quad A_{22} = 3\sum_{j = 0}^{\frac{N_0 }{4} - 1} {\frac{1}{(4j)!}\omega^{2j} } } \hfill \\ \end{array}$$
(34)

To obtain non-trivial Y, the determinant of A should be equal to zero, i.e., \(|{\bf{A}}| = 0\). The natural frequencies ωn (\(n =\) 1, 2, 3, \(\ldots\), N) can be worked out by DTM or seen in Ni et al. (2011). Then, after back substitution, the system’s mode functions will be obtained as follows:

$$y_n (\xi ) = \sum_{j = 0}^{\frac{N_0 }{4} - 1} {\frac{{\omega_n^{2j} }}{(4j + 2)!}\xi^{4j + 2} } - \frac{{\sum_{j = 0}^{\frac{N_0 }{4} - 1} {\frac{{\omega_n^{2j} }}{(4j)!}} }}{{\sum_{j = 0}^{\frac{N_0 }{4} - 1} {\frac{{\omega_n^{2j} }}{(4j + 1)!}} }}\sum_{j = 0}^{\frac{N_0 }{4} - 1} {\frac{{\omega_n^{2j} }}{(4j + 3)!}\xi^{4j + 3} }$$
(35)

For the other three kinds of pipes, similar results can be deduced and written as follows:

  1. (1)

    C–C pipe

    $$y_n (\xi ) = \sum_{j = 0}^{\frac{N_0 }{4} - 1} {\frac{{\omega_n^{2j} }}{(4j + 2)!}\xi^{4j + 2} } - \frac{{\sum_{j = 0}^{\frac{N_0 }{4} - 1} {\frac{{\omega_n^{2j} }}{(4j + 2)!}} }}{{\sum_{j = 0}^{\frac{N_0 }{4} - 1} {\frac{{\omega_n^{2j} }}{(4j + 3)!}} }}\sum_{j = 0}^{\frac{N_0 }{4} - 1} {\frac{{\omega_n^{2j} }}{(4j + 3)!}\xi^{4j + 3} }$$
    (36)
  2. (2)

    C–P pipe

    $$y_n (\xi ) = \sum_{j = 0}^{\frac{N_0 }{4} - 1} {\frac{{\omega_n^{2j} }}{(4j + 2)!}\xi^{4j + 2} } - \frac{{\sum_{j = 0}^{\frac{N_0 }{4} - 1} {\frac{{\omega_n^{2j} }}{(4j + 2)!}} }}{{\sum_{j = 0}^{\frac{N_0 }{4} - 1} {\frac{{\omega_n^{2j} }}{(4j + 3)!}} }}\sum_{j = 0}^{\frac{N_0 }{4} - 1} {\frac{{\omega_n^{2j} }}{(4j + 3)!}\xi^{4j + 3} }$$
    (37)
  3. (3)

    P–P pipe

    $$y_n (\xi ) = \sum_{j = 0}^{\frac{N_0 }{4} - 1} {\frac{{\omega_n^{2j} }}{(4j + 1)!}\xi^{4j + 1} } - \frac{{\sum_{j = 0}^{\frac{N_0 }{4} - 1} {\frac{{\omega_n^{2j} }}{(4j + 1)!}} }}{{\sum_{j = 0}^{\frac{N_0 }{4} - 1} {\frac{{\omega_n^{2j} }}{(4j + 3)!}} }}\sum_{j = 0}^{\frac{N_0 }{4} - 1} {\frac{{\omega_n^{2j} }}{(4j + 3)!}\xi^{4j + 3} }$$
    (38)

Although Eqs. (34)–(35) are obtained on the condition that N0 is an integer multiple of 4, in fact, as long as N0 is large enough, this result will always be obtained just by discarding the last few items.

In general, normalized mode functions are our subject, and they can be obtained by:

$$\hat{y}_n (\xi ) = \frac{y_n (\xi )}{{\int_0^1 {\left| {y_n (\xi )} \right|{\text{d}}\xi } }}$$
(39)

where \(\hat{y}_n (\xi )\)(\(n =\) 1, 2, 3, …, N) are just the undetermined \(\varphi_n (\xi )\) in Eq. (13).

It is commonly considered that higher-order natural frequencies contribute little to the system’s dynamics. As a result, most researchers mainly focus on the first few natural frequencies, meaning that N is not a large number here. In addition, in the next section, DTM-Galerkin will be used for convenience to indicate the proposed hybrid method combining DTM and Galerkin discretization.

5 Numerical Results

Dai et al. put DTM into the analysis practice of dynamics of a fluid-conveying straight pipe in Ni et al. (2011), where they concluded that \(N_0 = 60\) can output sufficiently accurate results with little time cost, and with increasing N0, the precision increases but more computing time is needed. Therefore, in order to balance accuracy and efficiency, N0 is directly chosen as 80 in the following calculations, and then determination of N is the only problem left.

5.1 Determination of N

Numerical experiments should be performed to find the appropriate value of N. During this process, DTM and GFM are chosen as the verification standards in calculating natural frequency and steady-state displacement response, respectively, since:

  1. (1)

    DTM has been verified to be of high efficiency and high precision in solving a homogeneous differential equation with high order in Mei (2008), Ni et al. (2011), Yalcin et al. (2009) and Chen and Chen (2009).

  2. (2)

    GFM can derive an analytical solution of a non-homogeneous differential equation in closed form, as shown in Li and Yang (2014), Zhao and Sun (2017), Li et al. (2014) and Abu-Hilal (2003, 2006).

With respect to natural frequency, if \(\beta = 0.5\) and a C–F pipe is taken as the research object, then the first four natural frequencies under different flow velocities can be numerically derived, and the results are shown in Table 1.

Table 1 First four natural frequencies under different flow velocities
Full size table

Table 1 reveals that as N increases, the results obtained by DTM-Galerkin are increasingly close to those of DTM, and when N increases to 8, the results of these two methods are in good agreement.

With respect to the steady-state displacement response, if the parameters are chosen as \(\beta = 0.5\), \(f_0 = 1.0\), \(a = 0.5\), and \(\overline{\omega } = 15.0\), then the amplitude of steady-state displacement response (denoted by ηmax) at \(\xi = 0.8\) of a C–F pipe can be calculated by GFM and DTM-Galerkin simultaneously, and the results are shown in Table 2.

Table 2 Amplitude of steady-state displacement response at \(\xi = 0.8\)
Full size table

Table 2 reveals that as N increases, the results of DTM-Galerkin are increasingly close to those of GFM, and when N increases to 8, the results of these two methods are very close to each other.

With the combination of Tables 1 and 2, it can be found that when \(N = 8\), the results of DTM-Galerkin accord well with those of existing methods; therefore, \(N = 8\) will be the first choice in the following calculations in this section.

5.2 Validity of the Current Method in Flow-Induced Vibration

5.2.1 Natural Frequency as a Function of Flow Velocity

If the mass ratio is taken as \(\beta = 0.262\), then calculations on the first four natural frequencies are performed and Fig. 2 shows the results. It is noteworthy that four curves composed of different markers correspond to the results by DTM, and four solid curves are obtained by DTM-Galerkin.

Fig. 2
figure 2

First four natural frequencies \({\text{Re}} (\omega )\) versus flow velocity u by DTM-Galerkin and DTM

Full size image

Figure 2 shows the variation in the first four natural frequencies following flow velocity, and the results of these two methods accord well with each other, revealing the effectiveness of DTM-Galerkin in calculating natural frequencies.

5.2.2 Modal Displacement Patterns of a P–P Pipe Under Different Flow Velocities

As was noted by Païdoussis (1998), the study of modal displacement patterns under different flow velocities is helpful in explaining the impact mechanism of flow velocity on the pipe’s conservative property; therefore, with the aid of DTM-Galerkin, modal displacement patterns of a P–P pipe under different flow velocities are shown in Fig. 3 along with the results by Païdoussis (1998), where uc is equal to \({\pi}\) for a P–P pipe (Ni et al. 2011; Païdoussis 1998).

Fig. 3
figure 3

Variation in modal forms of the fundamental mode of a P–P pipe of vanishing flexural rigidity during a period of oscillation

Full size image

From Fig. 3 it can be seen that the results by DTM-Galerkin accord well with those by Païdoussis (1998), confirming that the Coriolis term [\(2u\sqrt {\beta } \frac{\partial^2 \eta }{{\partial \xi \partial \tau }}\) in Eq. (8)] makes the system gyroscopic conservative, rather than just conservative (Païdoussis 1998) from the view of numerical calculation.

5.2.3 Eigenvalue of a C–F Pipe as a Function of Flow Velocity Under Different Mass Ratios

In order to clearly see variations in eigenvalues of fluid-conveying pipes following flow velocity, it is helpful to use an Argand diagram. The first four eigenvalues of a C–F pipe as functions of flow velocity under different mass ratios are then presented as shown in Fig. 4, where flow velocities have all been marked by black dots with specific values. In addition, results by Païdoussis (1998) are given for comparison.

Fig. 4
figure 4

First four eigenvalues of a C-F pipe versus flow velocity under different mass ratios

Full size image

As shown by Fig. 4, the results by DTM-Galerkin show good accordance with those by Païdoussis (1998) within the computing range of flow velocity, which reveals that DTM-Galerkin is effective in the current investigation.

5.2.4 Critical Velocities Under Given Conditions

The critical velocity for divergence (denoted by ucd) corresponds to \({\text{Re}} (\omega_i ) = {\text{Im}} (\omega_i ) = 0\), and the critical velocity for flutter (denoted by ucf) corresponds to \({\text{Re}} (\omega_i ) \ne 0\) and \({\text{Im}} (\omega_i ) = 0\) (Païdoussis 2008). Obeying this principle, some calculations are performed on critical velocities and Table 3 shows the results.

Table 3 Critical velocities of four kinds of pipes under given conditions
Full size table

As Table 3 shows, the results by DTM-Galerkin accord well with those in Païdoussis (1998); therefore, the correctness of DTM-Galerkin in calculating critical velocities is guaranteed.

5.2.5 Critical Velocity for Flutter of a C–F Pipe as a Function of Mass Ratio

Variation in critical velocity for flutter following the mass ratio is another key research point for a C–F pipe, and Fig. 5 shows both the scatter results for ucf as a function of β by DTM-Galerkin and the theoretical curve obtained by Païdoussis (1998).

Fig. 5
figure 5

Critical velocity for flutter ucf of a C-F pipe versus mass ratio β

Full size image

As Fig. 5 shows, it is clear that the results, especially those at inflection points, e.g., \(\beta \approx 0.3\), 0.65, 0.7, 0.85, or 0.93, by DTM-Galerkin are nearly identical to the theoretical curve (Païdoussis 1998) within the calculation range of mass ratio, further confirming the validity of DTM-Galerkin.

5.2.6 Critical Natural Frequency for Flutter of a C–F Pipe as a Function of Mass Ratio

As mentioned in the first sentence of Sect. 5.2.4, if flutter instability occurs, \({\text{Re}} (\omega_i ) \ne 0\) and \({\text{Im}} (\omega_i ) = 0\), the eigenvalues will degenerate to real numbers, namely the natural frequencies of a pipe. Then, using the same labeling protocol as ucf, ωcf can be used to denote the critical natural frequency for flutter below. As a simple example, the critical natural frequency for flutter of a C–F pipe as a function of mass ratio by DTM-Galerkin is shown in Fig. 6, where the theoretical curve obtained by Païdoussis (1998) is also given for comparison.

Fig. 6
figure 6

Critical natural frequency for flutter ωcf of a C-F pipe versus mass ratio β

Full size image

As depicted by Fig. 6, the scatter results for ωcf calculated by DTM-Galerkin perfectly match the theoretical curve (Païdoussis 1998) over the computing range of mass ratio, confirming the validity of DTM-Galerkin once again.

5.3 Validity of the Method in Calculating Steady-State Displacement Response

If \(\beta = 0.262\), \(u = 1.868\), \(f_0 = 0.686\), \(\overline{\omega } = 12.167\) and \(a = 0.5\), then DTM-Galerkin and GFM are used for comparison to calculate the amplitude of steady-state displacement response for all four kinds of pipes, and the results are shown in Fig. 7.

Fig. 7
figure 7

Amplitude of steady-state displacement response ηmax versus coordinate ξ by DTM-Galerkin and GFM

Full size image

Regardless of the supporting formats, Fig. 7 shows that the results of these two methods accord well with each other, confirming the effectiveness of DTM-Galerkin in calculating the steady-state displacement response.

6 Further Discussion: Implementation of the Current Method for Fluid-Conveying Curved Pipes

Inspired by the above investigation, we can naturally generalize our research objective to curved pipes with both ends rigidly supported (i.e., C–C, C–P, P–P pipes), for which the dimensionless in-plane governing equation can be written as follows (Zhao and Sun 2017):

$$\begin{array}{*{20}l} {\frac{\partial^6 \xi }{{\partial \theta^6 }} + 2\theta_{{\rm{op}}}^2 \frac{\partial^4 \xi }{{\partial \theta^4 }} + 2u\sqrt {\beta } \theta_{{\rm{op}}}^3 \left( {\frac{\partial^4 \xi }{{\partial \theta^3 \partial \tau }} + \theta_{{\rm{op}}}^2 \frac{\partial^2 \xi }{{\partial \theta \partial \tau }}} \right) + } \\ {\theta_{{\rm{op}}}^4 \left( {\frac{\partial^2 \xi }{{\partial \theta^2 }} + \frac{\partial^4 \xi }{{\partial \theta^2 \partial \tau^2 }}} \right) - \theta_{{\rm{op}}}^6 \frac{\partial^2 \xi }{{\partial \tau^2 }} = f(\theta ,\;\tau )} \\ \end{array}$$
(40)

with

$$\xi = \frac{w}{R},\;\theta = \frac{\Theta }{{\theta_{{\rm{op}}} }},\;\beta = \frac{{m_{\rm{f}} }}{{m_{\rm{f}} + m_{\rm{p}} }},\;u = RU\sqrt {{\frac{{m_{\rm{f}} }}{EI}}} ,\;\tau = \frac{t}{R^2 }\sqrt {{\frac{EI}{{m_{\rm{f}} + m_{\rm{p}} }}}} ,\;f(\theta ,\;\tau ) = \frac{R^3 }{{EI}}\frac{\partial F(\Theta ,\;t)}{{\partial \Theta }}$$
(41)

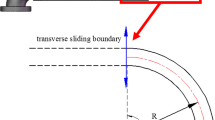
where w denotes tangential displacement, R is the constant radius of the centerline, Θ is the angle coordinate and θop is the opening angle of the pipe, mf and mp denote the mass per unit length of the fluid and pipe, respectively, the inner fluid flows with constant velocity U modeled by plug flow, EI represents the flexural stiffness, t is time, and F represents the excitation along the radial direction.

By the same manner as described in Sects. 3 and 4, the expressions of eigenfunction and steady-state displacement response by the proposed DTM-Galerkin will also be finally obtained, and a brief description will be given below. As Sects. 3 and 4 show, the core of DTM-Galerkin lies in the determination of normalized mode functions; therefore, to avoid repetition, some important intermediate results are given directly.

6.1 Normalized Mode Functions by DTM

The Euler–Bernoulli curved beam is used as the mechanical model deducing the normalized mode functions. Then, by neglecting fluid-related items, Eq. (40) degenerates into:

$$\frac{\partial^6 \xi }{{\partial \theta^6 }} + 2\theta_{{\rm{op}}}^2 \frac{\partial^4 \xi }{{\partial \theta^4 }} + \theta_{{\rm{op}}}^4 \left( {\frac{\partial^2 \xi }{{\partial \theta^2 }} + \frac{\partial^4 \xi }{{\partial \theta^2 \partial \tau^2 }}} \right) - \theta_{{\rm{op}}}^6 \frac{\partial^2 \xi }{{\partial \tau^2 }} = 0$$
(42)

Equation (42) is just the in-plane governing equation of the Euler–Bernoulli curved beam. Its solution can be expressed as follows:

$$\xi (\theta ,\;\tau ) = y(\theta )\exp ({\rm{i}}\omega \tau )$$
(43)

where \(\omega = \Omega R^2 \sqrt {{\frac{{m_{\text{p}} }}{EI}}}\) is the dimensionless characteristic variable, with mp, R, and EI having the same meaning as the curved pipe mentioned in Eqs. (40)–(41).

Substituting Eq. (43) into Eq. (42) and applying the DTM principle to this problem will yield the recursion formula written as follows:

$$Y(n_1 + 6) = - \frac{{2\theta_{{\text{op}}}^2 }}{{\prod_{i = 5}^6 {(n_1 + i)} }}Y(n_1 + 4) - \frac{{\theta_{{\text{op}}}^4 (1 - \omega^2 )}}{{\prod_{i = 3}^6 {(n_1 + i)} }}Y(n_1 + 2) - \frac{{\theta_{{\text{op}}}^6 \omega^2 }}{{\prod_{i = 1}^6 {(n_1 + i)} }}Y(n_1 )$$
(44)

where n1 denotes the n1th iteration in DTM.

If a C–C curved pipe is taken as an example, then differential transformations of its boundary conditions can be written as follows:

$$Y(0) = Y(1) = Y(2) = \sum_{n_1 = 0}^\infty {Y(n_1 )} = \sum_{n_1 = 1}^\infty {n_1 Y(n_1 )} = \sum_{n_1 = 2}^\infty {n_1 (n_1 - 1)Y(n_1 )} = 0$$
(45)

With the combination of Eqs. (44) and (45), and after further manipulations, the result can be expressed in matrix form as follows:

$${\bf{AY}} = {{\varvec{0}}}$$
(46)

where Aij (i, j = 1, 2, 3) are functions of ω and \({\bf{Y}} = \{ Y(3),Y(4),Y(5)\}^{{\varvec{T}}}\).

By solving \(|{\bf{A}}| = 0\), the natural frequencies ωn(\(n =\) 1, 2, 3, …, N) will be derived; in addition, Y(4) and Y(5) as functions of Y(3) can be obtained simultaneously. Therefore, the mode functions will be obtained after substituting the natural frequencies and Y(3), Y(4), Y(5) into

$$y_n (\theta ) = \sum_{n_1 = 0}^{N_1 } {\theta^{n_1 } Y(n_1 ,\;\omega_n )}$$
(47)

Normalizing \(y_n (\theta )\) will yield

$$\hat{y}_n (\theta ) = \frac{y_n (\theta )}{{\int_0^1 {\left| {y_n (\theta )} \right|{\text{d}}\theta } }}$$
(48)

where Y(3) is eliminated naturally and \(\hat{y}_n (\theta )\)(\(n =\) 1, 2, 3, …, N) are just the results as expected.

6.2 Deduction by Galerkin Method

The solution of Eq. (40) can be written as follows:

$$\xi (\theta ,\;\tau ) = \sum_{n = 1}^N {\hat{y}_n (\theta )q_n (\tau )}$$
(49)

where \(q_n (\tau )\) is the nth general coordinate, and N represents the number of normalized mode functions.

By the same procedures as Eqs. (14)–(16), a similar result will be obtained as follows:

$${{\varvec{K}}}_{N \times N} {{\varvec{q}}}_{N \times 1} + {{\varvec{G}}}_{N \times N} {\dot{\user2{q}}}_{N \times 1} + {{\varvec{M}}}_{N \times N} {\varvec{\ddot{q}}}{\,}_{N \times 1} = {{\varvec{f}}}_{N \times 1}$$
(50)

where

$$\begin{aligned} K_{mn} & = \int_0^1 {\hat{y}_m \left( {\frac{{{\text{d}}^6 \hat{y}_n }}{{{\text{d}}\theta^6 }} + 2\theta_{{\rm{op}}}^2 \frac{{{\text{d}}^4 \hat{y}_n }}{{{\text{d}}\theta^4 }} + \theta_{{\rm{op}}}^4 \frac{{{\text{d}}^2 \hat{y}_n }}{{{\text{d}}\theta^2 }}} \right){\rm{d}}\theta } ,\;G_{mn} = 2u\sqrt {\beta } \theta_{{\rm{op}}}^3 \int_0^1 {\hat{y}_m \left( {\frac{{{\text{d}}^3 \hat{y}_n }}{{{\text{d}}\theta^3 }} + \theta_{{\rm{op}}}^2 \frac{{{\text{d}}\hat{y}_n }}{{{\text{d}}\theta }}} \right){\rm{d}}\theta } \\ M_{mn} & = \int_0^1 {\hat{y}_m \left( {\theta_{{\rm{op}}}^4 \frac{{{\text{d}}^2 \hat{y}_n }}{{{\text{d}}\theta^2 }} - \theta_{{\rm{op}}}^6 \hat{y}_n } \right){\rm{d}}\xi } ,\;f_m = \int_0^1 {\hat{y}_m f(\xi ,\;\tau ){{\varvec{d}}}\xi } \\ \end{aligned}$$

The next steps for Eqs. (17)–(25) are the same as with the straight pipes, so there is no need to repeat them.

7 Conclusions

A new hybrid method combining differential transformation and Galerkin discretization is proposed for the first time to study the dynamics of fluid-conveying pipes, and some important conclusions are drawn as follows.

  1. (1)

    The proposed method combines the advantages of DTM in deducing mode functions and the Galerkin method in discretizing partial differential equations, thus demonstrating high accuracy and efficiency in solving governing equations of fluid-conveying straight pipes.

  2. (2)

    The same steps as those used for straight pipes can be taken for curved pipes, revealing that the proposed method can be easily extended to curved pipes.

  3. (3)

    The study combining DTM and Galerkin discretization can be extended to develop other hybrid algorithms, especially for the combination of the method that can deduce mode functions [e.g., VIM (Li and Yang 2017)] and the Galerkin method.

  4. (4)

    For further study, the application of the proposed method may be extended to the analysis for nonlinear static and dynamic responses of pipes conveying fluid.