1 Introduction

Two-phase flows of immiscible liquids appear in the context of several applications. Flows involving deformable droplets and slugs in a liquid carrier phase have the potential of enhancing heat transfer in microfluidic devices, as presented by Fischer et al. [1] and Bordbar et al. [2] in their study of thermal convective enhancement of microchannel heat sinks for electronics cooling. They observed that the droplets transport in a continuous phase, an enhanced convective thermal transport occurs as a result of blockage effects between subsequent droplets, causing vorticity rates and velocity distribution in the liquid slugs (see, e.g., Muzychka et al. [3]). Works related to the dynamics of temperature-actuated droplets have focused mainly on the generation and transport of liquid droplets (see, e.g., [4,5,6]). Most of these works have restricted their investigations through T-junctions and flow-focusing droplet formation devices that account for the effects of temperature-dependent viscosity and interfacial tension on the velocity and volume change (see [6, 7]), and rapid mixing within individual droplets [8]. Khater et al. [9] emphasized in their study that the physical behavior of dispersed droplets in response to a temperature change or heating source placed downstream far from the droplets ejection section requires further research on characterizing droplets thermal behavior within microchannels.

The main characteristic of two-phase droplet flows is the presence of a deformable interface separating the immiscible phases. Two-phase structures in immiscible fluids flows are subject to a high degree of topological change of the fluid interfaces (e.g., coalescence or breakup of droplets). Such topological changes make the interface tracking a challenging task (see [10, 11]). Difficulties in simulating the topological evolution of deformable interfaces come from the fact that its movement follows a material description, while the transport process is predicted from spatial descriptions; to merge these two frameworks are not straightforward (Santra et al. [11]). Standard strategies for tracking interfaces are the front-tracking method (see, e.g., [12,13,14,15]), sharp interface methods such as volume-of-fluid [2, 16, 17] and level-set [18,19,20]), and diffuse interface method (see [21, 22]); each one presenting advantages and drawbacks in representing the interface. As emphasized by Santra et al. [11], for example, the level-set and volume-of-fluid methods cannot handle the rapid spatial change in the micro-scale topology of the liquid interface. Standard treatments of two-phase droplet flows consider the interface between two phases as discontinuity surfaces. In contrast, the diffuse interface method assumes a three-dimensional transition zone separating the two phases; the material properties characterizing the bulk phases and interfacial forces vary smoothly. The diffuse interface method uses free energy for describing the interface that depends on the intermolecular forces of the components (Santra et al. [11]). The diffuse interface method provides a consistent thermodynamic formulation, which allows capturing topological changes; see Gurtin et al. [21]. Further, the diffuse interface method allows for the modeling of interfacial phenomena without a priori assumptions on the shape of the moving interface, which is represented by a thin, smooth transition layer; this is achieved by introducing a phase-field variable, which requires an evolution equation.

In this view, the Cahn–Hilliard equation [23, 24] or its non-conservative counterpart the Allen–Cahn equation [25] are commonly used to describe the dynamic evolution of the phase-field variable. When coupled to the Navier–Stokes equations, introduce interfacial stress given by the chemical potential and the gradient of the phase-field parameter (see Gurtin et al. [21]).

Phase-field modeling based on the Navier–Stokes–Cahn–Hilliard has been used for capturing the interfacial phenomena of multicomponent and multiphase flow within microfluidics, including droplet dynamics in unbounded flow, such as droplet formation and breakup; see, e.g., [26,27,28,29,30,31] or the presence of solid boundaries. De Menech [26] studied modeling of droplet breakup in a microfluidic T-shaped junction with a phase-field model in the hydrodynamic regime where capillary and viscous stresses dominate over inertial forces within microfluidic devices. In a recent study by Bai et al. [32], a three-dimensional droplet generation in a flow-focusing microchannel is studied by performing a phase-field method based on the Navier–Stokes equations coupled with the Cahn–Hilliard equation. These works have studied the dynamics of generation and transport of droplets in T-junction, co-flowing, and contraction-expansion microfluidic devices. Analysis of droplets transport within microfluidics is complicated due to the need for three-dimensional simulating of droplets. According to Khater et al. [9], most of the droplet generation and transport are limited to two-dimensional simulations aiming to study heat transfer enhancement and characterize internal vortices in liquid plugs in microchannels and within the droplets through the Marangoni effect (see, e.g., [1, 33]).

In this work, we study the thermal behavior of two-phase droplet transport within a co-flowing microtube subjected to a temperature change. Further, we analyze the effect of two-phase droplet frequency in terms of the flow rate ratio and recirculation between droplets on the heat transfer enhancement. For that, we use an axisymmetric phase-field model based on the Navier–Stokes–Cahn–Hilliard equations coupled with the heat equations for simulating droplets transport in the co-flowing microchannel.

The model is solved using a mixed finite element method implemented in the software COMSOL Multiphysics. Then, the model is applied to investigate the effects of the droplets dynamics on the temperature distribution within the microchannel. Further, we study the thermal convective enhancement within microchannel by the vortices in the continuous phase due to liquid–liquid interfaces. We assume a simplified model by considering droplets formation in a co-flowing microchannel and heat transfer as a Graetz problem.

We have structured the remainder of this work as follows. In Sect. 2, we introduce the problem definition and mathematical modeling for the two-phase flow. Then, in Sect. 3, we describe the numerical details to solve the physical problem using a mixed finite element implementation in the COMSOL Multiphysics. We present results and discussions in Sect. 4 and the conclusion in Sect. 5.

2 Problem definition and phase-field equations

2.1 Geometry of co-flowing microtube

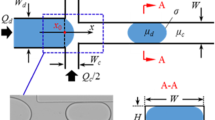
We adopted a co-flowing microtube geometry to reproduce a droplet two-phase flow regime studied by Fischer et al. [1]. The co-flowing liquid stream controls the generation and transport of dispersed droplets in a dripping regime (see, e.g., [34]), such that hydrodynamic forces are employed to control the pinching of the liquid–liquid interface, modifying the size of the droplets, and generation frequency. The geometry of the cylindrical microchannel, which comprises two aligned capillary tubes, is shown in Fig. 1), with the radius of the carrier cylindrical microchannel and injection capillary tube are \(R=500\,\upmu\)m and \(r_{\!i}=0.2R\), respectively. The total length is 50R to ensure full thermal development of droplet two-phase flow, which can also ensure the fully developed flow in the case of single-phase flow. The wall temperature distribution of the microtube is set to be 300 K for \(-30R< z< 0\) and 340 K for \(0< z< 20 R\), respectively.

Fig. 1
figure 1

Geometric model of the axisymmetric microtube in the co-flowing configuration

Full size image

Driven by pressure loads, the dispersed droplets (phase 2) flow into the continuous liquid (phase 1). A train of droplets is formed, detached, and immersed into the isothermic region of the capillary tube, \(-30R<z<0\). As they move with the continuous liquid, the flow develops around the droplets deforming the interface between the two phases and their surrounding, immiscible liquid. After that, the train of droplets enters into the thermally developing region of the microtube. Heat transfer of a single-phase-laminar flow in the cylindrical microchannel follows the classical Graetz problem; see, e.g., [35].

2.2 Phase-field equations

We apply a particular version of the Navier–Stokes–Cahn–Hilliard equations introduced in Gurtin et al. [21], which were originally developed for predicting separation of two-phase binary fluids, to study the following physical process occurring in the co-flowing cylindrical microchannel (Fig. 1): Droplet dynamics (formation, breakup, coalescence, and transport), convective heat transfer, and two-phase flow of immiscible liquids. In short, we use the phase-field model based on the Cahn–Hilliard equation to capture the interface between droplet and continuous phase. The Navier–Stokes and continuity equations are solved to simulate the flow field. Thus, the governing equations are given by

$$\left. {\begin{array}{*{20}l} {{\varrho }{\mathbf{\dot{v}}} = - {\text{grad}}\,p + {\text{div}}\left( {\nu ({\text{grad}}\,{\mathbf{v}} + ({\text{grad}}\,{\mathbf{v}})^{{ \top }} )} \right) + \mu {\mkern 1mu} {\text{grad}}{\mkern 1mu} \varphi ,} \hfill \\ {{\text{div}}{\mkern 1mu} {\mathbf{v}} = 0,} \hfill \\ {{\text{d}}\frac{{\partial \varphi }}{{\partial t}} + {\mathbf{v}} \cdot {\text{grad}}\varphi = m\Delta \mu ,} \hfill \\ {\mu = f^{\prime } (\varphi ) - \lambda \Delta \varphi ,} \hfill \\ \end{array} } \right\}$$
(1)

which must be solved for the gross velocity field \({\mathbf {v}}\), pressure p, phase-field variable \(\varphi\), and chemical potential \(\mu\); where \(\dot{{\mathbf {v}}}=\left( \frac{\partial {\mathbf {v}}}{\partial t} + {\mathbf {v}}\cdot \mathrm {grad}{\mathbf {v}}\right)\) denotes the material-time derivative, \(\varDelta\) denotes the Laplacian operator, and m is the mobility. The term \(\mu \,\mathrm {grad}\varphi\) accounts for surface tension force on the interface between two phases.

In addition, we coupled the phase-field model to the energy equation,

$$\begin{aligned} \varrho c_v\!\left( \frac{\partial T}{\partial t}+{\mathbf {v}}\cdot \mathrm {grad}\,T\right) = \mathrm {div}\big (k\,\mathrm {grad}\,T\big ), \end{aligned}$$
(2)

to describe thermal effects and temperature-dependent capillary, where T, \(c_v\), k are, respectively, the temperature field, specific heat capacity at constant volume, and thermal conductivity.

In the phase-field specialization, we assume that the two-phase fluids are immiscible except in a small interfacial region between the phases, which allows mixing and constituents diffusion (see [36]). Furthermore, the liquid phases are treated as incompressible with no phase change and mass transfer across the interface (see., e.g., [22]). The mass density \(\varrho\) of fluid in each phase is calculated as a smooth function of the phase-field variable \(\varphi\) by

$$\begin{aligned} \varrho =\frac{(1-\varphi )}{2}\varrho _d+\frac{(1+\varphi )}{2}\varrho _c, \end{aligned}$$
(3)

which allows the unmixed liquids to have different mass densities, \(\varrho _c\) and \(\varrho _d\); where subscripts d, c refer to dispersed and continuous phases, with \(\varphi _d=-1\) and \(\varphi _c=1\). In a similar way, the fluid viscosity \(\nu\), specific heat capacity at constant volume \(c_v\), and thermal conductivity of fluid in each phase are calculated as follows:

$$\begin{aligned} \begin{aligned}&\nu =\frac{(1-\varphi )}{2}\nu _d+\frac{(1+\varphi )}{2}\nu _c,\quad c_{v}=\frac{(1-\varphi )}{2}c_{v_d}+\frac{(1+\varphi )}{2}c_{v_c},\\&\quad k=\frac{(1-\varphi )}{2}k_{d}+\frac{(1+\varphi )}{2}k_{c}, \end{aligned} \end{aligned}$$
(4)

The Cahn–Hilliard Eq. (1\(_{3,4}\)) describes the transport of \(\varphi\), which is predicted on assuming that the free-energy density is given by a double-well potential with wells at \(\varphi _d=-1\) and \(\varphi _c=1\) as:

$$\begin{aligned} f(\varphi )=\frac{\uplambda }{4\varepsilon ^2}(\varphi ^2 - 1)^2. \end{aligned}$$
(5)

where \(\uplambda\) is the mixing energy per unit of length that can be related to the surface tension \(\sigma\) and interfacial thickness \(\varepsilon\) as [37]

$$\begin{aligned} \uplambda = \frac{3\sqrt{2}}{4}\varepsilon \sigma . \end{aligned}$$
(6)

Following Bai et al. [32] and Lim and Lam [38], we assume that the mobility is constant and given by

$$\begin{aligned} m = \chi \varepsilon ^2, \end{aligned}$$
(7)

where \(\chi\) is a positive parameter representing a mobility tuning that controls the magnitude of the diffusivity of the phase field. Thus, a large enough value of \(\chi\) is required to retain a constant interfacial thickness but small enough so that the convective term is not overdamped [38].

In the advective Cahn–Hilliard Eq. (1\(_3\)), \(m\varDelta \mu\) represents a term that minimizes the free energy of the system, which includes higher-order derivatives of \(\varphi\), designed to keep the interface compact. Note that \(m\varDelta \mu\) vanishes as m goes to zero, which gives a pure advective transport equation as in the level set method. However, the numerical solution with \(m\varDelta \mu =0\) is unstable and of small practical use in most cases. This diffusion term is analogous to numerical diffusion that stabilizes the numerical schemes and improves mass conservation.

The system of Eqs. (1) and (2) introduced above must be supplemented with physically appropriate boundary and initial conditions. The geometry of the co-flowing microtube is assumed to be axisymmetric, as shown in Fig. 1. We therefore adopt the top half of the geometry as a two-dimensional axisymmetric domain. We impose a symmetry boundary condition at the centerline of the microtube domain. We set uniform velocities \(u_d\) and \(u_c\) and temperature \(T_{w_1}\) to the inlet boundary conditions for the continuous and dispersed phases, while the outflow boundary condition with a fixed, zero-pressure constraint \(p_0=0\), and zero fluxes are imposed to the outlet (see, e.g., [39,40,41])

$$\begin{aligned} {\mathbf {n}}\cdot m\,\mathrm {grad}\mu =0,\quad {\mathbf {n}}\cdot \mathrm {grad}\varphi = 0,\quad {\mathbf {n}}\cdot k\,\mathrm {grad}\,T = 0, \end{aligned}$$
(8)

where \({\mathbf {n}}\) is the outward-pointing unit vector normal to the boundary. Further, we impose the no-slip, zero velocity \({\mathbf {v}}={\mathbf {0}}\) at the tube wall. Following Fischer et al. [1], we set a temperature distribution as a step function along the microchannel wall, 300 K on the isothermal entrance section and increased to 340 K on the heated section, as shown in Fig. 1. Furthermore, we assume that the liquid thermal behaviors are in thermal equilibrium with the wall at the liquid–solid interface (see, e.g., Gad-el-Hak [42] and Rosengarten et al. [43]). For droplet generation, the phases are set as \(\varphi _d=-1\) and \(\varphi _c=1\) at the inlet for dispersed and continuous, respectively. As a consequence, the dispersed phase flow forms a train of droplets; the droplets size and length between droplets can be adjusted by changing the flow rates \(Q_c\) when \(\varphi _c=1\) and \(Q_d\) when \(\varphi _d=-1\). The flow rate ratio \(\alpha\) is defined as \(\alpha = Q_d/Q_c\) and is used to control the droplets frequency generation.

We identify key controlling parameters of dispersed droplets generator. As in Khater et al. [9], these groups include the physical properties and flow rates of dispersed and continuous phases and the dimensions of microchannel. In our analysis, we will adopt three non-dimensional groups, say the Reynolds number \(\mathrm {Re}=\varrho _c{\bar{v}}_c R/\nu _c\), capillary number \(\mathrm {Ca}=\nu _c{\bar{v}}_c/\sigma\), and flow rate ratio \(\alpha = Q_d/Q_c\). These groups are calculated from the dimensional variables that include the volumetric flow rate Q, the viscosity \(\nu\), and interfacial tension \(\sigma\) between two immiscible liquids into the microtube, and the radius of the microtube as the characteristic length scale.

3 Numerical method

We have used the finite element software COMSOL Multiphysics to simulate the two-phase droplet and heat transfer in the microtube. In this case, the Navier–Stokes–Cahn–Hilliard and heat transfer Eqs. (1)–(2) are solved using a mixed finite-element method. The Cahn–Hilliard Eq. (1\(_{3,4}\)) is handled by adding an auxiliary variable to separate the fourth-order equation into two coupled second-order equations (see, e.g., [39, 41]).

The system of Eqs. (1) and (2) was implemented in the COMSOL Multiphysics using the Laminar Two-Phase Flow Module and coupled with the Heat Transfer Module. For the spatial discretization, we adopt Taylor–Hood elements (see, e.g., Ern and Guermond [44]) that are inf-sup stable elements. Thus, the velocity \({\mathbf {v}}\) and order parameter \(\varphi\) are interpolated by piecewise-quadratic functions, while the pressure p, chemical potential \(\mu\), and temperature T are interpolated by piecewise-linear functions. Furthermore, we apply an implicit second-order BDF method, with free time-stepping controlled by the solver to take larger or smaller time-steps sizes as required to satisfy the specified tolerances during the computations. At each time-step, the discrete mixed problem results in a system of nonlinear equations that is solved through a fully coupled approach using the damped Newton method. The direct solver PARDISO was selected to solve the discrete system.

3.1 Mesh independence

To study the heat transfer enhancement induced by the two-phase flow within the microchannel, as shown in Fig. 1, immiscible droplet liquid is injected in a co-flowing liquid stream at uniform temperature of 300 K, with the flow rate \(Q_c=64.2\) \(\mu\)l/s, which correspond to the Reynolds number of 50. The flow rate ratio was set at \(\alpha =0.223\), corresponding to a flow rate of 14.3 \(\mu\)l/s for the dispersed phase. Those choices have been made to reproduce the results presented in [1] in order to validate our results, as will be discussed in Sect. 4.1. Thus, Table 1 lists the physical properties of the continuous (water) and dispersed (oil PAO) phases used in the numerical simulations. Furthermore, we adopted an interfacial tension value \(\sigma _0=30\times 10^{-3}\) N/m at 300 K and a temperature coefficient \(\kappa =-0.06\times 10^{-3}\) N/(m K), such that the interfacial tension is given by \(\sigma =\sigma _0+\kappa (T-T_{w_1})\); see [1] for details.

Table 1 Physical properties of the liquids used in the study, see Ref. [45]
Full size table

As a measure of the heat transfer enhancement caused by the train of two-phase droplets flow, we have used the Nusselt number given by

$$\begin{aligned} N\!u_z=\frac{2Rq\vert _{w,z}}{k(T_b-T_{w,z})}, \end{aligned}$$
(9)

where \(q\vert _{w,z}\) is the heat flux at the wall, and the local bulk-mean-temperature \(T_b\) is calculated as follows:

$$\begin{aligned} T_b = \frac{\int _0^{R}\varrho c_v v_z T r \mathrm{d}r}{\int _0^{R}\varrho c_v v_z r \mathrm{d}r}. \end{aligned}$$
(10)

The axisymmetric, two-dimensional domain (Fig. 1) is meshed into different structured grids using \(n_{el}\) quadrilateral elements. To verify the independence of the results of the mesh choice, we compared the distributions of the normalized axial velocity and dimensionless temperature \(\vartheta = (T - T_{w,z})/(T_b - T_{w,z})\), where \(T_{w,z}\) is the wall temperature. As shown in Fig. 2, the axial velocity profiles in five meshes are coincident. The dimensionless temperature distribution presents a deviation between meshes with \(n_{el}=50,284\) and 70,038 that are almost negligible, as shown in Fig. 3. Since the two-phase droplet flow increases the local Nu(z) number in comparison to the single-phase flow in the microtube, the Nu number varies periodically in the axial direction. Thus, we adopt the equivalent \(N\!u^*\) number by space and time averaging Nu to verify the independence of meshes on the convective heat transfer. Figure 4 shows that Nu\(^*\) number tends to a plateau value as the number of elements \(n_{el}\) grows in the mesh. For the following studies, we employed mesh with 60,757 elements that satisfy mesh independence, with accuracy and small computational consumption.

Fig. 2
figure 2

Normalized axial velocity evaluated at \(z = 20R\) for different meshes

Full size image
Fig. 3
figure 3

Dimensionless temperature profiles evaluated at \(z = 20R\) for different meshes

Full size image
Fig. 4
figure 4

Average Nusselt number as a function of the number of elements in the mesh

Full size image

4 Results and discussion

4.1 Heat transfer enhancement of droplet two-phase flow

The flow patterns results are shown in Fig. 5 at the flow rate of 14.3 \(\mu\)l/s for dispersed phase. The dispersed phase generates from the tip of the internal microtube followed up with droplet growth, breakup and transport into the moving continuous phase under a dripping regime. Based on imposed hydrodynamic flow conditions, the simulations predicted that the spherical droplets are distanced by around 3.7R from each other and the droplet radius is around 0.8R, which are in agreement with the flow pattern obtained in the studies by Fischer et al. [1].

Fig. 5
figure 5

Snapshots of formation, breakup, and transport of dispersed droplets in the co-flowing microtube for \(Q_c=64.2\) \(\mu\)l/s and flow rate ratio \(\alpha =0.223\) at different time instant

Full size image

The results show convective heat transfer enhancement in the cylindrical microchannel and the influence of droplets frequency and internal circulation zones on the heat transfer rates. We compare the heat transfer rate predicted from droplets two-phase flow with results presented in the studies by Fischer et al. [1], which the focus was to study the effects of a train droplets on the local Nusselt number, without take into account the droplet generation. Figure 6 shows the local Nusselt number \(N\!u_z\) and temperature distribution in the axial z-direction at the steady state. As in the studies by Fischer et al. [1], a strongly thermal enhancement is achieved in comparison with a single-phase flow and the Graetz solution. The local Nusselt obtained from the classical approximated solution of the Graetz problem yields \(N\!u_z = 1.357\left( P\!e R/z\right) ^{1/3}\), where \(Pe=2\varrho _c{\bar{v}}_c c_p R/k_c\) is the Peclet number based on the properties of continuous phase.

From Fig. 6, we observe an augmentation of the local Nusselt number profile induced by the velocity of the recirculating zone between droplets being directed from the wall toward the center of the microchannel, meaning a enhancement in the convection transport. These recirculations zones appear periodically in the region between two subsequent droplets, as shown in zones I and III. The temperature distribution in the droplets and continuous phase suggests that the hotter liquid is transported from the heated wall toward the center line of the channel where the liquid is colder. Thus, the liquid in front of the droplets is hotter than the liquid in their tails, with a strong increase in the local Nusselt number. A similar process occurs within the droplets (see region II), where recirculations are observed, as shown in Fig. 7. The predicted local \(Nu_z\) along the co-flowing regime in the microtube is in good agreement with the front-tracking-based numerical results obtained by Fischer et al. [1]. The local Nusselt number calculated from the phase-field simulation exhibits a maximum value slightly above 12, in comparison to single-phase flow.

For model validation, we used the root-mean-squared percentage error to measure how well the predicted local Nusselt number agrees with Fischer et al. [1] simulations for liquid–liquid spherical droplets. In short, it is employed the standard formula (see, e.g., Cherbakov et al. [46])

$$\begin{aligned} \text{ Root-mean-squared } \text{ error }=\sqrt{\frac{\sum _1^n\left( \frac{P-F}{P}\right) ^2}{n}}\times 100, \end{aligned}$$
(11)

where P and F variables represent the predicted and Fischer et al. [1] local Nusselt numbers, respectively, and n is the number of data points. The root-mean-squared percentage error was determined to be around 5.5\(\%\).

Fig. 6
figure 6

Variation of Nu and temperature distribution along the co-flowing microtube in single-phase and two-phase droplets flows. The liquid in the droplets is polyalphaolefine (PAO) surrounded by water as continuous phase, with flow rate ratio \(\alpha =0.223\). The simulations are carried out for \(\mathrm {Re}=50\) and \(\mathrm {Ca}=2.6\times 10^{-3}\) in the continuous phase. The local Nu of the liquid–liquid droplet flow calculated by Fischer et al. [1]. The root-mean-squared percentage error for the predicted and Fischer et al. simulations was determined to be around 5.5\(\%\)

Full size image
Fig. 7
figure 7

Streamlines for a moving frame referential with the droplets mean velocity

Full size image

We consider the effect of dispersed droplets production frequency on the heat transfer enhancement. Figure 8 shows flow patterns predicted at flow rate ratios \(\alpha\) ranging from 0.1 to 0.3 (see, e.g., Asthana et al. [47]) in the dripping regime at steady state and fixed capillary number based on the bulk mean velocity Ca\(= 2.6 \times 10^{-3}\). Note that increasing the flow rate ratio \(\alpha\), the dispersed-phase frequency increases, and thus, more dispersed droplets flow through the microchannel. Figure 9 shows the influence of the frequency of the dispersed droplets on the temperature field in comparison to the temperature distribution in single-phase flow. The result shows that the convective heat transfer improvement is strongly associated with the distance between droplets in co-flowing. We associate the convective thermal enhancement with the flow structure shortening. The length of flow structures (the distance between droplets) is controlled using five values of the flow rate ratios \(\alpha\) to generate different dispersed-phase frequency and flow patterns. From Fig. 9, it can be verified that the temperature distribution between two droplets is affected in front of the droplet and in the rear of droplets as the flow rate ratio \(\alpha\) increases, as shown in Fig. 10, when considering the Nusselt number averaged over time. It is interesting to note that shortening the distance between droplets as increasing the flow rate ratio, the circulating flow between two droplets affects the convective thermal transport.

Fig. 8
figure 8

Flow patterns for different flow rate ratios at the steady state. a \(\alpha =0.1\), b \(\alpha =0.15\), c \(\alpha =0.2\), d \(\alpha =0.25\), and e \(\alpha =0.3\)

Full size image
Fig. 9
figure 9

Temperature distribution for two-phase droplets flows and different flow rate ratios at the steady state. a single-phase, b \(\alpha =0.1\), c \(\alpha =0.15\), d \(\alpha =0.2\), e \(\alpha =0.25\), and f \(\alpha =0.3\). The temperature field of the single-phase flow is added for comparison

Full size image
Fig. 10
figure 10

Nusselt averaged over time for different flow rate ratios \(\alpha\)

Full size image

By introducing the flow-type parameter (Lee et al. [48])

$$\begin{aligned} \omega = \frac{\vert {\mathbf {D}}\vert -\vert {\mathbf {W}}\vert }{\vert {\mathbf {D}}\vert +\vert {\mathbf {W}}\vert }, \end{aligned}$$
(12)

we quantify the flow structures within and between subsequent droplets, wherein \({\mathbf {D}}\) represents the symmetric strain rate tensor (stretching) that gives the local deformation and \({\mathbf {W}}\) is the skew part of the velocity gradient that gives the local rotation in the flow field; their respective magnitudes are defined as \(\vert {\mathbf {D}}\vert =\sqrt{\mathrm {tr}\,{\mathbf {D}}^2}\) and \(\vert {\mathbf {W}}\vert =\sqrt{-\mathrm {tr}\,{\mathbf {W}}^2}\) (see, e.g., [49]). The flow-type parameter \(\omega\) varies from \(-1\) (pure rotational flow) to 1 (pure extensional flow); \(\omega =0\) represents a pure shear flow. The distribution of \(\omega\) from Fig. 11 evidences the regions where rotation prevails over-stretching rates, regions with \(\omega <0\). When increasing the dispersed-phase frequency (distance between two droplets shortening), the recirculation structure decreasing in size between subsequent droplets and stretching zones prevails where \(\omega >0\). Thus, from Fig. 9, it can be found that these flow structures (recirculation zones) can affect the convective heat transfer. When compared with the heat transfer in the single-phase flow, we observe an increase of time-averaging Nu number, which suggests a bound limit for the heat transfer enhancement, as shown in Fig. 10. It is interesting to note that after the flow rate ratio reaches a critical value, the Nusselt number starts decreasing. Augmenting the flow rate ratio, the distance between two droplets decreases, presenting a smaller recirculation structure in size between droplets and stretching domains prevails with \(\omega >0\), as shown in Fig. 11.

Fig. 11
figure 11

Flow-type parameter field for a \(\alpha =0.1\), b \(\alpha =0.15\), c \(\alpha =0.2\), d \(\alpha =0.25\) and e \(\alpha =0.3\)

Full size image

We find from Fig. 12 the existence of an optimal flow rate ratio, which predicts a maximum heat transfer enhancement of two-phase droplet flow in the microtube.

Fig. 12
figure 12

Nusselt number spatial averaged for different flow rate and single phase (red dashed line)

Full size image

Figure 13 shows the pressure loss distribution as a function of flow rates. When the average Nu number augments around 34%, we find an increase of about 36.9% of pressure loss at the flow rate of 0.225.

Fig. 13
figure 13

Dimensionless pressure loss versus flow rate ratio

Full size image

4.2 Effects of capillary on the heat transfer

The Capillary number Ca relates viscous and interfacial forces. For low values of Ca, droplets tend to be elongated because the interfacial tension forces dominate over the actions of the viscous ones. As Ca augments, the breakup droplet rate steadily increases by the effect of the viscous forces accordingly grows, and droplet deformation decreases. For a sufficiently high capillary number, the droplet diameter becomes smaller and spherical droplets are formed, with the shear stress exerted on the droplet more concentrated in one point, as observed in Ref. [50].

Figure 14 shows two-phase droplet flow patterns taking into account different Ca numbers and fixed flow rate ratio. Since the Ca number influences the droplet’s shape and breakup rate, it strongly affects the convective heat transfer, as shown in Fig. 15. As Ca increases, droplets spacing and volume decrease while promoting an initial augmentation in the time-averaging Nusselt number. While Ca continues increasing, droplets become spherical and their diameter progressively smaller, which reduces recirculation between droplets in the dripping regime and, thus, the time-averaging Nusselt number decreases.

Fig. 14
figure 14

Droplet formation rate with different Ca and fixed flow rate ratios \(\alpha = 0.2\). a Ca\(= 0.5 \times 10^{-3}\), b Ca\(= 1 \times 10^{-3}\), c Ca\(= 2 \times 10^{-3}\), d Ca\(= 3 \times 10^{-3}\), e Ca\(= 4 \times 10^{-3}\), f Ca\(= 5.75 \times 10^{-3}\), and g Ca\(= 6 \times 10^{-3}\)

Full size image
Fig. 15
figure 15

Nusselt averaged over time for different capillary numbers and flow rate ratios \(\alpha = 0.2\)

Full size image

Figure 17 shows the dimensionless pressure loss as a function of the flow rate ratio for each value of the Ca number simulated; we find that the pressure loss steadily decreases as Ca augments. It is interesting to note that an optimum scenario regarding the heat transfer enhancement and pressure loss is obtained for \(Ca = 2.6 \times 10^{-3}\), as shown in Fig. 16 and 17.

Fig. 16
figure 16

Effect of flow rate ratio \(\alpha\) and capillary number Ca on the spatial average Nusselt number

Full size image
Fig. 17
figure 17

Dimensionless pressure loss for different flow rate ratios \(\alpha\) and capillary number Ca

Full size image

5 Conclusions

In this work, we employed a phase-field method based on the Navier–Stokes–Cahn–Hilliard equations coupled with the energy equation to simulate the heat transfer enhancement induced by a train of silicone-oil droplets in co-flowing microtube. Different from previous studies, we considered in the simulations droplets formation, breakup, and transport into the thermal entrance region. We found that with the presence of a train of droplets in the continuous phase flow, the heat transfer can be enhanced with an increase in the pressure loss relative to the single-phase flow. Moreover, the enhancement in the convective heat transfer varies non-monotonically with the flow rate ratio. By augmenting the droplet generation frequency, the distance between droplets decreases, and also the recirculation structure separating droplets, which improves the thermal mixing. Thus, the space-time-averaging Nu number over the heated region increases firstly and then decreases with the flow rate ratio. A comprehensive effect of such observation suggests an optimal flow rate ratio in which the heat transfer enhancement of two-phase droplet flows in the microtube reaches a maximum for the dripping regime. The time-averaging Nu number decreases as the capillary number augments. As a consequence, the heat transfer enhancement decreases since the droplets decrease their size.

As a final remark, numerical simulations compose an outstanding approach to the study of convective heat transfer enhancement induced by two-phase droplet flow in microchannels since they can predict complex two-phase flow conditions free from external interference. However, numerous factors point toward the requirement of a theoretical model for immiscible two-phase flow that accounts for temperature-dependent capillarity to describe the Marangoni effect. Thus, as a work-in-progress, we will propose a non-isothermal phase-field model for immiscible incompressible fluid flows with temperature-dependent capillarity in order to describe the Marangoni effect (or thermo-capillarity convection).