1 Introduction

Inkjet printing technology has found numerous applications since its original application of printing digital images or text on papers. In recent years, inkjet technology has been employed to deposit functional materials which are mixed with liquid, directly on a solid substrate. Example applications of inkjet printing include manufacturing of light-emitting diode (LED) display panel (Haskal et al. 2002; Koo et al. 2006; Ummartyotin et al. 2011), plastic transistor circuits (Sirringhaus et al. 2000), three-dimensional electronic circuits (Mei et al. 2005) and DNA micro-arrays (Heller 2002; Kumar et al. 2005). Impingement and spreading of a droplet on a solid substrate are the critical processes that determine the size and location of the features to be deposited.

Conventional inkjet material deposition for the creation of micron-sized feature is limited to a minimum of 20–50 μm (Sele et al. 2005) because of the difficulties in generating smaller droplet and controlling of droplet spreading. However, manufacturing of electronic devices such as field-effect transistors (FET) or active matrix display with thin-film transistor (TFT) circuit often demands highly accurate deposition of smaller feature (Tekin et al. 2008; Arias et al. 2004). A jetted droplet will also spread beyond its static diameter upon impingement and might contaminate adjacent droplets which are deposited at close proximity, for example, on a DNA micro-array. Among the solutions to overcome these problems, small grooves with width ranging from 5 to 15 μm have been embossed on the surface to guide the spreading of droplet (Hendriks et al. 2008). Surface energy patterning (to create hydrophobic and hydrophilic regions) has also been exploited to fabricate 15 μm to 500 nm features through the dewetting of droplets and preventing uncontrollable spreading of ink droplets on substrates (Sirringhaus et al. 2000; Wang et al. 2004; Lin et al. 2009). Droplet movement driven by heterogeneity in wettability (Bliznyuk et al. 2011; Chaudhury and Whitesides 1992; Kooij et al. 2012; Chu et al. 2010) has also been demonstrated and could be utilized as a potential mechanism to align and position droplet on the substrate. In this investigation, we focus on the spreading of an impinging droplet with a finite velocity on a surface with heterogeneous wettability. We assume that the wetted surface is smooth (roughness is small as compared to the size of the droplet).

To understand the spreading of droplets on a heterogeneous surface, various experimental and theoretical studies have been performed. Wenzel (1936) and Cassie and Baxter (1944) are among the first few researchers who presented the classical studies on the wetting of a sessile droplet on a heterogeneous surface. Further studies of three-phase contact-line dynamics on heterogeneous surfaces have been conducted for the dipping of a plate into a liquid bath (Joanny and Robbins 1990) and liquid column in a capillary tube (Raphael and de Gennes 1989). Léopoldès and Bucknall (2005) experimentally showed that, on a micro-stripe surface with high wettability contrast, a droplet spreads mainly along the stripe pattern direction, while the contact line is pinned in the perpendicular direction, resulting in an elongated droplet. In these experimental investigations, the droplet size is one to two order larger than the width of the stripe and the spreading behavior was shown to be dependent on the relative width of the hydrophilic and hydrophobic strips (Bliznyuk et al. 2009). Bliznyuk et al. (2010) also identified the two spreading regimes on a heterogeneous surface, namely the inertial regime where the droplet is only affected weakly by surface heterogeneity and the capillary regime where the droplet interacts with the surface heterogeneity.

Previous numerical and experimental studies typically allow the droplet to span over multiple heterogeneous stripes because the droplet size is much larger than the width of the micro-sized strips (Xia et al. 2012; Kooij et al. 2012; Jansen et al. 2012). These investigations highlighted the use of the multi-stripe pattern to elongate and move a droplet in a certain direction. However, accurate positioning of a jetted droplet on a specific location and its wettability pattern have not been investigated. The possible interference between adjacent droplets after impingement on a heterogeneous surface during the printing of densely packed features has also not been examined in the literature.

Numerous numerical simulations (Brandon et al. 1997; Schwartz and Eley 1998; Kusumaatmaja and Yeomans 2007; Kusumaatmaja et al. 2008) of spontaneous spreading of a partially wetting sessile droplet on a heterogeneous surface have also been performed. These studies focus on the spreading behavior of a sessile semi-spherical droplet or a spherical droplet which is initially in contact with the surface. However, numerical studies which consider a droplet traveling at a finite (nonzero) velocity before impingement typically assume a homogeneous surface (Yokoi et al. 2009; Lee and Liu 2010; Briones et al. 2010; Ganesan 2013). Recent numerical studies on droplet spreading and impingement are summarized in Table 1 with the corresponding Weber number We (which shows the ratio of impact inertia to surface tension) to highlight the novelty of our numerical investigation. Hitherto, simulations for a micro-droplet traveling at a finite velocity and impinging on a heterogeneous surface are lacking in the literature. Our studies extend the existing studies by focusing on the droplet impact and spreading behaviors on surfaces with heterogeneous wettability under a finite We or nonzero impact velocity. The spreading behaviors, i.e., evolution of contact angle, aspect ratio and equilibrium shape of the droplet, have been experimentally shown to differ between jetting a droplet on the surface and depositing the droplet slowly on a similar surface (Jansen et al. 2012). The behaviors of droplets under these conditions have practical implications such as inkjet printing with feature dimensions less than the droplet diameter. Unique behaviors, specifically the interaction of such droplet with wettability contrast and conformability of the droplet to the wettability pattern, are investigated in detail in our studies.

Table 1 Recent numerical simulations of droplet spreading and impingement on solid surface
Full size table

This investigation presents a numerical study of a micro-sized droplet impinging and spreading on a circular or stripe pattern with wettability contrast to the surrounding surface. The circular pattern is chosen for ease of analysis arising from its axisymmetry, while the rectangular stripe pattern is examined because of its application in the fabrication of FET, TFT and other electronic circuits. The outcome of this study can be applied to confine a jetted droplet to a specific area and control the spreading dynamics of the droplet upon impingement to prevent interference with adjacent droplets.

2 Numerical simulation

Droplet impingement and spreading have been simulated with various numerical models, for example, level-set method, volume of fluid, phase-field method, lattice Boltzmann method and arbitrary Lagrangian–Eulerian method (see Table 1). The pros and cons of these numerical models have been discussed in detail in a recent review paper by Wörner (2012). Recently, phase-field model based on Cahn–Hilliard equation has been successfully applied to the simulations of various multi-phase flow problems, including the wetting phenomenon of droplets (Takada and Tomiyama 2007; Liu and Zhang 2010), electro-hydrodynamics (Lin et al. 2012), flow in micro-channels (Wylock et al. 2012) and viscoelasticity (Zhou et al. 2010). One of the advantages of the phase-field method is that it naturally allows the contact line of a droplet to move along the wetted surface without any ad hoc treatment for stress singularity (see Sect. 2.2). Therefore, the model is favorable for simulations involving contact-line motion on a wetted surface. However, since phase-field model involves fourth-order derivative (see Eqs. 4, 5), numerical computation is more complex and time consuming. Hence, a simple boundary condition which is desirable for computational efficiency has been proposed in this study for the modeling of dynamic contact angle (Sect. 3.2).

2.1 Governing equations

Detailed theoretical development of the phase-field model and its application for fluid flow simulation as described here can be found in the literature (Yue et al. 2004; Jacqmin 1999, 2000). Only the basic concept of the model and governing equations employed for the current simulation are highlighted here. A phase-field model describes a system of two phases which are separated by a diffuse interface of finite thickness. The profile and thickness of the interface are determined by the molecular attraction and random molecular motion. The evolution of the interfacial layer is governed by a phase-field function ϕ through the Cahn–Hilliard equation (Yue et al. 2004),

$$\frac{\partial \phi }{{{\text{d}}t}} + {\mathbf{u}} \cdot \nabla \phi = \nabla \cdot \left( {\kappa \nabla G} \right)$$
(1)

where u = velocity field, κ = phase-field mobility and G = chemical potential. The concentrations or volume fractions of phase 1 and phase 2 are (1 − ϕ)/2 and (1 + ϕ)/2, respectively. ϕ assumes the value of −1 and +1 in the regions with only phase 1 and phase 2, respectively. At the thin interfacial region between the two fluids, ϕ varies sharply but continuously from −1 to +1.

The second term on the left-hand side of Eq. 1 governs the changes in ϕ through convective effect. The term on the right-hand side of Eq. 1 represents the diffusive effect due to the gradient of chemical potential G.

$$G = \lambda_{\text{m}} \left[ { - \nabla^{2} \phi + \frac{{\phi \left( {\phi^{2} - 1} \right)}}{{\varepsilon^{2} }}} \right]$$
(2)

where λ m = mixing energy density and ε = interfacial thickness. The first term on the right-hand side of Eq. 2 represents the interfacial energy, while the second term represents the bulk free energy.

Phase-field mobility κ determines the timescale of Cahn–Hilliard diffusion and relaxation time of the interface. κ should be chosen to be large enough to retain a constant interfacial thickness but small enough so that the convective term is not overdamped. The mixing energy density is related to the surface tension σ through the expression (Yue et al. 2004)

$$\sigma = \frac{2\sqrt 2 }{3}\frac{{\lambda_{\text{m}} }}{\varepsilon }$$
(3)

To facilitate the solving process, Eq. 1 which is a fourth-order partial differential equation (PDE) is separated into two second-order PDEs as follows:

$$\frac{\partial \phi }{{{\text{d}}t}} + {\mathbf{u}} \cdot \nabla \phi = \frac{{\kappa \lambda_{\text{m}} }}{{\varepsilon^{2} }}\nabla^{2} \psi$$
(4)
$$\psi = - \varepsilon^{2} \nabla^{2} \phi + \phi \left( {\phi^{2} - 1} \right)$$
(5)

Fluid flow is modeled with the Navier–Stokes equation and continuity equation:

$$\rho \left( {\frac{{{\text{d}}{\mathbf{u}}}}{{{\text{d}}t}} + {\mathbf{u}} \cdot \nabla {\mathbf{u}}} \right) = - \nabla p + \mu \nabla^{2} {\mathbf{u}} + \rho {\mathbf{g}} + G\nabla \phi$$
(6)
$$\nabla \cdot {\mathbf{u}} = 0$$
(7)

where p = pressure and g = gravitational acceleration. The density and dynamic viscosity are written with respect to the volume fraction of fluid 2 V f as

$$\rho = \rho_{1} + (\rho_{2} - \rho_{1} )V_{\text{f}} ,\quad \mu = \mu_{1} + (\mu_{2} - \mu_{1} )V_{\text{f}} ;\quad V_{\text{f}} = (1 + \phi )/2$$
(8)

where ρ 1 and ρ 2 are the densities of phase 1 and phase 2, respectively, and μ 1 and μ 2 are the dynamic viscosities of phase 1 and phase 2, respectively. Hence, the properties of the fluids/phases vary continuously with phase-field function across the thin interfacial region. The last term of Eq. 6 represents the surface tension force. Although it is implemented as a body force, the surface tension force only has a finite value at the interfacial region where the gradient of ϕ is nonzero.

The governing equations (Eqs. 1, 6 and 7) are non-dimensionalized based on characteristic length D (diameter of droplet before impact), impact velocity U (u = U u*), gravitation acceleration g (g = g g*), time (t = t*D/U) and pressure (p = p* ρ U 2):

$$\frac{\partial \phi }{{{\text{d}}t^{*} }} + {\mathbf{u}}^{*} \cdot \nabla \phi = \frac{3}{2\sqrt 2 }\frac{1}{Pe}\nabla^{2} \left[ { - Cn^{2} \nabla^{2} \phi + \phi \left( {\phi^{2} - 1} \right)} \right]$$
(9)
$$\left( {\frac{{{\text{d}}{\mathbf{u}}^{*} }}{{{\text{d}}t^{*} }} + {\mathbf{u}}^{*} \cdot \nabla {\mathbf{u}}^{*}} \right) = - \nabla p^{*} + \frac{1}{Re}\nabla^{2} {\mathbf{u}}^{*} + \frac{1}{Fr}{\mathbf{g}}^{*} + \frac{3}{2\sqrt 2 }\,\frac{1}{Cn \cdot We}\left[ { - Cn^{2} \nabla^{2} \phi + \phi \left( {\phi^{2} - 1} \right)} \right]\nabla \phi$$
(10)
$$\nabla \cdot {\mathbf{u}}^{*} = 0$$
(11)

From the dimensionless governing equations, the following dimensionless numbers can be identified:

$$Pe = \frac{DU\varepsilon }{\kappa \gamma },\quad Cn = \frac{\varepsilon }{D},\quad Re = \frac{\rho UD}{\mu },\quad Fr = \frac{{U^{2} }}{gD},\quad We = \frac{{\rho U^{2} D}}{\sigma }.$$
(12)

Peclet number Pe defines the ratio of convective to diffusive mass transport of the two-phase system. Cahn number Cn shows the relative thickness of the interfacial layer with respect to the diameter of the droplet. Reynolds number Re describes the ratio of inertial force to viscous force, while Weber number We shows the ratio between inertial force to surface tension force. Froude number Fr defines the ratio of the velocity of the droplet to the gravitational acceleration. In our studies, U ranges from 0.5 to 4 m s−1 (see Sect. 3.4.3) and ε is set to 1 μm (see Sect. 3.1). Based on the liquid properties shown in Table 2, these dimensionless parameters are calculated to be Pe = 3.4–27, Cn = 0.018, Re = 31–247, We = 0.18–12 and Fr = 463–29,654.

Table 2 Symbols and constants in numerical simulation
Full size table

The simulation is divided into three parts. In the first part, the simulation of a droplet impinging and spreading on a homogeneous surface was conducted. The simulation result was compared with experimental results available in the literature to validate the model. It also serves as a benchmark and as a special case for the second part of the simulation. The second part of the simulation investigated droplet impinging and spreading on a circular area with a lower contact angle (higher wettability) than the surrounding surface. Water droplet tends to wet a surface with lower contact angle (higher surface energy) instead of a surface with higher contact angle (lower surface energy) to lower the overall energy of the system. Therefore, on a circular area with a lower contact angle than the surrounding surface, the droplet is expected to be contained and conformed to the circular pattern. In the third part, a droplet impinging on a long rectangular stripe pattern with a lower contact angle as compared to the surrounding surface was presented. In this study, evaporation effect can be neglected in the simulation of droplet impingement due to the 4 order of magnitude difference in their characteristic timescale (Briones et al. 2010). The surface is also assumed to be smooth, and the change in wettability is due to chemical heterogeneity alone. The droplet and surface are also assumed to be isothermal. No splashing of droplet is expected since We is lower than 100 (Mani et al. 2010) in all our simulations.

2.2 Boundary conditions

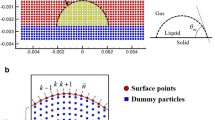
The numerical model was implemented with the finite element method (FEM) software, COMSOL Multiphysics. The first two parts of the simulations are axisymmetrical, and the simulation domain is shown in Fig. 1. When a droplet partially wets a solid surface, typical contact-line models which assume a moving sharp interface separating the two phases (with no flux through the interface) would induce a singularity at the contact line upon the imposition of no-slip boundary condition. However, under the phase-field model which assumes a diffusive interface, no-slip boundary condition can be applied without any complication at the contact line (Seppecher 1996). The interface in a phase-field model can move across the wetted surface with a diffusive effect instead of just the convective effect while maintaining the interface form and stability (Jacqmin 2000).

Fig. 1
figure 1

Computation domain for axisymmetry simulation

Full size image

The contact angle boundary condition at the wetted surface is specified according to the following equation:

$$\cos \theta_{\text{a}} = \frac{{{\mathbf{n}} \cdot \nabla \phi }}{{\left| {\nabla \phi } \right|}}$$
(13)

where θ a = apparent contact angle and n = normal vector into the wetted surface. In the first part of the simulation, three different types of boundary conditions related to the definition of apparent contact angle are examined. The simplest condition is to set the apparent contact angle to be the static contact angle (SCA) θ s of the droplet, with the assumption that the apparent contact angle is constant throughout the wetting process. In general, the dynamic contact angle (DCA) at the moving contact line differs from its static value and changes throughout the spreading process. Specifically, the advancing DCA is greater than the SCA, while the receding DCA is smaller than the SCA. There are two major approaches to describe these changes of apparent contact angle with respect to the velocity of contact line, namely hydrodynamic approach (Cox 1986; Voinov 1976) and molecular–kinetic approach (Blake and De Coninck 2002).

According to hydrodynamics theory, the change of dynamic contact angle is caused by viscous bending of liquid–gas interface on a mesoscopic scale. In its simplest form, it can be expressed (Voinov 1976) by

$$\theta_{\text{a}}^{3} - \theta_{\text{m}}^{3} = 9{\text{Ca}}_{\text{s}} \ln \left( {\frac{L}{{L_{\text{m}} }}} \right),\quad \theta_{\text{a}} < \frac{3}{4}\pi$$
(14)

where Cas = spreading capillary number and θ m = microscopic contact angle which is often assumed to be the static contact angle θ s. L and L m are the macroscopic and microscopic characteristic lengths, respectively, and are often regarded as fitting parameters in most analyses. Here, the spreading capillary number is defined as μv cl/σ where v cl = contact-line velocity. Typically, L is set to 10 μm, which is the approximate distance from the wetting line where the contact angle can be measured, and L m = 1 nm which is of the order of molecular size, and thus, ln(L/L m) = 9.21 (Blake 2006; Cox 1986). Typical values of ln(L/L m) derived from curve fitting of experimental results are found to be around 10 (Seveno et al. 2009).

An alternative approach to model the change in dynamic contact angle is through a molecular kinetic approach. According to the molecular kinetic theory, the movement of the contact line is due to the displacement of molecules in one phase on the solid surface adsorption site by molecules from another phase. The out-of-balance surface tension, which is defined as σ(cosθ a − cosθ s), provides the energy for this molecular displacement process. It accounts for the deviation of dynamic contact angle from its static value (Blake and De Coninck 2002). The contact-line velocity v cl can be expressed as

$$v_{\text{cl}} = 2f_{\text{o}} \lambda \sinh \left[ {\frac{{\sigma \lambda^{2} }}{{2k_{\text{b}} T}}\left( {\cos \theta_{\text{s}} - \cos \theta_{\text{a}} } \right)} \right]$$
(15)

where f o = characteristic frequency of molecular displacement, λ = molecular displacement length, k b = Boltzmann constant and T = temperature. f o is defined as

$$f_{\text{o}} = \frac{{hf_{\text{o}}^{\text{s}} }}{{v_{\text{m}} \mu }}$$
(16)

where h = Planck constant, f so  = equilibrium frequency of molecular displacement when retarded only by solid–liquid interaction and v m = molecular flow volume. For this study, the simulation results will be compared with the experimental results obtained by Briones et al. (2010), with λ taken to be 0.2 nm following their analysis. Other simulation parameters and constants are shown in Table 2. Phase 1 refers to air, while phase 2 refers to water in this study.

As suggested by de Gennes (1985), for a partially wetting droplet, the out-of-balance surface tension which causes the deviation of dynamic contact angle from its static value can be compensated by 2 distinct channels of dissipation: dissipation in the bulk and in the microscopic region near the contact line. These two modes of dissipation correspond to the two types of DCA boundary conditions described here. Hydrodynamic model would better describe the situation where bulk viscous dissipation is dominant. Molecular–kinetic model would be more suitable if the dominant mode of dissipation is due to adsorption/desorption of fluid molecules on the solid surface near the contact line. More complicated models which incorporate both these dissipation channels will not be discussed here.

3 Results and discussions

3.1 Convergence of phase-field simulation

In a real physical system, the two-phase interface width is much smaller (in the order of a few angstroms) and sharper than the characteristic diffusive interface thickness ε adopted in most phase-field simulations. However, a numerical simulation with such fine interface width is not feasible due to limited computation resources as mesh size will have to be adjusted to the order of ε for accurate resolution of the phase-field function at the interface. Therefore, a phase-field simulation is only valid if the simulation result is not affected significantly by the change in interface width, i.e., the simulation produces result which converges according to a sharp-interface model.

Yue et al. (2010) proposed a criterion for the sharp-interface limit in the situation where a fluid interface contacts a solid wall:

$$Cn \le \frac{{4\sqrt {\kappa \mu_{\text{e}} } }}{D},\quad \mu_{\text{e}} = \sqrt {\mu_{1} \mu_{2} }$$
(17)

where μ e is the equivalent viscosity for the two fluids.

The first set of simulations will be conducted based on SCA boundary condition with three different mesh sizes for a convergence test. The value of interfacial thickness ε is typically set to half of the mesh size employed in the simulation. Smaller mesh size and ε provide better resolution to capture the sharp change in phase-field function ϕ across the fluid–air interface. The minimum value of ε is set to 0.5 μm for the convergence test because smaller ε and finer mesh require excessive computation time and memory. For a converged solution of a moving contact line problem, κ should be independent on ε (Yue et al. 2010). Based on the smallest mesh size which allows a solution to be obtained with our computational resources, the minimum κ is calculated to be 1.10 × 10−10 m3 s kg−1 (from Eq. 17), and this value is adopted for three different mesh sizes. The impact velocity is set to 2.45 m s−1, and the SCA θ s is set to 55° to compare with experimental results obtained from the literature [droplet C in Briones et al. (2010)]. The simulated time evolution of droplet spreading diameter for three values of ε (0.5, 1.0 and 2.0 μm, which correspond to Cn = 0.009, 0.018 and 0.036, respectively) is shown in Fig. 2. The spreading diameter of the droplet on the wetted surface can be obtained by integrating the volume fraction of fluid 2 (droplet), V f along the wetted surface. The dimensionless spread diameter D* is defined as

Fig. 2
figure 2

Comparisons between phase-field simulation based on SCA boundary condition with different interfacial thickness ε and experimental results (Briones et al. 2010). Both a droplet spread diameter D* and b height H* are non-dimensionalized with droplet initial diameter (D = 55 μm). Impact velocity, U = 2.45 m s−1; static contact angle θ s = 55°; We = 4.5. Dimensionless time t* = tU/D

Full size image
$$D*(t) = \frac{{2\int {V_{\text{f}} (t){\text{d}}r} }}{D}$$
(18)

Based on the definition of V f, V f = 1 at the surface wetted by the droplet and V f = 0 at the surface outside of the droplet. V f varies gradually from 1 to 0 at the interfacial region between liquid and air. The integrand in Eq. 18 is zero outside of the droplet, where V f = 0. Thus, the integration operation in Eq. 18 yields the equivalent radius of the droplet. Similarly, the height of the droplet H* can be obtained by integrating V f along the symmetry axis and non-dimensionalized with D. It is noted that the spreading diameter and droplet height for ε = 0.5 μm and ε = 1.0 μm do not differ significantly (see Fig. 2), indicating convergence has been achieved. The intermediate value ε = 1.0 μm is chosen for subsequent analysis because a relatively accurate solution can be obtained in an acceptable time frame.

To determine the stability of the phase-field function during spreading, the average gradient of phase-field function at the middle of the interfacial region (where the curve is approximately linear, see Fig. 3) on the wetted surface was determined from the numerical results for the three interfacial thicknesses throughout the wetting process. As expected, the average gradients of ϕ are dependent on the interface thickness and were determined to be 2.31 × 105 m−1 (standard deviation 0.078 × 105), 4.73 × 105 m−1 (standard deviation 0.123 × 105) and 9.69 × 105 m−1 (standard deviation 0.235 × 105) for ε values of 2, 1 and 0.5 μm, respectively. The phase-field function gradient at the interfacial region can be approximated as a constant, especially for ε = 0.5 μm and ε = 1 μm, where the standard deviations are less than 2.6 %. The solution is less accurate when ε is set to a large value due to the excessively diffused interfacial region. A simple scheme based on the interfacial gradient of phase-field function has been formulated to track the contact-line velocity for the specification of DCA boundary condition, as described in Sect. 3.2.

Fig. 3
figure 3

Contact-line velocity tracking scheme is illustrated with schematic showing spatial distribution of phase-field function ϕ at two time steps (t 1 and t 1 + Δt). If phase-field function gradient dϕ/dr is constant with time, contact-line velocity can be written as v cl = −(dϕ/dt)/(dϕ/dr)

Full size image

3.2 Tracking of contact-line velocity

The two models of DCA described in Sect. 2.2 require the specification of contact-line velocity at the wetted boundary/wall. Unlike other models which specify at the contact surface a slip velocity which can be prescribed in terms of the local fluid velocity, the phase-field model adopted in this study specifies a non-slip boundary condition at the wall. Hence, the fluid velocity at the wall is zero, and the contact-line velocity cannot be prescribed with respect to the local fluid velocity. A simple scheme for the tracking of contact-line velocity is proposed based on the phase-field function gradient in the interfacial region (see Fig. 3).

If the phase-field function gradient dϕ/dr is known, the velocity of the moving contact line can be written as a function of the local time derivative of phase-field function dϕ/dt, as follows:

$$v_{\text{cl}} (t) = - \frac{{{\text{d}}\phi /{\text{d}}t}}{{{\text{d}}\phi /{\text{d}}r}}$$
(19)

If dϕ/dr is assumed to be a constant during the spreading process, the contact-line velocity will assume a finite value at the interfacial region according to the time variation of ϕ; ϕ outside of the interfacial region (in the region with only air or liquid) is constant with time. When the contact line is advancing, ϕ at the interfacial region increases with time; when the contact line is receding, ϕ at the interfacial region decreases with time.

To determine whether the phase-field function gradient changes with surface wettability, a series of simulations for droplet spreading on surfaces of different contact angles was performed and the average interfacial phase-field gradient for each simulation was measured. Figure 4 shows that the interfacial phase-field gradient varies weakly with SCA of a surface, and a quadratic curve can be fitted through the points. In the simulation of droplet spreading on a surface with heterogeneous wettability, the interfacial phase-field gradient can be associated with the local SCA of the surface.

Fig. 4
figure 4

Average gradient of phase-field function at fluid–air interface on surfaces with different contact angles

Full size image

Although the spatial gradient of the phase-field function is constant during the spreading process, it is noted that the gradient does change for a short period of time, just when the droplet impinges on the surface. This transient behavior of the phase-field gradient during the impact process is not included in the boundary condition specification for this simplified model and will be investigated in future work.

3.3 Validation of phase-field model with experimental results

To verify the validity of the phase-field model and to determine the phenomenological constants for DCA boundary conditions, the numerical results were compared with experimental results obtained from the literature [droplet C in Briones et al. (2010)]. Figure 2 shows that the numerical results of the spreading diameter obtained from SCA boundary conditions as compared to the experimentally obtained spread diameter under the same conditions. The equilibrium droplet diameter predicted by the SCA model fits the experimental results very well. However, the numerical results show a high overshoot in spreading diameter upon impact and the predicted maximum spread diameter is 35 % larger than the spread diameter observed experimentally. Thus, SCA model cannot predict the droplet spreading dynamics upon impact accurately. Lunkad et al. (2007) reported that droplet spreading dynamics on a horizontal surface can only be modeled accurately with SCA model if the surface is less wettable (contact angle >90°). Therefore, DCA models, namely the hydrodynamic model and molecular–kinetic model, are considered in this study.

Three simulations based on the hydrodynamics approach for DCA boundary condition were conducted by taking values of ln(L/L m) as 9.2, 18 and 72 (see Fig. 5). As mentioned in Sect. 2.2, physically realistic values of ln(L/L m) should be around 10. However, a good fit of the hydrodynamic model on experimental spreading diameter (see Fig. 5) can only be obtained at ln(L/L m) = 72, which would result in subatomic value for the microscopic length scale L m. This indicates that viscous effect may not be the main mode of energy dissipation during the wetting process. For high contact-line velocity and larger contact angle, energy dissipation at the contact line due to molecular kinetics is dominant. In contrast, for lower contact angle with the displaced fluid of higher viscosity than the displacing fluid, energy dissipation is better described by hydrodynamic theory (Brochard-Wyart and de Gennes 1992). Hence, for our study here which involves high impact velocities, molecular–kinetic theory was employed for the specification of DCA boundary condition.

Fig. 5
figure 5

Comparisons between phase-field simulation based on DCA boundary condition formulated with hydrodynamic theory and experimental results (Briones et al. 2010). Both a droplet spread diameter D* and b height H* are non-dimensionalized with droplet initial diameter (D = 55 μm). Impact velocity U = 2.45 m s−1; static contact angle θ s = 55°; We = 4.5; dimensionless time t* = tU/D; L = macroscopic characteristic length scale, L m = microscopic characteristic length scale

Full size image

Three simulations based on molecular–kinetic approach for DCA boundary condition were conducted by assuming the characteristic frequency of molecular displacement f o = 10, 20 or 40 GHz (see Fig. 6). A good fit to the experimental results can be obtained with f o = 10 GHz, which has the same order of magnitude as most f o values employed in the literature (Seveno et al. 2004; Blake et al. 1997; Briones et al. 2010; Bhardwaj and Attinger 2008). The main mode of energy dissipation near the contact line can be attributed to the adsorption/desorption of fluid molecule on the solid surface in this case. Despite the accuracy in the prediction of spread diameter, the height of the droplet seems to be overdamped in the numerical simulation (see Fig. 6b), which is also reported by Briones et al. (2010). Molecular–kinetic approach (Blake’s formulation, Eq. 15) is adopted for subsequent simulation in Sect. 3.4 since it produces results which are closest to the experimental data.

Fig. 6
figure 6

Comparisons between phase-field simulation based on DCA boundary condition formulated with molecular–kinetic theory and experimental results (Briones et al. 2010). Both a droplet spread diameter D* and b height H* are non-dimensionalized with droplet initial diameter (55 μm). Impact velocity U = 2.45 m s−1; static contact angle θ s = 55°; We = 4.5; dimensionless time t* = tU/D; f o = characteristic frequency of molecular displacement

Full size image

3.4 Impact and spreading on circular pattern with wettability contrast

In this section, simulation results of a droplet impinging and spreading on a surface with a circular heterogeneous pattern are presented. All numerical results in Sect. 3.4 were obtained through the molecular–kinetic boundary condition on wetted surface (Eq. 15). The inner region of the circular pattern is more wettable than the surface surrounding it. The contact angle transition on the wetted surface was modeled with a smoothed Heaviside function. The effect of wettability contrast, circular pattern diameter and impact velocity were investigated and discussed in Sects. 3.4.1–3.4.3.

3.4.1 Effect of wettability contrast

In this series of simulations, the contact angle of the inner surface (see Fig. 1) is fixed at 50°, while the contact angle of the outer region is set to 4 different values ranging from 50° to 120°. The water contact angle on a surface is dependent on the property of the material. Some examples of contact angles for common substrates are poly(ethylene terephthalate) PET with SCA = 82° (Blake 2012), poly(methyl methacrylate) PMMA with SCA = 77° (Wang et al. 2011), polystyrene (PS) with SCA = 93° (Jung and Bhushan 2006) and silicon wafer with SCA = 51° (Tao and Bhushan 2006). The contact angles of these common substrates fall within the range of SCA simulated (50°–120°) and thus represent realistic properties of the surface. In addition, it should be noted that the contact angle or surface properties of a substrate can be modified selectively with methods such as chemical coating (Jung and Bhushan 2006), femto-second laser irradiation (Wang et al. 2011) or plasma treatment (Lai et al. 2006).

The diameter of the droplet and the impact velocity are set to 55 μm and 2.45 m s−1, respectively. The typical droplet diameter produced by an inkjet dispenser ranges from 10 to 100 μm (Hutchings and Martin 2013). The simulated droplet diameter of 55 μm is the average of the range. The diameter of the circular pattern D h is set to 70 μm (non-dimensionalized with the initial droplet diameter; D h * = 1.27), which is smaller than the final droplet spread diameter on a homogeneous surface (1.65D). Figure 7 shows the comparison between the simulated droplet impinging on a homogeneous surface and a circular region with 70° wettability contrast. On the surface with 70° wettability contrast, the droplet is confined in the circular region with a diameter of 70 μm which is smaller than the droplet’s final diameter on a homogeneous surface (91 μm).

Fig. 7
figure 7

Comparisons between simulated droplet impinging on a homogeneous surface with static contact angle = 50° and a circular area with 70° wettability contrast to surrounding surface. Droplet initial diameter D = 55 μm; impact velocity U = 2.45 m s−1; We = 4.5

Full size image

The time evolution of spreading diameter for two surfaces (the surface inside and outside of the circular pattern) with various wettability contrast is shown in Fig. 8a. The simulation results show that even a slight wettability contrast (such as 5°) produces a notable reduction in final spreading diameter. The final spread diameter reduces gradually with increasing wettability contrast and approaches an asymptotic limit beyond 70° difference (see Fig. 8b).

Fig. 8
figure 8

a Time evolution of droplet spread diameter (non-dimensionalized with droplet initial diameter) upon impingement on a circular pattern with various wettability contrasts Δθ to surrounding surface. Horizontal line at D h * = 1.27 indicates diameter of circular pattern. b Final droplet spread diameter and maximum spread diameter (non-dimensionalized with droplet initial diameter) for droplet impinging on a circular pattern with various wettability contrast Δθ to surrounding surface. Droplet initial diameter D = 55 μm; impact velocity U = 2.45 m s−1; We = 4.5; dimensionless time t* = tU/D

Full size image

In addition to the final spread diameter, the maximum spread diameter was also inspected. Similar to the final droplet diameter, the maximum diameter reduces with increasing wettability contrast (see Fig. 8b). Percentage overshoot is defined as (maximum spread diameter/final spread diameter − 1) × 100 %. For a homogeneous surface (0°) or a surface with small (5°) wettability contrast, the droplet reaches the final spread diameter without a significant overshoot (see Fig. 8b). However, with higher wettability contrast (20° and 40°), the spreading diameter shows a significant overshoot of 9–10 % before receding to the final diameter. For the surface with very large wettability contract (70°), the droplet exhibits a smaller overshoot (4 %) in spread diameter and conforms to the circular pattern. This illustrates that chemical surface patterning with a pattern of high wettability contrast is a viable technique to constrain the spreading of an impinging droplet to a specified area. In some applications where the deposited droplets are in close proximity to each other, sufficiently high wettability contrast is required to ensure that the droplet does not spread beyond the confined area and interfere with the adjacent droplets.

Ren and E (2011) investigated the effect of surface wettability contrast on the movement of contact line over a surface with sinusoidal contact angle (see Fig. 9a). Their analysis is adapted here for the current investigation of a droplet spreading over a surface with a step change of wettability (see Fig. 9b). If the argument of hyperbolic sine in Eq. 15 is small, the DCA boundary condition based on Eq. 15 can be approximated as (Ren and E 2011)

$$v_{\text{cl}} = \frac{{f_{\text{o}} \sigma \lambda^{3} }}{{k_{\text{b}} T}}\cos \left( {\theta_{\text{s}} - \cos \theta_{\text{a}} } \right)$$
(20)

Equation 20 can be rewritten as:

$$\sigma \cos \left( {\theta_{\text{s}} - \cos \theta_{\text{a}} } \right) = \beta v_{\text{cl}} ,\quad \beta = \frac{{k_{\text{b}} T}}{{f_{\text{o}} \lambda^{3} }}$$
(21)

where β = friction parameter, which describes the three-phase interaction at the contact line (Ren et al. 2010). Although Eq. 20 is only valid if the apparent contact angle is close to the static contact angle, this simplified analysis provides meaningful insight to gain an understanding of the numerical simulation results.

Fig. 9
figure 9

a Schematic of theoretical analysis by Ren and E (2011) on movement of contact line over surface with sinusoidal wettability. b Analysis performed in this study on spreading droplet across surface with step change of wettability

Full size image

For a droplet spreading on a heterogeneous surface, the following relationship can be established based on Young’s equation (Ren and E 2011):

$$\sigma \cos \theta_{\text{s}} (r) = \gamma_{2} (r) - \gamma_{1} (r)$$
(22)
$$\sigma \cos \theta_{\text{s}} (r) = \Updelta \sigma_{\text{o}} + f_{\varepsilon } (r)$$
(23)

where γ 1 = liquid–solid interfacial tension and γ 2 = air–solid interfacial tension. The difference between the two terms on the right-hand side of Eq. 22 has been decomposed into two components in Eq. 23: a constant Δσ o and a variable component f ε (r). In this study, Δσ o is written in terms of the static contact angle inside the circular pattern θ s1 (with lower contact angle), and Eq. 23 can be expressed as

$$\sigma \cos \theta_{\text{s}} (r) = \sigma \cos \theta_{\text{s1}} + f_{{{\varepsilon}}} (r)$$
(24)

Here, the variable component f ε (r) is defined as the defect force (per unit length) which represents the change of wettability/contact angle across the surface. The defect refers to the chemical heterogeneity of a surface. Substituting Eq. 21 into Eq. 24 yields

$$\sigma \left( {\cos \theta_{{{\text{s}}1}} - \cos \theta_{\text{a}} } \right) = \beta v_{\text{cl}} - f_{\varepsilon } (r)$$
(25)

Equation 25 shows that the out-of-balance surface tension is dissipated in two different channels if the droplet is spreading on a heterogeneous surface. The first term on the right-hand side of Eq. 25 is the energy dissipation in the interfacial region due to adsorption/desorption on a homogeneous surface, while the second term represents the additional dissipation due to the effect of heterogeneity on the surface. The latter reduces the maximum spread diameter on a surface with heterogeneous wettability which is demonstrated in the simulation, as the DCA tends to its static value. According to Eq. 24, the defect force (which is a negative value in this study) increases in magnitude when the wettability contrast between the two surfaces increases. If the defect force is zero, Eq. 25 simply becomes the conventional boundary condition of a homogeneous surface with a constant SCA of θ s1.

3.4.2 Effect of pattern diameter

The boundary condition on the wetted surface is varied to investigate the effect of wettability pattern diameter on droplet spreading. The diameter of the circular pattern is set to various values (40, 55 and 70 μm) which are smaller than the final spread diameter. On a homogenous surface, the final spread diameter of the droplet is 90 μm or 1.65 times of the droplet initial diameter. The wettability contrast is fixed at 70° with SCA of the inner and outer regions set to 50° and 120°, respectively. The simulation results are shown in Fig. 10a.

Fig. 10
figure 10

a Time evolution of droplet spread diameter (non-dimensionalized with droplet initial diameter) upon impingement on a circular pattern with 70° wettability contrast to surrounding surface (SCA of inner and outer regions are 50° and 120°, respectively). Diameter of the circular area is varied. Only selected results are shown for clarity. Horizontal lines indicate diameter of circular pattern D h *. Droplet initial diameter D = 55 μm; impact velocity U = 2.45 m s−1; We = 4.5; dimensionless time t* = tU/D. b Final droplet spread diameter on surface with different D h *. Two horizontal lines indicate final D* for homogenous surface with SCA of 50° and 120°, respectively

Full size image

As the diameter of the circular pattern is reduced, the final diameter of the droplet reduces accordingly as droplet spreading is confined by wettability contrast. Hence, the final spread diameter is linearly proportional to the diameter of heterogeneous pattern (see Fig. 10a). However, this linear relationship is not obeyed when the diameter of the circular pattern is reduced below a certain threshold. From Fig. 10b, it can be observed that when the diameter of the heterogeneous pattern is reduced to 0.86 times of the droplet diameter or smaller, the final spread diameter does not reduce further. In fact, the threshold diameter of the wettability confinement is the final spread diameter of a droplet on a homogeneous surface with the same contact angle as the outer region. In this case, the final spread diameter on a homogeneous surface with a contact angle of 120° is 0.86D. If D h * is smaller than 0.86D, the impinging droplet behaves as if the surface is homogeneous due to a lack of interaction between the contact line and the boundary between the two regions with an abrupt change in contact angle. Similar argument applies if D h * is larger than 1.65D which is the final droplet spread diameter on a surface with a contact angle of 50°.

3.4.3 Effect of impact velocity

The effect of impact velocity on droplet spreading behavior was investigated by varying the droplet impact velocity. The diameter of the inner circular area is set to the droplet initial diameter (D h * = 1). Droplet impact velocities for a typical drop-on-demand (DOD) inkjet dispenser are 1–8 m s−1 (Briones et al. 2010). The impact velocities in our studies are 0.5, 1, 2.45 and 4 m s−1 with We ranging from 0.19 to 12. Therefore, the velocities are realistic estimates of impact velocity for a DOD inkjet dispenser. The lowest velocity (0.5 m s−1) is meant to illustrate the effect of low impact velocity on the spreading behavior and serves as a comparison for the results at higher impact velocities. The simulated time evolution of the spreading diameter is shown in Fig. 11. At the early stages of droplet impingement, the spreading of droplet is governed by the impact velocity and initial diameter only (Rioboo et al. 2002). Higher impact velocity provides higher kinetic energy for the spreading of the droplet, resulting in larger maximum spread diameter. This causes a higher overshoot from the area of confinement with increasing impact velocity.

Fig. 11
figure 11

a Time evolution of droplet spread diameter (non-dimensionalized with droplet initial diameter) upon impingement on a circular area with 70° wettability contrast to surrounding surface (SCA of inner and outer regions are 50° and 120°, respectively). Droplet impact velocity U is varied; We = 0.19, 0.76, 4.5 and 12. Horizontal lines indicate diameter of circular area D h *. Droplet initial diameter D = 55 μm. Dimensionless time t* = tU/D. b Overshoot % with different impact velocities

Full size image

After reaching the maximum diameter, the droplet contact line recedes back to the boundary with wettability contrast and the droplet exhibits some oscillations near the boundary before reaching its equilibrium state. The final spread diameters of all droplets are the same regardless of impact velocities. This is because after the kinetic energy is depleted during the initial inertial-dominated spreading, the contact line movement is governed by surface tension and the wetted surface condition. The fluid properties and the surface condition in this series of simulations are the same. In this case of a surface with a single circular pattern of heterogeneity, the minimization of energy brings the droplet back into the circular region with a lower contact angle.

3.5 Impact and spreading on stripe pattern with wettability contrast

The simulation of a droplet impinging on a stripe pattern with a higher wettability than the surrounding surface was performed (see Fig. 12). For 3-dimensional (3D) phase-field simulations, the contact-line-tracking scheme proposed in Sect. 3.2 cannot be applied because the contact line moves in a plane instead on a line. A more complex formulation of the scheme which takes into consideration the change in phase-field gradient in both the x and y directions is required. However, this is not pursued in this study due to limited computation resources. Therefore, static contact angle boundary condition was applied at the surface as an approximation, and the results were compared with results obtained with axisymmetry SCA simulation performed in Sect. 3.3. Due to the large memory required and long computation time, the mesh employed in this 3D simulation is coarser than the axisymmetry case. The smallest mesh size on the surface is set to 4 μm, and the interfacial thickness ε is set to 2 μm accordingly. According to Fig. 2, the simulation result based on this mesh size would still give a good approximation to the results obtained from a finer mesh if κ is set to a value larger than 1.10 × 10−10 m3 s kg−1.

Fig. 12
figure 12

3D simulation domain for droplet impinging and spreading on striped pattern with wettability contrast. Only a quarter of the droplet is simulated with surface AEHD and EFGH as planes of symmetry; surface CDHG is wetted surface; the other surfaces are open boundaries. Droplet initial diameter D = 55 μm; impact velocity U = 2.45 m s−1; We = 4.5

Full size image

In the simulation, a droplet with 55 μm diameter impinges on an infinitely long stripe with a width of 70 μm at an impact velocity of 2.45 m s−1. The contact angles inside and outside of the stripe are 50° and 120°, respectively (see Figs. 12, 13). Only a quarter of the droplet was simulated due to symmetry. The full droplet is generated by mirroring the obtained simulation result at the two planes of symmetry. To show the anisotropic spreading behavior of the droplet, the droplet spread length in the parallel and perpendicular directions to the stripe are plotted in Fig. 14. The spreading of the droplet perpendicular to the stripe is constrained to 1.27D by the wettability contrast and is smaller than the equilibrium droplet diameter on a homogeneous surface with SCA of 50° (1.65D). Due to mass conservation, the droplet is forced to spread along the direction parallel to the stripe. The maximum spread length along the strip is 2.6D and is larger than the maximum droplet spread diameter on a homogeneous surface with SCA of 50° (2.1D). This resulted in an elongated droplet in the direction of the stripe pattern.

Fig. 13
figure 13

Top and side views of 55-μm-diameter droplet impinging on a striped pattern (width = 70 μm) with wettability contrast of 70° to surrounding surface. Impact velocity = 2.45 m s−1. We = 4.5

Full size image
Fig. 14
figure 14

Time evolution of droplet spread diameter upon impingement on a striped pattern with 70° wettability contrast to surrounding surface (SCA of inner and outer regions are 50° and 120°, respectively). Horizontal line indicates stripe width of 70 μm (1.27D). Droplet initial diameter D = 55 μm; impact velocity U = 2.45 m s−1; We = 4.5. Dimensionless time t* = tU/D

Full size image

4 Conclusions

The impingement and spreading of a micro-sized droplet with nonzero impact velocities on a solid surface were modeled numerically based on phase-field method through FEM. Numerical results based on static contact angle and dynamic contact angle boundary conditions were compared. A simple scheme was proposed to track the contact-line velocity which is required to prescribe the boundary condition for dynamic contact angle. The numerical results were verified with experimental results from the literature. Boundary condition of the wetted surface prescribed according to molecular–kinetic theory (Blake’s formulation) was found to provide the best fit to the experimental results with physically reasonable parameters, as compared to static contact angle boundary condition or hydrodynamic dynamic contact angle boundary condition.

The model was used to simulate the impingement and spreading of a droplet on a heterogeneous surface. For a circular pattern with a lower contact angle than the surrounding surface, the droplet final spread diameter decreases with increasing wettability contrast. High wettability contrast confines the droplet within the circular area. Decreasing diameter of the circular pattern with high wettability contrast reduces the final droplet spread diameter as the droplet conforms to the pattern. However, the diameter of the droplet cannot be reduced below a certain threshold, which is dictated by the final spread diameter of the droplet on a homogeneous surface with similar contact angle as the outer region of the circle. The droplet maximum spread diameter is larger at higher impact velocities. However, the final droplet diameter is independent of the impact velocity, as the droplet contact line recedes back into the circular pattern after it reaches its maximum diameter.

Impingement and spreading of a droplet on a long stripe pattern with a lower contact angle than the surrounding surface has been demonstrated in a 3D phase-field simulation. With a high wettability contrast between the inner and outer regions of the stripe, the droplet exhibits anisotropic spreading, with a longer spreading length in the direction parallel to the stripe and a smaller spreading length in the direction perpendicular to the stripe. This results in an elongated droplet in the direction of the stripe. These simulations demonstrated that a jetted droplet which impinges on a solid surface can be confined to a selected area through surface wettability patterning.