A study on the electroosmotic flow of micropolar fluid in a channel with hydrophobic walls

Abstract

In the present study, the equations governing the electroosmotic flow in a horizontal microchannel with hydrophobic walls are solved using the micropolar fluid model analytically. The effects of the influential parameters, including micropolar viscosity, the ratio of characteristic length of the fluid microstructures to the characteristic length of the flow (m), concentration coefficient, Debye–Hückel parameter, the ratio of pressure-driven velocity to electroosmotic velocity (U_r), and slip coefficient, were examined on the flow pattern. According to the results, the magnitude of the velocity profile decreases as the micropolar viscosity, m, and U_r (U_r < 0) increase. The flow velocity grows as the concentration coefficient-dependent microgyration flow distribution increases, and the velocity distribution increases as the U_r (U_r > 0) and Debye–Hückel parameter acting as the flow's electric driving force. The slip coefficient has a direct impact on the velocity profile, considerably increasing its value. Thus, it can be concluded that small-scale surface slip is highly significant and helps achieve the best design of microchannel walls to control the flow in microchannels accurately. In addition, the contrast between decreasing velocity profile and increasing micropolar viscosity makes the micropolar fluid model an appropriate tool to simulate the fluid behavior in microstructures, given that it assumes gyration in the boundaries due to the existence of an electric field.

1 Introduction

Given the great advances in the technologies for fabricating devices and systems on micro and nanoscales, especially electromechanical systems, electroosmotic micropumps are an efficient solution for fluid transport within microfluidic systems due to their numerous advantages, especially having no moving parts [1].

Electroosmosis is known as a major phenomenon in electrokinetic transport. This phenomenon was discovered in 1809 by Reuss [2], who observed the motion of water during the transport of an external electric field. Subsequently, numerous researchers showed interest in investigating this subject. Smoluchowski [3] was the first to propose an analytical solution for the electroosmotic flow (EOF) in a simple channel. In a study in 1998, Patankar and Hu [4] presented a finite volume-based numerical scheme to simulate EOFs in complex geometries. So far, extensive research has been performed on electrokinetic transport phenomena classified according to different factors, such as fluid type, microchannel type, and flow analysis type, examining the effects of various parameters, such as Joule heating, electric double-layer (EDL) potential, and external pressure gradient, on the heat transfer and flow behavior. Furthermore, different methods have been introduced for flow analysis. In a numerical study, Park et al. [5] investigated the EOF inside various microchannels using the Nernst–Planck and the Poisson–Boltzmann methods. They stated that in problems with small EDL thicknesses, the difference between the two models was very small. Moreover, the Poisson–Boltzmann model was more efficient in simple geometries and for modeling internal electric potential. However, the Nernst–Planck model was more suitable for complex geometries due to the significance of ion displacement and concentration. Over recent years, non-Newtonian fluids have received special attention due to their important engineering and industrial applications. However, given the diversity of the fundamental equations in these fluids and the fact that the Navier–Stokes equations cannot accurately represent the properties of Newtonian fluids, which do not contain suspended particles, micropolar models can be effective in better describing the behavior of Newtonian and non-Newtonian fluids. In 1965, Eringen [6] formulated the micropolar fluid theory for the first time to describe fluid behavior on a small scale.

The results of this study are practicable and can be helpful for the development of technologies such as capillary electrochromatography (CEC) [7].

1.1 Electroosmotic flow of a micropolar fluid

Investigations into the EOF of the micropolar fluids have indicated that considering the role of suspended particles in the fluid, along with the micropolar theory, plays a key role in understanding the pattern of flows subject to magnetic and electric fields, such as EOFs, especially in microstructures [8,9,10,11,12]. A review of the literature is performed as follows to gain a better understanding of this subject.

Misra et al. [13] conducted a semi-analytical study on the micropolar fluid flow in a microchannel under the effect of a variable electric field. They simulated blood flow between two plates with an infinite depth as a case of bio-microfluidics with micropolar properties. Their results indicated that changing the micropolarity of the fluid and the height between the two plates led to a change in the flow velocity, and using the nonzero boundary condition for the microgyrations altered the thickness of the EDL. Ding et al. [14] presented an analytical solution for the time-varying EOF of an incompressible micropolar fluid inside parallel microchannels. They realized that with an increase in the micropolarity of the fluid, the velocity range and the volumetric flow rate decreased to near zero. The results also showed that the electric potential effect on the micropolar fluid was similar to that on the Newtonian fluid. However, it could cause a difference in the microgyrations. Chaube et al. [15] conducted an analytical study on the peristaltic flows of biological micropolar fluids via the electroosmosis mechanism using a parallel plate microchannel. The results showed that the peristaltic pumping of a micropolar fluid escalated with the use of an external electric field and changed with the formation of an EDL. It was observed that since the flows were in one direction, the streamlines were trapped near the EDL, becoming parallel in the middle of the microchannel. However, when the EOF was not along the peristaltic flow, the flow was trapped in the middle of the microchannel.

In the most recent research on the EOF of a micropolar fluid, Tripathi et al. [16] carried out a numerical study considering the effects of double-diffusive convection heat transfer for a micropolar fluid flow created by a peristaltic pump and the electroosmotic mechanism inside an asymmetric microchannel. They showed that the Helmholtz–Smoluchowski velocity considerably affected the fluid particles' velocity, pressure gradient, and microgyration in tolerating the velocity slip, the buoyancy effect, and the EDL phenomenon. In addition, the temperature of the nano-fluid rose with the thermal diffusivity and the Prandtl number. Saleem et al. [17] proposed a comprehensive mathematical model to analyze the peristaltic flow of a Bingham viscoplastic micropolar fluid inside a wavy microchannel with an electroosmotic actuator. They stated that the electroosmotic effects mostly assisted the flow control, and higher electric field strengths resulted in lower axial velocity and higher microgyration velocity.

A disadvantage of microchannels is the large pressure drop along them compared to channels with conventional dimensions. Hence, using hydrophobic surfaces as a factor that reduces pressure drop is recommended. Hydrophobic surfaces repel water. This phenomenon is due to the unbalance between the molecular forces at the water–solid interface, which causes surface tension [18]. The behavior of water droplets on a surface can be associated with two factors: surface energy and wettability. When a material has larger energy on the surface, the surface is hydrophilic, and thus, a smaller contact angle is created. On the other hand, if the surface energy of a material is small, the molecules in the water droplets are more attracted to each other than to the surface, hence creating a larger contact angle and a hydrophobic surface. Moreover, wettability is the capability of a liquid in contact with a solid surface and results from intermolecular forces [19]. One of the most practical methods of creating a hydrophobic surface is using polymer composites that give hydrophobic properties to the textures surface and bond it to the substrate, thereby stabilizing the hydrophobic walls [18]. In addition, slip velocity and temperature jump are two factors affecting the heat transfer and pressure drop in hydrophobic surfaces [20]. The following reviews some of the previous research in this field.

1.2 Electroosmotic flow with hydrophobic surfaces

Soong et al. [21] performed an analysis of electrokinetic flows subject to pressure in a one-dimensional hydrophobic microchannel considering the effects of slip and slip-dependent zeta potential on Newtonian fluids. Their results showed that the slip effects were effective only in small length ranges, and the super-hydrophobicity of the channel walls was not effective in increasing the flow and saving pumping power. Sadeghi et al. [22] analyzed the fully developed EOF in hydrophobic microchannels with different cross sections with the Debye–Hückel approximation using the Navier slip condition. They demonstrated that the flow velocity increased linearly with the slip length for a thin EDL. Silkina et al. [23] proposed a theory for flat and cylindrical nano-channels containing hydrophobic surfaces. Their theory consisted of the movement of the attracted surface charges and hydrodynamic slip for describing EOFs. They also showed that the EDL and fluid slip near the hydrophobic surface affected the hydrodynamic diffusivity of the nano-structures. Rahmati et al. [24] presented a model using the lattice Boltzmann method to calculate the slip length in EOFs on hydrophobic walls. Their results indicated that slipping on the channel boundaries extended the flow development time, and slipping on the walls prevented lateral changes in the velocity profile while causing a significant quantitative increase, improving the performance of the electroosmotic pump. Noreen et al. [25] studied the effects of slippage and Joule heating in EOF through peristalsis in an asymmetric microchannel to investigate the entropy generation in a magnetohydrodynamic non-Newtonian Jeffery fluid flow numerically. They concluded that the axial velocity of the EOF in the Jeffrey fluid was higher than that of the Newtonian fluids, and the velocity generation increased in porous media and with parameters, such as the electroosmotic parameter and the zeta potential at the upper wall. However, the slip length and zeta potential at the lower wall reduced velocity production for a porous medium, and the Joule heating increased entropy generation.

In a recent study, Baños et al. [26] numerically examined the effects of rheology and slippage of non-Newtonian fluids on the mass transport of species due to an oscillatory electroosmotic flow using a power-law model. The results showed that by considering the slippage, more suitable conditions could be created for mass transport of species for different values of Schmidt number and a Womersley number of less than one.

To the best of knowledge of the authors of this study, the effect of slippage on electroosmotic flow of micropolar fluids has never been considered in other investigations. Micropolar fluid theory has proven to have higher accuracy in explaining fluid behavior in microscale in the presence of potential field. This innate quality gives this model a priority to be utilized in relevant physics, Therefore, this study has analytically investigated the effect of the influential parameters, including micropolar viscosity (K), the ratio of characteristic length of the fluid microstructures to the characteristic length of the flow (m), concentration coefficient (n), Debye–Hückel parameter (m₀), the ratio of pressure-driven velocity to electroosmotic velocity (U_r), and slip coefficient (b), on the flow behavior by examining the velocity and gyration profiles.

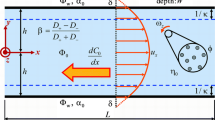
2 Problem geometry

Figure 1 shows a symbolic design of an EOF in a microchannel with hydrophobic walls. The basic equations governing an incompressible, axially symmetric micropolar fluid, ignoring the volumetric forces and gravity, are as follows [8]:

$$\nabla^{\user2{*}} .{\varvec{V}}^{\user2{*}} = 0$$

(1)

$$- (\mu + \chi )\nabla^{\user2{*}} \times \left[ {\nabla^{\user2{*}} \times {\varvec{V}}^{\user2{*}} } \right] + \chi \nabla^{\user2{*}} \times {\varvec{v}}^{\user2{*}} + \rho_{e}^{*} {\varvec{E}} - \nabla^{\user2{*}} .{\varvec{P}}^{\user2{*}} = \rho \left[ {{\varvec{V}}^{\user2{*}} .\nabla^{\user2{*}} } \right]{\varvec{V}}^{\user2{*}}$$

(2)

$$(\alpha + \beta + \gamma ){ }\nabla^{*} \left[ {\nabla^{*} .{\varvec{v}}^{*} } \right] - \gamma \nabla^{*} \times \left[ {\nabla^{*} \times {\varvec{v}}^{*} } \right] - 2\chi {\varvec{v}}^{*} + \chi \nabla^{*} \times { }{\varvec{V}}^{*} = \rho j_{0} \left[ {{\varvec{V}}^{*} .\nabla^{*} } \right]{\varvec{v}}^{*}$$

(3)

Fig. 1

Symbolic design of problem geometry and flow

The expressions ${\varvec{V}}$ and ${\varvec{v}}$ are the fluid velocity and microgyration, respectively, E is the applied electric field, P is the fluid pressure, and ρ and j₀ denote mass density and microinertia, respectively. Moreover, α, β, and γ are angular viscosity coefficients, and μ and χ are the dynamic and rotational viscosity coefficients, respectively.

3 Electric field equations

According to Fig. 1, the EOF is caused by creating a dual zone and applying the internal electric field in the vicinity of the charged walls of the channel. In order to calculate the velocity field, first, the distribution of the electric potential obtained through the Poisson equation is defined as follows:

$$\nabla^{2} \psi \left( y \right) = - \frac{{\rho_{e} }}{\epsilon}$$

(4)

where ρ_e is the electric charge density and $\epsilon$ is the permittivity of the solution. For small Debye lengths and zeta potentials, the electric potential can be considered the sum of the potential derived from the EDL ($\psi$) and the potential caused by the external electric field ($\phi$) [27].

$$\varphi = \left( {\phi+ \psi } \right)$$

(5)

By assuming that the electrolyte solution is symmetrical, Boltzmann distribution can be used for charge density within the electrolyte solution:

$$\rho_{{{e}}} = ze\left( {n^{ + } - n^{ - } } \right) = - {2}n_{{0}} ze\sinh \left( {\frac{ze\psi }{{k_{B} T}}} \right)$$

(6)

In the above equation, z represents valence of ions, e is the electron charge, n₀ is the desired ion concentration, k_B is the Boltzmann constant, and T denotes the absolute temperature in kelvin.

The Debye length is also much smaller than the height of the microchannel (h >  > λ_D) [8]:

$$\lambda_{D} = \sqrt {\frac{{\epsilon k_{B} T }}{{2n_{0} (ze)^{2} }}}$$

(7)

The characteristic velocity of an electric field can be defined as follows [8]:

$$U_{e} = - \frac{{{\epsilon}\psi_{0} E_{0} }}{\mu }$$

(8)

in which E₀ =|E|≥ 0 and $\psi$₀ is called zeta potential.

For an incompressible micropolar fluid, the continuity, momentum, and microgyration equations are defined using the dimensionless form as follows [8]:

$$\nabla .{\varvec{V}} = 0$$

(9)

$$- \nabla \times \left[ {\nabla \times {\varvec{V}}} \right] + {{K}} \nabla \times {\varvec{v}} + \rho_{e} \varvec E/E_{0} = \nabla \cdot {\varvec{P}} + Re[{\varvec{V}}. \nabla ]{\varvec {V}}$$

(10)

$$- \nabla \times \left[ {\nabla \times {\varvec{V}}} \right] - 2s\varvec v + w\nabla [\nabla .{\varvec{v}}] + s \nabla \times {\varvec{V}} = Ro[{\varvec{V}}. \nabla ]{\varvec v}$$

(11)

where K represents the micropolar viscosity, s and w are the couple stress parameters, Re denotes the Reynolds number, and Ro represents the microgyration Reynolds number.

According to Ref. [28], s equals $\frac{10K}{{m}^{2}(1+\frac{K}{2})}$, in which m indicates the ratio of characteristic length of the fluid microstructures to the characteristic length of the flow and varies between 0.1 and 1.

Based on the theory of electric field, the governing equation for the distribution of electrostatic potential in the Poisson equation is defined by substituting Eq. (6) in Eq. (4) as follows:

$$\nabla^{2} \psi \left( y \right) = \frac{{m_{0}^{2} }}{{\alpha_{0} }}\sinh \left[ {\alpha_{0} \psi \left( y \right)} \right]$$

(12)

and a group of dimensionless parameters is defined as follows:

$$\begin{gathered} K = {}\chi /\mu \quad {{s}} = \chi h^{2} /\gamma \quad w = \left( {\alpha + \beta + \gamma } \right)/\gamma \hfill \\ Re =\rho U_{e} h/\mu \quad P = \left( {p - p_{0} } \right)/(\frac{1}{2}\rho U_{e}^{2}) \quad U_{r} = U_{p} /U_{e} \hfill \\ U_{p} = - h^{2} \left( {dp/dx} \right)/\mu \quad Ro = \rho j_{0} U_{e} h/\gamma \quad m_{0} = h/ \lambda_{D} \hfill \\ \alpha_{0} = ze\psi_{0} /k_{B} T \hfill \\ \end{gathered}$$

(13)

The symbols U_p, U_r, m₀, and α₀ denote the pressure-driven flow velocity, the ratio of pressure-driven velocity to electroosmotic velocity, the Debye–Hückel parameter, and the ionic energy parameter, respectively.

By using the Taylor expansion, the hyperbolic sine function in Eq. (12) can be linearized:

$$\nabla^{2} \psi \left( y \right) = m_{0}^{2} \psi \left( y \right)$$

(14)

By solving the above general differential equation, Eq. (14) can be solved as follows:

$$\psi \left( y \right) = \frac{{\cosh \left( {m_{0} y} \right)}}{{\cosh \left( {m_{0} } \right)}}$$

(15)

Herein, the changes along the x-axis are ignored. Concerning the y-axis, the one-dimensional flow is smooth and symmetrical.

According to the definitions presented, Eqs. (9)–(11) provide the following two differential equations:

$$U^{\prime\prime}\left( y \right) + \frac{K}{K + 1}N^{\prime}\left( y \right) + \frac{1}{K + 1}\psi^{\prime\prime}\left( y \right) + \frac{{U_{{{r}}} }}{K + 1} = 0$$

(16)

$$N^{\prime\prime}\left( y \right) - sU^{\prime}\left( y \right) - 2sN\left( y \right) = 0$$

(17)

By integrating Eq. (16) and using Eq. (15), Eq. (18) is obtained as follows:

$$U^{\prime}\left( y \right) = - \frac{K}{K + 1}N\left( y \right) - \frac{{m_{0} \sinh \left( {m_{0} y} \right)}}{{\left( {K + 1} \right)\cosh \left( {m_{0} } \right)}} - \frac{{U_{{{r}}} }}{K + 1}y$$

(18)

Since the flow is symmetrical, we have:

$$U^{\prime}\left( 0 \right) = 0{ },{ }\psi^{\prime}\left( 0 \right) = 0$$

(19)

The boundary conditions intended for U(y) and $\psi$(y) are as follows:

$$U\left( { \pm 1} \right) = 0 , \psi \left( { \pm 1} \right) = 0$$

(20)

By substituting Eq. (18) in Eq. (17), we have:

$$N^{\prime\prime}\left( y \right) - \left( {2s - \frac{sK}{{K + 1}}} \right)N\left( y \right) + \frac{{sm_{0} \sinh \left( {m_{0} y} \right)}}{{\left( {K + 1} \right)\cosh \left( {m_{0} } \right)}} + \frac{{sU_{{{r}}} }}{K + 1}y = 0$$

(21)

By using the D-operator, the solution of the above equation is obtained as follows:

$$N\left( y \right) =\; ae^{{\sqrt {\left( {2s - \frac{sK}{{K + 1}}} \right)} y}} + be^{{ - \sqrt {\left( {2s - \frac{sK}{{K + 1}}} \right)} y}} + \frac{s}{{\left( {2s - \frac{sK}{{K + 1}}} \right)\left( {K + 1} \right)}}U_{r} y + \frac{{\frac{{sm_{0} }}{{\left( {K + 1} \right)\cosh \left( {m_{0} } \right)}}}}{{\left( {2s - \frac{sK}{{K + 1}}} \right) - m_{0}^{2} }}\sinh \left( {m_{0} y} \right)$$

(22)

The following provides the boundary conditions for the gyration on walls:

$$N ({ \pm 1} ) = - n\frac{dU}{{dy}}|_{y = \pm 1}$$

(23)

in which n is the microgyration boundary parameter (concentration coefficient). As for boundary conditions, various arguments provide analytical and numerical results in Ref. [8] for zero as well as nonzero, and if:

$$N (0) = 0 \to a + b = 0$$

(24)

the general solution of Eq. (22) is considered a coefficient like c whose value is calculated:

$$N\left( y \right) =\; c\sinh \left( {\sqrt {\left( {2s - \frac{sK}{{K + 1}}} \right)} y} \right) + \frac{s}{{\left( {2s - \frac{sK}{{K + 1}}} \right)\left( {K + 1} \right)}}U_{r} y + \frac{{\frac{{sm_{0} }}{{\left( {K + 1} \right)\cosh \left( {m_{0} } \right)}}}}{{\left( {2s - \frac{sK}{{K + 1}}} \right) - m_{0}^{2} }}\sinh \left( {m_{0} y} \right)$$

(25)

By using boundary conditions (24) in the above equation, the coefficient c is obtained:

$$\begin{gathered} N\left( y \right) = \left[ {\frac{{\frac{{ - \frac{{sm_{0} }}{{\left( {K + 1} \right)\cosh \left( {m_{0} } \right)}}}}{{\left( {2s - \frac{sK}{{K + 1}}} \right) - m_{0}^{2} }}\sinh \left( {m_{0} } \right) + \frac{{\frac{{nm_{0} \sinh \left( {m_{0} } \right)}}{{\left( {K + 1} \right)\cosh \left( {m_{0} } \right)}} + \frac{{nU_{{{r}}} }}{K + 1}}}{{1 - \frac{Kn}{{1 + K}}}} - \frac{{sU_{r} }}{{\left( {2s - \frac{sK}{{K + 1}}} \right)\left( {K + 1} \right)}}}}{{\sinh \left( {\sqrt {\left( {2s - \frac{sK}{{K + 1}}} \right)} } \right)}}} \right]\sinh \left( {\sqrt {\left( {2s - \frac{sK}{{K + 1}}} \right)} y} \right) + \hfill \\ \frac{{sU_{r} }}{{\left( {2s - \frac{sK}{{K + 1}}} \right)\left( {K + 1} \right)}}y + \frac{{\frac{{sm_{0} }}{{\left( {K + 1} \right)\cosh \left( {m_{0} } \right)}}}}{{\left( {2s - \frac{sK}{{K + 1}}} \right) - m_{0}^{2} }}\sinh \left( {m_{0} y} \right) \hfill \\ \end{gathered}$$

(26)

Then, equation U(y) could be solved by integrating Eq. (18) and considering the Navier slip boundary conditions on walls for hydrophobic walls. Therefore:

$$\begin{gathered} U\left( y \right) = \frac{{ - K\left[ {\frac{{\frac{{ - \frac{{sm_{0} }}{{\left( {K + 1} \right)\cosh \left( {m_{0} } \right)}}}}{{\left( {2s - \frac{sK}{{K + 1}}} \right) - m_{0}^{2} }}\sinh \left( {m_{0} } \right) + \frac{{\frac{{nm_{0} \sinh \left( {m_{0} } \right)}}{{\left( {K + 1} \right)\cosh \left( {m_{0} } \right)}} + \frac{{nU_{{{r}}} }}{K + 1}}}{{1 - \frac{Kn}{{1 + K}}}} - \frac{{sU_{r} }}{{\left( {2s - \frac{sK}{{K + 1}}} \right)\left( {K + 1} \right)}}}}{{\sinh \left( {\sqrt {\left( {2s - \frac{sK}{{K + 1}}} \right)} } \right)}}} \right]}}{{\left( {1 + K} \right)\sqrt {\left( {2s - \frac{sK}{{K + 1}}} \right)} }} \hfill \\ \left[ {\cosh \left( {\sqrt {\left( {2s - \frac{sK}{{K + 1}}} \right)} y} \right) - \cosh \left( {\sqrt {\left( {2s - \frac{sK}{{K + 1}}} \right)} } \right)} \right] - \left( {\frac{{U_{r} }}{{2\left( {K + 1} \right)}} + \frac{{KsU_{r} }}{{2\left( {K + 1} \right)^{2} \left( {2s - \frac{sK}{{K + 1}}} \right)}}} \right)\left( {\left( {y^{2} - 1} \right)} \right) \hfill \\ - \left( {\frac{{\frac{{Ksm_{0} }}{{\left( {K + 1} \right)\cosh \left( {m_{0} } \right)}}}}{{m_{0} \left( {1 + K} \right)\left( {\left( {2s - \frac{sK}{{K + 1}}} \right) - m_{0}^{2} } \right)}}} \right) \left[ {\cosh \left( {m_{0} y} \right) - \cosh \left( {m_{0} } \right)} \right] - \left( {\frac{1}{K + 1}} \right) \left[ {\frac{{\cosh \left( {m_{0} y} \right)}}{{\cosh \left( {m_{0} } \right)}} - 1} \right] \hfill \\ - b\left[ { - \frac{K}{K + 1}} \left[\left[ {\frac{{\frac{{ - \frac{{sm_{0} }}{{\left( {K + 1} \right)\cosh \left( {m_{0} } \right)}}}}{{\left( {2s - \frac{sK}{{K + 1}}} \right) - m_{0}^{2} }}\sinh \left( {m_{0} } \right) + \frac{{\frac{{nm_{0} \sinh \left( {m_{0} } \right)}}{{\left( {K + 1} \right)\cosh \left( {m_{0} } \right)}} + \frac{{nU_{{{r}}} }}{K + 1}}}{{1 - \frac{Kn}{{1 + K}}}} - \frac{{sU_{r} }}{{\left( {2s - \frac{sK}{{K + 1}}} \right)\left( {K + 1} \right)}}}}{{\sinh \left( {\sqrt {\left( {2s - \frac{sK}{{K + 1}}} \right)} } \right)}}} \right]\sinh \left( {\sqrt {\left( {2s - \frac{sK}{{K + 1}}} \right)} } \right) + \frac{{sU_{r} }}{{\left( {2s - \frac{sK}{{K + 1}}} \right)\left( {K + 1} \right)}} + \frac{{\frac{{sm_{0} }}{{\left( {K + 1} \right)\cosh \left( {m_{0} } \right)}}}}{{\left( {2s - \frac{sK}{{K + 1}}} \right) - m_{0}^{2} }}\sinh \left( {m_{0} } \right)\right] \begin{gathered} \hfill \\ - \frac{{m_{0} \sinh \left( {m_{0} } \right)}}{{\left( {K + 1} \right)\cosh \left( {m_{0} } \right)}} - \frac{{U_{{{r}}} }}{K + 1} \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered}$$

(27)

In the above equation, b indicates the slip coefficient of the surfaces.

Accordingly, Eqs. (26) and (27) form the boundary value solution for the steady-state flow of a micropolar fluid when the Debye–Hückel approximation is established [8].

4 Validation of the solution

The analytical solutions were validated with two different cases. First, the velocity profile of the flow with the electroosmotic/pressure actuator for different values of U_r was compared with the analytical solution of the electroosmotic/pressure-driven flow in a straight two-dimensional channel [29]. Then, the velocity distribution of the micropolar fluid at various Ks was compared to the analytical results of [30], which were presented for the Poiseuille flow of micropolar fluids. A very good agreement was obtained between the results (Figs. 2, 3).

Fig. 2

A comparison between the results of the present study and Ref. [29] to validate the velocity profiles with electroosmotic/pressure actuator for different values of U_r

Fig. 3

A comparison between the results of the present study and Ref. [30] to validate the velocity profiles of micropolar fluid for different values of K

5 Results and discussion

In this section, the results of the analytical solution are investigated, and the effect of the influential parameters, including micropolar viscosity, the ratio of characteristic length of the fluid microstructures to the characteristic length of the flow, concentration coefficient, Debye–Hückel parameter, the ratio of pressure-driven velocity to electroosmotic velocity, and slip coefficient, on the flow pattern are investigated. The following provides the distribution of velocities for the cases with the slip coefficients of 0, 0.05, and 0.1 for slippage walls, respectively.

5.1 Electrokinetic effects of micropolar fluids without slip

Figures 4 and 5 display the flow velocity and gyration profiles with an electroosmotic/pressure actuator in a micropolar fluid for different values of K in the range of 0–10. It is observed that with an increase in the micropolar viscosity, the velocity and gyration profiles experience a reduction in magnitude. Furthermore, when K equals zero, such behavior is qualitatively similar to that of Newtonian fluids.

Fig. 4

Velocity profile with electroosmotic/pressure actuator of micropolar fluid flow for different values of K at m₀ = 10, n = 0.1, m = 0.2, U_r = 1, b = 0

Fig. 5

Gyration profile with electroosmotic/pressure actuator of micropolar fluid flow for different values of K at m₀ = 10, n = 0.1, m = 0.2, U_r = 1

Figures 6 and 7 depict different concentration coefficients ranging from 0 to 1, versus velocity and gyration profiles with the electroosmotic/pressure actuator in a micropolar fluid. As can be seen, at n = 0, the fluid elements at the boundaries have no gyration. Hence, no movement is added to the flow in the microchannel given the gyration of fluid elements at the boundaries. Moreover, the magnitude of the velocity and gyration profiles has an increasing trend with the rise in n.

Fig. 6

Velocity profile with electroosmotic/pressure actuator of micropolar fluid flow for different values of n at m₀ = 10, K = 1, m = 0.2, U_r = 1, b = 0

Fig. 7

Gyration profile with electroosmotic/pressure actuator of micropolar fluid flow for different values of n at at m₀ = 10, K = 1, m = 0.2, U_r = 1

Figures 8 and 9 make a comparison between the flow velocity and gyration profiles for different values of the Debye–Hückel parameter in the range of 5–100, which is the main actuation factor of the flow. It is observed that higher values of this parameter lead to higher flow velocity and lower curvature of the velocity profile. This means a reduction in the thickness of the EDL. Moreover, given the definition of m₀, which is in the form of $\frac{h}{ {\uplambda }_{{D}}}$, ${\uplambda }_{{D}}$ becomes smaller than $h$, and the velocity distribution tends to a constant value.

Fig. 8

Velocity profile with pure electroosmotic actuator of micropolar fluid flow for different values of m₀ at K = 0, n = 0.1, m = 0.2, U_r = 0, b = 0

Fig. 9

Gyration profile with pure electroosmotic actuator of micropolar fluid flow for different values of m₀ at at K = 0, n = 0.1, m = 0.2, U_r = 0

Figures 10 and 11 demonstrate the velocity and gyration profiles of the micropolar fluid for different values of U_r (representing the ratio of pressure-driven velocity to electroosmotic velocity that the zeta potential can create in the flow via m₀) with its value ranging from -2 to 2. U_r > 0 means that the velocity field due to electroosmotic and pressure forces is applied in the direction of the flow, and the velocity distribution rises with the pressure. On the other hand, if U_r < 0, the velocity field is opposite to the direction of the flow, and the velocity distribution decreases. Moreover, it can be said that a zero value for this ratio means the absence of a pressure force in the flow, i.e., the fluid flow in the channel is totally driven by the electroosmotic actuator.

Fig. 10

Velocity profile with electroosmotic/pressure actuator of micropolar fluid flow for different values of U_r at K = 1, m₀ = 10, n = 0.1, m = 0.2, b = 0

Fig. 11

Gyration profile with electroosmotic/pressure actuator of micropolar fluid flow for different values of U_r at K = 1, m₀ = 10, n = 0.1, m = 0.2

In Figs. 12 and 13, the velocity and gyration profiles with an electroosmotic actuator in the micropolar fluid versus the channel width can be compared for different values of m ranging from 0.1 to 1. According to the figures, an increase in this parameter reduces the flow velocity. In addition, considering the concept of m, which represents the ratio of characteristic length of the fluid microstructures to the characteristic length of the flow, one can infer that the flow faces lower frictional resistance at lower ratios.

Fig. 12

Velocity profile with electroosmotic/pressure actuator of micropolar fluid flow for different values of m at K = 1, m₀ = 10, n = 0.1, U_r = 1, b = 0

Fig. 13

Gyration profile with electroosmotic/pressure actuator of micropolar fluid flow for different values of m at K = 1, m₀ = 10, n = 0.1, U_r = 1

Figure 14 indicates the effect of the slip coefficient in the range of 0–0.2 on the flow velocity with the electroosmotic/pressure actuator. As can be seen, as the slip coefficient rises, the resistive force of the fluid decreases, and the fluid exits the wall, increasing the flow velocity near the wall. It can be said that if a hydrophobic wall is used, the flow velocity on the wall is no longer zero. Accordingly, the slip length significantly affects the flow profile and increases its value.

Fig. 14

Velocity profile with electroosmotic/pressure actuator of micropolar fluid flow for different values of b at K = 1, m₀ = 10, n = 0.1, m = 0.2, U_r = 1

5.2 Electrokinetic effect of micropolar fluids in the presence of slip

The following resents the EOF velocity results in the presence of surface slip.

Figures 15 and 16 indicate the velocity profiles with the electroosmotic/pressure actuator in a micropolar fluid for different values of K considering wall slip. It was observed that the decreasing trend of the velocity profile decelerates as the micropolar viscosity and slip coefficient increase.

Fig. 15

Velocity profile with electroosmotic/pressure actuator of micropolar fluid flow for different values of K at m₀ = 10, n = 0.1, m = 0.2, U_r = 1, b = 0.05

Fig. 16

Velocity profile with electroosmotic/pressure actuator of micropolar fluid flow for different values of K at m₀ = 10, n = 0.1, m = 0.2, U_r = 1, b = 0.1

Figures 17 and 18 illustrate different concentration coefficients for velocity profiles in a micropolar fluid with the electroosmotic/pressure actuator in the presence of wall slip. As can be seen, with a rise in the concentration and wall slip, the velocity profile extends compared to the state without slip.

Fig. 17

Velocity profile with electroosmotic/pressure actuator of micropolar fluid flow for different values of n at m₀ = 10, K = 1, m = 0.2, U_r = 1, b = 0.05

Fig. 18

Velocity profile with electroosmotic/pressure actuator of micropolar fluid flow for different values of n at m₀ = 10, K = 1, m = 0.2, U_r = 1, b = 0.1

Figures 19 and 20 make a comparison of the velocity profiles with hydrophobic walls for different values of the Debye–Hückel parameter. The results indicate that the velocity distribution is significantly extended in the presence of slip. Moreover, the curvature of the velocity profile is decreased, i.e., the thickness of the EDL is decreased.

Fig. 19

Velocity profile with pure electroosmotic actuator of micropolar fluid flow for different values of m₀ at K = 0, n = 0.1, m = 0.2, U_r = 0, b = 0.05

Fig. 20

Velocity profile with pure electroosmotic actuator of micropolar fluid flow for different values of m₀ at K = 0, n = 0.1, m = 0.2, U_r = 0, b = 0.1

Figures 21 and 22 show the velocity profiles of the micropolar fluid for different values of U_r with wall slip. As mentioned previously, at U_r > 0, the velocity distribution increases with the pressure drive. In contrast, if U_r < 0, the velocity distribution declines, and the presence of a hydrophobic wall significantly magnifies the effect of this parameter on the flow velocity distribution.

Fig. 21

Velocity profile with electroosmotic/pressure actuator of micropolar fluid flow for different values of U_r at K = 1, m₀ = 10, n = 0.1, m = 0.2, b = 0.05

Fig. 22

Velocity profile with electroosmotic/pressure actuator of micropolar fluid flow for different values of U_r at K = 1, m₀ = 10, n = 0.1, m = 0.2, b = 0.1

In Figs. 23 and 24, the velocity profiles of the micropolar fluid with the electroosmotic actuator can be compared for different values of m considering wall slip. It is observed that an increase in this parameter in the presence of the slip effect decelerates the decreasing trend in the flow velocity.

Fig. 23

Velocity profile with electroosmotic/pressure actuator of micropolar fluid flow for different values of m at K = 1, m₀ = 10, n = 0.1, U_r = 1, b = 0.05

Fig. 24

Velocity profile with electroosmotic/pressure actuator of micropolar fluid flow for different values of m at K = 1, m₀ = 10, n = 0.1, U_r = 1, b = 0.1

6 Conclusions

The electroosmotic flow of a micropolar fluid model in a horizontal microchannel with hydrophobic walls is investigated analytically in this study. The findings were divided into two sections to examine the effects of the problem variables including micropolar viscosity (K), the ratio of characteristic length of the fluid microstructures to the characteristic length of the flow (m), concentration coefficient (n), Debye–Hückel parameter (m₀), the ratio of pressure-driven velocity to electroosmotic velocity (U_r), and slip coefficient (b). The first section examined the effect of these variables on velocity and gyration profiles without considering wall slip, and the second section examined the effect of these variables with wall slip.

The results indicated that increasing the K, m, and U_r (U_r < 0) parameters decreased the microchannel's velocity. With an increased U_r (U_r > 0), n and m₀ parameters, the velocity inside the microchannel increased. Additionally, increasing the m₀ results in a reduction in the thickness of the EDL. The slip coefficient directly affects the velocity profile, significantly increasing its value. It was observed that when the wall slip is considered, the trend toward increasing the flow velocity increases as the U_r (U_r > 0), n, and m₀ parameters are increased. At the same time, the decreasing trend of the velocity distribution declines by increasing the K, m, and U_r (U_r < 0) parameters and slip coefficient. Thus, increasing the slip coefficient on the wall results in an increase in the wall's velocity.

The present analysis indicates that slip boundary condition on a small scale is highly significant and helps achieve the best microchannel walls design for accurate control of flow in microchannels. The future studies would be focused on the effects of heat transfer within the present physics by different boundary conditions and the addition of nanoparticles.