1 Introduction

Application of Microelectromechanical systems (MEMS) and nanoelectromechanical systems is becoming considerably prevalent for variety of scientific and engineering applications [1, 2]. With the recent development of MEMS technologies, variety of studies has been performed in microfluidic systems. For instance, microvalves, micropumps, and flow sensors are interdisciplinary systems combining fluid mechanics and micromachining technologies [3,4,5]. Due to their ability to control and regulate precise and small volumes of fluids, micropumps are the most commonly employed components in biological, chemical, and medical applications such as microsyringes for diabetics. However, in many situations some of fluid properties which restrict certain principle to a small class of fluids, impact their performance considerably. Micropumps are mainly classified into two categories: mechanical and non-mechanical (without moving parts) micropumps [4]. Mechanical micropumps are actuated considering variety of actuating principles, such as, electrostatic, thermopneumatic, piezoelectric, and magnetic ones [6, 7]. Wear and fatigue of the input–output check valves and high-pressure drop across them, are common problems in those micropumps [8]. Hence, micropumps without movable parts such as electrohydrodynamic (EHD), magnetohydrodynamic (MHD) and valveless diffuser–nozzle micropumps were presented. A diffuser–nozzle valveless micropump was presented by Stemme and Stemme [8].The working principle of the micropump is that net volume from the inlet side to the outlet side is pumped since generally, for a given pressure drop, the volume flow is higher in diffuser than in nozzle direction.

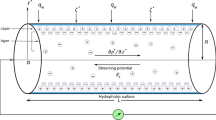
Comparatively high pump volume and simplicity are features of these kinds of pumps. The other type of non-mechanical micropumps, which principle was offered first around 1960, is EHD micropump [9]. Bart et al. and Richter et al. applied the EHD induction effect, which represents the formation and movement of stimulated charges at boundary layer of fluid–solid or fluid–fluid [10,11,12]. They also used the EHD injection effect, which is based on the electrochemical generation and motion of charged ions. In these micropumps, the pumping source is either the result of the interaction between a traveling wave of potential and conductivity gradient or the Coulomb force derived from electrochemical reactions which acts on ions injected into the fluid from an emitter electrode. These micropumps are only able of pumping the liquids with very low conductivities in the range of 10−12–10−6 S/m, such as methanol, ethanol, or several oils which are organic solvents [13]. Since aqueous solutions possess the high ionic conductivity, the application of these kinds of micropumps in biological or medical applications is restricted [14]. The other type of non-mechanical micropump is MHD micropump in which the electrically conducting liquids are pumped due to interaction of magnetic and electric fields [15]. Ritchie figured of that the utilization of an electric field perpendicular to a magnetic field led to pump the conducting liquid fluid in a microchannel [16]. The actuation principle of MHD has been mainly expanded in the MHD propulsion ship since the 1960s [17, 18]. Figure 1 demonstrates the primary principle of the MHD micropump, in which the Lorentz force is acting along the x-direction.

Fig. 1
figure 1

Schematic of the MHD micropump with Lorentz driving force

Full size image

Since a reversal of the magnetic field or electric current led to flow reflux, this pumping principle is bidirectional. Only small values for achievable pressure, e.g., 1.8 mbar and pump rate, 63 μl/min, can be generated by typical MHD micropumps for the device described in [19]. The ionic conductivity of the pumped fluid influences achievable pressure and pump rate, strongly. At the injection electrodes, DC operation can generate electrolytic bubble. Application of AC current injection with usage of an electromagnet instead of a permanent magnet can solve this problem. The Lorentz vector, and therefore, the fluid flow remain in the same direction by driving both the current injector and the magnet coil from synchronized AC sources. Electrolytic formation of gas bubbles could be prevented by choosing the high operation frequency. Taking disturbing effect in MHD pumps into account to generate dosing systems with high accuracy as a simple and supreme actuation principle, the electrolytic formation of gas bubbles can be exploited. Böhm mentioned the drug delivery as the first application of this principle in his work [20]. He generated gas bubbles applying current injection to a container with two immersed electrodes in electrolyte solution. A step-by-step or steady dislocation in an adjoining meander, which carries the fluid to be distributed, is generated by the corresponding increment of volume. This dosing system is capable of delivering fluid doses as small as 100 nl with a precision of at least 5 nl by a closed-loop control of the process of gas formation. For DC and AC MHD devices, experimental and theoretical investigations have been done. An applicative AC MHD pump was presented by Lemoff et al. and Lemoff and Lee in which an electrolytic solution propelled by the Lorentz force along the silicon microchannel [21, 22]. By applying the simple model, performance of a DC MHD micropump in single phase was obtained by Jang and Lee [19]. Theoretical and experimental analyze of various models of the MHD micropump flow for two types of magnetohydrodynamic stirrers have been done by Bau et al. and Yi et al. [23, 24]. Zhong et al. demonstrated the circulation of fluids in ceramic channels, using magnetohydrodynamic [25]. An AC magnetohydrodynamic micropump was developed and fabricated by Eijkel et al. for chromatographic application [26]. Application of MHD pumping in microfluidic networks and mixing systems has been studied too. To pump electrolytic solutions in microfluidic networks, MHD forces were utilized by Lemoff and Lee [27]. The function of a DC MHD micropump at high current densities was described by Homsy et al. to prevent gas bubbles production in pumping conduit [28]. Duwairi and Abdullah presented the theoretical study of the fully developed transient laminar flow and distribution of temperature in MHD micropumps. Also, they investigated the influence of various parameters on the temperature and transient velocity [29]. Kiyasatfar et al. studied a transient, laminar and fully developed electrically conducting fluids flow in MHD micropumps, and also, investigated the temperature distribution and effects of dimensionless parameters on the entropy generation rate [30]. The results indicate that at the small Hartmann numbers, the velocity and temperature profiles are parabolic and its increase leads to decrease in maximum velocity and temperature that makes their profiles getting flatten. Kiyasatfar et al. also investigated the flow and heat transfer characteristics of various working medium with different physical properties in MHD micropumps [31]. They studied effects of magnetic flux density, applied electric current and channel size on flow velocity field, thermal behavior as well as entropy generation rate. The results show that when the high electrically conductive fluids is used as a working medium in MHD pumps, the reverse induced Lorentz forces are significant and the peak velocity is happening in a specific value of magnetic flux density.

Currently, fluid dynamic theory’s evaluation is in advancement phase since electrically conducting fluids which behave like a non-Newtonian fluid are essential in industry and technology [32].

Considering the internal specifications of the subtractive particles, which are able to rotate, theory of molecular fluids by Eringen have been represented [33]. The foundation for a mathematical model for non-Newtonian fluids is provided by this theory because it considers the microscopic effects caused by the micro motions and local structure of the fluid elements. The micropolar fluid can be considered physically as a suspension of tiny, rigid cylindrical elements like huge dumbbell-shaped molecules where the deformation of the particles is ignored. An increased interest in the theory of micropolar fluids led to re-examination of many classical flows to characterize the influence of the fluid microstructure. These fluids consist of dilute suspension of rigid macromolecules with particular movements that are affected by spin inertia and support body moments and stress. The fluids which contain micro constituents that can undergo rotation, and impact the flow’s hydrodynamics in the way it can be considered non-Newtonian, are micropolar fluids. There are many practical applications for micropolar fluids, for instance, analyzing the behavior of human and animal blood, polymeric fluids, liquid crystals, exotic lubricants, additive suspensions, colloidal suspensions, coating, ink-jet printing, geological flows in the earth mantle, turbulent shear flow and so on. Many researches about various problems in micropolar fluids have been conducted since the time Eringen introduced it. Ariman et al. presented a pervasive review of micropolar fluids mechanically [34]. They study the influences of Hall and ion-slip on electrically conducting micropolar fluid flow inside a rectangular conduit while imposing a transverse magnetic field. Lukaszewicz presented the applications of micropolar fluids in the theory of porous media and the theory of lubrication. Furthermore, he offered the mathematical theory of equations for micropolar fluids [35]. The non-Newtonian micropolar fluids’ stagnation point flow without heat generation or vertical velocity at the surface was studied by Nazar et al. Classical Newtonian fluid as a special case was included in this study and also the couple stresses were sustained [36].

The widespread technical applications of magnetohydrodynamic (MHD) have made it favorable to extend many of the existing hydrodynamic solutions considering the electrically conducting fluid and the impacts of magnetic fields. The MHD micropump is one of the applications of magnetohydrodynamic (MHD) effect which offers several privileges, compared with other types of non-mechanical micropumps, such as bidirectional pumping capability, simple manufacturing process, producing continuous flow, and the availability of medium conducting liquid. The MHD micropump could be used in microfluidic propulsion device as the active control transducer of turbulent flow or biomedical devices such as a drug delivery system.

In this paper, a MHD micropump with side-walled electrodes which applies Lorentz force is studied. The continuous steady, incompressible and fully developed laminar conducting micropolar fluid is pumped through the square channel of the pump as a result of interaction between an applied electric field and a perpendicular magnetic field.

2 Formulation of the problem

Continues incompressible micropolar fluid flow through a micropump’s square duct is considered after reaching the steady state.

The Cartesian coordinate system was chosen, the x-axis along the axis of the conduit and y, z-axes along the sides. The dimensions of the channel in y- and z-directions are equal to h. The flow is subjected to a uniform magnetic field and a uniform electric field perpendicular to magnetic one and they are imposed in a plane perpendicular to the x-axis. It is assumed that the flow is steady and magnetic Reynolds number is very small so that the induced magnetic field can be neglected [37]. The ion slip and Hall effects can be neglected in this case since the frequency of electron–atom collision is considered to be relatively low. The fluid velocity vector is given as \(\bar{u} = \bar{u}(y,z)i\) and the microrotation vector as \(\bar{v} = \bar{v}_{1} (y,z)j + \bar{v}_{2} (y,z)k\).

Considering these assumptions, the equations that govern the MHD flow of micropolar fluid are obtained. The continuity equation is expressed as follows:

$$\frac{\partial u}{\partial x} = 0$$
(1)

In the microchannel under electromagnetic interactions, the Lorentz forces acting on the fluid particles are considered as a hydrostatic pressure head uniformly distributed over the entire channel region; hence, it is expressed as follows:

$$- \frac{\partial P}{\partial x} = \frac{\Delta P}{L}$$
(2)

where \(\Delta P\) is the pressure head along the channel with length L, caused by the interaction between magnetic and electric fields. That is:

$$\Delta P = \left( {J \times B} \right)L_{p}$$
(3)

From Eqs. (2) and (3), the pressure gradient generated by the applied DC electric and magnetic fields in the flow channel can be obtained. Equation (4) is obtained by substituting the pressure gradient into linear momentum equation.

Here electric current density is \(\vec{J} = \sigma \, (\vec{E} + \vec{u} \times \vec{B})\), σ is the fluid electrical conductivity, B is the magnetic flux density, E is the electric field intensity, L is length of microchannel and L p is the electrode length. In this study, it is assumed that the length of electrode is the same as the microchannel length.

$$\left( {\mu + k} \right)\left( {\frac{{\partial^{2} \bar{u}}}{{\partial y^{2} }} + \frac{{\partial^{2} \bar{u}}}{{\partial z^{2} }}} \right) + k\left( {\frac{{\partial \bar{v}_{2} }}{\partial y} - \frac{{\partial \bar{v}_{1} }}{\partial z}} \right) + \frac{{\sigma EBL_{p} }}{L} - \frac{{\sigma B^{2} \bar{u}L_{p} }}{L} = 0$$
(4)

Angular momentum equations are presented as following forms:

$$- 2k\bar{v}_{1} + k\frac{{\partial \bar{u}}}{\partial z} - \gamma \frac{\partial }{\partial z}\left( {\frac{{\partial \bar{v}_{2} }}{\partial y} - \frac{{\partial \bar{v}_{1} }}{\partial z}} \right) + (\alpha + \beta + \gamma )\frac{\partial }{\partial y}\left( {\frac{{\partial \bar{v}_{1} }}{\partial y} + \frac{{\partial \bar{v}_{2} }}{\partial z}} \right) = 0$$
(5)
$$- 2k\bar{v}_{2} - k\frac{{\partial \bar{u}}}{\partial y} + \gamma \frac{\partial }{\partial y}\left( {\frac{{\partial \bar{v}_{2} }}{\partial y} - \frac{{\partial \bar{v}_{1} }}{\partial z}} \right) + (\alpha + \beta + \gamma )\frac{\partial }{\partial z}\left( {\frac{{\partial \bar{v}_{1} }}{\partial y} + \frac{{\partial \bar{v}_{2} }}{\partial z}} \right) = 0$$
(6)

One of the essential characteristic of the micropump is its flow rate which is defined as the mass of fluid which can be pumped through a cross-section of the microchannel in unit of time. Considering the area of cross-sectional channel integral, the volumetric flow rate (Q) is given by:

$$Q = \iint {u(y,z)dydz}$$
(7)

In this work, variables of the flow are constant in the flow direction (x-direction).

The following inequalities are satisfied by the material constants α, β, γ, κ and μ [30]. Where α, β and γ, are the spin gradient viscosity coefficients, κ is the vortex viscosity coefficient and μ is the classical molecular viscosity coefficient.

$$\kappa \ge 0, \, 2\mu + \kappa \ge 0, \, 3\alpha + \beta + \gamma \ge 0,\gamma \ge \left| \beta \right|$$
(8)

To obtain the non-dimensional form of the Eqs. (4), (5) and (6), the following non-dimensional variables are introduced:

$$y = \frac{{\bar{y}}}{h},z = \frac{{\bar{z}}}{h},u = \frac{\mu }{{h^{2} \sigma EB}}\bar{u},v_{1} = \frac{\mu }{h\sigma EB}\bar{v}_{1} ,v_{2} = \frac{\mu }{h\sigma EB}\bar{v}_{2}$$
(9)

Afterwards the non-dimensional governing equations are presented as:

$$\frac{1}{1 - N}\frac{{\partial^{2} u}}{{\partial z^{2} }} + \frac{{h^{2} }}{{b^{2} (1 - N)}}\frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{hN}{b(1 - N)}\frac{{\partial v_{2} }}{\partial y} - \frac{N}{1 - N}\frac{{\partial v_{1} }}{\partial z} + 1 - Ha^{2} u = 0$$
(10)
$$- v_{1} + \frac{1}{2}\frac{\partial u}{\partial z} - \frac{h(2 - N)}{{bm^{2} }}\frac{{\partial^{2} v_{2} }}{\partial z\partial y} + \frac{2 - N}{{m^{2} }}\frac{{\partial^{2} v_{2} }}{{\partial z^{2} }} + \frac{1}{{L^{2} }}\frac{{\partial^{2} v_{1} }}{{\partial y^{2} }} + \frac{b}{{hL^{2} }}\frac{{\partial^{2} v_{2} }}{\partial y\partial z} = 0$$
(11)
$$- v_{2} + \frac{h}{2b}\frac{\partial u}{\partial y} - \frac{{h^{2} (2 - N)}}{{b^{2} m^{2} }}\frac{{\partial^{2} v_{2} }}{{\partial y^{2} }} + \frac{h(2 - N)}{{bm^{2} }}\frac{{\partial^{2} v_{2} }}{{\partial z^{2} }} + \frac{b}{{hL^{2} }}\frac{{\partial^{2} v_{1} }}{\partial y\partial z} + \frac{{b^{2} }}{{h^{2} L^{2} }}\frac{{\partial^{2} v_{2} }}{{\partial y^{2} }} = 0$$
(12)

where \(L^{2} = \frac{{2h^{2} \kappa }}{\alpha + \beta + \gamma }\), \(N = \frac{\kappa }{\mu + \kappa },(0 \le N \le 1)\) is the coupling number, \(m^{2} = \frac{{2h^{2} \kappa (2\mu + \kappa )}}{\gamma (\mu + \kappa )}\) is the micropolar parameter and \(Ha = hB\sqrt {\frac{\sigma }{\mu }}\) is the Hartmann number.

Considering usual hyper stick and no-slip boundary conditions, the following equations are obtained:

$$v_{ 1} \left( {x, y, 0} \right) = v_{ 1} \left( {x, y, h} \right) = v_{ 1} \left( {x, 0, z} \right) = v_{ 1} \left( {x, b, z} \right) = 0$$
(13)
$$v_{2} \left( {x, y, 0} \right) = v_{2} \left( {x, y, h} \right) = v_{2} \left( {x, 0, z} \right) = v_{2} \left( {x, b, z} \right) = 0$$
(14)
$$u\left( {x, 0, z} \right) = u\left( {x, b, z} \right) = u\left( {x, y, 0} \right) = u\left( {x, y, h} \right) = 0$$
(15)

Applying finite-difference method, the governing Eqs. (10), (11) and (12) with the boundary conditions Eqs. (13), (14) and (15) are numerically solved. A numerical experiment was conducted with various meshes in the rectangular region and axial step lengths in X and Y directions to check the independence of the mesh resolution of the numerical results. To describe the flow in this study with sufficient accuracy, the mesh distribution of 51 × 51 was selected.

To verify the validity of numerical results, the flow rate and velocity of a viscous fluid flow without considering micropolar effects were investigated for varying current and compared with the experimental ones presented by Ho for the fluid with conductivity of 1.5 S/m, the viscosity of 0.0006 Pa s and electrode length of 0.035 m. The channel depth width and length values are equal to 0.007, 0.003 and 0.08 m, respectively [38].

The numerical results showed a good agreement with experimental ones. A linear increment occurs in the average flow velocity with increment of current from 0.1 to 1.3 A. As it can be seen from the Fig. 2, deviation increases in higher applied current due to bubbles’ growth in solutions which affect the flow motion.

Fig. 2
figure 2

Comparison the flow velocity between numerical solution and experiment result with applied current

Full size image

3 Results and discussion

To investigate the impacts of different parameters like coupling number (N), magnetic parameter (Ha), and micropolar fluid parameter (m), on velocity and microrotation components explicitly, various values for these parameters were applied. After obtaining numerical solution of the equations for a grid of mesh points of square region, the results are illustrated graphically.

Figures 3, 4 and 5 demonstrate the velocity (u) profile and microrotation components (v 1 and v 2 ) profiles, respectively, for N = 0.4, Ha = 2, m = 5, l = 1.0. As it is expected, the maximum velocity occurred at the rectangle center and there is a symmetric flow in the y- and z-directions.

Fig. 3
figure 3

Profile of velocity component (u) for N = 0.4, Ha = 2, m = 5, l = 1.0

Full size image
Fig. 4
figure 4

Profile of microrotation component (v 1 ) for N = 0.4, Ha = 2, m = 5, l = 1.0

Full size image
Fig. 5
figure 5

Profile of microrotation component (v 2 ) for N = 0.4, Ha = 2, m = 5, l = 1.0

Full size image

It can be seen from the Figs. 4 and 5 that the microrotation components v 1 and v 2 are zero at the center of the rectangle.

Also it is obvious that v 1 and v 2 , respectively, are symmetric about the y (channel width) and z (channel height) axes.

For various amounts of N and for Ha = 2, l = 1.0, and m = 5, the velocity and microrotation components behavior along y at the centerline of the channel (i.e., z = 0.5) is demonstrated in Figs. 6, 7, and 8. (Since the microrotation component (v 1 ) is equal to zero at the centerline, the behavior of this component is demonstrated at z = 0.52).

Fig. 6
figure 6

The effect of N on velocity component (u)

Full size image
Fig. 7
figure 7

The effect of N on microrotation component (v 1 )

Full size image
Fig. 8
figure 8

The effect of N on microrotation component (v 2 )

Full size image

With increment of the coupling number the velocity u and microrotation component v 1 decrease. As the value of N approximates zero, the viscous fluid equations are obtained from Eqs. (6) and (7). Thus, it can be concluded that the velocity in the case of viscous fluid is more than that of micropolar fluid. With increasing N, the microrotation component v 2 rises adjacent to one side of the rectangle while it decreases near to the other side of the channel symmetrically, with a reverse rotation adjacent to the boundaries. Furthermore, it is obvious that the microrotation components increase symmetrically with increasing width of channel for constant N value; however, adjacent to the sides of the microchannel it shows a decreasing.

Figures 9, 10 and 11 demonstrate the influence of magnetic parameter (Ha) on the velocity and microrotations for N = 0.4, l = 1.0, and m = 5.

Fig. 9
figure 9

The effect of Ha on velocity component (u)

Full size image
Fig. 10
figure 10

The effect of Ha on microrotation component (v 1 )

Full size image
Fig. 11
figure 11

The effect of Ha on microrotation component (v 2 )

Full size image

As it is expected, Fig. 9 shows that as Ha increase the velocity component become smaller. The reason is that the applied magnetic field normal to the flow direction slows down the movement of the fluid by rising resistive force. The microrotation component v 1 decreases similarly by increasing Ha. On the other hand, increment of magnetic parameter led to increment of v 2 near to one side of the channel and decrement of it adjacent to the other side of the channel symmetrically.

The effect of various m amounts on the velocity and microrotation for Ha = 2, l = 1.0, and N = 0.4 are analyzed in Figs. 12, 13, 14.

Fig. 12
figure 12

The effect of m on velocity component (u)

Full size image
Fig. 13
figure 13

The effect of m on microrotation component (v 1 )

Full size image
Fig. 14
figure 14

The effect of m on microrotation component (v 2 )

Full size image

It can be deduced from the Fig. 12 that the velocity decreases as the m value increases. Similarly, the microrotation component v 1 increases with increment of m. Furthermore, with increasing micropolar parameter (m) adjacent to one side of the channel the microrotation component v 2 increases while it symmetrically decreases near to the other side of the channel.

Figure 15 illustrates the effect of different N and Ha parameters on the non-dimensional flow rate of the micropump. As it can be seen from Fig. 15, the flow rate is lower for higher Hartmann numbers due to the rising resistive force against the fluid movement caused by the applied magnetic field. The increment of coupling number (N) which demonstrates the increment of micropolarity of the fluid results in lower flow rates which is due to diminished velocity.

Fig. 15
figure 15

Flow rate versus N for different Ha values

Full size image

4 Conclusion

In this paper, a MHD micropump with the continuous flow of the micropolar fluid through it is studied. The flow is pumped as a result of Lorentz force, which is induced as a result of interaction between an applied electric field and a perpendicular magnetic field for the application of microfluidic systems. A theoretically simplified MHD flow model includes the theory of fluid dynamics and electromagnetics, and it is based upon the steady state, incompressible and fully developed laminar fluid flow across the square microchannel. The continuum fluid theory is no longer applicable in this study since the micropump dimensions are comparable to dimensions of the fluid molecules. Therefore, micropolar fluid theory is considered and governing equations of the corresponding momentum and angular momentums are derived under MHD effect. Afterward, the non-dimensional forms of the governing equations and their associated boundary conditions are obtained. Utilizing finite difference technique the resulting partial differential equations are solved numerically. Validity of the results was investigated considering experimental works. The velocity and microrotation profiles were obtained, and the coupling number, micropolar parameters and Hartmann number effects on velocity and microrotation components and flow rate were investigated. It can be concluded from the results that the increment of coupling number and Hartmann number led to decreasing the velocity and microrotation component and the flow rate consequently. However, increment of micropolar parameter resulted in increased microrotation component.