Simulation of slug flow initiation with adaptive numerical diffusion based on wavelength effect

Abstract

This study presents a methodology using the correlation of numerical diffusion with the standard two-fluid model to simulate the separated two-phase flow (gas–liquid) in a pipe. Firstly, different numerical schemes are examined to investigate the flow characteristics through the water faucet problem. For this, the shock-capturing method is developed to an algorithm scripted in Fortran; and the Force (first-order centred) scheme is selected for the models used in this work, due to the higher accuracy and less computations. For validation of the simulations, the results of instability range are compared to the calculations using the classic Kelvin–Helmholtz instability equation; and then, the methodology is used to evaluate the slug flow initiation and growth in a horizontal pipe. The results showed that the instability range is affected by the wavelengths as a decrease in the wavelengths led to inconsistency of the range. It is found that the short-wavelength perturbations induce the unbounded growth rates, and this halts the convergence of results. To remedy this deficiency, the methodology introduced in this study showed an excellent ability to damp the unbounded growth of instabilities, where the standard model is not well-posed. Indeed, comparing the flow property diagrams for the two studied conditions showed that the wavelengths below the specified cut-off are stabilized, and the converged results are achieved for the flow properties. Finally, for the slug flow initiation, a very good agreement is achieved between the results from the introduced approach and the experimental results.

1 Introduction

Multiphase flow has become increasingly significant in a wide variety of engineering systems for their optimum design and safe operation. It can be observed in many engineering sectors, such as marine, aerospace, power stations, nuclear power plants, oil and gas; or in many biological sectors including cardiovascular and breathing systems; or in natural phenomena, such as ocean waves, river flood, and fermentation devices [1,2,3,4,5]. Accurate prediction of multiphase flow properties is an outstanding challenge for the industry. The two-phase flow of gas and liquid is a simultaneous transfer of gas and liquid [6, 7]. Extensive usages in various engineering systems and their complicated behavior indicate the necessity of studying the concept of two-phase flows. It is important to note that the mathematical model chosen for the simulation is one of the fundamental challenges in predicting the flow dynamics [8].

In general, there are two different types of formulations called mixed fluid model (MFD) and two-fluid model (TFM) [9]. In fact, these formulations represent fundamentally different viewpoints about such flows. The first consists of a dispersed phase and a continuous phase. It is convenient for the two-phase flows, where phases are coupled strongly [10, 11]. The second formulation is based on two types of conservation equations. Each phase has its own pressure, velocity, and temperature [10, 12, 13]. The TFM is convenient for the flows, where phases are coupled together weakly, and the wave propagates at different velocities in each phase [12, 14]. The TFM presents more accurate details of flow properties and therefore, is the most complete model. For the reasons stated, this study used and focused on TFM.

Due to the existence of the changeable interface and compressibility of the gas phase, separated two-phase flow modeling is complicated [15]. The interface between the gas and liquid can arrange itself into a large variety of forms, and this deformability causes the fluid properties to change in the interface discontinuously [16, 17]. Shock interaction as a discontinuity in fluid properties, and interface discontinuity cause complexity in simulating and instabilities capturing in the interface [18, 19]. Consequently, although solving two-phase flows using the classic Navier–Stokes equations is possible theoretically, it is too complicated and impossible practically [12, 18].

Various forms of TFM have been developed, according to the performance of phase pressures: Pressure-Free Model (PFM) that the pressure does not appear in the equations, Single-Pressure Model (SPM), which both of the phase pressures are equal, and Two-Pressure Model (TPM) that the pressures are different and interactions between the phases are calculated by structural relations that have significant effects on the solution field [20,21,22,23]. The governing equations, coupled with numerical methods, should prepare a tool for investigating and predicting the mean flow features, with an understanding of the uncertainties and limitations in their specifications [10, 24]. Thus, building an appropriate physical model is the most important part of a simulation process. A numerical model developed from an inappropriate physical model can have large uncertainties, and lead to results that are clearly different from physics. Based on Hadamard’s well-posed theory, mathematical analysis and the well-posedness of the model’s equations is another challenge of a simulation [25]. Previous studies show two-fluid models are sensitive to the roots of the characteristic equation [9, 26]. According to the results, TPM is always hyperbolic and PFM and SPM are hyperbolic within a specified range [12, 27, 28]. However, one of the features of the TPM and SPM is the non-conservative aspect of their governing equations [19, 29]. Thus, the efficient and developed numerical methods that are suited for single-phase flows, are not applicable to them. Therefore, an additional method must be introduced for calculations of the non-conservative term, and this increases the complexity of the simulation. On the other hand, PFM equations are in the conservative form, but to determine a well-posed range, a hyperbolic analysis is required [9, 27]. Hyperbolic analysis shows ill-posedness is related to the unbounded growth of short-wavelength perturbations [15, 27]. Surface tension, which appears as a source term in the governing equations introduces a cut-off wavelength [24, 28]. This is suitable for short-wavelengths and on the contrary with long-wavelength assumptions, because of the wavelengths above the cut-off experience non-physical high growth rates [30, 31]. The grid diffusivity was used to annihilate the growth of short-wavelengths, but the grid independence verification was not achieved for all the conditions [27]. According to the non-physical nature of these instabilities, it seems a mathematical approach can lead to a convergent solution.

In the computational fluid dynamics, the words "numerical dissipation\dispersion" and "numerical diffusion", are frequently used interchangeably, and generally connote the diffusive behavior (which is purely numerical in origin) of a numerical solution. Numerical dissipation is a direct result of the even-order derivatives, and numerical dispersion is a result of the odd-order derivatives of the governing equations [32, 33]. Although numerical diffusion decreases the accuracy of a solution, on the contrary, it increases the stability [34]. Indeed, for many flow problems with strong gradients, such as shock waves, where shocks are captured within the flow by using a shock-capturing method, the addition of numerical diffusion is an appropriate approach to achieve a stable and smooth solution, whereas, without it, no solution would be attainable [32, 35]. Numerical diffusion, which is the result of even-order derivative terms in the Taylor expansion reduces strong gradients in the solution field, and provides a convenient termination to the existing model in the short-wavelength limit. The present study aims to explore the effects and possibility of adding a second-order numerical diffusion term to the two-fluid model. The matrix $\varepsilon$ is added to the original equations as numerical diffusion, and its effects on stability will investigate. A comparison of the numerical results with analytical and experimental results is done on the benchmark problems and showing a good agreement.

This paper is organized as follows: Sect. 2 presents governing equations and mathematical models; Sect. 3 describes the numerical calculation methods, giving special care to the scheme developed. Section 4 shows the comparison of the numerical results with analytical and experimental results and discussion; finally, Sect. 5 reports some conclusions.

2 Governing equations and mathematical models

In this paper, the TPM, SPM, and PFM have been chosen as the physical models, governing on the solution field. One dimensional form of TFM was obtained from surface integration (area averaging) of the three-dimensional equations of fluid properties over cross section of the flow [27]. Momentum transmission between the fluids and the pipe, and also dynamic interactions of phases at the interface, is calculated as a source term obtained from empirical relations [15, 27].

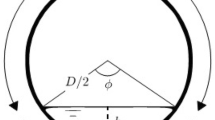
The present study is based on the transport equations for an isothermal flow, and therefore consists of conservation of mass and momentum for the gas and liquid. Figure 1 illustrates the schematic of the separated two-phase flow in a pipe.${u}_{k}$, ${s}_{i}$ and ${s}_{k}$ are velocities, wetted perimeters of interface and phases (k = l, g, and i are defined as the liquid, gas, and interface notations), respectively. ${\tau }_{i}$ and ${\tau }_{k}$ are the shear stresses of the interface and phase-wall, respectively.

Fig. 1

Schematic of the separated two-phase flow

2.1 TPM

The governing equations of TPM pioneered by Saurel and Abgrall include five equations and are expressed for a compressible two-phase model [23]:

Gas volume fraction evaluation equation:

$$ \partial _{t} \left( {\alpha _{g} } \right) + u_{i} \partial _{x} \left( {\alpha _{g} } \right) = r_{p} \left( {P_{g} - P_{l} } \right) $$

(1)

Mass conservation equations for gas and liquid phases:

$${\partial }_{t}\left({\rho }_{k}{\alpha }_{k}\right)+{\partial }_{x}\left({\rho }_{k}{\alpha }_{k}{u}_{k}\right)=0$$

(2)

Momentum conservation equations for gas and liquid phases:

$${\partial }_{t}\left({\rho }_{k}{\alpha }_{k}{u}_{k}\right)+{\partial }_{x}\left({\rho }_{k}{\alpha }_{k}{u}_{k}^{2} \right){={-\alpha }_{k}{\partial }_{x}\left({P}_{k}\right)-{\partial }_{x}\left(\left({P}_{k}-{P}_{ki}\right){\alpha }_{k}\right)-{\alpha }_{k}{\rho }_{k}G\mathit{sin}\theta }_{k}+{r}_{v}({u}_{g}-{u}_{l})-{\tau }_{k}{s}_{k}{A}^{-1}\mp {\tau }_{I}{s}_{I}{A}^{-1}$$

(3)

${\rho }_{k}$, ${a}_{k}$ and,$D$ are density, cross-section area, and pipe diameter. $G$ is the acceleration of gravity,${h}_{l}$ is liquid height and $\theta$ is pipe inclination (is required for inclined pipe).$A$ is the area of the whole cross-section of the pipe (gas and liquid). + and – of the ${\tau }_{I}{S}_{I}{A}^{-1}$ denote the flow direction as shown in Fig. 1. $P$ and ${P}_{i}$ are pressures of each phase and interface. ${u}_{i}$ is average interfacial velocity was suggested by Saurel and Abgrall [23]:

$${u}_{i}=\frac{{\sum }_{\forall k}{\alpha }_{k}{\rho }_{k}{u}_{k}}{{\sum }_{\forall k}{\alpha }_{k}{\rho }_{k}}$$

(4)

${r}_{p}$ and ${r}_{v}$ are the pressure and velocity relaxation terms, and are defined by equations recommended by Bestion [4], Munkejord [36, 37], and Ansari [16].

2.2 SPM

In the SPM, the pressure of both phases is equal, as well as the pressure of phases at the interface is the same. The governing equations are included two series of continuity and momentum equations are stated as follows:

Mass conservation equations for gas and liquid phases:

$${\partial }_{t}({\rho }_{k}{\alpha }_{k})+{\partial }_{x}({\rho }_{k}{\alpha }_{k}{u}_{k})=0$$

(5)

Momentum conservation equations for gas and liquid phases:

$${\partial }_{t}\left({\rho }_{k}{\alpha }_{k}{u}_{k}\right)+{\partial }_{x}\left({\rho }_{k}{\alpha }_{k}{u}_{k}^{2} {+ \alpha }_{k}P\right){={P}_{i}{\partial }_{x}({\alpha }_{k})-{\alpha }_{k}{\rho }_{k}Gs\mathit{in}\theta }_{k}-{\tau }_{k}{s}_{k}{A}^{-1}\mp {\tau }_{I}{s}_{I}{A}^{-1}$$

(6)

2.3 PFM

The PFM consists of two differential equations that include a hybrid mass and a hybrid momentum equation. Hybrid mass conservation equation is obtained by summing the gas and liquid mass equations of SPM with the incompressibility assumption of phases:

Hybrid continuity equation:

$${\partial }_{t}({\rho }_{l}{\alpha }_{l}+{\rho }_{g}{\alpha }_{g})+{\partial }_{x}({\rho }_{l}{\alpha }_{l}{u}_{l}+{\rho }_{g}{\alpha }_{g}{u}_{g})=0$$

(7)

Hybrid momentum conservation equation is obtained by combining (some mathematical operations) the gas and liquid momentum equations of the SPM:

$${\partial }_{t}\left({ \rho }_{l}{u}_{l}-{\rho }_{g}{u}_{g}\right)+{\partial }_{x}\left(0.5{ \rho }_{l}{u}_{l}^{2}-0.5{ \rho }_{g}{u}_{g}^{2}+\Delta \rho G\mathrm{cos}\theta {h}_{l}\right)=-\Delta \rho G\mathit{sin}\theta +\left({a}_{l}^{-1}+{a}_{g}^{-1}\right){\tau }_{i}{s}_{i}+{\tau }_{g}{s}_{g}{a}_{g}^{-1}-{\tau }_{l}{s}_{l}{a}_{l}^{-1}$$

(8)

In the PFM equations system ${\alpha }_{l}$ ،${\alpha }_{g}$ ،${u}_{g}$ and ${u}_{l}$ are unknowns. To find the primitive unknowns, Eqs. (7) and (8) must be supplemented by two more equations. The first is obtained by primary mass conservation equations. Since the fluids are assumed to be incompressible, algebraic constraint $C(t)$, which is a time-dependent function obtained by the relations suggested by Wallis [10, 27]:

$${\partial }_{x}\left({\alpha }_{l}{u}_{l}+{\alpha }_{g}{u}_{g}\right)=0 \to {\alpha }_{l}{u}_{l}+{\alpha }_{g}{u}_{g}=C\left(t\right)={({\alpha }_{l}{u}_{l}+{\alpha }_{g}{u}_{g})}_{inlet}$$

(9)

Another relation is obtained by the geometric constraint [10]:

$${a}_{l}+{a}_{g}=A \to {\alpha }_{g}={a}_{g}{A}^{-1}, {\alpha }_{l}={a}_{l}{A}^{-1}, {\alpha }_{g}+{\alpha }_{l}=1$$

(10)

2.4 Shear stress

The shear stresses are comprised of wall-phase shear stresses and shear stress at the interface of gas and liquid. Their distribution on the wall has a vital role in determining the turbulence structure inside the pipe as well as the flow resistance [38, 39]. Shear stresses are modeled, using single-phase friction equations, based on the Fanning friction factors and phase hydraulic diameter [30, 40]:

$$ \begin{gathered} \tau_{k} = 0.5 f_{k} \rho_{k} u_{k} \left| {u_{k} } \right| \hfill \\ \tau_{i} = 0.5 f_{i} \rho_{g} u_{g} \Delta u\left| {\Delta u} \right| \hfill \\ \end{gathered} $$

(11)

${f}_{k}$ and ${f}_{i}$ represent phases and interface friction factors, respectively:

$$ \begin{gathered} f_{k} = MAX\left( {16Re_{k}^{ - 1} ,0.046Re_{k}^{ - 0.2} } \right) \hfill \\ f_{i} = f_{g} \hfill \\ \end{gathered} $$

(12)

in which hydraulic diameter ${D}_{hk}$ is applied for calculation of Reynolds number ${Re}_{k}$ in each phase instead of inner diameter:

$${Re}_{k}={ \rho }_{k}{D}_{hk}\left|{u}_{k}\right|{\mu }_{l}^{-1}, {D}_{hl}={4a}_{l}{s}_{l}^{-1}, {D}_{hg}={4a}_{g}{({s}_{g}{+s}_{l})}^{-1}$$

(13)

${\mu }_{k}$ is dynamic viscosity. To calculate the wetted perimeter of each phase, geometric variables are used, which can be found in previous works [26, 41].

2.5 Hyperbolic analysis

The present study does not intend to scrutinize the methodologies of hyperbolic analysis and their validation. However, the result of the present approach will affect the analysis and improve its stability range.

Generally, there are two kinds of hyperbolic analysis methods, depending on the presence\absence of conservative terms in the governing equations [26]. To determine the stability range of interface waves, various relations are offered based on the classic Kelvin–Helmholtz relation [14, 28, 29]. SPM (as a non-conservative form) and PFM (as a conservative form) are sensitive whether their characteristic values are real or complex [26, 27]. If the values are characterized as complex, the model will be an ill-posed. Considerable basic work has been undertaken in the literature in measuring hyperbolicity shows that although approximate eigenvalues are always real, the true eigenvalues can be complex, and a numerical evaluation reveals that the condition of hyperbolicity or limit of validity of the SPM is similar to the PFM [9]. Previous studies are demonstrated that challenges are directly related to the velocity difference between the phases as follows:

$${u}_{g}-{u}_{l}\le K\sqrt{{(\alpha }_{g}{\rho }_{l}+{\alpha }_{l}{\rho }_{g})\frac{\Delta \rho }{{\rho }_{l}{\rho }_{g}}G\mathrm{cos}\theta \frac{a}{\frac{d{a}_{l}}{d{h}_{l}}}}$$

(14)

If Eq. (14) is not satisfied, the roots of the characteristic equation are imagined and the model is ill-posed, and the interface is physically unstable as well. It means that limit of physical instability at the interface is equal to the well-posing of the model. Ill-posing causes the results not to show realistic physics. In Eq. (14), for the inviscid assumption $K=1$ and for the viscous assumption $K$ is obtained by suggested equation [27, 34]:

$$K=\sqrt{1-\frac{{\left({C}_{V}-{C}_{IV}\right)}^{2}}{\frac{\Delta \rho }{\left({\rho }_{l}/{\alpha }_{l}\right)-\left({\rho }_{g}/{\alpha }_{g}\right)}G\mathrm{cos}\theta \frac{a}{\frac{d{a}_{l}}{d{h}_{l}}}}}$$

(15)

where ${C}_{IV}$ and ${C}_{V}$ are critical wave velocities from the inviscid and viscous stability analyses, respectively.

3 Numerical calculation methods

The transport equations were mentioned in the previous section can be rewritten in a compact generic form:

$${\partial }_{t}(\Phi )+{\partial }_{x}\left(\Psi \left(\Phi \right)\right)-\zeta {\partial }_{x}\left(\Phi \right)=\xi (\Phi )$$

(16)

The generic form helps to simplify and organize the logical algorithm in a computer code. $\Phi$, $\xi$ and $\Psi$ are, vector field of conservative variables, vector including all source terms, and conservative flux vector, respectively. On the other hand, $\zeta {\partial }_{x}\left(\Phi \right)$ contains all the non-conservative terms, which present in the selected model. If $\zeta$ is zero, the model is conservative and appropriate for PFM, and otherwise, is non-conservative and is appropriate for SPM and TPM.

3.1 Methods and discretization

By applying the shock capturing method algorithm to discretize the generic form, a forward approximation is used for time derivative, and central approximation is used for the spatial derivative [42]:

$${\Phi }_{j}^{n+1}={\Phi }_{j}^{n}+\Gamma \left({\Psi }_{j-1/2}^{n}-{\Psi }_{j+1/2}^{n}\right)+\Delta t\zeta {\partial }_{x}\left(\Phi \right)+\Delta t{ \xi }_{j},\Gamma =\frac{\Delta t}{\Delta x}$$

(17)

$n$, $n+1$, $\Delta t$, and $\Delta x$ are the old time and new time values, time step, and mesh size, respectively and j denotes cell position. ${\Psi }_{j+1/2}^{n}$ is a numerical flux that is an approximation of physical flux. Depending on the scheme that has been chosen for ${\Psi }_{j+1/2}^{n}$, various Riemann numerical solvers are achieved. In this study, various schemes, which are popular in multiphase simulations, are chosen and compared. Schemes are grouped into two categories, namely central schemes and characteristics-based schemes [32, 43]. Force and Richtmyer from the central schemes, and Rusanov and TVD Lax-Friedrichs from the characteristics-based schemes, are selected and implemented. They are selected, because they use a variety of approximations, and cover a wide range of resolutions.

3.1.1 Richtmyer method

Richtmyer method is a second-order explicit scheme in time and space, and calculated in two steps. In the first step, Lax-Friedrichs method is used and in the second step, Leap-Frog method is used [32, 44]. Flux expression can be calculated in the following form [42]:

$${\Phi }_{j+1/2}^{n}=0.5\left({\Phi }_{j}^{n}+{\Phi }_{j+1}^{n}\right)$$

(18)

$${\overline{\Phi } }_{j+1/2}={\Phi }_{j+1/2}^{n}-0.5\Gamma \left({\Psi }_{j+1}^{n}-{\Psi }_{j}^{n}\right)+0.5\Delta t\xi ({\Phi }_{j+1/2}^{n})$$

(19)

$${\Psi }_{j+1/2}^{RI}=\Psi ({\overline{\Phi } }_{j+1/2})$$

(20)

where ${\overline{\Phi } }_{j+1/2}$ and ${\Phi }_{j+1/2}^{n}$ are intermediate vector solution, and average vector, respectively.

3.1.2 Force method

Richtmyer method is dispersive and induces numerical spurious waves, and on the other hand Lax-Friedrichs method (where is a step of Richtmyer method) is diffusive and will damp most flow features [32]. Toro proposed a new first-order centered method to avoid the bad effects of Richtmyer and Lax-Friedrichs methods [35]. In Force method, the intercell flux is an arithmetic mean of the Richtmyer and Lax-Friedrichs fluxes, and calculated by [42, 45]:

$${\Psi }_{j+1/2}^{FORCE}= 0.5\left({\Psi }_{j+1/2}^{LF}+ {\Psi }_{j+1/2}^{RI}\right)$$

(21)

3.1.3 TVD Lax-Friedrichs method

In computational fluid dynamics, total variation diminishing schemes are used to capture sharper shock predictions without any spurious oscillations [32]. In order to improve Lax-Friedrichs method, which generates extreme diffusion in the solution field, a high-resolution TVD approach is used as follows [9, 32]:

$${\Psi }_{j+1/2}^{TVDLF}=0.5\left[\Psi \left({\Phi }_{j+1/2}^{Left}\right)+\Psi \left({\Phi }_{j+1/2}^{Right}\right)\right]-0.5{\Gamma }^{-1}{\Omega }_{j+1/2}^{LR}$$

(22)

$${\Phi }_{j+1/2}^{Left}={\Phi }_{j}^{n+1/2}+0.5\delta {\overline{\Phi } }_{j}^{n}, {\Phi }_{j+1/2}^{Right}={\Phi }_{j+1}^{n+1/2}-0.5\delta {\overline{\Phi } }_{j+1}^{n}$$

(23)

TVD Lax-Friedrichs method is a characteristic based flux method, where ${\Phi }^{Left}$, ${\Phi }^{Right}$, ${\Phi }^{n+1/2}$,${\Omega }_{j+1/2}^{LR}$, and ${\overline{\Phi } }^{n}$ are the left and right state vectors, predictor step value, dissipative limiter, and the limited differences, respectively. The predictor step value is given by:

$${\Phi }_{j}^{n+1/2}={\Phi }_{j}^{n}-0.5\Gamma \left[\Psi \left({\Phi }_{j}^{n}+0.5\delta {\overline{\Phi } }_{j}^{n}\right)-\Psi \left({\Phi }_{j}^{n}-0.5\delta {\overline{\Phi } }_{j}^{n}\right)\right]+0.5\Delta t\xi \left({\Phi }_{j}^{n}\right)$$

(24)

Dissipative limiter is obtained by using the maximum eigenvalue or characteristic of the model:

$${\Omega }_{j+1/2}^{LR}={\Gamma }^{-1}{\lambda }_{j+1/2}^{max}\left({\Phi }^{Right}-{\Phi }^{Left}\right)$$

(25)

where:

$${\lambda }_{j+1/2}^{max}=max\left|{0.5\lambda }_{k}\left({\Phi }^{Right}+{\Phi }^{Left}\right)\right|, k=1,Neq$$

(26)

In the present work one of the acceptable methods are used to calculate the flux limiter [9]:

$$\delta {\overline{\Phi } }_{j}^{n}=Min mod\left({\Phi }_{j}^{n}{-\Phi }_{j-1}^{n},{\Phi }_{j+1}^{n}-{\Phi }_{j}^{n}\right)$$

(27)

3.1.4 Rusanov method

Rusanov method is a characteristic-based flux scheme that is appropriate for one-dimensional non-linear systems. This explicit first-order scheme uses the maximum value of the characteristic model to produce the flux as follows [9]:

$${\Psi }_{j+1/2}^{RUS}=0.5\left[\Psi \left({\Phi }_{j}^{n}\right)+\Psi \left({\Phi }_{j+1}^{n}\right)-{\lambda }_{j+1/2}\left({\Phi }_{j+1}^{n}-{\Phi }_{j}^{n}\right)\right]$$

(28)

$${\lambda }_{j+1/2}=max\left(max\left|{\lambda }_{j}^{k}\right|,max\left|{\lambda }_{j+1}^{k}\right|\right) , k=1,Neq$$

(29)

$Neq$ and ${\lambda }_{j+1}^{k}$ are number of equations in the model, and average wave velocity, suggested by Hornung and Trangenstein [46].

3.1.5 Non-Conservative Terms

The numerical schemes described above are implemented for conservative models. In order to discretize the non-conservative term in Eq. (16) (for SPM and TPM), a second-order upwind discretization is used [9]:

$$\zeta {\partial }_{x}\left(\Phi \right)=\frac{{\zeta }_{j}^{n}}{\Delta x}Min mod\left[2\left({\Phi }_{j+1}^{n}-{\Phi }_{j}^{n}\right),0.5\left({\Phi }_{j+1}^{n}-{\Phi }_{j-1}^{n}\right),2\left({\Phi }_{j}^{n}-{\Phi }_{j-1}^{n}\right)\right]$$

(30)

The Min-mod in above equation is defined as following:

$$Min mod\left(x,y,z\right)=\left\{\begin{array}{c}S.min\left(\left|x\right|,\left|y\right|,\left|z\right|\right) if sign\left(\mathrm{x}\right)=sign\left(\mathrm{y}\right)=sign\left(\mathrm{z}\right)\\ 0 othewise\end{array}\right.$$

(31)

3.1.6 Numerical diffusion

As discussed in the previous section, the present study focuses on the implementation of numerical diffusion to regulate instabilities. Simulation results in Sect. 4 demonstrate that PFM is more convenient to use than the two others, in terms of process time and implementation of numerical methods in the benchmark problems. But this model still has spurious oscillations on the points with severe gradients on the solution field. To solve the deviance, matrix $\varepsilon$ is coupled with the original transport equation as a coefficient for second order derivative, as following:

$${\partial }_{t}\left(\Phi \right)+{\partial }_{x}\left(\Psi \left(\Phi \right)\right)-{\varepsilon \partial }_{\upsilon }\left(\Phi \right){\partial }_{xx}\left(\upsilon \right)=\xi (\Phi )$$

(32)

In fact, Eq. (32) is a rewritten form of Eq. (16) with a second-order tensor. Therefore, by reusing equations, the conservative part of the equation can be discretized. But for the newly added part of the equation, a new method must be used. Non-conservative second order tensor of ${\varepsilon \partial }_{\upsilon }\left(\Phi \right){\partial }_{xx}\left(\upsilon \right)$ complicates the solution, which cannot be solved by the methods mentioned above. In the present study, equations are solved using an alternating two-step mathematical technique, which consists of an implicit method and a finite volume method that are coupled together strongly [47]:

Step one: solving diffusion part of Eq. (32) by an implicit method:

$${\partial }_{t}\left(\upsilon \right)=\varepsilon {\partial }_{xx}\left(\upsilon \right)$$

(33)

It can be solved by using an implicit method like Crank–Nicholson in step one, such as following [43]:

$$\frac{{\upsilon }_{j}^{n+1}-{\upsilon }_{j}^{n}}{\Delta t}=0.5\frac{\varepsilon }{{\left(\Delta x\right)}^{2}}\left[\left({\upsilon }_{j+1}^{n+1}-2{\upsilon }_{j}^{n+1}{+\upsilon }_{j-1}^{n+1}\right)+\left({\upsilon }_{j+1}^{n}{-2\upsilon }_{j}^{n}+{\upsilon }_{j-1}^{n}\right)\right]$$

(34)

Variables are calculated by integration on the first half-time at time step $n$. The output data is used as the input data for step two.

Step two: solving advection–source term part of Eq. (32) by an explicit method in step two:

$${\partial }_{t}\left(\Phi \right)+{\partial }_{x}\left(\Psi \left(\Phi \right)\right)=\xi (\Phi )$$

(35)

where is the optimum method that has been chosen based on the results of simulation in Sect. 4. Updated variables are calculated by integration on the full-time step, and output data of this step is used as the input data of step one, but on the last half-time step at time step $n$. This alternating technique is a semi-implicit method, and the time step must be controlled to achieve convergence results.

3.2 Calculation Time Step

In the mentioned alternating technique, the first step is an implicit method, then is always stable. But the second step is explicit, and the size of the time step needs to be controlled and can be estimated from the following equation [48]:

$${\left(\Delta t\right)}^{n}=CFL\frac{\Delta x}{{\lambda }_{c,max}^{n}}$$

(36)

In order to calculate time step, value of the Courante-Friedrichs-Levy number is assumed 0.5 and ${\lambda }_{c,max}^{n}$ is the maximum eigenvalue of the Jacobian of the Eq. (36) which is equal to:

$${\lambda }_{c,max}^{n}={max}_{j}\left\{{max}_{j}\left|{\lambda }_{j}^{k}\right|\right\} \mathrm{for} j=\mathrm{1,2},\dots ,M k=1,Neq$$

(37)

where ${\lambda }_{j}^{k}$ is wave velocity in each computational cell [26].

3.3 Boundary conditions

The schematic of the computing domain of an internal flow can be illustrated by Fig. 2. Domain is discretized into M cells, and special conditions are at the boundary positions $x=0$ and $x=L$, where provide numerical fluxes ${\Psi }_{1/2}$ and $\Psi _{{m + 1/2}}$ to advance the extreme cells 1 and M to the next time level in Eq. (16). For this purpose, an artificial grid will be considered at the input and output, and zeroth-order extrapolation for the virtual points will be used for the flux in entry and outlet, which is denoted 0 and M + 1.

Fig. 2

Schematic of the computational domain of an internal flow

4 Results and discussion

In this section, the results of the simulation are presented, in order to demonstrate whether the addition of numerical diffusion renders it possible to have converging numerical solutions. Obviously, they are consistent with the long-wavelength assumption also for flow properties outside the classic Kelvin–Helmholtz range. Inviscid Burgers' equation and water faucet problem are used as benchmark cases to evaluate the accuracy and robustness of the numerical schemes, with the known analytical solutions. Then, the water faucet problem is used to test the role of numerical diffusion in the well-posedness of two-fluid models and stability analysis. Finally, the enhanced model is used to model the slug flow.

4.1 Problem geometry and validation of methods

4.1.1 Inviscid Burgers' equation

The classical Burgers equation is a non-linear partial differential equation [49]. This equation is one of the most helpful equations to investigate the behavior of the shock waves, fluid dynamics, turbulent flows, and gas dynamics, in which non-linear advection and diffusion can be observed [50]. On the other hand, it allows researchers to compare the quality of the numerical scheme applied to a non-linear equation [9]. For a fluid velocity field $u(x,t)$ and diffusion coefficient $\in$, the general form of Burgers' equation in one space dimension is the dissipative system [35, 51]:

$$\frac{\partial u}{\partial t}+ u\frac{\partial u}{\partial x}= \in \frac{{\partial }^{2}u}{\partial {x}^{2}}$$

(38)

If the diffusion term is absent, Burgers' equation becomes the inviscid Burgers' equation, which is given in the conservative form, and is a very useful model for flows, where severe gradients are anticipated [9]:

$$\frac{\partial u}{\partial t}+ \frac{\partial (\frac{{u}^{2}}{2})}{\partial x}=0$$

(39)

In the present work the pipe length is $2 m$ and the number of cells is set to 100.

4.1.2 Water faucet problem

This benchmark problem was stated by Ransom [52].The schematic of the water faucet problem is illustrated in Fig. 3 which is comprised of a free fall of a column of water in a pipe, where has a height of 12 m and a diameter of 1 m. At time $t=0$, the velocity of water is$10m/s$, the velocity of air is$0m/s$, and the volume fraction of water is assumed 0.8. The pressure in the pipe is equal to ${10}^{5}$ Pascal. Inlet conditions are equal to the initial values and for the outlet of the pipe, a fully developed condition is assumed. The density of air is $1.16Kg/{m}^{3}$ and density of water is considered$1000Kg/{m}^{3}$. In order to validate modeling accuracy, different types of numerical methods mentioned in the previous section are used, and the results are compared with the analytical solution.

Fig. 3

Schematic of the water faucet problem

4.2 Analytical solution

4.2.1 Inviscid Burgers' equation

An exact analytical solution for the inviscid Burgers' equation can be found in numerical books [35, 53]. The initial data for the inviscid Burgers' equation are given by [35]:

$$u\left(x,0\right)=\left\{\begin{array}{c}{u}_{L} x<{x}_{d}\\ {u}_{R} x>{x}_{d}\end{array}\right.$$

(40)

where ${x}_{d}$, ${u}_{R}$, and ${u}_{L}$ are the location of the discontinuity, constant right and left velocities. If the left velocity is greater than the right velocity, the Riemann problem is called shock wave, and for ${x}_{d}=0$ in Eq. (40), Toro has suggested an exact analytical solution as described in his book [35]:

$$\left.\begin{array}{c}\left.\begin{array}{c}u(x,t)=\left\{\begin{array}{c}{u}_{L} if x<Wt\\ {u}_{R }if x>Wt\end{array}\right\}\\ W=\frac{1}{2}\left({u}_{L}+{u}_{R}\right)\end{array}\right\} if {u}_{L}>{u}_{R}\\ u(x,t)=\left\{\begin{array}{c}{u}_{L} if \frac{x}{t}\le {u}_{L}\\ \frac{x}{t} if{ u}_{L}<\frac{x}{t}<{u}_{R}\\ {u}_{R }if \frac{x}{t}\ge {u}_{L}\end{array}\right\} if {u}_{L}\le {u}_{R}\end{array}\right\}$$

(41)

where, $W$ is the shock wave velocity. ${u}_{L}=1 m/s$ and ${u}_{R}=0.5 m/s$ are considered at $1.5 sec$ for this problem.

4.2.2 Water faucet problem

Evje and Flatten proposed an analytical solution using the assumption that the gas phase pressure changes are insignificant [54]:

$$ \begin{gathered} \alpha_{l} \left( {x,t} \right) = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\frac{{\alpha_{l}^{inlet} u_{l}^{inlet} }}{{\sqrt {\left( {u_{l}^{inlet} } \right)^{2} + 2Gx} }}} & { x \le u_{l}^{inlet} t + 0.5Gt^{2} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\alpha_{l}^{inlet} } & {{ }x > u_{l}^{inlet} t + 0.5Gt^{2} } \\ \end{array} } \\ \end{array} } \right. \hfill \\ \alpha_{g} \left( {x,t} \right) = 1 - \alpha_{l} \left( {x,t} \right) \hfill \\ \end{gathered} $$

(42)

$${u}_{l}\left(x,t\right)=\left\{\begin{array}{c}\begin{array}{cc}\sqrt{{\left({u}_{l}^{inlet}\right)}^{2}+2Gx}& x\le {u}_{l}^{inlet}t+0.5G{t}^{2}\end{array}\\ \begin{array}{cc}{u}_{l}^{inlet}+Gt& x>{u}_{l}^{inlet}t+0.5G{t}^{2}\end{array}\end{array}\right.$$

(43)

where $G$ is the acceleration of gravity. ${\alpha }_{l}^{inlet}$ is the liquid fraction at the pipe inlet and is equal to $0.8$. ${u}_{l}^{inlet}$ is the liquid phase velocity at the pipe inlet and is equal to $10 m/s$.

4.3 Simulation results

In order to observe the effects of schemes, the results of two simulation problems are presented, then the optimized model is used to simulate slug flow. The aim is to substantiate that the inclusions of numerical diffusion to the selected model can improve numerical solutions consistent with the long-wavelength assumption. All the simulations and algorithms are implemented in Fortran language, and results are compared with the analytical solution. In order to evaluate the performance of numerical schemes, the Burgers' equation problem is first investigated as a single-phase flow. Figure 4 shows the comparative results for the two central and two characteristic-based schemes with the exact solution. The Richtmyer results appear dispersive behavior and spurious oscillations near the discontinuity. It does not seem to be a suitable method for longer or more complex simulation cases. The TVD Lax-Friedrichs scheme, then the Rusanov and Force schemes are more accurate than the Richtmyer. The results show that the TVD Lax-Friedrichs and the Rusanov are less diffusive, and more accurate than the Force; however, they take a lot longer in the same meshes for simulation and are more complicated. Figure 5 shows the mesh refinement for the Force scheme.

Fig. 4

Inviscid Burgers' equation: comparison of numerical schemes with exact solution for velocity profile, cells 100

Fig. 5

Inviscid Burgers' equation: mesh refinement for Force scheme

Figures 6, 7, 8, and 9 show the liquid volume fraction profiles obtained from the water faucet problem by using the schemes, previously described. In order to evaluate various numerical effects on each model, the numerical schemes have been applied to TPM, SPM, and PFM, and compare with the analytical solution. All the results reported are obtained with a CFL value of 0.5 and using 100 cells. The results of Richtmyer scheme presented in Fig. 6 have dispersive behavior and oscillatory nature near the discontinuity. This is a second-order scheme and has a third-order error, where leads to numerical dispersion near the discontinuity in the solution field. Figures 7, 8, and 9 show the results of the Force, TVD Lax-Friedrichs, and Rusanov schemes, respectively. They are in accordance with our anticipation extracted from the inviscid Burgers' equation. Simulations indicated TVD Lax-Friedrichs is the most consistent with the exact solution. The results of Rusanov and Force are almost the same, and they are in the next position of accuracy in the simulation. A comparison between the performance of the TPM, SPM and PFM indicates that SPM and PFM models have higher accuracy than the TPM, and they are almost consistent in a same mesh. As already mentioned, the present study attempts to refine the simulation by adding the numerical diffusion to the original equation. TVD Lax-Friedrichs and Rusanov are characteristic-based schemes and require algebraic manipulation of the Jacobian of the flux vector, and information of the characteristics of the model. The processing time is another important criterion in any simulation, and it is obvious that a conservative form of a model takes less time than a non-conservative [32, 35]. With an overview on models that have been implemented in the present study, Force-PFM scheme is chosen as the most appropriate model for this case study, and adding diffusion term to the equation. Figure 10 shows the flowchart of the algorithm for developed numerical simulation.

Fig. 6

Water faucet problem: comparison of liquid volume fraction of TPM, SPM and PFM models of Richtmyer scheme with analytical solution for computational cells = 100 and CFL = 0.5

Fig. 7

Water faucet problem: comparison of liquid volume fraction of TPM, SPM and PFM models of Force scheme with analytical solution for computational cells = 100 and CFL = 0.5

Fig. 8

Water faucet problem: comparison of liquid volume fraction of TPM, SPM and PFM models of TVD Lax-Friedrichs scheme with analytical solution for computational cells = 100 and CFL = 0.5

Fig. 9

Water faucet problem: comparison of liquid volume fraction of TPM, SPM and PFM models of Rusanov scheme with analytical solution for computational cells = 100 and CFL = 0.5

Fig. 10

Flowchart that describes the numerical algorithm

Figure 11 shows the mesh refinement for the liquid volume fraction at time = 0.5 s, using the Force-PFM scheme. Mesh refinement indicates a very small and almost invisible overshoot appears for finer meshes (i.e., 250 cells). The results obtained by finer mesh produce clearly visible overshoots before and after the front of the discontinuity, resulting in a code crash for fine mesh simulations. These oscillatory spikes are related to the ill-posedness and the non-hyperbolicity of the model. In other words, the defect has a numerical nature, and is due to the limitations of the model used for this case. To improve and eliminate the defection, a new regulation must be used to the model.

Fig. 11

Water faucet problem: Mesh Refinement for the liquid volume fraction at time = 0.5 sec, using the Force-PFM scheme.

Figure 12 and 13 indicate the effects of adding numerical diffusion to the original equations for the water faucet problem. Comparative diagrams of liquid volume fraction and liquid velocity, are clearly indicating the effect of presence and absence of numerical diffusion in the conservation equations. It is evident that the simulations with numerical diffusion provide converging solutions as the grid is refined. According to this effectiveness, the optimized model has been used in the simulation of slug flow.

Fig. 12

Water faucet problem: Comparison of presence and absence of numerical diffusion for liquid volume fraction for computational cells = 850, CFL = 0.5, time = 0.5 s

Fig. 13

Water faucet problem: Comparison of presence and absence of numerical diffusion for liquid velocity for computational cells = 850, CFL = 0.5, time = 0.5 s

Figure 14 shows the initiation points of the slug flow map for different meshes using PFM-Force scheme. Despite the mesh independence in 6400 cells, for finer meshes, non-physical instabilities are appeared. Figure 15 shows the liquid volume fraction in both the presence and absence of the numerical diffusion in the mathematical model for computational cells 12,800. It clearly shows the effectiveness of adding numerical diffusion in slug flow simulation.

Fig. 14

Slug flow simulation: The initiation points of the slug flow for different computational cells using PFM-Force, CFL = 0.2

Fig. 15

Slug flow simulation: Comparison of presence and absence of numerical diffusion using PFM-Force scheme for computational cells = 12,800, CFL = 0.2

Figure 16 indicates the comparison of the initiation point of slug flow simulation with experimental results obtained by Ansari and Nariai [55]. They carried out a detailed investigation of the wave growth, and slug formation were analyzed by using a video camera. The experimental procedure was performed on a pipe with the length of 5 $m$, and the diameter of 0.078 $m$. The inlet superficial air velocity is 6.532 $m/s$, inlet superficial water velocity is 0.532 $m/s$, and the liquid volume fraction at the initial condition is 0.526. The densities of air and water are $1.14Kg/{m}^{3}$ and 1000 $Kg/{m}^{3}$, respectively. Because of the vast variety of different factors in empirical data, initiation point of slugging have occurred between 1.75 and 2.00 $m$, were called lower and upper limits. The results have demonstrated that achieving the grid-independent occurs at 1000 mesh number, the model is well-posed, and there are no unphysical instabilities that form, as the mesh number is increased. Furthermore, the slug initiation position was verified by comparing it with upper and lower experimental limits plotted.

Fig. 16

Slug flow simulation: Comparison experimental data with numerical solution using PFM-Force scheme with adding numerical diffusion for computational cells = 12,800, CFL = 0.2

5 Conclusions

It has been demonstrated that achieving grid-independent solutions is very important in any numerical simulation. In this work, an algorithm for two benchmark problems was developed and implemented in Fortran code. The developed model is used to simulate the slug flow. Results indicate the Force-PFM scheme is the most appropriate method for simulating the cases, but the use of fine meshes would lead to the growth of non-physical instabilities in the discontinuities. The ill-posedness of the original model emanates from the extrapolation of the long-wavelength assumption into the short-wavelength domain. Short-wavelength perturbations induce unbounded growth rates, and make it impossible to achieve converging numerical solutions. The approach taken in this article has been to adding numerical diffusion as a CFD technique that is used to remedy this deficiency. For the simulation containing a new approach, the short-wavelength perturbations have damped, while the larger wave grows softly and goes downstream. On the other hand, for the simulation without numerical diffusion, the short-wavelength disturbances have grown severely and created high-frequency and high-amplitude oscillations, and therefore make it an ill-posed problem. Diagrams of the flow parameters are compared for two conditions: with and without numerical diffusion, and results show that wavelengths below the specified cut-off are stabilized, and converging solutions are achieved for flow conditions that were ill-posed without adding the numerical diffusion.