Introduction

The phenomenon of fluid flow plays a vital role in various industrial and engineering applications [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]. A wide range of applications of heat and the mass transfer analysis due to flow of non-Newtonian fluids can be observed, such as petroleum reservoirs, heat exchangers, material process system. The non-Newtonian fluids are abundant in various involved industrial applications and heat transfer processes as compared to Newtonian fluids. The equation for the non-Newtonian fluids does not execute the linear connection across the shear stress and strain rate. The flow and heat transfer analysis of these fluids has been explained by various researchers with different physical situations.

In perspective on numerous such applications, Sheikholeslami et al. [18] commence the analytical study on MHD free convection of nanofluid considering the impacts of thermal radiation with a stretching sheet. Prasannakumara et al. [19] studied that in the case of nonlinear stretching sheet the Nusselt number and Sherwood number are higher with the effect of magnetic field on nanofluid radiative heat transfer. Sheikholeslami and Ellahi [20] investigated that the rise of Lorentz forces detracts the convection in a cubic cavity. MHD viscous flow due to a shrinking sheet has been done by Sajid and Hayat [21]. Hsiao [22] investigated the effects of stagnation-point flow on MHD nanofluid mixed convection with the existence of boundary slip on stretching sheet. Cortell [23] indicates that the magnetohydrodynamic flow and a nonlinear radiative heat transfer of a viscoelastic fluid over a stretching sheet with the generation/absorption of heat at energy aspect. The articles discussed by Sheikholeslami [15, 24,25,26,27,28,29] revealed the significant importance of magnetic field. Subsequently, many researchers extended this kind of work to Newtonian/non-Newtonian boundary layers flow with assorted velocity and the thermal boundary condition. In view of such extensive materials, many authors have made efforts to illustrate the analysis of flow and heat with non-Newtonian fluids along with a Sisko fluid model [30,31,32,33].

The above referred works concern the consistent physical properties of a cooling fluid, but in practical situations the physical properties are needed with variable characteristics. That is why the one such property is a thermal conductivity, which is considered to vary linearly with a temperature. The heat transfer analysis in a viscous fluids flow over a permeable surface along with temperature field is presented by Mahmood et al. [34]. Salahuddin et al. [35], using the Keller box method, discussed the combined impacts of variable thermal conductivity and the MHD flow on pseudoplastic fluid. Abel et al. [36] deliberated the effects of variable thermal conductivity in a power-law fluid past a stretching surface in the existence of non-uniform heat source. Recently, Malik et al. [37, 38] have initiated the flow of non-Newtonian fluids over a stretching cylinder and heat transfer with viscous dissipation and variable thermal conductivity. In one of these investigations, the physical properties of the fluids were thought to be consistent. Although it is notable that such properties increase or decrease with the temperature. Consequently, the related articles [39,40,41,42,43,44] demonstrate that this sort of flow has not been explored for power-law fluids within the sight of stretching sheet. Zhang et al. [45] presented another model on the temperature field by considering the impacts of power law, they expected that the temperature field is same as velocity field, while the thermal diffusivity shifts as a component of temperature slope. Yu and Choi [46] altered the Maxwell’s equation and the Hamilton’s Crosser relation for the effective thermal conductivity to incorporate the impact of requested nano-layers surrounding the particles. Jang and Choi [47] proposed a powerful thermal conductivity model by considering the impacts of Brownian motion particles. They concentrated on the heat transfer among particles and the carrier fluid, ignoring the blending because of irregular molecule movement.

Furthermore, some researchers focus on the combining investigation of non-Newtonian fluids with the convection process. A numerical studied on such types of heat transfer execution of nanofluids over a porous stretching sheet is exhibited by Das [48]. Huang et al. [49] also discussed the unsteady flow with a heat transfer enclosure held on a circular cylinder. Convection flow based on boundary layer from a circular cylinder with uniform surface heat flux transfer is explored by Bhowmick et al. [50].

All the overhead examinations were carried out for fluids having magnetic field, variable thermal conductivity and the mass diffusivity, right through the flow regime. Although it is realized that the physical properties change with the temperature, the effects of these quantities on the heat transfer have become more useful in engineering and applications process such as crude oil extraction, geothermal systems and ground water pollution. The main purpose of the current work is to study the dual nature of magnetohydrodynamics flow with the heat and mass transfer analysis embedded in permeable media under the impacts of thermal conductivity and the mass diffusivity. The governing PDEs have been solved by using bvp4c techniques in Matlab.

Mathematical formulation

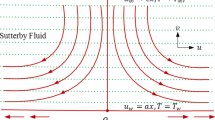
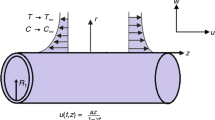
Here, we consider the steady, laminar and incompressible two-dimensional flow of a Sisko fluid originate by semi-infinite shrinking surface with the velocity \(u_{\text{w}}=cx^{\text{s}},\) in the region upper half plane. The velocity \(v_{{\rm w}}\) on the wall is perpendicular to the sheet. Further, it is assumed that the velocity \(v=v_{0}\) is the constant mass flux velocity which is taken to be positive in the case of suction while taking negative in the case of blowing on the sheet along the axial direction. In the positive y-direction, a uniform transverse magnetic field \(\left( B_{0}x^{(s-1)/2}\right)\) is applied normal to the stretching surface. And the effects of thermal conductivity and mass diffusivity are also considered. Moreover, \(T_{\text{w}}\) and \(C_{\text{w}}\) represent the temperature and the concentration at the wall surface of shrinking sheet, while \(T_{\infty }\) the temperature and \(C_{\infty }\) the concentration at the ambient surface such that (\(T_{\infty }<\) \(T_{\text{w}}\)) and (\(C_{\infty} < \) \(C_{\text{w}}\)). In this analysis, we considered the positive velocity gradient due to the boundary layer approximation the flow is over the shrinking surface (Fig. 1).

Fig. 1
figure 1

Physical geometry and coordinates system

Full size image

For the Sisko fluid model, the extra stress tensor is [51]:

$$\begin{aligned} \mathbf {S=}\left\{ a+b\left| \sqrt{\frac{1}{2}tr\left( \mathbf {A} _{1}\right) ^{2}}\right| ^{{\text{n}}-1}\right\} \mathbf {A}_{1}, \end{aligned}$$
(1)

with

$$\begin{aligned} \mathbf {A}_{1}=\nabla \mathbf {V+}\left( \nabla \mathbf {V}\right)^{\text{T}}. \end{aligned}$$
(2)

By using the above suppositions, the model equations are governed into the following form:

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0, \end{aligned}$$
(3)
$$\begin{aligned}& u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\frac{a}{\rho _{\text{f}}}\left( \frac{\partial ^{2}u}{\partial y^{2}}\right) +\frac{b}{\rho _{\text{f}}} \frac{\partial }{\partial y}\left( \frac{\partial u}{\partial y}\right) ^{\text{n}}- \frac{\sigma B_0^{2}}{\rho _{\text{f}}}u, \end{aligned}$$
(4)
$$\begin{aligned}&u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}+\delta _{\text{E}} \left[ \begin{array}{c} u^{2}\frac{\partial ^{2}T}{\partial x^{2}}+2uv\frac{\partial ^{2}T}{\partial x\partial y}+v^{2}\frac{\partial ^{2}T}{\partial y^{2}} \\ +\left( u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right) \frac{\partial T}{\partial x} \\ +\left( u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}\right) \frac{\partial T}{\partial y} \end{array} \right] \nonumber \\&\quad =\frac{1}{\rho c_{\text{f}}}\frac{\partial }{\partial y}\left( k(T)\frac{ \partial T}{\partial y}\right) , \end{aligned}$$
(5)
$$\begin{aligned}&u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}+\delta _{C} \left[ \begin{array}{c} u^{2}\frac{\partial ^{2}C}{\partial x^{2}}+2uv\frac{\partial ^{2}C}{\partial x\partial y}+v^{2}\frac{\partial ^{2}C}{\partial y^{2}} \\ +\left( u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right) \frac{\partial C}{\partial x} \\ +\left( u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}\right) \frac{\partial C}{\partial y} \end{array} \right] \nonumber \\&\quad =\frac{\partial }{\partial y}\left( D(C)\frac{\partial C}{\partial y} \right) , \end{aligned}$$
(6)

the BC’s are

$$\begin{aligned} u= & {} \chi u_{\text{w}}(x),v=v_{\text{w}}(x),T=T_{\text{w}},C=C_{\text{w}}\text { at}\ \ y=0, \nonumber \\ u= & {} 0,\upsilon =0,T=T_{\infty },C=C_{\infty }\text { as }y\rightarrow \infty , \end{aligned}$$
(7)

where u and v denote the velocity components in x- and y-directions, respectively, \(\sigma\) is the electrical conductivity, p is a fluid pressure, T denotes the fluid temperature and C the fluid concentration, respectively, \(\rho _{\text{f}}\) a fluid density and \(c_{\text{f}}\) the specific heat,  and \(\chi\) is shrinking \(\left( \chi <0\right)\) / stretching \(\left( \chi >0\right)\) parameter. Introducing a stream function \(\psi (x,y)\)

$$\begin{aligned} u=\frac{\partial \psi }{\partial y}\mathbf {\ }\text {and}\mathbf {\ }v=-\frac{ \partial \psi }{\partial x}, \end{aligned}$$

where \(\psi (x,y)=u_{\text{w}}x\mathrm{Re}_{\text{b}}^{-\frac{1}{{\text{n}}+1}}f(\eta ),\) with \(\mathbf {\ }f(\eta )\) is a dimensionless stream function where \(\eta =\frac{y}{x}\mathrm{Re}_{\text{b}}^{\frac{1}{{\text{n}}+1}}.\) Thus,

$$\begin{aligned}u&=u_{\text{w}}f^{\prime }(\eta ),v=-u_{\text{w}}\mathrm{Re}_{\text{b}}^{-\frac{1}{{\text{n}}+1}}\left[ \left\{ \frac{s\left( 2-n\right) -1}{1+n}\right\} \eta f^{\prime }(\eta )\right. \nonumber \\&\quad \left. +\left\{ \frac{s\left( 2n-1\right) +1}{1+n}\right\} f(\eta )\right] , \end{aligned}$$
(8)
$$\begin{aligned}&\theta (\eta )=\frac{T-T_{\infty }}{T_{\text{w}}-T_{\infty }},\mathbf {\ }\phi (\eta )=\frac{C-C_{\infty }}{C_{\text{w}}-C_{\infty }}, \end{aligned}$$
(9)

where \(\theta \left( \eta \right)\) and \(\phi \left( \eta \right)\) are the dimensionless temperature and concentration for the fluid. By using Eqs. (8) and (9) , Eqs. (3) to (6) transform into the following set of nonlinear ODEs as:

$$\begin{aligned}&\left( A+n(f^{\prime \prime })^{{\text{n}}-1}\right) f^{\prime \prime \prime }-sf^{\prime 2}+\left\{ \frac{s\left( 2n-1\right) +1}{1+n}\right\} ff^{\prime \prime }-Mf^{\prime }=0, \end{aligned}$$
(10)
$$\begin{aligned}&(1+\varepsilon _{1}\theta )\theta ^{\prime \prime }+\varepsilon _{1}\theta ^{\prime 2}+\Pr \left\{ \frac{s\left( 2n-1\right) +1}{1+n}\right\} f\theta ^{\prime }\nonumber \\&\quad -\Pr \lambda _{E}\left\{ \frac{s\left( 2n-1\right) +1}{1+n} \right\} \nonumber \\&\quad\times\left[ \{2+n+(n-2)s\}ff^{\prime }\theta ^{\prime }+\{s\left( 2n-1\right) +1\}f^{2}\theta ^{\prime \prime }\right] =0, \end{aligned}$$
(11)
$$\begin{aligned}&(1+\varepsilon _{2}\phi )\phi ^{\prime \prime }+\varepsilon _{2}\phi ^{\prime 2}+{{\rm Sc}}\left\{ \frac{s\left( 2n-1\right) +1}{1+n}\right\} f\phi ^{\prime }\nonumber \\&\quad -{{\rm Sc}}\lambda _{C}\left\{ \frac{s\left( 2n-1\right) +1}{1+n}\right\} \nonumber \\&\quad \times\left[ \{2+n+(n-2)s\}ff^{\prime }\phi ^{\prime }+\{s\left( 2n-1\right) +1\}f^{2}\phi ^{\prime \prime }\right] =0, \end{aligned}$$
(12)

and the BC’s become

$$\begin{aligned} \ f\left( \eta \right)&= S,\mathbf {\ }f^{\prime }\left( \eta \right) =\chi ,\theta \left( \eta \right) =1,\phi \left( \eta \right) =1\text { at }\eta =0, \nonumber \\ \ f^{\prime }(\eta )&= 0,\, \theta (\eta )=0,\, \phi (\eta )=0\text { as }\eta \rightarrow \infty , \end{aligned}$$
(13)

where \({{\rm Re}}_{\text{a}}\left( =\frac{\rho xu_{\text{w}}}{a}\right) ,\) and \({{\rm {Re}}}_{\text{b}}\left( = \frac{\rho x^{\text{n}}u_{\text{w}}^{2-{\text{n}}}}{b}\right) \) are the Reynolds numbers, \(A\left( =\frac{\mathrm{Re}_{\text{b}}^{\frac{2}{{\text{n}}+1}}}{\mathrm{Re}_{\text{a}}}\right)\) denotes the material parameter, \(M\left( =\frac{\sigma B_{0}^{2}}{a\rho }\right)\) is a magnetic field parameter, \(\lambda _{\text{E,C}}\left( =\frac{u_{\text{w}}\delta _{\text{E,C}}}{x} \right)\) is a relaxation parameters, \(\Pr \left( =\frac{xu_{\text{w}}}{a}\mathrm{Re} _{\text{b}}^{\frac{-2}{{\text{n}}+1}}\right)\) represents the generalized Prandtl number and \({{\rm {Sc}}}\left( =\frac{xu_{\text{w}}\mathrm{Re}_{\text{b}}^{\frac{-2}{{\text{n}}+1}}}{D}\right)\) is the generalized Schmidt numbers, and \(S\left( =-\frac{\upsilon _{\text{w}}}{\left( \frac{s\left( 2n-1\right) +1}{n+1}\right) u_{\text{w}}\mathrm{Re}_{\text{b}}^{\frac{-2}{{\text{n}}+1}} }\right)\) is the suction parameter.

From Eq. (10), it tends to be seen that for \(A=0\) and distinct values of a power-law index, different kinds of fluid behaviors are recovered. For \(n=1\), the behavior of the fluid is Newtonian and for \(n \ne 1\) the behavior of the fluid is non-Newtonian (\(n>1\) shear thickening and \(n<1\) shear thinning). Also when \(n=1,\) we have \({{\rm Re}}_{\text{a}}={{\rm Re}}_{\text{b}}\) which represents the global similarity. The physical attributes of \(C_{\text{f}}\) is described as

$$\begin{aligned} C_{\text{f}}=\frac{\tau _{\text{w}}}{\rho u_{\text{w}}^{2}}, \end{aligned}$$
(14)

where the shear stress \(\tau _{\text{w}}\) is defined as

$$\begin{aligned} \tau _{\text{w}}=\left[ a\left( \frac{\partial u}{\partial y}\right) +b\left( \frac{ \partial u}{\partial y}\right) ^{\text{n}}\right] _{y=0}. \end{aligned}$$
(15)

In dimensionless notation, the quantity skin friction becomes

$$\begin{aligned} C_{\text{f}}\mathrm{Re}_{\text{b}}^{\frac{-1}{{\text{n}}+1}}=Af^{\prime \prime }(0)+\left[ f^{\prime \prime }(0)\right] ^{\text{n}}. \end{aligned}$$
(16)

Solution methodology

The non-dimensional governing equations of the model problem are nonlinear PDEs in nature. Thus, to solve this system we first transform these into a new dimensionless form of ODEs along with boundary conditions depending on a single variable \(\eta .\) For further solving, we go toward numerical simulation. Therefore, the transformed governing ODEs in Eqs. (10–12) with conditions (13) are numerically integrated by using the bvp4c in Matlab. In utilizing this technique, the dimensionless system of equations are initially reduced into the set of first-order differential equations by familiarizing with some new variables given by

$$\begin{aligned} f=y_{1}, \ f^{\prime }=y_{2},f^{\prime \prime }=y_{3},\theta =y_{4},\theta ^{\prime }=y_{5},\phi =y_{6},\phi ^{\prime }=y_{7.} \end{aligned}$$
(17)

Therefore, the reduced system of first-order equations is

$$\begin{aligned}&\left( \begin{array}{c} y_{1}^{\prime } \\ y_{2}^{\prime } \\ y_{3}^{\prime } \\ y_{4}^{\prime } \\ y_{5}^{\prime } \\ y_{6}^{\prime } \\ y_{7}^{\prime } \end{array} \right) \nonumber \\&\quad =\left( \begin{array}{c} y_{2} \\ y_{3} \\ \frac{sf^{\prime 2}-\left( \frac{s(2n-1)+1}{n+1}\right) ff^{\prime \prime }+M^{2}f^{\prime }}{A+n(f^{\prime \prime })^{{\text{n}}-1}} \\ y_{5} \\ \frac{\Pr\lambda _{\text{E}}\left( \frac{s(2n-1)+1}{(n+1)^{2}}\right) \times \{2+n+(n-2)s\}ff^{\prime }\theta ^{\prime }-\Pr\left( \frac{s(2n-1)+1}{n+1} \right) f\theta ^{\prime }-\varepsilon _{1}\theta ^{\prime ^{2}}}{ 1+\varepsilon _{1}\theta -\Pr\lambda _{\text{E}}\left( \frac{s(2n-1)+1}{(n+1)^{2}} \right) \times \{s(2n-1)+1\}f^{2}} \\ y_{7} \\ \frac{{{\rm Sc}}\lambda _{\text{C}}\left( \frac{s(2n-1)+1}{(n+1)^{2}}\right) \times \{2+n+(n-2)s\}ff^{\prime }\phi ^{\prime }-{{\rm Sc}}\left( \frac{s(2n-1)+1}{n+1} \right) f\phi ^{\prime }-\varepsilon _{2}\phi ^{\prime ^{2}}}{1+\varepsilon _{2}\phi -{{\rm Sc}}\lambda _{\text{C}}\left( \frac{s(2n-1)+1}{(n+1)^{2}}\right) \times \{s(2n-1)+1\}f^{2}} \end{array} \right) , \end{aligned}$$
(18)

with conditions

$$\begin{aligned} \begin{array}{c} y_{1}(0)=S,\mathbf {\ }y_{2}\left( 0\right) =\chi ,\mathbf {\ }y_{2}\left( \infty \right) =0,\mathbf {\ }y_{4}\left( 0\right) =1, \\ y_{4}\left( \infty \right) =0,\mathbf {\ }y_{6}(0)=1,\mathbf {\ }y_{6}(\infty )=0. \end{array} \end{aligned}$$
(19)

Flow, heat and mass transfer problem of Sisko fluid is considered for testing the influence of various flow parameters with the help of numerical approach. In particular, all these effects are summarized in the form of first and second approximated values of local skin friction, Nusselt number and Sherwood number. However, these results are well correlated with results presented by Bhattacharyya [34] and Ishak et al. [35] as illustrated in Table 1.

Table 1 Comparison of \(f^{\prime \prime }(0)\) for first and second solutions with different values of shrinking parameter \(\chi\) by keeping \(n=s=1\), when the other parameters are zero
Full size table

Graphical results and discussion

Numerical solutions to the ordinary differential equations (10) to (12) along with the boundary conditions (13) were obtained by using one of the collocation methods in Matlab. In this techniques, the multiple solutions are obtained by setting different initial guesses for the values of \(f^{\prime \prime }\left( 0\right) , \mathbf {\ }\theta ^{\prime }\left( 0\right)\) and \(\phi \left( 0\right)\), where all profiles satisfy the boundary conditions asymptotically with different boundary layer thickness. The actual domain is infinite but the results concluded for finite domain because the software is working only for finite value of domain.

The variation of \(f^{\prime \prime }\left( 0\right)\) with shrinking parameter \(\chi\) for shear-thinning fluid in panel (a) and shear-thickening fluid in panel (b) is shown in Fig. 2 and Fig. 3 for the representative values of Sisko fluid parameter and mass suction parameter,  respectively. These figures show that there is a region of single solution for \(\chi \geqslant -1,\) dual (upper branch and lower branch) solutions for \(\left( \chi _{\text{c}}<\chi <-1\right)\) and there are no solutions for \(\left( \chi <\chi _{\text{c}}\right) .\) Here, \(\chi _{\text{c}}\) represent the critical values (turning points) of \(\chi\) that depend on A and S.

Figure 2 displays the impacts of skin friction for the surface of Sisko fluid parameter A for distant values of the shrinking parameter \(\chi .\) In shear-thinning fluid critical values are changing from \(\chi _{\text{c}}=\) \(-1.5065\) to \(\chi _{\text{c}}=\) \(-1.6360\), whereas in shear-thickening fluid critical values decrease from \(\chi _{\text{c}}=\) \(-2.3804\) to \(\chi _{\text{c}}=\) \(-3.4054\). Here, we also noted that the dual-nature solutions of skin friction are reduced with increasing the values of \(A=\{3,4,5\}\) and \(\ \{50\%,\ 60\%,83\%\}\) in percentage term.

Also, Fig. 3 depicts the evaluation for numerous values of mass suction parameter (\(S>0\)); the skin friction is sketched with reference to shrinking parameter \(\chi\). We noted that the critical values for shear-thinning fluid are decreasing from \(\chi _{\text{c}}=\) \(-2.2846\) to \(\chi _{\text{c}}=\) \(-2.6296\), whereas in shear-thickening fluid critical values are decreasing from \(\chi _{\text{c}}=\) \(-4.0094\) to \(\chi _{\text{c}}=\) \(-4.4094\). Thus, skin friction rises with rising the variation of \(S=\{3.0,3.1,3.2\}\)and \(\{75\%,77.5\%,\ 80\%\}\) in percentage term. Also we noted that multiple solutions of skin friction are higher for A as compared to the S.

The profile \(f^{\prime }(\eta )\) for the several values of Sisko fluid parameter A is shown in Fig. 4 with the first solution being shown by a full line and the second solutions by a broken line. It is depicted that the fluid velocity distribution decreases in the upper branch solution and increases in the lower branch solution, while in the case of shear thickening, the upper branch solution and the lower branch solution are showing a decreasing pattern. Also, the thickness of a momentum boundary layer increases with this effect.

Figure 5 shows the impacts of S on \(f^{\prime }(\eta ).\) It is perceived that the impact of suction parameter S has the opposite trend in upper branch and lower branch solutions, i.e., the strong influence of S causes the fluid velocity to increase in upper branch, while it causes the fluid velocity to decrease in the lower branch. Furthermore, the behavior of the boundary layer of the flow can also be analyzed through these figures. Thus, we observed that the related thickness is declined and is raised in the upper branch and lower branch solutions, respectively, with the increasing value of \(S=\{3.0,3.4,3.8\}\)and \(\{75\%,85\%,\ 95\%\}\) in percentage term.

Figure 6 shows the prominent attributes of shrinking parameter \(\chi\) on fluid velocity against the dimensionless parameter \(\eta\). For both the cases, the velocity increases with increasing the magnitude of \(\chi\) for the first branch, whereas opposite behavior is seen in the second branch. Consequently, the momentum boundary layer thickness is showing reduction in the upper branch case, while the reverse is true for the lower branch.

Figure 7 reveals the magnetic field effects on the momentum boundary layer. By analyzing these graphs, it is elucidated that the strong magnetic field improves the boundary layer in the upper branch, while it conflicts in the lower branch solution. Also we noted that due to the effect of Lorentz forces the magnitudes of the first velocity profile are lower with the variation of M and that the motion of the fluid is declined. On the other way, the velocity profile is not realizable physically; that is why in a physical situation the second solution is unstable. Here, we vary the value of M in percentage term as \(\ \{10\%,25\%,40\%\}.\)

The impact of Pr on dimensionless temperature distribution \(\theta \left( \eta \right)\) is shown in Fig. 8a. The percent values of Pr are increased in a manner \(\{32\%,33\%,35\%\}\) depending upon the convergence region of Pr. An increase in Pr physically implies a reduction of fluid thermal conductivity; thus, the decline is seen in the thickness of a thermal boundary layer. Also, the temperature profile is showing a decreasing behavior in the first branch and increasing one in second branch solution with increasing values of \(\Pr .\) So there is no effect of \(\Pr\) on the velocity fluid because the momentum equation is independent of the thermal one. Furthermore, from Fig. 8b we noted that as we increased the values of \(\lambda _{\text{E}}\), the fluid temperature and the thickness of the related boundary layers diminished. Physically, this is due to the reality that the liquid particle needs enough time to transport the heat to its nearest particles. Additionally, for the larger values of \(\lambda _{\text{E}}\) the conduct of liquid as a non-conductor which is in charge of the decrease of \(\theta \left( \eta \right)\) (Fig. 9). The fluctuation in the temperature distribution and the related boundary layer thickness for the \(\epsilon _{1}\) is shown in Fig. 10. It is concluded from the figure that the fluid temperature shows an increasing behavior with the enlargement of \(\varepsilon _{1}\) in upper branch and lower branch solutions, which is a result of the way that the thermal conductivity improves the temperature.

The variation of Sc and \(\lambda _{\text{c}}\) on concentration profile is shown in Fig. 10a,b. Schmidt number Sc causes the concentration profile to minimize in the first solution as well as in the second solution. The enhancment in Schmidt number decreases the concentration distribution as well as the associated boundary layer thickness and this is due to an inverse relation of Schmidt number with molecular diffusivity. So, concentration distribution and concentration boundary layer thickness diminished. The corresponding dual dimensionless concentration profiles are shown in Fig. 9b. For the second solution, the peak of the concentration overshoot increases with increasing concentration relaxation parameter and the thickness of a concentration boundary layer is always greater than that of the first solution. Figure 11 displays the concentration profile for distant values of \(\epsilon _{2}\). As we see from the figure, the related thickness for the first solution is greater than for the second solution. The concentration profile declines with the variation of \(\epsilon _{2}\) for the first solution, however increment for the second solution.

Fig. 2
figure 2

The impact of Sisko fluid parameter A on skin friction coefficient with shrinking parameter \(\chi\)

Full size image
Fig. 3
figure 3

The variation of skin friction at the surface with shrinking parameter \(\left( \chi \right)\) for distant values of mass suction parameter \(\left( S\right) .\)

Full size image
Fig. 4
figure 4

The dual behavior of \(f^{\prime }(\eta )\) with the variation of A

Full size image
Fig. 5
figure 5

The dual behavior of \(f^{\prime }(\eta )\) with the variation of S

Full size image
Fig. 6
figure 6

The dual behavior of \(f^{\prime }(\eta )\) with the variation of \(\chi\)

Full size image
Fig. 7
figure 7

The dual behavior of \(f^{\prime }(\eta )\) with the variation of M

Full size image
Fig. 8
figure 8

The dual behavior of \(\theta (\eta )\) with the variation of \(\Pr\) in (panel-a) and \(\lambda _{\text{E}}\) in (panel-b)

Full size image
Fig. 9
figure 9

The dual behavior of \(\theta (\eta )\) with the variation of \(\epsilon _{1}\)

Full size image
Fig. 10
figure 10

The dual behavior of \(\phi (\eta )\) with the variation of a Sc b \(\lambda _{\text{C}}\)

Full size image
Fig. 11
figure 11

The dual behavior of \(\phi (\eta )\) with the variation of \(\varepsilon _{2}\)

Full size image

Conclusions

A numerical simulation is employed to examine the dual-nature solutions for the MHD Sisko fluid flow over a uniformly shrinking sheet. In this work, magnetic field and suction effects were taken into the account for the fluid flow and heat transfer analysis. The results were obtained for the multiple (upper branch and lower branch) solutions of modeled problem by utilizing the Matlab built-in function, namely bvp4c. On the basis of the present work, we have concluded some remarkable features as follows:

  • The upper solution is physically stable, whereas the lower solution is unstable.

  • The more suction S into the Sisko fluid flow increases the fluid velocity in upper branch, while it reduces in the lower branch.

  • The thickness of momentum and thermal boundary layer are thinner in upper branch compared with the lower branch.

  • Temperature fluid rises with rising the values of variable thermal conductivity.