1 Introduction

Recent innovative methodologies have paved the way for the appearance of manufactured materials at nanometer scale. Nanoliquid possesses huge impact on the improvement of newly developed heat transfer liquids. Nanoliquid is innovative engineered materials having massive applications in biology, cancer diagnosis, nuclear industries, drilling and oil recovery. Moreover, nanofluids have been widely utilized for heat transport applications. Khan et al. [1] inspected the impact of heat sink–source and nanoparticles on an Oldroyd-B fluid. Sheikholeslami and Ellahi [2] considered the characteristics of cubic cavity for 3D flow of magneto-nanofluid. Khan and Khan [3] reported the analysis for Burgers fluid in existence of nanoparticles. Sandeep et al. [4] investigated the impact of convective heat/mass transfer mechanisms on non-Newtonian magneto-nanofluid. Rehman et al. [5] studied the characteristics of entropy generation by utilizing nanoparticles. Khan and Khan [6] demonstrated impact of zero mass flux condition for power-law nanofluid. Haq et al. [7] utilized two-phase relation for water and ethylene glycol-based Cu nanoparticles under effect of suction–injection. Steady-state 2D flow of Burgers fluid in existence of nanoparticles was demonstrated by Khan and Khan [8]. Zero mass flux relation has been employed by Khan et al. [9] to visualize behavior of Burgers fluid in the presence of nanoparticles. Rahman et al. [10] reported nanofluid flow for Jeffrey fluid. Raju et al. [11] studied the magneto-nanofluid flow in the presence of rotating cone with temperature-dependent viscosity. Recently, numerous investigators published their research work about heat transport [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37].

Disparity of concentration in chemically reacting species effecting on mass transfer mechanism. In these situations, chemical species moves from high to low concentrated area. Applications of chemical reactions include manufacturing of food, formation and dispersion of fog, manufacturing of ceramics, production of polymer, crops damage via freezing, hydrometallurgical industry, geothermal reservoirs, cooling of nuclear reactor and recovery of thermal oil. Some reactions have capacity to move slowly or not at all except in the existence of a catalyst. Activation energy plays an important role in enhancing the production speed of chemical reactions. Moreover, activation energy is smallest amount of energy that reactants must acquire to start a chemical reaction. The term activation energy was initially presented by Arrhenius in 1889. The applications of activation energy are very wide in geothermal, mechanics of water, chemical engineering and oil emulsions. Khan et al. [38] considered the chemical processes for 3D flow of Burgers fluid by utilizing the revised heat–mass flux relations. Khan et al. [39] analyzed the effects of chemical processes on 3D flow of Burgers fluid. Khan et al. [40] investigated the characteristics of convective flow in the presence of variable thicked surface. Khan et al. [41] examined the features of revised heat flux relation and chemical processes for Maxwell fluid. Khan et al. [42] inspected the impact of chemical reactions on generalized Burgers fluid by utilizing the nanoparticles. Mustafa et al. [43] examined the characteristics of activation energy and chemical mechanisms on magneto-nanofluid.

Our main focus here is to explore the impact of activation energy on 3D flow of cross-nanofluid with combined effects of heat sink–source and nonlinear thermal radiation. Heat transport phenomenon is scrutinized through variable thermal conductivity. Moreover, impacts of chemical processes and Lorentz’s forces are accounted. By employing transformations procedure, the governing PDE’s are converted into ODE’s which are then tackled numerically by bvp4c. Outcomes of physical parameters involved in this research work are analyzed through graphical and tabular data.

2 Physical model and problem statement

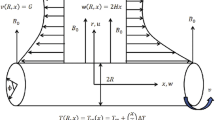
Geometry and boundary condition of physical model for steady 3D forced convective flow of cross-nanofluid is presented through Fig. 1. In this research work, we have utilized the thermally heated surface which can be utilized for various industrial products. Coordinate system is selected in such a way that sheet coincides with the plane \(z = 0\) and motion of the cross-nanofluid is confined in the half space \(z > 0\). Aspects of heat sink–source and thermal radiation are carried out in existing flow situation. Mass transport mechanism is scrutinized through activation energy. We have applied magnetic field of strength \(B_{0}\) in \(z\)-direction. Furthermore, the impact of induced magnetic field on the cross-nanofluid is neglected by utilizing the assumption of low Reynolds number. The sheet is kept at constant concentration \(C_{\text{w}}\), whereas the nanofluid outside the boundary is maintained at uniform temperature and concentration \(\left( {T_{\infty } ,\,C_{\infty } } \right)\), respectively. In areas such as geothermal, the governing equations are [see Ref. 9, 44]:

$${\frac{\partial u}{\partial x}} + {\frac{\partial v}{\partial y}} + {\frac{\partial w}{\partial z}} = 0,$$
(1)
$$u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} + w\frac{\partial u}{\partial z} = - \frac{1}{{\rho_{\text{f}} }}\frac{\partial P}{\partial x} + \nu \frac{\partial }{\partial z}\left[ {\frac{{\tfrac{\partial u}{\partial z}}}{{1 + \left\{ {\Gamma \left( {\tfrac{\partial u}{\partial z}} \right)} \right\}^{n} }}} \right] - \frac{{\sigma_{1} B_{0}^{2} u}}{{\rho_{\text{f}} }},$$
(2)
$$u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} + w\frac{\partial v}{\partial z} = - \frac{1}{{\rho_{\text{f}} }}\frac{\partial P}{\partial y} + \nu \frac{\partial }{\partial z}\left[ {\frac{{\tfrac{\partial v}{\partial z}}}{{1 + \left\{ {\Gamma \left( {\tfrac{\partial v}{\partial z}} \right)} \right\}^{n} }}} \right] - \frac{{\sigma_{1} B_{0}^{2} v}}{{\rho_{\text{f}} }},$$
(3)
$$\begin{aligned} u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} + w\frac{\partial T}{\partial z} = & \frac{1}{{\left( {\rho c} \right)_{\text{f}} }}\frac{\partial }{\partial z}\left( {k(T)\frac{\partial T}{\partial z}} \right) + \tau \left[ {D_{\text{B}} \frac{\partial C}{\partial z}\frac{\partial T}{\partial z} + \frac{{D_{\text{T}} }}{{T_{\infty } }}\left( {\frac{\partial T}{\partial z}} \right)^{2} } \right]\, \\ & - \frac{1}{{(\rho c)_{\text{f}} }}\frac{{\partial q_{r} }}{\partial z} + \frac{{Q_{0} }}{{(\rho c)_{\text{f}} }}(T - T_{\infty } ), \\ \end{aligned}$$
(4)
$$\begin{aligned} u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} + w\frac{\partial C}{\partial z} = &\, D_{\text{B}} \frac{{\partial^{2} C}}{{\partial z^{2} }} + \frac{{D_{\text{T}} }}{{T_{\infty } }}\frac{{\partial^{2} T}}{{\partial z^{2} }} \\ & - k_{\text{c}}^{2} \left( {C - C_{\infty } } \right)\,\left( {\frac{T}{{T_{\infty } }}} \right)^{m} \exp \left( { - \frac{{E_{\text{a}} }}{{k^{*} T}}} \right). \\ \end{aligned}$$
(5)

with

$$\begin{aligned} & u = U_{w} = ax,\quad v = V_{w} = by,\quad w = 0, \\ & - k\frac{\partial T}{\partial z} = h_{\text{f}} [T_{\text{f}} - T],\, \, D_{\text{B}} \frac{\partial C}{\partial z} + \frac{{D_{\text{T}} }}{{T_{\infty } }}\frac{\partial T}{\partial z} = 0\quad {\text{at}}\quad z = 0, \\ \end{aligned}$$
(6)
$$u \to 0,\, \, v \to 0,\, \, T \to T_{\infty } ,\, \, C \to C_{\infty } \, \quad {\text{as}}\quad z \to \infty ,$$
(7)

where

$$k(T) = k_{\infty } \left( {1 + \varepsilon \left( {\frac{{T - T_{\infty } }}{{T_{\text{f}} - T_{\infty } }}} \right)} \right),$$
(8)
$$q_{\text{r}} = - \frac{{4\sigma^{ * } }}{{3k^{ * } }}\frac{{\partial T^{4} }}{\partial z} = - \frac{{16\sigma^{ * } }}{{3k^{ * } }}\frac{\partial }{\partial z}\left( {T^{3} \frac{\partial T}{\partial z}} \right),$$
(9)

Substituting Eqs. (8) and (9) into Eq. (4), we have the following energy equation

$$\begin{aligned} u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} + w\frac{\partial T}{\partial z} = & \frac{1}{{\left( {\rho c} \right)_{\text{f}} }}\frac{\partial }{\partial z}\left( {k(T)\frac{\partial T}{\partial z}} \right) + \tau \left[ {D_{\text{B}} \frac{\partial C}{\partial z}\frac{\partial T}{\partial z} + \frac{{D_{\text{T}} }}{{T_{\infty } }}\left( {\frac{\partial T}{\partial z}} \right)^{2} } \right] \\ & + \frac{1}{{(\rho c)_{\text{f}} }}\frac{{16\sigma^{ * } }}{{3k^{ * } }}\frac{\partial }{\partial z}\left( {T^{3} \frac{\partial T}{\partial z}} \right) + \frac{{Q_{0} }}{{(\rho c)_{\text{f}} }}(T - T_{\infty } ). \\ \end{aligned}$$
(10)
Fig. 1
figure 1

Physical geometry for the problem

Full size image

Considering the following suitable conversions,

$$\begin{aligned} & u = axf^{\prime } (\eta ),\quad v = ayg^{\prime } (\eta ),\quad w = - (a\nu )^{{\tfrac{1}{2}}} \left[ {f(\eta ) + g(\eta )} \right], \\ & \theta (\eta ) = \frac{{T - T_{\infty } }}{{T_{\text{f}} - T_{\infty } }},\quad \varphi (\eta ) = \frac{{C - C_{\infty } }}{{C_{\infty } }},\quad \eta = z\sqrt {\frac{a}{\nu }} . \\ \end{aligned}$$
(11)

Equation (1) is automatically satisfied, and Eqs. (2)–(7) and (9) yield

$$\left[ {1 + \left( {1 - n} \right)\,\left( {We_{1} f^{\prime \prime } } \right)^{n} } \right]\,f^{\prime \prime \prime } - \left[ {1 + \left( {We_{1} f^{{^{\prime \prime } }} } \right)^{n} } \right]^{2} \left[ {f^{{^{\prime } 2}} - \left( {f + g} \right)\,f^{\prime \prime } + M^{2} f^{\prime } } \right] = 0,$$
(12)
$$\left[ {1 + \left( {1 - n} \right)\,\left( {We_{2} g^{\prime \prime } } \right)^{n} } \right]\,g^{\prime \prime \prime } - \left[ {1 + \left( {We_{2} g^{\prime \prime } } \right)^{n} } \right]^{2} \left[ {g^{\prime 2} - \left( {f + g} \right)g^{\prime \prime } + M^{2} g^{\prime } } \right] = 0,$$
(13)
$$\begin{aligned} & \frac{\text{d}}{{{\text{d}}\eta }}\left[ {\{ 1 + R_{\text{d}} \{ 1 + (\theta_{\text{f}} - 1)\theta \}^{3} \} \theta^{\prime } } \right] + \left( { \varepsilon \theta } \right)\theta^{\prime \prime } + \varepsilon \theta^{{{\prime }2}} \\ & \quad + \mathop {Pr}\limits \left[ {(f + g)\theta^{\prime } + N_{\text{b}} \theta^{\prime } \varphi^{\prime } + N_{\text{t}} \theta^{\prime 2} } \right] + \mathop {Pr}\limits \lambda \theta = 0, \\ \end{aligned}$$
(14)
$$\varphi^{\prime \prime } + Le\mathop {Pr}\limits (f + g)\varphi^{\prime } - Le\mathop {Pr}\limits \sigma \varphi \left( {1 + \delta \theta } \right)^{m} \exp \left( { - \frac{E}{1 + \delta \theta }} \right) + \frac{{N_{\text{t}} }}{{N_{\text{b}} }}\theta^{\prime \prime } = 0,$$
(15)
$$\begin{aligned} & f = 0,\quad g = 0,\quad f^{\prime } = 1,\quad g^{\prime } = \alpha , \\ & \theta^{\prime } (0) = - \gamma [1 - \theta (0)],\quad N_{\text{b}} \varphi^{\prime } (0) + N_{\text{t}} \theta^{\prime } (0) = 0,\quad {\text{at}}\quad \eta = 0, \\ \end{aligned}$$
(16)
$$f^{\prime } \to 0,\quad \, g^{\prime } \to 0,\quad \theta \to 0,\quad \, \varphi \to 0,\quad {\text{as}}\quad \eta \to \infty .$$
(17)

Mathematically, dimensionless parameters are defined as

$$\begin{aligned} & We_{1} =\Gamma ax\sqrt {\frac{a}{\nu }} ,\,We_{2} =\Gamma ay\sqrt {\frac{a}{\nu }} ,\,R_{\text{d}} = \frac{{16\sigma^{ * } T_{\infty }^{3} }}{{3k_{\infty } k^{ * } }},\,\alpha = \frac{b}{a},\,\theta_{\text{f}} = \frac{{T_{\text{f}} }}{{T_{\infty } }}, \\ & M = \frac{{\sigma_{1} B_{0}^{2} }}{{\rho_{\text{f}} a}},\,N_{\text{b}} = \frac{{\tau D_{\text{B}} C_{\infty } }}{\nu },\,N_{\text{t}} = \frac{{\tau D_{\text{T}} (T_{\text{f}} - T_{\infty } )}}{{\nu T_{\infty } }},\,\lambda = \frac{{Q_{0} }}{{a(\rho c)_{\text{f}} }},\, \\ & \mathop {Pr}\limits = \left( {\frac{\nu }{{\alpha_{1} }}} \right),\,Le = \frac{{\alpha_{1} }}{{D_{\text{B}} }},\,\sigma = \frac{{k_{\text{c}}^{2} }}{a},\,E = \frac{{E_{\text{a}} }}{{k^{ * } T_{\infty } }},\,\delta = \frac{{T_{\text{f}} - T_{\infty } }}{{T_{\infty } }}, \\ \end{aligned}$$
(18)

The mathematical relations of local skin frictions, local Nusselt number and local Sherwood number in dimensional form are expressed as

$$C_{{f_{x} }} = \frac{{2\tau_{xz} }}{{\rho_{\text{f}} U_{w}^{2} }},\quad C_{{f_{y} }} = \frac{{2\tau_{yz} }}{{\rho_{\text{f}} U_{w}^{2} }},$$
(19)
$$Nu_{x} = - \frac{x}{{\left( {T_{\text{f}} - T_{\infty } } \right)}}\left. {\left( {\frac{\partial T}{\partial z}} \right)} \right|_{z = 0} + \frac{{xq_{\text{r}} }}{{k\left( {T_{\text{f}} - T_{\infty } } \right)}},$$
(20)
$$Sh_{x} = - \frac{x}{{\left( {C_{\text{f}} - C_{\infty } } \right)}}\left. {\left( {\frac{\partial C}{\partial z}} \right)} \right|_{z = 0} .$$
(21)

Dimensionless form of overhead physical quantities is

$$C_{{f_{x} }} \left( {Re_{x} } \right)^{{\tfrac{1}{2}}} = \frac{{2f^{\prime \prime } \left( 0 \right)}}{{\left[ {1 + \left( {We_{1} f^{\prime \prime } \left( 0 \right)} \right)^{n} } \right]}},\,C_{{f_{y} }} \left( {Re_{y} } \right)^{{ - \tfrac{1}{2}}} = \frac{{2V_{w} g^{\prime \prime } \left( 0 \right)}}{{U_{w} \left[ {1 + \left( {We_{2} g^{\prime \prime } \left( 0 \right)} \right)^{n} } \right]}},$$
(22)
$$\left( {Re_{x} } \right)^{{ - \tfrac{1}{2}}} Nu_{x} = - \left[ {1 + R_{\text{d}} \{ 1 + (\theta_{\text{f}} - 1)\theta \}^{3} } \right]\,\theta^{{\prime }} (0),$$
(23)

where

$$Re_{x} = \frac{{ax^{2} }}{\nu }.$$

3 Numerical procedure

In this research work, bvp4c method is implemented for the considered problem. In this regard, system of ODEs along with boundary conditions is converted into system of first-order differential equations and solved numerically for involved physical parameters.

$$f = s_{1} ,\quad \, f^{\prime } = s_{2} ,\quad f^{\prime \prime } = s_{3} ,\quad f^{\prime \prime \prime } = s_{3}^{\prime } ,$$
(24)
$$g = s_{4} ,\quad g^{\prime } = s_{5} ,\quad g^{\prime \prime } = s_{6} ,\quad g^{\prime \prime \prime } = s_{6}^{{^{\prime } }} ,$$
(25)
$$\theta = s_{7} ,\quad \theta^{\prime } = s_{8} ,\quad \theta^{\prime \prime } = s_{8}^{\prime } ,$$
(26)
$$\varphi = s_{9} ,\quad \varphi^{\prime } = s_{10} ,\quad \varphi^{\prime \prime } = s_{10}^{\prime } ,$$
(27)

where

$$s_{3}^{\prime } = \frac{{\left( {1 + (We_{1} s_{3} )^{n} } \right)^{2} (M^{2} s_{2} + s_{2}^{2} - (s_{1} + s_{4} )s_{3} )}}{{A_{1} }},$$
(28)

here

$$s_{6}^{\prime } = \frac{{\left( {1 + (We_{2} s_{6} )^{n} } \right)^{2} (M^{2} s_{5} + s_{5}^{2} - (s_{1} + s_{4} )s_{6} )}}{{A_{2} }},$$
(29)
$$A_{1} = 1 + \left( {1 - n} \right)\,\left( {We_{1} s_{3} } \right)^{n} ,$$
(30)
$$A_{2} = 1 + \left( {1 - n} \right)\,\left( {We_{2} s_{6} } \right)^{n} ,$$
(31)
$$\begin{aligned} s_{8}^{\prime } = & \frac{{ - Pr((s_{1} + s_{4} )s_{8} + N_{\text{b}} s_{8} s_{10} + N_{\text{t}} s_{8}^{2} - \lambda s_{7} )}}{{A_{3} }} \\ & \quad \frac{{ - \varepsilon s_{8}^{2} - 3R_{\text{d}} (1 + (\theta_{\text{f}} - 1)s_{7} )^{2} (\theta_{\text{f}} - 1)s_{8}^{2} }}{{A_{3} }}, \\ \end{aligned}$$
(32)

here

$$A_{3} = 1 + \varepsilon s_{7} + R_{\text{d}} \left( {1 + \left( {\theta_{\text{f}} - 1} \right)\,s_{7} } \right)^{3} ,$$
(33)
$$s_{10}^{\prime } = - \mathop {Pr}\limits Le(s_{1} + s_{4} )s_{10} + \mathop {Pr}\limits Le\sigma ((1 + \delta s_{7} )^{m} )\exp ( - E/(1 + \delta s_{7} ))s_{9} - \frac{{N_{\text{t}} }}{{N_{\text{b}} }}s_{8}^{\prime } ,$$
(34)

with

$$\begin{aligned} & s_{1} \left( 0 \right) = 0,\,s_{4} \left( 0 \right) = 0,\,s_{2} \left( 0 \right) = 1,\,s_{5} \left( 0 \right) = \alpha ,\;s_{8} \left( 0 \right) + \gamma \left( {1 - s_{7} \left( 0 \right)} \right) = 0, \\ & N_{\text{b}} s_{10} \left( 0 \right) + N_{\text{t}} s_{8} \left( 0 \right) = 0, \\ \end{aligned}$$
(35)
$$s_{2} \to 0,\quad s_{5} \to 0,\quad s_{7} \to 0,\quad s_{9} \to 0\quad {\text{as}}\quad \eta \to \infty .$$
(36)

3.1 Validation with previous results

Table 1 certifies the appropriateness of obtained numerical outcomes by making a comparison for Newtonian fluid with the outcomes tabulated by Ariel [44]. The numerical data for \(- f^{\prime \prime } \left( 0 \right)\) and \(- g^{\prime \prime } \left( 0 \right)\) are computed, and legitimacy of work is ensured.

Table 1 A comparison of \(f^{\prime \prime } \left( 0 \right)\) and \(g^{\prime \prime } \left( 0 \right)\) for Newtonian fluid with \(We_{1} = We_{2} = M = 0\)
Full size table

4 Physical analysis

In the current research work, impact of activation energy and Lorentz forces on 3D forced convective flow of cross-nanofluid is demonstrated. Zero mass flux relation is employed for estimating cross-nanofluid properties. Features of heat transport for nanofluid are scrutinized through nonlinear radiation and heat source–sink. Numerical data of the present investigation are declared in terms of profiles of velocity, temperature and concentration. The surface drag forces, heat transfer rate and mass transfer rate for fluctuating various parameters are illustrated through tables.

4.1 Velocity profile

Figure 2a, b is plotted to demonstrate the behavior of velocity profile corresponding to change in local Weissenberg number We. It is observed from graphical that velocity of cross-nanofluid declines for augmented values of \(We_{1}\) and \(We_{2}\). Physical reason behind this behavior of cross-nanofluid is that as we raise value of \(We_{1}\) and \(We_{2}\) relaxation time enhances due to which velocity of cross-nanofluid deteriorates. Figure 3a, b presents the impact of \(n\) on velocity of cross-nanofluid. The examination of these figures reveals that progressive trend of velocity profile rises for shear-thinning regime. Physically, an uplift in the value of \(n\) less resistance is faced by shear-thinning fluid due to low viscosity which causes an enlargement in fluid velocity.

Fig. 2
figure 2

Profiles of velocity \(f^{\prime } (\eta )\) for various values of \(We_{1}\) for shear-thinning (a) and profiles of velocity \(g^{\prime } (\eta )\) for various values of \(We_{2}\) for shear-thinning (b)

Full size image
Fig. 3
figure 3

Profiles of velocity \(f^{\prime } (\eta )\) for various values of \(n\) for shear-thinning (a) and profiles of velocity \(g^{\prime } (\eta )\) for various values of \(n\) for shear-thinning (b)

Full size image

4.2 Temperature field

Figures 4, 5, 6, 7 and 8 are portrayed here to investigate the impact of \(\alpha ,\,N_{\text{t}} ,\,\lambda ,\) \(\theta_{\text{f}}\) and \(\gamma\) for \(n < 1\) and \(n > 1\) on temperature of cross-nanofluid. To exhibit the effects of \(\alpha\) on the temperature profile of cross-nanofluid, we have plotted Fig. 4a, b. These sketches show that the temperature of cross-nanofluid decreases as the values of \(\alpha\) are augmented. Furthermore, careful analysis of these sketches releases that decaying behavior of cross-nanofluid is more prominent for \(n < 1\). Figure 5a, b interprets the dependence of thermophoresis parameter \(N_{\text{t}}\) on the temperature of cross-nanofluid. The rise in the temperature of cross-nanofluid is detected for growing values of \(N_{\text{t}}\). Physically, \(N_{\text{t}}\) demonstrates the temperature difference of cross-nanofluid between the hot fluid behind the sheet and temperature of liquid at infinity. The ratio of hot fluid behind the sheet to temperature of liquid at infinity \(\theta_{\text{f}}\) and heat absorption parameter \(\lambda\) play a vital role in forced convective 3D flow of cross-nanofluid. Figures 6a, b and 7a, b present the impact of \(\lambda\) and \(\theta_{\text{f}}\) on temperature profile of cross-nanofluid. These figures depict that the augmented values of \(\theta_{\text{f}}\) and \(\lambda\) affect the heat transfer strongly. Physically, as \(\theta_{\text{f}}\) strengthens, the temperature of the wall become higher as compared to temperature of the nanoliquid at infinity. Thus, as a result, the temperature of nanofluid enhances. Figure 8a, b is sketched to perceive the dependence of 3D flow of cross-nanofluid on \(\gamma\) for \(n < 1\) and \(n > 1\). The exploration of these plots impart that Biot number leads to enhancement of nanofluid temperature. Physical reason behind this trend of \(\gamma\) is that less resistance is faced by the thermal wall which causes an enhancement in convective heat transfer to the fluid.

Fig. 4
figure 4

Profiles of temperature \(\theta (\eta )\) for various values of \(\alpha\) for shear-thinning (a) and shear-thickening liquids (b)

Full size image
Fig. 5
figure 5

Profiles of temperature \(\theta (\eta )\) for various values of \(N_{\text{t}}\) for shear-thinning (a) and shear-thickening liquids (b)

Full size image
Fig. 6
figure 6

Profiles of temperature \(\theta (\eta )\) for various values of \(\lambda\) for shear-thinning (a) and shear-thickening liquids (b)

Full size image
Fig. 7
figure 7

Profiles of concentration \(\varphi (\eta )\) for various values of \(\theta_{\text{f}}\) for shear-thinning (a) and shear-thickening liquids (b)

Full size image
Fig. 8
figure 8

Profiles of concentration \(\theta (\eta )\) for various values of \(\gamma\) for shear-thinning (a) and shear-thickening liquids (b)

Full size image

4.3 Concentration field

Figures 9, 10, 11, 12, 13, 14 and 15 are sketched to visualize the aspects of various physical parameters on concentration of cross-nanofluid. Concentration profiles of cross-nanofluid for different values of activation energy \(E\) are sketched through Fig. 9a, b. The growing values of \(E\) result in an augmentation in the concentration of cross-nanofluid. From the mathematical relation of Eq. (1), we detected that high activation energy and low temperature reduce the reaction rate due to which chemical reaction mechanisms slow down. Therefore, the concentration of cross-nanofluid enhances. The influence of chemical reaction parameter \(\sigma\) on the concentration profile is displayed in Fig. 10a, b. It is analyzed from these figures that the concentration profile declines with an increment in \(\sigma\). Figure 11a, b is plotted to detect the characteristics of fitted rate constant \(m\) on concentration of cross-nanofluid. Chemically, as we boost up the values of \(m\), destructive chemical mechanisms enhance due to concentration of cross-nanofluid declines. Figures 12a, b and 13a, b portray the concentration profile of cross-nanofluid for various vales of \(N_{\text{b}}\) and \(N_{\text{t}}\). It is detected from these sketches that concentration of cross-nanofluid declines with elevation in \(N_{\text{t}}\) while the reverse trend is observed for \(N_{\text{b}}\). Additionally, it is detected that physically, an uplift in the magnitude of \(N_{\text{b}}\) corresponds to rise in the rate at which nanoparticles in the base liquid move in random directions with different velocities. This movement of nanoparticles augments transfer of heat and therefore, declines the concentration profile. The influence of magnetic parameter \(M\) on the concentration profile of cross-fluid is displayed in Fig. 14a, b. It is analyzed from these figures that the concentration profile enhances with an increment in \(M\). The concentration of cross-nanofluid increases due to heat produced by \(M\). To investigate the aspects of the ratio of stretching rate parameter \(\alpha\) on the concentration profile, we have plotted Fig. 15a, b. These figures reveal that the concentration profile declines as the value of \(\alpha\) is augmented.

Fig. 9
figure 9

Profiles of concentration \(\varphi (\eta )\) for various values of \(E\) for shear-thinning (a) and shear-thickening liquids (b)

Full size image
Fig. 10
figure 10

Profiles of concentration \(\varphi (\eta )\) for various values of \(\sigma\) for shear-thinning (a) and shear-thickening liquids (b)

Full size image
Fig. 11
figure 11

Profiles of concentration \(\varphi (\eta )\) for various values of \(m\) for shear-thinning (a) and shear-thickening liquids (b)

Full size image
Fig. 12
figure 12

Profiles of concentration \(\varphi (\eta )\) for various values of \(N_{\text{b}}\) for shear-thinning (a) and shear-thickening liquids (b)

Full size image
Fig. 13
figure 13

Profiles of concentration \(\varphi (\eta )\) for various values of \(N_{\text{t}}\) for shear-thinning (a) and shear-thickening liquids (b)

Full size image
Fig. 14
figure 14

Profiles of concentration \(\varphi (\eta )\) for various values of \(M\) for shear-thinning (a) and shear-thickening liquids (b)

Full size image
Fig. 15
figure 15

Profiles of concentration \(\varphi (\eta )\) for various values of \(\alpha\) for shear-thinning (a) and shear-thickening liquids (b)

Full size image

4.4 Quantities of physical interest

Tables 2 and 3 are presented to demonstrate the achieved outcomes for surface drag forces \(\left( {C_{{f_{x} }} ,\,C_{{f_{y} }} } \right)\) and heat transfer rates (\(Nu_{x}\)). It is noticed from Table 2 magnitude of surface drag forces is greater for larger estimation of \(n,\,\alpha ,\,M\) while opposite trend is observed for \(We_{1}\) and \(We_{2}\). Table 3 reveals that magnitude of heat transport rate deteriorates for augmented values of \(\delta ,\,\sigma ,\,m\) and \(N_{\text{t}}\), while it rises for \(Pr\),\(E\) and \(n\).

Table 2 Numerical values of local skin frictions \(\left( { - C_{fx} \left( {Re_{x} } \right)^{1/2} , - C_{fy} \left( {Re_{x} } \right)^{1/2} } \right)\) for distinct values of escalating parameters
Full size table
Table 3 Numerical values of Local Nusselt number \(\left( {Re_{x} } \right)^{{ - \tfrac{1}{2}}} Nu_{x}\) for distinct values of escalating parameters when \(M = 0.8,\,We_{1} = We_{2} = 2.2,\,Le = 2.0,\,R_{\text{d}} = 0.5,\,\theta_{\text{f}} = 0.3,\,N_{\text{b}} = 0.2,\,\alpha = 0.3\) and \(\gamma = 0.5\)
Full size table

5 Main outcomes

Influence of Lorentz forces and chemical process on 3D flow of cross-nanofluid is investigated here. Impact of variable thermal conductivity on nanofluid is taken into consideration. Heat source–sink and thermal radiation mechanisms are deliberated here to characterize the heat transport mechanism. Influence of activation energy is considered. Main outcomes of this research work are pointed as

  • Temperature of cross-nanofluid is an increasing function of \(N_{\text{t}} .\)

  • Higher estimation of \(\lambda\) provides larger temperature of cross-nanofluid.

  • An increment in \(\alpha\) demonstrates decays in \(\theta (\eta )\).

  • Concentration field enriches for intensifying estimation of \(M\).

  • Concentration of cross-magnetonanofluid augments for improving values of \(E.\)

  • \(\varphi (\eta )\) decays via \(m\).

  • The profiles of concentration descent for escalating \(m\) and \(\sigma\).