Introduction

To reach the best design of a heat exchanger, both hydrothermal and second-law behaviors need to be considered. To enhance its efficiency, nanofluid can be considered as a working fluid in a heat exchanger. Nanofluids have many applications, such as in solar energy [1], solidification/melting enhancement [2, 3], condensation process [4]. Jafaryar et al. [5] suggested the innovative twisted tape with an alternate axis to generate secondary flows in a heat exchanger. They utilized nanofluid as an effective fluid. Jafaryar et al. [6] displayed turbulent migration of nanofluid through a pipe. They used two combined passive techniques to reach the best design. Haq et al. [7] depicted the MHD mixed convection over a sheet. Qi et al. [8] reported experimental results for nanofluid heat transfer augmentation in a heat exchanger. They analyzed the stability of working fluid. Sheikholeslami et al. [9] demonstrated exergy loss of nanofluid in a pipe with a swirling device. They presented correlations for destroyed exergy. Zheng et al. [10] demonstrated sensitivity analysis for a flat heat exchanger to find the impact of active parameters on the thermal behavior. Sajjadi and Kefayati [11] studied the turbulent-free convection in an enclosure. They used a mesoscopic approach in their attempt. Zheng et al. [12] utilized vortex rods for augmentation of efficiency of the heat exchanger. They simulated the current problem for laminar region. Astanina et al. [13] demonstrated the second- and first-law approach for ferrofluid natural convection within a cavity. They simulated the nanofluid behavior under the role of Lorentz forces. Choosing a good working fluid is the hot subject in recent decades [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43].

Although the hydrothermal behavior of nanofluid laminar flow within a heat exchanger has been reported by previous researchers, there are few papers in which researchers focus on entropy generation of nanofluid. Also, in the current paper, we present an innovative type of turbulator to enhance the efficiency. For better estimation of the behavior of working fluid, previous experimental models have been utilized. Impact of inlet velocity and revolution angle on nanofluid flow, frictional and thermal entropy generations is shown as contours.

Physical model

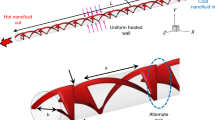
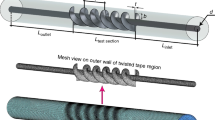
Two passive techniques have been employed in the current study. Using nanofluid and a turbulator can improve the heat transfer. Properties of H2O and CuO nanoparticles were depicted in Tables 1 and 2. Single phase was utilized for working fluid by employing experimental correlations. A new shape of the turbulator has been selected (see Fig. 1). Revolution angle was considered as a geometric variable. Length of the pipe is 900 mm, and the test section is central 300 mm. The reason for selecting such test section is because of the fact that test section should not appear any back flow. The inlet boundary was considered as velocity inlet and the outlet one was pressure outlet. The heat exchanger is heated by a constant heat flux.

Table 1 Coefficients of CuO–water
Full size table
Table 2 Properties of base fluid and nanoparticles
Full size table
Fig. 1
figure 1

Present heat exchanger

Full size image

Problem formulation

A heat exchanger with a turbulator is simulated in the current attempt. Turbulent nanofluid flow is considered. Governing partial equations for such flow are:

$$\frac{{\partial \left( {u_{\text{i}} } \right)}}{{\partial x_{\text{i}} }} = 0$$
(1)
$$\frac{\partial }{{\partial x_{\text{j}} }}\left( {\rho_{\text{nf}} u_{\text{i}} u_{\text{j}} } \right) = - \frac{\partial p}{{\partial x_{\text{i}} }} + \frac{\partial }{{\partial x_{\text{j}} }}\left( {\left( {\frac{{\partial u_{\text{i}} }}{{\partial x_{\text{j}} }} + \frac{{\partial u_{\text{j}} }}{{\partial x_{\text{i}} }}} \right)\mu_{\text{nf}} } \right) + \frac{\partial }{{\partial x_{\text{j}} }}\left( { - \rho_{\text{nf}} \overline{{u_{\text{j}}^{\prime } u_{\text{i}}^{\prime } }} } \right)$$
(2)
$$\frac{\partial }{{\partial x_{\text{i}} }}\left( {\rho_{\text{nf}} Tu_{\text{i}} } \right) = \frac{\partial }{{\partial x_{\text{i}} }}\left( {\left( {\varGamma_{\text{t}} + \varGamma } \right)\frac{\partial T}{{\partial x_{\text{i}} }}} \right),\quad \varGamma_{\text{t}} = \left( {\mu_{\text{t}} /Pr_{\text{t}} } \right),\quad \varGamma = \left( {\mu_{\text{nf}} /Pr_{\text{nf}} } \right),$$
(3)
$$\rho_{\text{nf}} \overline{{u^{\prime}_{\text{j}} u^{\prime}_{\text{i}} \,}}$$

and μt are:

$$- \rho_{\text{nf}} \overline{{u^{\prime}_{\text{i}} u^{\prime}_{\text{j}} }} = \left( {\frac{{\partial u_{\text{i}} }}{{\partial x_{\text{j}} }} + \frac{{\partial u_{\text{j}} }}{{\partial x_{\text{i}} }}} \right)\mu_{\text{t}} - \frac{2}{3}\rho_{\text{nf}} k\delta_{\text{ij}} - \frac{2}{3}\mu_{\text{t}} \frac{{\partial u_{\text{k}} }}{{\partial x_{\text{k}} }}\delta_{\text{ij}}$$
(4)
$$\mu_{\text{t}} = \frac{1}{\varepsilon }k^{2} C_{\upmu} \rho_{\text{nf}}$$
(5)

Due to strong swirling flow, we selected \(k - \varepsilon\) model and checked the limitation of this model. A homogenous model is employed for estimating nanofluid properties:

$$\frac{\partial }{{\partial x_{\text{j}} }}\left( {\left( {\mu_{\text{nf}} + \mu_{\text{t}} /\sigma_{\text{k}} } \right)\frac{\partial k}{{\partial x_{\text{j}} }}} \right) + G_{\text{k}} - \rho_{\text{nf}} \varepsilon = \frac{\partial }{{\partial x_{\text{i}} }}\left( {u_{\text{i}} k\rho_{\text{nf}} } \right),\quad G_{\text{k}} = - \rho_{\text{nf}} \frac{{\partial u_{\text{j}} }}{{\partial x_{\text{i}} }}\overline{{u^{\prime}_{\text{j}} u^{\prime}_{\text{i}} }}$$
(6)
$$\frac{\partial }{{\partial x_{\text{i}} }}\left( {u_{\text{i}} \rho_{\text{nf}} \varepsilon } \right) = \frac{\varepsilon }{k}G_{\text{k}} C_{1\varepsilon } - \rho_{\text{nf}} \frac{{\varepsilon^{2} }}{k}C_{2\varepsilon } + \frac{\partial }{{\partial x_{\text{j}} }}\left( {\left( {\frac{{\mu_{\text{t}} }}{{\sigma_{\varepsilon } }} + \mu_{\text{nf}} } \right)\frac{\partial \varepsilon }{{\partial x_{\text{j}} }}} \right)$$
(7)
$$C_{1\upvarepsilon } = 1.42,\quad C_{\upmu} = 0.0845,\quad C_{2\upvarepsilon } = 1.68,\quad Pr_{\rm{t}} = 0.85,\quad \sigma_{\rm{k}} = 1,\quad \sigma_{\upvarepsilon } = 1.3$$
(8)

ANSYS Fluent has been used for simulation. Pressure-based solver has also been used. We simulate a steady-state form. SIMPLE algorithm was selected for coupling of pressure and velocity. Upwind method was employed for discretization.

\(\rho_{\text{nf}} ,\;\left( {\rho C_{p} } \right)_{\text{nf}} ,\) \(\mu_{n\,f}\) and \(k_{\text{nf}}\)\(\mu_{\text{nf}}\) are [44]:

$$\rho_{\text{nf}} = \rho_{\text{f}} (1 - \phi ) + \rho_{\text{s}} \phi$$
(9)
$$\left( {\rho C_{\text{p}} } \right)_{\text{nf}} = - (\phi - 1)\left( {\rho C_{\text{p}} } \right)_{\text{f}} + \left( {\rho C_{\text{p}} } \right)_{\text{s}} \phi$$
(10)
$$\frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }} = \left[ {Prk_{\text{f}} } \right]^{ - 1} k_{\text{Brownian}} + \left( {1 - \phi } \right)^{ - 2.5}$$
(11)
$$\begin{aligned} \frac{{k_{\text{nf}} }}{{k_{\text{f}} }} & = 1 + 3\frac{{\phi \left( {kk - 1} \right)}}{{ - \phi \left( {kk - 1} \right) + \left( {2 + kk} \right)}} + 5 \times 10^{4} \phi \rho_{\text{f}} c_{\text{p,f}} \sqrt {\frac{{\kappa_{\text{b}} T}}{{\rho_{\text{p}} d_{\text{p}} }}} g^{\prime}(\phi ,d_{\text{p}} ,T) \\ g^{\prime}\left( {\phi ,d_{\text{p}} ,T} \right) & = \left( {a_{2} Ln\left( {d_{\text{p}} } \right) + a_{1} + a_{5} Ln\left( {d_{\text{p}} } \right)^{2} + a_{4} Ln\left( {d_{\text{p}} } \right)Ln\left( \phi \right) + a_{3} Ln\left( \phi \right)} \right)Ln\left( T \right) \\ & \quad + \left( {a_{10} Ln\left( {d_{\text{p}} } \right)^{2} + a_{6} + a_{8} Ln\left( \phi \right) + a_{7} Ln\left( {d_{\text{p}} } \right) + a_{9} Ln\left( {d_{\text{p}} } \right)Ln\left( \phi \right)} \right), \\ kk & = k_{\text{p}} /k_{\text{f}} \\ \end{aligned}$$
(12)

z = 0 and z = L have the following conditions:

$$v_{\text{i}} = 0,\quad w_{\text{i}} = cte,\quad u_{\text{i}} = 0,\quad I = 0.16(Re)^{{\frac{ - 1}{8}}},\quad T_{\text{i}} = cte$$
(13)
$$\frac{{\partial {{u}}}}{{\partial {{z}}}} = \frac{{\partial {{v}}}}{{\partial {{z}}}} = \frac{{\partial {{T}}}}{{\partial {{z}}}} = \frac{{\partial {{w}}}}{{\partial {{z}}}} = 0,$$
(14)

In the current work, the definitions of Nu and f are:

$$Nu = \frac{{hD_{\text{h}} }}{{k_{\text{nf}} }}$$
(15)
$$f = \frac{\Delta p}{{\frac{{\rho v_{\text{m}}^{2} }}{2}\frac{L}{{D_{\text{h}} }}}}$$
(16)

\(S_{\text{gen,th}}\) and \(S_{\text{gen,f}}\) were calculated as:

$$S_{\text{gen,th}} = \frac{{k_{\text{nf}} }}{{T^{2} }}\left[ {\left( {\frac{\partial T}{\partial z}} \right)^{2} + \left( {\frac{\partial T}{\partial y}} \right)^{2} + \left( {\frac{\partial T}{\partial x}} \right)^{2} } \right],$$
(17)
$$S_{\text{gen,f}} = \frac{{\mu_{\text{nf}} }}{T}\left\{ \begin{aligned} \left( {\frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}} \right)^{2} + 2\left[ {\left( {\frac{\partial u}{\partial x}} \right)^{2} + \left( {\frac{\partial w}{\partial z}} \right)^{2} + \left( {\frac{\partial v}{\partial y}} \right)^{2} } \right] \hfill \\ + \left( {\frac{\partial v}{\partial z} + \frac{\partial w}{\partial y}} \right)^{2} + \left( {\frac{\partial u}{\partial z} + \frac{\partial w}{\partial x}} \right)^{2} \hfill \\ \end{aligned} \right\}$$
(18)

Each numerical simulation should have outputs without dependence on mesh. For the current attempt, grid independency analysis has been checked, and we presented an example in Table 3. Also, to satisfy the condition of the chosen turbulent model, Y+ should be lower than 5. We checked this fact, which is presented in Table 4. For verification of the current code, a comparison with a previous article is depicted in Fig. 2 [45]. This figure proves great accuracy of the current code for nanofluid turbulent flow.

Table 3 Example of mesh independency for \(\beta = 90^{ \circ } ,\quad Re = 20000\)
Full size table
Table 4 Ranges of Y+ for outer wall at Re = 20,000
Full size table
Fig. 2
figure 2

Verification of our approach for h(x) [45]

Full size image

Results and discussion

Entropy generation of turbulent nanofluid flow within a duct with innovative swirling inserts was investigated in the current article. A homogenous model was considered. We selected two parameters as variables (inlet velocity and revolution angle). Finding the best performance in view of thermal and second-law behaviors was our main purpose.

Impacts of inlet velocity and \(\beta\) on velocity contours, thermal and viscous entropy generation contours are depicted in Figs. 3–8. As inlet velocity enhances, pressure drop and temperature gradient increase. As inlet velocity increases, a reduction in the thermal boundary layer thickness can be observed, and it makes convective flow stronger. Pressure loss enhances due to a more swirling flow.

Fig. 3
figure 3

Frictional and thermal entropy generation contours at \(\beta = 0^{ \circ } ,\quad Re = 5000\)

Full size image
Fig. 4
figure 4

Frictional, thermal entropy generation and velocity contours at \(\beta = 0^{ \circ } ,\quad Re = 20000\)

Full size image
Fig. 5
figure 5

Frictional and thermal entropy generation contours at \(\beta = 45^{ \circ } ,\quad Re = 5000\)

Full size image
Fig. 6
figure 6

Frictional, thermal entropy generation, and velocity contours at \(\beta = 45^{ \circ } ,\quad Re = 20000\)

Full size image
Fig. 7
figure 7

Frictional and thermal entropy generation contours at \(\beta = 90^{ \circ } ,\quad Re = 5000\)

Full size image
Fig. 8
figure 8

Frictional, thermal entropy generation and velocity contours at \(\beta = 90^{ \circ } ,\quad Re = 20000\)

Full size image

Secondary flow increases with augment of \(\beta\), and in turn convective flow increases. Stronger turbulent intensity occurs for higher values of \(\beta\). So, greater revolution angle makes to reach better nanofluid fluid mixing. The impact of \(\beta\) is more significant at lower inlet velocity because of thicker boundary layer in low Reynolds number. Also, disruption of thermal boundary is more pronounced in lower Re. \(\Delta P\) augments with an increase in \(\beta\) because of intensification in secondary flow.

Viscous entropy generation augments with augment of \(\Delta P\). So, \(S_{\text{gen,f}}\) intensifies with augment of inlet velocity and revolution angle. Thermal entropy generate act against pressure loss. \(S_{\text{gen,th}}\) intensifies with a reduction in \(\beta\) and \(\text{Re}\). The following formulas are derived for \(S_{\text{gen,th}} ,\,Be\) and \(S_{\text{gen,f}}\):

$$S_{\text{gen,th}} = 22.26 - 0.73\beta - 21.62\text{Re}^{*} + 0.64\beta \;\text{Re}^{*} + 0.57\beta^{2}$$
(19)
$$Be = 0.63 - 0.012\beta - 0.35Re^{*} - 0.012\beta \,Re^{*} + 0.012\beta^{2}$$
(20)
$$S_{\text{gen,f}} = 1.4 + 0.049\beta + 1.16\text{Re}^{*} + 0.039\beta \,\text{Re}^{*} - 0.048\beta^{2}$$
(21)

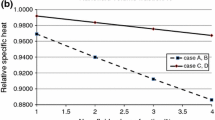
In the above equations, \(Re^{*} = 0.001Re\) and mean square error is 0.98. Figure 9 demonstrates the impacts of \(\beta\) and \(Re\) on entropy parameters. Secondary vortexes become stronger with an increase in both parameters. Therefore, \(S_{\text{gen,th}}\) is an augmenting function of Re and \(\beta\). Roles of significant parameters on \(S_{\text{gen,f}}\) are different from \(S_{\text{gen,th}}\). So, \(S_{\text{gen,th}}\) reduces with augment of Re and \(\beta\). Because of higher values of \(S_{\text{gen,th}}\) in comparison with \(S_{\text{gen,f}}\), it can be concluded that \(Be\) detracts with an increase in Re and \(\beta\).

Fig. 9
figure 9

Effects of Re and \(\beta\) on \(S_{\text{gen,f}} ,S_{\text{gen,th}} ,Be\)

Full size image

Conclusions

In the current article, we simulate nanofluid entropy generation and heat transfer to find the best design for the current heat exchanger. In industries, designers want to reach the highest heat transfer rate and the lowest entropy generation. So, we attempted to show not only the hydrothermal behavior but also frictional and thermal entropy generations. We demonstrated the contours for various cases and extracted new correlations for goal factors. To estimate characteristics of nanofluid, previous experimental formulas have been employed. Results demonstrated that Bejan number reduces with intensification of inlet velocity and revolution angle. Thermal entropy generation reduces with an increase in both variable factors.