An efficient finite element formulation for bending, free vibration and stability analysis of Timoshenko beams

Abstract

In this paper, a new three-node element is proposed for analysis of beams with shear deformation effect. In each node of this element, there exist translation and rotation degrees of freedom. The element’s formulation is based on the first-order shear deformation theory. For this aim, the displacement field of the element is approximated by a fifth-order polynomial. The shear strain is varied as a quadratic function within the element. It is worth noting that the quadratic function can be used for axial displacement field as well. By employing curvature and shear strain relations of Timoshenko beam theory, the exact and explicit shape functions of the displacement fields are obtained. By utilizing these shape functions, the stiffness matrix and the geometric stiffness matrix of the element are calculated. The mass matrices of the proposed element are derived from kinetic energy relation of the beam. Finally, several numerical tests are performed to assess the robustness of the developed element. The results of the numerical tests prove the absence of the shear locking and demonstrate high accuracy and efficiency of the proposed element for bending, free vibration and stability analysis of Timoshenko beams.

1 Introduction

Beams have a wide range of applications in various structures such as buildings and bridges. Two basic theories have been developed for analysis of beams. The Euler–Bernoulli approach neglects shear deformations. This model gives appropriate and acceptable assessments for thin beams, for which shear effects are indeed insignificant. However, as the beam thickness increases the accuracy of the response provided by the Euler–Bernoulli formulation lowers and the obtained results get inadequate. Correspondingly, the effect of shear deformation is formulated in Timoshenko theory. In this approach, the transverse shear strain is assumed to be constant along the thickness. Therefore, this model provides accurate responses for both thin and moderately thick beams.

Up to now, many elements have been proposed based on Timoshenko theory. These elements are classified into two groups which are simple and complex [1,2,3,4]. The simple elements consist of two nodes, and at each node, there are two degrees of freedom [1]. Distinctly, a complex element has more than two degrees of freedom at a node or more than two nodes. The first complex element with eight degrees of freedom was proposed by Kapur [5]. Lees and Thomas introduced a hierarchical Timoshenko beam finite element by assuming separate polynomial series for displacement and shear deformation [6, 7]. By using the concept of hierarchical functions, Tessler and Dong [8] presented conforming Timoshenko beam elements which include the effects of transverse shear deformation and rotary inertia. In the recent years, Falsone and Settineri by developing the Euler–Bernoulli beam theory presented a similar formulation for Timoshenko beams. They obtained a single governing differential equation expressed in terms of deflection for Timoshenko beams. It is important to note that the stiffness matrix for these elements with internal nodes is not symmetric [9]. Bouclier et al. developed a new non-uniform rational B-splines (NURBS) finite element for analysis of straight and curved Timoshenko beam problems. To alleviate shear and membrane locking, they utilized the selective reduced integration to evaluate the terms referring to shear and membrane energies [10]. Similarly, Cazzani et al. [11] developed a plane curved Timoshenko beam element based on NURBS interpolation for both geometry and displacements. Based on mixed finite element formulation, Lepe et al. [12] proposed a locking-free element for Timoshenko beams analysis. For analyzing such geomechanics problems as beam-type structures and deep pile foundations, Caillerie et al. [13] proposed a Timoshenko straight beam element with internal degrees of freedom. By using the flexibility and stiffness methods, Khajavi [14] introduced stiffness matrices for both Euler–Bernoulli and Timoshenko tapered and non-prismatic beams.

Free vibration analysis of shear deformable beams is an important stage for the design of skeletal structures. Dawe [15] presented a three-node element for free vibration of Timoshenko beams. Lee and Schultz [16] applied a pseudospectral method using the Chebyshev polynomials as the basis functions, for free vibration analysis of Timoshenko beams and radially symmetric Mindlin plates. By using Lagrange equations, free vibration analysis of Timoshenko beams with different boundary conditions was performed by Kocatürk and Simsek [17]. Ferreira [18] utilized the multiquadric radial basis function method to analyze free vibrations of Timoshenko beams and Mindlin plates. Also, Ferreira and Fasshauer [19], by combining collocation method, radial basis functions and pseudospectral method, presented a new high accuracy numerical scheme for free vibration analysis of Timoshenko beams with various support conditions. Xu and Wang [20] used discrete singular convolution (DSC) method for analyzing the free vibration of Timoshenko beam with various boundary conditions. Lee and Park [21] introduced an isogeometric approach for free vibration analysis of Timoshenko beams. Moallemi-Oreh and Karkon [22] proposed a two-node beam element with two nodal degrees of freedom at each node for stability and free vibration analysis of Timoshenko beams. Hsu [23] carried out free vibration analysis of Timoshenko beam by improving a simple linear two-node C⁰ element using two different enrichment formulations.

Similar to the free vibration case, buckling analysis of beam-columns is attractive for the researchers due to their wide application in the design of structures. Kosmatka [24], based upon Hamilton’s principle, developed a two-node beam element with four degrees of freedom for stability and free vibration analysis of Timoshenko beams. For stability analysis of deep beams, a one-dimensional higher-order theory has been developed by Matsunaga [25]. Więckowski and Golubiewski [26] by utilizing smoothed functions obtained with the aid of the least square technique improved the accuracy of the finite element method for stability analysis of Euler–Bernoulli and Timoshenko beams. Carrera et al. [27] by employing Carrera unified formulation (CUF) and dynamic stiffness method presented higher-order theories and exact solutions for buckling analysis of beam-columns.

In this article, a new three-node element has been suggested for bending, free vibration and stability analysis of beams based upon the Timoshenko beam theory. The shape functions, the stiffness matrix, the mass matrices and the geometric matrix of the element are explicitly derived. In the following, the accuracy and convergence rate of the presented element is evaluated with several numerical examples and the obtained results are compared with those of other researchers. At first stage, a static analysis of a two-member frame is performed and internal displacements and forces are calculated. In the second stage, the free vibration analyses of Timoshenko beams with different boundary conditions are performed for various values of thickness-to-length ratios. Finally, the stability analysis of simply supported beam is carried out for three different thickness-to-length ratios. The results prove that the suggested element is able to analyze the thick and thin beams with high level of accuracy.

2 Governing equations of Timoshenko beam

The strains and stresses in the Timoshenko beam theory can be written as:

$$\varepsilon = z\frac{{{\text{d}}\theta }}{{{\text{d}}x}},\quad \gamma = \frac{{{\text{d}}w}}{{{\text{d}}x}} - \theta$$

(1)

$$\sigma = E\varepsilon ,\quad \tau = 2G\gamma ,$$

(2)

where w and $\theta$ are transverse displacement and rotation field, respectively. On the other hand, the internal bending moments M and shear forces V are calculated in the following form:

$$M = \int_{A} {z\sigma {\text{d}}A} = EI\frac{{{\text{d}}\theta }}{{{\text{d}}x}}$$

(3)

$$V = k_{\text{s}} \int_{A} {\tau {\text{d}}A} = GAk_{\text{s}} \left( {\frac{{{\text{d}}w}}{{{\text{d}}x}} - \theta } \right),$$

(4)

where $k_{\text{s}}$, G and A denote the shear correction factor, shear modulus and cross-sectional area of beam, respectively. The equilibrium of moments and shear forces are:

$$V\left( x \right) - \frac{{{\text{d}}M}}{{{\text{d}}x}} = 0$$

(5)

$$\frac{{{\text{d}}V}}{{{\text{d}}x}} = - q\left( x \right).$$

(6)

Substituting Eqs. (3) and (4) into Eqs. (5) and (6) transforms the equilibrium equations into:

$$- \frac{\text{d}}{{{\text{d}}x}}\left( {{\text{GA}}k_{\text{s}} \gamma } \right) = q\left( x \right)$$

(7)

$${\text{GA}}k_{s} \gamma - \frac{\text{d}}{{{\text{d}}x}}\left( {{\text{EI}}\frac{{{\text{d}}\theta }}{{{\text{d}}x}}} \right) = 0.$$

(8)

3 Finite element formulation

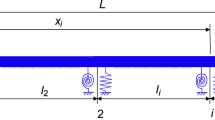
In the finite element method, displacement and rotation fields of the element are related to the nodal degrees of freedom via the shape functions. Figure 1 shows the proposed three-node Timoshenko beam element. In order to compute the shape functions of aforementioned beam element, a fifth-order and a second-order polynomial functions are used for deflection and shear strain field approximations, respectively:

Fig. 1

Three-node Timoshenko beam element

$$w = a_{1} + a_{2} \xi + a_{3} \xi^{2} + a_{4} \xi^{3} + a_{5} \xi^{4} + a_{6} \xi^{5} = \left[ {P_{w} } \right]\left\{ a \right\},\quad \xi = {{2x} \mathord{\left/ {\vphantom {{2x} l}} \right. \kern-0pt} l} - 1$$

(9)

$$\gamma = a_{7} + a_{8} \xi + a_{9} \xi^{2} .$$

(10)

In the FSDT beam theory, the rotation field of the element is calculated as:

$$\theta = \frac{{\text{d}w}}{{\text{d}x}} - \gamma = \frac{2}{l} \cdot \frac{{\text{d}w}}{{\text{d}\xi }} - \gamma .$$

(11)

It is worth emphasizing that the rotation field approximation is of fourth order. According to Eq. (8), the shear strain of the element can be written as follows:

$$\gamma = \lambda l^{2} \cdot \frac{{\text{d}^{2} \theta }}{{\text{d}x^{2} }},\quad \lambda = \frac{{\text{EI}}}{{\text{GA}k_{\text{s}} l^{2} }}.$$

(12)

By equating the shear strain of Eqs. (10) and (12), the unknown parameters $a_{7}$, $a_{8}$ and $a_{9}$ are rendered:

$$a_{7} = - \frac{48}{l}\left( {\lambda a_{4} + 80\lambda^{2} a_{6} } \right)$$

(13)

$$a_{8} = - \frac{192}{l}\lambda a_{5}$$

(14)

$$a_{9} = \frac{ - \,480}{l}\lambda a_{6} .$$

(15)

By substituting the parameters $a_{7}$, $a_{8}$ and $a_{9}$ in relation (11), the rotation field is obtained in the following form:

$$\theta = \frac{1}{l}\left[ {\begin{array}{*{20}c} 0 & 2 & {4\xi } & {6\left( {\xi^{2} + 8\lambda } \right)} & {8\xi \left( {\xi^{2} + 24\lambda } \right)} & {10\left( {\xi^{4} + 48\lambda \xi^{2} + 384\lambda^{2} } \right)} \\ \end{array} } \right]\left\{ a \right\} = \left[ {P_{\theta } } \right]\left\{ a \right\}.$$

(16)

In order to calculate the shape functions of the element, the indirect method is used. In this strategy, the element’s field functions $w$ and $\theta$ and nodal displacement vector $\left\{ D \right\}$ are expressed by the following equations:

$$\left\{ {\begin{array}{*{20}c} w \\ \theta \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\left[ {N_{w} } \right]} \\ {\left[ {N_{\theta } } \right]} \\ \end{array} } \right]\left\{ D \right\} = \left[ N \right]\left\{ D \right\}$$

(17)

$$\left\{ D \right\} = \left[ G \right]\left\{ a \right\}$$

(18)

$$\left\{ D \right\} = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {w_{i} } & {\theta_{i} } & {w_{k} } \\ \end{array} } & {\theta_{k} } & {w_{j} } & {\theta_{j} } \\ \end{array} } \right\}^{T} .$$

(19)

In expression (17), $\left[ {N_{w} } \right]$ and $\left[ {N_{\theta } } \right]$ denote the shape functions of the deflection and rotation field of the element. Also, the square matrix $\left[ G \right]$ in Eq. (18) is dependent on the element geometry, and its rows are formed by substituting the nodes’ coordinates or their derivatives in matrices $\left[ {P_{w} } \right]$ and $\left[ {P_{\theta } } \right]$:

$$\left[ G \right] = \frac{1}{l}\left[ {\begin{array}{*{20}c} l & { - \,l} & l & { - \,l} & l & { - \,l} \\ 0 & 2 & { - \,4} & {6\left( {8\lambda + 1} \right)} & { - 8\left( {24\lambda + 1} \right)} & {10\left( {384\lambda^{2} + 48\lambda + 1} \right)} \\ l & 0 & 0 & 0 & 0 & 0 \\ 0 & 2 & 0 & {48\lambda } & 0 & {3840\lambda^{2} } \\ l & l & l & l & l & l \\ 0 & 2 & 4 & {6\left( {8\lambda + 1} \right)} & {8\left( {24\lambda + 1} \right)} & {10\left( {384\lambda^{2} + 48\lambda + 1} \right)} \\ \end{array} } \right].$$

(20)

On the other hand, the following relation holds for the shape functions $\left[ N \right]$ and the approximants of the element unknowns:

$$\left[ N \right] = \left[ {\begin{array}{*{20}c} {\left[ {N_{w} } \right]} \\ {\left[ {N_{\theta } } \right]} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {P_{w} } \\ {P_{\theta } } \\ \end{array} } \right]\left[ G \right]^{ - 1} .$$

(21)

Therefore, the explicit forms of the deflection shape functions $\left[ {N_{w} } \right]$ can be found:

$$\left[ {N_{w} } \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {N_{1} } & {N_{2} } & {N_{3} } \\ \end{array} } & {N_{4} } & {N_{5} } & {N_{6} } \\ \end{array} } \right]$$

(22)

$$\begin{aligned} N_{1} & = - \frac{2}{\beta }\xi \left( {\xi - 1} \right)\left( {11520\lambda^{2} \xi + 5760\lambda^{2} - 144\lambda \xi^{3} - 24\lambda \xi^{2} + 456\lambda \xi + 120\lambda - 3\xi^{3} - \xi^{2} + 4\xi } \right) \\ N_{2} & = \frac{l}{\beta }\xi \left( {\xi^{2} - 1} \right)\left( {92160\lambda^{3} - 1152\lambda^{2} \xi^{2} + 768\lambda^{2} + 24\lambda \xi^{2} - 60\lambda \xi - 24\lambda + \xi^{2} - \xi } \right) \\ N_{3} & = - \frac{8}{\beta }\left( {60\lambda + 1} \right)\left( {\xi^{2} - 1} \right)\left( { - \xi^{2} + 48\lambda + 1} \right) \\ N_{4} & = - \frac{4l}{\beta }\xi \left( {48\lambda + 1} \right)\left( {\xi^{2} - 1} \right)\left( {960\lambda^{2} - 12\lambda \xi^{2} + 108\lambda - \xi^{2} + 1} \right) \\ N_{5} & = \frac{2}{\beta }\xi \left( {\xi + 1} \right)\left( {11520\lambda^{2} \xi - 5760\lambda^{2} - 144\lambda \xi^{3} + 24\lambda \xi^{2} + 456\lambda \xi - 120\lambda - 3\xi^{3} + \xi^{2} + 4\xi } \right) \\ N_{6} & = \frac{l}{\beta }\xi \left( {\xi^{2} - 1} \right)\left( {92160\lambda^{3} - 1152\lambda^{2} \xi^{2} + 768\lambda^{2} + 24\lambda \xi^{2} + 60\lambda \xi - 24\lambda + \xi^{2} + \xi } \right). \\ \end{aligned}$$

(23)

Parameter $\beta$ in these relations is defined as:

$$\beta = 23040\lambda^{2} + 864\lambda + 8.$$

(24)

Furthermore, the rotation shape functions $\left[ {N_{\theta } } \right]$ of the element are, similarly, obtained as:

$$\left[ {N_{\theta } } \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {N_{7} } & {N_{8} } & {N_{9} } \\ \end{array} } & {N_{10} } & {N_{11} } & {N_{12} } \\ \end{array} } \right]$$

(25)

$$\begin{aligned} N_{7} & = \frac{4}{\beta l}\xi \left( {\xi^{2} - 1} \right)\left( {15\xi - 480\lambda + 720\lambda \xi - 8} \right) \\ N_{8} & = - \frac{2}{\beta }\xi \left( {\xi - 1} \right)\left( {5760\lambda^{2} \xi^{2} + 5760\lambda^{2} \xi - 5760\lambda^{2} - 120\lambda \xi^{2} + 120\lambda \xi + 24\lambda - 5\xi^{2} - \xi + 2} \right) \\ N_{9} & = \frac{64}{\beta l}\xi \left( {60\lambda + 1} \right)\left( {\xi^{2} - 1} \right) \\ N_{10} & = \frac{8}{\beta }\left( {48\lambda + 1} \right)\left( {\xi^{2} - 1} \right)\left( {60\lambda \xi^{2} - 60\lambda + 5\xi^{2} - 1} \right) \\ N_{11} & = - \frac{4}{\beta l}\xi \left( {\xi^{2} - 1} \right)\left( {15\xi + 480\lambda + 720\lambda \xi + 8} \right) \\ N_{12} & = - \frac{2}{\beta }\xi \left( {\xi + 1} \right)\left( {5760\lambda^{2} \xi^{2} - 5760\lambda^{2} \xi - 5760\lambda^{2} - 120\lambda \xi^{2} - 120\lambda \xi + 24\lambda - 5\xi^{2} + \xi + 2} \right). \\ \end{aligned}$$

(26)

To derive the stiffness matrix, the strain matrix is required. The strains of the Timoshenko beam element are given by:

$$\left\{ \varepsilon \right\} = \left\{ {\begin{array}{*{20}l} {\frac{{\text{d}w}}{{\text{d}x}}} \hfill \\ {\frac{{\text{d}w}}{{\text{d}x}} - \theta } \hfill \\ \end{array} } \right\} = \left[ B \right]\left\{ D \right\}$$

(27)

$$\left[ B \right] = \left[ {\begin{array}{*{20}c} 0 & {\frac{\text{d}}{{\text{d}x}}} \\ {\frac{\text{d}}{{\text{d}x}}} & { - 1} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\left[ {N_{w} } \right]} \\ {\left[ {N_{\theta } } \right]} \\ \end{array} } \right],$$

(28)

where $\left[ B \right]$ is the strain matrix. The element stiffness matrix is then calculated as an integral:

$$\left[ {K^{e} } \right] = \int_{l} {\left[ B \right]^{T} \left[ C \right]\left[ B \right]\text{d}x} = \frac{l}{2}\int_{ - 1}^{1} {\left[ B \right]^{T} \left[ C \right]\left[ B \right]\text{d}\xi } .$$

(29)

In the present formula, $\left[ C \right]$ is the elastic rigidity matrix. For Timoshenko beam element, this matrix has the following shape:

$$\left[ C \right] = \left[ {\begin{array}{*{20}c} {\text{EI}} & 0 \\ 0 & {\text{GA}k_{\text{s}} } \\ \end{array} } \right].$$

(30)

By calculating expression (29), the stiffness matrix of the proposed element is:

$$\left[ {K^{e} } \right] = \frac{64}{{35l^{3} \beta^{2} }}\left[ {\begin{array}{*{20}c} {k_{11} } & {k_{12} } & {k_{13} } & {k_{14} } & {k_{15} } & {k_{16} } \\ {k_{12} } & {k_{22} } & {k_{23} } & {k_{24} } & { - k_{16} } & {k_{26} } \\ {k_{13} } & {k_{23} } & {k_{33} } & 0 & {k_{13} } & { - k_{23} } \\ {k_{14} } & {k_{24} } & 0 & {k_{44} } & { - k_{14} } & {k_{24} } \\ {k_{15} } & { - k_{16} } & {k_{13} } & { - k_{14} } & {k_{11} } & { - k_{12} } \\ {k_{16} } & {k_{26} } & { - k_{23} } & {k_{24} } & { - k_{12} } & {k_{22} } \\ \end{array} } \right].$$

(31)

The entries of this matrix are given in “Appendix,” see expressions (45). Note that the proposed element is free of shear locking. For thin beams, parameter $\lambda$ will be very small and, therefore, the presented shape functions and stiffness matrix degenerate to the shape functions and stiffness matrix of three-node Euler–Bernoulli element, which can be found in references [28,29,30]. Also, the nodal force vector of the element is obtained:

$$\left[ {F^{e} } \right] = \int_{l} {q\left[ {N_{w} } \right]^{T} \text{d}x} ,$$

(32)

where q is the load distributed along the element.

4 Mass matrix

The kinetic energy of a Timoshenko beam, including the effects of shear deformation and rotary inertia, can be written as:

$$T = \int_{l} {\rho A\dot{w}^{2} \text{d}x} + \int_{l} {\rho I\dot{\theta }^{2} \text{d}x} ,$$

(33)

where the dot denotes the time derivative. Moreover,$\rho$, A and I are the mass density of the material, area of the cross section and the second moment of area, respectively. By substituting Eq. (21) into (33) and applying Lagrange’s principle, one may arrive to an expression for the mass matrix:

$$\left[ {M^{e} } \right] = \left[ {M_{1}^{e} } \right] + \left[ {M_{2}^{e} } \right] = \frac{l}{2}\int_{ - 1}^{1} {\rho A\left[ {N_{w} } \right]}^{T} \left[ {N_{w} } \right]\text{d}\xi + \frac{l}{2}\int_{ - 1}^{1} {\rho I\left[ {N_{\theta } } \right]^{T} \left[ {N_{\theta } } \right]^{T} } \text{d}\xi ,$$

(34)

where the first term is associated with the translational inertia mass matrix and the second part is associated with the rotary inertia mass matrix. The translation mass matrix $\left[ {M_{1}^{e} } \right]$ is given by:

$$\left[ {M_{1}^{e} } \right] = \frac{64\rho A}{{3465\beta^{2} }}\left[ {\begin{array}{*{20}c} {m_{11} } & {m_{12} } & {m_{13} } & {m_{14} } & {m_{15} } & {m_{16} } \\ {m_{12} } & {m_{17} } & {m_{18} } & {m_{19} } & { - m_{16} } & {m_{110} } \\ {m_{13} } & {m_{18} } & {m_{111} } & 0 & {m_{13} } & { - m_{18} } \\ {m_{14} } & {m_{19} } & 0 & {m_{112} } & { - m_{14} } & {m_{19} } \\ {m_{15} } & { - m_{16} } & {m_{13} } & { - m_{14} } & {m_{11} } & { - m_{12} } \\ {m_{16} } & {m_{110} } & { - m_{18} } & {m_{19} } & { - m_{12} } & {m_{17} } \\ \end{array} } \right].$$

(35)

In addition, the explicit form of the rotary mass matrix $\left[ {M_{2}^{e} } \right]$ can be expressed as:

$$\left[ {M_{2}^{e} } \right] = \frac{32\rho I}{{315\beta^{2} }}\left[ {\begin{array}{*{20}c} {m_{21} } & {m_{22} } & {m_{23} } & {m_{24} } & {m_{25} } & {m_{26} } \\ {m_{22} } & {m_{27} } & {m_{28} } & {m_{29} } & { - m_{26} } & {m_{210} } \\ {m_{23} } & {m_{28} } & {m_{211} } & 0 & {m_{23} } & { - m_{28} } \\ {m_{24} } & {m_{29} } & 0 & {m_{212} } & { - m_{24} } & {m_{29} } \\ {m_{25} } & { - m_{26} } & {m_{23} } & { - m_{24} } & {m_{21} } & { - m_{22} } \\ {m_{26} } & {m_{210} } & { - m_{28} } & {m_{29} } & { - m_{22} } & {m_{27} } \\ \end{array} } \right].$$

(36)

The nonzero entries of the mass matrices $\left[ {M_{1}^{e} } \right]$ and $\left[ {M_{2}^{e} } \right]$ are given in formulas (46) and (47) of “Appendix.” It is well known that the equation of free vibration can be expressed as follows:

$$\left( {\left[ K \right] - \omega_{n}^{2} \left[ M \right]} \right)\left\{ {\phi_{n} } \right\} = 0,$$

(37)

where $\omega_{n}$ and $\phi_{n}$ represent the natural frequency and the mode shape associated with the nth mode. Also, $\left[ K \right]$ and $\left[ M \right]$ are the stiffness matrix and mass matrix of the whole structure, respectively.

5 Geometric stiffness matrix

The concept of the neutral state of equilibrium is used for buckling analysis of beam. As a result, the strain energy associated with axial load P can be expressed as follows:

$$\Delta W = \frac{P}{2}\int_{0}^{l} {\left( {\frac{{\text{d}y}}{{\text{d}x}}} \right)^{2} \text{d}x} .$$

(38)

Therefore, the element geometric stiffness matrix of the proposed element can be calculated as [31]:

$$\left[ {K_{g}^{e} } \right] = \int_{l} {\left[ {\frac{{\text{d}N_{w} }}{{\text{d}x}}} \right]^{T} P\left[ {\frac{{\text{d}N_{w} }}{{\text{d}x}}} \right]} \text{d}x$$

(39)

whose explicit form is:

$$\left[ {K_{g} } \right] = \frac{32}{{315\beta^{2} }}\left[ {\begin{array}{*{20}c} {k_{g1} } & {k_{g2} } & {k_{g3} } & {k_{g4} } & {k_{g5} } & {k_{g6} } \\ {k_{g2} } & {k_{g7} } & {k_{g8} } & {k_{g9} } & { - k_{g6} } & {k_{g10} } \\ {k_{g3} } & {k_{g8} } & {k_{g11} } & 0 & {k_{g3} } & { - k_{g8} } \\ {k_{g4} } & {k_{g9} } & 0 & {k_{g12} } & { - k_{g4} } & {k_{g9} } \\ {k_{g5} } & { - k_{g6} } & {k_{g3} } & { - k_{g4} } & {k_{g1} } & { - k_{g2} } \\ {k_{g6} } & {k_{g10} } & { - k_{g8} } & {k_{g9} } & { - k_{g2} } & {k_{g8} } \\ \end{array} } \right].$$

(40)

The entries of this matrix are given in “Appendix,” see expression (48). The equation of stability analysis can be expressed as:

$$\left( {\left[ K \right] - P_{{\text{cr},i}} \left[ {K_{g} } \right]} \right)\left\{ \varphi \right\} = 0\,.$$

(41)

Similar to free vibration analysis, $P_{{\text{cr},i}}$ and $\varphi$ represent the critical load and mode shape associated with the ith mode. Also, $\left[ K \right]$ and $\left[ {K_{g} } \right]$ are the stiffness matrix and the geometric stiffness matrix of the whole structure, respectively. The exact value of the beam-column buckling load with shear deformation effect can be written as [32]:

$$P_{{\text{cr},i}} = \frac{{\pi^{2} \text{EI}}}{{L_{{\text{eff}}}^{2} }}\left( {\frac{{\left( {L_{{\text{eff}}} i} \right)^{2} \text{GA}k_{\text{s}} }}{{L_{{\text{eff}}}^{2} \text{GA}k_{\text{s}} + \left( {\pi i} \right)^{2} \text{EI}}}} \right),$$

(42)

where $L_{{\text{eff}}}$ is the effective beam length and i indicates the mode number.

6 Numerical examples

In order to assess the accuracy of the proposed element, some numerical problems have been analyzed and the results are compared with the data available in the literature. At first, static analysis of a two-member plane frame is performed. In subsection 6.2, free vibration analysis of beams with different boundary conditions is considered. Finally, buckling analysis of simply supported beam is carried out for three thickness-to-length ratios.

6.1 Static analysis of a frame

In order to reveal the accuracy and robustness of the proposed element in static analysis, a two-member plane frame is considered. The frame geometry and its loading are shown in Fig. 2. It should be mentioned that the second-order polynomial function is used for the axial displacement approximation. The size of parameter a appearing in this figure is given equal to $a = 1\,\text{m}$. The material properties of the members are given as: Young’s modulus $E = 25 \times 10^{9} \,\text{N}/\text{m}^{2}$ and Poisson’s ratio $\nu = 0.25$. Moreover, the axial and bending stiffnesses of the vertical member of the frame are considered as $\text{EA} = 3 \times 10^{9} \,\text{N}$ and $\text{EI} = 4 \times 10^{7} \,\text{Nm}^{2}$, respectively. These quantities for the angled member are assumed to be $\text{EA} = 7.8125 \times 10^{9} \,\text{N}$ and $\text{EI} = 3.75 \times 10^{7} \,\text{Nm}^{2}$. Note that the shear correction coefficient for the Timoshenko beam element is taken to be $k_{\text{s}} = 5/6$. As shown in Fig. 2, the vertical member is loaded by a triangular distributed load, with maximum value $q = 30\,\text{kN/m}$. Additionally, two concentrated loads $P = 20\,\text{kN}$ are applied as: a horizontal force at the node 3 and a vertical force at the node 4. The structure is analyzed by using a single element of the proposed type for each member.

Fig. 2

Geometry and loading of plane frame

The diagrams of the displacements, rotations, internal moment and shear force along the vertical member are plotted in Figs. 3, 4, 5 and 6, respectively. The results obtained with the proposed element are compared with those of reduced integration element (RIE) [3], two-node interdependent interpolation element (IIE) [3], Falsone and Settineri three-node element [9] and exact solution. These figures reveal that the proposed element gives the exact solution in all the cases. It should be mentioned that the exact solution of this problem is a polynomial of fifth order and thus a single element per each member of the frame is sufficient to capture it.

Fig. 3

Transverse deflection along the vertical member

Fig. 4

Rotation along the vertical member

Fig. 5

Internal bending moment along vertical member

Fig. 6

Internal shear force along vertical member

6.2 Free vibration analysis

In order to assess the accuracy of the proposed element for free vibration analysis of shear deformable beams, four types of beams—simply supported (SS) beam, clamped–clamped (CC) beam, free–free (FF) beam and clamped-free beam (CF)—are analyzed and the results are compared with the references available in the literatures. For convenience, the following non-dimensional natural frequencies are introduced:

$$\lambda_{i}^{2} = \omega_{i} l^{2} \sqrt {\frac{\rho A}{{\text{EI}}}} .$$

(43)

To investigate the effect of the number of elements, at first, the free vibration behavior of a simply supported thin beam $\left( {{t \mathord{\left/ {\vphantom {t l}} \right. \kern-0pt} l} = 0.002} \right)$ is analyzed, and first fifteen non-dimensional frequency parameters are obtained. The results of the proposed element are compared with those of Lee and Schultz [16], Ferreira [18], Hsu [23] and Euler–Bernoulli beam theory solution (EBT). Table 1 reveals that the proposed element has high accuracy and a rapid rate of convergence. So that, by using the 32 proposed elements, the results of all fifteen frequencies will be converged. Figure 7 shows the reduction in the relative error for the first 8 frequencies of the simply supported thin beam with ${t \mathord{\left/ {\vphantom {t l}} \right. \kern-0pt} l} = 0.002$. The corresponding mode shapes are shown in Fig. 8.

Table 1 Non-dimensional frequency parameter $\lambda_{i}$ of the SS thin beam $\left( {{t \mathord{\left/ {\vphantom {t l}} \right. \kern-0pt} l} = 0.002} \right)$ for different meshes

Fig. 7

Error percentage for the first 8 frequencies of the SS beam

Fig. 8

First 8 mode shapes of the SS beam

In the following examples, frequencies of Timoshenko beams with different boundary conditions and aspect ratios $\left( {{t \mathord{\left/ {\vphantom {t l}} \right. \kern-0pt} l}} \right)$ are obtained, by utilizing meshes of 32 and 64 elements. The findings are compared with published results of the other researchers. The first fifteen non-dimensional frequency parameters of the SS beam are listed in Table 2. Furthermore, Table 3 lists these parameters for CC beam. The results of the FF beam and the CF beam are presented in Tables 4 and 5, respectively. These tables demonstrate that the proposed element has high accuracy, and the rate of convergence is quite independent of the boundary conditions. It is also observed that the thickness-to-length ratio does not have influence on the convergent rate, and the suggested element is free from the shear locking effect.

Table 2 Non-dimensional frequency parameter $\lambda_{i}$ of the SS Timoshenko beam with different thickness-to-length ratios

Table 3 Non-dimensional frequency parameter $\lambda_{i}$ of the CC Timoshenko beam with different thickness-to-length ratios

Table 4 Non-dimensional frequency parameter $\lambda_{i}$ of the FF Timoshenko beam with different thickness-to-length ratios

Table 5 Non-dimensional frequency parameter $\lambda_{i}$ of the CF Timoshenko beam with different thickness-to-length ratios

6.3 Stability analysis

In this section, the robustness of the proposed element for buckling analysis of shear deformable beams is evaluated. For this aim, a simply supported beam-column (SS) with three thickness-to-length ratios is analyzed and the first five buckling loads are obtained. For simplicity, the critical loads are given in non-dimensional form as follows:

$$\bar{P}_{{\text{cr},i}} = P_{{\text{cr},i}} \times \frac{{l^{2} }}{{\pi^{2} \text{EI}}}.$$

(44)

The results obtained using the proposed element are compared with those of Matsunaga [25], Carrera [27], the Euler–Bernoulli beam theory solution (EBT) and the Timoshenko beam theory solution (TBT) in Table 6. The data listed in this table confirm the element’s high accuracy and rapid convergence. Moreover, it is obvious that the obtained results converge to the TBT solution as the number of elements increases.

Table 6 Non-dimensional critical buckling loads $\bar{P}_{{\text{cr},i}}$ of the SS Timoshenko beam with different thickness-to-length ratios

7 Conclusion

In this study, a highly efficient three-node element was proposed for static, free vibration and buckling analysis of beams, based on the Timoshenko beam theory. For element formulation, deflection and shear strain fields’ approximants are chosen of fifth and second orders, respectively. By employing these fields and classical finite element method relations, the shape functions of the proposed element were calculated in the explicit form. Then, by utilizing these shape functions, the stiffness matrix, the geometric stiffness matrix and the mass matrices of the element were explicitly derived. Finally, the extensive numerical testing was performed to assess the accuracy and efficiency of the author’s formulation. The results reveal that the suggested three-node element has a very high accuracy and convergence rate for static, free vibration and buckling analysis of thick and thin beams. Moreover, the numerical experiments prove that the element is free of shear locking for extremely thin beams. In conclusion, the solution accuracies of the famous benchmark problems provide the justification of the suggested element.

Appendix

The nonzero entries of the stiffness matrix $\left[ {K^{e} } \right]$ is:

$$\begin{aligned} k_{11} & = 4\text{EI}\left( {401587200\lambda^{3} + 19440000\lambda^{2} + 292140\lambda + 1273} \right) \\ k_{12} & = 2\text{EI}l\left( { - 1857945600\lambda^{4} + 76723200\lambda^{3} + 6814080\lambda^{2} + 119340\lambda + 569} \right) \\ k_{13} & = - 3584\text{EI}\left( {60\lambda + 1} \right)^{3} \\ k_{14} & = 1920\text{EI}l\left( {48\lambda + 1} \right)^{2} \left( {1680\lambda^{2} + 180\lambda + 1} \right) \\ k_{15} & = - 4\text{EI}\left( {208051200\lambda^{3} + 9763200\lambda^{2} + 130860\lambda + 377} \right) \\ k_{16} & = 2\text{EI}l\left( { - 1857945600\lambda^{4} - 20044800\lambda^{3} + 1975680\lambda^{2} + 38700\lambda + 121} \right) \\ k_{22} & = 4\text{EI}l^{2} \left( {3715891200\lambda^{5} + 6220800\lambda^{4} + 15949440\lambda^{3} + 967980\lambda^{2} + 16605\lambda + 83} \right) \\ k_{23} & = - 896\text{EI}l\left( {60\lambda + 1} \right)^{3} \\ k_{24} & = 320\text{EI}l^{2} \left( {48\lambda + 1} \right)^{2} \left( { - 40320\lambda^{3} - 2640\lambda^{2} + 156\lambda + 1} \right) \\ k_{26} & = 2\text{EI}l^{2} \left( {7431782400\lambda^{5} - 277862400\lambda^{4} - 14065920\lambda^{3} + 116520\lambda^{2} + 5490\lambda + 19} \right) \\ k_{33} & = 7168\text{EI}\left( {60\lambda + 1} \right)^{3} \\ k_{44} & = 1280\text{EI}l^{2} \left( {48\lambda + 1} \right)^{2} \left( {20160\lambda^{3} + 3840\lambda^{2} + 192\lambda + 1} \right). \\ \end{aligned}$$

(45)

The nonzero entries of the translation mass matrix $\left[ {M_{1}^{e} } \right]$ is:

$$\begin{aligned} m_{11} & = l\left( {2189721600\lambda^{4} + 179055360\lambda^{3} + 5828688\lambda^{2} + 88554\lambda + 523} \right) \\ m_{12} & = \frac{3}{2}l^{2} \left( { - 729907200\lambda^{5} + 36495360\lambda^{4} + 2871360\lambda^{3} + 93060\lambda^{2} + 2061\lambda + 19} \right) \\ m_{13} & = 44l\left( {60\lambda + 1} \right)^{2} \left( {12096\lambda^{2} + 540\lambda + 5} \right) \\ m_{14} & = - 40l^{2} \left( {48\lambda + 1} \right)^{2} \left( { - 23760\lambda^{3} - 792\lambda^{2} + 177\lambda + 1} \right) \\ m_{15} & = \frac{1}{2}l\left( {1368576000\lambda^{4} + 141419520\lambda^{3} + 4440816\lambda^{2} + 49668\lambda + 131} \right) \\ m_{16} & = - \frac{1}{4}l^{2} \left( {4379443200\lambda^{5} - 218972160\lambda^{4} - 120960\lambda^{3} + 526680\lambda^{2} + 9546\lambda + 29} \right) \\ m_{17} & = l^{3} \left( {35035545600\lambda^{6} + 291962880\lambda^{5} - 11335680\lambda^{4} + 193536\lambda^{3} + 6774\lambda^{2} + 129\lambda + 2} \right) \\ m_{18} & = 22l^{2} \left( {60\lambda + 1} \right)^{2} \left( {72\lambda + 1} \right) \\ m_{19} & = - 3l^{3} \left( {48\lambda + 1} \right)^{2} \left( {10137600\lambda^{4} + 929280\lambda^{3} - 9440\lambda^{2} + 76\lambda + 1} \right) \\ m_{110} & = \frac{3}{4}l^{3} \left( {46714060800\lambda^{6} + 389283840\lambda^{5} - 15114240\lambda^{4} + 258048\lambda^{3} - 4168\lambda^{2} - 268\lambda - 1} \right) \\ m_{111} & = 1408l\left( {60\lambda + 1} \right)^{2} \left( {3024\lambda^{2} + 108\lambda + 1} \right) \\ m_{112} & = 32l^{3} \left( {48\lambda + 1} \right)^{2} \left( {1900800\lambda^{4} + 411840\lambda^{3} + 24960\lambda^{2} + 288\lambda + 1} \right). \\ \end{aligned}$$

(46)

The nonzero entries of the rotary mass matrix $\left[ {M_{2}^{e} } \right]$ is:

$$\begin{aligned} m_{21} &= \frac{12}{l}\left( {403200\lambda^{2} + 14880\lambda + 139} \right) \hfill \\ m_{22} & = - \left( {55987200\lambda^{3} + 1969920\lambda^{2} + 15444\lambda - 39} \right) \hfill \\ m_{23} &= - \frac{1536}{l}\left( {60\lambda + 1} \right)^{2} \hfill \\ m_{24} &= - 240\left( {48\lambda + 1} \right)^{2} \left( {60\lambda - 1} \right) \hfill \\ m_{25} &= \frac{12}{l}\left( {57600\lambda^{2} + 480\lambda - 11} \right) \hfill \\ m_{26} &= - \left( { - 2073600\lambda^{3} + 207360\lambda^{2} + 5076\lambda + 9} \right) \hfill \\ m_{27} &= 4l\left( {219801600\lambda^{4} + 9711360\lambda^{3} + 153144\lambda^{2} + 1263\lambda + 7} \right) \hfill \\ m_{28} &= 48\left( {60\lambda + 1} \right)^{2} \left( {336\lambda - 1} \right) \hfill \\ m_{29} &= - 8l\left( {48\lambda + 1} \right)^{2} \left( { - 18000\lambda^{2} + 600\lambda + 1} \right) \hfill \\ m_{210} &= l\left( {8294400\lambda^{4} + 2557440\lambda^{3} + 9936\lambda^{2} - 924\lambda - 5} \right) \hfill \\ m_{211} &= \frac{3072}{l}\left( {60\lambda + 1} \right)^{2} \hfill \\ m_{212} &= 256l\left( {48\lambda + 1} \right)^{2} \left( {3600\lambda^{2} + 60\lambda + 1} \right). \hfill \\ \end{aligned}$$

(47)

The nonzero entries of the geometric stiffness matrix $\left[ {K_{g} } \right]$ is:

$$\begin{aligned} k_{g1} & = \frac{12}{l}\left( {2409523200\lambda^{4} + 137721600\lambda^{3} + 2953800\lambda^{2} + 30156\lambda + 139} \right) \\ k_{g2} & = - 3\left( {22295347200\lambda^{5} + 597196800\lambda^{4} + 2695680\lambda^{3} + 80640\lambda^{2} + 1152\lambda - 13} \right) \\ k_{g3} & = - \frac{1536}{l}\left( {60\lambda + 1} \right)^{2} \left( {2520\lambda^{2} + 84\lambda + 1} \right) \\ k_{g4} & = 240\left( {48\lambda + 1} \right)^{2} \left( {241920\lambda^{3} + 26640\lambda^{2} + 228\lambda + 1} \right) \\ k_{g5} & = - \frac{12}{l}\left( {1248307200\lambda^{4} + 60307200\lambda^{3} + 880200\lambda^{2} + 4044\lambda + 11} \right) \\ k_{g6} & = - 9\left( {7431782400\lambda^{5} + 199065600\lambda^{4} - 714240\lambda^{3} - 7680\lambda^{2} + 576\lambda + 1} \right) \\ k_{g7} & = 4l\left( {66886041600\lambda^{6} + 398131200\lambda^{5} - 17418240\lambda^{4} + 483840\lambda^{3} + 15174\lambda^{2} + 471\lambda + 7} \right) \\ k_{g8} & = 48\left( {60\lambda + 1} \right)^{2} \left( {84\lambda - 1} \right) \\ k_{g9} & = - 8l\left( {48\lambda + 1} \right)^{2} \left( {29030400\lambda^{4} + 2592000\lambda^{3} - 30960\lambda^{2} + 420\lambda + 1} \right) \\ k_{g10} & = l\left( {267544166400\lambda^{6} + 1592524800\lambda^{5} - 69672960\lambda^{4} + 1935360\lambda^{3} - 55944\lambda^{2} - 2076\lambda - 5} \right) \\ k_{g11} & = \frac{3072}{l}\left( {60\lambda + 1} \right)^{2} \left( {2520\lambda^{2} + 84\lambda + 1} \right) \\ k_{g12} & = 256l\left( {48\lambda + 1} \right)^{2} \left( {1814400\lambda^{4} + 388800\lambda^{3} + 23040\lambda^{2} + 240\lambda + 1} \right). \\ \end{aligned}$$

(48)