1 Introduction

Of late, the studies of flow and heat transfer for Newtonian and non-Newtonian fluids inside thin films associated with a stretching surface are important for their theoretical and technical importance in fields of engineering, manufacturing operations, and technology. Some applications include design of heat exchangers and chemical reaction equipments, wire and fiber coatings, reactor fluidization, polymer processes, transpiration cooling, food stuff processing, etc. Many metallurgical processes, such as drawing, annealing, and strips of filaments, are done by drawing them through a quiescent fluid. So, the study of the fluid flow and heat transfer characteristics due to stretching surface has an immense attention from many researchers owing to its importance in many fields of industrial, technological, and engineering applications. For example, in a template of polymer sheet when it is in the case of solutions, at this case, the sheet is sometimes stretched. During this process, the properties of the final product may depend on both the rate of cooling and the rate of stretching by drawing such sheet through a cooling system. Since the pioneer study of Crane [1] who was believed to be the first to examine analytically the problem of flow and heat transfer characteristics for a steady, two-dimensional semi-infinite fluid layer driven by a continuous moving sheet with a velocity linearly proportional to the distance from a fixed point. Taking into account the Crane’s problem [1], various aspects of the accompanying heat transfer characteristics which occurs in the infinite fluid medium surrounding the stretching sheet have been studied by Gupta and Gupta [2]. In the same context, Grubka and Bobba [3] have examined the variable surface temperature effects on a stretching surface which moving with a linear velocity. Wang [4] initiated the hydrodynamic flow problem of a finite fluid layer over an unsteady stretching sheet with a specific type of velocity that allowed similarity analysis, and his similarity solution was found to satisfy the full Navier-Stokes equations as well as the boundary layer equations. Usha and Sridharan [5] studied the axisymmetric motion for a fluid which caused due to an unsteady stretching surface. The hydrodynamic flow problem of Wang [4] was investigated by Dandapat et al. [6] including the heat transfer and the thermocapillarity effect, by Wang [7] for viscous fluids, by Wang and Pop [8] for power-law fluids, by Hayat et al. [9] for MHD second grade fluids, and by Elgazery and Hassan [10] for viscous fluids through porous media. Recently, Santra and Dandapat [11] have examined the problem of flow and heat transfer which can be observed in a thin viscous liquid film owing to heated horizontal unsteady stretching surface. Abel et al. [12, 13] investigated the influence of viscous dissipation and non-uniform heat source on MHD fluid film over an unsteady stretching surface. Very recently, Mahmoud and Megahed [14] studied the effects of variable thermal conductivity and variable viscosity which assumed to be a function of temperature on the flow and the process of heat transfer for an electrically conducting non-Newtonian power-law fluid within a thin liquid film due to an unsteady stretching sheet taking into account a transverse magnetic field. Furthermore, Liu et. al [15] investigated numerically the effects of thermal radiation on the heat transfer characteristics of a viscous liquid film flow over an unsteady stretching sheet subject to variable heat flux. Until now, little interest can be observed through a literature review for the flow of non-Newtonian Eyring Powell fluid within thin liquid film layer in spite of its certain advantages over the other non-Newtonian fluid models. Some of this advantages may appear for this model in which it can approach to Newtonian behavior at low and high shear rates. Regarding the study of Powell-Eyring on fluid flow and heat transfer, some former attentions have been made in the studies [16–19]. In the same context, Patel and Timol [20] numerically examined the flow of Powell-Eyring model past a wedge. The problem of slider bearing lubricated with Eyring Powell model is presented numerically using Homotopy perturbation analysis by Islam et al. [21]. Very recently, the flow and heat transfer of Powell-Eyring fluid over a continuously moving surface in the presence of a free stream velocity is investigated by Hayat et al. [22].

All the studies mentioned above assumed that there is no effects for the slip velocity and non-uniform heat generation or absorption on the flow and heat transfer for a non-Newtonian Powell-Eyring thin film fluid due to an unsteady stretching sheet, and thus how to find the local skin-friction coefficient and the heat transfer rate between the stretching surface and the fluid in which of course an important issue in engineering applications. It is important to determine the extent to which the slip velocity will affect the film thickness response. Motivated by the literature above, the purpose of the present work is to study the effects of slip velocity and non-uniform heat generation/absorption on the flow and heat transfer of a non-Newtonian Powell-Eyring thin film fluid owing to a stretching sheet. To achieve this study, we use the well-known numerical technique, shooting method.

2 Formulation of the problem

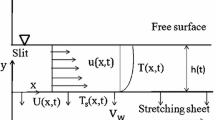
In this section, we will describe the proposed physical problem by considering a non-Newtonian Powell-Eyring fluid flow within a thin film with uniform thickness h(t) due to an unsteady stretching sheet. The x-axis is chosen along the plane of the sheet and the y-axis is taken normal to the plane. The continuous surface aligned with the x−axis at y = 0 moves in its own plane with a velocity U(x, t) and temperature distribution T s (x, t), see Fig. 1. Furthermore, the expression of stress tensor in the Powell-Eyring fluid can be expressed as [17]:

$$\tau_{ij}=\mu\frac{\partial u_{i}}{\partial x_{j}} +\frac{1}{\tilde{\beta}}{\sinh}^{-1}\left( \frac{1}{C}\frac{\partial u_{i}}{\partial x_{j}}\right), $$
(1)

where μ is the viscosity coefficient, \(\tilde {\beta }\) and C are the characteristics of non-Newtonian Powell-Eyring model with dimension m s2 kg−1 and s−1 respectively. Here, it must be mentioned that, to reduce the complexity of the second part of (1), we will consider that \({\sinh }^{-1}\left (\frac {1}{C}\frac {\partial u_{i}}{\partial x_{j}}\right )\cong \frac {1}{C}\frac {\partial u_{i}}{\partial x_{j}}-\frac {1}{6}\left (\frac {1}{C}\frac {\partial u_{i}}{\partial x_{j}}\right )^{3}\), \(|\frac {1}{C}\frac {\partial u_{i}}{\partial x_{j}}|\leq 1\).

Fig. 1
figure 1

Schematic of the physical system

Full size image

The basic equations for mass, momentum, and energy for the proposed model can be written as:

$$\begin{array}{@{}rcl@{}} \frac{\partial u}{\partial x}&\!\,+\,\!&\frac{\partial v}{\partial y}=0, \end{array} $$
(2)
$$\begin{array}{@{}rcl@{}} \frac{\partial u}{\partial t}&\!\,+\,\!&u\frac{\partial u}{\partial x}\,+\,v\frac{\partial u}{\partial y}\,=\,\frac{1}{\rho}\frac{\partial }{\partial y}\!\left( \!\mu\frac{\partial u}{\partial y}\,+\, \frac{1}{\tilde{\beta}C}\frac{\partial u}{\partial y}\,-\,\frac{1}{6\tilde{\beta}C^{3}} (\frac{\partial u}{\partial y})^{3}\!\right),\\ \end{array} $$
(3)
$$\begin{array}{@{}rcl@{}} \frac{\partial T}{\partial t}&\!\,+\,\!&u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{\kappa}{\rho c_{p}}\left( \frac{\partial^{2} T}{\partial y^{2}}\right)+\frac{q^{\prime\prime\prime}}{\rho c_{p}}, \end{array} $$
(4)

where u and v are the velocity components along x and y directions, respectively. ρ is the density for the non-Newtonian fluid, T is the temperature of the fluid, t is the time, κ is the thermal conductivity, c p is the specific heat at constant pressure, and q ″′ is the rate of the internal heat generation. The internal heat generation or absorption term q ″′ is modeled according to the following equation [13–23] and [24]:

$$ q^{\prime\prime\prime}={(\frac{\kappa Re_{x}}{x^{2}})}[a^{*}(T_{s}-T_{0})e^{-\eta}+b^{*}(T-T_{0})], $$
(5)

where \(Re_{x}=\frac {\rho U x}{\mu }\) is the local Reynolds number, T s is the surface temperature, and T 0 is the temperature at the slit. In (9), we must refer that the first part corresponds to the dependence of the internal heat generation or absorption on the space coordinates while the last part of the same equation represents its dependence on the temperature, so a ∗ is the pace-dependent heat source/sink parameter and b ∗ is the temperatures-dependent heat source/sink parameter. Here, we must mention that when both a ∗ > 0 and b ∗ > 0, the case will be internal heat generation while it will be internal heat absorption when both a ∗ < 0 and b ∗ < 0. The associated boundary conditions for the present problem are given by:

$$\begin{array}{@{}rcl@{}} u&=& U+ \gamma_{1}\left( \frac{\partial u}{\partial y}+ \frac{1}{\mu\tilde{\beta}C }\frac{\partial u}{\partial y}-\frac{1}{6\mu\tilde{\beta}C^{3}} (\frac{\partial u}{\partial y})^{3}\right),\\ v&=&0, T=T_{s}, \text{ at } y=0, \end{array} $$
(6)
$$\begin{array}{@{}rcl@{}} \left( \frac{\partial u}{\partial y}+ \frac{1}{\mu\tilde{\beta}C }\frac{\partial u}{\partial y}-\frac{1}{6\mu\tilde{\beta}C^{3}} (\frac{\partial u}{\partial y})^{3}\right)&=&0,\\ \frac{\partial T}{\partial y}&=&0,\quad at~y=h, \end{array} $$
(7)
$$\begin{array}{@{}rcl@{}} v=\frac{dh}{dt} ,\quad at \hspace{0.2 cm} y=h, \end{array} $$
(8)

where γ 1 is the slip factor which can be assumed as \(\gamma _{1}=\gamma \sqrt {1-a t}\); here, γ is the slip coefficient having dimension of length. It is worth reminding that the first part of (7) satisfy that the viscous shear stress vanish at the free surface. Also, the second part of the same equation reflect the absence of heat flux at the adiabatic free surface (y = h). The flow is caused by stretching the elastic surface at y = 0 such that the continuous sheet moves in the x-direction with the velocity:

$$ U=\frac{bx}{1-at}, $$
(9)

where a and b are positive constants with dimension (time −1), likewise, we must observe that our problem is valid only for a t < 1. The mathematical analysis of the problem is simplified by introducing the following dimensionless coordinates [13]:

$$ \eta=(\frac{b}{(\mu/\rho)})^{\frac{1}{2}}(1-at)^{\frac{-1}{2}} y, $$
(10)
$$ \psi=(\frac{\mu b}{\rho})^{\frac{1}{2}}(1-at)^{\frac{-1}{2}}x f(\eta), $$
(11)
$$ T=T_{0}-T_{ref}(\frac{d x^{2}}{(\mu/ \rho)})(1-at)^{-3/2} \theta(\eta), $$
(12)

where ψ is the stream function which automatically assures continuity (2) with \(u=\frac {\partial \psi }{\partial y}\) and \(v=-\frac {\partial \psi }{\partial x}\), d is a constant having a dimension of t −1, η is the dimensionless variable, 𝜃 is the dimensionless temperature of the fluid, and T r e f can be taken as a constant reference temperature such that 0 ≤ T r e f ≤ T 0.

Also, the surface temperature T s of the stretching sheet which varies with x and t can be written in the following form :

$$ T_{s}=T_{0}-T_{ref}(\frac{d x^{2}}{(\mu/ \rho)})(1-at)^{-3/2}. $$
(13)

Using (10)-(13), the mathematical problem defined in (2)–(7) is then transformed into a set of ordinary differential equations and their associated boundary conditions:

$$ f^{\prime\prime\prime}\left[1+\alpha(1-\beta f^{\prime\prime^{2}})\right]-S(f^{\prime}+\frac{1}{2}\eta f^{\prime\prime})-f^{\prime^{2}}+ff^{\prime\prime}=0 , $$
(14)
$$ \theta^{\prime\prime}+Pr\left[f\theta^{\prime}-2f^{\prime}\theta-S(\frac{3}{2}\theta+\frac{1}{2}\eta\theta^{\prime})\right]+a^{*}e^{-\eta}+b^{*}\theta=0, $$
(15)
$$\begin{array}{@{}rcl@{}} f(0)&=&0, f^{\prime}(0)=1+\lambda\left[(1+\alpha)f^{\prime\prime}(0)-\frac{\alpha\beta}{3}f^{\prime\prime^{3}}(0) \right],\\ \theta(0)&=&1, \end{array} $$
(16)
$$ \left[(1+\alpha)f^{\prime\prime}(\delta)-\frac{\alpha\beta}{3}f^{\prime\prime^{3}}(\delta) \right]=0,\quad\quad \theta^{\prime}(\delta)=0, \quad $$
(17)
$$ f(\delta)=\frac{1}{2}\delta S, $$
(18)

where a prime denotes ordinary differentiation with respect to η, \(S=\frac {a}{b}\) is the unsteadiness parameter, \(\lambda =\gamma \sqrt {\frac {b}{\nu }}\) is the slip velocity parameter, \(Pr=\frac {\mu c_{p}}{\kappa }\) is the Prandtl number, and \(\alpha =\frac {1}{C\mu \tilde {\beta }},\,\,\beta =\frac {\rho U^{3}}{2x\mu C^{2}}\) are the dimensionless Powell-Eyring fluid parameters. Here, it is worth mentioning that the parameter β is a local parameter which is a function of x and t, and its value varies locally throughout the thin film flow motion. On the other hand, the parameter λ depends on γ 1 which is a function of t, so the slip velocity parameter λ is also a local parameter. Therefore, the provided equation is valid only for a locally similar solution.

By examining the first part of (17), we can observe that there exist three different cases for f ″(δ) as follows: (i) f ″(δ) = 0, which means the vanishing for the shear stress at the free surface y = h, but without effects for the powell-Eyring parameters α and β. (ii) \(f^{\prime \prime }(\delta )=+\sqrt {\frac {3(1+\alpha )}{\alpha \beta }}\), which corresponds to the absence of the shear stress at the free surface with the influence of the powell-Eyring parameters α and β. Physically, for the flow next to a continuous stretching surface, the velocity gradient must not be positive. (iii) \(f^{\prime \prime }(\delta )=-\sqrt {\frac {3(1+\alpha )}{\alpha \beta }}\), which coincide with the demise for the shear stress at the free surface with the effect of the powell-Eyring parameters α and β. So, this condition is the suitable one to satisfy the first part of (17). Then, in our calculations, we used the condition \(f^{\prime \prime }(\delta )=-\sqrt {\frac {3(1+\alpha )}{\alpha \beta }}\) in (17). The actual film thickness can be found from the fact that η = δ as y = h, then

$$h(t)=\delta(\frac{b}{(\mu/\rho)})^{\frac{-1}{2}}(1-at)^{\frac{1}{2}}, $$
(19)

since δ is an anonymous constant, which should be calculated from the present boundary value problem. On the other hand, the kinematic constraint at y = h(t) which appears in (8) can be obtained by differentiating (19) with respect to t.

It is worth mentioning that when α = β = 0 (Newtonian model) and in the absence of the slip velocity parameter (λ = 0), our proposed problem reduces to those considered by Abel et al. [13].

For engineering and practical purposes, one is usually more interested in the values of the skin-friction or heat transfer than in the shape of the velocity or temperature profiles, so our interest lies in the investigation of the important physical quantities of the flow behavior and heat transfer characteristics by analyzing the non-dimensional local skin-friction coefficient (C f x ) or the frictional drag coefficient and the local Nusselt number (N u x ), which are defined, respectively, by the following relations:

$$ Cf_{x}=\frac{2\tau_{w}}{\rho U^{2}}, \quad\quad Nu_{x}=\frac{x q_{w}}{\kappa(T_{s}-T_{0})}, $$
(20)

where \(\tau _{w}= -\left [\mu \frac {\partial u}{\partial y}+ \frac {1}{\tilde {\beta }C}\frac {\partial u}{\partial y}-\frac {1}{6\tilde {\beta }C^{3}} (\frac {\partial u}{\partial y})^{3}\right ]_{y=0}\) and \(q_{w}=-\kappa \left [\frac {\partial T}{\partial y}\right ]_{y=0}\).

Using the non-dimensional (10)-(13), the local skin-friction coefficient and the local Nusselt number can be written as :

$$\begin{array}{@{}rcl@{}} \frac{Cf_{x}}{2}Re_{x}^{\frac{1}{2}}&=&-\left[(1+\alpha)f^{\prime\prime}(0)-\frac{\alpha\beta}{3}f^{\prime\prime^{3}}(0) \right],\\ Nu_{x}Re_{x}^{\frac{-1}{2}}&=&-\theta^{\prime}(0). \end{array} $$
(21)

From (21), we must observe that the values of the local skin-friction coefficient depends only on both the α parameter and β parameter, while the local Nusselt number is independent on them. But, actually from (14) to (15), we noticed that they are coupled, then we can conclude that α parameter and β parameter also have an indirect effect on the local Nusselt number. In order to validate the proposed numerical method, we have compared the values of f ″(0),𝜃(δ) and 𝜃 ′(0) (in the absence of α, β, λ and a ∗, b ∗) in the case of f ″(δ)=0(17) with those obtained by Abel et al. [13] (in the absence of M and E c) and found in good agreement as shown in the Tables 1 and 2.

Table 1 Comparison of δ and \(-f^{\prime \prime }(0)\) with α = β = λ = 0 using the previous work and the shooting method
Full size table
Table 2 Comparison of 𝜃(δ) with a ∗ = b ∗ = α = λ = 0 using the previous work and the shooting method
Full size table

3 Procedure Solution Using Shooting Method

A numerical procedure is used to solve the differential system (14)–(15). This system along with the boundary conditions (16)–(17) is integrated numerically by means of Runge-Kutta method with systematic estimate of f ″(0) and 𝜃 ′(0) with Newton-Raphson shooting technique until the boundary condition at adiabatic free surface 𝜃 ′(δ) vanish to zero, while \(f^{\prime \prime }(\delta )=-\sqrt {\frac {3(1+\alpha )}{\alpha \beta }}\). The following first-order system is set:

$$ y_{1}=f,\quad y_{2}=y_{1}^{\prime},\,\,\quad\,\, y_{3}=y_{2}^{\prime},\,\,\,\,\quad y_{4}=\theta,\,\,\,\,\quad y_{5}=y_{4}^{\prime}. $$
(22)

Equations 14–15 with the boundary conditions (16) and (18) are then reduced to a system of first-order ordinary differential equations, i.e.,

$$\begin{array}{@{}rcl@{}} y_{1}^{\prime}&=&y_{2},\quad\quad y_{1}(0)=0,\\ y_{2}^{\prime}&=&y_{3},\quad\quad y_{2}(0)=1+\lambda\left[(1+\alpha)y_{3}(0)-\frac{\alpha\beta}{3}{y_{3}^{3}}(0) \right], \end{array} $$
$$\begin{array}{@{}rcl@{}} y_{3}^{\prime}&\,=\,& \frac{1}{\left[1+\alpha(1-\beta {y_{3}^{2}})\right]}\!\left( S(y_{2}\,+\,\frac{1}{2}\eta y_{3})+{y_{2}^{2}}- y_{1}y_{3}\right),\\ y_{3}(0)&=&\varepsilon_{1}, \end{array} $$
(23)
$$\begin{array}{@{}rcl@{}} y_{4}^{\prime}=y_{5},\quad\quad y_{4}(0)=1 , \end{array} $$
$$\begin{array}{@{}rcl@{}} y_{5}^{\prime}&=&Pr\left[2y_{2}y_{4}-y_{1}y_{5}+S(\frac{3}{2}y_{4}+\frac{1}{2}\eta y_{5})\right]\\ &&-a^{*}e^{-\eta}-b^{*}y_{4},\quad\quad y_{5}(0)=\varepsilon_{2}. \end{array} $$

The shooting method is used to guess ε 1 and ε 2 by iteration until the outer boundary conditions (17) are satisfied. Therefore, the estimated value of δ is systematically adjusted until (18) is satisfied to within 10−7. Once the convergence is achieved, the resulting differential equations can be integrated using a fourth-order Runge-Kutta integration scheme. The above procedure is repeated until we get the results up to the desired degree of accuracy, 10−5.

4 Results and Discussion

In this section, we concentrate on the variations of the parameters governing the slip flow and heat transfer for Powell-Eyring viscous liquid film over an unsteady stretching sheet subject to non-uniform heat generation/aborbtion. In particular, the variations of the dimensionless Powell-Eyring fluid parameters α and β, the unsteadiness parameter S, slip velocity parameter λ, the space-dependent heat generation/absorption parameter a ∗, the temperature-dependent heat generation/absorption parameter b ∗, and the Prandtl number P r are emphasized. The typical dimensionless velocity profiles f ′(η) for selected values of unsteadiness parameter S are plotted in Fig. 2. It is apparent from this figure that due to the presence of slip velocity at the sheet, the fluid velocity along the sheet f ′(0) is an increasing function of S but the film thickness δ is a decreasing function of the same parameter and therefore the free surface velocity f ′(δ) enlarges as S increases.

Fig. 2
figure 2

The velocity profile for various values of S

Full size image

The effects of the same parameter S on the temperature profile 𝜃(η) are presented in Fig. 3. From this figure, it can be seen that both the temperature distribution and the free surface temperature 𝜃(δ) increases as the unsteadiness parameter increases.

Fig. 3
figure 3

The temperature profile for various values of S

Full size image

The effect of the non-Newtonian fluid parameter α on the dimensionless velocity profiles may be analyzed from Fig. 4. This graph reveal that the increase of α parameter results in the decrease of the fluid velocity along the sheet f ′(0). Also, from this figure, we observe that the increase of α parameter leads to an increase for both the film thickness δ and the free surface velocity f ′(δ).

Variations of temperature profiles as a function of η for various values of the same parameter α are shown in Fig. 5. It is interesting to note that an increase in the value of α leads to a decrease in both the temperature distribution and the free surface temperature 𝜃(δ).

Fig. 4
figure 4

The velocity profile for various values of α

Full size image
Fig. 5
figure 5

The temperature profile for various values of α

Full size image

Figure 6 represents the graph of velocity profile for different values of β parameter. It is seen that the effect of increasing β parameter is to increase both the film thickness δ and the free surface velocity f ′(δ).

Fig. 6
figure 6

The velocity profile for various values of β

Full size image

Figure 7 demonstrates that at any point the dimensionless temperature 𝜃(η) decreases with the increasing value of β parameter. Also, the free surface temperature 𝜃(δ) is observed to decrease with an increase in β parameter.

Fig. 7
figure 7

The temperature profile for various values of β

Full size image

The variation of dimensionless temperature against η for various values of the Prandtl number P r are displayed in Fig. 8. From this figure, it is seen that the effect of increasing Prandtl number P r is to decrease the temperature distribution throughout the liquid film which results in decrease in the free surface temperature 𝜃(δ). Based on the physical point of view, the increase of Prandtl number coincides with slow rate of thermal diffusivity.

Fig. 8
figure 8

The temperature profile for various values of P r

Full size image

The effects of the space-dependent heat source/sink parameter a ∗ and the temperature-dependent heat source/sink parameter b ∗ could be apparently seen in Fig. 9. Before discussing the results, we recollect the fact that the case a ∗ > 0, b ∗ > 0 correspond to internal heat generation and that a ∗ < 0, b ∗ < 0 correspond to internal heat absorption. It is interesting to note that the stronger heat source parameters a ∗ > 0 and b ∗ > 0, coincides with the stronger heat generation and the increasing for the temperature distribution throughout the liquid film and free surface temperature 𝜃(δ), but the influence of a ∗ < 0 and b ∗ < 0 resulting in temperature dropping throughout the liquid film.

Fig. 9
figure 9

The temperature profile for various values of a ∗,b ∗

Full size image

Figure 10 explains the variation of the slip velocity parameter λ on the velocity profiles when all other parameter are fixed. From here, we see that the velocity profiles decrease very rapidly throughout the liquid film with the increase of slip velocity parameter λ. Likewise, this figure shows that the effect of increasing the slip velocity parameter λ is to decrease the film thickness δ but the opposite effect is observed for the free surface velocity f ′(δ).

For various values of the slip velocity parameter λ, the profiles of the temperature distribution across the liquid film are shown in Fig. 11. It is obvious that an increase in the slip velocity parameter λ results in an increasing in both the temperature distribution throughout the thermal liquid film and the free surface temperature 𝜃(δ).

Fig. 10
figure 10

The velocity profile for various values of λ

Full size image
Fig. 11
figure 11

The temperature profile for various values of λ

Full size image

Now at this step, we reached to analyze Table 3 which is very interesting in evaluating the frictional drag or the local skin-friction coefficient \((Cf_{x}/2)Re_{x}^{\frac {1}{2}}\) and the rate of heat transfer or the local Nusselt number \(Nu_{x}Re_{x}^{\frac {-1}{2}}\) in which they can be affected by the unsteadiness parameter S, slip velocity parameter λ, the dimensionless Powell-Eyring fluid parameters α, β, space-dependent heat source/sink parameter a ∗, temperature-dependent heat source/sink parameter b ∗, and the Prandtl number P r. From this table, one sees that both the local skin-friction coefficient and the local Nusselt number increases as both the α parameter and β parameter increases. Also, results show that increasing the unsteadiness parameter tends to decrease both the local skin-friction coefficient and the local Nusselt number. Furthermore, it is analyzed from Table 3 that the effect of slip velocity parameter is to decrease both the local Nusselt number and the local skin-friction coefficient. Likewise, from the same table, it can be noted that the local Nusselt number enhances with the increase of the heat absorption parameter. This phenomenon reflect the fact that the presence of the heat absorption may be creates a thin layer of cold fluid adjacent to the heated surface and therefore the rate of heat transfer boost. Additionally, it is observed that increases in the values of the heat generation parameter has the effect of decreasing the local Nusselt number. This is because the heat generation mechanism will increase the fluid temperature near the surface of the sheet and thus temperature gradient at the surface decreases, thereby decreasing the heat transfer at the sheet. Finally, the heat loss to sheet or the local Nusselt number increases when the values of Prandtl number rise.

Table 3 Values of \((Cf_{x}/2)Re_{x}^{\frac {1}{2}}\) and \(Nu_{x}Re_{x}^{\frac {-1}{2}}\) for various values of α, β, P r, a ∗, b ∗, λ, and S
Full size table

5 Conclusions

This present investigation is a worthwhile attempt to study the problem which involves flow and heat transfer for non-Newtonian Powell-Eyring viscous liquid film flow past an unsteady stretching surface with slip velocity and non-uniform heat generation/absorption. Owing to the complicated nature of the governing equations, we employed a suitable dimensionless transformations to change the governing partial differential equations into ordinary ones. These equations were solved numerically by using shooting method. The results are presented graphically and the effects of the emerging flow parameters on the momentum and thermal thin films are discussed in detail with physical interpretations. It is found that both the α parameter and β parameter increases the thin film thickness, whereas the unsteadiness parameter has an opposite effect on the momentum thin film thickness. Likewise, along the sheet, the velocity decreases with increase in the α parameter, whereas it increases away from the sheet. Moreover, it is interesting to find that as the slip parameter increases in magnitude, permitting more fluid to slip past the sheet, the skin-friction coefficient decreases in magnitude and approaches to zero for higher values of the slip parameter, i.e., the flow behaves as though it were viscid. On the other hand, it was observed that the presence of heat generation or absorption parameters has prominent effects on the free surface temperature. Finally, it was found that an increase of Prandtl number results in decreasing the temperature distribution across the thin film. The reason is that smaller values of Prandtl number are equivalent to increasing the thermal conductivities, and therefore heat is able to diffuse away from the heated surface more rapidly than for higher values of Prandtl number.