The anisotropic elasto-plastic analysis using a natural neighbour RPIM version

Abstract

In this work, the natural neighbour radial point interpolation method (NNRPIM), an advanced discretization meshless technique, is used to study several solid mechanics benchmark examples considering an elasto-plastic approach. The NNRPIM combines the radial point interpolators (RPI) with the natural neighbour geometric concept. The nodal connectivity and the background integration mesh depend entirely on the nodal discretization and are both achieved using mathematic concepts, such as the Voronoï diagram and the Delaunay tessellation. The obtained interpolation functions, used in the Galerkin weak form, are constructed with the RPI and possess the delta Kronecker property, which facilitates the imposition of the natural and essential boundary conditions. Due to the organic procedure employed to impose the nodal connectivity, the obtained displacement and the stress field are smooth and accurate. Since the scope of this work is to extend and validate the NNRPIM in the anisotropic elasto-plastic analysis, it is used as nonlinear solution algorithm, the modified Newton–Raphson initial stiffness method. The efficient “backward-Euler” procedure is considered to return the stress to the Hill anisotropic yield surface. The elasto-plastic algorithm of solution is described. Several benchmark two-dimensional problems are solved, considering anisotropic elasto-plastic materials with anisotropic hardening, and the obtained solutions are compared with finite-element solutions, showing that the meshless approach developed is efficient and accurate.

1 Introduction

In the recent years, the significant development of advanced discretization meshless techniques permits them to be considered as a valid alternative to the finite-element method (FEM) [1, 2]. The complete freedom and flexibility in the domain discretization of meshless methods are very attractive. Within meshless methods, the solid domain can be discretized with an arbitrarily set of nodes rather with an element mesh [3]. In meshless methods, the nodal connectivity is imposed with the influence-domain concept, in opposition to the fixed size element used in the FEM. Furthermore, in contrast with the FEM, to enforce the nodal connectivity, the influence domains may and must overlap each other.

One of the first developed meshless methods is the smooth particle hydrodynamics (SPH) method. Initially, the SPH method was used to model astrophysical phenomena [4]. Later, the SPH was extended to solve solid mechanics problems using a strong formulation [5], as well as the SPH-corrected versions that, meanwhile, emerged [1].

More recently, other approximation meshless methods seeking the weak form solution were developed. The diffuse element method (DEM) [6] was one of the first fully developed approximation meshless methods. The DEM uses the moving least square (MLS) approximants to construct the approximation functions, which was initially proposed by Lancaster and Salkauskas [7] for surface fitting. Later, Belytschko evolved the DEM and developed one of the most popular meshless methods, the element-free Galerkin method (EFGM) [8]. In the same period, the reproducing kernel particle method (RKPM) was developed [9], as well as the meshless local Petrov–Galerkin (MLPG) method [10].

However, the aforesaid methods employ approximation functions, which mean that the constructed shape functions do not possess the Kronecker delta property. As a consequence, the treatment of the essential and natural boundary conditions is not as straightforward as within numerical methods using interpolation functions [1, 11, 12].

To overcome this drawback, in the last few years, several interpolator meshless methods were developed, such as the point interpolation method (PIM) [13, 14], the radial point interpolation method (RPIM) [15, 16], the natural neighbour finite-element method (NNFEM) [17, 18], the meshless finite-element method (MFEM) [19], more recently, the natural neighbour radial point interpolation method (NNRPIM) [11, 20, 21], and the radial natural element method (NREM) [22, 23, 24].

The NNRPIM uses mathematic concepts, such as the Voronoï diagrams [25] and the Delaunay tessellation [26], to construct the influence-cells (the basic structure of the nodal connectivity in the NNRPIM [3]) and the background integration mesh [3]. Both these numerical structures are totally dependent on the nodal discretization. Unlike the FEM, where geometrical restrictions on elements are imposed for the convergence of the method, in the NNRPIM, there are no such restrictions, permitting a random nodal distribution for the discretized problem. The NNRPIM interpolation functions, used in the Galerkin weak form, are constructed with the radial point interpolators (RPI) [15, 16, 27]. The RPI functions possess the delta Kronecker property, facilitating the enforcement of boundary conditions, which can be directly imposed as in the FEM. The RPI function construction is simple, and its derivatives are easily obtained [3].

In the literature, it is possible to find research works in which meshless methods were extended to the nonlinear structural analysis considering elasto-plastic materials. The elasto-plastic analysis using the EFGM was initially applied to fracture problems [28, 29, 30] and subsequently applied to 2D problems [31, 32] and to 3D problems [33, 34]. Afterwards, Belinha and Dinis extended the EFGM to the nonlinear analysis of thick plates [35] and composites [36] assuming anisotropic elasto-plastic materials with anisotropic hardening. Regarding the RKPM, Chen and coworkers [37] were able to study large deformation analysis of nonlinear elastic and inelastic structures using the RKPM. Other approximation methods were used to solve nonlinear problems considering elasto-plastic materials, such as the meshless integral method [38] and the MLPG [39].

Advanced discretization meshless techniques using interpolation functions were also successfully extended to the nonlinear analysis of structures considering elasto-plastic materials. Dai et al. [40] extended the RPIM to the inelastic analysis of 2D problems. In addition, it is possible to find some elasto-plastic research works on meshless methods using the natural neighbour concept, such as the meshless natural neighbour method [41] and the hybrid natural element method [42].

In this work, the NNRPIM is used to analyse two-dimensional problems considering a small strain formulation and assuming anisotropic elasto-plastic materials with anisotropic hardening. Thus, To extend and validate the NNRPIM in the elasto-plastic analysis, the used nonlinear solution algorithm is the modified Newton–Raphson initial stiffness method, and the stress state is returned to the yield surface using a backward-Euler scheme [43].

The outline of this study is as follows: In Sect. 2, the basic concepts of the used meshless method are presented. In Sect. 3, the small strain elasto-plastic formulation is presented. In Sect. 4, several well-known 2D elasto-plastic problems considering anisotropic hardening are solved using the NNRPIM. This work ends with conclusions and remarks in Sect. 5.

2 Natural neighbour radial point interpolation method

2.1 Natural neighbours

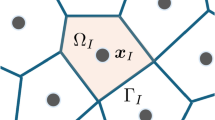
The concept of natural neighbours emerged in 1980 by Sibson [44], and it allows to impose the nodal connectivity in the NNRPIM [45]. This mathematical concept can be materialised by the Voronoï diagram of the discretized domain.

Thus, considering a problem domain $\varOmega \in {\mathbb{R}}^{d}$, bounded by a physical boundary $\varGamma \subset \varOmega$, which is discretized in several randomly distributed nodes $\varvec{N} = \left\{ {n_{1} ,n_{2} , \ldots ,n_{N} } \right\}$ scattered in the space domain: $\varvec{X} = \left\{ {\varvec{x}_{1} ,\varvec{x}_{2} , \ldots ,\varvec{x}_{N} } \right\} \in \varOmega$. The Voronoï diagram of $\varvec{N}$ is the partition of the domain defined by $\varOmega$ in subregions $V_{i}$, closed and convex. Each subregion $V_{i}$ is associated with the node $n_{i}$, in a way that any point in the interior of $V_{i}$ is closer to $n_{i}$ than any other node $n_{j}$, where $n_{j} \in \varvec{N} \wedge j \ne i$

$$V_{i} : = \left\{ {\varvec{x}_{I}} \in \varOmega \subset {\mathbb{R}}^{d} :\left\| {\varvec{x}_{I} - \varvec{x}_{i} } \right\| < \left\| {\varvec{x}_{I} - \varvec{x}_{j} } \right\|,\forall i \ne j \right\},$$

(1)

where $||\,\, \cdot \,\,||$ is the Euclidian metric norm and $\varvec{x}_{I} \in \varOmega$. The set of Voronoï cells $\varvec{V}$ defines the Voronoï diagram, $\varvec{V} = \left\{ {V_{\text{1}} ,V_{\text{2}} , \ldots ,V_{N} } \right\}$. In Fig. 1a, it is presented a Voronoï diagram. In the literature, it is possible to find several works addressing properly the Voronoï construction procedure [3, 11, 22].

Fig. 1

a Voronoï diagram. b Natural neighbours. c Subcells obtained by the overlap of a cell of the Voronoï diagram and the Delaunay tessellation of that cell. d Application of the quadrature points (one in each subcell) following the Gauss–Legendre integration scheme. e Mesh of the integration points

2.2 Nodal connectivity

Formed by a set of nodes in the neighbourhood of an interest node $\varvec{x}_{i} \in \varvec{X}$, the NNRPIM “influence-cell” concept permits to establish the nodal connectivity [11], allowing to organically determine the influence domain of an interest node $\varvec{x}_{i}$. Since it is simpler to represent, only the determination of the 2D influence-cell is presented; however, this concept is applicable to a $d$-dimensional space. In Fig. 1a, two types of influence-cells are shown: the first-degree influence-cell and the-second degree influence-cell. The first-degree influence-cell is composed by the first natural neighbours of the interest node $\varvec{x}_{i}$. The second-degree influence-cell, in addition to the first natural neighbours of the interest node $\varvec{x}_{i}$, contains the natural neighbours of the nodes belonging to the first degree influence-cell of node $\varvec{x}_{i}$. This procedure is well described in detail in the works of Belinha and coworkers [3, 11, 22].

It is possible to observe in Fig. 1a that the second-degree influence-cell enforces a higher nodal connectivity when compared with the first-degree influence-cell. The literature shows [11, 20, 46, 21, 47, 48, 49, 50] that regardless, the studied phenomenon, higher degree influence-cells, permits to achieve more accurate solutions. Therefore, due to the superior numerical behaviour, only the second degree influence-cells are considered in this work.

2.3 Numerical integration

After the definition of the Voronoï diagram, Fig. 1a, it is possible to construct the integration mesh required to numerically integrate the differential equation ruling the studied physical phenomenon. One of the numerical advantages of the NNRPIM is the complete dependency of the integration mesh on the nodal discretization, i.e., the integration mesh is constructed using only the information from the nodal spatial field $\varvec{X}$ and from the subsequent Voronoï diagram $\varvec{V}$. Thus, in opposition to the majority of the meshless methods, the NNRPIM only requires the nodal spatial field $\varvec{X}$ to determine: the nodal connectivity; the integration mesh; and the interpolation functions.

To obtain the integration mesh, first, the area of each Voronoï cell must be subdivided in several subareas. To perform this subdivision, the Delaunay triangulation [26] is applied, which can be determined by connecting the nodes whose Voronoï cells have common boundaries, as shown in Fig. 1b.

The Delaunay triangulation permits to divide the original Voronoï cell area, $A^{{V_{j} }}$, of an interest node $\varvec{x}_{j}$ in $k$ subareas $A_{k}^{{V_{j} }}$, being $A_{{}}^{{V_{j} }} = \sum\nolimits_{i = 1}^{k} {A_{i}^{{V_{j} }} }$, Fig. 1c. The distribution of integration points inside each subarea $A_{k}^{{V_{j} }}$, Fig. 1d, permits to obtain the integration mesh for the Voronoï cell $V_{j}$.

Repeating the process for the $N$ Voronoï cells discretizing the problem domain, it is possible to obtain the integration mesh of the entire domain, Fig. 1e, being $A^{\varOmega } = \sum\nolimits_{j = 1}^{n} {\sum\nolimits_{i = 1}^{k} {A_{i}^{{V_{j} }} } }$, as suggested in the previous NNRPIM works [3, 11, 21].

The distribution of the integration point inside each subarea $A_{k}^{{V_{j} }}$ follows the Gauss–Legendre quadrature rule. In Fig. 1d, only one quadrature point was applied in each one of the subareas, which is sufficient for the used NNRPIM formulation [3, 11].

2.4 Interpolation functions

In this work, the shape functions are obtained combining radial basis functions with polynomial basis functions [11, 15]. Consider a function space $T$ defined in the analysed domain $\varOmega \subset {\mathbb{R}}^{d}$. The finite-dimensional space $T_{h} \subset T$ discretizing the domain $\varOmega$ is defined by:

$$T_{h} : = \left\langle {r\left( {\varvec{x} - \varvec{x}_{i} } \right):i \in {\mathbb{N}} \wedge i \le N} \right\rangle + p_{m} (\varvec{x}),$$

(2)

where $p_{m} :{\mathbb{R}}^{d} \mapsto {\mathbb{R}}$ is defined in the space of polynomials of degree less than $m$ and $r:{\mathbb{R}}^{d} \mapsto {\mathbb{R}}$ is at least a $C^{1} -$ function. Since, in this work, only two-dimensional domains $\varOmega \subset {\mathbb{R}}^{2}$ are studied, the problem domain $\varOmega$ is discretized by a set of $N$ arbitrarily distributed nodes $\varvec{N}_{I} = \{ n_{1} ,n_{2} , \ldots ,n_{N} \}$ defined in the two-dimensional space by $\varvec{X} = \{ \varvec{x}_{1} ,\varvec{x}_{2} , \ldots ,\varvec{x}_{N} \} \wedge \varvec{x}_{i} \in {\mathbb{R}}^{2}$.

Consider now, for an interest point $\varvec{x}_{I} \subset \varOmega$, not necessarily coincident with any $\varvec{x}_{i} \in \varvec{X}$, an interpolation function $u^{h} (\varvec{x}_{I} )$ defined within the space of an influence-cell $\varOmega_{I} \subset \varOmega$ containing $n$ nodes. The radial point interpolators (RPI) [11, 15] permit to construct an interpolation function $u^{h} (\varvec{x}) \in T$ capable to pass through all nodes within the influence-cell, i.e., $u^{h} (\varvec{x}_{i} ) = u_{i}$, where $u_{i}$ is the nodal function value assumed on node $\varvec{x}_{i}$, $u_{i} = u(\varvec{x}_{i} )$.

Using a radial basis function $r(\varvec{x})$ and a polynomial basis function $p(\varvec{x})$, the interpolation function $u^{h} (\varvec{x}) \in T$ can be defined at the interest point $\varvec{x}_{I} \in {\mathbb{R}}^{2}$ by:

$$u^{h} (\varvec{x}_{I} ) = \sum\limits_{i = 1}^{n} {r_{i} (\varvec{x}_{I} )a_{i} } + \sum\limits_{j = 1}^{m} {p_{j} (\varvec{x}_{I} )b_{j} } = \varvec{r}(\varvec{x}_{I} )^{\text{T}} \varvec{a} + \varvec{p}(\varvec{x}_{I} )^{\text{T}} \varvec{b }=\,u(\varvec{x}_{I} ),$$

(3)

where $a_{i}$ is the non-constant coefficient of $r_{i} (\varvec{x}_{I} )$ and $b_{j}$ is the non-constant coefficient for $p_{j} (\varvec{x}_{I} )$. The integer $n$ is the number of nodes inside the influence-cell of the interest point $\varvec{x}_{I}$ and $m$ is the number of monomials of the polynomial basis $p(\varvec{x}_{I} )$. The vectors are defined by the following expressions:

$$\varvec{a}^{\text{T}} = \{ a_{1} ,a_{2} , \ldots ,a_{n} \}$$

(4)

$$\varvec{b}^{\text{T}} = \{ b_{1} ,b_{2} , \ldots ,b_{m} \}$$

(5)

$$\varvec{r}(\varvec{x})^{\text{T}} = \{ r_{1} (\varvec{x}),r_{2} (\varvec{x}), \ldots ,r_{n} (\varvec{x})\}$$

(6)

$$\varvec{p}(\varvec{x})^{\text{T}} = \{ p_{1} (\varvec{x}),p_{2} (\varvec{x}), \ldots ,p_{m} (\varvec{x})\} .$$

(7)

The radial basis function used in this work is the multiquadrics radial basis function (MQ-RBF), first proposed by Hardy [51]:

$$\varvec{r}_{i} (\varvec{x}_{I} ) = \varvec{s}(d_{iI} ) = \left( {d_{iI}^{2} + c^{2} } \right)^{p} = \left( {\left| {\left( {x_{i} - x_{I} } \right)^{2} + \left( {y_{i} - y_{I} } \right)^{2} } \right| + c^{2} } \right)^{p} ,$$

(8)

where $d_{iI}$ is the Euclidean distance between the interest point $\varvec{x}_{I} = \{ x_{I} ,y_{I} \}^{T}$ and the node $\varvec{x}_{i} = \{ x_{i} ,y_{i} \}^{T}$. The MQ-RBF requires the definition of the shape parameters $c$ and $p$. The variation of these parameters can affect the performance of the MQ-RBFs [11, 15, 16]. This work follows the conclusions of Dinis et al. [11], which suggest that the optimal values should be $c < < 1$ and $p \cong 1$. Thus, the values used in this work are $c = 0.0001$ and $p = 0.9999$.

To assure that the interpolation matrix of the RBF is invertible, the polynomial basis added to the RBF must be completed [11]. In this work, it was considered the use of a constant basis, being the polynomial basis, for the two-dimensional space $\varvec{x}_{i} = \{ x_{i} ,y_{i} \}^{T}$, defined as $\varvec{p}^{T} (\varvec{x}_{i} ) = \{ 1\}$ with $m = 1$.

Enforcing the interpolation to pass through all $n$ nodes within the influence-cell, it is possible to determine the coefficients $a_{i}$ and $b_{j}$ of Eq. (3) [3]. Thus, the interpolation at the $k^{th}$ node is defined by:

$$u^{h} (x_{k} ,y_{k} ) = \sum\limits_{i = 1}^{n} {r_{i} (x_{k} ,y_{k} )a_{i} } + \sum\limits_{j = 1}^{m} {p_{j} (x_{k} ,y_{k} )b_{j} = u_{k} ,\quad k = 1,2, \ldots ,n} .$$

(9)

The inclusion of the following polynomial term is an extra-requirement that guarantees unique interpolation [3]:

$$\sum\limits_{i = 1}^{n} {p_{j} (x_{i} ,y_{i} )a_{i} = 0,\quad \, j = 1,2, \ldots ,m} .$$

(10)

Thus, the computation of the shape functions is written in a matrix form as:

$$\left[ {\begin{array}{*{20}c} \varvec{R} & \varvec{P} \\ {\varvec{P}^{T} } & \varvec{Z} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} \varvec{a} \\ \varvec{b} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} \varvec{u} \\ \varvec{z} \\ \end{array} } \right\} \Leftrightarrow \varvec{G}\left\{ {\begin{array}{*{20}c} \varvec{a} \\ \varvec{b} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} \varvec{u} \\ \varvec{z} \\ \end{array} } \right\},$$

(11)

where $\varvec{G}$ is the complete moment matrix, $\varvec{Z}$ is a null matrix defined by $Z_{ij} = 0,\,\quad \forall \;\{ \{ i,j\} \in {\mathbb{N}}:\{ i,j\} \le m\}$, and the null vector $\varvec{z}$ can be represented by $z_{i} = 0,\,\;\forall \;\{ i \in {\mathbb{N}}:i \le m\}$. The vector for function values is defined as $u_{i} = u(\varvec{x}_{i} ),\,\;\forall \;\{ i \in {\mathbb{N}}:i \le n\}$. The radial moment matrix $\varvec{R}$ is represented as:

$$\mathop R\limits_{[n \times n]} = \left[ {\begin{array}{*{20}c} {r_{1} (x_{1} ,y_{1} )} & {r_{1} (x_{2} ,y_{2} )} & \cdots & {r_{1} (x_{n} ,y_{n} )} \\ {r_{2} (x_{1} ,y_{1} )} & {r_{2} (x_{2} ,y_{2} )} & \cdots & {r_{2} (x_{n} ,y_{n} )} \\ \vdots & \vdots & \ddots & \vdots \\ {r_{n} (x_{1} ,y_{1} )} & {r_{n} (x_{2} ,y_{2} )} & \cdots & {r_{n} (x_{n} ,y_{n} )} \\ \end{array} } \right]$$

(12)

and polynomial moment matrix $\varvec{P}$ is defined as:

$$\mathop P\limits_{[n \times m]} = \left[ {\begin{array}{*{20}c} {p_{1} (x_{1} ,y_{1} )} & {p_{2} (x_{1} ,y_{1} )} & \cdots & {p_{m} (x_{1} ,y_{1} )} \\ {p_{1} (x_{2} ,y_{2} )} & {p_{2} (x_{2} ,y_{2} )} & \cdots & {p_{m} (x_{2} ,y_{2} )} \\ \vdots & \vdots & \ddots & \vdots \\ {p_{1} (x_{n} ,y_{n} )} & {p_{2} (x_{n} ,y_{n} )} & \cdots & {p_{m} (x_{n} ,y_{n} )} \\ \end{array} } \right].$$

(13)

Notice that the distance is directionless, $r_{i} (x_{j} ,y_{j} ) = r_{j} (x_{i} ,y_{i} )$, i.e., $R_{ij} = R_{ji}$; therefore, $\varvec{R}$ matrix is symmetric. A unique solution is obtained if the inverse of the radial moment matrix $\varvec{R}$ exists:

$$\left\{ {\begin{array}{*{20}c} \varvec{a} \\ \varvec{b} \\ \end{array} } \right\} = \varvec{G}^{ - 1} \left\{ {\begin{array}{*{20}c} \varvec{u} \\ \varvec{z} \\ \end{array} } \right\}.$$

(14)

The solvability of this system is usually guaranteed by the requirements ${\text{rank}}(p) = m \le n$ [14]. Since, in this work, only the constant polynomial basis is used, the previous condition is largely satisfied. It is possible to obtain the interpolation with:

$$u^{h} (\varvec{x}_{I} ) = \left\{ {\varvec{r}(\varvec{x}_{I} )^{T} ;\varvec{p}(\varvec{x}_{I} )^{T} } \right\}\varvec{G}^{ - 1} \left\{ {\begin{array}{c} \varvec{u} \\ \varvec{z} \\ \end{array} } \right\} = \left\{ {\varPhi (\varvec{x}_{I} )^{T} ; \varPsi (\varvec{x}_{I} )^{T} } \right\}\left\{ {\begin{array}{c} \varvec{u} \\ \varvec{z} \\ \end{array} } \right\},$$

(15)

where the interpolation function vector $\varPhi (\varvec{x}_{I} )$ is defined by:

$$\varPhi (\varvec{x}_{I} ) = \left\{ {\varphi_{1} (\varvec{x}_{I} )\;\;\varphi_{2} (\varvec{x}_{I} )\; \cdots \;\varphi_{n} (\varvec{x}_{I} )} \right\}$$

(16)

and the residual vector $\uppsi(\varvec{x}_{I} )$, with no relevant physical meaning, is expressed as follows:

$$\varPsi (\varvec{x}_{I} ) = \left\{ {\psi_{1} (\varvec{x}_{I} )\;\;\psi_{2} (\varvec{x}_{I} )\;\; \cdots \;\;\psi_{m} (\varvec{x}_{I} )} \right\}.$$

(17)

The partial derivatives of the interpolated function can be easily obtained, as demonstrated in [3, 11]. The RPI test functions $\varPhi (\varvec{x}_{I} )$ depend uniquely on the distribution of scattered nodes and are linearly independent in the influence-cell [3, 11]. The RPI test functions possess several important and useful numerical properties, such as the Kronecker delta property, reproducing property, the consistency property and the unity partition property [3]. In addition, since the obtained RPI test functions have a local compact support, it is possible to assemble a well-conditioned and banded equation system matrix.

2.5 Discretized system equation of the NNRPIM for plane stress

Consider $\varOmega \subset {\mathbb{R}}^{\text{2}}$, the solid domain bounded by $\varGamma$, where $\varGamma \in \varOmega :\varGamma_{u} \cup \varGamma_{t} = \varGamma \wedge \varGamma_{u} \cap \varGamma_{t} = \emptyset$, where $\varGamma_{u}$ is the essential boundary and $\varGamma_{t}$ is the natural boundary. The linear elastostatic problem equilibrium equations can be expressed by:

$$\nabla {\varvec{\Lambda}} + \varvec{b} = {\mathbf{0}}\quad {\text{in }}\varOmega ,$$

(18)

where $\nabla$ is the divergence operator, ${\varvec{\Lambda}}$ is the Cauchy stress tensor, and $\varvec{b}$ is the body forces per unit volume. The natural boundary conditions are given by ${\varvec{\Lambda}}\,\,\varvec{n} = \bar{\varvec{t}}$ on $\varGamma_{t}$ and the essential boundary conditions are imposed with $\varvec{u} = \bar{\varvec{u}}$ on $\varGamma_{u}$, where $\bar{\varvec{u}}$ is the prescribed displacement on the essential boundary $\varGamma_{u}$, $\bar{\varvec{t}}$ is the traction on the natural boundary $\varGamma_{t}$ and $\varvec{n}$ is the unit outward normal to the boundary of domain $\varOmega$.

The Galerkin weak form of Eq. (18) can be written as:

$$\int\limits_{\varOmega } {\delta\varvec{\varepsilon}^{T}\varvec{\sigma}\, \text{d}\varOmega } - \int\limits_{\varOmega } {\delta \varvec{u}^{T} \varvec{b} \, \text{d}\varOmega } - \int\limits_{{\varGamma_{t} }} {\delta \varvec{u}^{T} \varvec{t} \, \text{d}\varGamma } = 0.$$

(19)

Within the NNRPIM, the discrete system of equations is developed first for every influence-cell, i.e., the weak form has local support. Afterwards, the local systems of equations are assembled into the global system of equations, and then, the final equation system is solved. Using the interpolation functions $\varphi_{i} (\varvec{x}_{I} )$ obtained from Eq. (15), it is possible to define for an interest point $\varvec{x}_{I} \subset \varOmega$ the following approximation:

$$u^{h} (\varvec{x}_{I} ) = \sum\limits_{i = 1}^{n} {\varphi_{i} (\varvec{x}_{I} )\,u(\varvec{x}_{i} )} ,$$

(20)

where $u(\varvec{x}_{i} )$ is the nodal parameter of the $i^{th}$ node belonging to the nodal set defining the influence-cell of interest node $\varvec{x}_{I}$. Since, in this work, only two-dimensional examples are studied, there are two degrees of freedom per node $\varvec{u}(\varvec{x}_{i} ) = \{ \begin{array}{*{20}c} {u(\varvec{x}_{i} )} & {v(\varvec{x}_{i} )} \\ \end{array} \}^{\text{T}}$. Thus, from Eq. (20), it is possible to obtain the virtual displacement approximation:

$$\delta \varvec{u}^{h} (\varvec{x}_{I} ) = \left\{ {\begin{array}{*{20}c} {\delta u^{h} (\varvec{x}_{I} )} \\ {\delta v^{h} (\varvec{x}_{I} )} \\ \end{array} } \right\} = \sum\limits_{i = 1}^{n} {\left[ {\begin{array}{*{20}c} {\varphi_{i} (\varvec{x}_{I} )} & 0 \\ 0 & {\varphi_{i} (\varvec{x}_{I} )} \\ \end{array} } \right]\,\left\{ {\begin{array}{*{20}c} {\delta u(\varvec{x}_{i} )} \\ {\delta v(\varvec{x}_{i} )} \\ \end{array} } \right\}} = \sum\limits_{i = 1}^{n} {\varvec{H}_{i} (\varvec{x}_{I} )\,\delta \varvec{u}(\varvec{x}_{i} )} .$$

(21)

The strain and stress vectors on Eq. (19) can be correlated with the Hooke law:

$$\varvec{\varepsilon}= \varvec{s}\,\varvec{\sigma}\Rightarrow \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{xy} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {s_{11} } & {s_{12} } & {s_{13} } \\ {s_{21} } & {s_{22} } & {s_{23} } \\ {s_{31} } & {s_{32} } & {s_{33} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\tau_{xy} } \\ \end{array} } \right\},$$

(22)

where $\varvec{s}$ is the compliance elasticity matrix for the general anisotropic material case, which is defined in Eqs. (23) and (24), respectively, for the plane stress and plane strain formulations:

$$\varvec{s}_{\text{plane stress}} = \left[ {\begin{array}{*{20}c} {\frac{1}{{E_{11} }}} & { - \frac{{\upsilon_{21} }}{{E_{22} }}} & 0 \\ { - \frac{{\upsilon_{12} }}{{E_{11} }}} & {\frac{1}{{E_{22} }}} & 0 \\ 0 & 0 & {\frac{1}{{G_{12} }}} \\ \end{array} } \right]$$

(23)

$$\varvec{s}_{{{\text{plane}}\;{\text{strain}}}} = \left[ {\begin{array}{*{20}c} {\frac{{1 - \upsilon_{{\text{31}}} \upsilon_{{\text{13}}} }}{{E_{{\text{11}}} }}} & { - \frac{{\upsilon_{{\text{12}}} + \upsilon_{{\text{31}}} \upsilon_{{\text{23}}} }}{{E_{{\text{22}}} }}} & 0 \\ { - \frac{{\upsilon_{{\text{12}}} + \upsilon_{{\text{32}}} \upsilon_{{\text{13}}} }}{{E_{{\text{11}}} }}} & {\frac{{1 - \upsilon_{{\text{32}}} \upsilon_{{\text{23}}} }}{{E_{{\text{22}}} }}} & 0 \\ 0 & 0 & {\frac{1}{{G_{{\text{12}}} }}} \\ \end{array} } \right],$$

(24)

where $E_{ij}$ is the elasticity modulus, $\upsilon_{ij}$ is material Poisson coefficient, and $G_{ij}$ is the distortion modulus in material direction $i$ and $j$. The stress vector can be obtained with the expression: $\varvec{\sigma}= \varvec{c}\,\varvec{\varepsilon}$, being $\varvec{c} = \varvec{s}^{ - 1}$.

Considering small strains, the virtual strain vector can be obtained with the following relation:

$$\delta\varvec{\varepsilon}= \varvec{L}\,\delta \varvec{u}\, \Rightarrow \left\{ {\begin{array}{*{20}c} {\delta \varepsilon_{xx} } \\ {\delta \varepsilon_{yy} } \\ {\delta \gamma_{xy} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\frac{\partial }{\partial x}} & 0 \\ 0 & {\frac{\partial }{\partial y}} \\ {\frac{\partial }{\partial y}} & {\frac{\partial }{\partial x}} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\delta u} \\ {\delta v} \\ \end{array} } \right\}.$$

(25)

Thus, using Eq. (21), it is possible to develop the virtual strain vector to the following expression:

$$\begin{aligned} \delta\varvec{\varepsilon}(\varvec{x}_{I} ) & = \varvec{L}\,\delta \varvec{u}^{h} (\varvec{x}_{I} ) = \varvec{L}\sum\limits_{i = 1}^{n} {\varvec{H}_{i} (\varvec{x}_{I} )\,\delta \varvec{u}(\varvec{x}_{i} )} = \sum\limits_{i = 1}^{n} {\left[ {\varvec{L}\,\varvec{H}_{i} (\varvec{x}_{I} )} \right]\,\delta \varvec{u}(\varvec{x}_{i} )} \\ & = \sum\limits_{i = 1}^{n} {\varvec{B}_{i} (\varvec{x}_{I} )\,\delta \varvec{u}(\varvec{x}_{i} )} = \sum\limits_{i = 1}^{n} {\left[ {\begin{array}{*{20}c} {\frac{{\partial \varphi_{i} (\varvec{x}_{I} )}}{\partial x}} & 0 \\ 0 & {\frac{{\partial \varphi_{i} (\varvec{x}_{I} )}}{\partial y}} \\ {\frac{{\partial \varphi_{i} (\varvec{x}_{I} )}}{\partial y}} & {\frac{{\partial \varphi_{i} (\varvec{x}_{I} )}}{\partial x}} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\delta u(\varvec{x}_{i} )} \\ {\delta v(\varvec{x}_{i} )} \\ \end{array} } \right\}} . \\ \end{aligned}$$

(26)

Substituting in Eq. (19) the virtual strain vector $\delta\varvec{\varepsilon}(\varvec{x}_{I} )$ obtained in Eq. (26), the stress vector by $\varvec{\sigma}(\varvec{x}_{I} ) = \varvec{c}\,\varvec{\varepsilon}(\varvec{x}_{I} )\text{ = }\varvec{c}\,\varvec{L}\,\varvec{u}(\varvec{x}_{I} )$ and the virtual displacement vector $\delta \varvec{u}^{h} (\varvec{x}_{I} )$ with Eq. (21), it is possible to rewrite Eq. (19) for an interest point $\varvec{x}_{I}$:

$$\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1}^{n} {\delta \varvec{u}_{i}^{T} } } \underbrace {{\int_{\varOmega } {\varvec{B}_{i}^{T} \varvec{cB}_{j} \, } {\text{d}}\varOmega }}_{{\text{(}\varvec{K}_{I} \text{)}_{ij} }}\varvec{u}_{j} - \sum\limits_{i = 1}^{n} {\delta \varvec{u}_{i}^{T} \underbrace {{\int_{\varOmega } {\varvec{H}_{i}^{T} \left\{ {\begin{array}{*{20}c} {b_{x} } \\ {b_{y} } \\ \end{array} } \right\} \, } {\text{d}}\varOmega }}_{{\text{(}\varvec{f}_{b} \text{)}_{i} }} - } \sum\limits_{i = 1}^{n} {\delta \varvec{u}_{i}^{T} \underbrace {{\int_{{\varGamma_{t} }} {\varvec{H}_{i}^{T} \left\{ {\begin{array}{*{20}c} {t_{x} } \\ {t_{y} } \\ \end{array} } \right\} \, } {\text{d}}\varGamma_{t} }}_{{\text{(}\varvec{f}_{t} \text{)}_{i} }} = 0} .$$

(27)

In the end, after assembling the stiffness matrices $\varvec{K}_{I}$ obtained for each interest point, Eq. (27) can be represented as the following linear system of equations:

$$\delta \varvec{u}^{T} \left[ {\varvec{K}\,\varvec{u} - \varvec{f}_{b} - \varvec{f}_{t} } \right] = 0 \Rightarrow \varvec{K}\,\varvec{u} = \varvec{f}_{b} + \varvec{f}_{t} .$$

(28)

Since the RPI test functions possess the Kronecker delta property, the essential boundary conditions are directly imposed in the global stiffness matrix $\varvec{K}$ [3].

3 Elasto-plastic formulation

To capture the nonlinear behaviour of an elasto-plastic material, it is necessary to define the mathematical law for the plastic component of the deformation. Therefore, three aspects should be considered: a yield criterion, indicating the stress level in terms of the stress tensor and permitting to analyse the beginning of the plastic regime; a flow rule, defining the relationship between stress and deformation after plastification; and a hardening law, describing if, and how, the yield criterion depends on the plastic deformation [52].

3.1 Anisotropic yield criterion

The yield criterion permits to define the beginning of the plastic regime. Usually, a yield criterion can be formulated as: $F(\varvec{\sigma},\kappa ) = f(\varvec{\sigma}) - \sigma_{Y} (\kappa ) = 0$, where $\varvec{\sigma}$ is the stress tensor and $\kappa$ is the hardening parameter. The yield function is the scalar function $f(\varvec{\sigma})$ and $\sigma_{Y} (\kappa )$ is the yield stress, defining the elastic limit of the material. If the stress state at a point leads to $f(\varvec{\sigma}) < \sigma_{Y} (\kappa )$, it means that the point shows an elastic behaviour, governed by the linear equations of the theory of elasticity [53], otherwise, it means that the point is in the plastic region ($f(\varvec{\sigma}) = \sigma_{Y} (\kappa )$), under a loading or unloading condition, depending on the flow vector direction.

The yield criterion used in this work is the generalised Huber–Mises criterion [54] for an anisotropic material, which is known as the Hill yield criterion:

$$f\left( \sigma \right) = \bar{\sigma } = \left[ {\alpha_{12} (\sigma_{xx} - \sigma_{yy} )^{2} + \alpha_{23} (\sigma_{yy} - \sigma_{zz} )^{2} + \cdots + \alpha_{31} (\sigma_{zz} - \sigma_{xx} )^{2} + 3(\alpha_{44} \tau_{xy}^{2} + \alpha_{55} \tau_{yz}^{2} + \alpha_{66} \tau_{zx}^{2} )} \right]^{{\frac{1}{2}}} .$$

(29)

This yield function can be developed and the following expression is obtained:

$$f\left( \sigma \right) = \bar{\sigma } = \left[ {a_{11} \sigma_{xx}^{2} + a_{22} \sigma_{yy}^{2} + a_{33} \sigma_{zz}^{2} + \cdots + a_{12} \sigma_{xx} \sigma_{yy} + a_{23} \sigma_{yy} \sigma_{zz} + a_{31} \sigma_{zz} \sigma_{xx} + a_{44} \sigma_{xy}^{2} + a_{55} \sigma_{yz}^{2} + a_{66} \sigma_{zx}^{2} } \right]^{{\frac{1}{2}}} ,$$

(30)

where $a_{ij}$ are the material anisotropic parameters defined by: $a_{11} = \alpha_{31} + \alpha_{12}$, $a_{22} = \alpha_{12} + \alpha_{23}$, $a_{33} = \alpha_{23} + \alpha_{31}$, $a_{12} = - 2\alpha_{12}$, $a_{23} = - 2\alpha_{23}$, $a_{31} = - 2\alpha_{31}$, $a_{44} = 3\alpha_{44}$, $a_{55} = 3\alpha_{55}$ and $a_{66} = 3\alpha_{66}$. Thus, Eq. (30) can be represented in the matrix form:

$$f\left(\varvec{\sigma}\right) = \bar{\sigma } = \left[ {\varvec{\sigma}^{\text{T}} \varvec{M}_{A}\varvec{\sigma}} \right]^{{\tfrac{1}{2}}} ,$$

(31)

where $\varvec{M}_{A}$ is the anisotropic parameters matrix, defined as:

$$\varvec{M}_{A} = \left[ {\begin{array}{*{20}c} {a_{11} } & {\frac{{a_{12} }}{2}} & {\frac{{a_{31} }}{2}} & 0 & 0 & 0 \\ {\frac{{a_{12} }}{2}} & {a_{22} } & {\frac{{a_{23} }}{2}} & 0 & 0 & 0 \\ {\frac{{a_{31} }}{2}} & {\frac{{a_{23} }}{2}} & {a_{33} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {a_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {a_{55} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {a_{66} } \\ \end{array} } \right].$$

(32)

The initial anisotropic parameters, before hardening, can be determined resorting to six independent yield tests. For each one of these tests, all the components of the stress vector are considered zero, except for the required component. However, as the previous works indicate [55, 56], the anisotropic parameters are dependent on the actualized yield stress. Thus, the anisotropic parameters will vary along the plastic process. In the literature [55, 56], the following parameters are suggested:

$$a_{11} = \left[ {\frac{{\bar{\sigma }_{0} }}{{\sigma_{Y1} }}} \right]^{2} = \frac{{\bar{\varvec{\sigma }}^{2} }}{{\frac{{E_{T1} }}{{E_{T} }}\left( {\bar{\varvec{\sigma }}^{2} - \bar{\varvec{\sigma }}_{0}^{2} } \right) + \sigma_{Y10}^{2} }}$$

(33)

$$a_{22} = \left[ {\frac{{\bar{\sigma }_{0} }}{{\sigma_{Y2} }}} \right]^{2} = \frac{{\bar{\varvec{\sigma }}^{2} }}{{\frac{{E_{T2} }}{{E_{T} }}\left( {\bar{\varvec{\sigma }}^{2} - \bar{\varvec{\sigma }}_{0}^{2} } \right) + \sigma_{Y20}^{2} }}$$

(34)

$$a_{33} = \left[ {\frac{{\bar{\sigma }_{0} }}{{\sigma_{Y3} }}} \right]^{2} = \frac{{\bar{\varvec{\sigma }}^{2} }}{{\frac{{E_{T3} }}{{E_{T} }}\left( {\bar{\varvec{\sigma }}^{2} - \bar{\varvec{\sigma }}_{0}^{2} } \right) + \sigma_{Y30}^{2} }}$$

(35)

$$a_{44} = \left[ {\frac{{\bar{\sigma }_{0} }}{{\tau_{Y12} }}} \right]^{2} = \frac{{\bar{\varvec{\sigma }}^{2} }}{{\frac{{G_{T12} }}{{E_{T} }}\left( {\bar{\varvec{\sigma }}^{2} - \bar{\varvec{\sigma }}_{0}^{2} } \right) + \tau_{Y120}^{2} }}$$

(36)

$$a_{55} = \left[ {\frac{{\bar{\sigma }_{0} }}{{\tau_{Y23} }}} \right]^{2} = \frac{{\bar{\varvec{\sigma }}^{2} }}{{\frac{{G_{T23} }}{{E_{T} }}\left( {\bar{\varvec{\sigma }}^{2} - \bar{\varvec{\sigma }}_{0}^{2} } \right) + \tau_{Y230}^{2} }}$$

(37)

$$a_{66} = \left[ {\frac{{\bar{\sigma }_{0} }}{{\tau_{Y31} }}} \right]^{2} = \frac{{\bar{\varvec{\sigma }}^{2} }}{{\frac{{G_{T31} }}{{E_{T} }}\left( {\bar{\varvec{\sigma }}^{2} - \bar{\varvec{\sigma }}_{0}^{2} } \right) + \tau_{Y310}^{2} }},$$

(38)

where $\bar{\varvec{\sigma }}_{0}$ is the yield stress in the material reference direction and $\sigma_{Yj0}$ is the yield stress in the material principal direction $j$ before hardening. $E_{T1}$, $E_{T2}$ and $E_{T3}$ are the tangential modulus in the directions 1, 2 and 3, respectively. $E_{T}$ is the effective tangential modulus. $G_{T12}$, $G_{T23}$ and $G_{T31}$ are the tangent shear modules. These quantities are independent and obtained experimentally.

To obtain $a_{12}$, it is necessary to submit a material sample obtained from the material plane 1–2 to an uniaxial tensile test [57]. Considering that the sample axis is oriented by an angle $\beta$ in relation to material direction 1, and $\sigma_{Y\beta 0}$ is the uniaxial yield stress in direction 1–2 before hardening, obtained in the aforementioned test, $a_{12}$ is defined as:

$$a_{12} = \frac{{\bar{\sigma }_{0} }}{{\left[ {\frac{{E_{T\beta } }}{{E_{T} }}\left( {\bar{\varvec{\sigma }}^{2} - \bar{\varvec{\sigma }}_{0}^{2} } \right) + \sigma_{Y\beta 0}^{2} } \right] \cdot \sin^{2} \beta \cdot \cos^{2} \beta }} - \frac{{a_{11} \cdot \cos^{4} \beta + a_{22} \cdot \sin^{4} \beta + a_{44} \cdot \cos^{2} \beta \cdot \sin^{2} \beta }}{{\cos^{2} \beta \cdot \sin^{2} \beta }},$$

(39)

where $E_{T\beta }$ is the tangential modulus in direction $\beta$. Applying the same procedure in direction 2–3, considering now the sample oriented with an angle $\varphi$ in relation to material direction 2, the parameter $a_{23}$ can be obtained with:

$$a_{23} = \frac{{\bar{\sigma }_{0} }}{{\left[ {\frac{{E_{T\varphi } }}{{E_{T} }}\left( {\bar{\varvec{\sigma }}^{2} - \bar{\varvec{\sigma }}_{0}^{2} } \right) + \sigma_{Y\varphi 0}^{2} } \right] \cdot \sin^{2} \varphi \cdot \cos^{2} \varphi }} - \frac{{a_{22} \cdot \cos^{4} \varphi + a_{33} \cdot \sin^{4} \varphi + a_{55} \cdot \cos^{2} \varphi \cdot \sin^{2} \varphi }}{{\cos^{2} \varphi \cdot \sin^{2} \varphi }}.$$

(40)

To obtain the parameter $a_{31}$, the sample is oriented with an angle $\phi$ in relation to material direction 3:

$$a_{31} = \frac{{\bar{\sigma }_{0} }}{{\left[ {\frac{{E_{T\phi } }}{{E_{T} }}\left( {\bar{\varvec{\sigma }}^{2} - \bar{\varvec{\sigma }}_{0}^{2} } \right) + \sigma_{Y\phi 0}^{2} } \right] \cdot \sin^{2} \phi \cdot \cos^{2} \phi }} - \frac{{a_{11} \cdot \sin^{4} \phi + a_{33} \cdot \cos^{4} \phi + a_{66} \cdot \cos^{2} \phi \cdot \sin^{2} \phi }}{{\cos^{2} \phi \cdot \sin^{2} \phi }}.$$

(41)

In this work, only two-dimensional analyses are performed, which permits to simplify the problem formulation. If the problem is analysed assuming the plane strain deformation theory, then $\tau_{yz} = \tau_{zx} = 0$, leading to an anisotropic parameter matrix $\varvec{M}_{A}$ with size $[4 \times 4]$. If the plane stress assumptions are considered, $\sigma_{zz} = \tau_{yz} = \tau_{zx} = 0$, the anisotropic parameter matrix $\varvec{M}_{A}$ becomes a $[3 \times 3]$ symmetric matrix.

In the numerical analyses where the principal material axes are not coincident with the global referential axis $(x,y)$, the anisotropic parameters must be transformed to the global reference system. Considering a material orientated with an angle $\theta$ with relation to the global 2D referential $Oxy$, the effective stress can be written in the form presented in Eq. (42), where the transformed matrix of the anisotropic parameters, $\bar{\varvec{M}}_{A}$, is obtained with Eq. (43). The transformation matrix $\varvec{T}$, defined in Eq. (44), permits to account the orientation of the material:

$$f\left(\varvec{\sigma}\right) = \bar{\sigma } = \left[ {\varvec{\sigma}^{T} \bar{\varvec{M}}_{A}\varvec{\sigma}} \right]^{{\tfrac{1}{2}}}$$

(42)

$$\bar{\varvec{M}}_{A} = \varvec{T}^{T} \varvec{M}_{A} \varvec{T}$$

(43)

$$\varvec{T} = \left[ {\begin{array}{*{20}c} {\cos^{2} \theta } & {\sin^{2} \theta } & 0 & { - \sin 2\theta } & 0 & 0 \\ {\sin^{2} \theta } & {\cos^{2} \theta } & 0 & {\sin 2\theta } & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ {\sin \theta \cdot \cos \theta } & { - \sin \theta \cdot \cos \theta } & 0 & {\cos^{2} \theta - \sin^{2} \theta } & 0 & 0 \\ 0 & 0 & 0 & 0 & {\cos \theta } & { - \sin \theta } \\ 0 & 0 & 0 & 0 & {\sin \theta } & {\cos \theta } \\ \end{array} } \right].$$

(44)

3.2 Plastic flow rule

In this works, it is considered the associated flow rule, since the plastic flow is associated with the yield criterion. The Prandtl-Reuss flow rule defines that the plastic strain is defined as:

$${\text{d}}\varvec{\varepsilon}_{p} = {\text{d}}\lambda \frac{\partial f}{{\partial\varvec{\sigma}}} = {\text{d}}\lambda \,\varvec{a,}$$

(45)

where ${\text{d}}\lambda$ is the plastic rate multiplier and $\varvec{a}$ is the flow vector, normal to the adopted yield function, $f$, defined by Eq. (42). The flow vector can be presented as:

$${\mathbf{a}} = \partial f/\partial\varvec{\sigma}= \left[ {\begin{array}{*{20}c} {\frac{\partial f}{{\partial \sigma_{xx} }}} & {\frac{\partial f}{{\partial \sigma_{yy} }}} & {\frac{\partial f}{{\partial \sigma_{zz} }}} & {\frac{\partial f}{{\partial \sigma_{xy} }}} & {\frac{\partial f}{{\partial \sigma_{yz} }}} & {\frac{\partial f}{{\partial \sigma_{zx} }}} \\ \end{array} } \right]$$

(46)

and considering the yield function defined in Eq. (42):

$$\frac{\partial f}{{\partial \sigma_{xx} }} = \frac{1}{{\bar{\sigma }}}\left[ {\bar{a}_{11} \sigma_{xx} + \bar{a}_{12} \sigma_{yy} + \bar{a}_{13} \sigma_{zz} } \right]$$

(47)

$$\frac{\partial f}{{\partial \sigma_{yy} }} = \frac{1}{{\bar{\sigma }}}\left[ {\bar{a}_{21} \sigma_{xx} + \bar{a}_{22} \sigma_{yy} + \bar{a}_{23} \sigma_{zz} } \right]$$

(48)

$$\frac{\partial f}{{\partial \sigma_{zz} }} = \frac{1}{{\bar{\sigma }}}\left[ {\bar{a}_{31} \sigma_{xx} + \bar{a}_{32} \sigma_{yy} + \bar{a}_{33} \sigma_{zz} } \right]$$

(49)

$$\frac{\partial f}{{\partial \sigma_{xy} }} = \frac{1}{{\bar{\sigma }}}\left[ {\bar{a}_{44} \sigma_{xy} } \right]$$

(50)

$$\frac{\partial f}{{\partial \sigma_{yz} }} = \frac{1}{{\bar{\sigma }}}\left[ {\bar{a}_{55} \sigma_{yz} } \right]$$

(51)

$$\frac{\partial f}{{\partial \sigma_{zx} }} = \frac{1}{{\bar{\sigma }}}\left[ {\bar{a}_{66} \sigma_{zx} } \right].$$

(52)

3.3 Hardening law

Following the linear elastic Hooke law, the following relation between the stress rate ${\text{d}}\varvec{\sigma}$ and the elastic strain rate ${\text{d}}\varvec{\varepsilon}_{e}$ is assumed:

$${\text{d}}\varvec{\sigma}= \varvec{c}\,{\text{d}}\varvec{\varepsilon}_{e} = \varvec{c}\left( {{\text{d}}\varvec{\varepsilon - }{\text{d}}\varvec{\varepsilon}_{p} } \right),$$

(53)

where ${\text{d}}\varvec{\varepsilon}$ is the total strain rate and ${\text{d}}\varvec{\varepsilon}_{p}$ is the plastic strain rate. Considering the associated flow rule, Eq. (45), and assuming that the yield surface, $F(\varvec{\sigma},\kappa )$, only depends on the magnitude of the applied principal stresses and of a hardening parameter $\kappa$, $F(\varvec{\sigma},\kappa ) = f(\varvec{\sigma},\kappa ) - \sigma_{Y} (\kappa ) = 0$, Eq. (53) can be rewritten as:

$${\text{d}}\varvec{\sigma}= \varvec{c}\left( {{\text{d}}\varvec{\varepsilon - }{\text{d}}\lambda \,\varvec{a}} \right).$$

(54)

The stress must remain on the yield surface to occur plastic flow. Therefore,

$${\text{d}}F = \frac{\partial f}{{\partial\varvec{\sigma}}}{\text{d}}\varvec{\sigma - }\frac{{\partial \sigma_{Y} }}{\partial \kappa }{\text{d}}\kappa = 0$$

(55)

or

$${\text{d}}F = \varvec{a}^{T} {\text{d}}\varvec{\sigma - }A\,{\text{d}}\lambda = 0,$$

(56)

where $A$ is an hardening parameter that depends on the hardening rule [52], defined by:

$$A = \frac{1}{{{\text{d}}\lambda }}\frac{{\partial \sigma_{Y} }}{\partial \kappa }{\text{d}}\kappa .$$

(57)

Applying Eq. (54) on Eq. (56),

$${\text{d}}\lambda = \frac{{\varvec{a}^{T} \varvec{c}\,{\text{d}}\varvec{\varepsilon}}}{{\varvec{a}^{T} \varvec{c a} + A}}.$$

(58)

Introducing the value of ${\text{d}}\lambda$ into Eq. (54), the stress rate can be written as:

$${\text{d}}\varvec{\sigma}= \varvec{c}\,{\text{d}}\varvec{\varepsilon}- \frac{{\varvec{a}^{T} \varvec{c }\,{\text{d}}\varvec{\varepsilon}}}{{\varvec{a}^{T} \varvec{c a} + A}} \cdot \varvec{c a}\,=\left( {\varvec{c} - \frac{{\varvec{c a a}^{T} \varvec{c}}}{{\varvec{a}^{T} \varvec{c a} + A}}} \right){\text{d}}\varvec{\varepsilon} = {c}_{t} \,{\text{d}}\varvec{\varepsilon ,}$$

(59)

where $\varvec{c}_{t}$ is the tangential constitutive matrix. To define explicitly the hardening parameter $A$, the work hardening hypothesis is employed [52] considering the associated flow rule. Since all the nonlinear materials used in the present work show a “linear elastic”-“linear plastic” hardening behaviour, the hardening parameter $A$ can be defined as [52]:

$$A = \frac{{E_{To} }}{{1 - \frac{{E_{To} }}{{E_{o} }}}},$$

(60)

where $E_{o}$ and $E_{To}$ are the elastic modulus and the tangential modulus in the reference direction, respectively.

3.4 Stress returning algorithm

In this work, the material behaviour is modelled in the form of an incremental relation between the incremental stress vector and the strain increment. To force the stress to return to the yield surface, the “backward-Euler” procedure [43] shown in Fig. 2 is considered.

Fig. 2

Backward-Euler scheme

Within this methodology, which solves the nonlinear equations acting on the level of the Gauss points, it is not require to determine the intersection point of the incremental load with the yield surface, point $A$. Thus, after the incremental load application, and for each Gauss point, it is verified if the achieved stress state is inside or outside the yield surface. The stress returning algorithm is called every time the stress state is outside the yield surface. Consider the stress on point $B$ represented in the two-dimensional Westergaard stress space, Fig. 2. Since point $B$ is outside the yield surface, it must be pushed back to point $C$, on the yield surface. To perform the returning of the stress state to the yield surface, the implemented algorithm starts with a predictor, simulating that point $B$ is on the surface of a ‘forward’ yield function $f_{B}$, consequently avoiding the computing of the intersection point $A$. The flow vector is calculated from point $B$, $\varvec{a}_{B}$, being the yield function in point $B$ defined by $f_{B} = \bar{\sigma }_{B} - \sigma_{Y}^{ * }$, where $\sigma_{Y}^{ * }$ is the updated yield stress. Next, using Eq. (54), an estimative of the stress in point $C$ is obtained:

$$\varvec{\sigma}_{C} \varvec{ = \sigma }_{B} - {\text{d}}\lambda \, \varvec{c} \, \varvec{a}_{B} .$$

(61)

To correctly obtain the stress in point $C$, it should be used the flow vector on point $C$, $\varvec{a}_{C}$. However, $\varvec{a}_{C}$ cannot be directly obtained with only the data from points $X$ and $B$. Hence, the information from point $B$ must be employed to estimate point $C$. This process continues iteratively until $C$ is satisfactorily approximated, concluding the process.

3.5 Nonlinear solution algorithm

The solution algorithm, used in the nonlinear NNRPIM code developed by the authors, is shown in Fig. 3 and summarised as follows.

Fig. 3

NNRPIM and KT0 algorithm

First, the problem domain is discretized with a nodal distribution and a nodal dependent integration mesh is constructed. Afterwards, the nodal connectivity is defined, and the interpolation functions are obtained for each integration point. Then, the linear elastic stiffness matrix, $\varvec{K}_{0}$, can be constructed, ending the preprocessing phase.

Since this work considers the elasto-plastic deformation problem, the incremental form of the discretized system [presented in Eq. (28)] within an incremental load can be written as:

$$\varvec{K}_{T} \Delta \varvec{u} - \Delta \varvec{f} = \varvec{f}^{\text{res}} ,$$

(62)

where $\varvec{K}_{T}$ is the tangent stiffness matrix, $\Delta \varvec{u}$ is the incremental displacement field and $\Delta \varvec{f}$ is the incremental load vector. The residual force vector is defined as $\varvec{f}^{\text{res}}$. This work considers a variation of the Newton–Raphson nonlinear solution method—initial stiffness method combined with an incremental solution (KT0)—to solve the nonlinear equations [43]. Within this approach, the stiffness matrix is calculated only once: at the preprocessing phase ($\varvec{K}_{0}$) assuming the elastic constitutive matrix. Thus, for any given increment, $j$: $\varvec{K}_{T}^{j} \varvec{ = K}_{0} ,\forall j \in {\mathbb{N}}$.

The overall solving process is given by the following algorithm. First, construct the initial stiffness matrix $\varvec{K}_{0}$ and set as ${\mathbf{0}}$ the vectors: $\varvec{u}$, $\varvec{f}$ and $\varvec{f}^{res}$. Then, begin the incremental procedure:

• 1. Set $\Delta \varvec{f}$ equal to the current increment load vector $\varvec{f}^{j}$: $\Delta \varvec{f = f}^{j}$.

• 2. Solve $\Delta \varvec{u = K}_{0} \Delta \varvec{f}$.

• 3. Set $\varvec{u}^{j} \varvec{ = u}^{j - 1} + \Delta \varvec{u}$.

• 4. For each integration point, evaluate the strain increment: $\Delta\varvec{\varepsilon}= \varvec{B}\Delta \varvec{u}$.

• 5. Using the elastic constitutive matrix ($\varvec{c} = \varvec{s}^{ - 1}$, from Eqs. (23) and (24)) evaluate, at each integration point, the incremental stress state: $\Delta\varvec{\sigma}= \varvec{c}\Delta\varvec{\varepsilon}$, and the trial total stress state: $\varvec{\sigma}_{\text{trial}}^{j} \varvec{ = \sigma }^{j - 1} + \Delta\varvec{\sigma}$.

• 6. At each integration point, evaluate $\varvec{\sigma}_{\text{trial}}^{j}$ to satisfy the yield criterion. If $f(\varvec{\sigma}_{\text{trial}}^{j} ) \le \sigma_{Y} (\kappa )$, then: $\varvec{\sigma}_{\text{new}}^{j} \text{ = }\varvec{\sigma}_{\text{trial}}^{j}$, otherwise, the algorithm described in Sect. 3.4 is applied and a new modified total stress state is obtained: $\varvec{\sigma}_{\text{new}}^{j} \ne\varvec{\sigma}_{\text{trial}}^{j}$. After the evaluation, it is possible to define the total stress field of the present increment: $\varvec{\sigma}^{j} =\varvec{\sigma}_{\text{new}}^{j}$. Notice that the incremental stress and strain resultant relation is valid under the assumption of a proportional loading path.

• 7. Evaluate the residual force vector: $\varvec{f}^{\text{res}} = \Delta \varvec{f} - \int_{\varOmega } {B^{T} (\varvec{\sigma}^{j} -\varvec{\sigma}^{j - 1} )} {\text{d}}\varOmega$.

• 8. Check the convergence using the following residual force convergence criteria: $E^{\text{res}} = \text{(}\varvec{f}^{\text{res}} \cdot \varvec{f}^{\text{res}} )^{1/2} \times \text{(}\varvec{f}^{j} \cdot \varvec{f}^{j} )^{ - 1/2} < {\text{toler}}$, where ${\text{toler}}$ is a specified tolerance.

• 9. If $E^{\text{res}} < {\text{toler}}$, the process moves to step 1. Else, the process moves to the iterative phase: step 10.

• 10. The iterative procedure starts with iteration $i = 0$, setting: $\varvec{u}_{0}^{j} = \varvec{u}_{{}}^{j}$, $\varvec{\sigma}_{0}^{j} =\varvec{\sigma}_{{}}^{j}$ and $\varvec{f}_{0}^{\text{res}} = \varvec{f}^{\text{res}}$. Afterwards, the iterative procedure continues:

  • 10.1 Set $\Delta \varvec{f}$ equal to the last residual force vector $\varvec{f}_{i - 1}^{\text{res}}$: $\Delta \varvec{f} = {f}_{i - 1}^{\text{res}}$.

  • 10.2. Solve $\Delta \varvec{u} = {K}_{0} \Delta \varvec{f}$.

  • 10.3. Set $\varvec{u}_{i}^{j} = \varvec { u}_{i - 1}^{j} + \Delta \varvec{u}$.

  • 10.4. For each integration point, evaluate the strain iterative increment: $\Delta\varvec{\varepsilon}= \varvec{B}\Delta \varvec{u}$.

  • 10.5. Using the elastic constitutive matrix ($\varvec{c} = \varvec{s}^{ - 1}$, from Eqs. (23) and (24)) evaluate, at each integration point, the iterative incremental stress state: $\Delta\varvec{\sigma}= \varvec{c}\Delta\varvec{\varepsilon}$, and the trial total stress state: $\text{(}\varvec{\sigma}_{\text{trial}}^{j} \text{)}_{i} \varvec{ = \sigma }_{i - 1}^{j} + \Delta\varvec{\sigma}$.

  • 10.6. At each integration point, evaluate $\text{(}\varvec{\sigma}_{\text{trial}}^{j} \text{)}_{i}$ to satisfy the yield criterion. If $f(\text{(}\varvec{\sigma}_{\text{trial}}^{j} \text{)}_{i} ) \le \sigma_{Y} (\kappa )$, then: $\text{(}\varvec{\sigma}_{\text{new}}^{j} \text{)}_{i} \text{ = (}\varvec{\sigma}_{\text{trial}}^{j} \text{)}_{i}$, otherwise, the algorithm described in Sect. 3.4 is applied and a new modified total stress state is obtained: $\text{(}\varvec{\sigma}_{\text{new}}^{j} \text{)}_{i} \ne \text{(}\varvec{\sigma}_{\text{trial}}^{j} \text{)}_{i}$. After the evaluation, it is possible to define the total stress field of the present iteration: $\varvec{\sigma}_{i}^{j} = \text{(}\varvec{\sigma}_{\text{trial}}^{j} \text{)}_{i}$.

  • 10.7. Evaluate the residual force vector: $\varvec{f}_{i}^{\text{res}} = \Delta \varvec{f} - \int_{\varOmega } {B^{T} (\varvec{\sigma}_{i}^{j} -\varvec{\sigma}_{i - 1}^{j} )} {\text{d}}\varOmega$.

  • 10.8. Check the convergence using: $E^{\text{res}} = \text{(}\varvec{f}_{i}^{\text{res}} \cdot \varvec{f}_{i}^{\text{res}} )^{1/2} \times \text{(}\varvec{f}^{j} \cdot \varvec{f}^{j} )^{ - 1/2} < {\text{toler}}$.

  • 10.9. If $E^{\text{res}} < {\text{toler}}$, the process moves to step (1). Else, the process continues in the iterative phase, moving to step (10.1).

4 Numerical examples

In this section, several two-dimensional benchmark examples are presented. The results obtained with the NNRPIM are compared with FEM solutions obtained by the commercial software ANSYS 14.0, considering exactly the same nodal spatial distribution and the same material properties. Regarding the FEM ANSYS analysis, it was used the linear quadrilateral finite element: PLANE182, with bilinear interpolation, indicated for 2D plane strain and 2D plane stress. In addition, concerning the plasticity model of ANSYS, to permit a fair comparison, it was considered the “generalised anisotropic Hill potential” option.

4.1 Cook’s membrane

The benchmark example of the Cook’s membrane with the geometry, properties and boundary conditions presented in Fig. 4a is analysed [58]. The problem was studied considering the plane stress assumptions, and the domain was discretized with the irregular nodal distribution shown in Fig. 4b. The same nodal discretization was used to obtain the NNRPIM and the FEM solutions using ANSYS.

Fig. 4

a Cook’s membrane; b Irregular nodal mesh with 414 nodes

In Fig. 5, the plots of horizontal, $u_{A}$, and vertical, $v_{A}$, displacement components of node $A$, Fig. 4a, versus the applied uniform distributed load $P$ are presented for both NNRPIM and FEM ANSYS solutions. As it is visible, the NNRPIM solution adjusts very well to the FEM ANSYS solution for both the displacement components.

Fig. 5

Load–displacement curve for: a the horizontal displacement of point A; b the vertical displacement of point A

Figure 6 shows the distribution of the normal stress $\sigma_{xx}$ along the membrane’s essential boundary ($x = 0$ and $y = [0,44]$) for increasing values of the applied uniform distributed load. Similar to the load–displacements curves presented in Fig. 5, a nearly close correlation between the NNRPIM and FEM ANSYS solution is obtained, even for higher load levels. As it would be expected, due to the type of the applied load and the geometry of the Cook’s membrane, it is possible to visualise a stress concentration in the top-left corner of the Cook’s membrane, at $\{ x,y\} = \{ 0,44\} \;{\text{m}}$. As a consequence, these nodes are the first to yield.

Fig. 6

Normal stress distribution along the membrane essential boundary for increasing load levels

Figure 7 shows the distribution of the shear stress $\tau_{xy}$ along the left boundary ($x = 0$). Once again, the NNRPIM solution shows a good correlation with the FEM ANSYS solutions. However, it is possible to observe that the two solutions are not as close as the solutions obtained for the normal stress $\sigma_{xx}$. The distribution of the normal stress $\sigma_{xx}$ and the shear stress $\tau_{xy}$ on the global problem domain are shown in Fig. 8 for different load levels.

Fig. 7

Shear stress distribution along the membrane essential boundary for increasing load levels

Fig. 8

Distribution of normal (σ _xx) and shear (τ _xy) stress along the Cook’s membrane for distinct stages of load

4.2 Infinite plate with a circular hole

The second example, considering only isotropic materials with isotropic hardening, is an infinite plate with a circular hole subjected to a traction pressure in the extremities. Due to the double symmetry of the infinite plate, the problem can be simplified, as shown in Fig. 9a. The material properties are shown in Fig. 9a. The problem domain was discretized with the nodal distribution shown in Fig. 9b. In this example, it was considered the plane stress deformation theory.

Fig. 9

a Quarter of an Infinite plate with a circular hole; b Irregular nodal mesh with 1654 nodes

The elasto-plastic results obtained with the NNRPIM and the FEM ANSYS regarding the punctual displacements evolution with the load increment in control points $A$, $B$ and $C$, Fig. 9a, are shown in Fig. 10. For the interest point $A$, it is shown the vertical displacement component: $v_{A}$, Fig. 10a. For the interest point $B$, it is presented the quadratic norm of the local displacement: $d_{B} = \sqrt {u_{B}^{2} + v_{B}^{2} }$, Fig. 10b. The horizontal displacement component: $u_{C}$, on interest point $C$ is shown in Fig. 10c. The results show that the NNRPIM solution is very close with the FEM ANSYS solution.

Fig. 10

Load displacement curve for: a the vertical displacement in point A; b the displacement in point B; and c the horizontal displacement in point C

Figure 11 shows the normal stress $\sigma_{xx}$ distribution along the vertical essential boundary ($x = 0$ and $y = [2,5]$) for increasing load levels. A close correlation between the NNRPIM and FEM ANSYS solution is obtained, even for higher values of load. As expected, the bottom nodes are the firsts to yield, since discontinuities introduce higher stresses.

Fig. 11

Normal stress distribution along the vertical essential boundary for increasing load levels

Regarding the stress distribution, it is possible to observe in Fig. 12 that the stress field’s distributions obtained, for distinct load levels, present a smooth variation. With Fig. 12, it is also possible to visualise the evolution of the stress along the plate.

Fig. 12

Stress field distribution (σ _xx) obtained for the infinite plate with a circular hole

4.3 Cantilever beam

In this section, the cantilever beam represented in Fig. 13, loaded in the free end with a vertical uniform distributed load, is analysed. The considered material properties for isotropic and anisotropic behaviour are the same assumed by Brünig [59], which are referred in Fig. 13.

Fig. 13

Cantilever beam

The problem was analysed considering the plane stress assumptions, and the domain was discretized with two distinct nodal distributions: a regular nodal discretization and an irregular nodal distribution, both with 516 nodes, Fig. 14a, b. Only the regular discretization was used to obtain FEM ANSYS solutions.

Fig. 14

Nodal meshes of the cantilever beam. a Regular nodal mesh; b Irregular nodal mesh

In Fig. 15, the plots of the vertical displacement component, $v_{A}$, on node $A$, Fig. 13, versus the uniform distribute load $P$ are presented for both NNRPIM and FEM ANSYS solutions.

Fig. 15

Cantilever Beam: load displacement curves for anisotropic and isotropic material behaviours

As it is visible, the NNRPIM solution adjusts very well to the FEM ANSYS solution, regardless the material used: isotropic or anisotropic. Due to the similarity of the NNRPIM results obtained with the regular (NNRPIM RM) and irregular (NNRPIM IM) nodal discretization for the isotropic material behaviour, only the regular nodal distribution was considered in the anisotropic analysis.

From Fig. 15, it is visible that, comparing the results from the analyses of the two materials (isotropic and anisotropic), the anisotropic material yields later and shows a higher load-carrying capacity during loading. As it can be seen from Fig. 15, while the anisotropic material shows only a vertical displacement $v = 35\;{\text{mm}}$ for an applied load of $5.5\;{\text{kN}}/{\text{m}}$, for the same load value, the isotropic material shows approximately a vertical displacement $v = 65\;{\text{mm}}$ in point $A$, which is almost the double.

Figure 16 shows the normal stress $\sigma_{xx}$ distribution along the clamped side ($x = 0$ and $y = [0,4]$) of the isotropic cantilever beam for increasing load values. From Fig. 16, it can be seen that the NNRPIM solution is very close with the FEM ANSYS solution, even for higher values of load.

Fig. 16

Cantilever beam: normal stress (σ _xx) distribution along the essential boundary for increasing load levels, considering isotropic material behaviour

Regarding the stress distribution along the domain of the cantilever beam and considering the isotropic material and the regular nodal discretization, it is possible to observe in Fig. 17 that the stress fields obtained for distinct load levels present a smooth variation. In Fig. 17, it is also possible to visualise the most stressed regions of the beam, where the yielding occurs first.

Fig. 17

Stress field distribution (σ _xx) obtained for the cantilever beam, considering distinct load levels

Figure 18 shows the formation of plastic zones (dark grey) during load, for isotropic and anisotropic materials. It also shows that yielding starts earlier in the isotropic case, being the results comparable, and very similar, to Brünig results [59].

Fig. 18

Formation of plastic zones

4.4 Punch pressure

In this section, another benchmark example is studied [59], in which a rigid punch is pressed over a solid. The problem is analysed assuming the plane strain deformation theory. The geometry, the boundary conditions and the material properties of the problem are shown in Fig. 19. The considered material properties for isotropic and anisotropic material behaviour are the same assumed by Brünig [59].

Fig. 19

Rigid punch

The problem domain was discretized with an irregular nodal distribution (1977 nodes), as shown in Fig. 20. As it is visible, the irregular discretization has a high concentration of nodes in the nearby region of application of the rigid punch, where higher stresses are expected.

Fig. 20

Rigid punch nodal meshes

In Fig. 21, it is presented the load–displacement curves of the vertical displacement $v_{A}$ of node $A$, the node immediately below the node with coordinates $\{ x,y\} = \{ 3,5.1\}$. The NNRPIM solutions are compared with the FEM ANSYS solutions.

Fig. 21

Rigid punch: load displacement curves for anisotropic and isotropic material behaviours considering an irregular nodal mesh

From Fig. 21, it is visible that NNRPIM solution shows a close correlation with FEM ANSYS solution. Figure 21 also shows that the load-carrying behaviour increases considerably when anisotropic materials are considered, as happened in the previous example, the cantilever beam.

The normal stress $\sigma_{yy}$ distribution along the vertical essential boundary ($x = 0$ and $y = [0,5.1]$) for increasing load levels is shown in Fig. 22. A close correlation between the NNRPIM and FEM ANSYS solution is obtained for all the load levels considered.

Fig. 22

Rigid punch: normal stress distribution (σ _yy) along the essential boundary with x = 0 for increasing load levels, considering isotropic material behaviour and an irregular nodal mesh

At last, Fig. 23 shows the distribution of the normal $\sigma_{yy}$ stresses along the geometry of the considered problem, for the different stages of applied loads. A smooth variation of the stress field is observed in all the distinct load levels considered (Fig. 23).

Fig. 23

Stress field distribution (σ _yy) obtained for the rigid punch example, considering distinct load levels and an irregular nodal mesh

5 Conclusions

In this work, the NNRPIM was extended to the analysis of nonlinear elasto-plastic examples, considering a small strain formulation. The modified Newton–Raphson initial stiffness method combined with an incremental solution (KT0) was used to solve the nonlinear system of equations. The generalised Huber–Mises criterion, also known as Hill yield criterion, was considered in the elasto-plastic formulation. To return the stress to the Hill anisotropic yield surface, it was assumed a “backward-Euler” procedure. From the results obtained in this work, it can be concluded that:

• i. The nonlinear solution algorithm was successfully implemented in the context of the used meshless method, as well as the algorithm to return the stress to the yield surface.

• ii. With the NNRPIM, the imposition of the boundary conditions is straightforward, reducing the computational time when compared with approximation methods, in which complex and computational expensive numerical procedures have to be considered.

• iii. The irregularity of the discretization does not significantly affect the final results. In addition, the convex boundaries of the problem, due to the NNRPIM node connectivity scheme, do not represent a setback, as in other meshless methods that for instances use the influence-domain concept.

• iv. The NNRPIM analysis produces a variable fields smooth, accurate and very close to the FEM ANSYS solution.

The major advantage of the NNRPIM is that it permits to define the nodal connectivity, the integration mesh and the interpolation functions using uniquely the information of the nodal discretization, which is a characteristic of truly meshless methods. This property allows the NNRPIM to analyse any numerical problem requiring only the information from the computational nodal distribution.

Nevertheless, it is important to mention the NNRPIM principal disadvantage. This meshless method technique, due to its heavy preprocessing phase, presents a higher computational cost when compared with FEM. The determination of the natural neighbours and the construction of the integration mesh represent most of the computational cost of the analysis.