The virtual stress boundary method to impose nonconforming Neumann boundary conditions in the material point method

Abstract

The material point method (MPM) is a popular and powerful tool for simulating large deformation problems. The hybrid Eulerian–Lagrangian nature of the MPM means that the Lagrangian material points and the Eulerian background mesh are often nonconforming. Once the material and mesh boundaries become misaligned, imposing boundary conditions, such as Neumann boundary conditions (i.e., traction), becomes a challenge. The recently developed virtual stress boundary (VSB) method allows for imposing nonconforming Neumann boundary conditions without explicit knowledge of the boundary position. This is achieved through a problem transformation where the original boundary traction problem is replaced by an equivalent problem featuring a virtual stress field. This equivalent problem results in updated governing equations which are ultimately solved using a combination of particle-wise and cell-wise quadrature. In the current work, a modification to the VSB method is proposed to eliminate the need for cell-wise quadrature. Despite removing cell-wise quadrature, the modified VSB method maintains the accuracy observed in the original approach. Several numerical examples, including 1D and 2D benchmark problems, as well as a 3D demonstration problem, are presented to investigate the accuracy and illustrate the capability of the modified VSB method. Mesh refinement studies are included to show the method’s good convergence behavior.

1 Introduction

The material point method (MPM) is a continuum-based particle method utilized for solving the governing equations through a combined Eulerian–Lagrangian approach [1, 2]. In the MPM, the material domain is discretized into a set of Lagrangian material points which are used in conjunction with an Eulerian background mesh to solve Newton’s equation of motion. The MPM is classified as a meshless method since the material points store all information throughout the simulation, and the background mesh primarily plays a supportive role in the calculation process, with Newton’s equations being solved at the mesh nodes. Utilizing mesh nodes to solve the equations of motion bears similarity to the approach used in the finite element method (FEM) [3]. However, in the MPM, the Eulerian nature of the mesh means there is no accumulated distortion within the mesh. The Lagrangian nature of the material points allows for the inclusion of history-dependent parameters, such as plasticity, in the MPM. This combined Eulerian–Lagrangian approach means that the MPM may provide advantages over the FEM in some situations, such as modeling large deformation problems, since the FEM often struggles with excessive numerical errors as mesh distortion accumulates. Recently, the MPM has been successfully used to simulate a wide variety of large deformation phenomena including hypervelocity impact [4,5,6,7], penetration [8, 9], explosion [10, 11], fracture evolution [12,13,14,15,16], fluid–structure interaction [17,18,19,20], multiphase flow [21], shear band evolution [22], geotechnical failure [23,24,25,26], etc. The reader is referred to [27,28,29] for a complete description of the MPM, more applications of the MPM, and further references.

Despite the widespread application of the MPM in many engineering fields, one critical aspect that still limits its application is the imposition of the boundary conditions, including both Dirichlet [30] and Neumann boundary conditions. Although some researchers have studied this issue in the previous publications [31,32,33], further advancements are necessary to fully address this challenge. Depending on whether the material boundary aligns with the computational mesh, the boundary conditions can be classified into two categories, namely, conforming boundaries and nonconforming boundaries. The imposition of conforming boundaries is straightforward [34, 35] where a homogeneous Dirichlet boundary (i.e., fixed boundary) is imposed by explicitly setting nodal velocity to zero in the fixed direction and a Neumann boundary (i.e., traction boundary) is imposed by adding equivalent forces at the corresponding nodes. However, nonconforming boundary conditions require additional attention, particularly for the MPM. Unlike Lagrangian mesh-based methods, the MPM discretizes the material domain into a set of particles, eliminating the explicit material boundary position. This characteristic makes it inconvenient to apply nonconforming boundary conditions even when employing regular background mesh [36].

Various strategies have been proposed to handle nonconforming boundary conditions within the MPM framework. The most common way is to define traction boundary conditions on the outermost layer of particles of the material domain and then map the equivalent forces to the related nodes [27, 37]. This approach requires mesh refinement in the near-boundary region to improve numerical accuracy, given that the particles are close to, but not precisely on, the material boundary [38, 39]. An improved method involves introducing massless points to track the boundary position, which enables the application of the boundary traction on a more accurate location compared with the previous approach. However, both methods need to update the particle/point area during the simulation using Nanson’s formula [40]. Updating the boundary area ranges from inconvenient for 3D problems that feature large deformation to impossible for problems where the boundary undergoes fracture.

Several alternative strategies are available for tracking the material boundary. The dual-grid concept [41] is an alternative framework to impose boundary conditions. This approach involves utilizing the standard background grid as well as an additional grid. However, even for 1D problems, this approach is sensitive to element size and boundary position. Bing et al. proposed a cubic B-spline boundary representation within the MPM framework [31, 42]. This method was integrated within the implicit boundary method (IBM) to handle both homogeneous and inhomogeneous Dirichlet boundary conditions as well as inhomogeneous Neumann boundary conditions. The Neumann boundary conditions were enforced by integrating the known traction along the boundary segment. However, the authors emphasized that boundaries must remain intact throughout the analysis (i.e., not fracture). If fracture occurs, additional detection routines are required to determine the new boundaries. Additionally, in the case of self-contact, routines are required such that boundaries cease to exist. Finally, the B-spline approach has been exclusively presented for 2D boundary representations.

Another alternative approach involves employing the concept of a moving mesh [37], where the background mesh remains dynamic rather than fixed, allowing for direct application of boundary conditions on the nodes akin to the FEM. This approach aims to convert nonconforming boundary conditions into conforming ones. However, it requires that the boundary maintains a consistent shape and undergoes relatively minor deformations, which contradicts the primary advantage of the MPM in effectively simulating large deformation problems compared to conventional mesh-based methods.

For nonconforming boundaries in fluid problems, the MPM has been recently extended into the Lagrangian–Eulerian stabilized collocation method (LESCM) [43, 44]. In the LESCM, both fluid and structures are represented using Lagrangian particles, with information from the Lagrangian particles mapped to the nodes in the Eulerian mesh using a reproducing kernel approximation. This approach has been demonstrated to be efficient for a variety of problems involving rigid structures, including fluid–structure interaction (FSI) and free surface flow. Additionally, the LESCM has been extended to determine Lagrangian coherent structures (LCSs) based on the simulated flow. Similar to the approaches described above, the nonconforming boundaries for rigid structures must be explicitly defined. Using this explicit definition, the LESCM employs a cell-cut algorithm to identify the cells where fluid and solid particles interact, and subsequently computes the appropriate interaction forces to account for the fluid flow and the rigid structures.

Different from the above methods that require boundary tracking or boundary reconstruction, Liang et al. recently proposed a new strategy [36] to impose Neumann boundary conditions without boundary representation, namely, the virtual stress boundary (VSB) method. To avoid the complexity of boundary representation, the VSB method transforms the original problem with a traction boundary condition into an equivalent problem with a virtual stress field. This virtual stress field is defined everywhere around the material boundary and necessitates modifications to the governing equation. The updated equations contain only volume integral terms which are subsequently computed using both particle-wise quadrature and cell-wise quadrature. The accuracy, efficiency, and capability have been demonstrated by several numerical examples, including problems in 3D with complex boundary geometry. In the current work, an additional modification is proposed to further simplify the governing equation so that the cell-wise quadrature in the original VSB method is avoided without any changes to the method’s numerical accuracy.

The remaining paper is structured as follows. First, Sect. 2 outlines the requisite strong and weak formulations for the balance of linear momentum. Additionally, this section includes the corresponding discretized formulation of the governing equation for the MPM. Next, Sect. 3 provides a review of the existing approaches to impose nonconforming Neumann boundary conditions. Particular emphasis is placed on summarizing the originally proposed VSB method. Furthermore, this section includes a proposed modification for the VSB method. Following that, Sect. 4 is comprised of three benchmark problems and one demonstration problem to assess the accuracy and capability of the proposed update for the VSB method. Finally, Sect. 5 presents the conclusion of this paper as well as suggestions for future works.

This paper has the following objectives:

• 1. Propose a modification for the VSB method which eliminates cell-wise quadrature to reduce some of the method’s complexity.

• 2. Show that the proposed modification for the VSB method is generally compatible with the MPM and exhibits acceptable convergence behavior.

• 3. Demonstrate that the VSB method may be used to explore 3D problems with evolving boundary geometry resulting from material damage and subsequent removal.

2 Problem discretization

This section presents the necessary discretized balance equations to solve solid mechanics problems using the MPM. Both the strong and weak formulations for the balance of linear momentum are provided before deriving the corresponding discretized formulation. The reader is referred to [27,28,29] for a complete description of the MPM including the computational algorithm, stress and velocity update schemes, and a number of numerical examples.

2.1 Strong formulation

In the updated Lagrangian frame of reference, the so-called strong formulation for the balance of linear momentum may be defined for a continuum body occupying the material domain, $\Omega$. This balance law is expressed as

$$\begin{aligned} \rho \ddot{\varvec{u}} = \rho \varvec{b} + \nabla \cdot {\varvec{\sigma }} , \end{aligned}$$

(1)

where $\rho$ is the current mass density, $\ddot{\varvec{u}}$ is the acceleration vector, ${\varvec{\sigma }}$ is the Cauchy stress tensor, and $\varvec{b}$ is the body force per unit mass vector. Bold symbols indicate that values are in tensor form. Additionally, single and double over dots, $\dot{\square }$ and $\ddot{\square }$, denote the first- and second-order material time derivatives, respectively. In Eq. (1), the second-order material time derivative links the material displacement to material acceleration.

Let $\Gamma$ represent the boundary of the material domain $\Omega$. This boundary may be decomposed into two parts: $\Gamma = \Gamma _{u} \cup \Gamma _{t}$, where $\Gamma _{u}$ and $\Gamma _{t}$ denote the Dirichlet boundary and the Neumann boundary, respectively. In solid mechanics problems, Dirichlet boundary conditions involve imposed displacement and Neumann boundary conditions involve imposed traction. Boundary conditions are required to solve Eq. (1) such that

$$\begin{aligned} \varvec{u}=\varvec{\hat{u}} \quad&\mathrm {on~}&\Gamma _{u} , \end{aligned}$$

(2)

$$\begin{aligned} \varvec{t}=\hat{\varvec{t}} \quad&\mathrm {on~}&\Gamma _{t} , \end{aligned}$$

(3)

where $\varvec{\hat{u}}$ and $\hat{\varvec{t}}$ are the imposed displacement and the imposed traction on $\Gamma _{u}$ and $\Gamma _{t}$, respectively. Note, the traction, $\varvec{t}$, may be defined in terms of the Cauchy stress tensor such that $\varvec{t}={\varvec{\sigma }}\cdot \varvec{\hat{n}}$, where $\varvec{\hat{n}}$ is the outward unit normal vector on $\Gamma _{t}$.

2.2 Weak formulation

The weak formulation can be derived from expressing the balance of linear momentum in an equivalent weighted residual form. This representation requires a virtual displacement, $\delta \varvec{u}$, where $\delta \varvec{u}\in \mathcal {W}$ (with $\mathcal {W}$ representing the space of admissible virtual displacements). The space of admissible virtual displacements is defined such that Dirichlet boundary conditions are automatically satisfied (i.e., $\delta u_i=0$ on $\Gamma _{u_i}$).

Following the establishment of $\delta \varvec{u}$, the weighted residual form is derived by multiplying Eq. (1) by the virtual displacement and integrating over the entire material domain. Then, using integration by parts, the divergence theorem, and the definition of space $\mathcal {W}$, the weak formulation can be written as

$$\begin{aligned}{} & {} \int _{\Omega } \delta \varvec{u}\cdot \rho \ddot{\varvec{u}} \textrm{d}\Omega + \int _{\Omega } \nabla \delta \varvec{u}:{\varvec{\sigma }} \textrm{d}\Omega - \int _{\Omega } \delta \varvec{u}\cdot \rho \varvec{b}d \Omega \nonumber \\{} & {} \quad - \int _{\Gamma _t} \delta \varvec{u}\cdot \hat{\varvec{t}} \textrm{d}\Gamma = 0 . \end{aligned}$$

(4)

2.3 Discretized formulation

Equation (4) is generally solved using a numerical approach, such as the MPM [1, 2]. Using the MPM requires the balance of linear momentum to be expressed in a discretized formulation.

First, the material domain, $\Omega$, is split into $n_p$ particles (i.e., material points) such that

$$\begin{aligned} \Omega = \sum _{n=1}^{n_p} V_p , \end{aligned}$$

(5)

where $V_p$ is the particle volume. Throughout the simulation, the particles store all information such as mass, velocity, stress, strain, and history-dependent parameters. Note, $\square _p$ denotes a variable is associated with particle p.

In the standard MPM, each particle has constant mass, $m_p$. Consequently, the conservation of mass is automatically enforced in the MPM. Additionally, particle density, $\rho _p$, may be defined using the standard relationship between mass and volume expressed as

$$\begin{aligned} \rho _p = m_p / V_p . \end{aligned}$$

(6)

In addition to storing all information throughout the simulation, particles are used as quadrature points in the MPM. Therefore, the volume integrals in Eq. (4) are approximated and rewritten as

$$\begin{aligned}{} & {} \sum _{p=1}^{n_p} \delta \varvec{u}_p \cdot m_p\ddot{\varvec{u}}_p + \sum _{p=1}^{n_p} \nabla \delta \varvec{u}_p: V_p{\varvec{\sigma }}_p - \sum _{p=1}^{n_p} \delta \varvec{u}_p \cdot m_p\varvec{b}_p\nonumber \\{} & {} \qquad = 0 . \end{aligned}$$

(7)

Notice that the boundary integral term in Eq. (4) is temporarily discarded in Eq. (7) since this term cannot be directly computed with particle quadrature. However, Sect. 3 outlines a variety of approaches to properly account for this boundary integral term.

In addition to particles, the MPM requires a background mesh consisting of nodes and cells (i.e., elements). The mesh nodes are used to solve the balance of linear momentum for each step in the simulation. Quantities, like displacement or acceleration, are mapped between the mesh nodes and particles using a nodal basis function, $N_I$, and the expression

$$\begin{aligned} \square _p = \sum _{I=1}^{n_n} N_{Ip} \square _I , \end{aligned}$$

(8)

where $n_n$ is the number of nodes and $N_{Ip}\equiv N_I(\varvec{\xi }_p)$ (i.e., the value of the basis function for node I at particle p with $\varvec{\xi }_p$ corresponding to the local coordinates of the particle). Note, $\square _I$ denotes a variable is associated with node I. Linear basis functions are employed in the current study. Others have shown that higher-order basis functions may be used in the MPM to map quantities between the particles and nodes [45, 46].

Using Eq. (8) to map displacement, the virtual displacement, and acceleration from the nodes to particles, then substituting the resulting expressions into Eq. (7), and invoking the arbitrariness of $\delta \varvec{u}_I$, leads to the discretized formulation for the balance of linear momentum at the mesh nodes. This is expressed as

$$\begin{aligned} \dot{\varvec{p}}_I = m_I \ddot{\varvec{u}}_I = \varvec{f}_{I}^{\textrm{int}} + \varvec{f}_{I}^{\textrm{ext}} + \varvec{f}_{I}^{\textrm{ext,traction}} \quad \quad \forall I \notin \Gamma _u , \end{aligned}$$

(9)

where $\varvec{f}_{I}^{\textrm{int}}$ and $\varvec{f}_{I}^{\textrm{ext}}$ are the internal and external nodal forces, respectively. Additionally, $\varvec{f}_{I}^{\textrm{ext,traction}}$ is the traction part of the external nodal force which is a consequence of the previously omitted boundary integral term in Eq. (4). In the traditional MPM, nodal mass is lumped via row summation to reduce computational cost. Internal and external nodal forces are defined as

$$\begin{aligned} \varvec{f}_{I}^{\textrm{int}}= & {} -\sum _{p=1}^{n_p} V_p \nabla N_{Ip}\cdot {\varvec{\sigma }}_p , \end{aligned}$$

(10)

$$\begin{aligned} \varvec{f}_{I}^{\textrm{ext}}= & {} \sum _{p=1}^{n_p} m_p N_{Ip}\varvec{b}_p . \end{aligned}$$

(11)

3 Treatment of nonconforming Neumann boundary conditions

Nonconforming boundaries arise when the material boundary and mesh boundary do not align. As discussed in Sect. 1, this misalignment is a common occurrence in the MPM due to the hybrid Eulerian–Lagrangian nature of the method. Conventional approaches to handle nonconforming boundaries rely on either boundary tracking or boundary reconstruction to apply nonconforming boundary conditions. The recently proposed VSB method [36] offers an alternative approach where explicit knowledge of the material boundary position is not required when imposing nonconforming Neumann boundary conditions. This section provides an overview of the conventional approaches to impose nonconforming boundary conditions, presents a summary of the original VSB method, and proposes a modification for the VSB method. The methods discussed in this section are demonstrated through various example problems presented in Sect. 4.

3.1 Imposing nonconforming Neumann boundary conditions with conventional methods

Conventional methods to impose nonconforming boundary conditions use boundary particles to explicitly track or reconstruct the material boundary. Once the material boundary has been explicitly defined, the boundary integral in Eq. (4) may be approximated or solved exactly.

Boundary tracking may be achieved by using so-called boundary particles. These particles, which form a subset of all particles in a simulation, are positioned close to, though not exactly on, the material boundary. Using boundary particles, the traction part of the external nodal force vector is computed as

$$\begin{aligned} \varvec{f}_{I}^{\textrm{ext,traction}} = \sum _{p=1}^{n_p} A_p N_{Ip}\hat{\varvec{t}}_p , \end{aligned}$$

(12)

where $A_p$ is the surface area associated with each particle. As the material domain deforms, the particle surface area must be updated using Nanson’s formula [47]. This approach inherently introduces error since the boundary traction is imposed within the material domain rather than directly on the material boundary.

Alternatively, boundary reconstruction is employed to impose nonconforming Neumann boundary conditions. In this method, the exact boundary location is described by a function (piece-wise polynomial, splines, Fourier series, etc.). Using the defined boundary function, the traction part of the external nodal force vector is computed as

$$\begin{aligned} \varvec{f}_{I}^{\textrm{ext,traction}} = \int _{\Gamma _t} N_{I}\hat{\varvec{t}}\textrm{d}\Gamma , \end{aligned}$$

(13)

where the integral in Eq. (13) is typically solved using particle quadrature. This approach also introduces some error since the quadrature points used to solve the integral are mapped to adjacent nodes, with some nodes located within the material domain while other nodes are positioned outside of the material boundary. The numerical error resulting from imposing nonconforming Neumann boundary conditions via boundary reconstruction is clearly demonstrated by the numerical example in Sect. 4.1.

3.2 Imposing nonconforming Neumann boundary conditions with the VSB method

The VSB method was developed to impose nonconforming Neumann boundary conditions without the need for explicit boundary tracking or reconstruction [36]. This is accomplished by utilizing a problem transformation where the original boundary conditions are transformed into an equivalent virtual stress field. Figures 1 and 2 illustrate the original problem with Neumann boundary conditions and the transformed problem with a virtual stress field, respectively.

Fig. 1

Illustration of the VSB method; original problem with Neumann boundary conditions

Fig. 2

Illustration of the VSB method; Neumann boundary conditions replaced with equivalent virtual stress field

3.2.1 Summary of the original VSB method

Let the virtual domain, $\bar{\Omega }$, entirely surround the material domain, $\Omega$, as shown in Fig. 2. Within the virtual domain, the imposed boundary traction, $\hat{\varvec{t}}$, is replaced with an equivalent virtual stress field, $\bar{{\varvec{\sigma }}}$. Although the Neumann boundary condition may only be defined along part of the material boundary, the virtual stress field is defined everywhere in the virtual domain such that

$$\begin{aligned} \bar{{\varvec{\sigma }}}\cdot \varvec{n} = {\left\{ \begin{array}{ll} \hat{\varvec{t}} &{} \quad \textrm{on}\quad \Gamma _{t} , \\ \varvec{0} &{} \quad \textrm{on}\quad \Gamma -\Gamma _{t} . \end{array}\right. } \end{aligned}$$

(14)

Considering the form of Eq. (14), it is apparent that the original problem (with a Neumann boundary condition) and the transformed problem (with a virtual stress field) are precisely equivalent. Note, $\bar{\square }$ denotes a term is virtual, such as the virtual stress field, $\bar{{\varvec{\sigma }}}$.

The virtual stress field, $\bar{{\varvec{\sigma }}}$, is user-defined based on the Neumann boundary conditions and problem geometry. Following [36], it is recommended to select the simplest conceivable virtual stress field which satisfies Eq. (14). A unique virtual stress field is not guaranteed to exist. However, any virtual stress field satisfying Eq. (14) is acceptable. For example, consider imposing a boundary traction due to constant pressure, p. In this case, the virtual stress field is most concisely defined as $\bar{{\varvec{\sigma }}} = -p\mathbb {I}$ where $\mathbb {I}$ is the second order identity matrix. In this scenario, Eq. (14) will be satisfied for all possible boundary orientations.

Recall that the balance of linear momentum, Eq. (1), describes the response within the material domain. In the same way, an additional governing equation is required to describe the response within the virtual domain. Thus, the balance of linear momentum in the virtual domain is given as

$$\begin{aligned} \bar{\rho }\ddot{\bar{\varvec{u}}} = \bar{\rho }\bar{\varvec{b}} + \nabla \cdot \bar{\varvec{\sigma }} \quad \textrm{in}\quad \bar{\Omega } , \end{aligned}$$

(15)

where $\bar{\rho }$, $\ddot{\bar{\varvec{u}}}$, and $\bar{\varvec{b}}$ are the virtual density, virtual acceleration, and virtual body force, respectively. Additionally, define $\bar{\varvec{\!\!f}}$ as the divergence of the virtual stress field such that

$$\begin{aligned} {\bar{\varvec{\!\!f}}} = \nabla \cdot \bar{\varvec{\sigma }} \quad \textrm{in}\quad \bar{\Omega } . \end{aligned}$$

(16)

Let $\bar{\mu }$ be an intermediate variable that distinguishes between the material domain and the virtual domain such that

$$\begin{aligned} \bar{\mu } = {\left\{ \begin{array}{ll} 1 &{} \quad \textrm{in}\quad \bar{\Omega } , \\ 0 &{} \quad \textrm{in}\quad \Omega . \end{array}\right. } \end{aligned}$$

(17)

An updated strong formulation is developed when multiplying Eq. (1) by $(1-\bar{\mu })$ and Eq. (16) by $\bar{\mu }$. The sum of these products is

$$\begin{aligned}{} & {} (1-\bar{\mu })\left( \nabla \cdot {\varvec{\sigma }} + \rho \varvec{b} - \rho \ddot{\varvec{u}} -\nabla \cdot \bar{{\varvec{\sigma }}} + \bar{\varvec{\!\!f}} \right) \nonumber \\{} & {} \quad + \left( \nabla \cdot \bar{\varvec{\sigma }} - \bar{\varvec{\!\!f}}\right) = 0 \quad \textrm{in}\quad \Omega \cup \bar{\Omega } . \end{aligned}$$

(18)

The corresponding weak formulation is formed when multiplying Eq. (18) by the virtual displacement and integrating over the combined material and virtual domains such that

$$\begin{aligned}{} & {} \int _{\Omega } \delta \varvec{u}\cdot \left( \nabla \cdot {\varvec{\sigma }} + \rho \varvec{b} - \rho \ddot{\varvec{u}} -\nabla \cdot \bar{{\varvec{\sigma }}} + \bar{\varvec{\!\!f}} \right) \textrm{d}\Omega \nonumber \\{} & {} \quad + \int _{\Omega \cup \bar{\Omega }} \delta \varvec{u}\cdot \left( \nabla \cdot \bar{\varvec{\sigma }} - \bar{\varvec{\!\!f}}\right) \textrm{d}\Omega = 0 . \end{aligned}$$

(19)

Note, the bounds of integration in Eq. (19) are a result of the definition of $\bar{\mu }$ since $(1-\bar{\mu })=0$ within the virtual domain. Vitally, Eqs. (4) and (19) are equivalent. However, Eq. (19) does not include any boundary integral terms. When using the VSB method within the MPM framework, integration over the material domain, $\Omega$, is computed using particle-wise quadrature, whereas integration over the total domain, $\Omega \cup \bar{\Omega }$, is computed using cell-wise quadrature.

The weak formulation may be developed into a discretized formulation following the procedure described in Sect. 2.3. This leads to the discretized formulation for the unbalanced nodal force being expressed as

$$\begin{aligned} \dot{\varvec{p}}_I = m_I \ddot{\varvec{u}}_I = \tilde{\varvec{\!\!f}}_{I}^{\textrm{int}} + \tilde{\varvec{\!\!f}}_{I}^{\textrm{ext}} \quad \quad \forall I \notin \Gamma _u , \end{aligned}$$

(20)

where $\tilde{\varvec{\!\!f}}_{I}^{\textrm{int}}$ and $\tilde{\varvec{\!\!f}}_{I}^{\textrm{ext}}$ are the internal and external nodal forces updated for the VSB method, respectively. As before, nodal mass is lumped via row summation for reduced computational cost. The updated internal and external nodal forces are defined as

$$\begin{aligned} \tilde{\varvec{\!\!f}}_{I}^{\textrm{int}}= & {} -\sum _{p=1}^{n_p} V_p \nabla N_{Ip}\cdot ({\varvec{\sigma }}_p - \bar{{\varvec{\sigma }}}_p) - \sum _{c=1}^{n_c} V_c\nabla N_{Ic} \cdot \bar{{\varvec{\sigma }}}_c \nonumber \\ \end{aligned}$$

(21)

$$\begin{aligned} \nonumber= & {} \varvec{f}_I^{\textrm{int}} + \sum _{p=1}^{n_p} V_p \nabla N_{Ip}\cdot \bar{{\varvec{\sigma }}}_p - \sum _{c=1}^{n_c} V_c\nabla N_{Ic} \cdot \bar{{\varvec{\sigma }}}_c , \\ \tilde{\varvec{\!\!f}}_{I}^{\textrm{ext}}= & {} \sum _{p=1}^{n_p} m_p N_{Ip}\varvec{b}_p + \sum _{p=1}^{n_p} V_p N_{Ip} \bar{\varvec{\!\!f}}_p - \sum _{c=1}^{n_c} V_c N_{Ic}\bar{\varvec{\!\!f}}_c \nonumber \\= & {} \varvec{f}_I^{\textrm{ext}} + \sum _{p=1}^{n_p} V_p N_{Ip} \bar{\varvec{\!\!f}}_p - \sum _{c=1}^{n_c} V_c N_{Ic}\bar{\varvec{\!\!f}}_c , \end{aligned}$$

(22)

where $n_c$ is the number of cell quadrature points and $N_{Ic}\equiv N_I(\varvec{\xi }_c)$ (i.e., the value of the basis function for node I at cell quadrature point c with $\varvec{\xi }_c$ corresponding to the local coordinates of the cell quadrature point). Note, $\square _c$ denotes a variable is associated with cell quadrature point c. If no boundary traction is applied, it is clear that Eqs. (21) and (22) become equivalent to the standard expressions for internal and external nodal forces given by Eqs. (10) and (11), respectively.

3.2.2 Proposed update for the VSB method

The current study introduces a modification for the VSB method that eliminates the need for cell-wise quadrature, which was required in the original VSB method.

The current study adopts the same problem setup and development of the strong formulation as the original VSB method, given by Eqs. (14)–(18). However, Eq. (19) may be further simplified when considering the definition for the divergence of the virtual stress field, $\nabla \cdot \bar{{\varvec{\sigma }}}-\bar{\varvec{\!\!f}}=0$, which can be expanded to still hold in the material domain $\Omega$ as its form is not limited within this domain. Therefore, the weak formulation is expressed as

$$\begin{aligned} \int _{\Omega } \delta \varvec{u} \cdot \left( \nabla \cdot {\varvec{\sigma }} + \rho \varvec{b} - \rho \ddot{\varvec{u}} -\nabla \cdot \bar{{\varvec{\sigma }}} + \bar{\varvec{\!\!f}} \right) \textrm{d}\Omega = 0 . \end{aligned}$$

(23)

Notice that Eqs. (4), (19), and (23) are all equivalent. However, Eq. (23) has the obvious advantage that the boundary traction term is imposed using only volume integrals and that the bounds of integration are limited to only the material domain, $\Omega$.

Using integration by parts, the divergence theorem, and Eqs. (3) and (14), the weak formulation is alternatively expressed as

$$\begin{aligned}{} & {} \int _{\Omega }\delta \varvec{u} \cdot \rho \ddot{\varvec{u}}\textrm{d}\Omega + \int _{\Omega }\nabla \delta \varvec{u}: {\varvec{\sigma }} \textrm{d}\Omega - \int _{\Omega }\nabla \delta \varvec{u}: \bar{{\varvec{\sigma }}} \textrm{d}\Omega \nonumber \\{} & {} \quad -\int _{\Omega }\delta \varvec{u} \cdot \rho \varvec{b}\textrm{d}\Omega - \int _{\Omega }\delta \varvec{u} \cdot \bar{\varvec{\!\!f}} \textrm{d}\Omega = 0 . \end{aligned}$$

(24)

It is noted that the integral term related to the material boundary $\Gamma _t$ in Eq. (4) is eliminated due to the virtual stress field. Then using the particles as quadrature points, Eq. (24) is approximated and rewritten as

$$\begin{aligned}{} & {} \sum _{p=1}^{n_p} \delta \varvec{u}_p \cdot m_p\ddot{\varvec{u}}_p + \sum _{p=1}^{n_p} \nabla \delta \varvec{u}_p: V_p{\varvec{\sigma }}_p - \sum _{p=1}^{n_p} \nabla \delta \varvec{u}_p: V_p\bar{{\varvec{\sigma }}}_p \nonumber \\{} & {} \quad - \sum _{p=1}^{n_p} \delta \varvec{u}_p \cdot m_p\varvec{b}_p - \sum _{p=1}^{n_p} \delta \varvec{u}_p \cdot V_p\bar{\varvec{\!\!f}}_p = 0 . \end{aligned}$$

(25)

Equation (8) is employed to map displacement, the virtual displacement, and acceleration between particles and nodes. Once the resulting expressions are substituted into Eq. (25), the arbitrariness of $\delta \varvec{u}_I$ is invoked, leading to the discretized expression for the unbalanced nodal force

$$\begin{aligned} \dot{\varvec{p}}_I = m_I \ddot{\varvec{u}}_I = \tilde{\varvec{\!\!f}}_{I}^{\textrm{int}} + \tilde{\varvec{\!\!f}}_{I}^{\textrm{ext}} \quad \quad \forall I \notin \Gamma _u . \end{aligned}$$

(26)

The updated internal and external nodal forces are redefined as

$$\begin{aligned} \tilde{\varvec{\!\!f}}_{I}^{\textrm{int}}= & {} -\sum _{p=1}^{n_p} V_p \nabla N_{Ip}\cdot ({\varvec{\sigma }}_p - \bar{{\varvec{\sigma }}}_p) , \end{aligned}$$

(27)

$$\begin{aligned} \nonumber= & {} \varvec{f}_I^{\textrm{int}} + \sum _{p=1}^{n_p} V_p \nabla N_{Ip}\cdot \bar{{\varvec{\sigma }}}_p , \\ \tilde{\varvec{\!\!f}}_{I}^{\textrm{ext}}= & {} \sum _{p=1}^{n_p} m_p N_{Ip}\varvec{b}_p + \sum _{p=1}^{n_p} V_p N_{Ip} \bar{\varvec{\!\!f}}_p , \\ \nonumber= & {} \varvec{f}_I^{\textrm{ext}} + \sum _{p=1}^{n_p} V_p N_{Ip} \bar{\varvec{\!\!f}}_p . \end{aligned}$$

(28)

Similar to the original VSB method, if no boundary traction is applied, Eqs. (27) and (28) degenerate into the standard expressions for internal and external nodal forces given by Eqs. (10) and (11), respectively. The modified VSB method removes all cell-wise quadrature found in Eqs. (21) and (22). Vitally, the nonconforming Neumann boundary conditions are still imposed without explicit boundary tracking or reconstruction. Therefore, the proposed update is equivalent to the original VSB method, but the cell-wise quadrature has been avoided.

3.2.3 Computer implementation

The original VSB method is easily embedded into the traditional MPM [36]. As shown in Sect. 3.2.1, only the expressions for internal and external nodal forces must be updated for the VSB method. Since the virtual stress field is defined to exist outside of the material domain, only nodes close to the material boundary need to rely on Eqs. (21) and (22). Following this rationale, the modified VSB method is also easily embedded into the traditional MPM. Similarly, only nodes close to the material boundary need to utilize the updated expressions for internal and external forces given by Eqs. (27) and (28), respectively.

Algorithm 1 provides the steps to determine the node set $\mathcal {N}_1$, which utilize the updated expressions for internal and external force. Let node set $\mathcal {N}_1$ be a subset of the active node set $\mathcal {A}$, where an active node is defined to have at least one particle located within its support domain.

Algorithm 1

Find the nodes related to the VSB method

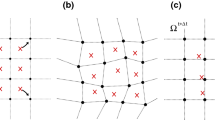
Algorithm 1 is depicted by Fig. 3: cells shaded red represent void cells and are members of cell set $\mathcal {E}_1$; cells shaded blue represent non-void cells and are members of cell set $\mathcal {E}_2$; red nodes are active nodes associated with $\mathcal {E}_1$ or $\mathcal {E}_2$, indicating that these nodes are members of node set $\mathcal {N}_1$. Active nodes that are not members of node set $\mathcal {N}_1$ are shown as black diamonds. In Fig. 3, most nodes are in node set $\mathcal {N}_1$. However, in more realistic situations, most active nodes will not be members of node set $\mathcal {N}_1$.

Fig. 3

Illustration of the VSB method; discretized problem with cell set $\mathcal {E}_1$, cell set $\mathcal {E}_2$, and node set $\mathcal {N}_1$

For each node in node set $\mathcal {N}_1$, all particles within its support domain are included in the sums involved in Eqs. (27) and (28). This implies that particles not located in either cell sets $\mathcal {E}_1$ or $\mathcal {E}_2$ may be used to impose the nonconforming Neumann boundary conditions.

Some nodes associated with elements in cell set $\mathcal {E}_1$ are inactive. Similar to the original VSB method, the modified VSB method does not require updated internal and external forces to be computed for inactive nodes. In other words, the degrees of freedom in the linear system described by Eq. (26) remain unchanged when using the VSB method compared to the traditional MPM.

4 Numerical examples

In this section, the numerical quality and capability of the proposed modification for the VSB method is demonstrated using four numerical examples:

• 1. A benchmark problem of a 1D column subjected to axial loading is simulated. This numerical example directly compares the imposition of nonconforming Neumann boundary conditions using explicit boundary reconstruction, the original VSB method, and the modified version of the VSB method.

• 2. A benchmark problem of an internally pressurized thick-walled cylinder is simulated in the 2D plane strain scenario. This numerical example demonstrates that the modified version of the VSB method can accurately impose traction on circular boundary geometry. Mesh refinement and particle per cell (PPC) refinement are studied to show that the modified VSB method exhibits acceptable convergence behavior.

• 3. A benchmark problem of an infinite plate with an elliptic hole under cavity pressure is simulated in the 2D plane strain scenario. The interaction between non-circular cavity geometry and anisotropic far-field stresses leads to a more intricate stress solution compared to the previous benchmark problems. Mesh refinement is studied to show that the proposed modification for the VSB method exhibits acceptable convergence behavior for a more complex problem.

• 4. A demonstration problem of propagating wellbore failure is simulated in 3D. Propagating failure means that the boundary changes throughout the simulation. This showcases the capability of the modified VSB method to impose nonconforming boundary conditions on an evolving boundary without any explicit boundary tracking or reconstruction.

All numerical examples rely on the modified update stress last (MUSL) stress update scheme. Additionally, they all employ the FLIP velocity update scheme.

4.1 Axially loaded column

The first numerical example is a 1D benchmark problem of an axially loaded column.

This benchmark problem illustrates that using the VSB method to impose nonconforming Neumann boundary conditions results in reduced error compared to using explicit boundary reconstruction via massless particles. Additionally, this benchmark problem demonstrates that the accuracy of the VSB method remains consistent regardless of the background mesh type (e.g., regular mesh versus isoparametric mesh). Finally, this benchmark problem directly compares the original VSB method with the modified VSB method.

Column geometry is illustrated in Fig. 4. The initial column length is set to $L_0=9.5$ m for all simulations. A homogeneous Dirichlet boundary condition is imposed at the left end of the column, while a Neumann boundary condition is imposed at the right end of the column. The Neumann boundary condition is a traction equal to $\hat{t}=1.0$ Pa (compressive).

Fig. 4

Geometry for axially loaded column: initial column length and location of the applied Neumann boundary condition. Problem discretization using combination of regular mesh and isoparametric mesh

Figure 4 shows the utilized long isoparametric, regular, and short isoparametric meshes. The regular mesh is entirely comprised of square elements with characteristic length of $h_e=1.0$ m. The long isoparametric mesh contains a non-square final element with a dimension of $1.5\times 1.0$ m and the short isoparametric mesh contains a non-square final element with a dimension of $0.5\times 1.0$ m. In each mesh, the Neumann boundary conditions are nonconforming due to the column compressing under the applied traction. All three meshes consist of nine fully filed elements and one partially filled element at the right end. The current study employs PPC = 8 in each of the full elements and PPC = 4 in the partially filled element.

The axially loaded column simulations utilize a linear elastic constitutive model. Table 1 summarizes the elastic material parameters.

Table 1 Linear elastic material parameters for axially loaded column

Time step, $\textrm{d}t$, is computed using

$$\begin{aligned} \textrm{d}t = \kappa \frac{h_e}{\sqrt{M/\rho }} , \end{aligned}$$

(29)

where $\kappa$ is the reduction factor from the critical time step and M is the constrained modulus. This benchmark problem uses a reduction factor of about $\kappa =0.3$. The column is initially unstressed before the boundary traction is slowly applied over 10,000 steps such that the problem remains approximately quasi-static. Additionally, Cundall damping of 0.05 is applied to reduce the number of steps required to reach the final steady-state solution [48].

Analytic displacement and analytic stress are represented by $u(x^0)$ and $\sigma (x^0)$, respectively, with the expressions for the displacement and stress given by Eqs. (A1) and (A2), respectively. For this benchmark problem, the stress distribution within the column is constant, meaning that the problem is essentially a patch test. Thus, the numerical solution will not improve under mesh refinement and a mesh refinement study is omitted for this numerical example. The displacement and stress errors are computed using the following expressions

$$\begin{aligned} e_u= & {} \sqrt{\frac{1}{n_p}\sum _{p=1}^{n_p} \left( \frac{u(x_p^0) - u_p}{L_0}\right) ^2} , \end{aligned}$$

(30)

$$\begin{aligned} e_{\sigma }= & {} \sqrt{\frac{1}{n_p}\sum _{p=1}^{n_p} \left( \frac{\sigma (x_p^0) - \sigma _p}{\hat{t}}\right) ^2} . \end{aligned}$$

(31)

Figure 5 shows a displacement profile along the column. While the solutions may seem comparable, Table 2 lists the computed error for each simulation. Using explicit boundary tracking or the original VSB method produces similar displacement errors with magnitudes around $1e-7$. Alternatively, the modified VSB method results in displacement errors on the order of $1e-11$. The difference in error stems from how the full cell volume is computed between Eq. (21) and Eq. (27). For the original VSB method, the full cell quadrature corresponds to sum of cell quadrature points which is always $\sum V_c=1.0$. However, for the modified VSB method, the full cell quadrature is computed as the sum of particle quadrature points or $\sum V_p=0.9990005$ (for the current scenario). The sum is less than 1.0 due to the slight compression of each particle under the applied boundary traction.

Fig. 5

Axial displacement profile along the 1D column

Table 2 Displacement and stress errors when imposing nonconforming Neumann boundary conditions with massless boundary particles and the VSB method

Figure 6 shows a stress profile along the column. By inspection, it is evident that the largest stress error occurs when using explicit boundary reconstruction to impose the nonconforming Neumann boundary conditions. The error is well understood and arises because the boundary is represented by a massless boundary particle which is mapped to the adjacent nodes. Thus, a portion of the boundary traction is applied outside of the material while the remaining part is applied inside of the material domain. As indicated in Table 2, both variations of the VSB method represent an improvement compared to the explicit boundary reconstruction approach. However, the original VSB method has error on the order of $1e-4$ while the updated VSB method has error on the order of $1e-11$. As before, the difference in error stems from computing elemental volume via the sum of cell quadrature points versus computing elemental volume via the sum of particle volumes.

Fig. 6

Axial stress profile along the 1D column

Previous studies have demonstrated that the original formulation of the VSB method has a reduced computational cost compared to other existing methods for imposing nonconforming Neumann boundary conditions [36]. The earlier study computed the additional computational cost for imposing a nonconforming traction boundary using three methods: directly applying traction to material points near the material boundary, applying traction to massless boundary particles corresponding to the exact material boundary, and the imposing traction with the original VSB method. This efficiency study has been extended to include the proposed variation of the VSB method.

Table 3 provides the time per particle per time step as a 1m $\times$ 1m $\times$ 10m column is simulated without imposing any Neumann boundary conditions, referred to as the base simulation. For the column, one end is fixed, and the other is free, similar to the column geometry depicted in Fig. 4. This table also reports the additional cost, as a percentage of the base simulation, when the column is loaded using various approaches to impose nonconforming boundary conditions. These approaches include imposing traction directly on existing material points located near the boundary, imposing traction on massless boundary particles that exactly represent the material boundary, employing the original VSB method, and employing the modified VSB method. The additional costs associated with these approaches are denoted using $\Delta t_{mp}$, $\Delta t_{bp}$, $\Delta t_{vsb}$, and $\Delta t_{vsb}^*$, respectively. All reported values are averaged over multiple consecutive simulations of 1000 steps using an Intel(R) Core(TM) i9-10900X CPU at 3.70 GHz.

Table 3 Cost per particle per time step for the base simulation; additional cost, as a percentage of the base simulation, when imposing nonconforming Neumann boundary conditions with material points near the boundary, massless boundary particles, the original VSB method, and the updated VSB method, or $\Delta t_{mp}$, $\Delta t_{bp}$, $\Delta t_{vsb}$, and $\Delta t_{vsb}^{*}$, respectively

In Table 3, as the number of particles increases, the relative efficiency of the VSB method becomes evident. When $h_e<1.0$ m, both the original and modified VSB methods correspond to lower additional costs compared to explicit boundary tracking or reconstruction approaches. For all simulations considered, the modified VSB method outperforms the original VSB method in terms of lower additional cost to impose the nonconforming Neumann boundary condition. The relatively lower cost is reasonable given the simplified formulation of the updated VSB method, which eliminates the cell-wise quadrature from the original approach. It is important to note that for more complex deformations, such as self-contact or fracture, explicit boundary tracking or reconstruction requires additional computational algorithms to handle the evolving boundary geometry. Alternatively, no additional considerations beyond what is described by Algorithm 1 are required for either variation of the VSB method when handling complicated deformations.

This benchmark problem illustrates three key points. Firstly, when imposing nonconforming Neumann boundary conditions, both variations of the VSB method exhibit higher accuracy compared to explicit boundary reconstruction via massless particles. The increase in accuracy is most evident when considering the stress profile along the 1D column in Fig. 6. Secondly, both variations of the VSB method demonstrate independence from the background mesh. Results summarized in Table 2 indicate that displacement and stress errors are approximately mesh independent. Thirdly, the modified VSB method is comparable to the original VSB method. In this case, error is lower for the updated version of the VSB method. However, it is shown that both variations of the VSB method are capable of imposing nonconforming Neumann boundary conditions.

4.2 Internally pressurized thick-walled cylinder

The second numerical example is a benchmark problem of an internally pressurized thick-walled cylinder, modeled using the 2D plane strain assumption.

In this numerical example, only the VSB method is used to impose the nonconforming Neumann boundary conditions. The influence of particle distribution and mesh shape is investigated through mesh refinement and PPC refinement studies. Overall, this benchmark problem demonstrates that modified version of the VSB method is capable of imposing nonconforming traction boundary conditions with acceptable convergence behavior.

Figure 7 shows the thick-walled cylinder geometry. The variables a and b correspond to the inner and outer radius, respectively, with $a=1$ and $b=5$ in the current study. Figure 7 also indicates that the imposed Neumann boundary condition is an isotropic pressure boundary applied along the inner cavity. In the current study, internal pressure is set as $p_i=100.0$ kPa (compressive). Due to symmetry of the thick-walled cylinder geometry and symmetry of the applied boundary condition, no additional constraints (e.g., Dirichlet boundary conditions) are required for the thick-walled cylinder to remain static.

Fig. 7

Geometry for thick-walled cylinder: inner radius, outer radius, and location of the applied Neumann boundary condition

Figure 8 illustrates the combinations of mesh shape and particle distribution utilized in the study, including regular mesh with uniform particles, regular mesh with concentric particles, and isoparametric mesh with concentric particles. Differences in mesh shape and particle distribution mean that the total quantity of particles for each specimen cannot be equal. Particular emphasis was placed on developing specimens with an approximately equal total number of particles.

First, the specimens with regular mesh and uniform particle distribution were developed. For these specimens, PPC $=N$ denotes equally spaced particles with an $N\times N$ distribution in the element.

Next, the specimens with isoparametric mesh and concentric particles were developed. Compared to the regular mesh, the isoparametric mesh was defined to have the same number of elements along the x-axis and y-axis. For these specimens, PPC $=N$ refers to an $N\times N$ distribution of particles with constant radial spacing and rotational offset in the radial and circumferential directions, respectively. The number of circumferential elements was selected such that the total quantity of particles was approximately equivalent to the specimens with regular mesh and uniform particle distribution.

Lastly, the specimens with regular mesh and concentric particles were generated by combining the previously developed regular mesh and concentric particle files. For these specimens, PPC$\approx N$ represents the average $N\times N$ distribution over all elements. In fact, more particles are located in cells in the near-cavity region, leading to a gradient of the actual PPC which decreases from the inner to outer radius.

Fig. 8

Thick-walled cylinder discretization using regular mesh with uniform material points, regular mesh with concentric material points, and isoparametric mesh with concentric material points

The thick-walled cylinder simulations utilize a linear elastic constitutive model. Table 4 summarizes the elastic material parameters.

Table 4 Linear elastic material parameters for thick-walled cylinder

Time step is computed using Eq. (29) with $\kappa =0.2$. Initially the thick-walled cylinder is unstressed before internal pressure is imposed using the updated VSB method. The magnitude of pressure is slowly increased over 0.2 seconds such that the simulation is approximately quasi-static. Additionally, Cundall damping of 0.05 is applied to achieve the steady-state solution and reduce the effect of dynamic loading [48].

The analytic solution for an internally pressurized thick-walled cylinder is well established in the literature [49]. The expressions for analytic displacement, radial stress, and hoop stress are given by Eqs. (A3), (A4), and (A5), respectively.

Error is redefined to consider each particle’s relative volume such that displacement error is computed using

$$\begin{aligned} e_u = \sqrt{\frac{1}{V_t}\sum _{p=1}^{n_p} V_p\left( \frac{u(\varvec{x}_p) - u_p}{a}\right) ^2} , \end{aligned}$$

(32)

and the stress error is computed using

$$\begin{aligned} e_{\sigma } = \sqrt{\frac{1}{V_t}\sum _{p=1}^{n_p} V_p\left( \frac{\sigma (\varvec{x}_p) - \sigma _p}{p_i}\right) ^2} , \end{aligned}$$

(33)

where $\sigma (\varvec{x}_p)$ and $\sigma _p$ correspond to the analytic and numerical solutions of stress, respectively. For this benchmark problem, the stress state is decomposed into the radial stress and hoop stress or $\sigma _{rr}$ and $\sigma _{\theta \theta }$, respectively.

Figure 9 shows representative contours for the normalized radials stress, hoop stress, and displacement in the near-cavity region for specimens with $h_e=0.25$ m. Stress contours for the regular mesh simulations (both the uniform and concentric particle distributions) show an obvious mesh dependency pattern for normalized radial and hoop stresses. These results are mostly due to the utilized linear basis functions and are consistent with previous simulations using the VSB method [36]. The normalized stress contours for the isoparametric mesh with concentric particles represent a better match with the analytic solution. This improvement occurs since the gradient of the linear basis functions is approximately oriented in the radial and circumferential directions which subsequently coincides with the orientation of the stress contours for radial and hoop stress. Overall, all displacement contours are well aligned between the analytic and each numerical solution.

Fig. 9

Analytic and numerical solutions for radial stress, hoop stress, and displacement in the near-cavity region (results for mesh with $h_e=0.25$ m)

4.2.1 Mesh refinement study

The influence of mesh refinement are studied for this benchmark problem.

Table 5 compares the total quantity of particles for the uniform particle distribution versus the concentric particle distribution. As noted above, specimens were developed such that the total quantity of particles is approximately equivalent between these two particle distributions. For the regular mesh with uniform particle distribution and the isoparametric mesh with concentric particle distribution, the total quantity of particles listed in Table 5 corresponds to PPC $=4$. Alternatively, for the regular mesh with concentric particles, the total quantity of particles listed in Table 5 corresponds to PPC$\approx 4$.

Table 5 also lists the characteristic length for each of the regular meshes, ranging from $h_e=0.0625$ m through $h_e=1.0$ m. Note, these values do not correspond to the characteristic length of the isoparametric mesh. However, the characteristic lengths listed in Table 5 are used for plotting the convergence behavior to directly compare the behavior of different combinations of mesh shape and particle distribution under mesh refinement. In reality, the characteristic length of the isoparametric mesh varies for each concentric ring of elements.

Table 5 Total quantity of material points used in mesh refinement study for thick-walled cylinder simulations

Displacement and stress errors are computed using Eqs. (32) and (33), respectively. Figure 10 shows the convergence behavior of errors under mesh refinement for the regular mesh with uniform particle distribution (“uniform”), regular mesh with concentric particle distribution (“concentric”), and isoparametric mesh with concentric particle distribution (“isoparametric”). Stress errors are expect to converge linearly and displacement errors are expected converge quadratically. The rates of convergence for radial and hoop stress errors are nearly linear and approximately constant under mesh refinement. For the “uniform” specimens, the rate of convergence for the displacement error starts as nearly quadratic but reduces to approximately linear as the mesh is refined. Alternatively, for the “concentric” specimens, the displacement errors diverge for the smallest mesh ($h_e=0.0625$ m). This divergence occurs due to an unavoidable increase in the quantity of cell crossing occurrences resulting from the combination of Cartesian mesh and circular particle distribution. For the “isoparametric” specimens, the rate of convergence for displacement is nearly quadratic for all meshes considered.

Fig. 10

Convergence behavior for radial stress, hoop stress, and displacement errors under mesh refinement for thick-walled cylinder simulations

Table 6 presents the calculated rates of convergence for stress and displacement errors for the three combinations of mesh shape and particle distribution. Overall, the isoparametric mesh with concentric particle distribution shows convergence behavior that is closest to the expected rates. This observation is consistent with Fig. 10, where the most accurate numerical stress and displacement contours are associated with the specimen utilizing the isoparametric mesh with concentric particle distribution.

Table 6 Convergence rates for radial stress, hoop stress, and displacement errors under mesh refinement for thick-walled cylinder simulations

In addition to comparing the various mesh shape and particle distributions, it is worth considering how the selection of the original versus updated VSB method influences simulation outputs. Therefore, Fig. 11 shows spatial convergence behavior for the stress and displacement errors, where both the original and updated variations of the VSB method are utilized. For both variations, a regular mesh with concentric particle distribution is utilized. Upon inspection, the stress errors are very similar for both approaches; the displacement errors exhibit similar rates of convergence and ultimately exhibit divergence due to the cell crossing noise. For displacement error results, there is more variability in terms of relative error between the two methods. Initially, the original VSB method exhibits lower error, whereas for smaller characteristic lengths, the updated VSB method exhibits reduced error.

Fig. 11

Convergence behavior for radial stress, hoop stress, and displacement errors under mesh refinement for thick-walled cylinder simulations

To better quantify the differences in simulation results, Table 7 lists the computed errors for each simulation. For all values of characteristic length considered, the radial and hoop stress errors are well aligned for both variations of the VSB method. In general, the updated VSB method has slightly reduced error compared to the original VSB method, and the maximum difference between the two stress errors is approximately 1.9e−3. The magnitude and trend of the displacement errors are also aligned, but exhibit a larger relative discrepancy than the stress errors. The maximum difference for the two displacement errors is approximately 1.8e−6.

Table 7 Radial stress, hoop stress, and displacement errors when imposing nonconforming Neumann boundary conditions with original VSB method and updated VSB method

4.2.2 Particle per cell study

The effects of PPC refinement is studied for this benchmark problem.

Table 8 lists the total quantity of particles for the uniform and concentric particle distributions. As discussed above, specimens were developed such that the total particles are approximately the same for both distributions. Recall that for the isoparametric mesh, the characteristic length in Table 5 does not accurately describe the size of the mesh. However, the value of PPC is exact for specimens with isoparametric mesh and concentric particle distribution. The same is true for values in Table 8. Additionally, for the regular mesh with concentric particle distribution, the value of PPC in Table 8 represents the approximate average PPC over the entire domain.

Table 8 Total quantity of material points used in PPC study for thick-walled cylinder simulations

Displacement and stress errors are computed with Eqs. (32) and (33), respectively. Figure 12 shows error behavior under PPC refinement. In general, there is not an expected convergence rate as the quantity of PPC increases. For specimens with regular mesh and uniform particle distribution (“uniform”), the radial stress error, hoop stress error, and displacement error decrease for all PPC refinement. For specimens with regular mesh and concentric particle distribution (“concentric”), the radial stress error and hoop stress error decrease for all PPC refinement. The displacement error initially decreases, but for PPC $=5$, the displacement error increases. The diverging error is caused by the inevitable increase in cell crossing quantity due to the combination of Cartesian mesh and circular particle distribution. For specimens with isoparametric mesh and concentric particle distributions (“isoparametric”), stress errors are relatively insensitive to PPC refinement. The lowest stress errors occur for PPC $=1$ with approximately constant error for the remaining values of PPC. For displacement, the largest error occurs for PPC $=1$ with approximately constant error for the remaining values of PPC.

Fig. 12

Convergence behavior for radial stress, hoop stress, and displacement errors under PPC refinement for thick-walled cylinder simulations (for mesh with $h_e=0.125$ m)

4.3 Infinite plate with elliptic hole under cavity expansion

The third numerical example and final benchmark problem is an infinite plate with elliptic hole under cavity expansion. This is a 2D plane strain benchmark.

The combination of non-circular cavity geometry and anisotropic far field stresses makes the analytic solution of stress more complex compared to the previous two benchmark problems. Therefore, this numerical example further verifies that the updated version of the VSB method is capable of accurately imposing nonconforming Neumann boundary conditions.

The geometry of this benchmark problem is illustrated by Fig. 13. The variables $a_0$ and $b_0$ correspond to the semimajor and semiminor axes of the elliptic hole, respectively. For the current numerical study, these axes are $a_0=2.0$ m and $b_0=1.5$ m. Figure 13 indicates that the Neumann boundary condition is an isotropic pressure applied along the elliptic cavity. The internal pressure is set as $p_i=12.5$ kPa (compressive). The infinite plate condition is approximately achieved by imposing the far-field stresses along the outer boundaries of the model. The far-field stress is set as $\sigma _0=10.0$ kPa (compressive) with varying values of K.

Fig. 13

Geometry for infinite plate with elliptic hole: semimajor axis, semiminor axis, location of applied Neumann boundary condition, and far-field stress condition

All simulations of the infinite plate are completed using regular mesh with a uniform particle distribution. PPC = 4 is consistently employed for this benchmark problem. Additionally, taking advantage of symmetry, only a quarter of the infinite plate is simulated. Vertical displacement is constrained to zero along the positive x-axis while horizontal displacement is constrained to zero along the positive y-axis.

The infinite plate simulations utilize a linear elastic constitutive model. Table 9 summarizes the elastic material parameters.

Table 9 Linear elastic material parameters for infinite plate with elliptic hole

Appropriate time step is computed using Eq. (29) with $\kappa =0.2$. The internal pressure is applied using the modified VSB method. The magnitude of pressure is slowly increased over 0.2 seconds such that the simulation remains approximately quasi-static. Cundall damping of 0.05 is used to quickly reach the steady-state solution [48].

The analytic solution for an infinite plate with a non-circular cavity and anisotropic far-field stresses can be determined using a conformal mapping function in conjunction with complex stress functions. This approach was first pioneered by G.V. Kolosov and subsequently detailed by Muskhelishvili (1953) [50]. A very brief summary of this method, along with explicit expressions for the Cartesian stresses, is provided in Appendix 3. Stress error is computed using Eq. (33).

The influence of mesh refinement is studied for this benchmark problem. Table 10 lists the characteristic length and associated total quantity of particles for the utilized meshes (using PPC $=4$). The characteristic length ranges from $h_e=0.0625$ m to $h_e=1.0000$ m.

Table 10 Total quantity of material points used in mesh refinement study for infinite plate with elliptic hole simulations

Figures 14, 15, and 16 plot the Cartesian stresses in the near-cavity region for $K=0.5$, $K=1.0$, and $K=2.0$, respectively. Each plot includes the analytic stresses, as well as the numeric solutions for the coarsest mesh ($h_e=1.0000$ m), medium mesh ($h_e=0.2500$ m), and finest mesh ($h_e=0.0625$ m). For the coarsest meshes, the solutions are noisy and do not necessarily exhibit the same stress distribution as the analytic solution. With the medium meshes, the solutions improve and the numeric and analytic stress contours are generally aligned. However, there still remains obvious mesh dependency due to the utilization of linear basis functions (similar to mesh dependency observed in the thick-walled cylinder simulations). The finest meshes display the smoothest stress distributions with further reduced numerical noise and generally provide a good match with the analytic solution.

Fig. 14

Analytic and numerical solutions in the near-cavity region for infinite plate with $K=0.5$

Fig. 15

Analytic and numerical solutions in the near-cavity region for infinite plate with $K=1.0$

Fig. 16

Analytic and numerical solutions in the near-cavity region for infinite plate with $K=2.0$

Figure 17 shows convergence behavior of the Cartesian stresses under mesh refinement. Overall, the error decreases with continued mesh refinement for each stress component and each value of K. Consider that the initial convergence behavior occurs as the mesh is refined from coarse mesh ($h_e=1.0000$ m) to medium mesh ($h_e=0.2500$ m). During this phase, the initial rate of convergence for $\sigma _{xx}$ ranges from $0.64-0.71$, while for $\sigma _{xy}$, it ranges from $0.64-0.69$. For $\sigma _{yy}$, the initial rate of convergence ranges from $0.51-1.06$ (where the rate of convergence when $K=1.0$ and $K=2.0$ is $>1.0$). The initial rates of convergence may be less than linear due to several factors. For instance, using a uniform particle distribution leads to a poorly resolved curved boundary, which could be alleviated by increasing the quantity of near-cavity particles. Moreover, the simulations employ linear basis functions while the analytic distributions of stress are highly nonlinear. With continued refinement, the magnitude of stress errors continues to decrease, but the rate of convergence tends to stagnate. This phenomenon has been observed in the MPM by others [46, 51], and is partly mitigated in certain variations of the MPM [52].

Fig. 17

Convergence behavior for Cartesian stresses under mesh refinement for infinite plate with elliptic hole simulations

4.4 3D simulation with evolving boundaries

The final numerical example simulates a 3D scenario of evolving boundaries arising from propagating failure in a wellbore. Instances of wellbore failure are well documented in both field observations [53] and laboratory testing [54,55,56,57]. Imposing Neumann boundary conditions along evolving boundaries in 3D poses significant numerical challenges if the boundary must be explicitly tracked or reconstructed. However, this numerical example illustrates that the VSB method is capable of imposing nonconforming Neumann boundary conditions, even under the complex conditions associated with evolving boundaries due to material failure and removal.

The wellbore is simulated using a 3D cylindrical shell with inner radius of $a=0.0127$ m, outer radius of $b=0.0762$ m, and height of $h=0.1524$ m (equivalent to 0.5 in, 3.0 in, and 6.0 in, respectively), as depicted in Fig. 18. An internal pressure of $p_i=7.0$ MPa (compressive) is applied to the inner cavity wall as the Neumann boundary condition using the modified VSB method. Additionally, fixed Dirichlet boundary conditions are imposed on the top and bottom of the 3D cylinder to constrain vertical displacements at these boundaries.

The simulation employs a regular mesh with characteristic length of $h_e=0.003$ m. Partials are initialized using PPC $=2$. For 3D specimens, PPC $=N$ signifies that particles are equally spaced with an $N\times N\times N$ distribution. Based on the specific combination of $h_e$, PPC, and the problem geometry, the model is ultimately comprised of 805,392 particles. Time step is compute using Eq. (29) with $\kappa =0.5$. The model utilizes a Mohr–Coulomb constitutive model with the material parameters listed in Table 11.

Table 11 Mohr–Coulomb material parameters for 3D cylindrical shell

Others have developed semi-analytic approaches to determine the episodic development of wellbore breakouts [58]. This approach treats the problems as a sequence of quasi-static problems. A similar procedure, outlined in Algorithm 2, is followed in the current study. Initially, the equilibrium state is computed based on fully applied boundary conditions and the current problem geometry. Subsequently, each particle is checked to determine whether it has exceeded the failure threshold. Failed particles are then removed from the simulation, resulting in an updated problem geometry. Since removing particles disrupts the equilibrium condition, the procedure must be repeated. The propagating failure may either reach a steady state where no more particles are removed from the model, or failure continues until total wellbore collapse. In the current study, Cundall damping of 0.05 is added to quickly reach the equilibrium state [48].

Algorithm 2

Simulate episodic development of wellbore failure

Several mechanisms are known to contribute to wellbore damage, including shear failure, tensile failure, volumetric failure, and fluid erosion failure [59, 60]. Considering the current boundary conditions, characterized by relatively high internal pressure, and the symmetric wellbore geometry, shear failure is expected to be the primary cause of damage [61]. Therefore, the failure threshold utilized in Algorithm 2 is established as the equivalent plastic deviatoric strain, $\varepsilon _q^p$. This parameter quantifies the magnitude of plastic shear deformation within the continuum and is defined as

$$\begin{aligned} \varepsilon _q^p = \sqrt{\frac{2}{3}\varvec{e}^p: \varvec{e}^p} , \end{aligned}$$

(34)

where $\varvec{e}^p$ is the deviatoric part of the plastic strain tensor, $\varvec{\varepsilon }^p$. In the current study, a constant failure threshold of $\varepsilon _{q}^{p}=0.003$ is utilized. Conducting a parametric investigation into the material parameters and the failure threshold can provide insights into critical aspects of wellbore failure. For instance, such studies may indicate factors that influence the rate and extent of material removal, conditions leading to either steady state or total wellbore collapse, and the impact of anisotropic stresses or geometric variations. However, these analyses are beyond the scope of the current study. The goal of this study is simply to demonstrate that the VSB method is capable of handling complex and evolving boundaries. A remapping (i.e., smoothing) procedure is employed for the equivalent plastic deviatoric strain when determining whether particles have exceeded the failure threshold (Step 2 in Algorithm 2). Alternatively, the true value of plastic strain is always utilized to determine the equilibrium state (Step 1 in Algorithm 2).

Figure 19 shows contours of the equivalent plastic deviatoric strain for the 3D cylindrical shell for each equilibrium state reached when repeatedly applying Algorithm 2. Initially, there is a very small damage zone in the near-cavity region with only one to two rows of particles exhibiting plastic strain greater than the removal threshold. After these failed particles are removed and the updated equilibrium state has been reached, it is observed that the material damage has propagated outwards. This is caused, in part, by the fact that the internal pressure remains constant, resulting in an increased force on the wellbore due to the larger wellbore surface area after the damaged particles are removed. Based on the problem geometry and the imposed cavity pressure, the damage pattern should always be axisymmetric. However, the observed damage zone appears “$+$”-shaped due to a mismatch between the orientation of the stress contours, background mesh, and particle distribution. Now, six to seven rows of particles have plastic strain greater than the removal threshold. After these failed particles are removed, material damage continues to propagate outwards until reaching approximately half of the model with nearly 20 rows of particles exhibiting plastic strain greater than the removal threshold. After removing the newly failed particles, the entire remaining model exhibits plastic strain above the failure threshold. Additionally, the specimen distorts due to the large internal forces relative to the remaining ring of particles. In short, the specimen exhibits total failure.

Fig. 18

Geometry for 3D cylindrical shell

Fig. 19

Contours of equivalent plastic deviatoric strain ($\varepsilon _q^p$) for each equilibrium state before specimen collapse

Overall, this demonstration highlights several advantageous components of the VSB method. It effectively imposes nonconforming Neumann boundary conditions for a problem with evolving boundary geometry. As a result of material damage and subsequent removal, the inner boundary evolves, but determining the precise position of the new material boundary, which presents clear numerical challenges in 3D, becomes unnecessary when utilizing the VSB method. Additionally, simulation results exhibit approximately symmetric outcomes in the x–y plane, as well as an approximately constant equivalent plastic deviatoric strain profile in the vertical direction. This suggests that even as particles are removed, the simulation remains numerically stable. The true damage pattern in the x–y plane should be perfectly axisymmetric. However, the numerical results exhibit planes of symmetry in the x–y plane due to mesh dependency arising from the utilization of Cartesian background mesh and uniform particle distribution. Section 4.2 demonstrates that adjusting particle distribution or mesh shape may mitigate a portion of the observed mesh-dependent behavior. Vertical symmetry confirms successful integration of the VSB method within the MPM framework. In particular, regions of the model subjected to both nonconforming Neumann boundary conditions and conforming Dirichlet boundary conditions show no spurious results. Furthermore, the approximately constant equivalent plastic deviatoric strain profile in the vertical direction illustrates that the resulting force due to internal pressure primarily acts in the radial directions, consistent with the expected resultant force within the pressurized cylindrical shell.

5 Conclusion

This paper introduces a modification to the VSB method that eliminates the need for cell-wise quadrature present in the original approach. Both the original and modified VSB methods rely on a problem transformation where a boundary traction is replaced with a virtual stress field. This transformation introduces a virtual domain containing the virtual stress field and necessitates an additional governing equation. This additional governing equation serves as the basis for developing an updated strong formulation and corresponding weak formulation. Essentially, the modified VSB method further simplifies the expression for the weak formulation found in the original approach. The simplified weak formulation is then utilized to develop a discretized formulation for the balance equations, enabling the imposition of nonconforming Neumann boundary conditions using only particle-wise quadrature. The modified VSB method is easily embedded in the MPM framework since only the expressions for internal and external nodal forces must be updated.

The numerical benchmark problems presented above cover a range of scenarios, including an axially loaded 1D column, internally pressurized thick-walled cylinder, and an infinite plate with elliptic hole under cavity expansion. These cases demonstrate the versatility of the VSB method, which can be applied to scenarios with various mesh type, particle distributions, and boundary geometries. In all cases, the computed results exhibit good agreement with the available analytic solutions and good spatial convergence. The final numerical example highlights the capability of the VSB method to impose Neumann boundary conditions for 3D scenarios with complex and evolving boundaries.

Future research should prioritize enhancing numerical accuracy and gaining insight into the factors that contribute to stagnating convergence rates.

Appendices

Appendix A: Summary of analytic solutions

Appendix A provides a summary of analytic solutions used for the three benchmark problems in the current study.

1.1 Axially loaded column

Analytic expressions for displacement and stress along the 1D column are represented by $u(x^0)$ and $\sigma (x^0)$, respectively. These terms are defined in terms of the initial position, $x^0$. The magnitude of displacement depends on both the true strain and the initial position such that

$$\begin{aligned} u(x^0) = x^0 \ln \left( 1 + \hat{t} /E\right) , \end{aligned}$$

(A1)

where $\hat{t}$ is the applied boundary traction (compression positive) and E is the Young’s modulus. Alternatively, stress is constant throughout the column such that

$$\begin{aligned} \sigma (x^0) = \hat{t}. \end{aligned}$$

(A2)

1.2 Internally pressurized thick-walled cylinder

Resulting from rotational symmetry of the thick-walled cylinder geometry, displacement and stress depend on only the radial position, r (and not the current orientation, $\theta$). The analytic expressions for radial displacement, radial stress, and hoop stress follow the notational conventions found in [63]. Analytic displacement, u(r), is given by

$$\begin{aligned} u(r) = \frac{\left( 1+\nu \right) }{E}\frac{p_i r}{\left( \left( \frac{b}{a}\right) ^2 -1\right) }\left( (1-2\nu ) + \left( \frac{b}{r}\right) ^2\right) , \end{aligned}$$

(A3)

where a, b, and r are the inner radius, outer radius, and radial position, respectively. Additionally, E is the Young’s modulus and $\nu$ is the Poisson ratio. Finally, $p_i$ is the applied internal pressure. Analytic radial stress and hoop stress, $\sigma _{rr}(r)$ and $\sigma _{\theta \theta }(r)$, respectively, are given by

$$\begin{aligned} \sigma _{rr}(r)= & {} \frac{p_i}{\left( \left( \frac{b}{a}\right) ^2 -1\right) }\left( 1-\left( \frac{b}{r}\right) ^2\right) , \end{aligned}$$

(A4)

$$\begin{aligned} \sigma _{\theta \theta }(r)= & {} \frac{p_i}{\left( \left( \frac{b}{a}\right) ^2 -1\right) }\left( 1+\left( \frac{b}{r}\right) ^2\right) . \end{aligned}$$

(A5)

Due to symmetry of the thick-walled cylinder geometry and applied pressure boundary, analytic shear stress is $\sigma _{r\theta }(r)=0$ throughout the entire domain.

1.3 Infinite plate with elliptic hole under cavity expansion

The elastic solutions for stress in an infinite plate with an elliptic hole under cavity expansion are derived using the conformal mapping function and complex stress functions. This methodology follows the classic work of G.V. Kolosov which has been widely shared in the translated work of Muskhelishvili [50]. Further insights into the development of explicit expression of stress are found in [64].

The conformal map function is defined as

$$\begin{aligned} z = w(\zeta ) = R\left( \frac{1}{\zeta } + m\zeta \right) , \end{aligned}$$

(A6)

where $z=x+iy$ and $\zeta =\xi + i\eta$ with $i^2=-1$. This function maps the interior of the unit disk in the phase plane to the exterior of an ellipse in the physical plane as illustrated by Fig. 20.

Fig. 20

Illustration of the conformal map between the exterior of an ellipse (physical space) and the interior of the unit disk (phase space)

The coefficients of R and m are defined based on problem geometry such that

$$\begin{aligned} R= & {} \frac{a_0 + b_0}{2} , \end{aligned}$$

(A7)

$$\begin{aligned} m= & {} \frac{a_0 - b_0}{a_0 + b_0}, \end{aligned}$$

(A8)

where $a_0$ and $b_0$ are the semimajor axis and semiminor axis of the ellipse, respectively.

Cartesian stresses are related to the conformal mapping function and complex stress functions by

$$\begin{aligned}{} & {} \sigma _{xx} + \sigma _{yy} = 4\text {Re}\left[ \frac{\phi '(\zeta )}{w'(\zeta )}\right] , \end{aligned}$$

(A9)

$$\begin{aligned}{} & {} \sigma _{yy} - \sigma _{xx} + 2i\sigma _{xy} = \frac{2}{w'(\zeta )} \left[ \overline{w(\zeta )} \left( \frac{\phi '(\zeta )}{w'(\zeta )}\right) ' + \psi '(\zeta ) \right] , \nonumber \\ \end{aligned}$$

(A10)

where $\phi (\zeta )$ and $\psi (\zeta )$ are the complex stress functions found in [64]. Note, $\square '$ indicates the first derivative of a function and $\overline{\square }$ indicates the complex conjugate of a function.

Equation (A9) is explicitly expressed as

$$\begin{aligned}{} & {} \sigma _{xx} + \sigma _{yy}\nonumber \\{} & {} \;\; = 4\text {Re}\left[ \frac{-4 p_i m \zeta ^2 + \sigma _0\left( 1+K+K(m-2)\zeta ^2+(m+2)\zeta ^2\right) }{4m\zeta ^2 - 4}\right] ,\nonumber \\ \end{aligned}$$

(A11)

where $p_i$ is internal pressure, $\sigma _0$ is the far-field stress, and K is the ratio between horizontal and vertical stress in the far field. Likewise, Eq. (A10) is explicitly expressed as

$$\begin{aligned}{} & {} \sigma _{yy} - \sigma _{xx} + 2i\sigma _{xy}\nonumber \\{} & {} \quad = \frac{-4\zeta ^2(\zeta ^2+m\rho ^4)}{\rho ^2(m\zeta ^2-1)^3}\left( -p_i m + \frac{(1+K)\sigma _0 m}{2} + \frac{(1-K)\sigma _0}{2}\right) \nonumber \\{} & {} \quad \quad -(1-K)\sigma _0 -2p_i \frac{(1+m^2)(1+m\zeta ^2)\zeta ^2}{(m\zeta ^2 -1)^3} \nonumber \\{} & {} \quad \quad +(1+K)\sigma _0 \frac{(1+m^2)(1+m\zeta ^2)\zeta ^2}{(m\zeta ^2 -1)^3} \nonumber \\{} & {} \quad \quad +(1-K)\sigma _0 \frac{\zeta ^2\left[ (m^2-1)m\zeta ^4+(3-m^2)\zeta ^2+2m\right] }{(m\zeta ^2 -1)^3},\nonumber \\ \end{aligned}$$

(A12)

where $\rho$ is the absolute value of the phase space complex coordinate $\zeta$.

Appendix B: List of symbols

Roman symbols (lower)
a	Inner radius of thick-walled cylinder
$a_0$	Semimajor axis of ellipse
b	Outer radius of thick-walled cylinder
$b_0$	Semiminor axis of ellipse
$\varvec{b}$	Body force per unit mass vector
$\bar{\varvec{b}}$	Virtual body force per unit mass vector
$\textrm{d}t$	Time step
$\varvec{e}^p$	Deviatoric part of the plastic strain tensor
$e_u$	Displacement error
$e_{\sigma }$	Stress error
$\varvec{f}^{\textrm{ext}}$	External force vector
$\varvec{f}^{\textrm{ext,traction}}$	Traction part of external force vector
$\varvec{f}^{\textrm{int}}$	Internal force vector
$\tilde{\varvec{f}}^{\textrm{ext}}$	Updated external force vector
$\tilde{\varvec{f}}^{\textrm{int}}$	Updated internal force vector
$\bar{\varvec{f}}$	Divergence of the virtual stress field
$h_e$	Characteristic length
m	Mass
$\varvec{n}$	Outward unit normal
$\varvec{\hat{n}}$	Outward unit normal on Neumann boundary
$n_c$	Number of cell quadrature points
$n_n$	Number of nodes
$n_p$	Number of particles
p	Pressure
$p_i$	Internal pressure
$\varvec{p}$	Momentum vector
$\dot{\varvec{p}}$	Rate of momentum vector
r	Radial position
$\hat{\varvec{t}}$	Imposed traction vector
$\varvec{u}$	Displacement vector
$\hat{\varvec{u}}$	Imposed displacement vector
$\ddot{\varvec{u}}$	Acceleration vector
$\ddot{\bar{\varvec{u}}}$	Virtual acceleration vector
$\varvec{x}$	Position vector
$\varvec{x}^0$	Initial position vector

Roman symbols (upper)
A	Boundary surface area
E	Young’s modulus
K	Ratio between horizontal and vertical stress
$L_0$	Initial column length
M	Constrained modulus
$N_{I}$	Linear basis function
V	Particle volume
Letter-like symbols
$\mathcal {A}$	Active node set
$\mathcal {E}_1$	Cell set 1
$\mathcal {E}_2$	Cell set 2
$\mathbb {I}$	Second-order identity matrix
$\mathcal {N}_1$	Node set 1
$\mathcal {W}$	Space of admissible virtual displacements
Greek symbols (lower)
$\delta \varvec{u}$	Virtual displacement
${\varvec{\varepsilon }}^p$	Plastic strain tensor
$\varepsilon _q^p$	Equivalent plastic deviatoric strain
$\theta$	Rotation above x-axis
$\kappa$	Time step reduction factor
$\bar{\mu }$	Virtual stress field variable
$\nu$	Poisson ratio
$\varvec{\xi }$	Local coordinate vector
$\rho$	Density
$\bar{\rho }$	Virtual density
$\sigma _0$	Far-field stress
$\sigma _{rr},~\sigma _{\theta \theta },~\sigma _{r\theta }$	Polar stresses
$\sigma _{xx},~\sigma _{yy}, ~\sigma _{xy}$	Cartesian stresses
${\varvec{\sigma }}$	Cauchy stress tensor
$\bar{{\varvec{\sigma }}}$	Virtual stress tensor
Greek symbols (upper)
$\Gamma$	Material boundary
$\Gamma _{t}$	Neumann (traction) boundary
$\Gamma _{u}$	Dirichlet (displacement) boundary
$\Omega$	Material domain
$\bar{\Omega }$	Virtual domain