1 Introduction

In past few decades, the boundary layer flow and heat/mass transfer over stretching sheet has attracted the attention of researchers because of its valuable applications in many engineering and industrial processes. The most common applications of such phenomenon are glass fibre and paper production, packed sphere bed, hot rolling and continuous casting of metal and spinning of fibers, etc. In view of all these numerous applications many researchers worked on such problems. The effects of heat transfer on flow of non-Newtonian fluid over stretching sheet has been analyzed by many researchers [1–10]. The primary interest of such investigations is to predict the variation of skin friction coefficient and local Nusselt number with non-Newtonian parameters. The mathematical equivalence of the thermal boundary layer problem with the concentration analogue has provided the liberty to use the results obtained for heat transfer to the case of mass transfer by replacing the Prandtl number by Schmidt number. However, such equivalence is not possible when chemical reaction term is introduced in the mass diffusion equation. In such cases, the mass transfer equations must be solved along with momentum and energy equation to analyze the concentration field.

Alharbi et al. [11] discussed heat and mass transfer characteristics with chemical reaction on steady flow of viscoelastic fluid through porous medium over stretching sheet. Hayat et al. [12] investigated the effects of heat and mass transfer on second grade fluid in presence of chemical reaction. Veena et al. [13] obtained the non-similar solution of electrically conducting viscoelastic fluid with heat and mass transfer. Some more useful contributions regarding heat and mass transfer analysis of boundary layer flow with chemical reaction can be found in Refs. [14–18].

Sometimes heat and mass transfer occur simultaneously in moving fluid, then it is often observed that heat flux can be generated not only by temperature gradients but also by concentration gradients. The phenomenon of Soret (Thermal diffusion) is occurrence of diffusion flux due to temperature gradient. The reciprocal of Soret effect is known as Dufour effect, the occurrence of energy flux due to chemical potential gradient. Soret and Dufour effects play a vital role in geoscience and chemical engineering. Anghel [19] analyzed Soret and Dufour effects on free convection boundary layer flow over a vertical surface embedded in porous medium. Postelnicu [20] investigated the phenomenon of heat and mass transfer by natural convection from a vertical surface embedded in a saturated porous medium by considering Soret and Dufour effects. Srinivasacharya et al. [21] studied mixed convection viscous fluid over an exponentially stretching vertical surface subject to Soret and Dufour effects. Beg et al. [22] focused their research to investigate Soret and Dufour effects on laminar magnetohydrodynamic flow of viscous fluid. Soret and Dufour’s effects on Hiemenz flow through porous medium over stretching surface were investigated by Tsai [23]. Ahmed [24] reported the influence of Soret and Dufour effects by analyzing the similarity solution for free convection heat and mass transfer over a permeable stretching surface. Hayat et al. [25] analyzed the Soret and Dufour’s effects on mixed convection boundary layer flow of a viscoelastic fluid over a vertical stretching surface. In another contribution, Hayat et al. [26] discussed Soret and Dufour effects on mixed convection boundary layer flow of a Casson fluid. Bazid et al. [27] presented the numerical solution of stagnation point flow towards a stretching surface in the presence of buoyancy force and Soret and Dufour effects. Pal et al. [28] discussed the Soret and Dufour effects on MHD non-Darcian mixed convection heat and mass transfer over a stretching sheet with non-uniform heat source/sink. Nayak [29] discussed the Soret and Dufour effects on mixed convection unsteady boundary layer flow over a stretching sheet in porous medium by using Runge–Kutta method with shooting technique.

Then above mentioned studies deals with the fluid motion due to stretching of the sheet alone. However, there are situations where the sheet is stretched as well as oscillate periodically in its own plane. In this direction Wang [30] performed an analysis for the flow of a viscous fluid over an oscillatory stretching sheet. Zheng et al. [31] investigated Soret and Dufour effects in MHD viscous flow over an oscillatory stretching sheet. They used homotopy analysis method to solve the governing problem. A glance at the literature reveals that very little attention has been given to the flow, heat and mass transfer effects of non-Newtonian fluids. Keeping this fact in mind we investigated the Soret and Dufour effects in the presence of thermal radiation on unsteady flow of viscoelastic fluid over porous oscillatory stretching sheet in this paper. In fact, this study extends the analysis of Zheng et al. [31] in three directions. Firstly, by considering viscoelastic fluid, secondly assuming porous oscillatory stretching sheet and lastly including radiation effects. Well known analytical technique namely homotopy analysis method (HAM) is used to compute the solution of nonlinear partial differential equations. It is remarked here that HAM is well established tools for solving many complicated nonlinear problems arising in various scientific disciplines [32–36]. The paper is structured as follows: Sect. 2 presents the flow geometry and governing equation. The framework of HAM for solving the equations obtained in Sect. 2 is illustrated in Sect. 3. The convergence of HAM solution is discussed in Sect. 4. The effects of emerging parameters on various flow features are illustrated in Sect. 5. Important conclusions are listed in Sect. 6.

2 Governing equations

Constitutive equation for a second grade fluid is [37]

$$\tau^{ij} = - p\delta^{ij} + \mu A^{(1)ij} + \alpha_{1} A^{(1)ik} A^{(1)jk} + \alpha_{2} A^{(2)ij} ,\,$$
(1)

where τ ij are the components of Cauchy stress tensor, p is the pressure, δ ij are components of the identity tensor, μ is the dynamic viscosity, α 1, α 2 are material constants where μ ≥ 0, α 1 ≥ 0, α 1 + α 2 = 0 and A (1)ij, A (2)ij are the components of first and second Rivlin-Ericksen tensors defined as

$$A^{(1)ij} = V^{i,\,j} + V^{j,\,i} ,\,$$
(2)
$$A^{(2)ij} = a^{i,\,j} + a^{j,\,i} + 2V^{m,\,i} V^{m,\,j} ,\,$$
(3)
$$a^{i} = \frac{{\partial V^{i} }}{\partial t} + V^{j} V^{i,\,j} ,\,$$
(4)

where V i and a i are the components of velocity and acceleration respectively. Equations governing the flow, heat and mass transfer are

$$v_{,\,i}^{i} = 0,\,$$
(5)
$$\rho a^{i} = S_{,\,j}^{ij} + \rho b^{i} + R^{i} ,\,$$
(6)
$$\rho c_{p} \left[ {\frac{\partial T}{\partial t} + v^{r} T_{,\,r} } \right] = \alpha T_{,\,ii} + \frac{{\rho D_{m} k_{T} }}{{c_{s} }}C_{,\,ii} - \frac{{\partial q_{r} }}{{\partial \overline{y} }},\,$$
(7)
$$\frac{\partial C}{\partial t} + v^{r} C_{,\,r} = D_{m} C_{,\,ii} + \frac{{D_{m} k_{T} }}{{T_{m} }}T_{,\,ii} ,\,$$
(8)

where ρ is the fluid density, b i are the components of body force per unit volume, R i are the Darcy resistance, c p is the specific heat, α is the thermal diffusivity, T is the temperature, C is the concentration, D m is the molecular diffusivity of the species concentration, k T is the thermal diffusion ratio, c s is the concentration susceptibility, T m is the mean fluid temperature and q r is the radiative heat flux. Since fluid is subject to a constant magnetic field, therefore, the body force in this case is given by

$$b^{i} = \varepsilon_{jk}^{i} J^{j} B^{k} ,\,$$
(9)

where ɛ ijk, J j and B k are the components of the Levi–Civita symbol, current density and magnetic field strength respectively. Under the low magnetic Reylonds number approximation, we have neglected the induced magnetic field. It is also assumed that electric current is negligible as comparison to the current density. In such a situation current density can be obtained using Ohm’s law as follows

$$J^{i} = \sigma \varepsilon_{jk}^{i} V^{j} B_{0}^{k} ,\,$$
(10)

and therefore

$$\rho b^{i} = \sigma \varepsilon_{{^{ijk} }} \varepsilon_{{^{jmn} }} V^{m} B_{0}^{n} B_{0}^{k} ,\,$$
(11)
$$\rho b^{i} = \sigma \varepsilon_{{^{jki} }} \varepsilon_{{^{jmn} }} V^{m} B_{0}^{n} B_{0}^{k} ,\,$$
(12)
$$\rho b^{i} = \sigma \left( {\delta_{km} \delta_{in} - \delta_{kn} \delta_{im} } \right)\,V^{m} B_{0}^{n} B_{0}^{k} ,\,$$
(13)
$$\rho b^{i} = \sigma B_{0}^{m} \left( {V^{m} B_{0}^{i} - V^{i} B_{0}^{m} } \right).$$
(14)

3 Statement of problem

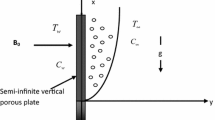
Let us consider two-dimensional boundary layer flow of incompressible electrically conducting second grade fluid in a porous medium over permeable oscillatory stretching sheet in the presence of Soret and Dufour effects. It is further assumed that a constant magnetic field of strength B o is applied in the transverse direction. The sheet performs periodic oscillations back and forth and stretched with a velocity \(u = b\bar{x}\sin \omega t\) (where b is the stretching rate and ω is the angular frequency). The schematic diagram of the flow is shown in Fig. 1.

Fig. 1
figure 1

Schematic diagram of the flow situation

Full size image

In the present flow situation we have

$$V^{i} {\mathbf{ = }}\left[ {u\left( {\bar{x},\,\bar{y},\,t} \right),\,v\left( {\bar{x},\,\bar{y},\,t} \right),\,0} \right]\,,$$
(15)

and B i = [0, B 0, 0]

therefore

$$\rho b^{i} = \left[ { - \sigma B_{0}^{2} u,\,0,\,0} \right].$$
(16)

Furthermore, the modified Darcy law for a second grade fluid is given by [38]

$$R^{i} = \frac{\phi }{k}\left[ {\mu + \alpha_{1} \frac{\partial }{\partial t}} \right]\,V^{i} ,\,$$
(17)

Substituting Eqs. (15–17) in Eqs. (5–9) and using the usual boundary layer approximations [39], we have

$$\frac{\partial u}{{\partial \bar{x}}} + \frac{\partial v}{{\partial \bar{y}}} = 0,\,$$
(18)
$$\frac{\partial u}{\partial t} + u\frac{\partial u}{{\partial \bar{x}}} + v\frac{\partial u}{{\partial \bar{y}}} = \nu \frac{{\partial^{2} u}}{{\partial \bar{y}^{2} }} + \frac{{\alpha_{1} }}{\rho }\left[ {\frac{{\partial^{3} u}}{{\partial t\partial \bar{y}^{2} }} + \frac{\partial }{{\partial \bar{x}}}\left( {u\frac{{\partial^{2} u}}{{\partial \bar{y}^{2} }}} \right) + \frac{\partial u}{{\partial \bar{y}}}\frac{{\partial^{2} v}}{{\partial \bar{y}^{2} }} + v\frac{{\partial^{3} u}}{{\partial \bar{y}^{3} }}} \right]\, - \frac{{\sigma B_{0}^{2} }}{\rho }u - \frac{\phi }{\rho k}\left( {\mu + \alpha_{1} \frac{\partial }{\partial t}} \right)\,u,\,$$
(19)
$$\frac{\partial T}{\partial t} + u\frac{\partial T}{{\partial \bar{x}}} + v\frac{\partial T}{{\partial \bar{y}}} = \alpha \frac{{\partial^{2} T}}{{\partial \bar{y}^{2} }} + \frac{{D_{m} k_{T} }}{{c_{s} c_{p} }}\frac{{\partial^{2} C}}{{\partial \bar{y}^{2} }} - \frac{1}{{\rho c_{p} }}\frac{{\partial q_{r} }}{{\partial \bar{y}}},\,$$
(20)
$$\frac{\partial C}{\partial t} + u\frac{\partial C}{{\partial \bar{x}}} + v\frac{\partial C}{{\partial \bar{y}}} = D_{m} \frac{{\partial^{2} C}}{{\partial \bar{y}^{2} }} + \frac{{D_{m} k_{T} }}{{T_{m} }}\frac{{\partial^{2} T}}{{\partial \bar{y}^{2} }}.$$
(21)

The model Eq. (19) is valid for small values of elastic parameter α 1 since it has been derived to the first order in elasticity representing the short memory fluid with smaller relaxation time. By using Rosseland approximation for radiation [40], we write

$$q_{r} = - \frac{{4\sigma^{ * } }}{{3k^{ * } }}\frac{{\partial T^{4} }}{{\partial \bar{y}}},\,$$
(22)

where σ * represents the Stefan–Boltzmann constant, k * is the mean absorption coefficient. Expanding using Tayler series, we get

$$T^{4} \cong 4TT_{\infty }^{3} - 3T_{\infty }^{4} .$$
(23)

In view of Eqs. (22) and (23), Eq. (20) becomes

$$\frac{\partial T}{\partial t} + u\frac{\partial T}{{\partial \bar{x}}} + v\frac{\partial T}{{\partial \bar{y}}} = \left( {\alpha + \frac{{16\sigma^{ * } T_{\infty }^{3} }}{{3k^{ * } }}} \right)\,\frac{{\partial^{2} T}}{{\partial \bar{y}^{2} }} + \frac{{D_{m} k_{T} }}{{c_{s} c_{p} }}\frac{{\partial^{2} C}}{{\partial \bar{y}^{2} }},\,$$
(24)

Let T w be temperature of the sheet and T ∞ denotes the ambient temperature in free stream, while C w and C ∞ correspond to surface concentrations and ambient concentration, respectively. The corresponding initial and boundary conditions are

$$u = u_{\omega } = b\bar{x}\sin \omega t,\, \, v = v_{w} ,\,\;\;\;T = T_{w} = T_{\infty } + A\bar{x} , { }C = C_{w} = C_{\infty } + B\bar{x} \quad {\text{ at}}\;\;\;\;\;\bar{y} = 0,\, \, t > 0,\,$$
(25)
$$u = 0,\, \, \frac{\partial u}{{\partial \bar{y}}} = 0,\, \, T \to T_{\infty } , \quad C \to C_{\infty } \quad {\text{ at}} \quad \bar{y} \to \infty .$$
(26)

To non-dimentionalize the flow problem, we introduce the following dimensionless variable:

$$y = \sqrt {\frac{b}{\nu }} \bar{y},\, \, \tau = t\omega ,\, \, u = b\bar{x}f_{y} \left( {y,\,\tau } \right),\, \, v = - \sqrt {\nu b} f\left( {y,\,\tau } \right),\,$$
(27)
$$\theta (y,\,\tau ) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }},\,\;\phi (y,\,\tau ) = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }}.$$
(28)

With the help of Eqs. (27) and (28) the continuity equation is identically satisfied and Eqs. (19, 21) and (24) reduce to

$$S(1 + \lambda K)f_{y\tau } + f_{y}^{2} - ff_{yy} + M^{2} f_{y} + \lambda f_{y} = f_{yyy} + K\left( {Sf_{yyy\tau } + 2f_{y} f_{yyy} - f_{yy}^{2} - ff_{yyyy} } \right),\,$$
(29)
$$\frac{1}{\Pr }\left( {1 + N_{r} } \right)\,\theta_{yy} + Du\phi_{yy} + f\theta_{y} - S\theta_{\tau } - \theta f_{y} = 0,\,$$
(30)
$$\phi_{yy} + S_{c} \left( {Sr\theta_{yy} + f\phi_{y} - S\phi_{\tau } - \phi f_{y} } \right) = 0.$$
(31)

In above equations, the dimensionless parameters \(K = \tfrac{{b\alpha_{1} }}{\nu \rho }\) is the dimensionless viscoelastic parameter and is of O (δ 2), δ being the boundary layer thickness [41]. Here K = 0 corresponds to the case of a Newtonian fluid, S ≡ ω/b is the ratio of oscillation frequency of the sheet to its stretching rate, \(M = \sqrt {\sigma B_{0}^{2} /\rho b}\) represents Hartmann number, \(\lambda = \tfrac{\nu \phi }{kb}\) denotes the porosity parameter, Pr = ν/α is the Prandtl number, Sc = ν/D m is the Schmidt number, \(\;Du = \tfrac{{D_{m} k_{T} \left( {C_{w} - C_{\infty } } \right)}}{{c_{s} c_{p} \nu \left( {T_{w} - T_{\infty } } \right)}}\) is the Dufour number \(,\,\;Sr = \tfrac{{D_{m} k_{T} \left( {T_{w} - T_{\infty } } \right)}}{{T_{m} \nu \left( {C_{w} - C_{\infty } } \right)}}\) represents Soret number \(,\,\;\;\gamma = \tfrac{{ - v_{w} }}{{\sqrt {a\nu } }}\) is the mass transfer parameter with γ > 0 for suction and γ < 0 for injection and \(N_{r} = \tfrac{{16\sigma^{ * } T_{\infty }^{3} }}{{3\alpha k^{{^{ * } }} }}\) is the radiation parameter.

Following Magyari and Pantokratoras [42], we write Eq. (30) as

$$\frac{1}{{\Pr_{eff} }}\theta_{yy} + Du\phi_{yy} + f\theta_{y} - S\theta_{\tau } - \theta f_{y} = 0,\,$$
(32)

where Preff = Pr/(1 + N r ) represents the effective Prandtl number. Magyari and Pantokratoras [42] pointed out that there is no need to solve energy Eq. (32) by using two parameter approach i.e. for different values of Pr and N r . They showed that in fact the investigation of heat transfer characteristics with and without thermal radiation is exactly the same task. They further emphasized that the radiation problem admits the same solution for infinite set of parameter values (N r , Pr) which corresponds to same effective Prandtl number. Following Magyari and Pantokratoras [42], we solve the Eq. (32) for various values of effective Prandtl number.

The boundary conditions (25) and (26) take the form

$$f_{y} \left( {0,\,\tau } \right) = \sin \tau ,\quad f\left( {0,\,\tau } \right) = \gamma ,\quad \theta (0,\,\tau ) = 1,\,\;\;\phi (0,\,\tau ) = 1,\,$$
(33)
$$f_{y} \left( {\infty ,\,\tau } \right) = 0,\quad f_{yy} \left( {\infty ,\,\tau } \right) = 0, \quad \theta (\infty ,\,\tau ) = 0,\,\;\;\phi (\infty ,\,\tau ) = 0.$$
(34)

We define the skin-friction coefficient C f , local Nusselt number Nu x and local Sherwood number as

$$C_{f} = \frac{{\tau_{w} }}{{\rho u_{w}^{2} }},\,\; \, Nu_{x} = \frac{{\bar{x}q_{w} }}{{k\left( {T_{w} - T_{\infty } } \right)}},\,\; \, Sh_{x} = \frac{{\bar{x}q_{m} }}{{D\left( {C_{w} - C_{\infty } } \right)}},\,$$
(35)

where τ w is the shear stress, q w represents the heat flux and q m is mass flux at wall, which can be defined as

$$\tau_{w} = \mu \left( {\frac{\partial u}{{\partial \bar{y}}}} \right)_{{\overline{y} = 0}} + \alpha_{1} \left( {\begin{array}{*{20}c} {\tfrac{{\partial^{2} u}}{{\partial t\partial \bar{y}}} + u\tfrac{{\partial^{2} u}}{{\partial \bar{y}\partial \bar{x}}}} \\ { + v\tfrac{{\partial^{2} u}}{{\partial \bar{y}^{2} }} - 2\tfrac{\partial u}{{\partial \bar{y}}}\tfrac{\partial v}{{\partial \bar{y}}}} \\ \end{array} } \right)_{{_{{\bar{y} = 0}} }} ,\,q_{w} = - k\left( {\frac{\partial T}{{\partial \bar{y}}}} \right)_{{\bar{y} = 0}} ,\,q_{m} = - D\left( {\frac{\partial C}{{\partial \bar{y}}}} \right)_{{\bar{y} = 0}} .$$
(36)

In view of (27) and (28), Eqs. (35) and (36) become

$$\left\{ {\begin{array}{*{20}l} {\text{Re}_{x}^{1/2} C_{f} = \left[ {f_{yy} + K\left( {Sf_{yy\tau } + 3f_{y} f_{yy} - ff_{yyy} } \right)} \right]_{{\overline{y} = 0}} ,} \hfill \\ {\text{Re}_{x}^{ - 1/2} Nu_{x}^{ * } = - \theta_{y} \left( {0,\,\tau } \right),} \hfill \\ {\text{Re}_{x}^{ - 1/2} Sh = - \phi_{y} \left( {0,\,\tau } \right).} \hfill \\ \end{array} } \right.\,$$
(37)

where Nu * x  = Nu x /(1 + N r ) the effective local Nusselt number and \(\text{Re}_{x} = u_{w} \bar{x}/\nu\) represents the local Reynold number.

4 Homotopy analysis method

In view of boundary conditions, we choose the following initial guesses and linear operators for velocity, temperature and concentration fields

$$f_{0} (y,\,\tau ) = \gamma + \sin \tau (1 - \exp ( - y)),\,$$
(38)
$$\theta_{0} (y) = \exp ( - y).$$
(39)
$$\phi_{0} (y) = \exp ( - y).$$
(40)
$$L_{f} = \frac{{\partial^{3} f}}{{\partial y^{3} }} - \frac{\partial f}{\partial y},\,$$
(41)
$$L_{\theta } = \frac{{\partial^{2} \theta }}{{\partial y^{2} }} - \theta ,\,$$
(42)
$$L_{\phi } = \frac{{\partial^{2} \phi }}{{\partial y^{2} }} - \phi ,\,$$
(43)

which has following properties

$$L_{f} [C_{1} + C_{2} \exp ( - y) + C_{3} \exp (y)] = 0,\,$$
(44)
$$L_{\theta } [C_{4} \exp (y) + C_{5} \exp ( - y)] = 0,\,$$
(45)
$$L_{\phi } [C_{6} \exp (y) + C_{7} \exp ( - y)] = 0,\,$$
(46)

where C i (i = 1–5) are arbitrary constants.

4.1 Zeroth order deformation problems

We construct the following zeroth order deformation problems

$$(1 - p)L_{f} [\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p) - f_{0} (y,\,\tau ) = ph_{f} N_{f} [\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)],\,$$
(47)
$$(1 - p)L_{\theta } [\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (y,\,\tau ;\,p) - \theta_{0} (y,\,\tau ) = ph_{\theta } N_{\theta } [\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (y,\,\tau ;\,p),\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (y,\,\tau ;\,p),\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)],\,$$
(48)
$$(1 - p)L_{\phi } [\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (y,\,\tau ;\,p) - \phi_{0} (y,\,\tau ) = ph_{\theta } N_{\theta } [\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (y,\,\tau ;\,p),\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (y,\,\tau ;\,p),\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)],\,$$
(49)
$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (0,\,\tau ;\,p) = 0,\,\left. {\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)}}{\partial y}} \right|_{y = 0} = \sin \tau ,\,\left. {\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)}}{\partial y}} \right|_{y = \infty } = 0,\,\left. {\frac{{\partial^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)}}{{\partial y^{2} }}} \right|_{y = \infty } = 0$$
(50)
$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (0,\,\tau ;\,p) = 1,\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (\infty ,\,\tau ;\,p) = 0,\,$$
(51)
$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (0,\,\tau ;\,p) = 1,\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (\infty ,\,\tau ;\,p) = 0,\,$$
(52)

where p ∊ [0, 1] is an embedding parameter and h f , h θ , h ϕ . The zeroth-order deformation are nonzero auxiliary nonlinear parameters. The nonlinear operators N f , N θ and N ϕ are

$$\begin{aligned} N_{f} [\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)] & & & & & & = \frac{{\partial^{3} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)}}{{\partial y^{3} }} - S\left( {1 + \lambda K} \right)\,\frac{{\partial^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)}}{\partial y\partial \tau } + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)\frac{{\partial^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)}}{{\partial y^{2} }} \\ & & \quad - \;\left( {\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)}}{\partial y}} \right)^{2} - M^{2} \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)}}{\partial y} - \lambda \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)}}{\partial y} \\ & & \quad + K\left( {\begin{array}{*{20}c} {S\tfrac{{\partial^{4} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)}}{{\partial^{3} y\partial \tau }} + 2\tfrac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)}}{\partial y}\tfrac{{\partial^{3} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)}}{{\partial y^{3} }}} \\ { - \left( {\tfrac{{\partial^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)}}{{\partial y^{2} }}} \right)^{2} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)\tfrac{{\partial^{4} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)}}{{\partial y^{4} }}} \\ \end{array} } \right),\, \\ \end{aligned}$$
(53)
$$\begin{aligned} & N_{\theta } [\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (y,\,\tau ;\,p),\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p),\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (y,\,\tau ;\,p)] = \frac{1}{{\Pr _{{{\text{eff}}}} }}\frac{{\partial ^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (y,\,\tau ;\,p)}}{{\partial y^{2} }} \\ & \quad + \;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)\tfrac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (y,\,\tau ;\,p)}}{{\partial y}} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (y,\,\tau ;\,p)\tfrac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)}}{{\partial y}} \\ & \quad + \;Du\tfrac{{\partial ^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (y,\,\tau ;\,p)}}{{\partial y^{2} }} - S\tfrac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (y,\,\tau ;\,p)}}{{\partial \tau }},\, \\ \end{aligned}$$
(54)
$$N_{\theta } [\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (y,\,\tau ;\,p),\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p),\,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (y,\,\tau ;\,p)] = \frac{{\partial^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (y,\,\tau ;\,p)}}{{\partial y^{2} }} + Sc\left( {\begin{array}{*{20}c} { + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)\tfrac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (y,\,\tau ;\,p)}}{\partial y} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (y,\,\tau ;\,p)\tfrac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)}}{\partial y}} \\ { + Sr\tfrac{{\partial^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (y,\,\tau ;\,p)}}{{\partial y^{2} }} - S\tfrac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (y,\,\tau ;\,p)}}{\partial \tau }} \\ \end{array} } \right)\,$$
(55)

problems defined above have the following solutions corresponding to p = 0 and p = 1

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,0) = f_{0} (y,\,\tau ),\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,1) = f(y,\,\tau ),\,$$
(56)
$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (y,\,\tau ;\,0) = \theta_{0} (y,\,\tau ) \quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (y,\,\tau ;\,1) = \theta (y,\,\tau ),\,$$
(57)
$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (y,\,\tau ;\,0) = \phi_{0} (y,\,\tau ) \quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (y,\,\tau ;\,1) = \phi (y,\,\tau ).$$
(58)

Expanding \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)\) \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (y,\,\tau ;\,p)\) and \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (y,\,\tau ;\,p)\) in a Taylor’s series with respect to p, we get

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p) = f_{0} (y,\,\tau ) + \mathop {\mathop {\mathop \sum \limits }\limits^{\infty } }\limits_{m = 1} f_{m} (y,\,\tau )p^{m} ,\,$$
(59)
$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (y,\,\tau ;\,p) = \theta_{0} (y,\,\tau ) + \mathop {\mathop {\mathop \sum \limits }\limits^{\infty } }\limits_{m = 1} \theta_{m} (y,\,\tau )p^{m} ,\,$$
(60)
$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (y,\,\tau ;\,p) = \phi_{0} (y,\,\tau ) + \mathop {\mathop {\mathop \sum \limits }\limits^{\infty } }\limits_{m = 1} \phi_{m} (y,\,\tau )p^{m} ,\,$$
(61)
$$f_{m} (y,\,\tau ) = \left. {\frac{1}{m!}\frac{{\partial^{m} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} (y,\,\tau ;\,p)}}{{\partial p^{m} }}} \right|_{p = 0} ,\,\theta_{m} (y,\,\tau ) = \left. {\frac{1}{m!}\frac{{\partial^{m} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\theta } (y,\,\tau ;\,p)}}{{\partial p^{m} }}} \right|_{p = 0} ,\,\phi_{m} (y,\,\tau ) = \left. {\frac{1}{m!}\frac{{\partial^{m} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } (y,\,\tau ;\,p)}}{{\partial p^{m} }}} \right|_{p = 0} ,\,$$
(62)

4.2 mth-order deformation problems

The mth order problems can be expressed as

$$L_{f} [\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f}_{m} (y,\,\tau ) - \chi_{m} f_{m - 1} (y,\,\tau ) = h_{f} R_{m}^{f} (y,\,\tau ),\,$$
(63)
$$L_\theta [\theta_{m} (y,\,\tau ) - \chi_{m} \theta_{m - 1} (y,\,\tau ) = h_{\theta } R_{m}^{\theta } (y,\,\tau ),\,$$
(64)
$$L_\phi [\phi_{m} (y,\,\tau ) - \chi_{m} \phi_{m - 1} (y,\,\tau ) = h_{\theta } R_{m}^{\phi } (y,\,\tau ),\,$$
(65)
$$\begin{aligned} f_{m} (0,\,\tau ;\,p) = & 0,\,\left. {\frac{{\partial f_{m} (y,\,\tau ;\,0)}}{\partial y}} \right|_{y = 0} = \left. {\frac{{\partial f_{m} (y,\,\tau ;\,0)}}{\partial y}} \right|_{y = \infty } = \left. {\frac{{\partial f_{m}^{2} (y,\,\tau ;\,0)}}{{\partial y^{2} }}} \right|_{y = \infty } = 0,\, \\ \theta_{m} (0) = & 0,\,\theta_{m} (\infty ) = 0,\,\;\;\phi_{m} (0) = 0,\,\phi_{m} (\infty ) = 0,\, \\ \end{aligned}$$
(66)
$$\begin{aligned} R_{m}^{f} (y,\,\tau ) & = \frac{{\partial^{3} f_{m - 1} }}{{\partial y^{3} }} - S\left( {1 + \lambda K} \right)\,\frac{{\partial^{2} f_{m - 1} }}{\partial y\partial \tau } - M^{2} \frac{{\partial f_{m - 1} }}{\partial y} - \lambda \frac{{\partial f_{m - 1} }}{\partial y} + \mathop {\mathop {\mathop \sum \limits }\limits^{m - 1} }\limits_{k = 0} \left( {\begin{array}{*{20}c} {f_{m - 1 - k} \tfrac{{\partial^{2} f_{k} }}{{\partial y^{2} }}} \\ { - \tfrac{{\partial f_{m - k - 1} }}{\partial y}\tfrac{{\partial f_{k} }}{\partial y}} \\ \end{array} } \right)\, \\ & \quad + KS\frac{{\partial^{4} f_{m - 1} }}{{\partial y^{3} \partial \tau }} + K\mathop {\mathop {\mathop \sum \limits }\limits^{m - 1} }\limits_{k = 0} \left( {\begin{array}{*{20}c} {2\tfrac{{\partial f_{m - k - 1} }}{\partial y}\tfrac{{\partial^{3} f_{k} }}{{\partial y^{3} }}} \\ { - \tfrac{{\partial^{2} f_{m - k - 1} }}{{\partial y^{2} }}\tfrac{{\partial^{2} f_{k} }}{{\partial y^{2} }} - f_{m - k - 1} \tfrac{{\partial^{4} f_{k} }}{{\partial y^{4} }}} \\ \end{array} } \right),\, \\ \end{aligned}$$
(67)
$$\begin{aligned} R_{m}^{\theta } (y,\,\tau ) = & \frac{1}{{\Pr_{eff} }}\frac{{\partial^{2} \theta_{m - 1} }}{{\partial y^{2} }} + Du\left( {\frac{{\partial^{2} \phi_{m - 1} }}{{\partial y^{2} }}} \right) - S\left( {\frac{{\partial \theta_{m - 1} }}{\partial \tau }} \right)\, \\ & + \mathop {\mathop {\mathop \sum \limits }\limits^{m - 1} }\limits_{k = 0} \left[ {f_{m - 1 - k} \frac{{\partial \theta_{k} }}{\partial y} - \theta_{m - 1 - k} \frac{{\partial f_{k} }}{\partial y}} \right],\, \\ \end{aligned}$$
(68)
$$\begin{aligned} R_{m}^{\phi } (y,\,\tau ) = & \frac{{\partial^{2} \phi_{m - 1} }}{{\partial y^{2} }} + Sc\left( {Sr\frac{{\partial^{2} \theta_{m - 1} }}{{\partial y^{2} }}} \right) - Sc\left( {S\frac{{\partial \phi_{m - 1} }}{\partial \tau }} \right)\, \\ & + Sc\left( {\mathop {\mathop {\mathop \sum \limits }\limits^{m - 1} }\limits_{k = 0} \left[ {f_{m - 1 - k} \frac{{\partial \phi_{k} }}{\partial y} - \phi_{m - 1 - k} \frac{{\partial f_{k} }}{\partial y}} \right]} \right),\, \\ \end{aligned}$$
(69)
$$\chi_{m} = \left\{ {\begin{array}{*{20}c} {0,\quad m \le 1,} \\ {1,\quad m > 1,} \\ \end{array} } \right..$$
(70)

The general solution of Eqs. (63)–(65) are

$$f(y,\,\tau ) = f_{{_{m} }}^{ * } (y,\,\tau ) + C_{1} + C_{2} \exp ( - y) + C_{3} \exp (y),\,$$
(71)
$$\theta (y,\,\tau ) = \theta_{{_{m} }}^{ * } (y,\,\tau ) + C_{4} \exp (y) + C_{5} \exp ( - y),\,$$
(72)
$$\phi (y,\,\tau ) = \phi_{{_{m} }}^{ * } (y,\,\tau ) + C_{6} \exp (y) + C_{7} \exp ( - y).$$
(73)

where \(f_{{_{m} }}^{ * } (y,\,\tau ),\,\;\theta_{{_{m} }}^{ * } (y,\,\tau )\) and \(\phi_{{_{m} }}^{ * } (y,\,\tau )\) denote the special solutions.

5 Convergence of HAM solution

We see that Eqs. (47–49) consist of nonzero auxiliary parameters h f , h θ and h ϕ . The convergence of series solution can be controlled by proper choice of these auxiliary parameters. Figure 2a–c are plotted to find the plausible values of h f , h θ and h ϕ at 10th order of approximation. We note from these figures that for convergent solution −1 ≤ h f  < −0.1, −1.2 ≤ h θ  <−0.1 and −1.3 ≤ h ϕ  <−0.1.

Fig. 2
figure 2

The h-curve at 10th order of approximation a velocity field, b temperature field and c concentration field

Full size image

6 Results and discussion

The main aim of this work is to investigate the effects of various parameters of interest on velocity profile, temperature field and concentration field. Figure 3a–d shows the effects of viscoelastic parameter K, Hartmann number M, porosity parameter λ and suction/injection parameter γ on the time series of velocity profile f ′ at fixed distance y = 0.25 from the surface. From Fig. 3a it is noticed that amplitude of velocity increases by increasing viscoelastic parameter K because of increased effective viscosity. Further, it can be seen that a phase shift occurs which increases with an increase in viscoelastic parameter K. Figure 3b elucidate the variation of Hartmann number M on the time series of velocity profile by taking S = 0.5, K = 0.5, γ = 0.2 and λ = 1. This figure show that the amplitude of velocity is suppressed by increasing magnetic parameter M. Since magnetic lines of force behaves like elastic bands in the fluid motion therefore, fluid motion is suppressed and thus amplitude is reduced. Figure 3c gives the variation of porosity parameter λ on the time series of velocity profile by keeping other parameters fixed. We note from this figure that the influence of porosity parameter is similar to Hartmann number i.e., the amplitude of velocity decreases with increase of porosity parameter λ. In fact, an increase in the porosity parameter decrease the permeability of the porous medium and hence increase the resistance to flow. The effects of suction/injection parameter γ on f ′ are illustrated in Fig. 3d. In the case of suction (γ > 0), the amplitude of velocity decreases periodically. However, in the case of injection (γ < 0) an opposite behavior is observed, i.e. the amplitude of the velocity increases.

Fig. 3
figure 3

Time-series of the velocity profile f’ in the first five periods τ ∊ [0, 10π] at a fixed distance to the sheet, y = 0.25 a influence of K, b influence of M, c influence of λ and d influence of γ

Full size image

Figures 4, 5, 6 and 7 demonstrate the effects of viscoelastic parameter K, Hartmann number M, suction/injection parameter γ and porosity parameter λ on transverse profile of f ′ at a fixed time τ = 8.5 π. Figure 4 shows the effects of viscoelastic parameter K on velocity field f ′. It is noted from this figure that f ′ increases with the increase of viscoelastic parameter K. The momentum boundary layer thickness also increases by increasing viscoelastic parameter. The dimensionless form of the viscoelastic parameter suggests that K is inversely proportional to the viscosity and thus increase in K reduces the viscosity as a result velocity is increased. Figure 5 shows a decrease in f ′ with the increase of Hartmann number M. The momentum boundary layer thickness is also seems to be suppressed for higher values of Hartmann number M. This is in accordance with the fact that a constant magnetic field suppresses the bulk motion and alters the boundary layers. The porous medium also offers resistance to the flow and thus Fig. 6 depicts a decrease in velocity. Figure 7 shows the same behavior as observed in Fig. 6 i.e. the velocity decreases significantly with the increase in the suction (γ > 0) while in the case of blowing (γ < 0) the velocity of fluid increases. It is also noted that in the case of wall suction (γ > 0), a decrease in momentum boundary layer thickness is observed.

Fig. 4
figure 4

Influence of K on velocity profile

Full size image
Fig. 5
figure 5

Influence of M on velocity profile

Full size image
Fig. 6
figure 6

Influence of λ on velocity profile

Full size image
Fig. 7
figure 7

Influence of γ on velocity profile

Full size image

The effects of effective Prandtl number Preff, viscoelastic parameter K, Dufour numbers Du, Hartmann number M, suction/injection parameter γ and porosity parameter λ on the temperature profile are illustrated in Figs. 8, 9, 10, 11, 12 and 13. It is observed from Fig. 8 that increase of effective Prandtl number Preff temperature and thermal boundary layer thickness decreases. An increase in effective Prandtl number means that thermal diffusivity is decreased and as a result temperature of the fluid decreases.

Fig. 8
figure 8

Influence of Preff on temperature profile

Full size image
Fig. 9
figure 9

Influence of Du on temperature profile

Full size image
Fig. 10
figure 10

Influence of M on temperature profile

Full size image
Fig. 11
figure 11

Influence of K on temperature profile

Full size image
Fig. 12
figure 12

Influence of γ on temperature profile

Full size image
Fig. 13
figure 13

Influence of Sc on concentration profile

Full size image

Figure 9 depicts that with the increase of Dufour number Du, the thickness of thermal boundary layer reduces. Figure 10 depicts that graph of non-dimensional temperature profile θ(η) for different values of Hartmann number M. Increase of magnetic parameter means increase of Lorentz force which creats enhancement in the dimensionless temperature and thermal boundary layer thickness.

It is evident from this figure that temperature increase with the increase of Hartmann number M. Figure 11 shows that temperature decreases with the increase viscoelastic parameter K. The effects of suction/injection parameter on θ(η) are illustrated in Fig. 12. Since fluid has maximum temperature at the surface and the suction causes flow near to the plate to sink down therefore, temperature of the fluid decreases as expected.

The variation of concentration field at τ = π/2 is illustrated in Figs. 14, 15, 16, 17, 18 and 19 for various values of Schmidt number Sc, Soret number Sr, Hartmann number M, viscoelastic number K, porosity parameter λ and suction/injection parameter γ.

Fig. 14
figure 14

Influence of Sr on concentration profile

Full size image
Fig. 15
figure 15

Influence of M on concentration profile

Full size image
Fig. 16
figure 16

Influence of K on concentration profile

Full size image
Fig. 17
figure 17

Influence of λ on concentration profile

Full size image
Fig. 18
figure 18

Influence of γ on concentration profile

Full size image
Fig. 19
figure 19

Time-series of the skin friction coefficient \(\text{Re}_{x}^{1/2} C_{f}\) in the first five periods τ ∊ [0, 10π] at a fixed distance to the sheet, y = 0.25 a influence of K, b influence of λ

Full size image

Figure 13 represents the effects of Schmidt number Sc on dimensionless concentration profile. The concentration profile as well as concentration boundary layer thickness decreases for higher values of Schmidt number. As Schmidt number Sc is the ratio of momentum to mass diffusivities, hence mass diffusivity decreases for higher values of Schmidt number Sc which leads to a decrease in the concentration profile. These effects may be attributable to the increase in the rate of solute transfer from the surface by increasing the Schmidt number. The influence of dimensionless Soret number Sr is discussed in Fig. 14. This figure shows that concentration profile is an increasing function of Soret number. The variation of Hartmann number M on concentration field ϕ is shown in Fig. 15. Likewise temperature, the concentration increases with increase of Hartmann number M. Figure 16 demonstrates the effects of viscoelastic parameter K on dimensionless concentration profile. The concentration profile decreases with an increase in viscoelastic parameter K. The thickness of concentration boundary layer also decreases for lager values of viscoelastic parameter. The variation of porosity parameter λ on concentration profile is plotted in Fig. 17. An increase in porosity parameter λ causes a rise in concentration. The concentration boundary layer thickness increases by increasing porosity parameter λ. Figure 18 shows the effects of suction/injection parameter on concentration profile. It is evident from these figures that concentration field decreases in the case of suction while increases in case of injection. The concentration boundary layer reduced because of suction of decelerated fluid particles through the porous wall. The concentration boundary layer thickness is higher in the case of injection.

The time-series of skin friction coefficient for different values of K and λ is illustrated in Fig. 19a, b. Figure 19a shows that skin friction coefficient oscillates with time and with increase of viscoelastic parameter K. Figure 19b depicts the influence of λ on time series of skin friction coefficient. It is observed that again the amplitude of skin friction coefficient increases by increasing λ. It is also observed that phase shift occur which increases for larger values of λ.

Table 1 shows the numerical values of effective local Nusselt number at fixed time τ = π/2. It is observed from this table that effective local Nusselt number increase with increase of Preff, Sr, γ and K while it decrease with increase of M, Sc, Du, and λ parameters. The numerical values of local Sherwood number are illustrated in Table 2. From this table we observe that local Sherwood number increases with Sc, Du, K and γ while it shows opposite behavior by increasing Preff, Sr, M and λ.

Table 1 The numerical values of effective local Nusselt number \(\text{Re}_{x}^{-1/2} Nu_{x}^{*}\) when S = 0.5 and τ =π
Full size table
Table 2 The numerical values of local Sherwood number \(\text{Re}_{x}^{-1/2} Sh\) when S = 0.5 and τ =π/2
Full size table

7 Conclusion

The effects of Soret and Dufour for an unsteady boundary layer flow of a second grade fluid over a porous oscillatory stretching sheet has been investigated in this paper. Heat transfer analysis has been performed in presence of thermal radiation. The governing equations has been derived by using tensorial components. The number of independent variables in governing equations has been reduced by using useful dimensionless variables. Well known analytical technique namely, Homotopy analysis method has been used to solve dimensionless nonlinear partial differential equations. The solutions are illustrated through various plots. The main findings are

  • Increasing the viscoelastic parameter K causes the increase of the amplitude of the flow velocity. The amplitude of flow velocity decreases for larger values of Hartmann number M, porosity parameter λ and suction/injection parameter γ.

  • Velocity inside the boundary layer increases with the increase of viscoelastic parameter K while it decreases with the increase of magnetic parameter M and porosity parameter λ.

  • It is observed that velocity decreases in case of suction.

  • With the increase of the effective Prandtl number Preff, the heat transfer from the plate to fluid becomes slower and the thermal boundary layer thickness decreases. However, increase in Dufour number Du, porosity parameter λ and suction/injection parameter γ leads to enhanced the fluid temperature.

  • An enhancement in Hartmann number M increases the temperature and concentration.

  • Concentration is higher for larger values of Soret number Sr while effects of Schmidt number Sc are opposite.

  • The effective local Nusselt number is an increasing function of effective Prandtl number Preff, Soret number Sr, suction/injection γ and viscoelastic parameter K while it shows opposite behavior by increasing Hartmann number M, Schmidt number Sc, Dufour number Du and porosity parameter λ.

  • The local Sherwood number is found to be increase for higher values of Schmidt number Sc, Dufour number Du and viscoelastic parameter K while it decreases with the increase of effective Prandtl number Preff, Soret number Sr, porosity parameter λ and Hartmann number M.

  • The amplitude of skin friction coefficient increases by increasing viscoelastic parameter K and porosity parameter λ.