MHD viscoelastic fluid flow through porous medium over a stretching sheet in the presence of non-uniform heat source/sink

Abstract

The boundary layer flow, heat and mass transfer of an electrically conducting viscoelastic fluid over a stretching sheet embedded in a porous medium has been studied. The effect of transverse magnetic field, non-uniform heat source and chemical reaction on the flow has been analyzed. The Darcy linear model has been applied to account for the permeability of the porous medium. The method of solution involves similarity transformation. The confluent hypergeometric function (Kummer’s function) has been applied to solve the governing equations. Two aspects of heat equation namely, (1) prescribed surface ure and (2) prescribed wall heat flux are considered. The study reveals that the loss of momentum transfer in the main direction of flow is compensated by increasing in transverse direction vis-à-vis the corresponding velocity components due to magnetic force density. The application of magnetic field of higher density produces low solutal concentration and a hike in surface temperature.

1 Introduction

Flow of an incompressible viscoelastic fluid over a stretching sheet has an important bearing on many technological application, to be specific, in the extrusion of the polymer in the malt-spinning processes, exudates from the die is generally drawn and simultaneously stretched into a sheet which is after wards solidfyed through quenching or gradual cooling by direct contact with water. Further, glass blowing, continuous casting of metal and spinning of fiver involve the flow due to a stretching surface. In all these applications, the quality of the final product depends on the rate of heat transfer at the stretching surface. Crane [1] studied two dimensional boundary layer flow due to stretching of a sheet which move in its own plane with a velocity varying linearly with the distance from a fixed point. Carragher and Crane [2] analyzed the heat transfer aspect of the same problem. Andersson and Dandapat [3] analyzed the flow of a non-Newtonian fluid (Power law fluid) past a stretching surface. Wang [4] investigated the three dimensional flow due to the stretching surface.

Further, Pavlov [5] studied the MHD flow over a stretching surface in a electrically conducting fluid and obtained an exact similarity solution. Besides the above mentioned works Chakrabarti and Gupta [6], Anderson [7], Pop et al. [8], Bhatacharya and Layek [9] have contributed to enrich the litrature.

Recently, the flow of incompressible fluid due to a shrinking sheet is gaining attention of modern day researchers because it’s increasing applications to many engineering problems. Wang [10] studied the flow behavior of liquid film over an unsteady stretching sheet. The existence and uniqueness of the solution of steady viscous flow over a shrinking sheet was established by Miklavcic and Wang [11]. Bhukta et al. [12] considered heat and mass transfer on MHD flow of a viscoelastic fluid through porous media over a shrinking Sheet. Kandasamy and Khamis [13] discussed the effects of heat and mass transfer on nonlinear MHD boundary layer flow past a shrinking sheet subject to suction. Fang and Zhang [14] obtained a closed form solution for steady MHD flow over a porous shrinking sheet subjected to mass suction. Numerical investigation on heat and mass transfer effect of micropolar fluid over a stretching sheet has been carried out by Tripathy et al. [15]. Fang and Zhang [16] obtained the exact analytical solution of thermal boundary layer over a shrinking sheet with mass transfer. On the other hand, Wang [17] studied the stagnation-point flow towards a shrinking sheet. The work of Wang [17] was extended by Ishak et al. [18]. Bhattacharya et al. [19] studied the effects of suction/blowing on steady boundary layer stagnation-point flow and heat transfer towards a shrinking sheet with thermal radiation. Baag et al. [20] attempted numerical investigation on MHD micropolar fluid flow toward a stagnation point on a vertical surface with heat source and chemical reaction.

The study of heat transfer in hydrodynamic boundary layer flow over porous stretching/shrinking sheet gains more importance when internal heat generation or absorption occurs. Effects of heat source/sink on the boundary layer flow over a stretching sheet were studied by Vajravelu and Hadjinjcolaou [21], Elbashbeshy and Bazid [22], Bataller [23], Layek et al. [24] and Chen [25], Acharya et al. [26]. Further, Abel et al. [27] have considered non-uniform heat generation on heat transfer phenomenon in viscoelastic boundary layer flow. Though the present study is a straight forward generalization of [27], still it enjoys its specialty in following aspects:

• (i) Application of magnetic field, considering the flow of viscoelastic liquid is a conducting one, which is more practical and realistic. Thereby interaction with a resistive force of electromagnetic origin is accounted for.

• (ii) The inclusion of mass transfer of diffusing species of low concentration level neglecting the Soret-Dufour (thermal diffusion and diffusion-thermo) effects. This contributes significantly affecting the flow and heat transfer phenomena. Moreover, in the present study we have considered the convective contribution (convective terms) acceleration in momentum, heat and mass transfer equations which render the equations coupled.

• (iii) To account for a resistive body force due to porous medium by linear Darcy model.

2 Mathematical formulation

Consider the steady two-dimensional laminar flow of an incompressible electrically conducting viscoelastic fluid (Walters’ ${B}'$ model) which represents an approximation to the first order in elasticity i.e. for short / rapidly fading memory fluid, on a semi-infinite, vertical impermeable sheet embedded in a saturated porous medium at the plane $y=0$, the flow being confined to $y>0$. In present analysis we have taken x-axis along the wall in the direction of motion of the flow, the y-axis being normal to it and u and v are the velocities along X-axis and Y-axis respectively. Two equal and opposite forces are applied along the X-axis to stretch the flat sheet keeping the origin fixed. The applied magnetic field is perpendicular to the flat sheet. Further, we assume that fluid possesses strong viscous property than elastic property (Fig. 1).

Fig. 1

Flow geometry

The governing equations of viscoelastic fluid of Walters ${B}'$ model and the boundary conditions following Abel et al. [27] are given by

$$\begin{aligned} \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}= & {} 0 \end{aligned}$$

(1)

$$\begin{aligned} u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}= & {} \upsilon \frac{\partial ^{2}u}{\partial y^{2}}-k_0 \left\{ {\left. {u\frac{\partial ^{3}u}{\partial x\partial y^{2}}+v\frac{\partial ^{3}u}{\partial y^{3}}+\frac{\partial u}{\partial x}\frac{\partial ^{2}u}{\partial y^{2}}-\frac{\partial u}{\partial y}\frac{\partial ^{2}u}{\partial x\partial y}} \right\} } \right. -\frac{\sigma B_0^2 u}{\rho }\nonumber \\&\quad -\frac{\upsilon u}{K{p}'} \end{aligned}$$

(2)

$$\begin{aligned} \rho c_p \left( {u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}} \right)= & {} \kappa \frac{\partial ^{2}T}{\partial y^{2}}+\mu \left( {\left. {\frac{\partial u}{\partial y}} \right) ^{2}} \right. +{q}''' \end{aligned}$$

(3)

$$\begin{aligned} u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}= & {} D\frac{\partial ^{2}C}{\partial y^{2}}-Kc^{\prime }(C-C_\infty ) \end{aligned}$$

(4)

$$\begin{aligned} \left. {\begin{array}{lll} \left. {\begin{array}{lll} u_w (x)=bx, v=0 , \\ T=T_w =T_\infty +A\left( {\frac{x}{l}} \right) ^{2}, (PST \, case) \\ -k\frac{\partial T}{\partial y}=q_w =d\left( {\frac{x}{l}} \right) ^{2}, (PHF \, case) \\ -D\frac{\partial C}{\partial y}=m_w =E_1 x^{2} \\ \end{array}} \right\} \quad \hbox {at} \, y=0 \\ u \rightarrow 0 ,T\rightarrow T_\infty ,C\rightarrow C_\infty \quad \hbox {as} \, y\rightarrow \infty \\ \end{array}} \right\} \end{aligned}$$

(5)

where u and v are the velocities along x and y directions respectively, $k_0$, the co-efficient of viscoelasticity, $\rho$, the density, $\sigma$, the electrical conductivity of the fluid, $c_p$, the specific heat at constant pressure, $\kappa$, the thermal conductivity, $\mu$, the viscosity, $Kp^{\prime }$, porosity of the medium, D, the mass diffusivity, $K_c ^{\prime }$, the non-dimensional chemical reaction parameter, C, the concentration of the fluid, $C_\infty$, the ambient concentration,$\upsilon$, the kinematic viscosity, b, the stretching rate, T, the non-dimensional temperature, $T_w$, the temperature of the wall, $T_\infty$, the ambient temperature, $A, E_1$ and d are constants, $q_w$, the heat flux and $m_w$, the mass flux.

When a viscoelastic liquid is in flow, a certain amount of energy is stored up in the material as strain energy in addition to viscous dissipation. This strain energy is responsible for recovery to the original state. In the present study we have assumed that the fluid possesses strong viscous property in comparison with the elastic property. Also the effect of elastic deformation terms might not be significant as the momentum boundary layer equation is valid at low shear rate and small values of elastic parameter [28]. Numerous works are also reported in the literature relating to viscoelastic boundary layer flow which recognizes this fact while studying heat transfer.

Further, ${q}'''$, the space and temperature dependent internal heat generation/absorption (non-uniform heat source/sink) [29], can be expressed in simplest form as

$$\begin{aligned} {q}'''=\left( {\left. {\frac{\kappa u_w (x)}{x\upsilon }} \right) } \right. \left( {A^{*}(T_w -T_\infty ){f}'(\eta )+B^{*}(T-T_\infty )} \right) \end{aligned}$$

(6)

where $A^{*} \hbox {and} B^{*}$ are space and temperature dependent parameters. It is to be noted that $A^{*}>0$ and $B^{*}>0$ correspond to internal heat generation while $A^{*}<0$ and $B^{*}<0$ correspond to internal heat absorption. The solution of Eq. (3) depends on the nature of the prescribed boundary conditions. The constant A depends on the thermal properties of the liquid and $l=\sqrt{\upsilon /b}$ is a characteristic length.

3 Method of solution

Equations (1) and (2), subjected to boundary condition (5), admit self-similar solution in terms of the similarity function f and the similarity variable $\eta$ defined by

$$\begin{aligned} u=b x {f}'(\eta ),\quad v=- \sqrt{b\upsilon } \, f(\eta ),\quad \eta =\sqrt{\frac{b}{\upsilon }} y \end{aligned}$$

(7)

Clearly u and v as defined above satisfy the continuity Eq. (1). On substitution of Eq. (7), Eq. (2) becomes

$$\begin{aligned} {f}'''+f{f}''-{f}'^{2}-Rc\left\{ {\left. {2{f}' {f}'''-f{{f}''''}-{f}''^{2}} \right\} } \right. -\left( {M+\frac{1}{Kp}} \right) {f}'=0 \end{aligned}$$

(8)

where $Rc=\frac{k_0 b}{\upsilon }$, the viscoelastic parameter, $M=\frac{\sigma B_0^2 }{\rho b}$, the magnetic field parameter and $Kp=\frac{bK{p}'}{\upsilon }$, the porous matrix.

The corresponding boundary conditions are

$$\begin{aligned} \begin{array}{l} {f}'(\eta ) =1, \,\quad f(\eta ) =0 \quad \hbox {at} \quad \eta \rightarrow 0, \\ {f}'(\eta )\rightarrow 0 \quad \quad \hbox {as} \quad \eta \rightarrow \infty \\ \end{array} \end{aligned}$$

(9)

It is to be noted that the boundary condition (9) is not sufficient to solve Eq. (8) uniquely. So using (9), Rajagopal et al. [28] obtained corresponding solution of Eq. (8), which is an exact solution, satisfying the boundary condition (9), is given by

$$\begin{aligned} f(\eta ) =\frac{1-e^{-\alpha \eta }}{\alpha } \quad \text{ with } \, \alpha =\sqrt{\frac{1+M+\frac{1}{Kp}}{1-Rc}} \quad \text{ and }\quad \, 0<Rc<1 \end{aligned}$$

(10)

Therefore, the velocity components are

$$\begin{aligned} u=bxe^{-\alpha \eta } \, \hbox {and} \, v=-\sqrt{b\upsilon } \left( {\frac{1-e^{-\alpha \eta }}{\alpha }} \right) \end{aligned}$$

(11)

The shear stress at the wall is defined as

$$\begin{aligned} C_f =\mu \left( {\frac{\partial u}{\partial y}-k_0 \left\{ {\left. {u\frac{\partial ^{2}u}{\partial x\partial y}+v\frac{\partial ^{2}u}{\partial y^{2}}-2\frac{\partial u}{\partial y}\frac{\partial v}{\partial y}} \right\} } \right. } \right) _{y=0} =\frac{-1}{\sqrt{\mathrm{Re}_x }}{f}''(0)(1-3Rc) \end{aligned}$$

(12)

where $\mathrm{Re}_x =\frac{u_w x}{\upsilon }$ is the local Reynolds number.

4 Temperature distribution

4.1 Case A: Prescribed surface temperature (PST case)

Introducing dimensionless scaled temperature

$$\begin{aligned} \theta (\eta )=\frac{T-T_\infty }{T_w -T_\infty } \end{aligned}$$

(13)

and using (5), the Eq. (3) can be transformed to

$$\begin{aligned} {\theta }''(\eta )+\Pr \, f(\eta ){\theta }'(\eta )-(2\Pr \, {f}'(\eta )-B^{*})\theta (\eta )=-(Ec\Pr \, {f}''^{2}(\eta )+A^{*}{f}') \end{aligned}$$

(14)

where $Ec=\frac{b^{2}l^{2}}{Ac_p }$, the Eckert number and $\Pr =\frac{\mu c_p }{\kappa }$, the Prandtl number.

The non-dimensional boundary conditions are

$$\begin{aligned} \begin{array}{l} \theta (\eta )=1 \quad \hbox {at} \quad \eta =0 \\ \theta (\eta )\rightarrow 0 \quad \hbox {as} \quad \eta \rightarrow \infty \\ \end{array} \end{aligned}$$

(15)

Introducing a new variable $\zeta =-\frac{\Pr }{\alpha ^{2}}e^{-\alpha \eta }$, the Eq. (14) and boundary condition (15) are reduced to

$$\begin{aligned}&\zeta \frac{d^{2}\theta }{d^{2}\zeta }+\left[ {\left( {1-a_0 } \right) -\zeta } \right] \frac{d\theta }{d\zeta }+\left( {2+\frac{B^{*}}{\alpha ^{2}\zeta }} \right) \theta =\frac{1}{\Pr }\left[ {A^{*}-Ec\alpha ^{4}\zeta } \right] \end{aligned}$$

(16)

$$\begin{aligned}&\theta \left( {\zeta =-\frac{\Pr }{\alpha ^{2}}} \right) =1,\theta (\zeta =0)=0 \end{aligned}$$

(17)

The Eq. (16), subject to boundary conditions (17), admit hypergeometric Kummer’s function as the solution

$$\begin{aligned} \theta (\eta )=c_1 \left( {e^{-\alpha \eta }} \right) ^{\frac{a_0 +b_0 }{2}}F\left( {\frac{a_0 +b_0 }{2}-2,1+b_0 ;-\frac{\Pr }{\alpha ^{2}}e^{-\alpha \eta }} \right) +c_2 e^{-\alpha \eta }+c_3 e^{-2\alpha \eta } \end{aligned}$$

(18)

where

$$\begin{aligned} \begin{array}{l} a_0 =\frac{\Pr }{\alpha ^{2}}, b_0 =\sqrt{a_0^2 -\frac{4B^{*}}{\alpha ^{2}}}, c_1 =\frac{1-(c_2 +c_3 )}{F\left( {\frac{a_0 +b_0 }{2}-2,1+b_0 ;-\frac{\Pr }{\alpha ^{2}}} \right) }, \\ c_2 =\frac{-A^{*}}{(4\alpha ^{2}-2\Pr +B^{*})} \quad \hbox {and} \quad c_3 =\frac{-Ec\alpha ^{2}\Pr }{(4\alpha ^{2}-2\Pr +B^{*})} \end{array} \end{aligned}$$

The non-dimensional wall temperature gradient derived from Eq. (18) is

$$\begin{aligned}&-{\theta }'(0)=c_1 \left[ -\alpha \left( {\frac{a_0 +b_0 }{2}} \right) F\left( {\frac{a_0 + b_0 -4}{2},1+ b_0 ;-\frac{\Pr }{\alpha ^{2}}} \right) \right. \nonumber \\&\quad \left. +\left( {\frac{a_0 + b_0 -4}{2(1+ b_0 )}} \right) \frac{\Pr }{\alpha }F\left( {\frac{a_0 + b_0 -2}{2},2+ b_0 ;-\frac{\Pr }{\alpha ^{2}}} \right) \right] -c_2 \alpha -2c_3 \alpha \end{aligned}$$

(19)

4.2 Case B: Prescribed heat flux (PHF case)

Introducing dimensionless scaled temperature

$$\begin{aligned} \psi (\eta )=\frac{T-T_\infty }{T_w -T_\infty } \end{aligned}$$

(20)

$$\begin{aligned} T_w -T_\infty =\frac{d}{k}\left( {\frac{x}{l}} \right) ^{2}\sqrt{\frac{\upsilon }{b}} \end{aligned}$$

(21)

Using Eqs. (20) and (21) in (3) we get

$$\begin{aligned} {\psi }''(\eta )+\Pr \, f(\eta ){\psi }'(\eta )-(2\Pr \, {f}'(\eta )-B^{*})\psi (\eta )=-(Ec\Pr \, {f}''^{2}+A^{*}{f}') \end{aligned}$$

(22)

where $Ec=\frac{\kappa b^{2}l^{2}}{dc_p }\sqrt{\frac{b}{\upsilon }}$ and the boundary conditions take the form

$$\begin{aligned} \begin{array}{l} {\psi }'(\eta )=-1 \quad \hbox {at} \quad \eta =0 \\ \psi (\eta )\rightarrow 0 \quad \quad \hbox {as} \quad \eta \rightarrow \infty \\ \end{array} \end{aligned}$$

(23)

With the help ‘$\zeta$’ as defined earlier, the Eq. (22) becomes

$$\begin{aligned} \zeta \frac{d^{2}\psi }{d^{2}\zeta }+\left[ {\left( {1-a_0 } \right) -\zeta } \right] \frac{d\psi }{d\zeta }+\left( {2+\frac{B^{*}}{\alpha ^{2}\zeta }} \right) \psi =\frac{1}{\Pr }\left[ {A^{*}-Ec\alpha ^{4}\zeta } \right] \end{aligned}$$

(24)

and corresponding boundary conditions are

$$\begin{aligned} {\psi }'\left( {\zeta =-\frac{\Pr }{\alpha ^{2}}} \right) =-1,\psi (\zeta =0)=0 \end{aligned}$$

(25)

The solution of Eq. (24), subject to the boundary condition (25) can be obtained in terms of hypergeometric Kummer’s function $[F(\alpha ;\beta ;x)]$ as

$$\begin{aligned} \psi (\eta )=c_4 e^{-\alpha \left( {\frac{a_0 +b_0 }{2}} \right) \eta }F\left( {\frac{a_0 +b_0 }{2}-2,1+b_0 ;-\frac{\Pr }{\alpha ^{2}}e^{-\alpha \eta }} \right) +c_2 e^{-\alpha \eta }+c_3 e^{-2\alpha \eta } \end{aligned}$$

(26)

where $a_0 , b_0 , c_2 \, \hbox {and }c_3$ are as defined earlier in the PST case and $c_4$ is given by

$$\begin{aligned} c_4 =\frac{(c_2 +2c_3 )\alpha -1}{\left[ {-\alpha \left( {\frac{a_0 +b_0 }{2}} \right) F\left( {\frac{a_0 +b_0 -4}{2},1+b_0 ;-\frac{\Pr }{\alpha ^{2}}} \right) +\left( {\frac{a_0 +b_0 -4}{2(1+b_0 )}} \right) \frac{\Pr }{\alpha }F\left( {\frac{a_0 +b_0 -2}{2},2+b_0 ;-\frac{\Pr }{\alpha ^{2}}} \right) } \right] } \end{aligned}$$

(27)

The non-dimensional wall temperature derived from Eq. (26) is given by

$$\begin{aligned} \psi (0)=c_4 F\left( {\frac{a_0 +b_0 }{2}-2,1+b_0 ;-\frac{\Pr }{\alpha ^{2}}} \right) +c_2 +c_3 \end{aligned}$$

(28)

5 Solutal concentration distribution

Introducing the similarity transformation $C-C_\infty = \frac{E_1 x^{2}}{D} \sqrt{\frac{\upsilon }{b}} \phi (\eta )$ where $\phi$ is the concentration profile and using (7) in Eq. (5) we get,

$$\begin{aligned} {\phi }''(\eta )+Scf(\eta ){\phi }'-Sc(2f_\eta (\eta )+Kc)\phi (\eta )=0 \end{aligned}$$

(29)

where $Sc=\frac{\upsilon }{D}$, the Schmidt number and $Kc=\frac{{K}'_c }{b}$, the chemical reaction parameter with the boundary conditions

$$\begin{aligned} \begin{array}{l} {\phi }'=-1 \quad \hbox {at} \quad \eta =0 \\ \phi \rightarrow 0 \quad \quad \hbox {as} \quad \eta \rightarrow \infty \\ \end{array} \end{aligned}$$

(30)

Again introducing a new variable $\zeta =-\frac{Sc}{\alpha ^{2}}e^{-\alpha \eta }$, the Eq. (29) becomes

$$\begin{aligned} \zeta \frac{d^{2}\phi }{d^{2}\zeta }+\left[ {\left( {1-s_1 } \right) -\zeta } \right] \frac{d\phi }{d\zeta }-\left( {2-\frac{Kc}{\alpha ^{2}\zeta }} \right) \phi =0 \end{aligned}$$

(31)

The corresponding boundary conditions are

$$\begin{aligned} \phi (\zeta =0)=0, \quad {\phi }'\left( {\zeta =-\frac{Sc}{\alpha ^{2}}} \right) =-\frac{\alpha }{Sc} \end{aligned}$$

(32)

The exact solution of Eq. (29) subject to the boundary condition (30) is given by

$$\begin{aligned} \phi (\eta )=\frac{e^{- \frac{\alpha (s_1 +s_2 )}{2}\eta }{ }_1F_1 \left( {\frac{s_1 +s_2 -4}{2};1+s_1 ;-\frac{Sce^{-\alpha \eta }}{\alpha ^{2}}} \right) }{\frac{\alpha (s_1 +s_2 )}{2}{ }_1F_1 \left( {\frac{s_1 +s_2 -4}{2};1+s_1 ;-\frac{Sc}{\alpha ^{2}}} \right) -\frac{Sc}{\alpha }\left( {\frac{s_1 +s_2 -4}{2(1+s_1 )}} \right) { }_1F_1 \left( {\frac{s_1 +s_2 -2}{2};2+s_1 ;-\frac{Sc}{\alpha ^{2}}} \right) } \end{aligned}$$

(33)

where $s_1 =\frac{Sc}{\alpha ^{2}}$ and $s_2 =\sqrt{s_1 ^{2}+\frac{4Kc}{\alpha ^{2}}}$.

The non-dimensional wall concentration gradient derived from Eq. (33) is

$$\begin{aligned} -{\phi }'(0)=\frac{\frac{-\alpha (s_1 +s_2 )}{2}{ }_1F_1 \left( {\frac{s_1 +s_2 -4}{2};1+s_1 ;-\frac{Sc}{\alpha ^{2}}} \right) +{ }_1F_1 \left( {\frac{s_1 +s_2 -2}{2};2+s_1 ;-\frac{Sc}{\alpha ^{2}}} \right) }{\frac{\alpha (s_1 +s_2 )}{2}{ }_1F_1 \left( {\frac{s_1 +s_2 -4}{2};1+s_1 ;-\frac{Sc}{\alpha ^{2}}} \right) -\frac{S_c }{\alpha }\left( {\frac{s_1 +s_2 -4}{2(1+s_1 )}} \right) { }_1F_1 \left( {\frac{s_1 +s_2 -2}{2};2+s_1 ;-\frac{Sc}{\alpha ^{2}}} \right) } \end{aligned}$$

(34)

6 Results and discussion

We have got an analytical solution of the Navier–Stokes equation which represents steady two-dimensional flow of an incompressible viscoelastic fuid of Walters${B}'$model. The following discussion reveals the effect of elasticity, porosity and magnetic field parameters on the flow phenomena. The effects of non-unform heat source and sink are to be discussed along with other parameters. The discussion also brings to its fold surface criterion such as skin friction and Nusselt number relating to shearing stress and the rate of heat transfer on the plate surface. Finally, for verification of the results of the present study we have compared with Abel et al. [27] in the absence of magnetic field.

Figures 2 and  3 exhibit the longitudinal and transverse component of velocity distribution. Form Eq.(10) we have

$f(\eta ) =\frac{1-e^{-\alpha \eta }}{\alpha }$ (Transverse), $\eta \rightarrow \infty \, f(\eta )\rightarrow 1/\alpha$, where $\alpha =\sqrt{\frac{1-Rc}{1+M+(1/Kp)}},Rc\ne 1$.

${f}'(\eta ) =e^{-\alpha \eta }$ (Longitudinal),   $\eta \rightarrow \infty \, {f}'(\eta )\rightarrow 0$

Thus, the attainment of ambient state of transverse velocity depends upon the parameters M, Kp and Rc with restriction $Rc\ne 1$. Therefore this flow model is valid for viscoelastic flow with small Rc i.e. slightly elastic which has been already mentioned. Whereas, the longitudinal velocity is independent of the parameters. Again $\eta \rightarrow 0$, longitudinal velocity ${f}'(\eta )\rightarrow 1$ whereas transverse velocity $f(\eta )\rightarrow 0$. From the above analysis it is clear that as the flow proceeds the loss of momentum transfer in the main direction of flow is compensated by increasing in transverse direction. Therefore, longitudinal velocity suddenly falls in a few layers near the plate whereas transverse velocity increases. This causes a decay versus growth type of variation in velocity components leading to momentum conservation.

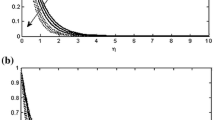
The effects of the parameters can be analyzed from the analytical expressions also. However, from the graph it is clear that an increase in magnetic force density (M), ${f}'(\eta )$ decreases for both Newtonian $(Rc=0)$ and non-Newtonian fluids $(Rc\ne 0)$. This decrease is due to magnetic force density, which is equivalent to a viscous breaking force. It tries to cancel the velocity component i.e. orthogonal to direction of magnetic field $\overline{B}$ [30]. Elastic parameter Rc as well as porosity parameter Kp also reduce the velocity at all the points producing a thinner boundary layer (Fig. 2). The effect of porosity parameter is significant in comparison with other parameters. Similar effect is observed on the transverse velocity component also.

Fig. 2

Longitudinal velocity profile

Fig. 3

Transverse velocity profile

Fig. 4

a Effect of Rc on temperature profile (PST case). b Effect of Rc on temperature profile (PHF case)

From Fig. 4a, b it is seen that both magnetic field, elasticity and porosity contributed to the growth of thermal boundary in both PST and PHF cases. On careful observation it is seen that the little hike in temperature for PST case is marked for Curve-V $(Rc=0.2,M=2,Kp=0.5)$. Thus, this hike in temperature can be interpreted as the contribution of heat energy due to combined effects of resistive magnetic force and porous matrix as well as stored energy due to elastic property of the fluid.

The variation of Prandtl number in the presence/absence of magnetic parameter on temperature profile for both PST and PHF cases are shown in the fig. 5a, b. The value of the elastic parameter $Rc(=0.2)$ is fixed with the space and time dependent heat source $A^{*}=0.3 \quad \hbox {and} \quad B^{*}=0.3$ respectively. It is observed that the presence of magnetic parameter enhances the temperature at all points within the thermal boundary layer whereas, increase in Prandtl number reduces it due to a low thermal diffusivity. The Prandtl number is a relative measure of the mechanism of heat conduction and viscous stresses. For gases, $\Pr$ is of the order of unity implies that heat conduction and viscosity of the gas enjoy same priority. In the present case we have considered the value of $\Pr >1$. From the temperature profiles it is clear that temperature decreases with an increase in $\Pr$ implies flow of liquids with low thermal diffusivity and high viscous stresses causes a fall in temperature in producing thinner boundary layer.

Figure 6a, b show the temperature distribution in PST and PHF cases. The profiles display similar nature of variation only exhibiting the effect of Eckert number Ec. It is seen that an increase in viscous dissipative heat contributes to the rise in temperature in the presence / absence of porous matrix. Thus, the dissipative heat is responsible for the rise in temperature within fluid layers in the presence / absence of porous medium.

Fig. 5

a Effect of Pr on temperature profile (PST case). b Effect of Pr on temperature profile (PHF case)

Fig. 6

a Effect of Ec on temperature profile (PST case). b Effect of Ec on temperature profile (PHF case)

Fig. 7

Concentration profile

Figure 7 depicts the concentration distribution in forming solutal boundary layer. It is seen that an increase in M, leads to increase in concentration whereas an increase in Sc, Rc and Kc resulted in a decrease in concentration level at all points. Thus, the magnetic field parameter contributed to the growth of solutal boundary layers same as thermal but the heavier species exhibiting viscoelastic nature with destructive reaction produces the thinner boundary layer.

Table 1 presents the shearing stress at the stretching surface. The table shows that the elasticity increases the skin friction with or without the effect of magnetic field on the other hand, an increase in magnetic parameter reduces the skin friction. Therefore, higher magnetic force density aids to flow stability by reducing the skin friction.

Tables 2 and 3 present the rate of heat transfer and solutal distribution at the stretching surface. One remarkable point is to note that Nu becomes negative when $\Pr =4.0$ (liquid), $\Pr$ being the relative measure of momentum diffusion. The increase in $\Pr$ gives rise to slow rate of thermal diffusion hence higher value of $\Pr$ results in the decrease in temperature at a particular point of flow region. This is supported by Fig. 5a, b. Therefore, decrease in temperature produces a cooling effect on the stretching surface.

For PHF case, an increase in magnetic parameter (M) and elastic parameter (Rc) increase the rate of heat transfer (Nu) at the surface producing a cooling effect but for PST case, the reverse effect is observed. To sum up, magnetic force density ad elasticity of the fluid produce a cooling effect on the stretching surface on the presence of heat flux but the reverse effect is observed when the bounding surface is subjected to a prescribe temperature. As regard to the effect of Ec, it is seen that an increase in Ec leads to increase the temperature for both PST and PHF cases. The Eckert number measures frictional heat due to viscosity of the fluid which resists the motion. The table 2 shows that an increase in Ec, increases the rate of heat transfer for both PST and PHF cases.

Table 1 Skin friction

Table 2 Nusselt number

Table 3 presents the rate of solutal concentration at the plate. It is seen that rate of mass transfer at the surface increases with an increase in elasticity (Rc), chemical reaction rate coefficient (Kc) and heavier species, higher value of Sc but magnetic parameter reduces it. Thus, for reduction of solutal concentration at the surface one is to apply a magnetic field of higher density.

Thus, surface condition shearing stress, rate of heat transfer and solutal concentration are to be regulated at the stretching surface as per the design requirement of the final product.

7 Conclusion

Heat transfer problem in hydrodynamic boundary layer flow over porous stretching/shrinking sheet has been solved by using Runge-Kutta method followed by shooting technique. From the above the following conclusions are obtained.

• The loss of momentum transfer in the layers near the stretching surface in the main direction of flow is compensated by increase in transverse direction. This causes decay versus growth type of variation in the velocity components. This supports the conservation of momentum on the boundary layer.

• The resistive magnetic force density which is equivalent to a viscous braking force opposes the motion.

• Hike in temperature is due to combined effects of resistive magnetic force and porous matrix as well as stored energy is due to elastic property of the fluid.

• Low thermal diffusivity and high viscous stresses causing a fall in temperature.

• The increase in viscous dissipation leads to increase the temperature for both PST and PHF cases.

• For reduction of solutal concentration at the bounding surface, one is to apply a magnetic field of higher density.

• Heavier chemical reactive diffusing species exhibiting elasticity property decreases the solutal concentration.

• Surface temperature (PST) and heat flux (PHF) show opposite behavior on the rate of heat transfer.

• Rate of solutal concentration falls at the plate in the presence of magnetic field ignoring the effect of elasticity.

Table 3 Sherwood number