An FEM-based method to evaluate and optimize vibration power flow through a beam-to-plate connection

Abstract

Power flow is an important measure in vibratory energy propagation path analysis. For one-dimensional structural elements, i.e., bars or beams, power flow is obtained using a relationship involving degrees of freedom (DOF) of interest, and the respective internal forces. Several published works on vibration analysis involving the finite element method (FEM) and its optimization describe measures of interest only in terms of DOF (such as displacement and mean square velocity). However, in scenarios involving the coupling of different structures, these measures are inadequate. For example, minimizing only dynamical displacements at specific points in a structure could result in the internal forces at those points becoming unacceptably large. In such cases, minimizing power flow is preferable over minimizing displacements. In this manuscript, using FEM and a gradient-based optimization method, the authors propose a technique to evaluate and optimize vibratory power flow specifically in cases involving beam–plate coupling. The total power flow at the connection point is defined as a function of the global displacement vector, and it is evaluated for a given frequency by harmonic analysis; the relevant sensitivities are obtained using elementary matrices and the adjoint method. Geometrical parameters of the beam are used as design variables. A description of the methodology and two examples of its application to beam–plate structures are presented.

1 Introduction

Two main groups of methods are usually considered for solving vibration control problems: passive and active. Passive methods usually involve parametric and structural modifications or addition of structural damping. It is often observed that in some cases, traditional vibration control methods using passive elements are not as effective as active methods. The limitations can be ascribed mainly to two reasons: lower effectiveness at low frequencies and optimality of solution being valid only under the specific conditions assumed in project design. However, active methods require that additional energy be supplied to the system, which, in many cases, can be avoided by using passive methods [14] when designing mechanical components.

Structural optimization has proved to be an effective vibration control procedure. However, for effectiveness, the objective functions must be defined properly. The most common objective functions (or constraints) found in the literature for gradient-based dynamic structural optimization are: dynamic compliance [16, 25] obtained from the internal product of the applied force vector and the resulting displacement vector; quadratic dynamic displacement [8] of a given point or set of points; sound radiation [5, 26] of a plate structure; and mode distribution [4, 18], which entails allocating sets of structural modes at desired frequencies. All these quantities are related to the behaviors of unique and continuous structural bodies (beam, plate, etc.).

However, vibration power flow is an important measure of the flow of energy between connected structures. Vibration in a given component can be controlled by minimizing power flow from the source structure (which receives external harmonic load) to the final structure (which propagates this vibration and usually radiates sound to the surrounding media). In this work, harmonic power flow from a beam to a plate is investigated to minimize its transmission between these structures. This minimization is achieved by changing the geometric parameters of the beam. The finite element method (FEM) is used to solve the associated dynamic problem and to obtain the sensitivities needed for optimization.

Research works on vibrational power flow appears regularly on scientific journals. For e.g., we can mention a recent one from Weisser et al. [23] which is dedicated to the structural characterization of power flowing inside the structure to study the power transmitted at the interface. But, to the best of the authors’ knowledge, few works in the literature deal with optimization of vibration power flow in structural systems. Sorokin et al. [19, 20] proposed a methodology to analyze in-plane flexural and longitudinal vibrations in a structure composed of elastic tubular beams; their method was based on a boundary equation method and varying the location, stiffness, mass, and damping of supports. An analytical formulation was used to solve the dynamic problem and minimize total power flow through the beams. Sorokin et al. [21] studied energy transmission through a pipe system using the general theory of elastic cylindrical shells with internal fluid loading, again using an analytical boundary equation method. However, these methods are not straightforward for solving problems characterized by complex geometry and boundary conditions. Kim et al. [10] and Cho et al. [2] used the energy finite element method to analyze and optimize power flow in structures at high frequencies, and employed Young’s modulus and densities as design variables. More recently, Niu and Olhoff [15] published their work on the minimization of vibration transmission from a machine source to its supporting structure.

Apart from strictly structural applications, there are several interesting works in photonics related to power transmission, which may go unnoticed by researchers working on structural vibration power flow. Jensen and Sigmund presented a series of articles describing the use of FEM for optimizing power transmission of E-polarized waves through waveguides. One such article [9] discusses the application of topology optimization [1] by using information about finite element shape functions to obtain the objective function and the sensitivities. This methodology is considered powerful and adaptable to other areas of engineering.

Based on the above-mentioned studies, this article proposes a technique to evaluate and optimize harmonic vibration power flow from a beam to a plate, with both structural members modeled using FEM. Here, we consider a structural plate perpendicularly connected to a hollow pipe (beam), which is excited by an external force. The design variables are the external diameters of the pipe (which is divided in several elements of constant cross-section), while the plate is, in this work, assumed as a non-design region. There are few analytical studies on a stepped beam perpendicularly coupled to a plate in the literature. However, some works report on vibration propagation in beams with cross-sectional discontinuities. For example, Mead [14] shows that, for a local change of a beam cross-section, the two sections of different diameters will have different wave numbers and, at any frequency, part of the incident wave that reaches the junction is reflected, thus changing the power transmission ratio. The greater the changes in section, the lower is the portion of power transmitted forward. Moreover, Liu and Hussein [12] investigated the benefits of using a stepped beam in a periodic arrangement, showing the appearance of a frequency band-gap in vibration propagation. The optimization method used in the present work involves performing structural modifications by varying the external diameters of the pipe to generate the desired power flow reduction at connection point of the coupled system.

Several authors in structural vibration analysis, such as [3, 11, 13], directly apply local responses and local internal forces obtained using commercial FEM packages to calculate power flow information, thus hindering the use of a gradient-based optimization method. In this paper, authors propose a new technique in which beam finite element matrices are used to calculate power flow as a function of the global displacement vector and to obtain the required sensitivities. The method of moving asymptotes (MMA) [22] is used as the gradient-based optimization algorithm for this problem. The mean square velocity of the plate is used to verify the vibratory behavior improvement. After a brief overview of the theory involved and the related numerical developments, this paper presents the results of two examples to demonstrate the effectiveness of the proposed technique.

2 Vibration power flow modeled using beam and plate finite elements

The instantaneous structural intensity $\mathbf {i}$ is defined at an interior point of an elastic solid as follows [6]:

$$\begin{aligned} \mathbf {i}(t)=-\varvec{\sigma }(t) \cdot \mathbf {v}(t), \end{aligned}$$

(1)

where $\mathbf {\sigma }$ is the Cauchy stress tensor and $\mathbf {v}$ is the velocity vector at the mentioned point. The intensity represents the total mechanical power over a unit area, and it is a function of location and time. Using stress and velocity components, one can rewrite (1) in indicial notation as follows:

$$\begin{aligned} i_p(t)=-\sigma _{pq}(t)v_q(t), \end{aligned}$$

(2)

where p and q are directional indices (p, q $=$ x, y, z according to the coordinate system in use). For a solid structure, at a given point (x, y, z), the structural intensity along the x-direction, for example, is $i_x(t)=-\sigma _{xx}(t)v_x(t)-\sigma _{xy}(t)v_y(t)-\sigma _{xz}(t)v_z(t)$. For vibrating structures, the time-averaged intensity $I_p$ for a vibration period $T$ can be expressed as follows:

$$\begin{aligned} I_p=\left\langle i_p(t)\right\rangle _t=\frac{1}{T}\int ^{T}_{0} -\sigma _{pq}(t)v_q(t)\mathrm{d}t. \end{aligned}$$

(3)

The symbol $\left\langle \right\rangle _t$ represents the time domain average. In the frequency domain, considering a harmonic analysis, the averaged intensity can be calculated by

$$\begin{aligned} I_p(t)=\frac{1}{2}\mathrm{Re}\{-\sigma _{pq}(\omega ){{v}_q}^*(\omega )\}, \end{aligned}$$

(4)

where symbols $^*$ and $\mathrm{Re}\{ \}$ represent the conjugate complex and real parts, respectively.

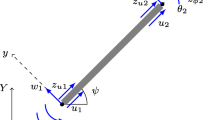
Consider a structure modeled by linear beam finite elements, as shown in Fig. 1. Each beam element has six degrees of freedom (DOF) at each node: three translational motions along the nodal x, y and z directions $(U_1, U_2$ and $U_3)$ and three rotation motions about the nodal x, y and z directions $(U_4, U_5$ and $U_6)$. By analyzing a cross-section of this beam, we found six resultant internal forces: three translational forces along the nodal x, y and z directions $(F_1, F_2$ and $F_3)$, and three moments about the x, y and z axes $(F_4, F_5$ and $F_6)$. In this case, the forces, moments, translations and rotations are evaluated along the center line of the beam for a given frequency $\omega$.

Fig. 1

Structure modeled using beam finite elements and convention employed for DOFs. Node $\textit{n}_3$ is shared by elements $\textit{e}_2$ and $\textit{e}_3$

Fig. 2

Beam–plate structure

The net power flow $\Phi$ at a cross-section of the beam can be obtained by integration of (4) over the total cross-sectional area [6], according to the following expression (observing the direction convention in Fig. 1):

$$\begin{aligned} \Phi (\omega )=\frac{1}{2}\omega \sum ^{6}_{p=1} \mathrm{Re}\{-jF_p(\omega ){{U}_p}^*(\omega )\}, \end{aligned}$$

(5)

where velocities are replaced by displacements by using complex algebra and assuming harmonic motion. In Fig. 1, if the excitation is imposed only on node $n_1$, the total power flows along the positive x-axis. In this work, there is only external excitation in one of the two connected bodies, and the total power flow must be calculated at the inlet port of the final structure. For example, in Fig. 1, if one considers a body $B_1$ composed of elements $e_1$ and $e_2$, and a body $B_2$ composed of elements $e_3$ and $e_4$, the total power flow must be obtained using node $n_3$ and element $e_3$, which “receives” the net energy.

Consider now a structure composed of a beam connected to a plate, as shown in Fig. 2. The plate is modeled using linear shell finite elements, where each element has six DOFs at each of the four nodes.

The system is considered a damped beam–plate structure, such that its dynamic behavior can be obtained via harmonic finite element analysis as follows:

$$\begin{aligned} (\mathbf {K}+j\omega \mathbf {C} - {\omega }^2\mathbf {M})\mathbf {U}(\omega )=\mathbf {P}(\omega ). \end{aligned}$$

(6)

Here, $\mathbf {U}$ is the complex displacement amplitude vector (translations and rotations); $\mathbf {K}$, $\mathbf {C}$ and $\mathbf {M}$ are stiffness, damping, and mass matrices, respectively; and $\mathbf {P}$ is the external force amplitude vector (transverse/axial forces and moments). Proportional Rayleigh damping is used as $\mathbf {C}=\alpha \mathbf {M}+\beta \mathbf {K}$. The commercial FE software ANSYS is employed in this paper to solve (6), and element types PIPE16 and SHELL63 are used for modeling the beam and plate parts, respectively.

The objective is to minimize power flow at a beam–plate connection by changing the external diameters of the beam part, which is modeled as a pipe in this study. Information about the energy flowing from the beam to the plate is obtained from the node and the beam element of the connection. In this case, the analyzed element belongs to the excitation source structure, where the interface nodal forces have opposite signals with respect to the forces on the plate (which is the “receiver” of the net energy). In this way, for a p DOF of this node,

$$\begin{aligned} \Phi _p(\omega )=\frac{1}{2}\omega \mathrm{Re}\{jF_p(\omega ){{U}_p}^*(\omega )\}. \end{aligned}$$

(7)

Next, the power flow expression (7) is rewritten in terms of the global displacement vector $\mathbf {U}$ to perform posterior sensitivity analysis for optimization. Suppose that the kth DOF of the entire structure is associated with the connection node. This DOF is the kth entry of the global vector $\mathbf {U}.$ The following matrix relations are introduced for a two-node beam element $\bar{e}$, where $\Phi _k$ will be calculated ($\bar{e}$ is the beam element at the connection):

$$\begin{aligned} \mathbf {F}_{\bar{e}}=(\mathbf {K}_D)_{\bar{e}}\mathbf {U}_{\bar{e}}, \end{aligned}$$

(8)

and

$$\begin{aligned} F_k=\mathbf {q}_{{\bar{e}}k}^{T}(\mathbf {K}_D)_{\bar{e}}\mathbf {U}_{\bar{e}}. \end{aligned}$$

(9)

$\mathbf {F}_{\bar{e}}$ is the vector of all internal forces of finite element $\bar{e},$ and $\mathbf {U}_{\bar{e}}$ is the respective set of all components of displacements; $(\mathbf {K}_D)_{\bar{e}}$ is the dynamic elementary matrix $(\mathbf {K}_D)_{\bar{e}}=\mathbf {K}_{\bar{e}}+j\omega \mathbf {C}_{\bar{e}}-\omega ^2 \mathbf {M}_{\bar{e}}$, and $\mathbf {q}_{{\bar{e}}k}$ is defined as

$$\begin{aligned} \mathbf {q}_{{\bar{e}}k}= \left[ \begin{array}{cccccccc} 0&\ldots&0&0&1&0&\ldots&0 \end{array}\right] ^T, \end{aligned}$$

(10)

which is a vector with dimensions $\text {NGL}_{\bar{e}} \times 1$, where $\text {NGL}_{\bar{e}}$ is the total number of DOFs of element $\bar{e}$. The vector $\mathbf {q}_{{\bar{e}}k}$ identifies the DOF k to be analyzed, while localizing in vector $\mathbf {F}_{\bar{e}}$ the respective component $F_k$ of the internal force. For the beam element model considered, $\mathrm{NGL}_{\bar{e}}=12$. For example, if the kth DOF is associated with the moment about x-axis for the second node of a beam element, the vector $\mathbf {q}_{{\bar{e}}k}$ is given as:

$$\begin{aligned} \mathbf {q}_{{\bar{e}}k}= \left[ \begin{array}{ccccccccccccc} 0&0&0&0&0&0&|&0&0&0&1&0&0 \end{array}\right] ^T. \end{aligned}$$

(11)

Applying a similar procedure to obtain the element nodal displacements $\mathbf {U}_{\bar{e}}$ from the global vector $\mathbf {U}$, we can rewrite (9) as follows:

$$\begin{aligned} F_k=\mathbf {q}_{{\bar{e}}k}^{T}(\mathbf {K}_D)_{\bar{e}}\mathbf {L}_{\bar{e}}\mathbf {U}, \end{aligned}$$

(12)

where $\mathbf {L}_{\bar{e}}$ is a zero algebraic entity with unit values for the entries associated with all of element $\bar{e}$’s DOFs ($\mathbf {U}_{\bar{e}}$). Each DOF of element $\bar{e}$ is identified from the columns of matrix $\mathbf {L}_{\bar{e}}$, which represent the NGL DOFs of the entire structure (beam $+$ plate). For example, in Fig. 2, the beam element $e_4$ connects with the plate, and it is composed of nodes $n_4$ and $n_5$, which are associated with DOFs $U(19)$ to $U(30)$. $\mathbf {L}_{\bar{e}}$ for element $e_4$ can be written as:

(13)

All resultant entries related to the plate DOFs are null.

The local displacement $U_p$ required in (7), which is $U_k$ here, can be determined using the same methodology as above. Thus,

$$\begin{aligned} {{U}_k}^*=\mathbf {r}_{k}^{T}{\mathbf {U}}^*, \end{aligned}$$

(14)

where

$$\begin{aligned} \mathbf {r}_k=\left[ \begin{array}{ccccccccc} 0&0&\ldots&0&0&1&0&\ldots&0 \end{array}\right] ^T, \end{aligned}$$

(15)

which is a vector of dimensions $\text {NGL} \times 1$ such that $\mathbf {r}_k$ has only a unit value at the kth entry.

Using these relationships, Eq. (7) can be rewritten as follows:

$$\begin{aligned} \Phi _k=\frac{1}{2}\omega \mathrm{Re}\left\{ j[\mathbf {q}_{{\bar{e}}k}^T(\mathbf {K}_D)_{\bar{e}}\mathbf {L}_{\bar{e}}\mathbf {U}][\mathbf {r}_{k}^{T}{\mathbf {U}}^*]\right\} . \end{aligned}$$

(16)

Because the products $\mathbf {q}_{{\bar{e}}k}^T(\mathbf {K}_D)_{\bar{e}}\mathbf {L}_{\bar{e}}\mathbf {U}$ and $\mathbf {r}_{k}^{T}{\mathbf {U}}^*$ are scalar quantities, and $\mathbf {r}_{k}^{T}{\mathbf {U}}^*={(\mathbf {U}}^*)^T\mathbf {r}_{k}$, the expression is rearranged as:

$$\begin{aligned} \mathbf {S}_k=\mathbf {r}_{k}\mathbf {q}_{{\bar{e}}k}^T(\mathbf {K}_D)_{\bar{e}}\mathbf {L}_{\bar{e}}. \end{aligned}$$

(17)

So,

$$\begin{aligned} \Phi _k=\frac{1}{2}\omega \mathrm{Re}\left\{ j\mathbf {U}^H\mathbf {r}_{k}\mathbf {q}_{{\bar{e}}k}^T(\mathbf {K}_D)_{\bar{e}}\mathbf {L}_{\bar{e}}\mathbf {U}\right\} , \end{aligned}$$

(18)

or

$$\begin{aligned} \Phi _k=\frac{1}{2}\omega \mathrm{Re}\{j\mathbf {U}^H\mathbf {S}_{k}\mathbf {U}\}, \end{aligned}$$

(19)

where the symbol $^H$ represents the conjugate transpose of a complex vector. Here, $\mathbf {S}_k$ is a non-symmetric matrix, and shows dependency on the properties of element $\bar{e}$.

In this methodology, the auxiliary vectors $\mathbf {r}_{k}$ and $\mathbf {q}_{\bar{e}k}$, and the matrix $\mathbf {L}_{\bar{e}}$, which are based on the DOFs of the connection node and on the connectivity of the interface element $\bar{e}$, are used in association with the respective finite element matrix to calculate power flow as a function of global displacement vector. To the best of authors’ knowledge, this procedure is not found in the literature, and it can be applied to other types of elements such as bars, beams and shells elements. The use of a gradient-based optimization algorithm to minimize power flow between two different structures is an application for this method of evaluation, as presented in the following sections.

3 Formulation of optimization problem

The objective of this work is to change the external diameters of a pipe connected to a plate in order to minimize the total power flow $\Phi$ transferred from the pipe to the plate at their connection point. For a given frequency $\omega$, the problem can be formulated as follows:

$$\begin{aligned}& \min \left\{ \Phi (\mathbf {D})=\sum ^{6}_{p=1}\Phi _p=\sum ^{6}_{p=1}\frac{1}{2}\omega \mathrm{Re}\{j\mathbf {U}^H\mathbf {S}_{p}\mathbf {U}\}\right\} , \\&\text{subject to }(\mathbf {K}+j\omega \mathbf {C} - {\omega }^2\mathbf {M})\mathbf {U}(\omega )=\mathbf {P}(\omega ) \text{ and }D_{\min }\le D_m\le D_{\max },\end{aligned}$$

(20)

where $\mathbf {D}$ is the vector of beam external diameters, and $D_{\min }$ and $D_{\max }$ are the bound values of the mth design variable. The state equation may be rewritten as:

$$\begin{aligned} (\mathbf {K}+j\omega \mathbf {C} - {\omega }^2\mathbf {M})\mathbf {U}(\omega )=\mathbf {P}(\omega )\rightarrow \mathbf {K}_{D}\mathbf {U}=\mathbf {P}, \end{aligned}$$

(21)

where $\mathbf {K}_{D}$ is the global dynamic stiffness matrix.

Notably, $\mathbf {S}_{p}$ is explicitly dependent on the variable vector $\mathbf {D}$, owing to the dependency of $(\mathbf {K}_D)_e$ on the element diameter. Here, we consider the sum of all six components $\Phi _p$ of power flow given that the connection node has six DOFs. In a numerical implementation, the value of $p$ is related to the position of these DOFs at the global displacement vector. Although the present work is focused on a single frequency $\omega$, the problem can be extended to applications where power flow is to be minimized over specific frequency intervals. This can be achieved by adding a weighted sum of the frequencies of interest in (20).

4 Sensitivity analysis

To solve the problem described by (20), we chose to use the MMA algorithm, which requires gradients of objective function and constraints. The power flow for a single DOF p is a real function described in terms of the design variable vector $\mathbf {D}$ and the complex displacement vector $\mathbf {U}$. The latter can be written considering its real and imaginary parts, $\mathbf {U}_R$ and $\mathbf {U}_I$, so that $\mathbf {U}=\mathbf {U}_R+j\mathbf {U}_I$. In this way, the function $\Phi _p$ can be represented as follows:

$$\begin{aligned} \Phi _p&=\frac{1}{2}\omega \mathrm{Re}\{j\mathbf {U}^H\mathbf {S}_{p}\mathbf {U}\} \nonumber \\&= \frac{1}{2}\omega (-\mathbf {U}_R^T\mathbf {S}_{p}\mathbf {U}_I + \mathbf {U}_I^T\mathbf {S}_{p}\mathbf {U}_R). \end{aligned}$$

(22)

An augmented objective function $\bar{\Phi }_p$ that allows for adjoint sensitivity analysis can be obtained as follows [7]:

$$\begin{aligned} \bar{\Phi }_p&=\Phi _p+\frac{1}{2}\mathbf {\lambda }_1^T(\mathbf {K}_D \mathbf {U}-\mathbf {P}) \nonumber \\&\quad +\frac{1}{2}\mathbf {\lambda }_2^T(\mathbf {K}_D^* \mathbf {U}^*-\mathbf {P}^*), \end{aligned}$$

(23)

where $\mathbf {\lambda }_1$ and $\mathbf {\lambda }_2$ are Lagrange multiplier vectors.

The sensitivities of (23) are calculated as:

$$\begin{aligned} \frac{\mathrm{d}\bar{\Phi }_p}{\mathrm{d}D_e}&=\frac{\partial \Phi _p}{\partial D_e}+\frac{\partial \Phi _p}{\partial \mathbf {U}_R}\frac{\partial \mathbf {U}_R}{\partial D_e}+\frac{\partial \Phi _p}{\partial \mathbf {U}_I}\frac{\partial \mathbf {U}_I}{\partial D_e} \nonumber \\&\quad + \frac{1}{2}\mathbf {\lambda }_1^T\frac{\partial }{\partial D_e}(\mathbf {K}_D \mathbf {U}-\mathbf {P}) \nonumber \\&\quad + \frac{1}{2}\mathbf {\lambda }_2^T\frac{\partial }{\partial D_e}(\mathbf {K}_D^* \mathbf {U}^*-\mathbf {P}^*). \end{aligned}$$

(24)

After algebraic manipulation, it can be found that two adjoint problems are required to eliminate expressions involving $\frac{\partial \mathbf {U}_R}{\partial D_e}$ and $\frac{\partial \mathbf {U}_I}{\partial D_e}$:

$$\begin{aligned} \mathbf {K}_D\mathbf {\lambda }_1=-\left( \frac{\partial \Phi _p}{\partial \mathbf {U}_R}-j\frac{\partial \Phi _p}{\partial \mathbf {U}_I}\right) ^T, \end{aligned}$$

(25)

and

$$\begin{aligned} \mathbf {K}_D^*\mathbf {\lambda }_2=-\left( \frac{\partial \Phi _p}{\partial \mathbf {U}_R}+j\frac{\partial \Phi _p}{\partial \mathbf {U}_I}\right) ^T. \end{aligned}$$

(26)

Comparing (25) and (26) after taking the complex conjugate of (26), one can note that $\mathbf {\lambda }_2=\mathbf {\lambda }_1^*$. Changing the nomenclature to $\mathbf {\lambda }=\mathbf {\lambda }_1$, and knowing that in this work the external force $\mathbf {P}$ is not dependent on the element diameters, (24) changes to

$$\begin{aligned} \frac{\mathrm{d}\bar{\Phi }_p}{\mathrm{d}D_e}=\frac{\partial \Phi _p}{\partial D_e}+\frac{1}{2}\mathbf {\lambda }^T\frac{\partial \mathbf {K}_D }{\partial D_e}\mathbf {U}+ \frac{1}{2}\mathbf {\lambda }^H\frac{\partial \mathbf {K}_D^* }{\partial D_e}\mathbf {U}^*.\end{aligned}$$

(27)

From (23), $\bar{\Phi }_p=\Phi _p$. And, rearranging (27),

$$\begin{aligned} \frac{\mathrm{d}\Phi _p}{\mathrm{d}D_e}=\frac{\partial \Phi _p}{\partial D_e}+\mathrm{Re}\left\{ \mathbf {\lambda }^T\frac{\partial \mathbf {K}_D}{\partial D_e}\mathbf {U}\right\} , \end{aligned}$$

(28)

where $\mathbf {\lambda }$ is the solution of the adjoint problem

$$\begin{aligned} \mathbf {K}_D\mathbf {\lambda }=-\left( \frac{\partial \Phi _p}{\partial \mathbf {U}_R}-j\frac{\partial \Phi _p}{\partial \mathbf {U}_I}\right) ^T. \end{aligned}$$

(29)

The sensitivities of a real function such as (22) and the adjoint problem above were obtained in a general form by [7], and specifically for power transmission in photonics by [9].

After algebraic calculation, the partial derivatives on the right hand side of (29) are obtained by:

$$\begin{aligned} \frac{\partial \Phi _p}{\partial \mathbf {U}_R}=\frac{1}{2}\omega (\mathbf {U}_I^T(\mathbf {S}_{p} - \mathbf {S}_{p}^T)), \end{aligned}$$

(30)

and

$$\begin{aligned} \frac{\partial \Phi _p}{\partial \mathbf {U}_I}=\frac{1}{2}\omega (\mathbf {U}_R^T(\mathbf {S}_{p}^T - \mathbf {S}_{p})). \end{aligned}$$

(31)

Taking into account that $\mathbf {S}_p$ is a non-symmetric, complex matrix, the adjoint problem changes to:

$$\begin{aligned} \mathbf {K}_D\mathbf {\lambda }=j\frac{1}{2}\omega \left( \mathbf {S}_p^H - \mathbf {S}_p\right) ^T\mathbf {{U}}^*. \end{aligned}$$

(32)

Since $\Phi _p$, which is obtained using (19), is dependent explicitly on $\mathbf {D}$ (owing to the dependency of $\mathbf {S}_p$ on the diameter of the connection element $\bar{e}$), its partial derivative in (28) exists and can be found by:

$$\begin{aligned} \frac{\partial \Phi _p}{\partial D_e}=\frac{1}{2}\omega \mathrm{Re}\left\{ j\mathbf {U}^H\frac{\partial \mathbf {S}_p}{\partial D_e}\mathbf {U}\right\} . \end{aligned}$$

(33)

However, $\mathbf {S}_p$ is dependent only on the diameter of element $\bar{e}$. In this way, $\frac{\partial \mathbf {S}_p}{\partial D_e}$ is null for all other elements.

Using (33) in (28), the final expression for the sensitivity of the pth component of power flow at the connection point can be found as:

$$\begin{aligned} \frac{\mathrm{d}\Phi _p}{\mathrm{d}D_e}=\mathrm{Re}\left\{ j\frac{1}{2}\omega \mathbf {U}^H\frac{\partial \mathbf {S}_p}{\partial D_e}\mathbf {U}+\mathbf {\lambda }^T\frac{\partial \mathbf {K}_D}{\partial D_e}\mathbf {U}\right\} , \end{aligned}$$

(34)

where $\mathbf {\lambda }$ can be determined by solving (32).

To comply with the objective function of (20), the sensitivities can be obtained directly by:

$$\begin{aligned} \frac{\mathrm{d}\Phi }{\mathrm{d}D_e}=\sum ^{6}_{p=1}\frac{\mathrm{d}\Phi _p}{\mathrm{d}D_e}. \end{aligned}$$

(35)

Thus, one can determine analytically the sensitivity of the structural power flow using the global displacement vector $\mathbf {U}$, local characteristic matrix $\mathbf {S}_p$, and global dynamic stiffness $\mathbf {K}_D$. In beam–plate coupling, where the external diameters of the beam are the only design variables, the following considerations should be made:

• $\frac{\partial \mathbf {K}_D}{\partial D_e}$ is null for all shell elements of the structure;

• $\mathbf {\lambda }^T\frac{\partial \mathbf {K}_D}{\partial D_e}\mathbf {U}=\mathbf {\lambda }_e^T\frac{\partial (\mathbf {K}_D)_e}{\partial D_e}\mathbf {U}_e$ for each design variable $D_e$;

• $\frac{\partial \mathbf {S}_p}{\partial D_e}$ is null for all elements, except for the beam element at the connection;

• the adjoint problem (32) is solved for the entire system. The pseudo-load $j\frac{1}{2}\omega \left( \mathbf {S}_p^H - \mathbf {S}_p\right) ^T\mathbf {U}^*$ results in excitations only at the connection node, owing to the nature of the matrix $\mathbf {S}_p$; therefore, $\mathbf {\lambda }$ is not null, and it sets the influence of each element at the connection point. This excitation is a localized pseudo-load that results in a non-null pseudo-response $\mathbf {\lambda }$ along the connected beam.

5 Computational implementation

The proposed optimization procedure was implemented using a MATLAB version of MMA. A simple program interface was written for reading and writing the relevant data from (and to) the files used in both the FEM software and the MMA optimizer, and to calculate numerically the objective/constraint function sensitivities. It was defined an iterative procedure composed of the following steps:

• (a) Define the auxiliary vectors $\mathbf {r}_{p}$ and $\mathbf {q}_{\bar{e}p}$, and matrix $\mathbf {L}_{\bar{e}}$ based on the connection node number and connectivity of the interface element $\bar{e}$. Each $p$ DOF related to the connection node is identified in a manner similar to that in the simple example shown in Sect. 3.

• (b) Input initial design values (generally, entire beam structure with uniform external diameter).

• (c) Enter the optimization loop. It calls the FEM program (after writing the current iteration values of the design variables to a file) to run a harmonic analysis in batch mode and return the displacement vector $\mathbf {U}$ for the frequency of interest to the optimization procedure. Next, calculate the objective function and sensitivities in the interface module and send these data to the MMA.

• (d) If the stopping criteria are fulfilled, plot the optimized design. Otherwise, repeat from (c).

Fig. 3

Cross-section of pipe beam element

To obtain the sensitivities indicated by (34), we are required to calculate $\frac{\partial (\mathbf {K}_D)_e}{\partial D_e}$ and $\frac{\partial \mathbf {S}_p}{\partial D_e}$. For the pipe element having the cross-section shown in Fig. 3, the stiffness and mass matrices are written as functions of material properties, element length and position (nodal coordinates), and diameters $d$ and $D_e$ [17]. Given that only $D_e$ changes in the optimization procedure, $\frac{\partial (\mathbf {K}_D)_e}{\partial D_e}$ can be calculated with ease. In addition, for the connection element, Eq. (17) is valid, so

$$\begin{aligned} \frac{\mathrm{d}\mathbf {S}_p}{\mathrm{d}D_e}=\mathbf {r}_{p}\mathbf {q}_{{\bar{e}}p}^T\frac{\partial (\mathbf {K}_D)_{\bar{e}}}{\partial D_e}\mathbf {L}_{\bar{e}}. \end{aligned}$$

(36)

Owing to the numerical characteristics of MMA, two volume constraints are imposed on the optimization problem: the material volume of the pipe may be between the minimum possible volume (all elements with external diameter $D_{\min }$) and the maximum (all elements with diameter $D_{\max }$). The elementary sensitivities of these constraints are easy to obtain owing to their simple dependency on the element diameters.

Due to the adoption of the FEM in the methodology proposed in this work, one can suggest novel external diameter distributions for a beam structure by minimizing power flow to the plate for any spatial configuration of the beam.

6 Numerical examples

A steel pipe with the following properties is considered: Young’s modulus $=$ $210$ GPa, and material density = $7800 \,\mathrm{kg}/m^3$. The total length $L_b=0.5$ m and internal diameter $d=0.002$ m are fixed, while the external diameter $D_e$ of each element is a design variable.

This pipe is connected to a thin rectangular plate, measuring $0.5$ m (width) $\times$ $0.35$ m (height) $\times$ $0.002$ m (thickness). The material properties are the same as those of the pipe. The dimensions of this beam–plate structure are typical of components used, for example, in domestic refrigeration devices, such as gas discharge tubes and hermetic compressor casings.

Fig. 4

Example 1—simple beam–plate structure modeled using FEM

Fig. 5

Total power flow from beam to plate and mean square normal velocity of plate for Example 1

For performing harmonic analysis, we consider the proportional damping model with $\alpha =0$ and $\beta =10^{-6}$. These values were estimated from experimental frequency response functions measured in similar structures.

For a maximum analysis frequency of 1000 Hz, 10 elements per wavelength were used, i.e., 40 elements for the beam part and 1120 elements for the plate part.

Because only external diameters $D_e$ were allowed to vary during optimization, 40 design variables were used to define the optimal configuration. The bound values were defined based on typical applications and they were set to $D_{\min }=0.003$ m and $D_{\max }=0.01$ m.

Fig. 6

Example 1—a, c total power flow from beam to plate at the case of optimization for 420 and 716 Hz, respectively. b, d Mean square velocity of the plate at the case of optimization for 420 and 716 Hz, respectively

6.1 Example 1—simple beam–plate structure

In this example, the plate is simply supported at all vertices, as shown in Fig. 4, with the beam connected perpendicularly at its geometric center, which is excited by a harmonic translational external force $P=(0.01 N;0.01 N;0.01 N)$.

The optimization objective function is the total structural power flow at point A (the connection node between the beam and plate). Two cases are presented, for two specific and arbitrary frequencies of interest: 420 and 716 Hz. Although, in general, any frequency could be used, the values used here correspond to peaks in the spectrum.

The initial design is defined with all diameters $D_e$ set to $0.006$ m. The total power flow at node A, and the mean square normal velocity of the plate are plotted in Fig. 5, for a frequency range of 1–1000 Hz with a frequency increment of 2 Hz. One can see in Fig. 5 that the mean square normal velocity of the plate, which is directly related to its radiated sound power [5], has the same spectral shape as the total power flow from the beam part.

In this example, two separated subcases are considered: total power flow at (a) 420 Hz and (b) 716 Hz are minimized to reduce the plate velocity response at each of these frequencies separately.

Owing to the use of a gradient method, the optimization procedure can lead to a local minimum, which may be satisfactory depending on the application.

The transmitted power flow and the mean square velocity of the plate incorporated in the final designs are shown in Fig. 6. The case with all external diameters equal to $D_{\max }$ is shown in Fig. 6 as well. Moreover, the final beam designs are shown in Figs. 7 and 8.

Fig. 7

Example 1—optimized diameter distribution for 420 Hz (a) and 716 Hz (b)

Fig. 8

Example 1—optimized diameter distribution for 420 Hz (top) and 716 Hz (bottom)

Fig. 9

Example 1—sensitivities for a 420 Hz and b 716 Hz

For the 420-Hz case, a reduction in power flow transmission from beam to plate is observed and, consequently, a reduction in the plate normal mean velocity; this is true for the 716-Hz case too. However, the reduction in case of the first frequency is much localized compared with the reduction in case of the second frequency. This is because near 420 Hz, in the initial design, there are two near-vibration modes: 418.9 and 421 Hz. The change in beam design during optimization causes separation of these modes owing to changes in the coupling dynamic characteristics. For 716 Hz, there is no vibration mode in the vicinity (nearest eigenfrequencies are: 620.3, 716.7, 756 Hz), and optimization leads to more effective power flow reduction. In this study, the authors are more focused on showing that the optimization procedure can solve the problem at hand systematically.

To verify the analytical sensitivities of power flow at the connection point, the forward finite difference method is applied for the two frequencies above. All external diameters of the pipe are fixed as $D_e=0.006$ m, while the variation of each design variable is fixed as $\delta D_e=10^{-9}$ m. A comparison between the two methods of calculation is shown in Fig. 9.

In addition, one can choose to minimize the average power flow in a given frequency range, which is considered in this work as

Fig. 10

Example 1—total power flow from beam to plate over 2–1000 Hz frequency range

Fig. 11

Example 1—optimized diameter distribution over 2–1000 Hz frequency range

$$\begin{aligned} \bar{\Phi }={\frac{1}{(\omega _2 - \omega _1)}}{\int ^{\omega _2}_{\omega _1}}\left( {\sum ^{6}_{pd=1}\Phi _p}\right) \mathrm{d}\omega \cong {\frac{1}{N_\omega }}\sum ^{N_\omega }_{n=1}\left( {\sum ^{6}_{p=1}\Phi _p}\right) , \end{aligned}$$

(37)

where $N_\omega$ is the number of frequency steps considered in a harmonic analysis from $\omega _1$ to $\omega _2$. Once this new function is a sum of known functions, the new sensitivities can be obtained directly. For the above example, the 2–1000 Hz frequency range with frequency steps of 2 Hz is selected to minimize the total power flow calculated using (37). The transmitted power flow at the connection point in the original and optimized configurations is shown in Fig. 10, and the final beam design is shown in Fig. 11.

6.2 Example 2—curved beam–plate structure

The plate described in Sect. 6.1 is now connected perpendicularly to a curved pipe having length $L_b=0.5$ m and arc radius $R_b=0.5$ m on the XY plane at the same connection point, as shown in Fig. 12. The beam is excited by an external force $P=(0.01 N;0.01 N;0.01 N)$ at the free extremity.

Fig. 12

Example 2—curved beam–plate structure modeled using FEM

Fig. 13

Example 2—total power flow from curved beam to plate and mean square normal velocity of plate

The initial design is defined with all diameters set to $0.006$ m. The total power flow at node A and the mean square normal velocity of the plate are shown in Fig. 13, for the frequency range from 1 to 1000 Hz.

The optimization objective function is the total structural power flow at point A for a specific and arbitrary frequency of interest: 562 Hz. The same FE mesh discretization as in Example 1 is applied.

Fig. 14

Example 2—optimized diameter distribution for 562 Hz

Fig. 15

Example 2—optimized diameter distribution for 562 Hz (geometry)

The objective of this example is to apply the methodology to a non-straight beam in order to show the generality of application of the developed method. Figure 13 shows that the mean square normal velocity of the plate is strongly related to the total power flow at the connection point.

In this example, the total power flow at 562 Hz is minimized to reduce the plate velocity response at this frequency. The problem formulated in (20) is applied to this specific frequency, and the final shape design of the beam is shown in Figs. 14 and 15.

The final power flow and mean square velocity of the plate are shown in Fig. 16. The case with all external diameters equal to $D_{\max }$ is presented in Fig. 16 as well.

The forward finite difference method is applied for verifying the analytical sensitivities using the same parameters as in Example 1, and a comparison between the two methods of calculation is shown in Fig. 17.

This example of a curved beam coupled to a plate shows that the proposed methodology can be applied to complex beam paths owing to the direct use of finite element information for obtaining power flow and sensitivities.

As in Sect. 6.1, one can also choose to minimize the average power flow in a given frequency range obtained using (37). A frequency range between 2 and 1000 Hz with frequency steps of 2 Hz is selected. The power flow at the connection point in the original and optimized configurations is shown in Fig. 18. The final beam design is presented in Fig. 19.

Fig. 16

Example 2: a total power flow from beam to plate at 562 Hz and b mean square velocity of plate at 562 Hz

Fig. 17

Example 2—sensitivities for 562 Hz

Fig. 18

Example 2—total power flow from beam to plate over 2–1000 Hz frequency range

Fig. 19

Example 2—optimized diameter distribution over 2–1000 Hz frequency range

For the example shown in this section (and in Sect. 6.1), Eq. (5) is used to obtain the total net power flow from the beam to the plate, which is a result of the interaction between the incident and reflected vibration waves at the connection point [24]. Once this measure is used to refer to the resultant (net) power transferred from the beam to the plate, its value does not change if calculated from the viewpoint of the plate (using shell elements adjacent to the connection node). From Fig. 20, it can be noted that four shell elements share the connection node for the structure analyzed in the current section. Thus, using these elements, the internal forces in this node can be obtained by an adaptation of Eq. (9) as follows:

$$\begin{aligned} F_k=\sum ^{4}_{\bar{e}=1}\mathbf {q}_{{\bar{e}}k}^{T}(\mathbf {K}_D)_{\bar{e}}\mathbf {U}_{\bar{e}}, \end{aligned}$$

(38)

Fig. 20

Shell elements connected to beam in Example 2

Fig. 21

Total power flow from beam to plate in Example 2

where $\bar{e}$ represents each shell element adjacent to the connection node and $(\mathbf {K}_D)_{\bar{e}}$ is the dynamic stiffness matrix associated with each element $\bar{e}$. The remainder of the procedure is maintained and repeated for the other DOFs of the connection. Elementary matrices of SHELL63 elements can be extracted from ANSYS in Harwell-Boeing format (to a text file). This data can then be interpreted by the algorithm implemented in this work. The power flow spectra calculated using beam element and shell elements (at the interface) are shown in Fig. 21. As expected, the curves are identical. This is true for other examples and diameter beam configurations as well.

7 Conclusions

A new technique was implemented and tested to evaluate vibration power flow at the connection point of a beam coupled perpendicularly to a plate. The direct use of finite element concepts and algebraic computation allows us to obtain power flow as a function of the global displacement vector of the coupled structure, which facilitates analytical determination of the sensitivities. Two simple examples show the potential of the method for improving the dynamical behavior of structures at specific frequencies of interest.

In the present work, the physical meaning of power flow minimization is related to the variation of cross-section along a beam, as well as local changes in the beam–plate connection. The developed optimization method involves varying the beam’s external diameters to minimize the transfer of vibration energy to the plate.

The use of auxiliary algebraic entities that localize internal forces and displacements in elementary and global displacement vectors for a given node in the beam is essential in the developed procedure. This technique allows for rearranging the power flow equation, thereby enabling the use of a general method for obtaining its sensitivities.

In the academic and simplified examples presented in this work, it can be observed that the diameter of the beam element coupled directly to the plate has excessive sensitivity. In fact, any change in this local property affects the dynamic behavior of the connection, as noted in (34) through the term $\frac{\partial \mathbf {S}_p}{\partial D_e}$. In cases where this excessive sensitivity leads to weak structures in the connection region, one could eliminate the diameter of the interface beam element from the design variables vector or impose new bound values for this local variable.

The examples presented herein focused on minimizing power flow at one single frequency, but the methodology can be easily expanded for a given frequency range of interest, as described in the article. Furthermore, this methodology can be applied to other types of parameterization, depending on how easy it is to find the derivatives of structural FE matrices with respect to the design variables.