On the finite load capacity in misaligned journal bearings

Abstract

We study some qualitative properties of a misaligned journal bearing. The device consists of two cylinders closely spaced: an inner rotating cylinder (the shaft) whose symmetry axis is not parallel to the one of the outer cylinder (the bearing). We consider the load capacity of the system, defined as the force exerted by the pressure. It is given by the integral of the pressure times the normal vector to the bearing surface. We obtain finite load capacity, even in the limit case when a point contact occurs. It was also verified by numerical simulations. We used an adapted Preconditioned Conjugate Gradient Method for solving the direct problem, preserving the A-orthogonality property of the search directions, even after a restarting process. The solution of the related inverse problem is based on an interior, trust-region algorithm. To validate the numerical proposal, the predicted pressure values at the bearing mid-plane, are compared to published experimental data.

1 Introduction

A journal bearing is a mechanical device consisting of two cylinders closely spaced and in relative motion. The annular gap between them is filled with a fluid, the lubricant, to prevent contact. Ideally, the axes of both cylinders are parallel when installed and remain so during the operation, under an imposed load and speed [25].

Actually, this ideal condition hardly exists and the inner cylinder, the shaft, tends to experience some degree of misalignment while rotating within the outer cylinder, the bearing. In this paper, considering misalignment, cavitation and a radial loading, we provide a mathematical proof to demonstrate the finite load capacity of the system for the point contact case. We also present numerical simulations that verify this result. We consider a stationary regime of a Newtonian, isoviscous, isothermal and incompressible lubricant.

Misalignment is known to have a harmful effect on the steady-state performance of a journal bearing. It can reduce the fluid film thickness, decreasing the load capacity and finally altering the entire pressure field [25]. On the other hand, cavitation, represented through the Reynolds or the Elrod–Adams cavitation model has been also considered in journal bearings. The differences between these two cavitation models are based on the conditions imposed to the pressure at the boundary that separates the cavitated and the full filled area, see [19, 37]. In presence of cavitation, it has been shown that the maximum pressure of a misaligned journal bearing is shifted to the bearing ends. Actually, it is greater than that for the aligned bearing and an increase in the degree of misalignment could yield two peak values in the pressure, axially near both ends [25]. A comprehensive study on misalignment and cavitation can be found in [28].

Representative numerical studies about loaded misaligned journal bearings in [2, 23, 32, 39], suggest that misaligned bearings have a finite load capacity as the end-plane film thickness goes to zero (the point contact case), as opposed to perfectly aligned journal bearings which then have a theoretically infinite load capacity (the line contact case), see [12, 33]. Conversely, Boedo and Booker suggest that misaligned bearings have infinite load and moment capacity as the end-plane minimum film thickness approaches zero under transient journal squeeze motion and under steady load and speed conditions [6]. These results differ markedly from finite capacity trends reported in this work, and in previously mentioned numerical and experimental studies. Our result is based on the generation of over-pressures at the boundary of the point contact. Such over-pressures, although unbounded, produce a finite load capacity, since the integral of the pressure is bounded at such boundary. On the other hand, far from the contact point, there is not over-pressures that can make the pressure to blow up. So, our result is independent of the cavitation model used, since it is a local behaviour, where the pressure is always positive. A similar proof on sliders can be found in [11].

Considering the numerical resolution of the model, the Finite Element Method (FEM) have been widely used. The discrete problem has been solved by the classical Gauss–Seidel method or a point-overrelaxation method, including both a projection technique to consider cavitation [8, 16]. We also do a FEM discretization, and solve the system of equations by a Preconditioned Conjugate Gradient Method (PCG) with both projection and restarting strategies. In most of the previous studies, the film thickness function h is a given datum and the pressure p is the main unknown. However, in real engineering applications the position of the shaft is unknown and consequently the film thickness function h. Thus, to get that position the Newton’s second law is introduced. The problem consists in finding the pressure of the lubricant, the shaft position and the projections of the angular misalignment when considering this last phenomenon. It is referred as an inverse problem, where the coefficient h depends on the unknown p. This problem has been addressed by several authors, from the simple case in which the surfaces are two parallel planes to a more general geometry, including the Reynolds cavitation model, see [11, 12, 18] for details. Furthermore, it has been proved the existence of shaft equilibrium positions when the hydrodynamic force created by the pressure film balances an external radial force [13]. The authors also considered the problem for both cases, a rigid surface moving over a flat plane and the elastohydrodynamic problem, see [14]. Nevertheless, none of these works considered misalignment.

As for the numerical resolution of the inverse problem we can mention the work of [20]. They used an implicit Euler method to deal with the dynamical shaft problem coupled with the fluid hydrodynamic problem. At each time step, the Broyden method combined with the Armijo–Goldstein criterion to choose a proper step length in the descent direction, is used to solve the resulting non-linear system. Conversely, Lombera and Tello proposed a different approach to deal with the shaft model [27]. It was based on first solving the Elrod–Adams equation for a known position by minimizing a convex and lower semi-continuous functional and then using an iterative method to reach the equilibrium, namely a trust-region strategy. A similar approach will be used in this work but adding to the shaft model two more equations, to consider the torque components in presence of angular misalignment.

The outline of the paper is the following. In Sect. 2 we derive the expression for the fluid film thickness and pose a suitable variational formulation for the hydrodynamic problem considering misalignment and the Reynolds cavitation model. We also present the admissible range of misalignment angle projections. In Sect. 3 we prove the finite load capacity of a misaligned journal bearing for the point contact case. In Sect. 4 we consider a finite element discretization and perform the minimization stage by a PCG, adapted with both projection and restarting strategies to account for cavitation. Section 5 is devoted to explaining the resolution of the inverse problem by an interior, trust-region algorithm subject to bounds. Numerical experiments and discussion are provided in Sect. 6. A grid convergence study and the validation of the whole numerical approach are presented in Sect. 7.

2 Mathematical model

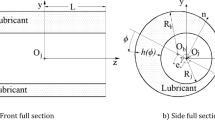
In this section, we depict a 3D formulation of the hydrodynamic behaviour of misaligned journal bearings. In Fig. 1a we show the journal bearing axes along with their projections on the XY-plane and the XZ-plane respectively. The origin O is located at the centre of the bearing “left” end-plane and the shaft rotates at a constant velocity $\omega$ about the X axis. The coordinate system has been rotated, in favour of the graphic comprehension. A typical misaligned journal bearing is presented in Fig. 1b.

Fig. 1

Misalignment in a journal bearing

Notice that the axis is rotated an angle $\psi$, characterized by its projections $\varphi$ and $\beta$ on the XY-plane and the XZ-plane respectively. We create a cross section of the inner cylinder along the plane $X=x$. The cross section is approximated by a circumference. We compute the position of the inner cylinder centre, on that plane, considering the eccentricity $\lambda$ of its axis.

Taking into account the auxiliary coordinate system $(x', y', z')$ located in the YZ-plane, at the position $(\rho \sin \alpha , \rho \cos \alpha )$, the coordinates of the shaft, on the plane $X=x$, will be:

$$\begin{aligned} S_y= & {} \nu _y + \rho \sin \alpha = x\tan \varphi + \rho \sin \alpha ,\\ S_z= & {} \nu _{{z}} + \rho \cos \alpha = x\tan \beta + \rho \cos \alpha . \end{aligned}$$

Therefore, the eccentricity for the cross section located at X=x is:

$$\begin{aligned} \lambda= & {} \left( S_y^2 + S_z^2\right) ^{1/2},\\ \lambda= & {} \left[ (x\tan \varphi + \rho \sin \alpha )^2 + (x\tan \beta + \rho \cos \alpha )^2\right] ^{1/2}, \\ \lambda= & {} \left( x^2 \tan ^2\varphi + 2x\rho \tan \varphi \sin \alpha + x^2\tan ^2\beta + 2x\rho \tan \beta \cos \alpha + \rho ^2\right) ^{1/2}. \end{aligned}$$

We introduce the angle $\gamma$, computed as a function of the eccentricity components:

$$\begin{aligned} \gamma= & {} \arctan \frac{S_y}{S_z}, \\ \gamma= & {} \arctan \frac{x\tan \varphi + \rho \sin \alpha }{x\tan \beta + \rho \cos \alpha }. \end{aligned}$$

By analogy to the parallel case, see [21, 28] for instance, we approximate the fluid film thickness as follows:

$$\begin{aligned} h(\rho , \alpha , \varphi , \beta , \theta , x)= & {} C + \lambda (\rho , \alpha , \varphi , \beta , x)\cos (\theta -\gamma (\rho , \alpha , \varphi , \beta , x)), \end{aligned}$$

(1)

where C represents the radial clearance and $\theta$ represents a point on the external circumference at the height $Z=z$.

In the following, we briefly discuss the governing equations for modelling, in a stationary regime, the hydrostatic pressure in a misaligned journal bearing considering a thin fluid film thickness and the cavitation phenomenon. Let L, R be the length and the cross section radius respectively of the shaft. We consider the unfolded circumferential coordinate $z \in (0, 2 \pi R)$ and the axial coordinate $x \in (0, L)$. We define the region $\varOmega : [0, 2 \pi R] \times [0, L]$. The unknowns of the problem are:

$$\begin{aligned} \begin{array}{ll} p(z, x):\varOmega \rightarrow {\mathbb {R}}^{+}, &{}\quad \text{ fluid } \text{ pressure, } \\ \rho \in [0, C), &{}\quad \text{ left } \text{ end-plane } \text{ eccentricity, }\\ \alpha \in [0, 2\pi ], &{}\quad \text{ left } \text{ end-plane } \text{ angular } \text{ position, } \\ \beta \in {[-C/L;C/L]}, &{}\quad \text{ misalignment } \text{ angle } \text{ projection } \text{ on } \text{ the } XZ-\text {plane,}\\ \varphi \in {[-C/L;C/L]}, &{}\quad \text{ misalignment } \text{ angle } \text{ projection } \text{ on } \text{ the } XY\text {-plane,} \end{array} \end{aligned}$$

and they satisfy the constraint of positivity of the gap h or equivalently:

$$\begin{aligned}&C^2> \lambda ^2,\\&\text{ i.e. }\\&C^2 >x^2 \tan ^2\varphi + 2x\rho \tan \varphi \sin \alpha + x^2\tan ^2\beta + 2x\rho \tan \beta \cos \alpha + \rho ^2. \end{aligned}$$

We then use the Reynolds cavitation model to describe the cavitation phenomenon, whose weak formulation is the following inequality:

$$\begin{aligned} \int _{\varOmega } h^3 \nabla p \nabla (\phi -p)\mathrm {d}z\mathrm {d}x\ge & {} \int _{\varOmega }6\mu h\mathbf {U}\nabla (\phi -p)\mathrm {d}z\mathrm {d}x \quad \forall \phi \in K , \end{aligned}$$

(2)

with

$$\begin{aligned} K= & {} \left\{ \phi \ge 0, \ \left( \int _{\varOmega } (\nabla \phi )^2\mathrm {d}z\mathrm {d}x \right) ^{1/2} + \left( \int _{\varOmega } \phi ^2\mathrm {d}z\mathrm {d}x\right) ^{1/2} < \infty \right\} , \nonumber \\&\phi (z,0)=\phi (z,L)= p_{\mathrm{a}},\nonumber \\&p_{\mathrm{a}} = \text{ atmospheric } \text{ pressure. } \end{aligned}$$

(3)

In (2), $\mu$ stands for the fluid viscosity, h stands for the fluid film thickness and the velocity $\mathbf {U}=(v_x,v_y,v_z)$ makes reference to the shaft velocity vector.

For steady-state bearing operation the shaft presents only one non-zero velocity component, $v_z = \omega R$, with $\omega$ the angular velocity. Then, (2) becomes:

$$\begin{aligned} \int _{\varOmega } h^3 \nabla p \nabla (\phi -p)\mathrm {d}z\mathrm {d}x\ge & {} \int _{\varOmega }6\mu h v_z\frac{\partial (\phi -p)}{\partial z}\mathrm {d}z\mathrm {d}x, \quad \forall \phi \in K , \end{aligned}$$

(4)

defined in (3).

We define the bilinear form a and the function f by:

$$\begin{aligned} a(p,\phi ):= & {} \int _{\varOmega } h^3 \nabla p \nabla \phi \mathrm {d}z\mathrm {d}x,\\ f:= & {} - 6 \mu div (h \mathbf {U}) \in H^{-1}(\varOmega ), \end{aligned}$$

and reformulate (4) as follows:

$$\begin{aligned} a(p, \phi -p)&\,\ge \,&\langle f,\phi -p\rangle , \end{aligned}$$

where notation $\langle , \rangle$ represents the $L^2$-inner product. We express the problem as a minimization problem of the following convex functional:

$$\begin{aligned} J(\phi )= & {} \frac{1}{2}a(\phi , \phi )-\langle f,\phi \rangle \,\, \text{ on } K. \end{aligned}$$

(5)

Taking the parameters of (4) and substituting them in (5) we obtain the dimensional functional to minimize:

$$\begin{aligned} J(\phi )= & {} \frac{1}{2} \int _\varOmega h^3(\nabla \phi )^T \nabla \phi \mathrm {d}z\mathrm {d}x \,-\, \int _\varOmega 6\mu h v_z \frac{\partial \phi }{\partial z}\mathrm {d}z\mathrm {d}x , \end{aligned}$$

(6)

with h defined in (1).

To make our solution to suffice for a variety of different problems, we introduce the following dimensionless variables:

$$\begin{aligned} \theta= & {} \frac{z}{R}, \quad \mathrm {d}z = R\mathrm {d}\theta ,\\ {\bar{x}}= & {} \frac{x}{L}, \quad \mathrm {d}x = L\mathrm {d}{\bar{x}},\\ {\bar{\phi }}= & {} \frac{C^2}{\mu _0 \omega R^2}\phi , \quad {\bar{\mu }} = \frac{\mu }{\mu _0},\quad {\bar{w}} = \frac{v_z}{\omega R},\quad {\bar{h}} = \frac{h}{C},\quad {\bar{\rho }} = \frac{\rho }{C}, \quad {\bar{\lambda }} =\frac{\lambda }{C}, \end{aligned}$$

where $\mu _0$ stands for the reference viscosity. Thus, we transform our domain into the dimensionless domain ${\bar{\varOmega }} = [0, 2\pi ]\times [0, 1]$ for the $(\theta , {\bar{x}})$ coordinates.

Then, the dimensionless equation for the functional in (6) is:

$$\begin{aligned} J({{\bar{\phi }}})= & {} \frac{1}{2} \int _{{\bar{\varOmega }}} LR{\bar{h}}^3 (\nabla {\bar{\phi }})^T \nabla {\bar{\phi }}\mathrm {d}\theta \mathrm {d}{\bar{x}} \,-\, \int _{{\bar{\varOmega }}} 6{\bar{\mu }}{\bar{h}}{\bar{w}}\frac{\mu _0\omega LR^2}{C^2} \frac{\partial {\bar{\phi }}}{\partial \theta }\mathrm {d}\theta \mathrm {d}{\bar{x}} , \end{aligned}$$

(7)

with ${\bar{h}}$ defined as:

$$\begin{aligned} {\bar{h}}({\bar{\rho }}, \alpha , \varphi , \beta , \theta , {\bar{x}})= & {} 1 + {\bar{\lambda }}({\bar{\rho }}, \alpha , \varphi , \beta , {\bar{x}})\cos (\theta -{\bar{\gamma }}({\bar{\rho }}, \alpha , \varphi , \beta , {\bar{x}})), \end{aligned}$$

(8)

where

$$\begin{aligned} {\bar{\lambda }}({\bar{\rho }}, \alpha , \varphi , \beta , {\bar{x}})= & {} \frac{1}{C}\left( ({\bar{x}}\tan \varphi + C{\bar{\rho }}\sin \alpha )^2 + ({\bar{x}}\tan \beta + C{\bar{\rho }}\cos \alpha )^2\right) ^{1/2}, \end{aligned}$$

and

$$\begin{aligned} {\bar{\gamma }}({\bar{\rho }}, \alpha , \varphi , \beta , {\bar{x}})= & {} \arctan \frac{{\bar{x}}\tan \varphi + C{\bar{\rho }}\sin \alpha }{{\bar{x}}\tan \beta + C{\bar{\rho }}\cos \alpha }. \end{aligned}$$

We now present the admissible range for the misalignment angle projections and the eccentricity, to satisfy the constraint $C> \lambda$. The limit cases are the contact case in ${\bar{x}}=0$ and ${\bar{x}}=1$. The former is obtained with ${{\bar{\rho }}}=1$, and we will focus on the latter by studying the condition ${{\bar{\lambda }}}^2 < 1$, which expands to:

$$\begin{aligned} ({\bar{x}}\tan \varphi + C{{\bar{\rho }}}\sin \alpha )^2 + ({\bar{x}}\tan \beta + C{{\bar{\rho }}}\cos \alpha )^2 < C^2. \end{aligned}$$

Working on the first term we get:

$$\begin{aligned} ({\bar{x}}\tan \varphi + C{{\bar{\rho }}}\sin \alpha )^2 < C^2. \end{aligned}$$

Considering the negative solution and the contact:

$$\begin{aligned}&-\tan \varphi - C{{\bar{\rho }}}\sin \alpha< C, \nonumber \\&\quad -C(1 + {{\bar{\rho }}}\sin \alpha ) < \tan \varphi . \end{aligned}$$

(9)

Considering the positive solution and the contact:

$$\begin{aligned}&\tan \varphi + C{{\bar{\rho }}}\sin \alpha< C, \nonumber \\&\quad \tan \varphi < C(1 - {{\bar{\rho }}}\sin \alpha ). \end{aligned}$$

(10)

Putting (9) and (10) together we can set the range for $\tan \varphi$:

$$\begin{aligned} -C(1 + {{\bar{\rho }}}\sin \alpha )< \tan \varphi <C(1 - {{\bar{\rho }}}\sin \alpha ). \end{aligned}$$

(11)

Following the same procedure we set the range for $\tan \beta$ as a function of $\tan \varphi$:

$$\begin{aligned}&-(C^2 - (\tan \varphi + C{{\bar{\rho }}}\sin \alpha )^2)^{\frac{1}{2}} - C{{\bar{\rho }}}\cos \alpha \nonumber \\&< \tan \beta < (C^2 - (\tan \varphi + C{{\bar{\rho }}}\sin \alpha )^2)^{\frac{1}{2}} - C{{\bar{\rho }}}\cos \alpha . \end{aligned}$$

(12)

To simplify the notation, we drop arguments of function ${\bar{h}}$, ${\bar{\lambda }}$ and ${\bar{\gamma }}$ from now on.

On the other hand, we state the equilibrium of forces and torques acting on the device as constraints that the problem (7) must satisfy. The resultant dimensional fluid film force components, acting on the bearing and accordingly to Fig. 1a are:

$$\begin{aligned} \int _{\varOmega } p(\theta , x)\sin \theta \mathrm {d}\theta \mathrm {d}x= & {} F_{\mathrm{y}}, \\ \int _{\varOmega } p(\theta , x)\cos \theta \mathrm {d}\theta \mathrm {d}x= & {} F_{\mathrm{z}}, \end{aligned}$$

where $\sin (\theta )$ and $\cos (\theta )$ stand for the unitary normal vector components to the bearing surface. The resultant dimensional torque components acting on the bearing are:

$$\begin{aligned} -\int _{\varOmega }xp(\theta , x)\cos \theta \mathrm {d}\theta \mathrm {d}x= & {} \tau _{y},\\ \int _{\varOmega }xp(\theta , x)\sin \theta \mathrm {d}\theta \mathrm {d}x= & {} \tau _{z}. \end{aligned}$$

Accordingly to (7), we get the following dimensionless expressions for the equilibrium of force and torque components:

$$\begin{aligned} \frac{1}{|\mathbf {F}|}\int _{{\bar{\varOmega }}}\frac{\mu _0\omega L R^3}{C^2}{\bar{\phi }}\sin \theta \mathrm {d}\theta \mathrm {d}{\bar{x}}= & {} {\bar{F}}_{\mathrm{y}}, \end{aligned}$$

(13)

$$\begin{aligned} \frac{1}{|\mathbf {F}|}\int _{{\bar{\varOmega }}}\frac{\mu _0\omega L R^3}{C^2}{\bar{\phi }}\cos \theta \mathrm {d}\theta \mathrm {d}{\bar{x}}= & {} {\bar{F}}_{\mathrm{z}}, \end{aligned}$$

(14)

$$\begin{aligned} - \frac{1}{|\varvec{\tau }|}\int _{{\bar{\varOmega }}}\frac{\mu _0\omega L^2 R^3}{C^2}{\bar{x}}{\bar{\phi }}\cos \theta \mathrm {d}\theta \mathrm {d}{\bar{x}}= & {} {\bar{\tau }}_{\mathrm{y}}, \end{aligned}$$

(15)

$$\begin{aligned} \frac{1}{|\varvec{\tau }|}\int _{{\bar{\varOmega }}}\frac{\mu _0\omega L^2 R^3}{C^2}{\bar{x}}{\bar{\phi }} \sin \theta \mathrm {d}\theta \mathrm {d}{\bar{x}}= & {} {\bar{\tau }}_{\mathrm{z}}, \end{aligned}$$

(16)

where $|\mathbf {F}|$ and $|\varvec{\tau }|$ denote the modulus of the external load $\mathbf {F}$ and torque $\varvec{\tau }$ respectively, used for scaling. The right-hand side terms ${\bar{F}}_{\mathrm{y}}$, ${\bar{F}}_{\mathrm{z}}$, ${\bar{\tau }}_{y}$ and ${\bar{\tau }}_{z}$ stand for the normalized components of $\mathbf {F}$ and $\varvec{\tau }$. Then, the problem is the following:

To find ${\bar{\phi }} \in K$ such that it minimizes (7) satisfying the constraints (13), (14), (15) and (16) with ${\bar{h}}$ given by (8).

3 Finite load capacity for the point contact case

We prove in Theorem 1 that the force exerted by the pressure is indeed finite.

Theorem 1

Let ${\bar{h}}({\bar{x}}, \alpha , \theta , \beta ) = 1 + \frac{{\bar{x}}}{C}\tan \beta \cos (\theta - \alpha )$ be the fluid film thickness for ${\bar{x}} \in [0, 1]$, such that $\min \{{\bar{h}}\}=0$ with a contact point at ${\bar{x}}=1$ if $\tan \beta = C$, ${\bar{\rho }}=0$ and $\theta -\alpha =\pi$. Then, we have that: $\lim \limits _{\tan \beta \rightarrow C}\int _{{\bar{\varOmega }}}{\bar{\phi }}\mathrm {d}{\bar{x}}\mathrm {d}\theta < k(\beta , C, {\bar{\rho }}, \alpha )$, where ${{\bar{\phi }}}$ is the solution of the variational Reynolds Eq. (2).

Proof

We first prove that the term

$$\begin{aligned} \int _{{\bar{\varOmega }}} {\bar{h}}^3 |\nabla {\bar{\phi }}|^2 \mathrm {d}{\bar{x}}\mathrm {d}\theta \end{aligned}$$

(17)

is uniformly bounded. The proof is obtained from the inequality:

$$\begin{aligned} \int _{{\bar{\varOmega }}} {\bar{h}}^3 |\nabla {\bar{\phi }}|^2 \mathrm {d}{\bar{x}}\mathrm {d}\theta= & {} \varLambda \int _{{\bar{\varOmega }}} {\bar{h}}\frac{\partial {\bar{\phi }}}{\partial \theta }\mathrm {d}{\bar{x}}\mathrm {d}\theta , \nonumber \\\le & {} \frac{1}{2} \int _{{\bar{\varOmega }}} {\bar{h}}^3 |\nabla {\bar{\phi }}|^2 \mathrm {d}{\bar{x}}\mathrm {d}\theta + \frac{\varLambda ^2}{2} \int _{{\bar{\varOmega }}} {\bar{h}}^{-1} \mathrm {d}{\bar{x}}\mathrm {d}\theta , \end{aligned}$$

(18)

providing

$$\begin{aligned} \int _{{\bar{\varOmega }}} {\bar{h}}^{-1} \mathrm {d}{\bar{x}}\mathrm {d}\theta \le k<\infty , \end{aligned}$$

and hence the boundedness of (17). We introduce the set $\varOmega _1$ defined by:

$$\begin{aligned} \varOmega _1=({\bar{x}}, \alpha ) \in (0,1) \times \left( \alpha + \frac{5 \pi }{6}, \alpha +\frac{7 \pi }{6}\right) , \end{aligned}$$

and $\varOmega _2 = {\bar{\varOmega }}- \varOmega _1$, i.e. a region where no over-pressures nor contacts occur, then:

$$\begin{aligned} \int _{\varOmega _1} {\bar{h}}^{-1} \mathrm {d}{\bar{x}}\mathrm {d}\theta\le & {} \int _{\alpha +\frac{5\pi }{6}}^{ \alpha +\frac{7\pi }{6}} C\Bigg [\frac{\ln (C+\tan \beta \cos (\theta -\alpha ))}{\tan \beta \cos (\theta -\alpha )} - \frac{\ln (C)}{\tan \beta \cos (\theta -\alpha )}\Bigg ]\mathrm {d}\theta ,\\\le & {} \frac{C}{\tan \beta }\Bigg [\int _{\alpha +\frac{5\pi }{6}}^{ \alpha +\frac{7\pi }{6}} \frac{\ln (C+\tan \beta \cos (\theta -\alpha ))}{\cos (\theta -\alpha )}\mathrm {d}\theta - k_0\Bigg ] < \infty . \end{aligned}$$

We have, in view of

$$\begin{aligned} \min _{({\bar{x}}, \theta ) \in \varOmega _2} {\bar{h}}^{-1} \ge h_0>0, \end{aligned}$$

the following result:

$$\begin{aligned} \int _{\varOmega } {\bar{h}}^{-1} \mathrm {d}{\bar{x}}\mathrm {d}\theta \le k_0 < \infty . \end{aligned}$$

(19)

Then, we have:

$$\begin{aligned} \int _{{\bar{\varOmega }}} {\bar{h}}^3 |\nabla {\bar{\phi }}|^2 \mathrm {d}{\bar{x}}\mathrm {d}\theta \le k <\infty , \end{aligned}$$

which implies:

$$\begin{aligned} \lim _{\tan \beta \rightarrow C} \int _{{\bar{\varOmega }}} {\bar{h}}^3 |\nabla {\bar{\phi }}|^2 \mathrm {d}{\bar{x}}\mathrm {d}\theta \le k <\infty , \end{aligned}$$

and therefore:

$$\begin{aligned} \int _{{\bar{\varOmega }}} {\bar{h}}^3 |\nabla {\bar{\phi }}|^2 \mathrm {d}{\bar{x}}\mathrm {d}\theta \le k <\infty , \qquad \forall \beta \le \arctan C. \end{aligned}$$

(20)

Thanks to (20) we have:

$$\begin{aligned} \int _{\varOmega _2} {\bar{h}}^3 |\nabla {\bar{\phi }}|^2 \mathrm {d}{\bar{x}}\mathrm {d}\theta \le k <\infty . \end{aligned}$$

Since $h \ge h_0$ in $\varOmega _2$ we have that:

$$\begin{aligned} \int _{\varOmega _2} |\nabla {\bar{\phi }} |^2 \mathrm {d}{\bar{x}}\mathrm {d}\theta \le k, \end{aligned}$$

and in particular we have that:

$$\begin{aligned} {\bar{\phi }}\in L^q(\varOmega _2), \ \text{ for } \text{ any } q<\infty . \end{aligned}$$

(21)

We also have that:

$$\begin{aligned} \left| \int _{{\bar{\varOmega }}} {\bar{\phi }} \cos (\theta - \alpha ) \mathrm {d}{\bar{x}}\mathrm {d}\theta \right|&= \left| \int _{{\bar{\varOmega }}} {\bar{\phi }} \frac{\partial }{\partial {\bar{x}}} {\bar{x}} \cos (\theta - \alpha )\mathrm {d}{\bar{x}}\mathrm {d}\theta \right| ,\\&= \left| k_0 \int _{{\bar{\varOmega }}} {\bar{\phi }} \frac{\partial {\bar{h}}}{\partial {\bar{x}}} \mathrm {d}{\bar{x}}\mathrm {d}\theta \right| ,\\&= \left| k_0 \int _{{\bar{\varOmega }}} {\bar{h}} \frac{\partial {\bar{\phi }}}{\partial {\bar{x}}} \mathrm {d}{\bar{x}}\mathrm {d}\theta \right| ,\\&\le \left| k_0 \left( \frac{1}{2} \int _{{\bar{\varOmega }}} {\bar{h}}^3 |\nabla {\bar{\phi }}|^2 \mathrm {d}{\bar{x}}\mathrm {d}\theta + \frac{\varLambda ^2}{2} \int _{{\bar{\varOmega }}} {\bar{h}}^{-1} \mathrm {d}{\bar{x}}\mathrm {d}\theta \right) \right| , \end{aligned}$$

and we obtain:

$$\begin{aligned} \left| \int _{{\bar{\varOmega }}} {\bar{\phi }} \cos (\theta - \alpha ) \mathrm {d}{\bar{x}}\mathrm {d}\theta \right| \le k_0. \end{aligned}$$

(22)

Since

$$\begin{aligned} \int _{{\bar{\varOmega }}} {\bar{\phi }} \cos (\theta -\alpha ) \mathrm {d}{\bar{x}}\mathrm {d}\theta = \int _{\varOmega _1} {\bar{\phi }} \cos (\theta -\alpha ) \mathrm {d}{\bar{x}}\mathrm {d}\theta + \int _{\varOmega _2} {\bar{\phi }} \cos (\theta -\alpha ) \mathrm {d}{\bar{x}}\mathrm {d}\theta , \end{aligned}$$

we have that:

$$\begin{aligned} \frac{1}{2} \int _{\varOmega _1} {\bar{\phi }} \mathrm {d}{\bar{x}}\mathrm {d}\theta \le \left| \int _{{\bar{\varOmega }}} {\bar{\phi }} \cos (\theta -\alpha ) \mathrm {d}{\bar{x}}\mathrm {d}\theta \right| + \left| \int _{\varOmega _2} {\bar{\phi }} \cos (\theta -\alpha ) \mathrm {d}{\bar{x}}\mathrm {d}\theta \right| , \end{aligned}$$

and thanks to (22) and (21)

$$\begin{aligned} \lim _{\tan \beta \rightarrow C}\int _{\varOmega _1} {\bar{\phi }}\mathrm {d}{\bar{x}}\mathrm {d}\theta <\infty . \end{aligned}$$

Then, in view of the previous inequality and (20) we obtain that:

$$\begin{aligned} \lim _{\tan \beta \rightarrow C}\int _{{\bar{\varOmega }}} {\bar{\phi }} \mathrm {d}{\bar{x}}\mathrm {d}\theta <\infty , \end{aligned}$$

(23)

which ends the proof. $\square$

However, in [6] the authors suggest that misaligned bearings have infinite load and moment capacity as the end-plane minimum film thickness approaches zero under transient journal squeeze motion and under steady load and speed conditions. Those results represent a relevant difference from this proof and from finite capacity trends reported in previous numerical and experimental studies.

Corollary 1

As a consequence of the previous theorem we have that:

$$\begin{aligned}&\int _{{\bar{\varOmega }}} {\bar{\phi }} \sin (\theta -\alpha ) \mathrm {d}{\bar{x}}\mathrm {d}\theta , \quad \int _{{\bar{\varOmega }}} {\bar{\phi }}\cos (\theta -\alpha ) \mathrm {d}{\bar{x}}\mathrm {d}\theta , \\&\quad \int _{{\bar{\varOmega }}} {\bar{x}}{\bar{\phi }} \sin (\theta -\alpha ) \mathrm {d}{\bar{x}}\mathrm {d}\theta , \quad \int _{{\bar{\varOmega }}} {\bar{x}} {\bar{\phi }}\cos (\theta -\alpha ) \mathrm {d}{\bar{x}}\mathrm {d}\theta , \end{aligned}$$

are uniformly bounded at the contact point limit. Therefore, for $|\mathbf {F}|$ or $|\varvec{\tau }|$ large enough we do not have a solution for the problem.

Nevertheless, the inequality (23) does not guarantee the boundedness of the pressure in $L^{\infty }(\varOmega )$.

Remark 1

The proof of Theorem 1 is given for the variational Reynolds model. Notice that the proof for the Elrod–Adams cavitation model is equivalent to the one presented before, if we replace (18) by the inequality:

$$\begin{aligned} \int _{{\bar{\varOmega }}} {\bar{h}}^3 |\nabla \phi |^2 \mathrm {d}{\bar{x}}\mathrm {d}\theta= & {} -\varLambda \int _{{\bar{\varOmega }}} \frac{\partial H(\phi ) {\bar{h}}}{\partial \theta } \phi \mathrm {d}{\bar{x}}\mathrm {d}\theta \nonumber \\= & {} \varLambda \int _{{\bar{\varOmega }}} H(\phi ) {\bar{h}}\frac{\partial \phi }{\partial \theta } \mathrm {d}{\bar{x}}\mathrm {d}\theta \nonumber \\\le & {} \frac{1}{2} \int _{{\bar{\varOmega }}} {\bar{h}}^3 |\nabla \phi |^2 \mathrm {d}{\bar{x}}\mathrm {d}\theta + \frac{\varLambda ^2}{2} \int _{{\bar{\varOmega }}} {\bar{h}}^{-1} \mathrm {d}{\bar{x}}\mathrm {d}\theta \end{aligned}$$

(24)

where $H(\phi )$ is the Heaviside function describing the concentration of the fluid in the cavitated region.

Remark 2

Notice that the gap function in [6] is defined as follows:

$$\begin{aligned} h=C-e^{x}\cos \theta -e^{y}\sin \theta - z \phi ^{y }\cos \theta + z\phi ^{ x }\sin \theta , \end{aligned}$$

where $e^{x}$, $e^{y}$ are components of mid-plane journal eccentricity, and $\phi ^{ x}$, $\phi ^y$ are components of journal axial misalignment angle. In this work, we define the gap h in terms of $\lambda$ defined by:

$$\begin{aligned} h= & {} C+ \lambda \cos (\theta - \gamma ),\\ \lambda= & {} \left( x^2 \tan ^2\varphi + 2x\rho \tan \varphi \sin \alpha + x^2\tan ^2\beta + 2x\rho \tan \beta \cos \alpha + \rho ^2\right) ^{1/2}, \end{aligned}$$

that can be written as:

$$\begin{aligned} \lambda = \left( (x \tan \varphi + \rho \sin \alpha )^2 + (x\tan \beta + \rho \cos \alpha )^{2} \right) ^{1/2}. \end{aligned}$$

Considering the Taylor polynomial of the square root function, and that the deviations $\beta$ and $\phi$ are close to zero, we may approximate $\lambda$ (as a function of $\tan \beta$ and $\tan \varphi$), by the following function:

$$\begin{aligned} \lambda \approx \rho + \frac{x}{\sqrt{\rho }} \tan \beta \cos \alpha + \frac{x}{\sqrt{\rho }} \tan \varphi \sin \alpha . \end{aligned}$$

Since

$$\begin{aligned} \cos (\theta - \gamma )=\cos \theta \cos \gamma + \sin \theta \sin \gamma , \end{aligned}$$

we have that:

$$\begin{aligned} h \approx C+ ( \rho + \frac{x}{\sqrt{\rho }} \tan \beta \cos \alpha + \frac{x}{\sqrt{\rho }} \tan \varphi \sin \alpha )(\cos \theta \cos \gamma + \sin \theta \sin \gamma ), \end{aligned}$$

i.e.

$$\begin{aligned} h\approx & {} C + \left[ \rho \cos \gamma + \frac{x}{\sqrt{\rho }}( \tan \beta \cos \alpha + \tan \varphi \sin \alpha ) \cos \gamma \right] \cos \theta \\&+\left[ \rho \sin \gamma + \frac{x}{\sqrt{\rho }}(\tan \beta \cos \alpha + \tan \varphi \sin \alpha )\sin \gamma \right] \sin \theta , \end{aligned}$$

which corresponds to the gap defined in [6] for:

$$\begin{aligned} e^x= - \rho \cos \gamma ,\qquad \phi ^{y}= -( \tan \beta \cos \alpha + \tan \varphi \sin \alpha ) \cos \gamma , \end{aligned}$$

and

$$\begin{aligned} e^y=- \rho \sin \gamma , \qquad \phi ^{x}= - ( \tan \beta \cos \alpha + \tan \varphi \sin \alpha ) \sin \gamma \end{aligned}$$

when the axes are renamed following the corresponding notation.

Since the proof is based on the boundedness of $\int _{\varOmega } h^{-1} \mathrm {d}{\bar{x}}\mathrm {d}\theta$ and the approximation in [6] also satisfies such condition, the proof is also valid for the gap defined in [6].

4 Direct problem resolution

We first consider the direct problem, where the position of the inner cylinder is known, i.e. h is a given datum determined by $\alpha$, $\rho$, $\varphi$ and $\beta$. Taking advantage of the region under study, we perform the spatial approximation by piecewise quadrangular Lagrange $Q_1$ finite elements. That is, ${\bar{\phi }}$ is approximated as follows:

$$\begin{aligned} {\bar{\phi }} \approx \phi _{\mathrm{f}}= & {} \sum _{{i}=1}^n N_{{i}} \phi _{{i}}, \end{aligned}$$

where subscript $\mathrm f$ stands for the finite element approximation.

The topology of the used mesh is shown in Fig. 2. As in [6], we use a uniform mesh density along the circumferential direction, whereas in the axial direction the mesh density becomes finer when moving from the bearing mid-plane to the bearing ends. An attenuation factor $\delta$ is used for this purpose.

Fig. 2

The mesh topology used in this work (dimensionless)

On the other hand, the discretized form of the dimensionless functional in (7) will be:

$$\begin{aligned} J(\phi _{\mathrm{f}})= & {} \frac{1}{2} \sum _{j=1}^n \sum _{k=1}^n \int _{{\bar{\varOmega }}} LR{\bar{h}}^3 \left[ \nabla \big (N_j\phi _j \big )\right] ^T \nabla \big (N_k\phi _k \big )\mathrm {d}\theta \mathrm {d}{\bar{x}} \nonumber \\&- \sum _{j=1}^n \int _{{\bar{\varOmega }}} 6{\bar{\mu }}{\bar{h}}{\bar{w}}\frac{\mu _0\omega LR^2}{C^2} \frac{\partial \big (N_j\phi _j\big )}{\partial \theta }\mathrm {d}\theta \mathrm {d}{\bar{x}}, \nonumber \\ J(\phi _{\mathrm{f}})= & {} \frac{1}{2} \sum _{j=1}^n \sum _{k=1}^n \phi _j \left( \int _{{\bar{\varOmega }}} LR{\bar{h}}^3 (\nabla N_j)^T (\nabla N_k) {\mathrm {d}\theta \mathrm {d}{\bar{x}}} \right) \phi _k \nonumber \\&- \sum _{j=1}^n \phi _j \int _{{\bar{\varOmega }}} 6{\bar{\mu }}{\bar{h}}{\bar{w}}\frac{\mu _0\omega LR^2}{C^2} \frac{\partial N_j}{\partial \theta }\mathrm {d}\theta \mathrm {d}{\bar{x}} . \end{aligned}$$

(25)

It can be easily verified that this functional can be written as a quadratic functional in the form of $\frac{1}{2}\phi ^TA\phi - \phi ^Tb$.

Therefore, for the resolution of the direct problem we propose a PCG, adapted with a projection technique to account for cavitation. Since it is well known that the convergence rate of the Conjugate Gradient Method (CG) without restart is only linear, we also perform a restarting process whenever a projection occurs, see [17] for details. This approach corrects at each iteration j the pressure value components $\phi _j^i$ and takes up the necessary zero gradients implicitly, whenever the first one is detected out of the convex set. We use the projection technique $\max (\phi _j^i, 0)$, also proposed in [10].

We determined the following expressions to properly compute the new descent directions after a restarting procedure when considering preconditioning. In what follows, the search direction $d_j$ and the residual $r_j$ applied to the restarting process for the PCG will all be marked by $\tilde{}$ , except the deflection parameter $\xi _j$ and the correction parameter $\zeta _j$, see [5, p. 430] for details. Thus, for the direction ${\tilde{d}}_{j+1}$ with $j \ge 2$ we have:

$$\begin{aligned} {\tilde{d}}_{j+1}= & {} {\tilde{r}}_{j+1} + \xi _j {\tilde{d}}_j + \zeta _j {\tilde{d}}_1. \end{aligned}$$

Let $\varPsi$ be a non-singular matrix derived from the decomposition of the preconditioner M of the matrix A. Due to back transformation

$$\begin{aligned} \phi= & {} \varPsi ^{-T}{\tilde{\phi }}, \end{aligned}$$

the algorithm has the search direction

$$\begin{aligned} d_j= & {} \varPsi ^{-T}{\tilde{d}}_j, \end{aligned}$$

for the transformed iterate

$$\begin{aligned} \phi _j= & {} \varPsi ^{-T}{\tilde{\phi }}_j. \end{aligned}$$

(26)

The residual $r_j$ in $\phi _j$ is given by:

$$\begin{aligned} r_j= & {} b - A\phi _j = \varPsi (c - B{\tilde{\phi }}_j)= \varPsi {\tilde{r}}_j, \end{aligned}$$

(27)

where $B = \varPsi ^{-1} A \varPsi ^{-T}$ and $c = \varPsi ^{-1}b$ are the system matrix and the right-hand side term respectively after applying a split preconditioning process. Then:

$$\begin{aligned} {\tilde{d}}_{j+1}= & {} \varPsi ^{-1} r_{j+1} + \xi _j {\tilde{d}}_j + \zeta _j {\tilde{d}}_1, \\ \varPsi ^{-T}{\tilde{d}}_{j+1}= & {} \varPsi ^{-T}\varPsi ^{-1} r_{j+1} + \xi _j \varPsi ^{-T}{\tilde{d}}_j + \zeta _j \varPsi ^{-T}{\tilde{d}}_1, \\ d_{j+1}= & {} \varPsi ^{-T}\varPsi ^{-1} r_{j+1} + \xi _j d_j + \zeta _j d_1, \\ d_{j+1}= & {} M^{-1} r_{j+1} + \xi _j d_j + \zeta _j d_1, \end{aligned}$$

with

$$\begin{aligned} \zeta _j= & {} \frac{\langle -{\tilde{r}}_{j+1}, B {\tilde{d}}_1\rangle }{\langle {\tilde{d}}_1, B {\tilde{d}}_1\rangle }, \\= & {} \frac{\langle - \varPsi ^{-1} r_{j+1}, \varPsi ^{-1} A \varPsi ^{-T} \varPsi ^{T}d_1\rangle }{\langle \varPsi ^{T}d_1, \varPsi ^{-1} A \varPsi ^{-T} \varPsi ^{T}d_1\rangle }, \\= & {} \frac{\langle - \varPsi ^{-1} r_{j+1}, \varPsi ^{-1} A d_1\rangle }{\langle \varPsi ^{T}d_1, \varPsi ^{-1} A d_1\rangle }, \end{aligned}$$

where notation $\langle ,\rangle$ stands for the inner product of both n-dimensional vectors. Taking the inner product:

$$\begin{aligned} \zeta _j= & {} \frac{(- \varPsi ^{-1} r_{j+1})^T \varPsi ^{-1} A d_1}{(\varPsi ^{T}d_1)^T \varPsi ^{-1} A d_1}, \\= & {} \frac{- r_{j+1}^T \varPsi ^{-T} \varPsi ^{-1} A d_1}{d_1^T \varPsi \varPsi ^{-1} A d_1}, \\= & {} \frac{- r_{j+1}^T M^{-1} A d_1}{d_1^T A d_1}. \end{aligned}$$

If we denote $\sigma _1 = A d_1$ we have:

$$\begin{aligned} \zeta _j= & {} \frac{- r_{j+1}^T M^{-1} \sigma _1}{d_1^T \sigma _1}. \end{aligned}$$

Notice that we need additionally to solve the system of equations $M s_\sigma = \sigma _1$, but only when a restarting procedure occurs. The solution is carried out by easily solving two triangular systems with coefficient matrices $\varPsi$ and $\varPsi ^T$, respectively. Finally, we have:

$$\begin{aligned} \zeta _j= & {} \frac{\langle - r_{j+1}, s_\sigma \rangle }{\langle d_1, \sigma _1\rangle }. \end{aligned}$$

A flow chart for the proposed PCG algorithm considering cavitation with the restarting technique included is presented in Fig. 3.

Fig. 3

Flow chart for the PCG considering cavitation and the restarting technique

As a summary, in the regular iteration when there is no cavitation nor restarting (steps 2, 4, 6, 8), we have the following expressions:

$$\begin{aligned} \phi _{j+1}= & {} \phi _{j} + \varepsilon _j d_j, \qquad \qquad \; \varepsilon _j = \frac{\langle r_j, s_j\rangle }{\langle d_j, Ad_j\rangle },\nonumber \\[0.3em] r_{j+1}= & {} r_j - \varepsilon _j Ad_j, \qquad \; \, s_{j+1} = M^{-1}r_{j+1},\nonumber \\[0.3em] d_{j+1}= & {} s_{j+1} + \xi _j d_j,\qquad \xi _j = \frac{\langle r_{j+1}, s_{j+1}\rangle }{\langle r_j, s_j\rangle }. \end{aligned}$$

(28)

Whenever we detect cavitation $(\phi _j^i < 0)$, we set the negative pressure and residual components to zero. We solve $s_j$ in (28), but using the updated residual value $r_j$. We prepare the restarting procedure by setting $d_j=s_j$, computing the inner product $\langle s_j, r_j\rangle$ and defining two flags (step 3). Then, in the first iteration of the restarting (when $\kappa _{\mathrm{iter}}==\mathrm{true}$) we set and compute (step 5):

$$\begin{aligned} d_1= & {} d_j, \qquad \qquad \qquad \qquad \quad \text{ same } \text{ value } \text{ as } s_j,\\ d_{j+1}= & {} s_j + \xi _j d_1, \qquad \qquad \qquad \text{ for } \text{ j } \text{= } \text{1 },\\ s_\sigma= & {} M\setminus \sigma _1, \qquad \qquad \qquad \quad \text{ computed } \text{ just } \text{ once } \text{ per } \text{ restarting },\\ \sigma _1= & {} Ad_1. \end{aligned}$$

Subsequent iterations (when $\kappa _{iter} == \textsf {false}$ and Restart== textsftrue) consider the search direction computed as follows (step 7):

$$\begin{aligned} d_{j+1}= & {} s_{j+1} + \xi _j d_j + \zeta _j d_1, \qquad \, \text{ for } j \ge 2,\\ \zeta _j= & {} \frac{\langle - r_{j+1}, s_\sigma \rangle }{\langle d_1, \sigma _1\rangle }. \end{aligned}$$

Since we deal with a quadratic functional and our proposal guarantees the search directions $\{d_{j}\}$ to be A-orthogonal, by Theorem 8.8.3 in [5, p. 405], the CG produces an optimal solution after one complete application of the main step, that is, after at most n line searches¹ have been performed. We consider the energy norm $\Vert \phi \Vert _A = (\phi ^T A \phi )^{1/2}$, induced by the energy scalar product. Due to the deduction of the PCG, see [26] for instance, and the identity

$$\begin{aligned} \Vert \phi _j - \phi \Vert _A = \Vert {\tilde{\phi }}_j - {\tilde{\phi }}\Vert _B, \end{aligned}$$

(29)

which results from (26) and the definition of B in (27), the approximation properties for the CG in (30) (see [26, p. 225] for its proof) also hold for the PCG method, if the spectral condition number $\kappa (A)$ is replaced by $\kappa (B) = \kappa (M^{-1}A)$. Notice that, since $\varPsi ^{-T}B\varPsi ^{T} = M^{-1}A$ and $\varPsi B\varPsi ^{-1} = AM^{-1}$, B, $M^{-1}A$ and $A M^{-1}$ have the same eigenvalues, and hence the same spectral condition number $\kappa$. Therefore, the error $(\phi _j - \phi )$ at the j^th step in the energy norm $\Vert .\Vert _A$ is:

$$\begin{aligned} \Vert \phi _j - \phi \Vert _A \le 2 \left( \frac{\kappa ^{1/2}-1}{\kappa ^{1/2}+1}\right) ^j\Vert \phi _0 - \phi \Vert _A, \end{aligned}$$

(30)

with $\kappa =\kappa (M^{-1}A)$. The algorithm stops when either the maximum iteration number is reached or $\Vert r\Vert \le tol \Vert b\Vert$, with tol the chosen tolerance.

5 Inverse problem numerical solution

For solving the dimensionless inverse problem we first consider the balance of force and torque components involved. We define the residual E as follows:

$$\begin{aligned} E({\bar{\rho }}, \alpha , \varphi , \beta ) = \left[ \begin{array}{ccc} {\bar{F}}_{\mathrm{y}} &{}-&{}\frac{1}{|\mathbf {F}|}\int _{{\bar{\varOmega }}}\frac{\mu _0\omega L R^3}{C^2}{\bar{\phi }}\sin \theta \mathrm {d}\theta \mathrm {d}{\bar{x}}\\ {\bar{F}}_{\mathrm{z}} &{}-&{} \frac{1}{|\mathbf {F}|}\int _{{\bar{\varOmega }}}\frac{\mu _0\omega L R^3}{C^2}{\bar{\phi }}\cos \theta \mathrm {d}\theta \mathrm {d}{\bar{x}}\\ {\bar{\tau }}_{\mathrm{y}} &{}+&{} \frac{1}{|\varvec{\tau }|}\int _{{\bar{\varOmega }}}\frac{\mu _0\omega L^2 R^3}{C^2}{\bar{x}}{\bar{\phi }}\cos \theta \mathrm {d}\theta \mathrm {d}{\bar{x}} \\ {\bar{\tau }}_{\mathrm{z}} &{}-&{} \frac{1}{|\varvec{\tau }|}\int _{{\bar{\varOmega }}}\frac{\mu _0\omega L^2 R^3}{C^2}{\bar{x}}{\bar{\phi }} \sin \theta \mathrm {d}\theta \mathrm {d}{\bar{x}} \end{array}\right] . \end{aligned}$$

The numerical approach is to minimize the $L^2$-norm of the residual E in least squares sense, i.e. $min |E|_2^2$. We note that to obtain the dimensionless pressure ${\bar{\phi }}$, four unknown parameters are needed: ${\bar{\rho }} \in [0, 1)$, $\alpha \in [0, 2\pi ]$, $\varphi \in {[-C/L, C/L]}$ and $\beta \in {[-C/L, C/L]}$ which determine the shaft position and misalignment in the system. We use an iterative method in the set of admissible positions $({\bar{\rho }} , \alpha , \varphi , \beta )$ to minimize $|E|_2^2$, where ${\bar{\phi }}$ is the solution to the hydrodynamic direct problem in (7), whose coefficient depends on ${\bar{\rho }}$, $\alpha$, $\varphi$ and $\beta$.

For the optimization routine we propose a trust-region algorithmic strategy [30]. Following the idea behind a trust-region method, the information gathered about E is used to construct an approximation of E in a neighbourhood of $d_k$ (the trust region) which we denote by $m_k$. We find the step $s_k = d_{k+1} - d_k$ by solving the following subproblem:

$$\begin{aligned} \min _{s_k \in {\mathbb {R}}^4} m_k(d_k + s_k), \quad \text{ where } \quad d_k + s_k \quad \text{ lies } \text{ inside } \text{ the } \text{ trust } \text{ region. } \end{aligned}$$

Let $He$ and G be defined by:

$$\begin{aligned} He(d_k) := \nabla ^2 E(d_k), \qquad G(d_k) := \nabla E(d_k). \end{aligned}$$

Then, let l and u be the lower and upper bounds of $d_k$, we define a vector function $r(d_k): {\mathbb {R}}^n \rightarrow {\mathbb {R}}^n$ as follows:

Definition 1

The vector $r(d_k) \in {\mathbb {R}}^n$ is defined:

• (i) if $G(d_k)_i < 0$ and $u_i < \infty$, then $r_i = (d_k)_i - u_i$,

• (ii) if $G(d_k)_i \ge 0$ and $l_i > -\infty$, then $r_i = (d_k)_i - l_i$,

For any $a \in {\mathbb {R}}^n$, diag(a) denotes an n-by-n diagonal matrix with the vector a defining the diagonal entries in their natural order. So, we define:

$$\begin{aligned} D(d_k)= & {} diag(|r(d_k)|^{-1/2}). \end{aligned}$$

In this manner and because we are facing a determined non-linear system of equations and a bounded admissible set of parameters, we propose the following scaled trust-region subproblem as in [15]:

$$\begin{aligned} \min _{s_k \in {\mathbb {R}}^4} m_k(s)= & {} s_k^{T}G_k+ \frac{1}{2} s_k^{T}M_{k}s_k, \end{aligned}$$

(31)

where

$$\begin{aligned} J^r(d_k)= & {} diag(sgn(G(d_k))), \\ C(d_k)= & {} D(d_k)diag(G(d_k))J^r(d_k)D(d_k), \\ M(d_k)= & {} B(d_k) + C(d_k), \end{aligned}$$

where $B(d_k)$ is the discretization of $He$.

As the notation indicates, $m_k$ and E are in agreement to first order at the current iterate $d_k$. The matrix $M_k$ and the diagonal matrix $D_k$ are chosen this way such that there is no need to handle constraints explicitly. Since the quadratic model $m_k$ is defined to include the constraint information, a natural extension to the classical definition of the ratio $\eta _k$ also takes place, see [30]. It is given by:

$$\begin{aligned} \eta _k= & {} \frac{E(d_k + s_k) -E(d_k) + \frac{1}{2}s_k^TC(d_k)s_k}{m_k(s_k)}, \end{aligned}$$

and measures the agreement between the nonlinear function $E(d_k)$ and its quadratic approximation at each iteration; see the work of [15] for a wide explanation on this selection. With this approach, it is possible to obtain an approximate trust-region solution which can guarantee second-order convergence by simply solving an unconstrained trust-region subproblem. Each iteration involves the approximate solution of the problem in (31), using the classical PCG. When the squared 2-norm of E is below the prescribed tolerance, the algorithm finishes. An implementation of the routine used for the inverse problem can be found in MATLAB (e.g. lsqnonlin).

It is important to remark that the numerical approach returns the equilibrium position, which could be in contact with the bearing geometry or outside the region of admissible positions. If any of them occurs, verified with (11) and (12), we assume that the solution is the contact. We have considered three cases in which the algorithm for the inverse problem stops:

• 1. The equilibrium position is found within the region of admissible positions.

• 2. The equilibrium position is found, in contact with the bearing geometry or outside the region of admissible positions. We noticed for the latter case, that the solution is outside the geometry but it is still close (about 1 $\upmu$m)² to its boundary, in such a way that the algorithm is still able to find it. We say the surfaces are in contact to each other. The algorithm does not crash.

• 3. There is a contact but the equilibrium position is not found. Before it occurs, the adapted PCG, running inside the trust-region algorithm, warns the system matrix is no longer positive definite for the current iteration of the forward problem. In addition, it shows that the candidate solution of the inverse problem places the shaft too far from the geometry boundary and, therefore, the mathematical model is not valid. After several attempts, trying to find a solution for the inverse problem in a smaller trust region, the algorithm throws an exception. We catch and handle the exception and say that surfaces are in contact.

6 Numerical results and discussion

In this section, we present numerical tests to verify the finite load capacity in misaligned journal bearings. The dimensionless domain ${\bar{\varOmega }}=[0, 2 \pi ] \times [0, 1]$ is discretized using a $400\times 160$ finite elements mesh (64000 four-noded quadrangles) and an attenuation factor $\delta =0.93$. Unless other values are specified, the geometrical and physical constants of the journal bearing used during the experiments are those in Table 1. They are real values taken from an experimental analysis accomplished in [7].

Table 1 Geometrical and physical constants

Although the problem is solved in a dimensionless domain, most of the results are back transformed and presented in their real scales and units when it does not affect the visualization purpose. From now on, the terms front and rear ends of the bearing will be used in place of the left and right end-planes respectively.

In Fig. 4 we present the behaviour of the minimum film thickness hMin with respect to the position of the applied force, in both front and rear ends of the device. This case has been conducted using different forces of 1000 N, 2000 N and 3000 N for an angular velocity of 1500 rpm. The force position, as a way of generating different torques, has been applied every 2 mm from the bearing mid-plane to its rear end (21 points in total).

Fig. 4

Behaviour of the minimum gaps at the end-planes, related to the force applying position

In Fig. 4a the behaviour at the rear end is presented. Notice that, when the position of the application of the force increases, the minimum film thickness monotonically decreases, reaching even some contact point detected by the algorithm and shown as a black square marker. This result proves numerically, that the device is unable to generate a force that can balance a large imposed load under that operating conditions. Thus, we found finite load capacity as stated in [2, 23, 32, 39]. Also, notice that for higher force values the same pattern get repeated, but the contact is reached faster.

In Fig. 4b we present the same study at the front end. The behaviour is no longer strictly monotone. This obeys the fact that at the beginning, when the force is applied at the mid-plane (centre of mass), there is not misalignment and both end-planes centres decrease their position in the same way. Nevertheless, when the distance between the centre of mass and the application point of the force increases, the centre of the front end goes up due to the torque, and the film thickness at that end-plane increases as well. At some point, the centre of the front end crosses the closest point to the bearing axis (where the film thickness is maximum) and subsequent movements decrease the film thickness again, since the shaft is now approaching towards the bearing top at this end.

We show in Fig. 5 the paths of both end-planes centres for the case conducted with a force of 3000 N in Fig. 4.

Fig. 5

Paths of both centres at their end-planes for a $F = 3000$ N. Both views are seen from the front end of the bearing

Similarly, if some contact point is found the position where the centre is located is shown as a black square marker. Notice that both views are seen from the front end of the bearing. It can be easily confirmed the behaviour of both centres, as described above. On the other hand, Fig. 6 presents a similar experiment as in Fig. 4, but increasing the angular velocity to 3000 rpm. As expected the carrying capacity increases, and in consequence the contact points disappear. This demonstrates the influence of the velocity and also the consistence of our proposal.

Fig. 6

Behaviour of the minimum gaps at the end-planes, related to the force applying position for an angular velocity of 3000 rpm

Additionally, Fig. 7 shows the effect on the force exerted by the pressure when the slenderness ratio (L/D) changes.

Fig. 7

The effect on the force exerted by the pressure when the ratio (L/D) changes

In the experiment the bearing length varies from 10 to 160 mm, with a step of 10 mm. The force was always computed for $\alpha = 0.610865$ rad, $\rho = 82.25~\upmu$m, $\beta = -0.000067$ rad and $\varphi = -0.000047$ rad. We notice, as stated in the literature, how the carrying capacity of the journal bearing is compromised as the slenderness ratio is much less than about 1/4, see [40].

Finally, it is important to remark that in [8], the authors solved the associated system of equations $Ax=b$ by the classical Gauss–Seidel, projecting over a convex set to account for cavitation, at each iteration. Its convergence is also guaranteed for this problem, since it is well known that the Gauss–Seidel algorithm converges globally if the system matrix A is symmetric and positive definite. Let M be the iteration matrix used in the definition of the Gauss–Seidel algorithm; if matrix and vector norms applied are consistent, then its convergence is monotone in the sense $\Vert e^{(k+1)}\Vert \le \Vert M\Vert \Vert e^k\Vert$, and hence the condition $\Vert M\Vert < 1$ must meet, see [22, 26]. Its convergence is also guaranteed if the matrix A is strictly diagonal dominant, which implies that $\Vert M\Vert _{\infty } < 1$, see [22, p. 295] for details. But these qualitative statements of convergence do not say anything about the usefulness of the Gauss–Seidel method for finite element discretization. Actually, it has been proved that, when solving the Poisson equation on a rectangular domain, if the number of interior nodes grows, the rate of convergence becomes worse. The effort to gain an approximative solution, which means to reduce the error level below a given threshold $\epsilon$, is proportional to the number of iteration $\times$ operations for an iteration, as it was discussed in [26, p. 206]. Therefore, the classical Gauss–Seidel is of use for only moderately large matrices. Our proposal, which includes preconditioning, not only presents better approximation properties according to (30), but also low memory space requirements and number of operations per iteration. Our proposal also finds the solution in a finite number of steps and in particular preserves the A-orthogonality of the search directions after the restarting process, without sacrificing preconditioning. This is our contribution to ensure that the adapted PCG holds its convergence properties when solving the direct problem (7). It is important to remark that PCG has proved to be extremely effective in dealing with general objective functions and it is considered a powerful solution scheme for solving unconstrained optimization problems, especially for large-scale problems [17, 29].

7 Grid convergence study

In this section we conduct a convergence study for verification of calculation, as suggested in [34, 36]. Since the exact solution for the force exerted by the fluid pressure is unknown we perform three computations of forces, on a different grid each. We then calculate two Grid Convergence Indexes (GCIs) from fine grid to intermediate (GCI$_{12}$) and from intermediate to coarse grid (GCI$_{23}$). The GCI indicates how much the computed force will change with an additional refinement of the grid [35]. A small value is preferable, since it suggests the force is within the asymptotic range. The grid information for the convergence study is provided in Table 2. It includes, for each experiment, the corresponding force value for the direct problem, computed for $\alpha = 0.523599$ rad, $\rho = 58.75~\upmu$m, $\beta = 0.000017$ rad and $\varphi = 0.000017$ rad. Notice also that every grid has twice the number of elements as the previous grid on each direction. The geometrical and physical constants used are those in Table 1.

Table 2 Grid information for the convergence study

We determine the order of convergence $p_g$ according to the force values. As we use in the convergence study a constant refinement ratio $r=2$, we can perform a direct evaluation of $p_g$ by (32), see [34]:

$$\begin{aligned} p_g= & {} \ln \left( \frac{F_3 - F_2}{F_2 - F_1}\right) \Bigg / \ln {r},\nonumber \\ p_g= & {} \ln \left( \frac{7.390402\times 10^3~\mathrm{N} - 7.353513\times 10^3~\mathrm{N}}{7.353513\times 10^3~\mathrm{N} - 7.335851\times 10^3~\mathrm{N}}\right) \Bigg / \ln {2},\nonumber \\ p_g= & {} 1.0625. \end{aligned}$$

(32)

The GCI for the fine grid solution is then computed. It is defined as:

$$\begin{aligned} GCI_{jk} = \frac{f_s}{(r^{p_g} - 1)} \left| \frac{F_j - F_k}{F_j}\right| , \end{aligned}$$

where $f_s$ is a factor of safety, recommended to be $f_s=1.25$ for comparisons of three grids, see [35]. The GCI for grids 1 and 2 is:

$$\begin{aligned} GCI_{12}= & {} \frac{1.25}{(2^{1.0625} - 1)} \left| \frac{7.335851\times 10^3~\mathrm{N} - 7.353513\times 10^3~\mathrm{N}}{7.335851\times 10^3~\mathrm{N}}\right| ,\\ GCI_{12}= & {} 0.0028. \end{aligned}$$

Similarly, the GCI for grids 2 and 3 is:

$$\begin{aligned} GCI_{23}= & {} \frac{1.25}{(2^{1.0625} - 1)} \left| \frac{7.353513\times 10^3~\mathrm{N} - 7.390402\times 10^3~\mathrm{N}}{7.353513\times 10^3~\mathrm{N}}\right| ,\\ GCI_{23}= & {} 0.0058. \end{aligned}$$

We then check that these solutions are within the asymptotic range of convergence by (33):

$$\begin{aligned} GCI_{23}= & {} r^{p_g}GCI_{12},\nonumber \\ \frac{0.0058}{2^{1.0625}\,0.0028}= & {} 0.997598, \end{aligned}$$

(33)

which is approximately 1 and indicates that the test succeeded.

Based on this study we can also estimate the exact solution $F_e$ by the Richardson extrapolation, using (34), see [34]:

$$\begin{aligned} F_e&\approxeq&F_1 + \frac{F_1 - F_2}{r^{p_g} - 1},\nonumber \\ F_e&\approxeq&7.335851\times 10^3~\mathrm{N} + \frac{7.335851\times 10^3~\mathrm{N} - 7.353513\times 10^3~\mathrm{N}}{2^{1.0625} - 1},\nonumber \\ F_e&\approxeq&7.319626\times 10^3~\mathrm{N}. \end{aligned}$$

(34)

Finally, we could say that the force exerted by the fluid pressure, for the direct problem depicted, is estimated to be $7.319626\times 10^3$ N with an error band of $0.0028$.

7.1 Validation

To validate the whole numerical approach, we compare the predicted pressure values at the bearing mid-plane with published experimental measurements reported in [31]. For that, the work of Pierre et al. was used, where the same geometrical and physical constants of the journal bearing were considered. Two experiments, one showing the maximum pressure and the other one showing the pressure field both for different misalignment torques are presented. For both simulations the pressure values at the bearing mid-plane were collected at the equilibrium position, after solving the corresponding inverse problem for each different misalignment torque. As in [31], we performed the simulation for an angular velocity of 4000 rpm and a radial load of 9000 N. The misalignment torques, taken with respect to the bearing mid-plane, vary from 0 Nm (aligned case) to 70 Nm.

In Fig. 8a we show the maximum pressure computed by the algorithm in the bearing mid-plane and the experimental data, as shown in [31]. Comparison between the experimental and the numerical results shows small discrepancies for all the misalignment torques. In Fig. 8b we present the pressure field obtained in the bearing mid-plane for both the experiment and the numerical approach.

Fig. 8

Validation of the numerical results comparing the predicted pressure to experimental data

The differences can be related to the fact that not all the surrounding phenomena (as temperature) are considered in our numerical model. Nevertheless, both experiments show an acceptable agreement between the output of our model and the experimental data. Such differences do not influence the determination of the maximum pressure (discrepancy less than 0.0963 MPa), which is an essential factor when designing a journal bearing. Thus, it makes us think that the algorithm can be used as a first prediction of the final position of a journal bearing under an imposed radial loading, considering misalignment and the cavitation phenomenon. In addition, it could be verified that misalignment tends to decrease the maximum pressure at the bearing mid-plane, as stated in the literature, see [7].

8 Future work

In many lubricated devices, the high pressure values can deform the surfaces in contact (elastohydrodynamic regime), and a pressure gap relation needs to be introduced, see [4]. Other significant topics have also received attention, as non-Newtonian fluids, thermohydrodynamic lubrication and roughness, see [1, 1, 3, 24, 25, 38, 41] for instance. These various aspects are taken into account by plugging into the Reynolds equation these new relations. Nevertheless, the general characterization of the behaviour of misaligned journal bearings considering all mentioned factors and including the prediction of its final position is a very complex task. We plan to continue our work in the future, adding these realistic factors to the current problem. In particular, studying the influence of misalignment on the elastic behaviour of the surfaces is our first interest, to investigate whether the elastohydrodynamic characteristics can also easily deviate from their desired state due to this factor [9].

9 Conclusions

We considered a misaligned journal bearing device with an unknown inner cylinder position. The position of the inner cylinder presents four degrees of freedom, which are obtained by the Newton’s second law. We assumed that the lubricant filling the gap between the cylinders satisfies the Reynolds cavitation model. In this paper we presented a mathematical proof of the finite load capacity in misaligned journal bearings, which was also numerically verified by providing an algorithm to get the position of the inner cylinder at the equilibrium state. The adapted PCG used for solving the direct problem, preserves the A-orthogonality property of the search directions after a restarting process. The numerical simulations showed the existence of contact points for finite loading when misalignment occurs. The results also showed the continuous dependence of the maximum load capacity of the bearing on the shaft angular velocity, in such a way that it increases with the latter. In addition, the numerical experiments showed an acceptable agreement with experimental data.