1 Introduction

Solitons are those waves that maintain their structures by propagating at a particular speed. Solitons or solitary waves formed due to the cancellation of dispersive and nonlinear effects in the plasma. For the first time, the Korteweg de-Vries (KdV) soliton has been studied to describe the ion-acoustic solitons in an inhomogeneous plasma [1]. The propagation of ion-acoustic solitary waves has also been studied in an inhomogeneous plasma system [2]. Theoretically, Kuehl [3] studied the ion-acoustic soliton reflection in the inhomogeneous plasma. He observed variations in the amplitudes of the incident and reflected solitons in the plasma. Later, considering fluid equations of plasma, Kuehl and Imen [4] investigated the propagations of ion-acoustic soliton in inhomogeneous plasmas. Nejoh [5] studied the impact of ion temperature on the nature of solitary waves propagating in a collisionless relativistic plasma. Singh and Dahiya [6] employed the Reductive Perturbation Technique (RPT) to obtain the KdV equation in inhomogeneous plasmas. Many plasma physics researchers have worked on soliton or solitary waves and their properties in different physical conditions in plasma. Several attempts were made to study soliton in inhomogeneous plasma under the effect of dust grains [7], negative ions [8,9,10,11], and finite ion temperature [12, 13] in the plasma. Rao and Shukla [14] have investigated the propagation of dust-acoustic solitons in the presence of fluctuating dust grains in an inhomogeneous plasma. Mukherjee et al. [15] investigated the bending of solitons in inhomogeneous unmagnetized plasmas. Dehingia and Deka [16] have studied the structural variations in solitary waves in various situations in an inhomogeneous plasma. Rani and Yadav [17] have discussed the propagation of nonlinear electro-acoustic waves consisting of degenerate quantum electrons in magnetized plasma. Chen et al. studied the nonlinear soliton dynamics in quantum plasmas under the effect of higher order dispersion [18]. Prayitno and Budi [19] have numerically discussed the soliton energy of ion-acoustic solitons in the KdV equation of inhomogeneous plasma. Lu and Liu [20] studied the small amplitude solitary waves in the presence of ions and κ-distributed electrons in the plasma.

Dusty plasma is one of the fundamental research topics in plasma physics. Dusty plasma supports a wide variety of interesting phenomena. In this system, plasma particles and dust grains together take part in the plasma system. Due to the addition of these dust grains in the plasma system, the plasma system becomes more complex in its behaviours. Therefore, they are termed complex systems. Goertz [21] and Northrop [22] theoretically studied dusty plasmas for the inhomogeneous plasma system. Shukla and Silin [23] studied the Dust Ion-Acoustic Solitary Waves (DIAWs) for the isothermal plasma. They found that some novel low-frequency waves exist in the presence of charged dust particles in the plasma. They have also declared that there would have been some relation between those low-frequency waves and Saturn's F-ring. Many authors have studied Dust Acoustic Waves (DAWs) [24] and Dust Lattice Waves (DLW) [25] in different physical situations in the plasma. To understand the characteristics and properties of DLWs, DAWs, and DIAWs, researchers have tried several theoretical [21,22,23] and experimental studies [26, 27]. Later, many studies have done on Dust-Acoustic Solitary Waves (DASWs) in inhomogeneous plasma under many physical situations. Dusty plasma has various connections with phenomena in astrophysical environments, space plasmas, fusion reactors, and as well as in laboratory experiments [28, 29]. Gogoi and Deka [30] have investigated soliton propagation under the effect of dust charge and dust fluctuations in an inhomogeneous plasma. Theoretically, the DAWs have been studied in the presence of ions fluid, K-distributed superthermal electrons [31], and negatively charged grains in the plasma. Akhtar et al. [32] studied the dust-cyclotron wave and modulational instability of DAWs with ions, electrons, and dust grains in magnetized plasma. Rehman et al. [33] investigated the linear and nonlinear magneto-acoustic wave propagation with pair-ion fullerene in an inhomogeneous plasma. Mushinzimana et al. [34] studied the propagation of DIASWs and double layers under the effect of ions, Cairns-distributed electrons, and adiabatic positively charged dust grains in an inhomogeneous plasma. Dehingia and Deka [35] have recently studied the impact of dust grains on DASWs propagating in an inhomogeneous dusty plasma under the effect of the magnetic field. Dehingia and  Deka [36] have studied the variations in the structures of DASWs propagating in an inhomogeneous unmagnetized plasma under the influence of isothermal electrons. Thus, realizing the significance of studying DASWs in various astrophysical conditions, we have chosen our problem to investigate the propagation of nonlinear DASWs under the effect of non-extensive electrons in inhomogeneous collisional magnetized dusty plasma. In this problem, we have used RPT to derive the modified Zakharov-Kuznetsov (m-ZK) equation. The solution of the m-ZK equation indicates the propagation of nonlinear DASWs in the plasma. In this study, we also discuss the variations of DA soliton amplitude and width depending on the variations of the inhomogeneity parameter and non-extensive electrons in the plasma. Results of this investigations concerning relations among the width, phase velocity, and amplitude of the DASWs are demonstrated in the earth’s magnetospheric plasma environment in the model.

2 Governing equations

We consider a three-dimensional, collisional, inhomogeneous warm dusty plasma with variation in number density for its components. The plasma model consists of Boltzmannean ions, non-extensive electrons, and massive dust grains with an external magnetic field in the plasma. All the components of plasma and magnetic field \({B}_{0}={B}_{0}\widehat{x}\) are taken along \(x-\) direction. The dimensionless governing equations of continuity equation, momentum equation, Poisson’s equation, Boltzmannean distribution of ions, nonextensive electron distribution, respectively, are given by

$$\frac{\partial n_d }{{\partial t}} + \vec{\nabla }.\left( {n_d \vec{u}_d } \right) = 0,$$
(1)
$$\frac{{\partial \vec{u}_d }}{\partial t} + \left( {\vec{u}_d .\vec{\nabla }} \right)\vec{u}_d + \frac{5}{3}\sigma n_d^{ - \frac{1}{3}} \vec{\nabla } \phi + \Omega \left( {\vec{u}_d \times \hat{x}} \right) + \Gamma \vec{u}_d = 0,$$
(2)
$$\vec{\nabla }^2 \phi = n_d + \frac{{\left( {n_e - \delta n_i } \right)}}{{\left( {\delta - 1} \right)}},$$
(3)
$$n_i = n_{i0} \left( x \right)e^{ - s\phi } ,$$
(4)
$$n_e = n_{e0} \left( x \right)[1 + (q - 1)\phi ]^{\frac{{\left( {q + 1} \right)}}{{2\left( {q - 1} \right)}}} .$$
(5)

Here, for equilibrium condition, the charge neutrality equation is given by \(\delta {n}_{i0}\left(x\right)={n}_{e0}\left(x\right)+\left(\delta -1\right){n}_{d0}\left(x\right)\) where \(\delta =\frac{{ n}_{i0}\left(x\right)}{{n}_{e0}\left(x\right)}\). Also, we consider \({n}_{e0}\left(x\right)\) and \({n}_{i0}\left(x\right)\) are as unperturbed electron and ion number densities in the plasma. In our above equations, \(\Gamma\) is the collision frequency for neutral dust grains, \(\Omega\) is the dust cyclotron frequency, \(\phi\) is the electrostatic potential, \({n}_{d}\) is the number density of dust grains, and \({\overrightarrow{u}}_{d}\) is the dust fluid velocity in the plasma. We have also considered the normalized dimensionless parameters are \(\Omega =\frac{e{B}_{0}{Z}_{d}}{{m}_{d}c},\) \(\sigma =\frac{{T}_{d}}{{{Z}_{d}T}_{e}},\) and \(s=\frac{{T}_{e}}{{T}_{i}}\) where \(c\) is velocity of light, \({m}_{d}\) is the mass of dust grains, \({Z}_{d}\) is dust charge numbers, \({T}_{d}\) is dust temperature, \({T}_{i}\) is ion temperature, and \({T}_{e}\) is electron temperatures in the plasma. Here, \({\alpha }_{e}\) and \({\alpha }_{i}\) are defined as the density gradient scale length for the electrons and ions, respectively, which can take either positive or negative values for growing number densities. In our problem, we have used some physical parameters \(k,\Omega ,\Gamma ,\) and \(q\) to investigate the characteristics of DASWs depending on the typical nonthermal values [37, 40] of the dusty plasma in the system. In the governing Eqs. (1, 2, 3, 4, 5) we have considered the physical quantities are as follows:

$$\nabla \lambda_{Dd} = \nabla \left( {\sqrt {\frac{T_e }{{4\pi e^2 Z_d }}} } \right),\Gamma = \left( {\frac{1}{{\omega_{pd} }}} \right)\lambda_{Dd} ,$$

where \({\upomega }_{\mathrm{pd}}\) and \({\uplambda }_{\mathrm{Dd}}\) are the plasma frequency for dust grains and modified Debye length, respectively. In this problem, for \(q\to 1\), the electrons are distributed in Boltzmannean distribution, on the other hand for the real number \(q>-1,\) the electrons are considered to be in the form of unnormalized non-extensive electron distribution [39].

3 Derivation of m-ZK equation

To study the nonlinear propagation and characteristics of DAWs in inhomogeneous Magnetized Dusty Plasma (MDP) system, we use the RPT to derive the m-ZK equation. In order to use RPT [16, 36, 37], we employ the standard stretched coordinates are as follows [37]:

$$\xi = \varepsilon^\frac{1}{2} \left( {\mathop \smallint \limits_0^x \frac{\partial x^/ }{{\lambda \left( {x^/ } \right)}} - t} \right),X = \varepsilon^\frac{3}{2} x,Y = \varepsilon^\frac{1}{2} y,Z = \varepsilon^\frac{1}{2} z,{\Gamma } = \varepsilon^\frac{3}{2} f_1$$
(6)

Here, \(M\) is the phase velocity of DASWs and \(\varepsilon\) is a smallness parameter which measures the size of the perturbation amplitude. To use RPT, we use some dependent variables are as follows:

$$\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {n_i } \\ {n_e } \\ {n_d } \\ {u_{dx} } \\ \end{array} } \\ {u_{dy} } \\ {u_{dz} } \\ \phi \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {n_{i0} \left( X \right)} \\ {n_{e0} \left( X \right)} \\ {n_{d0} \left( X \right)} \\ {u_{dx0} \left( X \right)} \\ 0 \\ 0 \\ {\phi_0 (X)} \\ \end{array} } \right] + \varepsilon \left[ {\begin{array}{*{20}c} {n_{i1} } \\ {n_{e1} } \\ {n_{d1} } \\ {u_{dx1} } \\ 0 \\ 0 \\ {\phi_1 } \\ \end{array} } \right] + \varepsilon^\frac{3}{2} \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ {u_{dy1} } \\ {u_{dz1} } \\ 0 \\ \end{array} } \right] + \varepsilon^2 \left[ {\begin{array}{*{20}c} {n_{i2} } \\ {n_{e2} } \\ {n_{d2} } \\ {u_{dx2} } \\ {u_{dy2} } \\ {u_{dz2} } \\ {\phi_2 } \\ \end{array} } \right] + \cdots$$
(7)

Using RPT, we obtain the spatial gradient relations from the above Eqs. 1, 2, 3, 4, 5, 6, 7 is as follows:

$$\frac{\partial }{\partial \xi }\left( {n_{i,e,d0} } \right) = \frac{\partial \lambda }{{\partial \xi }} = \frac{\partial }{\partial \xi }\left( {u_{dx0} } \right) = \frac{\partial }{\partial \xi }\left( {\phi_0 (X)} \right) = 0.$$
(8)

At an equilibrium condition, we obtain

$$\left. {\begin{array}{*{20}c} {\frac{\partial }{\partial X}\left( {n_{d0} u_{dx0} } \right) = 0} \\ {5\sigma \frac{\partial }{\partial X}\left( {n^\frac{2}{3}_{d0} } \right) + \frac{\partial }{\partial X}\left( {u^2_{dx0} } \right) - 2\frac{\partial \phi_0 }{{\partial X}} + 2u_{dx0} f_1 = 0 } \\ \end{array} } \right\}.$$
(9)

Substituting the Eqs. (6) and (7) in the governing Eqs. 1, 2, 3, 4, 5, and comparing the coefficients of \(\varepsilon\) for the smallest order, we have

$$\left. {n_{d1} = - n_{d0} R\phi_1 , \;u_{dx1} = - \lambda^/ R\phi_1 ,\;u_{dz1} = \frac{{\lambda^{/2} R\partial \phi_1 }}{\Omega \partial Z},\; u_{dz1} = \frac{{\lambda^{/2} R\partial \phi_1 }}{\Omega \partial Z}} \right\}$$
(10)

where \(R=\frac{1}{\left({{\lambda }^{/}}^{2}-\alpha {n}_{d0}\right)}\), \(\alpha =\frac{1}{\sqrt[3]{{n}_{d0}}}\frac{5}{3}\sigma\) and \({\lambda }^{/}=\lambda -{u}_{dx0}\). The value of phase velocity \(\lambda\) is found to have in the form as

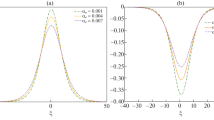
$$\lambda = u_{dx0} + \left( {\alpha n_{d0} + \frac{{n_{d0} \left( {\delta - 1} \right)}}{{\left( {\frac{1 + q}{2}} \right)n_{e0} \left[ {1 - \left( {\frac{q - 3}{2}} \right)\phi_0 } \right] + s\delta n_{i0} \left( {1 - s\phi_0 } \right)}}} \right)^\frac{1}{2} .$$
(11)

Eq. (11) represents the phase velocity \(\left(\lambda \right)\) of the DAWs in the inhomogeneous plasma system.

Similarly, comparing the coefficients of \(\varepsilon\) for the higher order perturbations, we have

$$\begin{aligned} - \lambda \frac{{\partial n_{d0} }}{\partial \xi } & + n_{d0} \frac{{\partial n_{dx2} }}{\partial \xi } + \frac{\partial }{\partial \xi }\left( {n_{d1} u_{dx1} } \right) + \lambda \left[ {\frac{\partial }{\partial X}\left( {n_{d0} u_{dx1} + n_{d1} u_{dx0} } \right)} \right] \\ + \lambda \left[ {\frac{\partial }{\partial Y}\left( {n_{d0} u_{dy2} } \right) + \frac{\partial }{\partial Z}\left( {n_{d0} u_{dz2} } \right)} \right] = 0 \\ \end{aligned}$$
(12)
$$\begin{aligned} - \lambda \frac{{\partial u_{dx2} }}{\partial \xi } & - u_{dx1} \frac{{\partial u_{dx1} }}{\partial \xi } + \lambda \frac{\partial }{\partial X}\left( {u_{dx0} u_{dx1} } \right) + \alpha \frac{{\partial n_{d2} }}{\partial \xi } + \alpha \lambda \frac{{\partial n_{d1} }}{\partial X} \\ - 1/3\alpha \lambda (n_{d0} )^{ - 1} n_{d1} \frac{{\partial n_{d0} }}{\partial X} - \frac{1}{3}\lambda \alpha \left( {n_{d0} } \right)^{ - 1} n_{d1} \frac{{\partial n_{d1} }}{\partial \xi } - \lambda \frac{\partial \phi_1 }{{\partial X}} - \lambda f_1 u_{dx1} = 0, \\ \end{aligned}$$
(13)
$$\frac{1}{\lambda^2 }\frac{\partial^2 \phi_1 }{{\partial \xi^2 }} + \frac{\partial^2 \phi_1 }{{\partial Y^2 }} + \frac{\partial^2 \phi_1 }{{\partial Z^2 }} - n_{d2} - \frac{1}{{\left( {\delta - 1} \right)}}\left( {n_{e2} - \delta n_{i2} } \right) = 0,$$
(14)

Where

$$u_{dy2} = - \frac{{\lambda^{/3} R}}{\Omega^2 \lambda }\left( {\frac{\partial^2 \phi_1 }{{\partial \xi \partial Z}}} \right),u_{dz2} = - \frac{{\lambda^{/3} R}}{\Omega^2 \lambda }\left( {\frac{\partial^2 \phi_1 }{{\partial \xi \partial Y}}} \right).$$
(15)

Equation (13) shows the dependency of the phase velocity of soliton w.r.t. the variation in \({\phi }_{0}\) and \(x/L\) where \(L\) refers as the density scale length taken to be an arbitrary value of 200. We have shown the graph for these variation in Figs. 1, 2 and 3, respectively. It also shows the decrease in the values of \(\lambda\) with the increasing values of \(q\) or \(x/L\) On the other hand, the phase velocity \(\lambda\) increases rapidly with the increase in the values of\({\phi }_{0}\). However, the decrease in the values of \({\phi }_{0}\) (negative values) and decreases the phase velocity of the DASW. Proceeding in this way, we observe an identical situation in the case of non-thermal ions present in the inhomogeneous dusty plasma system.

Fig. 1
figure 1

Plotting of \(\lambda\) vs \(x/L\) for \(\sigma ={10}^{-2},s=3,{\alpha }_{i}=0.9, {\alpha }_{e}=0.5,{u}_{dx0}=0.02\)

Full size image
Fig. 2
figure 2

Plotting of \(\lambda\) vs \(x/L\) for \(\delta =2,s=2,x/L=2,\) \({\alpha }_{e}=0.5,\) \({\alpha }_{i}=0.9,\sigma ={10}^{-2},{u}_{dx0}=0.02\)

Full size image
Fig. 3
figure 3

Plotting of \(A\) vs \(x/L\) for \(\sigma ={10}^{-2},s=3,{\alpha }_{i}=0.9, {\alpha }_{e}=0.5,{u}_{dx0}=0.02,\delta =2,\Gamma =0.001,{\phi }_{0}=0.2,\Omega =0.05\)

Full size image

Using the Eqs. in Eqs. (10), (11) and (15) in Eqs. (12), (13), (14) we eliminate second-order perturbed quantities and obtain the modified ZK (m-ZK) equation is in the form as follows:

$$\frac{\partial \phi_1 }{{\partial X}} + A\phi_1 \frac{\partial \phi_1 }{{\partial \xi }} + B\phi_1 \left( {\frac{\partial^2 \phi_1 }{{\partial Y^2 }} + \frac{\partial^2 \phi_1 }{{\partial Z^2 }}} \right) + C\frac{\partial^3 \phi_1 }{{\partial \xi^3 }} + D\phi_1 = 0,$$
(16)

where,

$$A = E\left[ {\frac{{\left\{ {3R^2 n_{d0} \left( {\lambda^{/2} - \frac{1}{9}\alpha n_{d0} } \right)} \right\}}}{{ - \frac{1}{{R\left( {\delta - 1} \right)}}\left\{ {\frac{1}{4}n_{e0} \left( {q - 3} \right)\left( {q - 1} \right) + \delta s^2 n_{i0} } \right\}}}} \right],B = - E\left( {\frac{{\lambda^{/4} Rn_{d0} }}{\partial X} + \frac{1}{R}} \right),C = - \frac{E}{\lambda^2 R},$$
$$\begin{gathered} D = - E\lambda \left[ {\lambda^/ \frac{\partial }{\partial X}\left( {\lambda Rn_{d0} } \right) + \lambda^/ \frac{\partial }{\partial X}\left( {Rn_{d0} u_{dx0} } \right) + n_{d0} \frac{\partial }{\partial X}\left( {\lambda^/ u_{dx0} R} \right) + \alpha n_{d0} \frac{\partial }{\partial X}\left( {Rn_{d0} } \right) - \frac{1}{3}\alpha n_{d0} R\frac{{\partial n_{d0} }}{\partial X} + \lambda^/ n_{d0} Rf_1 } \right], \hfill \\ E = \frac{1}{{2\lambda^2 \lambda^/ Rn_{d0} }}. \hfill \\ \end{gathered}$$

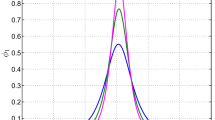
The above Eq. (16) is known as the modified ZK (m-ZK) Eq. [37]. Equation 16 indicates the propagation of nonlinear DASWs in the presence of non-extensive electron and inhomogeneity number density in an inhomogeneous dusty plasma. In the above m-ZK equation, \(A\) and \(C\) are the nonlinear and dispersive terms. However, the coefficient \(E\) occurs due to the inhomogeneity number density and the collision effect in the inhomogeneous dusty plasma system. In Fig. 4, we have seen that there is a variation in A, which is a function of \(x/L\). Figure 4 also describes the dressed solitons for \(A< 0 \left(0 < x/L <1.2\right)\) and \(A>0\).

Fig. 4
figure 4

Plotting of \(G(X)\) vs \(x/L\) for \(\delta =2,s=4,{\alpha }_{e}=0.5,\) . \({\alpha }_{i}=0.9,\sigma ={10}^{-2},{u}_{dx0}=0,\Gamma =0.1,\Omega =0.05,\) \({\phi }_{0}=-1\)

Full size image

4 Solution of m-ZK equation and result discussion

To obtain the soliton solution of the derived m-ZK equation, we employ a standard transformation equation is as follows [38]:

$${\phi }_{1}=H\left(X,Y,Z,\xi \right)G\left(X\right),$$
(17)

where the amplitude factor \(G(X)\) is obtained as follows:

$$G\left( X \right) = \frac{1}{{\left( {R\lambda \sqrt {\lambda^- n_{d0} } } \right)}}e^{ - \mathop \smallint \limits_0^x \frac{f_1 }{{2\lambda }}dx^- }$$
(18)

Substituting Eq. (17) in (16), we obtain

$$\frac{\partial H}{{\partial \tau }} + A^/ H\frac{\partial H}{{\partial \eta_1 }} + \frac{\partial }{\partial \eta_1 }\left( {\frac{\partial^2 H}{{\partial \eta_2^2 }} + \frac{\partial^2 H}{{\partial \eta_3^2 }}} \right) + \frac{\partial^3 H}{{\partial \eta_1^3 }} = 0,$$
(19)

where \({A}^{/},\) \(\tau\), \({\eta }_{1}\), \({\eta }_{2},\) and \({\eta }_{3}\) have their usual meaning which are defined as,

$$\tau = \smallint^X \sqrt {\frac{{A^{/3} }}{C}} dX^/ , A^/ = A\left( X \right)G\left( X \right),$$
$$\eta_1 = \sqrt {\frac{A^/ }{C}} \xi ,\eta_2 = \sqrt {\frac{A^/ }{B}} Y,{\text{and}}\;\eta_3 = \sqrt {\frac{A^/ }{B}} Z$$

Now, we define a new variable \(\eta ={L}_{x}{\eta }_{1}+{L}_{y}{\eta }_{2}+{L}_{z}{\eta }_{3}-V\tau\) where \(V\) is the constant velocity. Here, \({L}_{x},{L}_{y},{L}_{z}\)are the direction cosines of the wave vectors along the \(\xi -\) axes, \(Y-\) axes, and \(Z-\) axes, respectively. Using the boundary conditions; for \(\left|\eta \right|\to \infty ,\) we put \(H\left(\eta \right)\to 0, \frac{\partial H}{\partial {\eta }_{1}}\to 0, \frac{{\partial }^{2}H}{\partial {\eta }_{2}^{2}}\to 0\). Then, we obtain,

$$H\left(\eta \right)={H}_{m}^{/}{sech}^{2}\left(\frac{\eta }{W}\right)$$
(20)

Here, \({H}_{m}^{/}=\frac{6V}{{L}_{x}}\) is amplitude and \(W=2\sqrt{\frac{{L}_{x}}{V}}\) is width of the DASWs in the plasma. Now, when we choose, \(\phi ={\phi }_{1}\), and after performing some calculations, we obtain,

$$\phi ={A}_{m}{sech}^{2}\left(\frac{\zeta }{\omega }\right),$$
(21)

where \({A}_{m}\) and \(\Delta\) are the soliton amplitude and width of the DASWs in the plasma and are given by\({A}_{m}=\left(\frac{6V}{{L}_{x}}\right){\phi }_{0}{\phi }^{/}\) and \(\Delta =2\sqrt{\frac{C}{V{L}_{x}A{\phi }_{0{\phi }^{/}}}} .\)Here, at \(x=0,\) the amplitude factor of electrostatic potential is \({\phi }_{0}\) and we consider \({\phi }^{/}=\frac{{\phi }^{/}(x)}{{\phi }_{0}}\). Also, the Mach number \(M\) for DASW is obtained as follows:

$$M = \sqrt {\left( {\frac{L_x \lambda }{{L_x + V\lambda A\phi \phi^/ }}} \right)^2 + \frac{B}{C}\left\{ {\frac{{L_x^2 \left( {1 - L_x^2 } \right)}}{L_y^2 + L_z^2 }} \right\}} .$$
(22)

In the above investigations, Fig. 4 indicates the variations in \(G(X)\) versus \(x/L\) shown in Eq. \((20).\) We have observed that \(G\left(X\right)\) attains its maximum value at the critical point \({\left(x/L\right)}_{c}\approx 2.4\). As the value of the non-extensive parameter \((q)\) increases, decreases the value of critical point\({\left(x/L\right)}_{c}\). Due to the dominance of the inhomogeneity parameter on the collision of the plasma particles, increases the value of \(G(X)\) w.r.t.\(x/L\). Also, with the increasing value of\({x/L=\left(x/L\right)}_{c}\), a rapid decrease in the value of \(G(X)\) is seen accordingly. Similarly, when \({\left({x}\!\left/ L\right.\right)}_{c}<x\!\left/ L\right.,\) the value of \(G(X)\) decreases due to the contraction of plasma inhomogeneities relative to the collisional effect in the plasma. Consequently, for the higher values of \(x/L\), \(G(X)\) obtains relatively smaller values in the above considered plasma system.

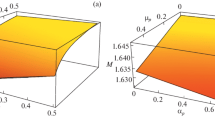
On the contrary, Fig. 5, indicates the variations in the characteristics of DA solitons with \(x/L\) and\(q\). In Fig. 6, we have seen that there is a decrease in Mach number\(M\), with the increase in \(\Omega\) or \(x/L\). Consequently, the variations of three-dimensional electrostatics potential \(\phi\) and \(x/L\) are shown in Figs. 7 and 8. From all the above observations, we have seen the width and amplitude of DASWs increase with increase in the value of \(x/L\). On the other hand, with the increase in the non-extensive effect \((q)\) slightly decrease the soliton amplitude but gets wider the width of the soliton in the plasma. Figures 7 and 8 also imply the movement of soliton towards \(\xi -\) direction with the increasing value of \(x/L\) in the above considered dusty plasma model.

Fig. 5
figure 5

Plotting of \(\Delta\) vs \(x/L\) for \(s=4,\sigma ={10}^{-3},{\alpha }_{i}=0.6, {\alpha }_{e}=0.5,{u}_{dx0}=0.2,\Gamma =0.001,{\delta =0,\Omega =0.5,\phi }_{0}=0.2\)

Full size image
Fig. 6
figure 6

Plotting of \(M\) vs \(x/L\) for \(\sigma =0,s=3,{\alpha }_{i}=0.9,\). \({\alpha }_{e}=0.5,{u}_{dx0}=0, {\phi }_{0}=-1,\Gamma =0.01,q=1,\delta =4\)

Full size image
Fig. 7
figure 7

Plotting of \(\phi\) vs \(x/L\) and \(\xi\) for \(\sigma =0,{\alpha }_{i}=0.9,q=2, {\alpha }_{e}=0.5,s=3,{u}_{dx0}=0, {\phi }_{0}=-1,\Gamma =0.01,q=1,\delta =4\)

Full size image
Fig. 8
figure 8

Plotting of \(\phi\) vs \(\xi\) and \(q\) for \(\sigma =0,{\alpha }_{i}=0.9,\). \(x/L=2,{\alpha }_{e}=0.5,s=3,{u}_{dx0}=0, {\phi }_{0}=-1,\Gamma =0.01,\) \(q=1,\delta =4\)

Full size image

5 Conclusion

In this paper, we have presented a study on the nonlinear characteristics of the DASWs propagating in an inhomogeneous collisional magnetized plasma. The plasma system consists of non-extensive electrons, positively and Boltzmannean distributed ions, and charged dust grains. Due to the effect of non-extensive electrons, collisional and magnetic field in the plasma, the variations of the soliton amplitude and widths are observed during the investigations of the plasma. All these things are studied in details in our present study. We have observed that the phase velocity of all the DASWs decreases with the increase in the gradient parameter connecting inhomogeneous factors \(x/L\) and non-extensive electrons \((q)\). However, using the RPT, we have derived a modified ZK (m-ZK) equation with variable coefficients. During this investigation, we have observed a critical point for the nonlinear propagation of dressed (rarefactive/compressive) solitons in the plasma. After using a transformation equation, we obtained two type of soliton solution. One of them is amplitude factor, and the other is of \({sech}^{2}\) type soliton solution which is of bell shaped. The above results and discussions also indicate that with the increase in the \(x/L\) or \(q\), increases the width of DASW in the plasma. It is also observed that the variation of soliton amplitude remains same under the influence of magnetic field in the given considered plasma. But the magnetic field influences the speed of solitons or the phase velocity \(M\). Our study may be helpful in understanding the various nonlinear wave phenomena of dusty plasma under the effect of non-extensive electrons and other physical situations for both theoretical and experimental studies.