Cost optimization analysis for an $M^{X}/M/c$ vacation queueing system with waiting servers and impatient customers

Abstract

This paper deals with the study of an $M^{X}/M/c$ Bernoulli feedback queueing system with waiting servers and two different policies of synchronous vacations (single and multiple vacation policies). During vacation period, the customers may leave the system (reneging), and using certain customer retention mechanism, the reneged customers may be retained in the system. The probability generating function (PGF) has been used to obtain the steady state probabilities of the model. Various performances measures of the system are derived. Then, a cost model is developed. Further, a cost optimization problem is considered using quadratic fit search method. Finally, a variety of numerical illustrations are discussed for the applicability of the model.

1 Introduction

Performance of modeling vacation queueing systems has attracted many researchers owing to their large applications in many real life congestion problems including computer and communication systems, manufacturing and production systems along with other queueing systems having industrial importance. A detailed surveys of the literature devoted to such systems are found in Doshi [9], Takagi [20], Tian and Zhang [21] and references therein.

Modeling vacation queueing models with impatient customers is very important in order to obtain novel managerial insights. The lost revenues due to impatience in several industries may be enormous. Literature analysis has shown an extensive studies of these models. Altman and Yechiali [1] dealt with customers’ impatience in queues with server vacation. Zhang et al. [27] gave the analysis of an M / M / 1 / N queueing model with balking, reneging and server vacations. Later, Ammar [3] carried out the transient analysis of an M / M / 1 queue with impatient behavior and multiple vacations. Panda and Goswami [16] studied the equilibrium balking strategies for a GI / M / 1 queue with Bernoulli-schedule vacation and vacation interruption. Recently, in Ammar [4], the transient solution of an M / M / 1 vacation queue with a waiting server and impatient customers has been established. For more literature on customer’s impatience in vacation queues, the authors can be referred to Yue et al. [25], Padmavathy et al. [15], Misra and Goswami [13], Yue et al. [24], Sun et al. [19], Bouchentouf and Yahiaoui [7], and references therein.

Queueing systems with batch arrival represent the case where arrivals enter the system in batches rather than one by one. Few examples of arrivals in batches to a system are customers in elevators, supermarkets, banks, etc. Considerable works on vacation models with batch arrivals were conducted by many researchers. Lee et al. [12] analyzed the fixed bulk service queueing system with single and multiple vacations. Later, Jau-Chuan Ke [10] dealt with a $M^{X}/G/1$ queueing model with balking and variant vacation policy, Wang et al. [22] presented the maximum entropy analysis of the $M^{X}/M/1$ queueing system with multiple vacations and server breakdowns. Then, Baruah et al. [5] treated the balking and the re-service in a vacation queueing model with batch arrival and two types of heterogeneous service. Baruah et al. [6] dealt with a batch arrival queue with second optional service and reneging during vacation periods. Recently, Sasikala et al. [18] presented the steady state behaviour of $M^{X}/G^{K}/1$ queueing model with control policy on request for re-service, N-policy, balking and multiple vacations.

The study of multi-server vacation systems with impatient customers is far more complex compared to impatience in single server vacation models, consequently, a limited literature is available. The M / M / c / N queuing system with balking, reneging and synchronous vacations of some partial servers together was presented by Yue et al. [23]. Altman and Yechiali [2] treated the infinite-server queues with system’s additional tasks and impatient customers. Then, a computational algorithm and parameter optimization for a multi-server queue with unreliable server and impatient customers have been discussed by Chia and Jau-Chaun [8]. Later, Yue et al. [26] dealt with an M / M / c queueing system with impatient customers and synchronous vacation, where impatience is due to the servers’ vacation. Recently, the analysis of a M / M / c queueing model with single and multiple synchronous working vacations was presented in Majid and Manoharan [14].

This paper deals with an infinite buffer multi-server vacation queueing system with batch arrival, Bernoulli feedback and waiting servers wherein customers may renege during vacation period, and they can be retained in the system, via certain strategy (convinced to stay in order to be serviced). The steady-state probabilities of the queueing system are obtained through probability generating functions (PGFs). Useful performance measures of the queueing system are derived. The cost profit analysis of the model is carried out. The optimization of the model is performed using quadratic fit search method (QFSM) in order to minimize the total expected cost of the system with respect to the service rate. A numerical study is presented to illustrate the impact of various system parameters on different performance measures and total expected profit of the system. The analysis carried out in this paper is very important and useful to any insurance firm. Among the advantages of the obtained results is to show the positive impact of waiting server and customer retention strategy.

The rest of paper is arranged as follows. Section 2 provides a general description of the model with multiple and single vacation policies. In Sect. 3, we develop the queueing model under multiple vacation policy (MVP) and carry out the steady-state analysis of the system, then we derive the explicit expressions of the various performance measures of the queueing system. The model under single vacation policy (SVP) is analyzed in Sect. 4 following the same methodology presented in the previous section. In Sect. 5, we develop a model for the costs incurred and perform the appropriate optimization using a quadratic fit search method (QFSM). Section 6 presents numerical examples in order to demonstrate the applicability of the theoretical investigation, and finally we conclude the paper in Sect. 7.

2 Model description

We consider an $M^{X}/M/c$ Bernoulli feedback queueing system under single and multiple vacations wherein customers may leave the system due to impatience during the absence of the servers. Using certain retention customer mechanism, the reneged customers may be retained in the system. The model considered in this work is based on following assumptions:

(i) Customers arrive in batches according to a Poisson process with rate $\lambda .$ The sizes of successive arriving batches are i.i.d. random variables $X_{1},$$X_{2},\ldots$distributed with probability mass function $P(X=l)=b_{l};\,\ l=1,2,3,\ldots$.

(ii) The customers are served on a First-Come First-Served (FCFS) queue discipline. The service times are assumed to follow exponential distribution with mean $1/\mu .$

(iii) When the busy period is finished the servers wait a random duration of time before beginning on a vacation. This waiting duration is exponentially distributed with mean $1/\eta .$

(iv) The queueing model consists of c servers. In synchronous vacation policy, all the servers leave for a vacation simultaneously, once the system becomes empty and they also comeback to the system as one at the same time.

In multiple vacation policy (MVP), the servers continue to take vacations until they find the system nonempty at a vacation completion instant. While, in single vacation policy (SVP), when the vacation ends and servers find the system empty, they remains idle until the first arrival occurs. Vacation periods are assumed to be exponentially distributed with mean $1/\phi .$

(v) Customers in batches are supposed to enter the queueing system, join the queue, if the servers are unavailable due to vacation, a batch of customers activates an independent impatience timer T,  with exponentially distributed duration, with mean $1/\xi .$ If T expires while the servers are still on vacation, the customers may abandon the system. Further, using certain mechanism, each impatient customer may abandon the system, with probability $\alpha ,$ and can be retained in the queue, with complementary probability $(1-\alpha ).$ Moreover, If the service is uncomplete or unsatisfactory, the customers can either leave the system definitively, with probability $\beta ,$ or rejoin the end of the queue of the system for another service, with complementary probability $(1-\beta ).$ Note that $\varrho =\frac{\lambda E(X)}{c\beta \mu }<1$ is the stability condition of the system, where E(X) is the mean of a batch of arrivals.

(vi) We assume that the inter-arrival times, batch sizes, server waiting times, vacation times, service times and impatience times are independent of each other.

Let $\{L(t); t \ge 0\}$ be the number of customers in the system at time t,  and S(t) be the state of servers at time t,  where S(t) is defined as follows:

$$\begin{aligned} S(t) = \left\{ \begin{array}{ll} 1, &{} \hbox {when the servers are in busy period at time }t; \\ 0, &{} \hbox {when the servers are in vacation period at time }t. \end{array}\right. \end{aligned}$$

Then, $\{(S(t),L(t)); t \ge 0\}$ defines a two-dimensional continuous Markov process with state space

$$\begin{aligned} \Omega = \{(s,n): s= 0,1,\,\ n = 0,1,\ldots \}. \end{aligned}$$

Let

$$\begin{aligned} P_{s,n} = \lim _{n\rightarrow \infty } P\{ S(t) = s, L(t) = n\}, \quad s = 0,1, n = 0,1,\ldots , \end{aligned}$$

denote the system steady-state probabilities.

3 Analysis of the model under MVP

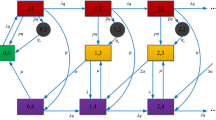
In this section, we study the model considered in Sect. 2 under multiple vacation policy, the state-transition-rate diagram is presented in Fig. 1.

Fig. 1

State-transition-rate diagram of the model under MVP

3.1 Steady state solution of the model

Using the Markov theory, the set of steady-state equations are written as follows

$$\begin{aligned} \lambda P_{0,0}= & {} \alpha \xi P_{0,1}+ \eta P_{1,0}, \end{aligned}$$

(1)

$$\begin{aligned} (\lambda +\phi +\alpha \xi )P_{0,1}= & {} \lambda b_{1}P_{0,0}+2\alpha \xi P_{0,2},\quad n=1, \end{aligned}$$

(2)

$$\begin{aligned} (\lambda +\phi +n\alpha \xi )P_{0,n}= & {} \lambda \displaystyle \sum _{m=1}^{n}b_{m}P_{0,n-m}+(n+1)\alpha \xi P_{0,n+1},\quad n\ge 2, \end{aligned}$$

(3)

$$\begin{aligned} (\lambda + \eta ) P_{1,0}= & {} \beta \mu P_{1,1}, \end{aligned}$$

(4)

$$\begin{aligned} (\lambda +\beta \mu )P_{1,1}= & {} \lambda b_{1}P_{1,0}+ 2\beta \mu P_{1,2}+\phi P_{0,1},\quad n=1, \end{aligned}$$

(5)

$$\begin{aligned} (\lambda +n\beta \mu )P_{1,n}= & {} \lambda \displaystyle \sum _{m=1}^{n}b_{m}P_{1,n-m}+ (n+1)\beta \mu P_{1,n+1} + \phi P_{0,n},\nonumber \\&2\le n\le c-1, \end{aligned}$$

(6)

$$\begin{aligned} (\lambda +c\beta \mu )P_{1,n}= & {} \lambda \displaystyle \sum _{m=1}^{n}b_{m}P_{1,n-m}+ c\beta \mu P_{1,n+1} + \phi P_{0,n},\quad n\ge c. \end{aligned}$$

(7)

And the normalizing condition is given as

$$\begin{aligned} \displaystyle \sum _{n=0}^{\infty }P_{0,n}+\displaystyle \sum _{n=0}^{\infty }P_{1,n}=1. \end{aligned}$$

(8)

The probability generating function (PGF) of $P_{s,n}$ is defined as

$$\begin{aligned} G_{s}(z)=\sum _{n=0}^{\infty }P_{s,n}z^{n},\quad s=0,1. \end{aligned}$$

(9)

The probability generating function (PGF) of the batch size X is as

$$\begin{aligned} B(z)=\sum _{l=1}^{\infty }b_{l}z^{l},|z|\le 1,\quad \hbox {with} \quad B(1)=\sum _{l=1}^{\infty }b_{l}=1. \end{aligned}$$

(10)

The steady-state probabilities of the queueing system are obtained by solving the Eqs. (1)–(7) using PGF.

By multiplying Eqs. (1)–(3) by $z^{n},$ and summing over n,  then re-arranging all the terms, we get

$$\begin{aligned} (1-z)\alpha \xi G_{0}'(z)+[\lambda (B(z)-1)-\phi ]G_{0}(z)=-[\phi P_{0,0}+\eta P_{1,0}]. \end{aligned}$$

(11)

In a similar manner, form Eqs. (4)–(7), we have

$$\begin{aligned}{}[\lambda z (B(z)-1)+c\beta \mu (1-z)]G_{1}(z)+z\phi G_{0}(z)= & {} \beta \mu (z-1)\displaystyle \sum _{n=0}^{c-1}(n-c)P_{1,n}z^{n}\nonumber \\&\quad +\, z[\eta P_{1,0}+\phi P_{0,0}]. \end{aligned}$$

(12)

Then, by taking $z=1$ in Eqs. (11) or (12), we obtain

$$\begin{aligned} \phi G_{0}(1)=\eta P_{1,0} + \phi P_{0,0}. \end{aligned}$$

(13)

We solve the differential Eq. (11) using the same method used in Altman and Yechiali [1]. Thus Eq. (11) can be written as

$$\begin{aligned} G_{0}'(z)+\bigg [\frac{\lambda }{\alpha \xi }H'(z)-\frac{\phi }{\alpha \xi (1-z)}\bigg ]G_{0}(z) =-\bigg [\frac{\phi }{\alpha \xi (1-z)}P_{0,0}+\frac{\eta }{\alpha \xi (1-z)}P_{1,0}\bigg ], \end{aligned}$$

(14)

where

$$\begin{aligned} H(z)=\displaystyle \int _{0}^{z}\frac{B(x)-1}{1-x}dx \quad \mathrm{and} \quad H'(z)=\displaystyle \frac{B(z)-1}{1-z}. \end{aligned}$$

Then, we multiply both sides of Eq. (14) by $e^{\frac{\lambda }{\alpha \xi }H(z)}(1-z)^{\frac{\phi }{\alpha \xi }},$ we get

$$\begin{aligned} \frac{d}{dz}\left( e^{\frac{\lambda }{\alpha \xi }H(z)}(1-z)^{\frac{\phi }{\alpha \xi }}G_{0}(z) \right) =-\bigg [\frac{\phi }{\alpha \xi }P_{0,0}+\frac{\eta }{\alpha \xi }P_{1,0}\bigg ]e^{\frac{\lambda }{\alpha \xi }H(z)}(1-z)^{\frac{\phi }{\alpha \xi }-1}. \end{aligned}$$

(15)

Now, integrating Eq. (15) from 0 to z,  we get

$$\begin{aligned} G_{0}(z)=e^{-\frac{\lambda }{\alpha \xi }H(z)}(1-z)^{-\frac{\phi }{\alpha \xi }}\bigg \{ G_{0}(0)-\frac{K(z)}{\alpha \xi }\bigg [\phi P_{0,0}+ \eta P_{1,0}\bigg ]\bigg \}, \end{aligned}$$

(16)

where

$$\begin{aligned} K(z)=\displaystyle \int _{0}^{z}e^{\frac{\lambda }{\alpha \xi }H(x)}(1-x)^{\frac{\phi }{\alpha \xi }-1}dx. \end{aligned}$$

(17)

Since $G_{0}(1)=P_{0,.} =\sum \nolimits _{n=0}^{\infty } P_{0,n} >0$ and $z = 1$ is the root of the denominator of the right hand side of Eq. (16), so $z = 1$ must be the root of the numerator of the right hand side of Eq. (16).

Thus, we get

$$\begin{aligned} P_{0,0}=G_{0}(0)=\frac{K(1)}{\alpha \xi }\bigg [\phi P_{0,0}+ \eta P_{1,0}\bigg ], \end{aligned}$$

(18)

with

$$\begin{aligned} K(1)=\displaystyle \int _{0}^{1}e^{\frac{\lambda }{\alpha \xi }H(x)}(1-x)^{\frac{\phi }{\alpha \xi }-1}dx. \end{aligned}$$

(19)

From Eq. (18), it yields

$$\begin{aligned} P_{1,0}=\theta _{0}P_{0,0},\,\,\hbox {where}\,\,\theta _{0}=\frac{\alpha \xi -\phi K(1)}{\eta K(1)}. \end{aligned}$$

(20)

By substituting Eq. (20) into Eq. (16), we obtain

$$\begin{aligned} G_{0}(z)=e^{-\frac{\lambda }{\alpha \xi }H(z)}(1-z)^{-\frac{\phi }{\alpha \xi }} \bigg \{1-\frac{K(z)}{K(1)}\bigg \}P_{0,0}. \end{aligned}$$

(21)

And by substituting Eq. (20) into Eq. (13), we find the probability that the servers are in vacation period, ($G_{0}(1)=P_{0,.}=\sum \nolimits _{n=0}^{\infty }P_{0,n}$),

$$\begin{aligned} G_{0}(1)=\frac{\alpha \xi }{\phi K(1)}P_{0,0}. \end{aligned}$$

(22)

It is clearly seen that Eq. (12) expresses $G_{1}(z)$ in terms of $P_{0,0},P_{1,0},P_{1,n}$ and $G_{0}(z).$ From Eq. (21), we see that $G_{0}(z)$ is expressed in terms of $P_{0,0},$ then in Eq. (20), $P_{1,0}$ is given in terms of $P_{0,0}.$ Thus, to define $G_{1}(z)$ in terms of $P_{0,0},$ we need to express $P_{1,n}$ in terms of $P_{0,0}$. To this end, we firstly have to write $P_{0,n}$ in terms of $P_{0,0}.$

From Eq. (1), using Eq. (20), we get

$$\begin{aligned} P_{0,1}=\omega _{1}P_{0,0}, \end{aligned}$$

(23)

where $\omega _{1}=\frac{\lambda -\eta \theta _{0}}{\alpha \xi }.$

From Eq. (2), using Eq. (23), we find

$$\begin{aligned} P_{0,2}=\omega _{2}P_{0,0}, \end{aligned}$$

(24)

where $\omega _{2}=\psi _{1}\omega _{1}-\frac{\lambda }{2\alpha \xi }b_{1}\omega _{0}, \,\, \psi _{1}=\frac{\lambda +\phi +\alpha \xi }{2\alpha \xi },$ and $\omega _{0}=1.$

Then, from Eq. (3), for $n=2,$ using Eqs. (23) and (24), we obtain

$$\begin{aligned} P_{0,3}=\omega _{3}P_{0,0}, \end{aligned}$$

(25)

where $\omega _{3}=\psi _{2}\omega _{2}-\frac{\lambda }{3\alpha \xi }(b_{1}\omega _{1}+b_{2}\omega _{0}),\,\hbox {and}\, \psi _{2}=\frac{\lambda +\phi +2\alpha \xi }{3\alpha \xi }.$

Then, recursively, it yields

$$\begin{aligned} P_{0,n}=\omega _{n}P_{0,0}, \end{aligned}$$

(26)

where

$$\begin{aligned}\omega _{n} =\left\{ \begin{array}{ll} 1, &{} \hbox {if }n=0, \\ \frac{\lambda -\eta \theta _{0}}{\alpha \xi }, &{} \hbox {if }n=1,\\ \psi _{n-1}\omega _{n-1}-\displaystyle \frac{\lambda }{n \alpha \xi }\sum \nolimits _{i=1}^{n-1}b_{i}\omega _{n-1-i}, &{} \hbox {if }2\le n\le c-1, \end{array} \right. \end{aligned}$$

with

$$\begin{aligned} \psi _{n-1}=\frac{\lambda +\phi +(n-1)\alpha \xi }{n \alpha \xi }. \end{aligned}$$

Next, we need to write $P_{1,n}$ in terms of $P_{0,0}.$ Via Eq. (4), using Eq. (20), we get

$$\begin{aligned} P_{1,1}=\theta _{1}P_{0,0}, \end{aligned}$$

(27)

where $\theta _{1}=\frac{\lambda +\eta }{\beta \mu }\theta _{0}.$

From Eq. (5), using Eqs. (20), (23) and (27), we obtain

$$\begin{aligned} P_{1,2}=\theta _{2}P_{0,0}, \end{aligned}$$

(28)

where $\theta _{2}=\rho _{1}\theta _{1}-\frac{\phi }{2\beta \mu }\omega _{1}-\frac{\lambda }{2\beta \mu }b_{1}\theta _{0},$ and $\rho _{1}=\frac{\lambda +\beta \mu }{2\beta \mu }.$

Then, from Eq. (6), for $n=2$, using Eqs. (20), (24), (27) and (28), we find

$$\begin{aligned} P_{1,3}=\theta _{3}P_{0,0}, \end{aligned}$$

(29)

where $\theta _{3}=\rho _{2}\theta _{2}-\frac{\phi }{3\beta \mu }\omega _{2}-\frac{\lambda }{3\beta \mu }\bigg (b_{1}\theta _{1} +b_{2}\theta _{0}\bigg ),$ and $\rho _{2}=\frac{\lambda +2\beta \mu }{3\beta \mu }.$

Then, recursively, we get

$$\begin{aligned} P_{1,n}=\theta _{n}P_{0,0}, \end{aligned}$$

(30)

where

$$\begin{aligned}\theta _{n} =\left\{ \begin{array}{ll} \theta _{0}, &{} \hbox {if }n=0, \\ \frac{\lambda +\eta }{\beta \mu }\theta _{0}, &{} \hbox {if }n=1,\\ \rho _{n-1}\theta _{n-1}-\displaystyle \frac{\phi }{n \beta \mu }\omega _{n-1}-\displaystyle \frac{\lambda }{n \beta \mu }\sum \nolimits _{i=1}^{n-1}b_{i}\theta _{n-1-i},&{} \hbox {if } 2\le n\le c-1, \end{array} \right. \end{aligned}$$

with

$$\begin{aligned} \rho _{n-1}=\frac{\lambda +(n-1)\beta \mu }{n\beta \mu }. \end{aligned}$$

Finally, using Eqs. (12), (20), (21), and (30), $G_{0}(z)$ and $G_{1}(z)$ are expressed in terms of $P_{0,0}.$ So, it remains to determine this quantity. From Eq. (14), applying L’Hopital rule, we find

$$\begin{aligned} \lim _{z\rightarrow 1}G'_{0}(z)=G'_{0}(1)=\frac{\lambda B'(1)}{\alpha \xi +\phi }G_{0}(1). \end{aligned}$$

(31)

Next, substituting Eq. (22) in Eq. (31), we obtain

$$\begin{aligned} G'_{0}(1)=\frac{\alpha \xi \lambda B'(1)}{(\alpha \xi +\phi )\phi K(1)}P_{0,0}. \end{aligned}$$

(32)

Then, substituting Eq. (13) in Eq. (12), we get

$$\begin{aligned} G_{1}(z)=\frac{\beta \mu (1-z)R(z)P_{0,0}-z\phi (G_{0}(z)-G_{0}(1))}{\lambda z (B(z)-1)+c\beta \mu (1-z)}, \end{aligned}$$

(33)

where

$$\begin{aligned} R(z)=\displaystyle \sum _{n=0}^{c-1}(c-n)\theta _{n}z^{n}. \end{aligned}$$

From Eq. (33), applying L’Hopital rule, we obtain the probability that the servers are in busy period, ($G_{1}(1)=P_{1,.}=\sum \nolimits _{n=0}^{\infty }P_{1,n}$),

$$\begin{aligned} \lim _{z\rightarrow 1}G_{1}(z)=G_{1}(1) =\frac{ \phi G'_{0}(1) + \beta \mu R(1)P_{0,0} }{c\beta \mu -\lambda B'(1)}, \end{aligned}$$

(34)

with

$$\begin{aligned} R(1)=\displaystyle \sum _{n=0}^{c-1}(c-n)\theta _{n}. \end{aligned}$$

Finally, by substituting Eqs. (22), (32) and (34) in Eq. (8), we find

$$\begin{aligned} P_{0,0}=\bigg \{\frac{\beta \mu }{c\beta \mu -\lambda B'(1)}R(1)+\frac{\alpha \xi }{\phi K(1)}\bigg (\frac{\phi \lambda B'(1)}{(c\beta \mu -\lambda B'(1))(\alpha \xi +\phi )}+1\bigg )\bigg \}^{-1}. \end{aligned}$$

3.2 Performance measures

Once the steady-state probabilities are obtained, one can evaluate different performance measures of the considered model.

• The mean system size (E[L]). Let L denote the number of customers in the system. The mean system size is given as

  $$\begin{aligned} E[L]=E[L_{0}]+E[L_{1}]. \end{aligned}$$

• $*$ Let $L_{0}$ be the system size when the servers are in vacation period. Then, the mean system size when the servers are in vacation period $(E[L_{0}])$ is given as

  $$\begin{aligned} E[L_{0}]=\lim _{z\rightarrow 1}G_{0}'(z)=G_{0}'(1), \end{aligned}$$

  which is a direct consequence of Eq. (32).

• $*$ Let $L_{1}$ be the system size when the servers are in busy period. Then, the mean system size when the servers are in busy period ($E[L_{1}]$) is given as

  $$\begin{aligned} E[L_{1}]=\lim _{z\rightarrow 1}G_{1}'(z)=G_{1}'(1). \end{aligned}$$

Via Eq. (33), using L’Hopital rule, we obtain

$$\begin{aligned} E[L_{1}]= & {} G'_{1}(1)=\displaystyle \frac{\phi }{2(c\beta \mu -\lambda B'(1))}G''_{0}(1)+\displaystyle \frac{\phi (2c\beta \mu +\lambda B''(1))}{2(c\beta \mu -\lambda B'(1))^{2}}G'_{0}(1)\nonumber \\&+\bigg (\displaystyle \frac{\beta \mu \lambda (2B'(1)+B''(1))}{2(c\beta \mu -\lambda B'(1))^{2}}R(1)+\displaystyle \frac{\beta \mu }{c\beta \mu -\lambda B'(1)}R'(1)\bigg )P_{0,0}, \end{aligned}$$

(35)

where $G_{0}''(1)$ is obtained by differentiating twice $G_{0}(z)$ at $z=1.$ Thus, using Eq. (11), we find

$$\begin{aligned} G_{0}''(1)=\frac{2\lambda B'(1)}{2\alpha \xi +\phi }G_{0}'(1)+\frac{\lambda B''(1)}{2\alpha \xi +\phi }G_{0}(1). \end{aligned}$$

(36)

Further

$$\begin{aligned} R'(1)=\displaystyle \sum _{n=1}^{c-1}n(c-n)\theta _{n}. \end{aligned}$$

Then, substituting Eq. (36) in Eq. (35), we get

$$\begin{aligned} E[L_{1}]= & {} \bigg (\displaystyle \frac{\phi (2c\beta \mu +\lambda B''(1))}{2(c\beta \mu -\lambda B'(1))^{2}}+\frac{\lambda \phi B'(1)}{(c\beta \mu -\lambda B'(1))(2\alpha \xi +\phi )}\bigg )E[L_{0}] \nonumber \\&+\,\bigg (\displaystyle \frac{\beta \mu \lambda (2B'(1)+B''(1))}{2(c\beta \mu -\lambda B'(1))^{2}}R(1)+\displaystyle \frac{\beta \mu }{c\beta \mu -\lambda B'(1)}R'(1)\bigg )P_{0,0}\nonumber \\&+\,\displaystyle \frac{\lambda \phi B''(1)}{2(c\beta \mu -\lambda B'(1))(2\alpha \xi +\phi )}G_{0}(1). \end{aligned}$$

• The mean number of customers in the queue $(E[L_{q}]).$

  $$\begin{aligned} E[L_{q}]=\displaystyle \sum _{n=0}^{\infty }n P_{0,n}+\displaystyle \sum _{n=c+1}^{\infty }(n-c)P_{1,n}=E[L]-c(1-P_{v})+R(1)P_{0,0}. \end{aligned}$$

• The probability that the servers are in vacation period $(P_{v})$. From Eq. (22), we obtain

  $$\begin{aligned} P_{v}=G_{0}(1)=\frac{\alpha \xi }{\phi K(1)}P_{0,0}. \end{aligned}$$

• The probability that the servers are idle during busy period $(P_{e})$. From Eq. (20), we get

  $$\begin{aligned} P_{e}=\frac{\alpha \xi -\phi K(1)}{\eta K(1)}P_{0,0}. \end{aligned}$$

• The probability that the servers are working (serving customers) during busy period $(P_{b}).$

  $$\begin{aligned} P_{b}=1-P_{v}-P_{e}. \end{aligned}$$

• The mean number of customers served per unit time $(N_{s}).$

  $$\begin{aligned} N_{s}=\beta \mu \displaystyle \sum _{n=0}^{c-1} n P_{1,n}+c\beta \mu \displaystyle \sum _{n=c}^{\infty } P_{1,n}=\beta \mu \left( c(P_{b}-P_{e})+R(1)P_{0,0}\right) \!. \end{aligned}$$

• The average rate of abandonment of customers due to impatience $(R_{a}).$

  $$\begin{aligned} R_{a}=\alpha \xi \sum _{n=0}^{\infty }n P_{0,n}=\alpha \xi E[L_{0}]. \end{aligned}$$

• The average retention rate of impatient customers $(R_{e}).$

  $$\begin{aligned} R_{e}=(1-\alpha )\xi \sum _{n=0}^{\infty }n P_{0,n}=(1-\alpha )\xi E[L_{0}]. \end{aligned}$$

4 Analysis of the model under SVP

This section is devoted to the study of the system under single vacation policy. The transition-rate diagram depicting the state of the system is shown in Fig. 2.

4.1 Steady state solution of the model

Via the Markov theory, the set of steady-state equations are as follows

$$\begin{aligned} (\lambda +\phi )P_{0,0}= & {} \alpha \xi P_{0,1}+\eta P_{1,0}, \end{aligned}$$

(37)

$$\begin{aligned} (\lambda +\phi +\alpha \xi )P_{0,1}= & {} \lambda b_{1}P_{0,0}+2\alpha \xi P_{0,2},\quad n=1, \end{aligned}$$

(38)

$$\begin{aligned} (\lambda +\phi +n\alpha \xi )P_{0,n}= & {} \lambda \displaystyle \sum _{m=1}^{n}b_{m}P_{0,n-m}+(n+1)\alpha \xi P_{0,n+1},\quad n\ge 2, \end{aligned}$$

(39)

$$\begin{aligned} (\lambda + \eta ) P_{1,0}= & {} \phi P_{0,0}+\beta \mu P_{1,1}, \end{aligned}$$

(40)

$$\begin{aligned} (\lambda +\beta \mu )P_{1,1}= & {} \lambda b_{1}P_{1,0}+ 2\beta \mu P_{1,2}+\phi P_{0,1},\quad n=1, \end{aligned}$$

(41)

$$\begin{aligned} (\lambda +n\beta \mu )P_{1,n}= & {} \lambda \displaystyle \sum _{m=1}^{n}b_{m}P_{1,n-m}+ (n+1)\beta \mu P_{1,n+1} + \phi P_{0,n},\nonumber \\&2\le n\le c-1, \end{aligned}$$

(42)

$$\begin{aligned} (\lambda +c\beta \mu )P_{1,n}= & {} \lambda \displaystyle \sum _{m=1}^{n}b_{m}P_{1,n-m}+ c\beta \mu P_{1,n+1} + \phi P_{0,n},\quad n\ge c, \end{aligned}$$

(43)

The normalizing condition is given in Eq. (8).

The PGF of $P_{s,n}$ is given in Eq. (9), and that of the batch size X has already been done in (10).

The state probabilities are obtained by solving the Eqs. (37)–(43) using PGF.

Fig. 2

State-transition-rate diagram of the model under SVP

Now, multiplying Eqs. (37)–(39) by $z^{n},$ and summing n,  then re-arranging all the terms, we have

$$\begin{aligned} (1-z)\alpha \xi G_{0}'(z)+[\lambda (B(z)-1)-\phi ]G_{0}(z)=-\eta P_{1,0}. \end{aligned}$$

(44)

In a similar manner, form Eqs. (40)–(43), it yields

$$\begin{aligned}{}[\lambda z (B(z)-1)+c\beta \mu (1-z)]G_{1}(z)+z\phi G_{0}(z)=\beta \mu (z-1)\displaystyle \sum _{n=0}^{c-1}(n-c)P_{1,n}z^{n}+\eta z P_{1,0}. \end{aligned}$$

(45)

By taking $z=1$ in Eqs. (44) or (45), we obtain

$$\begin{aligned} \phi G_{0}(1)=\eta P_{1,0}. \end{aligned}$$

(46)

We solve Eq. (44) by following the method presented in Altman and Yechiali [1].

Using Eq. (40), we get

$$\begin{aligned} P_{1,0}=\frac{\phi }{\lambda +\eta } P_{0,0}+\frac{\beta \mu }{\lambda +\eta }P_{1,1}. \end{aligned}$$

(47)

Equation (44) can be written as

$$\begin{aligned} G_{0}'(z)+\bigg [\frac{\lambda }{\alpha \xi }H'(z)-\frac{\phi }{\alpha \xi (1-z)}\bigg ]G_{0}(z)=-\bigg [\frac{\delta _{1} }{\alpha \xi (1-z)}P_{0,0}+\frac{\delta _{2}}{\alpha \xi (1-z)} P_{1,1}\bigg ], \end{aligned}$$

(48)

where

$$\begin{aligned} \delta _{1}=\frac{\eta \phi }{\lambda +\eta },\quad \delta _{2}=\frac{\eta \beta \mu }{\lambda +\eta }. \end{aligned}$$

The solution of the Eq. (44) is computed as before and given as follows

$$\begin{aligned} G_{0}(z)=e^{-\frac{\lambda }{\alpha \xi }H(z)}(1-z)^{-\frac{\phi }{\alpha \xi }}\bigg \{ G_{0}(0)-\frac{K(z)}{\alpha \xi }\bigg [\delta _{1}P_{0,0}+\delta _{2}P_{1,1}\bigg ]\bigg \}. \end{aligned}$$

(49)

Since $G_{0}(1)=P_{0,.} =\sum \nolimits _{n=0}^{\infty } P_{0,n} >0$ and $z = 1$ is the root of the denominator of the right hand side of Eq. (49), thus $z = 1$ must be the root of the numerator of the right hand side of Eq. (49).

Consequently,

$$\begin{aligned} P_{0,0}=G_{0}(0)=\frac{\delta _{1} P_{0,0}+\delta _{2} P_{1,1}}{\alpha \xi }K(1). \end{aligned}$$

(50)

This implies

$$\begin{aligned} P_{1,1}=M_{1}P_{0,0},\quad \hbox {where} \quad M_{1}=\frac{\alpha \xi (\lambda +\eta )}{\eta \beta \mu K(1)}-\frac{\phi }{\beta \mu }. \end{aligned}$$

(51)

Consequently,

$$\begin{aligned} G_{0}(z)=e^{-\frac{\lambda }{\alpha \xi }H(z)}(1-z)^{-\frac{\phi }{\alpha \xi }} \bigg \{1-\frac{K(z)}{K(1)}\bigg \}P_{0,0}. \end{aligned}$$

(52)

Next, substituting Eqs. (51) into (40), and Eq. (53) into (46), we get respectively

$$\begin{aligned} P_{1,0}=M_{0}P_{0,0}, \quad \hbox {where} \quad M_{0}=\frac{\alpha \xi }{\eta K(1)}, \end{aligned}$$

(53)

and

$$\begin{aligned} G_{0}(1)=\frac{\alpha \xi }{\phi K(1)}P_{0,0}. \end{aligned}$$

(54)

Now, Eq. (52) shows that $G_{0}(z)$ can be expressed in terms of $P_{0,0}$ and Eq. (53) expresses $P_{1,0}$ in terms of $P_{0,0}.$ So, to get $P_{1,n}$ in terms of $P_{0,0}$ for $n=0,\ldots ,c-1,$ at first we have to express $P_{0,n}$ in terms of $P_{0,0}$ for $n=0,\ldots ,c-1.$

Using Eqs. (37)–(39), recursively, we get

$$\begin{aligned} P_{0,n}=\gamma _{n}P_{0,0}, \end{aligned}$$

(55)

with

$$\begin{aligned}\gamma _{n} =\left\{ \begin{array}{ll} 1, &{} \hbox {if }n=0, \\ \frac{\lambda +\phi -\eta M_{0}}{\alpha \xi }, &{} \hbox {if }n=1,\\ \psi _{n-1}\gamma _{n-1}-\displaystyle \frac{\lambda }{n \alpha \xi }\sum \nolimits _{i=1}^{n-1}b_{i}\gamma _{n-1-i} , &{} \hbox {if }2\le n\le c-1. \end{array} \right. \end{aligned}$$

Next, via Eqs. (40)–(42), using recursive method, we obtain

$$\begin{aligned} P_{1,n}=M_{n}P_{0,0}, \end{aligned}$$

(56)

where

$$\begin{aligned}M_{n} =\left\{ \begin{array}{ll} M_{0}, &{} \hbox {if }n=0, \\ M_{1}, &{} \hbox {if }n=1,\\ \rho _{n-1}M_{n-1}-\displaystyle \frac{\phi }{n \beta \mu }\gamma _{n-1}-\displaystyle \frac{\lambda }{n \beta \mu }\sum \nolimits _{i=1}^{n-1}b_{i}M_{n-1-i},&{} \hbox {if } 2\le n\le c-1. \end{array} \right. \end{aligned}$$

Thus, $G_{0}(z)$ and $G_{1}(z)$ can be easily deduced in terms of $P_{0,0}.$

From Eq. (44), using Eq. (46), and applying L’Hopital rule, we have

$$\begin{aligned} \lim _{z\rightarrow 1}G'_{0}(z)=G'_{0}(1)=\frac{\lambda B'(1)}{\alpha \xi +\phi }G_{0}(1). \end{aligned}$$

(57)

Substituting Eq. (54) into Eq. (57), we obtain

$$\begin{aligned} G'_{0}(1)=\frac{\alpha \xi \lambda B'(1)}{\phi K(1)(\alpha \xi +\phi )}P_{0,0}. \end{aligned}$$

(58)

Next, substituting Eq. (46) into Eq. (45), we have

$$\begin{aligned} G_{1}(z)=\frac{\beta \mu (1-z)Q(z)P_{0,0}-z\phi (G_{0}(z)-G_{0}(1))}{\lambda z (B(z)-1)+c\beta \mu (1-z)}, \end{aligned}$$

(59)

where

$$\begin{aligned} Q(z)=\displaystyle \sum _{n=0}^{c-1}(c-n)M_{n}z^{n}. \end{aligned}$$

From Eq. (59), applying L’Hopital rule, it yields

$$\begin{aligned} G_{1}(1)=\frac{ \phi G'_{0}(1) + \beta \mu Q(1)P_{0,0} }{c\beta \mu -\lambda B'(1)}, \end{aligned}$$

(60)

with

$$\begin{aligned} Q(1)=\displaystyle \sum _{n=0}^{c-1}(c-n)M_{n}. \end{aligned}$$

Next, substituting Eq. (58) into Eq. (60), we get

$$\begin{aligned} G_{1}(1)=\bigg \{\frac{\alpha \xi \lambda B'(1)}{K(1)(\alpha \xi +\phi )(c\beta \mu -\lambda B'(1))}+\frac{\beta \mu }{c\beta \mu -\lambda B'(1)}Q(1)\bigg \}P_{0,0}. \end{aligned}$$

(61)

Finally, by substituting Eqs. (54) and (61) into Eq. (8), we get

$$\begin{aligned} P_{0,0}=\bigg \{\frac{\alpha \xi }{\phi K(1)}\bigg (1+\frac{\phi \lambda B'(1)}{(c\beta \mu -\lambda B'(1))(\alpha \xi +\phi )}\bigg )+\frac{\beta \mu }{c\beta \mu -\lambda B'(1)}Q(1)\bigg \}^{-1}. \end{aligned}$$

4.2 Performance measures

• The mean system size (E[L]). L is the number of customers in the system.

  $$\begin{aligned} E[L]=E[L_{0}]+E[L_{1}]. \end{aligned}$$

• $*$ Let $L_{0}$ be the system size when the servers are in vacation period, the mean system size when the servers are on vacation $(E[L_{0}])$ has been already given in Eq. (58).

• $*$ Let $L_{1}$ be the system size when the servers are in busy period, $(E[L_{1}])$ be the mean system size when the servers are on busy period. From Eq. (59), taking $z=1$ and using L’Hopital rule, we obtain

  $$\begin{aligned} E[L_{1}]= & {} G'_{1}(1)=\displaystyle \frac{\phi }{2(c\beta \mu -\lambda B'(1))}G''_{0}(1)+\displaystyle \frac{\phi (2c\beta \mu +\lambda B''(1))}{2(c\beta \mu -\lambda B'(1))^{2}}G'_{0}(1)\nonumber \\&+\bigg (\displaystyle \frac{\beta \mu \lambda (2B'(1)+B''(1))}{2(c\beta \mu -\lambda B'(1))^{2}}Q(1)+\displaystyle \frac{\beta \mu }{c\beta \mu -\lambda B'(1)}Q'(1)\bigg )P_{0,0}, \end{aligned}$$

  (62)

where $G_{0}''(1)$ is obtained by differentiating twice $G_{0}(z)$ at $z=1$, therefore, using Eq. (44), we get

$$\begin{aligned} G_{0}''(1)=\frac{2\lambda B'(1)}{2\alpha \xi +\phi }G_{0}'(1)+\frac{\lambda B''(1)}{2\alpha \xi +\phi }G_{0}(1), \end{aligned}$$

(63)

and

$$\begin{aligned} Q'(1)=\displaystyle \sum _{n=1}^{c-1}n(c-n)M_{n}. \end{aligned}$$

Now, substituting Eqs. (63) into (62), we get

$$\begin{aligned} E[L_{1}]= & {} \bigg (\displaystyle \frac{\phi (2c\beta \mu +\lambda B''(1))}{2(c\beta \mu -\lambda B'(1))^{2}}+\frac{\lambda \phi B'(1)}{(c\beta \mu -\lambda B'(1))(2\alpha \xi +\phi )}\bigg )E[L_{0}] \nonumber \\&+\,\bigg (\displaystyle \frac{\beta \mu \lambda (2B'(1)+B''(1))}{2(c\beta \mu -\lambda B'(1))^{2}}Q(1)+\displaystyle \frac{\beta \mu }{c\beta \mu -\lambda B'(1)}Q'(1)\bigg )P_{0,0}\nonumber \\&+\,\displaystyle \frac{\lambda \phi B''(1)}{2(c\beta \mu -\lambda B'(1))(2\alpha \xi +\phi )}G_{0}(1). \end{aligned}$$

• The mean number of customers in the queue $(E[L_{q}]).$

  $$\begin{aligned} E[L_{q}]=\displaystyle \sum _{n=0}^{\infty }n P_{0,n}+\displaystyle \sum _{n=c+1}^{\infty }(n-c)P_{1,n}=E[L]-c(1-P_{v})+Q(1)P_{0,0}. \end{aligned}$$

• The probability that the servers are in vacation period $(P_{v})$. From Eq. (54), we obtain

  $$\begin{aligned} P_{v}=G_{0}(1)=\frac{\alpha \xi }{\phi K(1)}P_{0,0}. \end{aligned}$$

• The probability that the servers are idle during busy period $(P_{e}).$ From Eq. (53), we get

  $$\begin{aligned} P_{e}=\frac{\alpha \xi }{\eta K(1)}P_{0,0}. \end{aligned}$$

• The probability that the servers are working (serving customers) during busy period $(P_{b}).$

  $$\begin{aligned} P_{b}=1-P_{v}-P_{e}. \end{aligned}$$

• The mean number of customers served per unit time $(N_{s}).$

  $$\begin{aligned} N_{s}=\beta \mu \displaystyle \sum _{n=0}^{c-1} n P_{1,n}+c\beta \mu \displaystyle \sum _{n=c}^{\infty } P_{1,n}=\beta \mu \left( c(P_{b}-P_{e})+ Q(1)P_{0,0} \right) \!. \end{aligned}$$

• The average rate of abandonment of customers due to impatience $(R_{a}).$

  $$\begin{aligned} R_{a}=\alpha \xi \sum _{n=0}^{\infty }n P_{0,n}=\alpha \xi E[L_{0}]. \end{aligned}$$

• The average retention rate of impatient customers $(R_{e}).$

  $$\begin{aligned} R_{e}=(1-\alpha )\xi \sum _{n=0}^{\infty }n P_{0,n}=(1-\alpha )\xi E[L_{0}]. \end{aligned}$$

5 Cost model

Practically, queueing managers are interested in minimizing operating cost of unit time. In this part of paper, we first formulate a steady-state expected cost function per unit time, where the service rate $\mu$ is the decision variable. Our main goal is to determine the optimum value of $\mu$ in order to minimize the expected cost function. To this end, we have to define the following cost elements:

• $C_{1}:$ Cost per unit time when the servers are working during busy period.

• $C_{2}:$ Cost per unit time when the servers are idle during busy period.

• $C_{3}:$ Cost per unit time when the servers are in vacation period.

• $C_{4}:$ Cost per unit time when customers join the queue and wait for service.

• $C_{5}:$ Cost per service per unit time.

• $C_{6}:$ Cost per unit time of serving a feedback customer.

• $C_{7}:$ Cost per unit time when a customer reneges.

• $C_{8}:$ Cost per unit time when a customer is retained in the system.

• $C_{9}:$ Fixed server purchase cost per unit.

• R :  The revenue earned by providing service to a customer.

  Let

• $\mathcal {T}_{c}$ be the total expected cost per unit time of the system:

  $$\begin{aligned} \mathcal {T}_{c}=C_{1}P_{b}+C_{2}P_{e}+C_{3}P_{v}+C_{4}E[L_{q}]+ c \mu (C_{5} + \beta 'C_{6} )+ C_{7}R_{a}+ C_{8}R_{e}+ cC_{9}. \end{aligned}$$

• $\mathcal {T}_{r}$ be the total expected revenue per unit time of the system:

  $$\begin{aligned} \mathcal {T}_{r}= R\times N_{s} \end{aligned}$$

• $\mathcal {T}_{p}$ be the total expected profit per unit time of the system:

  $$\begin{aligned} \mathcal {T}_{p}=\mathcal {T}_{r}-\mathcal {T}_{c}. \end{aligned}$$

5.1 Quadratic fit search method

This part considers the cost optimization problem under a given cost structure via quadratic fit search method (QFSM), this technique utilizes a 3-point pattern for fitting a quadratic function that has a unique optimum, see Rardin [17]. So, we focus on the optimization of the service rate $\mu$ in different cases in order to minimize the expected cost function $\mathcal {T}_{c}$ denoted in this part by F. Assume that all system parameters have fixed values, and the only controlled parameter is the service rate $\mu .$

Thus, the optimization problem can be illustrated mathematically as:

$$\begin{aligned} {\hbox {Minimize}:} \,\ F(\mu )=C_{1}P_{b}+C_{2}P_{e}+C_{3}P_{v}+C_{4}E[L_{q}]+ c \mu (C_{5} + \beta 'C_{6} )+ C_{7}R_{a}+ C_{8}R_{e}+ cC_{9}. \end{aligned}$$

As it has been mentioned in Laxmi et al. [11], given a 3-point pattern, we may fit a quadratic function via corresponding functional values that has a unique minimum, $x^{q}$, for the given objective function F(x). Quadratic fit utilizes this approximation to improve the current 3-point pattern by replacing one of its points with optimum $x^{q}$. The unique optimum $x^{q}$ of the quadratic function agreeing with F(x) at 3-point operation $(x^{l},x^{m},x^{u})$ is given as

$$\begin{aligned} x^{q}\cong \displaystyle \frac{1}{2}\bigg [\displaystyle \frac{F(x^{l})((x^{m})^{2}-(x^{u})^{2})+F(x^{m})((x^{u})^{2}-(x^{l})^{2})+F(x^{u})((x^{l})^{2}-(x^{m})^{2})}{F(x^{l})(x^{m}-x^{u})+F(x^{m})(x^{u}-x^{l})+F(x^{u})(x^{l}-x^{m})}\bigg ]. \end{aligned}$$

6 Numerical results

In this section, we illustrate the obtained resulting formulas numerically, we first carry out the optimization of the queueing system, using quadratic fit search method (QFSM) to minimize the expected cost function F with respect to the service rate, then we discuss the influence of different system parameters on the various performance measures of the queueing system as well as on total expected cost, total expected revenue and total expected profit. We assume that the batch size X follows a geometric distribution with parameter p, that is,

$$\begin{aligned} b_{l}=P(X=l)=(1-p)^{l-1}p,\,\, 0<p<1\,\, (l=1,2,\ldots ). \end{aligned}$$

Then, it is easy to observe that

$$\begin{aligned} B(z)=\frac{pz}{1-(1-p)z}, E(X)=B'(1)=\frac{1}{p}, \quad \hbox {and} \quad E(X^{2})=B''(1)=\frac{2(1-p)}{p^{2}}. \end{aligned}$$

For the whole analysis in this numerical part, we fixe $C_{1}=40,$$C_{2}=25,$$C_{3}=20,$$C_{4}=30,$$C_{5}=50,$$C_{6}=20,$$C_{7}=20,$$C_{8}=30,$ and $C_{9}=10.$

6.1 Optimization analysis

In order to carry out the numerical analysis on the parameter optimisation for the queueing system under consideration, we consider the values for default parameters as $c=2,$$p=0.70,$$\lambda =1.00,$$\beta =0.80,$$\eta =3.00,$$\phi =2.20,$$\alpha =0.60,$ and $\xi =0.20,$ and the tolerance of QFSM is $\epsilon =10^{-6}.$

Fig. 3

The optimum service rate $\mu ^{*}$ under multiple vacation policy

Fig. 4

The optimum service rate $\mu ^{*}$ under single vacation policy

From Figs. 3, 4, we clearly see the convexity of the curves, which shows that there exists a certain value of the service rate $\mu$ that minimizes the total expected cost function for the chosen set of model parameters. By adopting QFSM and choosing the initial 3-point pattern as $(\mu ^{l},\mu ^{m},\mu ^{u})=(1.05, 2.75, 3.5),$ in multiple vacation, and $(\mu ^{l},\mu ^{m},\mu ^{u})=(1.05, 2.75, 3.5),$ in single vacation, and after finite iterations, we observe that the minimum expected operating cost per unit time converges to the solution $F=262.045100$ at $\mu ^{*}=1.443674,$ under multiple vacation and converges to $F=260.584500$ at $\mu ^{*}=1.446983,$ under single vacation.

Further, from Tables 1, 2, and Figs. 3, 4, we observe that the optimum service rate $\mu ^{*}$ of multiple vacation model is smaller than that of single vacation model, while the minimum expected cost $F(\mu ^{*})$ of multiple vacation model is bigger than that of single vacation model.

Table 1 Search for optimum service rate $\mu ^{*}$ under multiple vacation policy

Table 2 Search for optimum service rate $\mu ^{*}$ under single vacation policy

Table 3 The optimal values $\mu ^{*}$ and $F(\mu ^{*})$ for different values of $\lambda$

Table 4 The optimal values $\mu ^{*}$ and $F(\mu ^{*})$ for different values of $\phi$

Table 5 The optimal values $\mu ^{*}$ and $F(\mu ^{*})$ for different values of $\eta$

Fig. 5

$\mathcal {T}_{c}$ versus $\lambda$ and $\mu$ in MVP

Fig. 6

$\mathcal {T}_{c}$ versus $\lambda$ and $\mu$ in SVP

Fig. 7

$\mathcal {T}_{c}$ versus $\phi$ and $\mu$ in MVP

Fig. 8

$\mathcal {T}_{c}$ versus $\phi$ and $\mu$ in SVP

Fig. 9

$\mathcal {T}_{c}$ versus $\eta$ and $\mu$ in MVP

Fig. 10

$\mathcal {T}_{c}$ versus $\eta$ and $\mu$ in SVP

Using QFS technique, the optimal values of $\mu$ and the minimum expected cost $F(\mu ^{*})$ are shown in Tables 3, 4 and 5 for various values of $\lambda ,$$\phi$ and $\eta ,$ respectively. We observe from Table 3 that for both single and multiple vacations, as the arrival rate $\lambda$ increases, both the optimal service rate and the minimum expected cost increase, the increase in the optimal service rate with $\lambda$ is as expected in view of the stability of the system. Moreover, it is quite clear from Figs. 5 and 6 that for both MVP and SVP, the total expected cost increases with $\lambda$ and $\mu ,$ as intuitively expected. Then, from Table 4, we observe that for both single and multiple vacation policies, the optimal service rate increases with $\phi ,$ while the minimum expected cost decreases as $\phi$ increases. On the other hand, Figs. 7 and 8 show that for both MVP and SVP, the total expected cost decreases with $\phi ,$ which agrees with our intuition, while it is not monotone with the parameter $\mu ;$ it first decreases if the service rate $\mu$ is less than some threshold parameter, then it increases when $\mu$ is above this threshold value. Further, from Table 5, it is clearly seen that the optimal service rate decreases with $\eta ,$ whereas, the minimum expected cost increases as $\eta$ increases, this is quite obvious. Moreover, Figs. 9 and 10 point out that for both MVP and SVP, the total expected cost increases with $\eta ,$ whereas it is not monotone with $\mu ;$ it first decreases when the service rate $\mu$ is below a certain threshold value, then it increases when $\mu$ is greater than this threshold value. The non-monotonicity of the total expected cost with $\mu ,$ displayed in Figs.  7, 8, 9 and 10, can be due to the choice of the system parameters.

6.2 Performance and cost-profit analysis

In this subsection, we perform a sensitivity analysis to understand how different performance measures, total expected cost, total expected revenue, and total expected profit vary with different system parameters.

6.2.1 Impact of arrival rate $(\lambda )$ and batch size (p)

Let the values for default parameters be fixed as $c=2,$$\beta =0.90,$$\eta =3.00,$$\phi =1.50,$$\alpha =0.60,$$\xi =3.50,$ and $\mu =1.50.$

Table 6 Impact of $\lambda$ and p

From Table 6, we observe that for both single and multiple vacation policies, for fixed p,  with the increases of $\lambda ,$ the mean system size E[L] increases, which results in the increasing of the mean number of customers served $N_{s}.$ Further, along the increasing of $\lambda ,$ the probability that the servers are idle during busy period $P_{e}$ decreases in the model with SVP, while it is not monotone in the model with MVP; it increases, then decreases, when $p=0.65,$ and increases in the case where $p=0.75,0.85$. This is due to the choice of the system parameters. In addition, $\mathcal {T}_{c},$$\mathcal {T}_{r},$ and $\mathcal {T}_{p}$ all increase with $\lambda .$ This is quite reasonable, the bigger the arrival rate, the larger the number of customers served and the greater the total expected cost, the total expected revenue and the total expected profit.

On the other hand, for both policies, for fixed $\lambda ,$ with the increasing of p,  the probability that the servers are idle $P_{e}$ increases, while E[L] and $N_{s}$ decrease with the parameter p,  this leads to a decrease in $\mathcal {T}_{c},$$\mathcal {T}_{r},$ and $\mathcal {T}_{p},$ as intuitively expected.

Fig. 11

Impact of $\lambda$ on $E[L_{q}]$ in MVP and SVP

Fig. 12

Impact of $\lambda$ on $E[L_{0}]$ in MVP and SVP

Figures 11, 12 show the effect of the arrival rate $\lambda$ on the expected number of customers in the queue $E[L_{q}]$ and on the size of the system when the servers are on vacation $E[L_{0}],$ for different values of batch size p,  under multiple and single vacation policies. It can be observed that for fixed p,  with the increase of $\lambda ,$$E[L_{q}]$ increases monotonically as it should be. While $E[L_{0}]$ first increases, then decreases in the case where $\lambda >0.80$ and $p=0.60,$$\lambda >1.00$ and $p=0.70,$ and $\lambda >1.10$ and $p=0.80.$ Obviously, $E[L_{q}]$ increases with 1 / p,  while $E[L_{0}]$ decreases with the parameter 1 / p, which is coherent with the fact that increasing the arrival rates increase the queue length during the busy period and decreases the system size when the servers are in vacation.

Further, one may also observe that for higher values of p,  $E[L_{q}]$ of multiple vacation model is smaller than that of single vacation model, while $E[L_{0}]$ of multiple vacation model is higher than that of single vacation model. This is due to the fact that in single vacation policy, whenever the busy period ended, the servers switch to the busy period and stay there until the first arriving customer enters the system, consequently the queue length $E[L_{q}]$ increases and $E[L_{0}]$ decreases. Contrariwise, in multiple vacation policy, once the vacation period is finished, the servers switch to the busy period, if at that moment no customer is observed in the queue, they immediately comeback to the vacation period, which results in the increasing of the size of the system during this period $E[L_{0}].$

6.2.2 Impact of waiting rate of the severs $(\eta )$ and vacation rate $(\phi )$

In this subpart, we fixed the parameters as $c=2,$$p=0.70,$$\lambda =0.90,$$\beta =0.80,$$\eta =3.00,$$\phi =0.50,$$\alpha =0.60,$$\xi =3.20,$ and $\mu =2.20.$

Table 7 System performance measures vs. $\eta$

Table 8 System performance measures vs. $\phi$

Table 9 $\mathcal {T}_{c},$$\mathcal {T}_{r},$ and $\mathcal {T}_{c}$ vs. $\eta$

Table 10 $\mathcal {T}_{c},$$\mathcal {T}_{r},$ and $\mathcal {T}_{c}$ vs. $\phi$

Fig. 13

Impact of $\eta$ on $E[L_{0}]$ in MVP and SVP

Fig. 14

Impact of $\lambda$ on $E[L_{0}]$ in MVP and SVP

The impact of waiting rate of the servers $\eta$ and vacation rate $\phi$ in single and multiple vacations are shown in Tables 7, 8, 9 and 10. It is clearly seen that for both multiple and single vacation policies, $P_{v},$$E[L_{0}],$$R_{a}$ and $R_{e}$ all increase with $\eta$ and decrease with $\phi .$ While $P_{b},$$E[L_{1}],$ and $N_{s}$ decrease with $\eta$ and increase with $\phi .$ Therefore, for both policies, $\mathcal {T}_{c},$$\mathcal {T}_{r},$ and $\mathcal {T}_{p}$ decrease with $\eta$ and increase with $\phi .$ These results are consistent with our intuition; the probability of busy period increases with $\phi$ (resp. decreases with $\eta$), thus the mean number of customers served increases with $\phi$ (resp. decreases with $\eta$), therefore, the total expected profit increases with $\phi$ (resp. decreases with $\eta$). On the other hand, the probability of vacation period decreases with the parameter $\phi$ (resp. increases with the parameter $\eta$). Consequently, the average rate of reneging decreases with $\phi$ (resp. increases with $\eta$). Consequently, the total expected profit increases with increasing values of $\phi$ and decreases along the increasing of $\eta .$

From Figs. 13, 14 we see that for both single and multiple vacations, $E[L_{0}]$ increases with $\eta$ and decreases with $\lambda$ and $\phi ,$ as it should be expected. Then, evidently for lower values of $\phi ,$$E[L_{0}]$ of multiple vacation model is higher than that of single vacation model. On the other hand, for higher values of $\eta ,$$E[L_{0}]$ of multiple vacation model is greater than that of single vacation model. Consequently, we can conclude that the model with waiting servers outperforms the model without this policy.

6.2.3 Impact of impatience rate $(\xi )$ and non-retention probability $(\alpha )$

In this subpart, we choose the default parameters as $c=2,$$p=0.70,$$\lambda =0.90,$$\beta =0.80,$$\eta =2.00,$$\phi =1.50,$$\mu =2.20.$

Table 11 Impact of $\xi$ and $\alpha$

Table 11 illustrates the impact of $\xi$ and $\alpha ,$ for both single and multiple vacation policies. As expected, for both MVP and SVP, increases in $\xi$ and $\alpha$ implies a decrease in E[L] and $N_{s}.$ This is because the size of the system decreases with the increasing of $\xi$ and $\alpha .$ Thus, the mean number of customers served decreases as the two parameters $\xi$ and $\alpha$ increase. Further, $R_{a}$ increases with $\xi$ and $\alpha ,$ whereas, $R_{e}$ increases with $\xi$ and decreases with $\alpha ,$ as it should be. Therefore, $\mathcal {T}_{c},$$\mathcal {T}_{r},$ and $\mathcal {T}_{p}$ monotonically decrease with $\alpha ,$$\mathcal {T}_{c}$ is not monotone with $\xi ,$ while $\mathcal {T}_{r}$ and $\mathcal {T}_{p}$ decrease significantly with the increasing values of $\xi ,$ this is because of the significant number of lost customers. From this, it is clearly obvious that the retention probability has a positive impact on the economy of the system, this probability is very useful for any firm operating in the field of finance, supply chain, manufacturing, and so on.

Fig. 15

Impact of $\xi$ on $E[L_{0}]$ in MVP

Fig. 16

Impact of $\xi$ on $E[L_{0}]$ in SVP

Figures 15, 16 depict the effect of $\xi$ for different values of $\alpha$ in both single and multiple vacation policies. From the figures, it can be seen that as the impatience rate $\xi$ increases, the mean system size when the servers are on vacation period $E[L_{0}]$ monotonically decreases for any $\alpha ,$ as intuitively expected. Moreover, from both figures, we observe that $E[L_{0}]$ is high when the non-retention probability $\alpha$ is small. Further, as it should be expected, $E[L_{0}]$ of multiple vacation model is greater than that of single vacation model.

6.2.4 Impact of non-feedback probability $(\beta )$ and number of the severs (c).

In this part, we take $p=0.70,$$\lambda =0.90,$$\eta =2.00,$$\phi =1.50,$$\alpha =0.60,$$\xi =1.00,$ and $\mu =2.20.$

Table 12 Impact of c and $\beta$

Fig. 17

Impact of $\mu$ on $N_{s}$ in MVP

Fig. 18

Impact of $\mu$ on $N_{s}$ in SVP

From Table 12 and Figs. 17, 18, we see that for both single and multiple vacations, $N_{s}$ increases with $\mu ,$c,  and $\beta ,$ respectively. Further, for both MVP and SVP, for fixed $\beta ,$ the total expected cost, the total expected revenue, and the total expected profit increase significantly with the increasing of c. This is quite reasonable, the greater the number of servers in the system, the larger the number of customers served and the higher the total expected profit. In addition, in both MVP and SVP, for fixed c,  the total expected revenue and the total expected profit decrease when $\beta$ increases. While in the model with SVP, $\mathcal {T}_{c}$ decreases with the parameter $\beta ,$ and in the model with MVP, it decreases with $\beta ,$ when $c=2,$ and increases along the increasing of $\beta ,$ when $c=3.$ Thus, we can say that a feedback probability has a nice effect on the economy of the system. Moreover, as intuitively expected, $N_{s}$ of single vacation model is higher than that of multiple vacation model.

7 Conclusion and future scope

In this paper, we carried out a study of a infinite-buffer multi-server Bernoulli feedback queueing system with batch arrivals, waiting servers, impatient customers and retention of reneged customer, under single and multiple vacation policies. We obtained the closed-form expressions for the steady-state probabilities of the queueing model, using the probability generating function (PGF). Various performance measures of the system are evaluated. We also performed a cost model and considered a cost optimization problem using quadratic fit search method (QFSM) in order to obtain the optimum values of the service rate for different values of arrival rate, waiting rate of the servers and vacation rate. Important numerical results have been illustrated, which may be useful to explore the impact of system parameters on different performance measures and total expected cost, total expected revenue and total expected profit, respectively. The obtained results have potential applications in modeling computer and telecommunication systems, computer networks, manufacturing, and so on. For further works, it will be interesting to apply the technique used in this paper in order to study more complex models such as $Geo^{X}/Geo/c$ and $M^{X}/M/c$ with breakdowns, impatient customers and asynchronous multiple and single vacations. Furthermore, the model under investigation can be analyzed under the provision of time dependent arrival and service rates which leads the system to more realistic environment.