Markovian working vacation queue with imperfect service, balking and retrial

Abstract

Markovian queue with working vacation, retrial and impatient customers has been investigated by including the feature of imperfect service during working vacation. If the server is occupied, an incoming customer may either decide to balk from the system or join the retrial orbit following the classical retrial policy. When there is no customer in the system, the server switches over to a working vacation (WV) mode. The customers who enter into the system during working vacation are also served at a slower speed. The probability generating functions (PGFs) are derived for evaluating the distributions of the number of customers in the system and orbit, which are further utilized to derive several performance metrics in closed form. The sensitivity analysis has been done to explore the sensitiveness of various descriptors on the system performance measures. Finally, a cost function is constructed and minimized using quasi-Newton method (QNM) and genetic algorithm (GA).

1 Introduction

In daily as well industrial scenarios, there are many circumstances in which, we can notice delay in the service which results is waiting in the queue. The study of such queues is important to reduce congestion causing inconvenience in our life and can be seen at many places including ATMs, hospitals, banks, call centres, railway counters, etc. Sometimes by finding the service counter busy, the customer decides not to join the queue and after some random period, he/she retries again to get service. The customers who find the server busy, join the orbit known as retrial orbit. Retrial queues are mostly seen in many congestion problems encountered in communication systems, internet networks, data centres, etc. Sherman and Kharoufeh (2006) studied Markovian retrial queue where server is prone to failures and after repair, capable of rendering the service again. They used the stability condition to find several stochastic decomposability results and other queueing performance indices. Azhagappan et al. (2018) analyzed Markovian retrial queue with reneging from orbit and obtained the transient probability distribution of orbit size and several other performance measures. Chang et al. (2018) derived various system characteristics for the queue with re-attempt by incorporating customer’s impatience and feedback behaviour. They dealt with Markovian model by using the matrix geometric method (MGM) to derive the queue length distribution and further optimal control parameters for the cost optimization.

Sometimes, it may happen that when the system becomes empty, the server goes for the vacation for a random period of time. In case when, the vacationing server works at a slower rate, rather than stopping service completely during a vacation, this type of vacation is known as a working vacation (WV). WV has numerous applications in analyzing many queueing systems such as service/distribution centres, production/manufacturing systems, data/internet networks, computer/communication systems, etc. During the last two decades, working vacation scenarios have been well studied broadly using this concept since the first study on WV done by Servi and Finn (2002). Liu et al. (2007) studied the stochastic decompositions of Markovian queue with WV and investigated the distribution of queue size as well as delay characteristics. Tian (2007) proposed Markovian single server model with WV and vacation interruptions using matrix geometric method (MGM) to establish the stochastic decomposition of the number of customers in the waiting line and some other indices related to the queue size. Zhang and Hou (2012) dealt with the non-Markovian WV queue with repeated attempts and analyzed the queue lengths in the waiting line and in the orbit. Using the PGF approach, Selvaraju and Goswami (2013) obtained the analytical solution of Markovian queue with impatient customers by considering the single working vacation (SWV) as well as multiple working vacations (MWV). An M/M/1 retrial queueing model with WV interruption and Bernoulli feedback under N-policy was developed by Tao et al. (2014). The state dependent M/M/1 model with inspection and WV was suggested by Jain et al. (2014). They used MGM to examine the throughput, mean delay time and various other performance indices. Several authors studied Markovian models with WV period in a variety of situations (Ammar 2015; Jain et al. 2017; Vijayashree and Janani 2016; Li et al. 2016). The transient queueing scenarios of a multiple vacation (MV) queue with an impatient customer have been discussed by Ammar (2017). He used the probability generating function (PGF) to derive mean and variance of queue size distributions by using the QBD process. Recently, the notable work on working vacation was also done by Xu et al. (2018) via fluid approximation approach by including the concept of negetive customers.

When the customer finds that there are too many clients in the queue, he may opt not to enter; this situation in queueing literature is called balking. Balking behaviour of the customers in congestion scenarios is a common event in everyday life and can be noticed in industrial scenarios also. A general re-attempt queue with balking customer under Bernoulli feedback was studied by Ke and Chang (2009) to derive some performance indices. Al-Seedy et al. (2009) developed the multi-server Markovian model wherein balking and impatient customers’ behaviour are taken into account. PGF technique was used to derive the transient state probabilities by taking modified Bessel function. Ammar et al. (2013) discussed the busy period of Markovian queue with discouragement due to both balking and reneging behaviour of the customers. They derived an explicit result for the busy period distribution. Further, some researchers studied on Markovian single server queue by including some specific features including balking behaviour of the customers (Wang and Zhang 2013; Laxmi and Jyothsna 2014; Dhakad and Jain 2016). The optimization of vacation and polling models with retrial customers was investigated by Abidini et al. (2016). The WV queue with impatient customer was considered by Vijaya Laxmi and Rajesh (2017) by employing probability generating function to obtain the expected system size and some performance indices. Sudhesh et al. (2017) provided analytical formulae for the transient model of Markovian queue with WV period, service failure, and customers’ impatience behaviour. Markovian queue under multiple vacation (MV) was investigated by Afroun et al. (2018) by incorporating the noble concept of balking and retention of the impatient customers. They employed a Q-matrix method to provide the analytical and numerical results of queueing performance measures of the system size and discussed the system stability also. More recently, to study the queue with multiclass orbit and balking customer, was presented by Morozov et al. (2019). They dealt with two ways communication model with exponential distribution by using MGM method. Jain and Sanga (2017) presented numerical results of various performance indices of finite retrial queue and obtained cost optimization by using computational QNM method.

In this research work, we consider the working vacation concept involve in Markovian queueing scenario involving balking behaviour of the customers. The service station is capable of rendering the service during WV at a low speed rather than not allowing the service. However, a few customers may not be satisfied with the service received during WV with slow pace and demand for additional service also. We cite an example of the proposed model which has wide applications in many areas where unpleasant scenarios of delay occur. Consider a doctor’s clinic where patients visit to get treatment. If the doctor is free, the patient will immediately treated by the doctor. However, if the doctor is busy, then the patient will wait in a retrial orbit for a random interval of time. The patient will retry to get the service again and again from retrial orbit. If the doctor is free then the patient will immediate receive the attention of doctor, and leave the clinic after receiving the service. If the doctor switches over to the WV mode, he attends the patient with slower rate rather than the normal rate in normal busy period. During WV period, the served patient sometimes may not satisfied and request for some additional service also. The balking behaviour of the patient can also be noticed due to delay in service in case of many patients already present in the retrial orbit.

Present study devoted to analyze Markovian WV queue with balking is structured into different sections as follows. In Sect. 2, we outline the preliminaries of quasi-Newton method (QNM) and genetic algorithm (GA) which have been used for cost optimization of the concerned model. In Sect. 3, Markov model formulation by the assumptions, has been done. In Sect. 4, the governing equations and PGF of the queue length in the orbit are established. In Sect. 5, we mention several queueing indices and cost optimization. In Sect. 6, the numerical results and sensitivity analysis are facilitated by taking a suitable illustration.

2 Preliminaries of quasi-newton method (QNM) and genetic algorithm (GA)

For the concerned model, we are interested in determining the optimal service parameters for which we conduct the cost optimization. The classical optimization methods are difficult to be implemented due to non-linear characteristics and involvement of integral terms. To minimize the total cost, we implement the numerical technique QNM as well as soft computing technique GA.

2.1 Quasi-newton method (QNM)

QNM is the numerical technique for finding optimal decision parameters of a non-linear function. To outline QNM, we define the vector $\overrightarrow {M}$ corresponding to decision parameters which are the service rates $\mu$ and $\eta$ during busy and WV respectively, and obtain a cost gradient $\overrightarrow {\nabla } TC\left( {\overrightarrow {M}_{0} } \right) = \left[ {\frac{\partial TC}{{\partial \mu }} \, \frac{\partial TC}{{\partial \eta }} \, } \right]^{T}$. Let $\left( {\mu^{*} ,\eta^{*} } \right)$ be the optimal value of $\left( {\mu ,\eta } \right)$.

The following algorithmic steps of quasi-Newton’s approach are used:

• (i) ${\text{Set the initial solution }}\overrightarrow {M}_{0} { = }\left[ {\mu ,\eta } \right]{\text{, and tolerance }}\delta .$

• (ii) ${\text{Evaluate }}TC\left( {\overrightarrow {M}_{0} } \right){.}$

• (iii) Determine gradient and Hessian matrix cost function at the point $\overrightarrow {M}_{0}$ as $\overrightarrow {\nabla } TC\left( {\overrightarrow {M}_{0} } \right) = \left. {\left[ {\frac{\partial TC}{{\partial \mu }} \, ,\frac{\partial TC}{{\partial \eta }} \, } \right]^{T} } \right|_{{\overrightarrow {M}_{0} }}$ and $\, H\left( {\overrightarrow {M}_{j} } \right) = \left[ \begin{gathered} \frac{{\partial^{2} TC}}{{\partial \mu^{2} }} \, \frac{{\partial^{2} TC}}{\partial \mu \partial \eta } \hfill \\ \frac{{\partial^{2} TC}}{\partial \eta \partial \mu } \, \frac{{\partial^{2} TC}}{{\partial \eta^{2} }} \hfill \\ \end{gathered} \right].$

• (iv) ${\text{Obtain new solution }}\overrightarrow {M}_{j + 1} { = }\overrightarrow {M}_{j} - \left[ {{\text{H}}\left( {\overrightarrow {M}_{j} } \right)} \right]^{ - 1} \, \overrightarrow {\nabla } TC\left( {\overrightarrow {M}_{j} } \right).$

• (v) ${\text{Set }}j = j + 1{\text{ and repeat steps (iii) - (iv) until Max}}\left( {\left| {\frac{\partial TC}{{\partial \mu }}} \right|,\left| {\frac{\partial TC}{{\partial \eta }}} \right|} \right) < \delta {.}$

• (vi) Compute the global minima of cost function at $\overrightarrow {M}_{0} { = }\left( {\mu^{*} ,\eta^{*} } \right)$ using $TC\left( {\mu^{*} ,\eta^{*} } \right) = TC(\overrightarrow {M}_{j} ).$

2.2 Genetic algorithm (GA)

For optimization, GA is widely used soft computing method for solving linear and non-linear optimization problems (OP). GA is based on the natural selection and ethics of genetics used for biological evaluation and it has three main elements (i) Crossover (ii) Mutation (iii) Selection for each step. Genetic algorithm selects several parents (current population) to produce children (new generation), named as off-springs. GA operator, i.e., crossover and mutation are applied for mating of parents. The selection of parents and producing of children are repeated until the stopping rule is satisfied. The selection probability of every chromosome to be chosen is relative to its fitness value. Sanga and Jain (2019) obtained optimal service rate by implementing the cost optimization of Markovian queue with general retrial times by using genetic algorithm. In the present investigation, GA approach is used to create a new generation under some selection rules to optimizes the cost function.

To solve OP, the following steps are used in GA (Sanga and Jain 2019):

• Step 1: Population initialization.

  The number of genes of chromosomes are generated randomly in the initial population. First of all fix the initial population size $U$ by genes ${U}_{\eta },{U}_{\mu }$ and bits ${U}_{\eta }(0~ \mathrm{or}~ 1)$, ${\text{U}}_{\eta }$$(0~ \mathrm{or} ~1)$. Initial population-based on high-quality chromosomes are selected by genes and high-quality chromosomes increase the possibility of a good quality clustering solution.

• Step 2: Fitness solution.

  To evaluate minimum average cost $TC({\mu }^{*},{\eta }^{*})$ per unit time, the fitness of a chromosome is evaluated.

• Step 3: Selection.

  For going on next genetic operators namely crossover and mutation, GA chooses chromosomes arisen by the cost function. The chance of a chromosome to be chosen is relative to its fitness value. To get better fitness of chromosomes, a fraction of population (say 1/5 of total population) is considered for the next generation.

• Step 4: Crossover.

  After selecting every pair of chromosomes, GA applies crossover operation on every pair of chromosomes at a multi-point. A pair of genes commute to each other and produce a new offsprings (children) chromosomes. If the new offspring chromosomes have better solution than earlier old generation, then crossover operator is evolved. For implementing GA for cost optimization of our model, two crossover-point method is selected where the probability of crossover is 100%.

• Step 5: Mutation.

  Offsprings are produced by crossover operator but mutation operator is used on offsprings with mutation rate. Mutation operators can change the selected one or more genes from chromosomes with a mutation rate. We have used mutation probability as 0.08, and generated values in the interval [0 1]. This mutation operator can be applied as often as a random number between 0 and 1 on any offspring. If the mutation probability is greater than the chosen random number, then the string value is opposite (either 1 to 0 or 0 to 1).

• Step 6: Continue the steps 2 to 5 until the fixed number of population (say 50) generation is met.

3 Retrial model

The retrial queueing system with balking, WV and imperfect service during WV, is analyzed under Markovian arrival/service set up. Markovian M/M/1 (WV) model is formulated under the assumption that the customers arrive in Poisson process with arrival rate $\lambda$ and service is done following exponential distribution (Exp-D) rate $\mu$. As soon as the server becomes idle, he moves to WV mode; the working vacation time is considered by Exp-D with rate $\theta$. During WV, if the customer is not satisfied with probability $p$ by the primary service, he needs additional service; both primary and additional services rendered by the server during WV are governed by Exp-D with rates $\eta$ and $\eta_{a}$, respectively. On the contrary, if the customer is satisfied with the primary service during WV, he departs from the system with probability $p$. The customer may be discouraged if the server is busy during WV period or during normal busy period, and enters in the system with probability $q$. Upon arrival, the customer gets service if the server is free and otherwise he enters into the orbit and wait for re-attempts. From the orbit, the customers make reattempts with state dependent retrial rates; if the service counter is busy then they go back to the orbit, and this process of re-attempts continues till the customers get the server free; the time spent by the customers in the retrial orbit is Exp-D with rate $n\alpha$, where n is the orbit size.

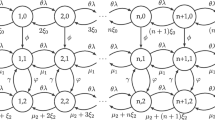
Let us consider the bivariate Markov process $\{ \left( {N\left( t \right), \, S\left( t \right)} \right), \, t \ge 0\}$, $N\left( t \right)$ being the number of customers in the orbit and $S\left( t \right)$ represents the status of the server at time $t$. The possible values that r.v. $S\left( t \right)$ takes at a time $t$ are given as follows:

$$S(t) = \left\{ \begin{gathered} 0,{\text{ the server is in WV and there is no customers in the system}} \hfill \\ 1,{\text{ the server is in WV and rendering the primary service}} \hfill \\ {\text{2, the server is in WV and rendering the additional service}} \hfill \\ {\text{3, the server is in normal busy mode (NBM) but server is free and }} \hfill \\ {\text{ there is no customer in the system}} \hfill \\ {\text{4, the server is in NBM and rendering the service to the customers}} \hfill \\ \end{gathered} \right.$$

The transition rates of Markov chain $\{ \left( {N\left( t \right), \, S\left( t \right)} \right), \, t \ge 0\}$ are given by

$$\begin{gathered} q_{(n,i)(n + 1,i)} = \lambda q, \, n \ge 0, \, i = 1,4 \hfill \\ q_{(0,4)(0,0)} = \mu , \, n \ge 0; \, q_{(n,4)(n,3)} = \mu , \, n \ge 1 \hfill \\ q_{(n,1)(n,2)} = \overline{p}\eta , \, n \ge 0; \, q_{(n,0)(n,3)} = \theta , \, n \ge 0 \hfill \\ q_{(0,1)(0,0)} = p\eta \, ; \, q_{(n,1)(n,3)} = p\eta , \, n \ge 1 \hfill \\ q_{(0,2)(0,0)} = \eta_{a} ; \, q_{(n,2)(n,3)} = \eta_{a} , \, n \ge 1 \hfill \\ q_{(n,3)(n - 1,4)} = n\alpha , \, n \ge 1; \, q_{(n,3)(n,4)} = \lambda , \, n \ge 1 \hfill \\ \end{gathered}$$

The transition rates of different system states are depicted in Fig. 1

Fig. 1

Transition rate diagram

4 Governing equations and probability generating functions (PGFs)

Let us denote, the transient probability  by $P_{n,i} (t) = \left\{ {N\left( t \right) = n, \, S\left( t \right) = i} \right\}$, steady state probability by $P_{{\text{n,i}}} = \mathop {{\text{Lt}}}\limits_{t \to \infty } P_{{\text{n,i}}} ({\text{t)}}$, and $\overline{p} = 1 - p$. For different system states following governing equations are framed:

$$\lambda qP_{0,0} = p\eta P_{0,1} + \mu P_{0,4} + \eta_{a} P_{{_{0,2} }}$$

(1)

$$\left( {\lambda q + p\eta + \overline{p}\eta + \theta } \right)P_{0,1} = \lambda qP_{0,0}$$

(2)

$$\eta_{a} P_{0,2} = \overline{p}\eta P_{0,1}$$

(3)

$$\left( {\lambda q + \mu } \right)P_{0,4} = \alpha P_{1,3} + \theta P_{0,1}$$

(4)

$$\left( {\lambda q + p\eta + \overline{p}\eta + \theta } \right)P_{n,1} = \lambda qP_{n - 1,1} \, , \, n \ge 1$$

(5)

$$\eta_{a} P_{n,2} = \overline{p}\eta P_{n,1} \, , \, n \ge 1$$

(6)

$$\left( {\lambda + n\alpha } \right)P_{n,3} = p\eta P_{n,1} + \eta_{a} P_{n,2} + \mu P_{n,4} \, , \, n \ge 1$$

(7)

$$\left( {\lambda q + \mu } \right)P_{n,4} = \lambda P_{n,3} + \lambda qP_{n - 1,4} + (n + 1)\alpha P_{n + 1,3} + \theta P_{n,1} \, , \, n \ge 1$$

(8)

Now define the PGFs by

$$\Omega_{i} (z) = \sum\limits_{n = 0}^{\infty } {P_{n,i} z^{n} ,} {\text{ for }}i{ = 1, 2, 4}\quad {\text{and }}\Omega_{3} (z) = \sum\limits_{n = 1}^{\infty } {P_{n,3} z^{n} } \,$$

(9)

Multiplying Eqs. (5) and (6) by $z^{n}$ and taking summation over $n$ and then adding, we get

$$(\lambda q + p\eta + \overline{p}\eta + \theta - \lambda qz)\Omega_{1} (z) = \lambda qP_{0,0}$$

(10)

$$\eta_{a} \Omega_{2} (z) = \overline{p}\eta \Omega_{1} (z)$$

(11)

In the similar way, from Eqs. (7) and (1), we get

$$\lambda \Omega_{3} (z) + \alpha z\Omega^{\prime}_{3} (z) + \lambda qP_{0,0} = p\eta \Omega_{1} (z) + \eta_{a} \Omega_{2} (z) + \mu \Omega_{4} (z) \,$$

(12)

Also from Eqs. (8) and (4), we have

$$\left( {\lambda q + \mu - \lambda qz} \right)\Omega_{4} (z) = \theta \Omega_{1} (z) + \lambda \Omega_{3} (z) + \alpha \Omega^{\prime}_{3} (z)$$

(13)

Solving Eqs. (10) and (11), we get

$$\Omega_{1} (z) = \frac{\lambda q}{{(\lambda q + \eta + \theta - \lambda qz)}}P_{0,0}$$

(14)

$$\Omega_{2} (z) = \frac{{\overline{p}\eta \lambda q}}{{\eta_{a} (\lambda q + \eta + \theta - \lambda qz)}}P_{0,0}$$

(15)

From Eq. (13), we obtain

$$\Omega_{4} (z) = \frac{\theta }{{\left( {\lambda q + \mu - \lambda qz} \right)}}\Omega_{1} (z) + \frac{\lambda }{{\left( {\lambda q + \mu - \lambda qz} \right)}}\Omega_{3} (z) + \frac{\alpha }{{\left( {\lambda q + \mu - \lambda qz} \right)}}\Omega^{\prime}_{3} (z)$$

(16)

Here superscript ‘${^{\prime}}$’ denotes the derivative with respect to ‘$z$’.

Using Eqs. (12)–(16) and after some manipulation, we get

$$\begin{gathered} \Omega^{\prime}_{3} (z) - \frac{{\lambda^{2} q}}{\alpha (\mu - \lambda qz)}\Omega_{3} (z) = \frac{\lambda q}{\alpha }\left[ {\frac{\lambda q}{{(\mu - \lambda zq)}} + 1} \right](1 - z)^{ - 1} P_{0,0} \hfill \\ \;\;\;\;\;\;\;\; - \frac{1}{\alpha }\left[ {\frac{\lambda qp\eta + \mu \theta }{{(\mu - \lambda zq)}} - p\eta } \right](1 - z)^{ - 1} \Omega_{1} (z) \, - \left[ {\frac{{\eta_{a} \lambda q}}{\alpha (\mu - \lambda zq)} - \frac{{\eta_{a} }}{\alpha }} \right](1 - z)^{ - 1} \Omega_{2} (z) \hfill \\ \end{gathered}$$

(17)

Solving Eq. (17), we have

$$\begin{gathered} \Omega_{3} (z) = (\mu - \lambda qz)^{{ - \frac{\lambda }{\alpha }}} \left[ {\frac{{\lambda^{2} q^{2} }}{\alpha }I_{1} (z) + \frac{\lambda q}{\alpha }I_{2} (z) - \left( {\frac{\lambda q\eta }{\alpha }} \right)I_{3} (z)} \right. \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. { - \left( {\frac{{\lambda q(\lambda pq\eta + \mu \theta ) + \lambda^{2} q^{2} \eta }}{\alpha }} \right)I_{4} (z)} \right]P_{0,0} \hfill \\ \end{gathered}$$

(18)

where

$$\left. \begin{gathered} I_{1} (z) = \int\limits_{0}^{z} {\frac{{(\mu - \lambda qx)^{{\frac{\lambda }{\alpha } - 1}} }}{(1 - x)}} dx \, ; \, I_{2} (z) = \int\limits_{0}^{z} {\frac{{(\mu - \lambda qx)^{{\frac{\lambda }{\alpha }}} }}{(1 - x)}} dx \, \hfill \\ I_{3} (z) = \int\limits_{0}^{z} {\frac{{(\mu - \lambda qx)^{{\frac{\lambda }{\alpha }}} }}{(1 - x)(\lambda q + \eta + \theta - \lambda qx)}} dx{\text{ ; I}}_{4} (z) = \int\limits_{0}^{z} {\frac{{(\mu - \lambda qx)^{{\frac{\lambda }{\alpha } - 1}} }}{(1 - x)(\lambda q + \eta + \theta - \lambda qx)}} dx \hfill \\ \end{gathered} \right\}$$

(19)

Eliminating $\Omega^{\prime}_{3} (z)$ from Eq. (12) and rewriting Eq. (13), we obtain

$$\Omega_{4} (z) = \frac{{(p\eta + \theta z)\Omega_{1} (z) + \eta_{a} \Omega_{2} (z) + \lambda (z - 1)\Omega_{3} (z) - \lambda qP_{0,0} }}{(\lambda qz - \mu )(1 - z)}$$

(20)

From Eqs. (14), (15), (18) and (20), we notice that all probability generating functions $\Omega_{i} (z)$, $i = 1,2,3,4$ are in terms of $P_{0,0}$. Now, we find $P_{0,0}$ by using normalization condition and derive other performance measures as follow.

For  obtaining $P_{0,0}$, from the Eqs. (14) and (15), we have

$$\Omega_{1} (1) = \frac{\lambda q}{{\eta + \theta }}P_{0,0}$$

(21)

$$\Omega_{2} (1) = \frac{{\overline{p}\eta \lambda q}}{{\eta_{a} (\eta + \theta )}}P_{0,0} \,$$

(22)

Equation (18), implies that

$$\Omega_{3} (1) = W{.}P_{0,0} = \frac{{(\mu - \lambda q)^{{\frac{ - \lambda }{\alpha }}} }}{\alpha }\left[ {\lambda^{2} q^{2} I_{1} (1) + \lambda qI_{2} (1) - \lambda q\eta I_{3} (1)} \right.\left. { - \left( {\lambda q(\lambda pq\eta + \mu \theta ) + \lambda^{2} q^{2} \eta } \right)I_{4} (1)} \right]P_{0,0}$$

(23)

Using L, Hospital rule in Eq. (20), we obtain

$$\begin{gathered} \Omega_{4} (1) = \mathop {\lim }\limits_{z \to 1} \Omega_{4} (z) \, \hfill \\ \quad \quad { = }\frac{{\theta \Omega_{1} (1) + (p\eta + \theta )\Omega^{\prime}_{1} (1) + \eta_{a} \Omega^{\prime}_{2} (1) + \lambda \Omega_{3} (1)}}{(\mu - \lambda q)} \hfill \\ \quad \quad = \frac{{\lambda W\left( {\eta + \theta } \right) + \theta \lambda q + \lambda^{2} q^{2} }}{{\left( {\eta + \theta } \right)(\mu - \lambda q)}}P_{0,0} \hfill \\ \end{gathered}$$

(24)

Now normalization condition becomes

$$P_{0,0} + \sum\limits_{i = 1}^{4} {\Omega_{i} (1)} = 1$$

(25)

Taking results from Eqs. (21), (22), (23), (24) and inserting into Eqs. (25), we have

$$P_{0,0} = \left[ {1 + \frac{\lambda q}{{\eta + \theta }} + \frac{{\overline{p}q\eta \lambda }}{{\eta_{a} \left( {\eta + \theta } \right)}} + W{ + }\frac{{\lambda W\left( {\eta + \theta } \right) + \theta \lambda q + \lambda^{2} q^{2} }}{{\left( {\eta + \theta } \right)\left( {\mu - \lambda q} \right)}}} \right]^{ - 1} \,$$

(26)

Now we can evaluate (21)–(24) easily in terms of $P_{0,0}$.

5 Performance measures

In this section, we obtain the analytical results for the average number of customers in the orbit $E[L]$, the average number of customers in the system $E[L_{s} ]$ and throughput $TP$. We also derive the analytical formulae for the average time in the orbit $E[W_{O} ]$ and in the system $E[W_{S} ]$.

Let us denote the mean orbit size by $E\left[ {L_{i} } \right]$ when the server’s status is $S\left( t \right) = i, \, i{ = 1,2,3,4}$. Differentiating Eqs. (14) and (15) w.r.t. ‘$z$’ and further taking $z \to 1$, we get

$$E\left[ {L_{1} } \right] = \mathop {\lim }\limits_{z \to 1} \Omega^{\prime}_{1} (z) = \frac{{\lambda^{2} q^{2} }}{{(\eta + \theta )^{2} }}P_{0,0}$$

(27)

$$E\left[ {L_{2} } \right] = \mathop {\lim }\limits_{z \to 1} \Omega^{\prime}_{2} (z) = \frac{{\overline{p}\eta \lambda^{2} q^{2} }}{{\eta_{a} (\eta + \theta )^{2} }}P_{0,0}$$

(28)

From Eq. (13), we have

$$\begin{gathered} E\left[ {L_{3} } \right] = \mathop {\lim }\limits_{z \to 1} \Omega^{\prime}_{3} (z) \hfill \\ \, = - \frac{\theta }{\alpha }\Omega_{1} (1) - \frac{\lambda }{\alpha }\Omega_{3} (1) + \frac{\mu }{\alpha }\Omega_{4} (1) \hfill \\ \end{gathered}$$

(29)

Differentiating Eq. (24) w.r.t ‘$z$’ and then employing L’ Hospital rule, we find

$$E\left[ {L_{4} } \right] = \frac{\begin{gathered} 2\lambda \left( {\mu - \lambda q} \right)E\left[ {L_{3} } \right] + \left( {\mu - \lambda q} \right)\left( {p\eta + \theta } \right)\Omega^{\prime\prime}_{1} \left( 1 \right) + \eta_{a} \left( {\mu - \lambda q} \right)\Omega^{\prime\prime}_{2} \left( 1 \right) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + 2E\left[ {L_{1} } \right]\left( {\theta \mu + \lambda qp\eta } \right) + \, 2\lambda q\left( {\lambda \Omega_{3} (1) + \theta \Omega_{1} (1)} \right) + 2\lambda q\eta_{a} E\left[ {L_{2} } \right] \, \hfill \\ \end{gathered} }{{2(\lambda q - \mu )^{2} }}$$

(30)

where $\Omega^{\prime\prime}_{1} (1) = \frac{{2\lambda^{3} q^{3} }}{{\left( {\eta + \theta } \right)^{3} }}P_{0,0} { ,~ }\Omega^{\prime\prime}_{2} (1) = \frac{{2\overline{p}\eta \lambda^{3} q^{3} }}{{\eta_{a} \left( {\eta + \theta } \right)^{3} }}P_{0,0} \,$

The PGFs mean orbit size and mean system size are respectively, given by

$$\Omega_{O} (z) = P_{0,0} + \sum\limits_{i = 1}^{4} {\Omega_{i} (z)}$$

(31)

$$\Omega_{S} (z) = {\rm P}_{0,0} + z\Omega_{1} (z) + z\Omega_{2} (z) + \Omega_{3} (z) + z\Omega_{4} (z)$$

(32)

The probability of the server having different status viz. probability that the server is busy $\left( {P_{{\text{B}}} } \right)$, probability that the server is free $\left( {P_{F} } \right)$, probability that the server is in WV mode $\left( {P_{WV} } \right)$ and probability that the server is in a normal service mode $\left( {P_{N} } \right)$ respectively, are obtained as follows:

$$P_{{\text{B}}} = \Omega_{1} (1) + \Omega_{2} (1) + \Omega_{4} (1)$$

(33)

$$P_{{\text{F}}} = 1 - P_{{\text{B}}}$$

(34)

$$P_{WV} = P_{0,0} + \Omega_{1} (1) \, + \Omega_{2} (1)$$

(35)

$$P_{N} = \Omega_{3} (1) + \Omega_{4} (1)$$

(36)

The mean orbit length, mean system length and throughput are respectively, given by

$$E\left[ L \right] = \sum\limits_{i = 1}^{4} {E\left[ {L_{i} } \right]}$$

(37)

$$E\left[ {L_{S} } \right] = E\left[ L \right] + \Omega_{1} \left( 1 \right) + \Omega_{2} \left( 1 \right) + \Omega_{4} \left( 1 \right)$$

(38)

$$TP = \eta \Omega_{1} (1) + \mu \Omega_{4} (1) + \eta_{a} \Omega_{2} (1)$$

(39)

Using Little’s formula, the mean waiting time of a customer in the orbit $E[W_{O} ]$ and in the system $E[W_{S} ]$ are given by

$$E[W_{O} ] = \frac{E[L]}{{\lambda_{eff} }}\quad {\text{and }}E[W_{S} ] = \frac{{E[L_{S} ]}}{{\lambda_{eff} }}$$

(40)

where $\lambda_{eff} = \lambda q\left( {\Omega_{1} \left( 1 \right) + \Omega_{2} \left( 1 \right) + \Omega_{4} \left( 1 \right)} \right) + \lambda \Omega_{3} \left( 1 \right)$.

5.1 Cost function

The prime goal of the queueing analysis of a service system is to increase revenue by lowering the company’s costs. With better service and less waiting for the customer, the system can provide good quality service but at the same time cost will be increased. Now we frame the cost function in which mean service rates of the server in WV as well as in normal busy period are considered as decision variables. The cost function includes some cost factors per unit time which are defined as follows:

• $C_{1}$: holding cost of the customer waiting in the orbit.

• $C_{2}$: cost/unit time spent on the server during NBM when server is busy.

• $C_{3}$: cost/unit time spent when the server renders additional service during WVM.

• $C_{4}$: cost/unit time spent when the sever renders service during WVM.

• $C_{5}$: fixed cost/unit time spent on the free server during NBM.

We evaluate an expected total cost per unit time as

$$TC(\mu ,\eta ) \, = \, C_{1} E[L] + C_{2} \mu + C_{3} p\eta_{a} + C_{4} \overline{p}\eta + C_{5} \theta$$

(41)

6 Numerical results

For the performance prediction of service system, the computational tractability of queueing indices is validated by taking an illustration. Now, we present sensitivity analysis of some key parameters and cost optimization by making code in ‘MATLAB’ software.

6.1 Sensitivity analysis

We set the default parameters for computational purpose as follows: $\lambda = 3,q = 0.3,\mu = 5$ $\alpha = 5,\,{\text{p = 0}}{.2, }\eta_{a} = 2,\;\theta { = 0}{\text{.3, }}\eta { = 2}$. For different balking probabilities (q), Figs. 2, 3, 4, 5, and 6 show the trends of mean orbit length $E[L]$ by varying parameters of working vacation rate ($\eta$), retrial rate $\left( \alpha \right)$, arrival rate $\left( \lambda \right)$, exponential service rate $\left( \mu \right)$, vacation time $\left( \theta \right)$, respectively.

Fig. 2

a $E[L]$ vs. $\eta$ for different values of ${\text{q}}$, b $E[L_{S} ]$ vs. $\eta$ for different values of ${\text{q}}$, c $E[L]$ vs. $\eta$ for different values of $\theta$, d $E[L_{S} ]$ vs. $\eta$ for different values of $\theta$

Fig. 3

a $E[L]$ vs. $\alpha$ different values of ${\text{q}}$, b $E[L_{S} ]$ vs. $\alpha$ different values of ${\text{q}}$, c $E[L]$ vs. $\alpha$ for different values of $\theta$, d $E[L_{S} ]$ vs. $\alpha$ for different values of $\theta$

Fig. 4

a $E[L]$ vs. $\lambda$ different values of ${\text{q}}$, b $E\left[ {L_{S} } \right]$ vs. $\lambda$ different values of ${\text{q}}$, c $E[L]$ vs. $\lambda$ different values of $\theta$, d $E\left[ {L_{S} } \right]$ vs. $\lambda$ different values of $\theta$

Fig. 5

a $E\left[ L \right]$ vs. $\mu$ different values of ${\text{q}}$, b $E\left[ {L_{S} } \right]$ vs. $\mu$ different values of ${\text{q}}$, c $E\left[ L \right]$ vs. $\mu$ for different values of $\theta$, d $E\left[ {L_{S} } \right]$ vs. $\mu$ for different values of $\theta$

Fig. 6

a $E\left[ L \right]$ vs. $\theta$ different values of ${\text{q}}$, b $E\left[ {L_{S} } \right]$ vs. $\theta$ different values of ${\text{q}}$, c $E\left[ L \right]$ vs. $\theta$ different values of ${\text{p}}$, d $E\left[ {L_{S} } \right]$ vs. $\theta$ different values of ${\text{p}}$

The indices seems to change significantly affected by varying different parameters as presented below:

6.2 Effect of $\eta$

In Fig. 2a–c, the performance indices namely expected orbit length $E[L]$ and expected system length $E[L_{S} ]$ are initially decreasing rapidly by varying parameter $\eta$ up to 0.5. It is noticed that $E[L]$ and $E[L_{S} ]$ also decrease moderately when $\eta$ increases from $\eta = 0.5$ to $\eta = 2$ for different values of $q$ and $\theta$ as shown in Fig. 2a–b and c–d, respectively. After $\eta = 3.5$, both expected orbit length $E[L]$ and expected system length $E[L_{S} ]$ do not change much for any values of $q$ and $\theta$.

From Table 1, for a fixed balking probability $q$, it is observed that the mean waiting in the orbit $E[W_{O} ]$ is reducing with increasing values of service rate $\left( \eta \right)$ during WV. For a fixed service rate $\left( \eta \right)$ during WV, the decreasing trends in $P_{F}$ and increasing trends in $P_{B}$ with the increment in discouragement probability $(q)$ are observed from the numerical results given in Table 1.

Table 1 Performance indices by varying parameter $\eta$

6.3 Effect of $\alpha$

Figure 3a–d show that the expected orbit length and expected system length both slow down with the growth in the retrial rate. But in case, when $q = 0.3$ then there are no significant changes in $E\left[ L \right]$ and $E\left[ {L_{S} } \right]$ as both the queue lengths remain constant which is observed from Fig. 3a, b.

From Table 2, it is observed that for a fixed retrial rate $\left( \alpha \right)$, there is the reducing trends in $P_{F}$, $P_{WV}$ and growing up trends in $P_{B}$, $P_{N}$ with an increment of balking probability $q$. Also, from Table 2, we notice that there is increasing trend of $P_{WV}$ and decreasing trend of $P_{N}$ for a fixed joining probability $\left( q \right)$ with increasing retrial rate $\left( \alpha \right)$. From Fig. 7c, it is noticed that the throughput (TP) has significant change with the increase in the retrial rate. However, when joining probability $\left( q \right)$ increases, the throughput (TP) seems to increase prominently.

Fig. 7

a $TP$ vs. $\lambda$ for different values of ${\text{q}}$, b $TP$ vs. μ for different values of ${\text{q}}$, c $TP$ vs. $\alpha$ for different values of ${\text{q}}$

Table 2 Performance indices by varying parameter $\alpha$

6.4 Effect of $\lambda$

It is noticed from the Fig. 4a–d that the expected orbit length and expected system length both significantly change by enhancing the arrival rate. It is also marked that both $E\left[ L \right]$ and $E\left[ {L_{S} } \right]$ reveal no considerable impact of varying values of $\theta$.

The average waiting time in the system $\left( {E\left[ {W_{S} } \right]} \right)$ can be observed from Table 3. We observe that probabilities $\left( {P_{F} , \, P_{WV} } \right)$ and $\left( {P_{B} , \, P_{N} } \right)$ change with an increment in the arrival rate $\left( \lambda \right)$ for a constant value of joining probability $\left( q \right)$. Also, from Table 3, for a constant value of $\lambda$, increment in probabilities $\left( {P_{B} , \, P_{N} } \right)$ and reduction in probability $\left( {P_{F} , \, P_{WV} } \right)$ for increasing joining probability $\left( q \right)$ are observed. The throughput (TP) reveals the rapidly increasing trends with the increment in arrival rate $\left( \mu \right)$ as shown in Fig. 7a.

Table 3 Performance indices by varying parameter $\lambda$

6.5 Effect of $\mu$

From Fig. 5a–d, it is evident that the expected orbit length and expected system length both are rapidly decreasing with growing service rate up to $\mu = 1.5$, but from Fig. 5a–b, when $q = 0.3$, $E\left[ L \right]$ and $E\left[ {L_{S} } \right]$ seem to be almost constant.

There is a significant change in the probability $P_{N}$ for different values of $q$ and $\mu$ which is shown in Table 4. Moreover, from Table 4, it is observed that for a fixed value of joining probability $\left( q \right)$, the expected waiting times in the orbit and in the system both reduce with an increment in the service rate $\left( \mu \right)$. Similarly, for a constant value of $q$, probability $P_{B}$ $\left( {P_{wv} } \right)$ is reducing (growing) with the growing values of normal service rate $\left( \mu \right)$. From Fig. 7b, we see that the throughput (TP) increases with the increment in the service rate $\left( \mu \right).$

Table 4 Performance indices by varying parameter $\mu$

6.6 Effect of $\theta$

From Fig. 6a–d, we notice that the expected orbit length and system length are both rapidly decreasing by an increment of vacation rate $\left( \theta \right)$. But from Fig. 6c and d, it is noticed that expected orbit length $E\left[ L \right]$ and expected system length $E\left[ {L_{S} } \right]$ are quickly decreasing with vacation rate $\left( \theta \right)$ for different joining probabilities $\left( p \right)$ (Fig. 7).

6.7 Cost optimization

In the queueing model, the most important issue is to find the optimal service rate during the WV period as well as in a normal busy periods and corresponding expected minimum cost. The cost function which is given in Eq. (41) is non-linear and complex so it is difficult to evaluate the optimum value by analytical approach. At first, we construct the average cost function per unit time in which the service rate in a normal busy period as well as in the WV periods both being the decision variables. Two search methods like QNM and GA, (Sanga and Jain 2019) can be applied to find the optimal service rates in the WV period as well as a normal service period. By finding the optimum values of the parameters $\mu ,\eta$, we find the minimum cost $TC(\mu,\eta)$.

First of all we set three cost-sets, which will have different cost-elements as seen from Table 5 and other parameters such as $\mu = 5, \, \lambda = 3, \, \eta = 2,\;\theta = 0.3$, etc. In Table 5, cost function for three cost sets are obtained using in quasi-Newton’s method with initial values $\mu = 5, \, \eta = 2$. We evaluate the optimal values of service rates ($\mu^{*} ,\eta^{*}$) and then extract the corresponding minimum expected cost and summarize in Table 6. The cost optimization results are shown in Fig. 8a–c corresponding to fixed arrival rate $\lambda = 3$ for $\alpha = 5,7,9$.

Table 5 Cost set for several cost elements

Table 6 $(\mu ^*,\eta ^*,TC(\mu ^*,\eta^ *)$ for different values of $\lambda$ using QNM and GA

Fig. 8

a–c Total cost varying joint values $\mu$ and $\eta$

From Fig. 8a–c, it is noticed that the tendency of minimum expected cost increases with the enhancement of different values of retrial rates $\left( \alpha \right)$ for a fixed arrival rate ($\lambda$). In Table 6, for cost set with the initial value of service rate as $\mu = 5,\eta = 2$, it is observed that the minimum expected cost 470.81/unit time is incurred at $\mu^{*} = 3.0795,\eta * = 0.401$ by using QNM. The curve representing the expected cost function is shown in Fig. 8a–c. It is clear that the cost function given in Eq. (41) is convex. From Table 6, it is noticed that as arrival rate is increasing, the cost is increasing and the corresponding optimal values $\left( {\mu^{*} ,\eta^{*} } \right)$ are also increasing.

GA discussed in Sect. 2.2, is considered for deriving the optimal parameters. By similarity to genetics, the strings is translated as chromosomes with singular bits indicating the appearance or non-appearance bit = 1 or 0 of a gene. In our investigation, the wellness (cost) function of a chromosome is dictated by the related estimation of the function that is being optimized. To implement GA, the following input and output are taken into account:

• Input: $\eta ,\theta ,p,C_{1} ,C_{2} ,C_{3} ,C_{4} ,C_{5}$, genes $\left( {U_{\mu } ,U_{\eta } } \right)$, population size, probability of mutation, probability of crossover.

• Output: Approximation solution of ${\mu }^{*},{\eta }^{*},\mathrm{ expected cost} ~TC({{\mu }^{*},\eta }^{*})$.

Now we obtain the optimal value of $(\mu^ *,\eta ^*)$ and expected minimum cost $TC(\mu ^*,\eta^ *)$ for various values of $\lambda$ which are shown in Table 6. The following findings are observed from Table 6:

• (i) The minimum expected cost $TC(\mu^ *,\eta ^*)$ increases as $\lambda$ increses.

• (ii) The optimal value ${\mu }^{*}$ decreases as $\lambda$ increases.

• (iii) For a fixed $\lambda$, when retrial rate enhances, the optimum cost also increases but the optimal service rate decreases.

We have found that optimal values of service rates, minimum expected cost obtained by the quasi-Newton method are in agreement with the optimal values of same derived by GA as shown in Table 6.

7 Conclusion

Markovian retrial queue by considering the concept of working vacation, balking behaviour of the customers and imperfect service studied in the present investigation, has several real-time applications in communication networks, production and manufacturing organizations, call and cyber centres, etc. In this model if a customer is not satisfied by the service provided by the server during the working vacation period (WV), he needs additional service; after getting service he departs from the system. The probability generating function can be easily used for providing the exact analytical results. The solution of the governing equations and various performance indices such as expected system length/queue length, expected waiting time etc. presented can be utilized for better quality of service of concerned organization. The cost optimization done might be advantageous to procure more benefits and minimize response time in a few queueing situations of routine life as well as industrial set up. The work done can be further extended by considering unreliable server or threshold based control policies viz. F-policy to control admission or N-policy to control the starting of service. It is to be mentioned that analytical analysis for such models will become tedious however, numerical results via soft computing techniques can be obtained.