Singularly perturbed delay differential equations of convection–diffusion type with integral boundary condition

Abstract

In this paper we consider a class of singularly perturbed delay differential equations of convection diffusion type with integral boundary condition. A finite difference scheme with an appropriate piecewise Shishkin type mesh is suggested to solve the problem. We prove that the method is of almost first order convergent. An error estimate is derived in the discrete norm. Numerical experiments support our theoretical results.

1 Introduction

Differential Equations with integral boundary conditions have plenty of applications. A Parabolic equation with nonlocal boundary conditions arising from electro chemistry is well studied by Choi and Chan [8]. In [10], Day have discussed Parabolic equations and thermodynamics. Cannon [6] have worked for the solution of the heat equation subject to the specification of energy. etc. The authors of [4, 12, 19] have proved that the problem of differential equations with integral boundary conditions is well posed. The authors of [1, 5, 7, 17, 26] have developed various numerical schemes on uniform meshes for singularly perturbed first and second order differential equations with integral boundary conditions.

A differential equation is said to be singularly perturbed delay differential equation, if it includes at least one delay term, involving unknown functions occuring with various different arguments and also the highest derivative term is multiplied by a small parameter. Such type of delay differential equations play a very important role in the mathematical models of science and engineering, such as, the human pupil-light reflex with mixed delay type [20], variational problems in control theory with small state problem [13], models of HIV infection [9] and signal transition [11], etc.

The standard numerical methods used for solving singularly perturbed differential equation are some time ill posed and fail to give analytical solution when the perturbation parameter $\varepsilon$ is small. Therefore, it is necessary to improve suitable numerical methods which are uniformly convergent to solve this type of differential equations. Many authors have worked on singularly perturbed differential equations with small and large delay using uniformly convergent numerical methods. In [18], Lange and Miura have discussed singularly perturbed linear second order differential-difference equations with small delay. In [14,15,16, 21, 23,24,25] finite difference and finite element methods are proposed to solve this kind of equations with large and small shifts.

In the present paper, motivated by the works of [1,2,3], we analyze a fitted finite difference scheme on a piecewise uniform mesh for the numerical solution of second order singularly perturbed convection diffusion equations with negative shift and integral boundary condition.

The present paper is arranged as follows. Statement of the problem is given in Sect. 2. In Sect. 3, maximum principle, stability result and appropriate bounds for the derivatives of the solution of the problem are presented. Section 4 describes the numerical method. Error analysis for approximate solution is given Sect. 5. Numerical results are given in Sect. 6. Conclusion are given in Sect. 7.

Throughout our analysis C and $C_1$ are generic positive constants that are independent of the parameter $\varepsilon$ and number of mesh points 2N. We assume that $\varepsilon \le CN^{-1}$, ${\overline{\varOmega }}=[0,2], \varOmega =(0,2), \varOmega _1=(0,1)$ and $\varOmega _2=(1,2)$. Further, $\varOmega ^*=\varOmega _1\cup \varOmega _2$, ${\overline{\varOmega }}^{2N}$ is denoted by  $\{0,1,2,\ldots ,2N\}$, ${\varOmega _1^{2N}}$ is denoted by  $\{1,2,\ldots ,N-1\}$, ${\varOmega _2^{2N}}$ is denoted by $\{N+1,N+2,\ldots ,2N-1\}$. The supremum norm used for studying the convergence of the numerical solution to the exact solution of a singular perturbation problem is

$$\begin{aligned} \Vert u\Vert _{\varOmega }=\sup _{x\in \varOmega }|u|. \end{aligned}$$

2 Statement of the problem

We consider the following singularly perturbed delay differential equation with integral boundary condition:

$$\begin{aligned} {\mathcal {L}}u(x)= & {} -\varepsilon u''(x)+a(x)u'(x)+b(x)u(x)+c(x)u(x-1)=f(x),~~ x\in \varOmega , \end{aligned}$$

(1)

$$\begin{aligned} u(x)= & {} \phi (x), ~~x\in [-\,1,0], \end{aligned}$$

(2)

$$\begin{aligned} {\mathcal {K}}u(2)= & {} u(2)-\varepsilon \int \limits _0^2g(x)u(x)dx=l, \end{aligned}$$

(3)

where $\phi (x)$ is sufficiently smooth on $[-\,1,0]$. For all $x\in {\overline{\varOmega }}$, it is assumed that the sufficient smooth functions a(x), b(x) and c(x) satisfy $a(x)> \alpha _1> \alpha > 0, b(x)\ge \beta \ge 0, c(x)\le \gamma \le 0$, $\alpha +\beta +\gamma >0$ and $\beta +\gamma \ge 0$.

Furthermore, g(x) is non negative and monotonic with $\int \nolimits _0^2g(x)dx<1$.

 The above assumptions ensure that $u\in X = C^{0}({\overline{\varOmega }})\cap C^{1}(\varOmega )\cap C^{2}(\varOmega _1\cup \varOmega _2).$

The problem (1)–(3) is equivalent to

$$\begin{aligned} {\mathcal {L}}u(x)=F(x), \end{aligned}$$

where

$$\begin{aligned} {\mathcal {L}}u(x)= & {} {\left\{ \begin{array}{ll} {\mathcal {L}}_{1}u(x)=-\varepsilon u''(x)+a(x)u'(x)+b(x)u(x),&{}\quad x\in \varOmega _1 ,\\ {\mathcal {L}}_{2}u(x)=-\varepsilon u''(x)\\ \qquad \quad +\,a(x)u'(x)+b(x)u(x)+c(x)u(x-1), &{}\quad x\in \varOmega _2 \end{array}\right. } \end{aligned}$$

(4)

$$\begin{aligned} F(x)= & {} {\left\{ \begin{array}{ll} f(x)-c(x)\phi (x-1),&{}\quad x\in \varOmega _1, \\ f(x),&{}\quad x\in \varOmega _2, \end{array}\right. } \end{aligned}$$

(5)

with boundary conditions

$$\begin{aligned} u(x)= & {} \phi (x),\quad x\in [-\,1,0], \end{aligned}$$

(6)

$$\begin{aligned} u(1^-)= & {} u(1^+), \quad u'(1^-)=u'(1^+), \end{aligned}$$

(7)

$$\begin{aligned} {\mathcal {K}}u(2)= & {} u(2)-\varepsilon \int \limits _0^2g(x)u(x)dx=l. \end{aligned}$$

(8)

3 Stability result

Lemma 1

(Maximum Principle) Let $\psi (x)$ be any function in X such that $\psi (0)\ge 0, {\mathcal {K}}\psi (2)\ge 0$, ${\mathcal {L}}_1\psi (x)\ge 0, \forall x\in \varOmega _1$, ${\mathcal {L}}_2\psi (x)\ge 0, \forall x\in \varOmega _2$, and $[\psi '](1)\le 0$ then $\psi (x)\ge 0$, $\forall x\in {\overline{\varOmega }}$.

Proof

Define a test function

$$\begin{aligned} s(x)= {\left\{ \begin{array}{ll} \frac{1}{8}+\frac{x}{2}, &{}\quad x\in [0,1] \\ \frac{3}{8}+\frac{x}{4}, &{}\quad x\in [1,2] \end{array}\right. } \end{aligned}$$

(9)

Note that $s(x)>0, \forall x \in {\overline{\varOmega }}$, ${\mathcal {L}} s(x)>0, \forall x\in \varOmega _1\cup \varOmega _2$, $s(0)>0$ , ${\mathcal {K}}s(2)>0$ and $[s'](1)<0$. Let

$$\begin{aligned} \mu =\max \left\{ \frac{-\psi (x)}{s(x)}:x\in {\overline{\varOmega }}\right\} . \end{aligned}$$

Then there exists $x_0\in {\overline{\varOmega }}$ such that $\psi (x_0)+\mu s(x_0)=0$ and $\psi (x)+\mu s(x)\ge 0,\forall x\in {\overline{\varOmega }}$. Therefore, the function $(\psi +\mu s)$ attains its minimum at $x=x_0$. Suppose the theorem does not hold true, then $\mu >0$.

Case (i)$x_0=0$

$$\begin{aligned} 0<(\psi +\mu s)(0)=\psi (0)+\mu s(0)=0 \end{aligned}$$

It is a contradiction.

Case (ii)$x_0\in \varOmega _1$

$$\begin{aligned} 0<{\mathcal {L}}(\psi +\mu s)(x_0)= & {} -\varepsilon (\psi +\mu s)''(x_0)+a(x_0)(\psi +\mu s)'(x_0)\\&+\, b(x_0) (\psi +\mu s)(x_0)\le 0 \end{aligned}$$

It is a contradiction.

Case (iii)$x_0=1$

$$\begin{aligned} 0\le [(\psi +\mu s)'](1)=[\psi '](1)+\mu [s'](1)<0 \end{aligned}$$

It is a contradiction.

Case (iv)$x_0\in \varOmega _2$

$$\begin{aligned} 0<{\mathcal {L}}(\psi +\mu s)(x_0)= & {} -\varepsilon (\psi +\mu s)''(x_0)+a(x_0)(\psi +\mu s)'(x_0)\\&+\, b(x_0)(\psi +\mu s)(x_0)+c(x_0)(\psi +\mu s)(x_0-1)\le 0 \end{aligned}$$

It is a contradiction.

Case (v)$x_0=2$

$$\begin{aligned} 0<{\mathcal {K}}(\psi +\mu s)(2)=(\psi +\mu s)(2)-\varepsilon \int \limits _0^2 g(x)(\psi +\mu s)(x)dx\le 0. \end{aligned}$$

It is a contradiction. Hence the proof of the theorem. $\square$

Lemma 2

(Stability Result) The solution u(x) of the problem (1)–(3), satisfies the bound

$$\begin{aligned} |u(x)|\le C \max \left\{ |u(0)|,|{\mathcal {K}}u(2)|,\sup _{x\in \varOmega ^*}|{\mathcal {L}}u(x)| \right\} ,\quad ~x\in {\overline{\varOmega }} \end{aligned}$$

Proof

This theorem can be proved by using Lemma 1 and the barrier functions $\theta ^{\pm }(x)=CMs(x)\pm u(x),~ x\in {\overline{\varOmega }}$, where $M= \max \left\{ |u(0)|,|{\mathcal {K}}u(2)|,\sup _{x\in \varOmega ^-\cup \varOmega ^+}\right. \left. |{\mathcal {L}}u(x)|\right\}$ and s(x) is the test function as in Lemma 1. $\square$

Lemma 3

Let u(x) be the solution of (1)–(3). Then we have the following bounds:

$$\begin{aligned} \Vert u^{(k)}(x)\Vert _{\varOmega ^*}\le C\varepsilon ^{-k}, \quad for \quad k=1,2,3 \end{aligned}$$

Proof

To bound $u'(x)$ on the interval $\varOmega _1$, we consider,

$$\begin{aligned} {\mathcal {L}}_{1}u(x)=-\varepsilon u''(x)+a(x)u'(x)+b(x)u(x)=f(x). \end{aligned}$$

Integrating the above equation on both sides,we have

$$\begin{aligned} -\, \varepsilon (u'(x)-u'(0))= & {} -[a(x)u(x)-a(0)u(0)]+\int \limits _0^x a'(t)u(t)dt\\&-\, \int \limits _0^x b(t)u(t)dt+\int \limits _0^x [f(t)-c(t)\phi (t-1)]dt \end{aligned}$$

Therefore,

$$\begin{aligned} \varepsilon u'(0)= & {} \varepsilon u'(x)-[a(x)u(x)-a(0)u(0)]+\int \limits _0^x a'(t)u(t)dt\\&-\,\int \limits _0^x b(t)u(t)dt+\int \limits _0^x [f(t)-c(t)\phi (t-1)]dt \end{aligned}$$

Then by the Mean value theorem, there exits $z\in (0,\varepsilon )$ such that $|\varepsilon u'(z)|\le C(\Vert u(x)\Vert ,\Vert f(x)\Vert ,\Vert \phi \Vert _{[-1,0]})$ and $|\varepsilon u'(0)|\le C(\Vert u(x)\Vert +\Vert f(x)\Vert +\Vert \phi (x)\Vert )$.

Hence,

$$\begin{aligned} |\varepsilon u'(x)|\le C~ \text {max}(\Vert u(x)\Vert ,\Vert f(x)\Vert ,\Vert \phi \Vert ). \end{aligned}$$

By a similar argument we can bound $u'(x)$ on $\varOmega _2$, as $|\varepsilon u'(x)|\le C$. From (4) and (5) we have $\Vert u^{(k)}(x)\Vert _{\varOmega ^{*}}\le C\varepsilon ^{-k}, k=2,3$. Hence the proof. $\square$

3.1 Decomposition of the solution

The Shishkin decomposition of the solution u(x) of (1)–(3) is $u(x)=v(x)+w(x)$, where v(x) and w(x) are regular and singular components respectively. Also $v(x)=v_0(x)+\varepsilon v_1(x)+\varepsilon ^2 v_2(x)$ where $v_0(x),v_1(x)$ and $v_2(x)$ are solutions of the following problems respectively:

$$\begin{aligned}&a(x)\frac{dv_0(x)}{dx}+b(x)v_0(x)+c(x)v_0(x-1)=f(x),x\in \varOmega \cup \{2\} \nonumber \\&\quad v_0(x)=\phi (x), \quad x\in [-1,0{]} \end{aligned}$$

(10)

Find $v_1(x)\in C^0({\overline{\varOmega }})\cap C^1(\{0\}\cup \varOmega ^*)$ such that

$$\begin{aligned}&a(x)\frac{dv_1(x)}{dx}+b(x)v_1(x)+c(x)v_1(x-1)=v''_0(x),~~~~x\in \varOmega ^{*}\cup \{2\} \nonumber \\&\quad v_0(x)=0, \quad x\in [-1,0{]} \end{aligned}$$

(11)

Find $v_2(x)\in X$ such that

$$\begin{aligned}&-\varepsilon \frac{d^2 v_2(x)}{dx^2}+a(x)\frac{dv_2(x)}{dx}+b(x)v_2(x)+c(x)v_2(x-1) = v''_1(x),~x\in \varOmega ^{*} \nonumber \\&\quad v_2(x)=0, \quad x\in [-\,1,0], \quad {\mathcal {K}}v_2(2)=0, \end{aligned}$$

(12)

The smooth component v(x) satisfies the following problem:

Find $v(x)\in C^0({\overline{\varOmega }})\cap C^2(\varOmega ^*)$, such that

$$\begin{aligned}&{\mathcal {L}}v(x)=-\varepsilon \frac{d^2 v(x)}{dx^2}+a(x)\frac{dv(x)}{dx}+b(x)v(x)+c(x)v(x-1)=f(x),~x\in \varOmega ^{*} \nonumber \\&\quad v(x)=\phi (x),x\in [-\,1,0], \quad v(1)=v_0(1)+\varepsilon v_1(1)+\varepsilon ^2 v_2(1),\nonumber \\&\quad {\mathcal {K}}v(2)={\mathcal {K}}v_0(2)+ \varepsilon {\mathcal {K}}v_1(2), \end{aligned}$$

(13)

Further w(x) satisfies the following problem:

Find $w(x)\in C^0({\overline{\varOmega }})\cap C^2(\varOmega ^*)$ such that

$$\begin{aligned}&{\mathcal {L}}w(x)=-\varepsilon \frac{d^2 w(x)}{dx^2}+a(x)\frac{dw(x)}{dx}+b(x)w(x)+c(x)w(x-1)=0,~x\in \varOmega ^{*} \nonumber \\&\quad w(x)=0,\quad x\in [-1,0], \quad [w'](1)=-[v'](1), \quad {\mathcal {K}}w(2)={\mathcal {K}}u(2)-{\mathcal {K}}v(2).\nonumber \\ \end{aligned}$$

(14)

We further decompose w(x) as $w(x)=w_B(x)+w_I(x)$,where the function $w_B(x)$ is boundary layer component and $w_I(x)$ is interior layer component, which are the solution of the following problems respectively:

Find $w_B(x)\in X$ such that

$$\begin{aligned}&{\mathcal {L}}w_B(x)=-\varepsilon \frac{d^2 w_B(x)}{dx^2}+a(x)\frac{dw_B(x)}{dx}+b(x)w_B(x)+c(x)w_B(x-1)=0, \nonumber \\&\quad w_B(x)=0, \quad x\in [-\,1,0], \quad {\mathcal {K}}w_B(2)={\mathcal {K}}u(2)-{\mathcal {K}}v(2). \end{aligned}$$

(15)

Find $w_I(x)\in C^0({\overline{\varOmega }})\cap C^2(\varOmega ^*)$ such that

$$\begin{aligned}&{\mathcal {L}}w_I(x)=-\varepsilon \frac{d^2 w_I(x)}{dx^2}+a(x)\frac{dw_I(x)}{dx}+b(x)w_I(x)+c(x)w_I(x-1)=0,\nonumber \\&\quad w_I(x)=0,\quad x\in [-1,0], \quad [w'_I](1)=-[v'](1), \quad {\mathcal {K}}w_I(2)=0. \end{aligned}$$

(16)

Theorem 1

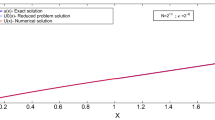
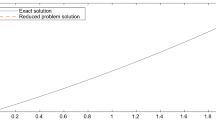
Let u(x) be the solution of the problem (1)–(3) and $v_0(x)$ be the reduced problem solution defined by (10). Then,

$$\begin{aligned} |u(x)-v_0(x)|\le C\left( \varepsilon +exp\left( \frac{-\alpha (2-x)}{\varepsilon }\right) \right) ,\quad x\in {\overline{\varOmega }} \end{aligned}$$

Proof

Consider the barrier functions

$$\begin{aligned} \theta ^\pm (x)=C\left( \varepsilon s(x)+exp\left( \frac{-\alpha (2-x)}{\varepsilon }\right) \right) \pm (u(x)-v_0(x)),\quad x\in {\overline{\varOmega }}. \end{aligned}$$

Clearly $\theta ^\pm (x)\in C^0({\overline{\varOmega }})\cap C^2(\varOmega _1\cup \varOmega _2)$. Note that, $\theta ^\pm (0)\ge 0$,

$$\begin{aligned} {\mathcal {K}}\theta ^\pm (2)= & {} \theta ^\pm (2)-\varepsilon \int \limits _0^2g(x)\theta ^\pm (x)dx\\= & {} C\varepsilon \left[ s(2)-\varepsilon \int \limits _0^2g(x)s(x)dx \right] \\&+\,C \left[ 1-\varepsilon \int \limits _0^2g(x)exp\left( \frac{-\alpha (2-x)}{\varepsilon }\right) dx \right] \pm {\mathcal {K}}u(2)\\\ge & {} C\varepsilon {\mathcal {K}}s(2)+C \left[ 1-\varepsilon \int \limits _0^2g(x)dx \right] \pm {\mathcal {K}}u(2)\\\ge & {} C \varepsilon {\mathcal {K}}s(2) \pm {\mathcal {K}}u(2)\ge 0. \end{aligned}$$

for a suitable choice of $C>0$.

Let $x\in \varOmega _1$. Then

$$\begin{aligned} {\mathcal {L}}_1\theta ^\pm (x)= & {} C\left[ \left( \frac{\alpha }{\varepsilon }(a(x)-\alpha )+ b(x)\right) exp\left( \frac{-\alpha (2-x)}{\varepsilon }\right) \right. \\&\left. +\, \varepsilon (a(x)+b(x)s(x))\right] \pm \varepsilon v''_0(x),\\\ge & {} C\left[ \left( \frac{\alpha }{\varepsilon }(\alpha _1-\alpha )+\beta \right) exp\left( \frac{-\alpha (2-x)}{\varepsilon } \right) + \varepsilon \left( \alpha +\frac{\beta }{8}\right) \right] \pm C\varepsilon ,\\\ge & {} 0. \end{aligned}$$

for a suitable choice of $C>0$.

Let $x\in \varOmega _2$. Then

$$\begin{aligned} {\mathcal {L}}_2\theta ^\pm (x)= & {} C\left[ \left( \frac{\alpha }{\varepsilon }(a(x)-\alpha )+ b(x)+c(x)exp\left( -\frac{\alpha }{\varepsilon }\right) \right) exp\left( \frac{-\alpha (2-x)}{\varepsilon }\right) \right. \\&\left. +\,\varepsilon (a(x)+b(x)s(x)+c(x)s(x-1)\right] \pm \varepsilon v''_0(x),\\\ge & {} C\left[ \left( \frac{\alpha }{\varepsilon }(\alpha _1-\alpha )+\beta +\gamma exp\left( -\frac{\alpha }{\varepsilon }\right) \right) exp\left( \frac{-\alpha (2-x)}{\varepsilon }\right) \right. \\&\left. +\,\varepsilon \left( \alpha +\frac{\beta }{8}+\frac{\gamma }{8}\right) \right] \pm C\varepsilon ,\\\ge & {} 0. \end{aligned}$$

for a suitable choice of $C>0$.

Then by the Lemma 1,we have $\theta ^\pm (x)\ge 0,x\in {\overline{\varOmega }}$. Hence the proof of the theorem. $\square$

Lemma 4

The regular component v(x) and the singular component w(x) of the solution u(x) satisfy the following bounds.

$$\begin{aligned}&\displaystyle \Vert v^k(x)\Vert _{\varOmega ^*} \le C(1+\varepsilon ^{2-k}),~~\ for ~ k=0,1,2,3 \end{aligned}$$

(17)

$$\begin{aligned}&\displaystyle |w_B^k(x)| \le C\varepsilon ^{-k}exp\left( \frac{-\alpha (2-x)}{\varepsilon }\right) ,\quad x\in \varOmega ^*, \quad k=0,1,2,3 \end{aligned}$$

(18)

$$\begin{aligned}&\displaystyle |w_I^k(x)| \le C {\left\{ \begin{array}{ll} \varepsilon ^{1-k}exp(\frac{-\alpha (1-x)}{\varepsilon }), &{}\quad x\in \varOmega _1, \\ \varepsilon ^{1-k}, &{}\quad x\in \varOmega _2, \end{array}\right. } \quad k=0,1,2,3 \end{aligned}$$

(19)

Proof

Integrating (10) and (12) and using the stability result, the inequality (17) can be proved easily.

To prove the inequalities (18), consider the barrier functions

$$\begin{aligned} \varPhi ^\pm (x)=C_1\left( exp\left( \frac{-\alpha (2-x)}{\varepsilon }\right) \right) \pm w_B(x),\quad x\in {\overline{\varOmega }}. \end{aligned}$$

It easy to see that $\varPhi ^\pm (0)\ge 0$.

Further,

$$\begin{aligned} {\mathcal {K}}\varPhi ^\pm (2)= & {} \varPhi ^\pm (2)-\varepsilon \int \limits _0^2g(x)\varPhi ^\pm (x)dx\\= & {} C \left[ 1-\varepsilon \int \limits _0^2g(x)exp\left( \frac{-\alpha (2-x)}{\varepsilon }\right) dx \right] \pm {\mathcal {K}}w_B(2)\\\ge & {} 0 \end{aligned}$$

and also

$$\begin{aligned} {\mathcal {L}}\varPhi ^\pm (x)= & {} C_1\bigg [ \frac{\alpha }{\varepsilon }(a(x)-\alpha )+ b(x)+c(x)exp\bigg (-\frac{\alpha }{\varepsilon }\bigg )\bigg ]\\&\quad \times exp\bigg (\frac{-\alpha (2-x)}{\varepsilon }\bigg ) \pm ~~{\mathcal {L}}w_B(x)\\\ge & {} C_1\bigg [ \frac{\alpha }{\varepsilon }(\alpha _1-\alpha )+\beta +\gamma exp\bigg (-\frac{\alpha }{\varepsilon }\bigg )\bigg ] exp\bigg (\frac{ -\alpha (2-x)}{\varepsilon }\bigg ) \pm ~0\\\ge & {} 0. \end{aligned}$$

By the Lemma 1,

$$\begin{aligned} |w_B(x)| \le Cexp\left( \frac{-\alpha (2-x)}{\varepsilon }\right) . \end{aligned}$$

Integration of (15) yields the estimates of $|w'_B(x)|$. From the differential equations (14), one can derive the rest of the derivative estimates (18).

To prove the inequalities (19), consider the barrier functions

$$\begin{aligned} \varPhi ^\pm (x)=C_1\varepsilon \left( \text {exp}\left( \frac{-\alpha (1-x)}{\varepsilon }\right) \right) \pm w_I(x), \quad x\in [0,1]. \end{aligned}$$

Clearly, $\varPhi ^\pm (0)\ge 0$ and $\varPhi ^\pm (1)\ge 0$ and also ${\mathcal {L}}_1\varPhi (x_i)\ge 0$, easily proves first inequality.

Similarly, consider the following barrier function

$$\begin{aligned} \varPhi ^\pm (x)=C_1x\varepsilon \pm w_I(x),\quad x\in [1,2]. \end{aligned}$$

Note that $\varPhi ^\pm (1)\ge 0$, and

$$\begin{aligned} {\mathcal {K}}\varPhi ^\pm (2)= & {} \varPhi ^\pm (2)-\varepsilon \int \limits _0^2g(x)\varPhi ^\pm (x)dx\\= & {} C\varepsilon \left[ 2-\varepsilon \int \limits _0^2xg(x)dx \right] \pm {\mathcal {K}}w_I(2)\\= & {} 2C\varepsilon \left[ 1-\varepsilon \int \limits _0^2g(x)dx \right] \pm ~0\\\ge & {} 0\\ {\mathcal {L}}_2\varPhi ^\pm (x)= & {} -\varepsilon (\varPhi ^\pm )''(x)+a(x)(\varPhi ^\pm )'+b(x)\varPhi ^\pm (x) +c(x)\varPhi ^\pm (x-1)\ge 0 \end{aligned}$$

Hence the proof. $\square$

Note: From the above theorem, it is not difficult to prove

$$\begin{aligned} |u(x)-v(x)|\le C {\left\{ \begin{array}{ll} \varepsilon ~ exp(\frac{-\alpha (1-x)}{\varepsilon })+exp(\frac{-\alpha (2-x)}{\varepsilon }), &{}\quad x\in \varOmega _1 \\ \varepsilon + exp(\frac{-\alpha (2-x)}{\varepsilon }), &{}\quad x\in \varOmega _2. \end{array}\right. } \end{aligned}$$

(20)

4 The discrete problem

4.1 Mesh selection procedure

The BVP (1)–(3) exhibits strong boundary layer at $x=2$ and interior layer at $x=1$.

The interval [0, 1] is partitioned into $[0,1-\sigma ]$ and $[1-\sigma ,1]$ and the interval [1, 2] is partitioned as $[1,2-\sigma ]$ and $[2-\sigma ,2],$ where $\sigma$ is transition parameter for this mesh defined by

$$\begin{aligned} \sigma =\min \left\{ \frac{1}{2}, 2{\frac{\varepsilon }{\alpha }}\ln N \right\} . \end{aligned}$$

The mesh ${\bar{\varOmega }}^{2N}=\{x_0,x_1,\ldots ,x_{2N}\}$ is defined by

$$\begin{aligned}\begin{array}{rcl} &{}&{} x_0=0,\\ &{}&{} x_i=x_0+iH, i=1 to \frac{N}{2}\\ &{}&{} x_{i+\frac{N}{2}} =x_{\frac{N}{2}}+ih,i=1 to \frac{N}{2}\\ &{}&{} x_{i+{N}} =x_{N}+iH,i=1 to \frac{N}{2}\\ &{}&{} x_{i+\frac{3N}{2}} =x_{\frac{3N}{2}}+ih, i=1 to \frac{N}{2} \end{array} \end{aligned}$$

where $h=\frac{2\sigma }{N}$, $H=\frac{2(1-\sigma )}{N}$.

4.2 Discrete problem

The discrete scheme corresponding to the original problem (1)–(3) is as follows:

For i $=$ 1, 2, ..., $N-1,$

$$\begin{aligned} {\mathcal {L}}_1^NU_i=f_i-b_i\phi _{i-N}, \end{aligned}$$

(21)

For i $= N+1,\ldots ,2N-1$,

$$\begin{aligned} {\mathcal {L}}_2^NU_i=f_i, \end{aligned}$$

(22)

subject to the boundary conditions:

$$\begin{aligned}&U_i = \phi _i,\ i=-N,-N+1,\ldots ,0 \end{aligned}$$

(23)

$$\begin{aligned}&{\mathcal {K}}^NU_{2N}=U_{2N}-\sum \limits _{i=1}^{2N} \frac{g_{i-1}U{i-1}+g_iU_i}{2}h_i \end{aligned}$$

(24)

and

$$\begin{aligned} D^-U_N=D^+U_N \end{aligned}$$

(25)

where

$$\begin{aligned}&\displaystyle {\mathcal {L}}_1^NU_i=-\varepsilon \delta ^2U(x_i)+a(x_i)D^{-}U(x_i)+b(x_i)U(x_i)\\&\displaystyle {\mathcal {L}}_2^NU_i=-\varepsilon \delta ^2U(x_i)+a(x_i)D^{-}U(x_i)+b(x_i)U(x_i)+c(x_i)U(x_{i-N}) \end{aligned}$$

Lemma 5

(Discrete Maximum Principle) Assume that

$$\begin{aligned} \sum \limits _{i=1}^{2N}\frac{g_{i-1}+g_i}{2}h_i=\rho <1 \end{aligned}$$

and mesh function $\varPsi (x_i)$ satisfies $\varPsi (x_0)\ge 0$, and ${\mathcal {K}}^{N}\varPsi (x_{2N})\ge 0$, Then ${\mathcal {L}}_1^N\varPsi (x_i)\ge 0$, $\forall ~ x_i \in \varOmega _1^{2N}$, ${\mathcal {L}}_2^N\varPsi (x_i)\ge 0,$$\forall ~ x_i\in \varOmega _2^{2N}$ and $D^+(\varPsi (x_N))-D^-(\varPsi (x_N))\le 0$ imply that $\varPsi (x_i)\ge 0$, $\forall ~ x_i \in {\overline{\varOmega }}^{2N}$.

Proof

$$\begin{aligned} \text {Define}~~ s(x_i)= {\left\{ \begin{array}{ll} \frac{1}{8}+\frac{x_i}{2}, &{}\quad x_i\in [0,1]\cap {\overline{\varOmega }}^{2N}, \\ \frac{3}{8}+\frac{x_i}{4}, &{}\quad x_i\in [1,2]\cap {\overline{\varOmega }}^{2N}, \end{array}\right. } \end{aligned}$$

Note that $s(x_i)>0, \forall x_i \in {\overline{\varOmega }}^{2N}$, ${\mathcal {L}}s(x_i)>0, \forall x_i\in \varOmega _1^{2N}\cup \varOmega _2^{2N}$, $s(0)>0$ , ${\mathcal {K}}s(x_{2N})>0$ and $[s'](x_N)<0$. Let

$$\begin{aligned} \mu =\max \left\{ \frac{-\psi (x_i)}{s(x_i)}:x_i\in {\overline{\varOmega }}^{2N}\right\} . \end{aligned}$$

Then there exists $x_k\in {\overline{\varOmega }}^{2N}$ such that $\psi (x_k)+\mu s(x_k)=0$ and $\psi (x_i)+\mu s(x_i)\ge 0,\forall x_i\in {\overline{\varOmega }}^{2N}$. Therefore, the function $(\psi +\mu s)$ attains its minimum at $x=x_k$. Suppose the theorem does not hold true, then $\mu >0$.

Case (i): $x_k=x_0$

$$\begin{aligned} 0<(\psi +\mu s)(x_0)=0 \end{aligned}$$

It is a contradiction.

Case (ii): $x_k\in \varOmega _1^{2N}$

$$\begin{aligned} 0<{\mathcal {L}}_1^N(\psi +\mu s)(x_k)\le 0 \end{aligned}$$

It is a contradiction.

Case (iii): $x_k=x_N$

$$\begin{aligned} 0\le [D(\psi +\mu s)](x_N)<0 \end{aligned}$$

It is a contradiction.

Case (iv): $x_k\in \varOmega _2^{2N}$

$$\begin{aligned} 0<{\mathcal {L}}_2^N(\psi +\mu s)(x_k)\le 0 \end{aligned}$$

It is a contradiction.

Case (v): $x_k=x_{2N}$

$$\begin{aligned}&0< {\mathcal {K}}^N(\psi +\mu s)x_{2N}=(\psi +\mu s)x_{2N}\nonumber \\&\quad -\sum \limits _{i=1}^{2N} \frac{g_{i-1}(\psi +\mu s)x_{i-1}+g_i(\psi +\mu s)x_{i}}{2}h_i\le 0 \end{aligned}$$

It is a contradiction. Hence the proof of the theorem. $\square$

Lemma 6

Let $\varPsi (x_i)$ be any mesh function then for $0\le i\le 2N$,

$$\begin{aligned} |\varPsi (x_i)|\le C \max \bigg \{ |\varPsi (x_0)|,|{\mathcal {K}}^N\varPsi (x_{2N})|,\max _{i\in \varOmega _1^{2N}\cup \varOmega _2^{2N}}|{\mathcal {L}}^N\varPsi (x_i)| \bigg \}. \end{aligned}$$

Proof

Consider the barrier functions

$$\begin{aligned} \theta ^\pm (x_i)=CM\pm \varPsi (x_i), ~~~\forall ~ x_i \in {\overline{\varOmega }}^{2N}. \end{aligned}$$

(26)

where

$$\begin{aligned} M=\max \{|\varPsi (x_0)|,|{\mathcal {K}}^{N}\varPsi (x_{2N})|,\max _{i\in \varOmega _1^{2N}\cup \varOmega _2^{2N}}|{\mathcal {L}}^N\varPsi (x_i)| \}. \end{aligned}$$

From Eq. (26) it is clear that $\theta ^\pm (x_0)\ge 0$ and ${\mathcal {K}}^{N}\theta ^\pm (x_{2N})\ge 0$,

$$\begin{aligned}&{\mathcal {L}}_1^N\theta ^\pm (x_i) \ge 0,\quad \forall ~ x_i \in \varOmega _1^{2N},\\&{\mathcal {L}}_2^N\theta ^\pm (x_i) \ge 0,\quad \forall ~ x_i\in \varOmega _2^{2N},\\&D^+\theta ^\pm (x_N)- D^-\theta ^\pm (x_N) \le 0. \end{aligned}$$

Using Lemma 5, $\theta ^\pm (x_i)\ge 0$,    $\forall ~ x_i \in {\overline{\varOmega }}^{2N}.$$\square$

5 Error estimate

To calculate the error estimate for the numerical solution, we decompose the discrete solution $U(x_i)$ into $V(x_i)$ and $W(x_i)$ as $U(x_i)=V(x_i)+W(x_i),$ where $V(x_i)$ and $W(x_i)$ satisfy the following differential equations respectively.

$$\begin{aligned} {\mathcal {L}}^NV(x_i)= & {} -\varepsilon \delta ^2V(x_i)+a(x_i)D^{-}V(x_i)+b(x_i)V(x_i)\nonumber \\&+\,c(x_i)V(x_{i}-x_{N})=f_i,~~~~{i\in I_{2N\setminus \{0,N,2N\}}} \nonumber \\ V(x_0)= & {} v(0),~ [D]V(x_{N})=[v'](1),~{\mathcal {K}} V(x_{2N})={\mathcal {K}}v(2). \end{aligned}$$

(27)

$$\begin{aligned} {\mathcal {L}}^NW(x_i)= & {} -\varepsilon \delta ^2W(x_i)+a(x_i)D^{-}W(x_i)+b(x_i)W(x_i) \nonumber \\&+\,c(x_i)W(x_{i}-x_{N})=f_i,~~~~{i\in I_{N \setminus \{0,N,2N\}}} \nonumber \\ W(x_0)= & {} w(0),~ [D]W(x_{N})=-[D]V(x_{N}),~ {\mathcal {K}} W(x_{2N})={\mathcal {K}} w(2). \end{aligned}$$

(28)

Theorem 2

Let $U(x_i)$ be a numerical solution of (1)–(3) defined by (21)–(25) and $V(x_i)$ be a numerical solution of (13) defined by (27). Then

$$\begin{aligned} |U(x_i)-V(x_i)|\le C {\left\{ \begin{array}{ll} N^{-1}, \quad i=0,1,\ldots ,\frac{3N}{2} \\ N^{-1}+|l-V(x_{2N})|, \quad i=\frac{3N}{2}+1,\ldots ,2N. \end{array}\right. } \end{aligned}$$

Proof

Consider the barrier functions

$$\begin{aligned} \theta ^\pm (x_i)=C_1 N^{-1}s(x_i)+C_1 x_i \varPsi (x_i)\pm (U(x_i)-V(x_i)), \forall x_i \in {\overline{\varOmega }}^{2N}, \\ \text {where}\quad \varPsi (x_i)= {\left\{ \begin{array}{ll} 0, \quad i=0,1,\ldots ,\frac{3N}{2}, \\ |l-V(x_{2N})|, \quad i=\frac{3N}{2}+1,\ldots ,2N. \end{array}\right. } \end{aligned}$$

It is clear that $\theta ^\pm (x_0)\ge 0$ and ${\mathcal {K}}\theta ^\pm (x_{2N})\ge 0.$

If $\forall ~ x_i \in \varOmega _1^{2N}$

$$\begin{aligned} {\mathcal {L}}_1^N\theta ^\pm (x_i)\ge 0 \end{aligned}$$

If $\forall ~ x_i \in \varOmega _2^{2N}$

$$\begin{aligned} ~~{\mathcal {L}}_2^N\theta ^\pm (x_i) \ge 0, \text {and} \end{aligned}$$

$[D]^+\theta ^\pm (x_{N})=-C_1 \frac{N^{-1}}{4}\pm [v'](1)<0$ for a suitable choice of $C_1>0.$

By Lemma 5, this thorem gets proved. $\square$

Theorem 3

Let $V(x_i)$ be a numerical solution of (13) defined by (27). Then

$$\begin{aligned} |v(x_i)-V(x_i)|\le CN^{-1},~~x_i \in {\overline{\varOmega }}^{2N}. \end{aligned}$$

Proof

If $x_i \in \varOmega _1^{2N}$ and $x_i\in \varOmega _2^{2N}$ then by [22], we have

$$\begin{aligned} |L^{N}(v(x_i)-V(x_i))|\le CN^{-1}, i\in \varOmega _1^{2N}\cup \varOmega _2^{2N}. \end{aligned}$$

By the Lemma 6, we have

$$\begin{aligned} |v(x_i)-V(x_i)|\le CN^{-1},~~ i\in \varOmega _1^{2N}\cup \varOmega _2^{2N}. \end{aligned}$$

At the point $x_i=x_{2N}$,

$$\begin{aligned} {\mathcal {K}}^{N}(V-v)(x_{2N})= & {} {\mathcal {K}}^{N}V(x_{2N})-{\mathcal {K}}^{N}v(x_{2N})\\= & {} l-{\mathcal {K}}^{N}v(x_{2N})\\= & {} {\mathcal {K}}v(x_{2N})-{\mathcal {K}}^{N}v(x_{2N})\\= & {} v(x_{2N})-\int \limits _{x_0}^{x_{2N}}g(x)v(x)dx-v(x_{2N})+\sum \limits _{i=1}^{2N}\frac{g_{i-1}v_{ i-1} +g_iv_i}{2}h_i\\ |{\mathcal {K}}^{N}(V-v)(x_{2N})|\le & {} C\varepsilon ((h_1^3v''(\chi _1)+\dots +h_{2N}^3v''(\chi _{2N}))\\\le & {} C\varepsilon (h_1^3+\dots +h_{2N}^3)\\\le & {} CN^{-2}\\\le & {} CN^{-1},~~~\text {where} ~~x_{i-1}\le \chi _i\le x_i, 1\le i\le 2N. \end{aligned}$$

Applying Lemma 6 we have $|\mathcal (V-v)(x_{2N})|\le CN^{-1}$.

Hence $|v(x_i)-V(x_i)|\le CN^{-1},~~ i\in {\overline{\varOmega }}^{2N}.$$\square$

Theorem 4

Let $W(x_i)$ be a numerical solution of (14) defined by (28). Then

$$\begin{aligned} |w(x_i)-W(x_i)|\le CN^{-1} ln^{2}N, ~~x_i\in {\overline{\varOmega }}^{2N} \end{aligned}$$

Proof

Note that

$$\begin{aligned} |w(x_i)-W(x_i)|\le |u(x_i)-U(x_i)|+|v(x_i)-V(x_i)| \end{aligned}$$

Then by (20), Theorems 1 and 3, we have

$$\begin{aligned} |u(x_i)-U(x_i)|\le |U(x_i)-V(x_i)|+|v(x_i)-V(x_i)|+|u(x_i)-v(x_i)|. \end{aligned}$$

Now,

$$\begin{aligned} |w(x_i)-W(x_i)|\le & {} |U(x_i)-V(x_i)|+2|v(x_i)-V(x_i)|+|u(x_i)-v(x_i)|,\nonumber \\\le & {} C_1 N^{-1}+C_1 \exp (\frac{-\alpha (2-x)}{\varepsilon })+\varepsilon \nonumber \\\le & {} C_1 \exp (\frac{-\alpha \sigma }{\varepsilon })+ C_1 N^{-1}\le CN^{-1}, i=0~ \text {to}~\frac{3N}{2} \end{aligned}$$

(29)

Consider mesh functions

$$\begin{aligned}&\phi ^\pm (x_i)=C_1N^{-1}s(x_i)+ C_1 N^{-1} \frac{\sigma }{\varepsilon ^2}(x_i-(2-\sigma ))\\&\quad \pm \, (w(x_i)-W(x_i)) ~~x_i\in [2-\sigma ,2]\cap {\overline{\varOmega }}^{2N}. \end{aligned}$$

From (29), it is easy to check $\phi ^\pm (x_\frac{3N}{2})\ge 0$ and ${\mathcal {K}}\phi ^\pm (x_{2N})\ge 0.$ For a suitable choice of $C_1\>0$.

$$\begin{aligned} {\mathcal {L}}^N\phi ^\pm (x_i)\ge 0 \end{aligned}$$

Then by the Lemma 5, we have $\phi ^\pm (x_i)\ge 0, ~~x_i\in {\overline{\varOmega }}^{2N}$. Therefore

$$\begin{aligned} |w(x_i)-W(x_i)|\le CN^{-1} ln^{2}N, ~~x_i\in {\overline{\varOmega }}^{2N} \end{aligned}$$

Hence the proof. $\square$

Theorem 5

Let $U(x_i)$ be the numerical solution of (1)–(3) defined by (21)–(25). Then

$$\begin{aligned} |u(x_i)-U(x_i)|\le CN^{-1} ln^{2}N, ~~x_i\in {\overline{\varOmega }}^{2N} \end{aligned}$$

Proof

The descried estimate follows from the fact that $u_k=v_k+w_k$ , $U_k=V_k+W_k$ and from the above Theorems 3 and 4. $\square$

6 Numerical experiments

In this section, four examples are given to illustrate the numerical method discussed above. The exact solution of the test problems are not known. Therefore, we use the double mesh principle to estimate the error and compute the experiment rate of convergence to the computed solution. For this we put

$$\begin{aligned} D_\varepsilon ^N=\max _{0 \le i \le 2N}|U_i^N-U_{2i}^{2N}| \end{aligned}$$

where $U_i^N$ and $U_{2i}^{2N}$ are the ith components of the numerical solutions on meshs of N and 2N, respectively. We compute the uniform error and the rate of convergence as

$$\begin{aligned} D^N=\max _\varepsilon D_\varepsilon ^N \quad \text {and} \quad p^N=log_2 \left( \frac{D^N}{D^{2N}}\right) \end{aligned}$$

The numerical results are presented for the values of the perturbation parameter $\varepsilon \in \{2^{-2},2^{-3},\ldots ,2^{-20}\}$

Example 6.1

$$\begin{aligned}&-\varepsilon u^{''}(x)+3u'(x)+u(x)-u(x-1) = 1,\quad \text {for}\quad x\in (0,1)\cup (1,2),\\&\quad u(x)=1 \quad \text {for} \quad x\in [-1,0],~{\mathcal {K}}u(2)= u(2)-\varepsilon \int \limits _0^2 \frac{x}{3} u(x)dx=2. \end{aligned}$$

Example 6.2

$$\begin{aligned}&-\varepsilon u^{''}(x)+5u'(x)+(x+1)u(x)-u(x-1)= x^2, \quad \text {for} \quad x\in (0,1)\cup (1,2),\\&\quad u(x)=1 \quad \text {for} \quad x\in [-1,0],{\mathcal {K}}u(2)=u(2)-\varepsilon \int \limits _0^2 \frac{x}{3} u(x)dx=2. \end{aligned}$$

Example 6.3

$$\begin{aligned}&-\varepsilon u^{''}(x)+3u'(x)-u(x-1)=0,\quad \text {for} \quad x\in (0,1)\cup (1,2),\\&\quad u(x)=1 \quad \text {for} \quad x\in [-1,0],~{\mathcal {K}}u(2)=u(2)-\varepsilon \int \limits _0^2 \frac{x}{3} u(x)dx=2. \end{aligned}$$

Example 6.4

$$\begin{aligned}&-\varepsilon u^{''}(x)+(x+10)u'(x)-u(x-1)=x^2,\quad \text {for} \quad x\in (0,1)\cup (1,2),\\&u(x)=1 \quad \text {for} \quad x\in [-1,0],{\mathcal {K}}u(2)=u(2)-\varepsilon \int \limits _0^2 \frac{x}{3} u(x)dx=2. \end{aligned}$$

7 Conclusion

We have solved singularly perturbed delay differential equations of convection diffusion type with integral boundary condition (1)–(3), using finite difference method on Shishkin mesh. The method is shown to be of order $O(N^{-1}\ln ^2N)$, that is, the method has almost first order convergence with respect to $\varepsilon$. Four examples are given to illustrate the numerical method. Our numerical results reflect the theoretical estimates. Maximum pointwise errors and order of convergence of the Examples 6.1, 6.2, 6.3 and 6.4 are given in Tables 1, 2, 3 and 4 respectively. The maximum errors of Examples 6.1, 6.2, 6.3 and 6.4 are shown in Figs. 1, 2, 3, and 4 respectively.

Table 1 Computed maximum pointwise errors $D_\varepsilon ^N$, computed $\varepsilon$-uniform errors $D^N$ and the $\varepsilon$-uniform orders of convergence $p^N$ for Example 6.1

Table 2 Computed maximum pointwise errors $D_\varepsilon ^N$, computed $\varepsilon$-uniform errors $D^N$ and the $\varepsilon$-uniform orders of convergence $p^N$ for Example 6.2

Table 3 Computed maximum pointwise errors $D_\varepsilon ^N$, computed $\varepsilon$-uniform errors $D^N$ and the $\varepsilon$-uniform orders of convergence $p^N$ for Example 6.3

Table 4 Computed maximum pointwise errors $D_\varepsilon ^N$, computed $\varepsilon$-uniform errors $D^N$ and the $\varepsilon$-uniform orders of convergence $p^N$ for Example 6.4

Fig. 1

Maximum pointwise error of the numerical solution of Example 6.1

Fig. 2

Maximum pointwise error of the numerical solution of Example 6.2

Fig. 3

Maximum pointwise error of the numerical solution of Example 6.3

Fig. 4

Maximum pointwise error of the numerical solution of Example 6.4