Numerical solutions of a class of linear and nonlinear Volterra integral equations of the third kind using collocation method based on radial basis functions

Abstract

In this paper, we use a method based on radial basis functions and the collocation method for the numerical solution of a class of Volterra integral equations of the third kind, using zeros of the shifted Legendre polynomial as the collocation points. The principal benefit of this scheme is that it does not require any discretization and so it is independent of the geometry of the domains and can thus be applied to the solution of various kinds of integral equations. The procedure is more flexible for the majority of classes of Volterra integral equations of the third kind. The construction of the suggested technique has been introduced. The convergence analysis of the presented method is investigated. Finally, certain numerical examples are included to show the accuracy and efficiency of the new technique. The numerical results obtained and their comparison with other methods demonstrate the reliability of this method. Our proposed method gives acceptable accuracy with a small use of data, which also reduces the computational costs.

1 Introduction

The integral equations appear as reformulations of other mathematical problems, such as partial differential equations and ordinary differential equations. Over the last few years, the theory and application of integral equations of the third kind have been a major theme in applied mathematics. Researchers have conducted extensive scientific studies on these equations. Third kind Volterra integral equations have received greater attention; they have appeared in many problems in different branches of science and engineering, such as heat transfer, population growth models, and shock wave problems. In recent years, meshless methods have attracted the attention of mathematicians and engineers. Therefore, there are several works on meshless approximation methods in various branches of science. For instance, RBFs are extensively applied for the approximation of multivariate functions or the interpolation of sparse data. The main purpose of this paper is to study the numerical solution by meshless techniques of a class of linear and nonlinear VIEs of the third kind in the following form:

$$\begin{aligned} t^{\beta }u(t)=t^{\beta }f(t)+\int _{0}^{t} s^{\beta -1} k(t, s) G(u(s)) d s, \quad t \in I, \end{aligned}$$

(1)

and

$$\begin{aligned} t^{\beta } u(t)=t^{\beta }f(t)+\int _{0}^{t} s^{\beta -1} k(t, s) u(s) d s, \quad t \in I, \end{aligned}$$

(2)

in which $s^{\beta -1} k(t, s) \in C\left( D\right)$, $t^{\beta }f(t) \in C(I)$, $I=[0, T]$, u(t) is an unknown function, $D:=\{(t, s), 0 \le s \le t, t \in I\}$ and $G \in C^1(\mathbb {R})$. The Eq. (1) can be written in the form of the equivalent cordial integral equation

$$\begin{aligned} u(t)=f(t)+\left( \mathcal {V}_{k, \beta }\right) (u)(t), \quad t \in I, \end{aligned}$$

in which

$$\begin{aligned} \left( \mathcal {V}_{k, \beta }\right) (u)(t)=\int _0^t t^{-1} \phi \left( \frac{s}{t}\right) k(t, s) G(u(s)) d s, \end{aligned}$$

where $\phi (r)=r^{\beta -1} \in L^1(0,1)$.

Whereas, the Eq. (2) can be written in the form of the equivalent cordial integral equation

$$\begin{aligned} u(t)=f(t)+\left( \mathcal {V}_{k}\right) (u)(t), \quad t \in I, \end{aligned}$$

in which

$$\begin{aligned} \left( \mathcal {V}_{k}\right) (u)(t)=\int _0^t t^{-1} \phi \left( \frac{s}{t}\right) k(t, s) u(s) d s, \end{aligned}$$

where $\phi (r)=r^{\beta -1} \in L^1(0,1)$ is called the core (Vainikko 2009). Many researchers in different branches of science and engineering have been interested in the numerical solution of integral equations of the third kind. We would like to review some of the most recent work concerning the numerical solution of these equations, like the spectral collocation method presented by Dastjerdi and Shayanfard (2021). In Shayanfard et al. (2019) the multistep collocation method is applied to solve linear Volterra integral equations of the third kind. The existence, uniqueness, and regularity of the solution of linear VIEs of the third kind are examined in Allaei et al. (2015). For a detailed discussion of the analytical properties of solutions of linear and nonlinear VIEs of the third kind, see also Song et al. (2019), Vainikko (2009, 2010b). Whereas for equations with compact operators, the numerical analysis is analogous to that of classical VIEs of the second kind (see, for example, Brunner et al. 1999; Brunner 2004). A numerical analysis of collocation methods for third-kind VIEs is investigated in Allaei et al. (2017). The superconvergence analysis of collocation methods is presented in Song et al. (2022). Over the past few decades, meshless techniques have attracted the attention of various researchers in many fields of applied sciences and engineering. The meshless approximations have important applications in various computational mathematics problems, such as integral equations (Aourir et al. 2024). Meshless methods don’t need a structured grid and use only a scattered set of collocation points. The RBFs are efficient procedures for interpolating an unknown function on a scattered set of points that have been used in the past few decades. It is important to mention that the RBF method does not require any domain elements, so it is meshless. The history of RBF estimates dates back to 1968. The most common basic meshless techniques are known in the literature as radial basis functions (RBFs) and moving least squares (MLS) methods. In this paper, we propose a new method based on the RBF method for the solution of a class of linear and nonlinear third kind Volterra integral equations of the form (1) and (2). We use RBFs with collocation nodes $\left\{ t_j\right\} _{j=1}^N$ which are the zeros of the shifted Legendre polynomial $L_N(t), 0 \leqslant t \leqslant 1$. The shifted Legendre polynomials $L_i(t)$ are defined on the interval [0, 1]

$$\begin{aligned} \begin{aligned}&L_0(t)=1, \quad L_1(t)=2 t-1 \\&L_{i+1}(t)=\frac{2 i+1}{i+1}(2 t-1) L_i(t)-\frac{i}{i+1} L_{i-1}(t), \quad i=1,2,3, \ldots \end{aligned} \end{aligned}$$

The outline of this paper contains the following sections

• Section 2: Existence and uniqueness of solutions are presented.

• Section 3: We introduce the radial basis function.

• Section 4: The proposed method is introduced and applied to linear and nonlinear VIEs of the third kind of the form (1) and (2).

• Section 5: The convergence of this method is analyzed.

• Section 6: Numerical experiments are carried out in comparison with other existing methods to show the accuracy and efficiency of the proposed method.

• Section 7: Conclusions and further work.

2 Existence and uniqueness of solutions of class of third-kind VIEs

2.1 Class of nonlinear VIEs of the third kind

Theorem 1

(Brunner 2017) Let’s assume that

• (a) $\phi \in L^1(0,1), f \in C(I)$ and $k \in C(D)$,

• (b) $G^{\prime }(u) \in C(E)$, where E is some open set in $\mathbb {R}$. Then, (1) has a unique solution $u\in C(I)$.

Theorem 2

(Brunner 2017) Let’s suppose that

• (a) $\phi \in L^1(0,1)$,

• (b) $k \in C^m$ (D) for certain $m \ge 1$. Therefore, for each $f \in C^m(I)$, (1) has a unique solution $u\in C^m(I)$.

Remark 1

For $0<\beta <1$ or $\beta =1$ and $k(0,0)=0$, the operator $\mathcal {V}_{k, \beta }$ is compact (Song et al. 2019).

2.2 Class of linear VIEs of the third kind

The existence and uniqueness of the solution of linear VIEs of the third kind are discussed in Vainikko (2009, 2010a) and Yang (2015).

Theorem 3

Let $0<\beta \le 1, k \in C(I)$. Then the operator $\mathcal {V}_k$ has the following properties:

• (i) For $\beta \in (0,1)$, the operator $\mathcal {V}_k$ is compact, and the operator $\mathcal {I}-\mathcal {V}_k$ has a bounded inverse operator from $L^{\infty }(I)$ to $L^{\infty }(I)$.

• (ii) For $\beta =1$, the operator $\mathcal {V}_k$ is compact if and only if $k(0,0)=0$.

• (iii) For $\beta =1$, the spectrum of the operator $\mathcal {V}_k$ is given by

  $$\begin{aligned} \sigma \left( \mathcal {V}_k\right) =\{0\} \cup \left\{ k(0,0)(1+\lambda )^{-1}: {\text {Re}} \lambda \ge 0\right\} . \end{aligned}$$

• (iv) For $\beta =1$, the operator $\mathcal {I}-\mathcal {V}_k$ has a bounded inverse from $L^{\infty }(I)$ to $L^{\infty }(I)$ if and only if $k(0,0)<1$.

Theorem 4

Let’s suppose that $k \in C(D)$. So, for all $f \in C(I)$ (2) has a unique continuous solution u on C(I) if any of the following characteristics is satisfied

• (i) $0<\beta <1$.

• (ii) $\beta =1, \ \ k(0,0)=0$.

• (iii) $\beta =1, \ \ k(0,0) \ne 0$ and $1 \notin \sigma _0\left( \mathcal {V}_{k}\right)$.

3 An outline of the RBF approximation

In this section, we review some definitions and properties of the RBFs method (Wendland 2005). The radial basis function (RBF) method for multivariate approximation is one of the most frequently applied tools in modern approximation theory due to its accuracy. The good conditionality of the interpolation problem for scattered data by the RBFs method is that the function $\phi$ used in constructing the RBFs is positive definite, then the corresponding interpolation matrix is also positive definite and so nonsingular. The meshless method does not need a mesh to discretize the problem domain under consideration, and the estimated solution is constructed entirely on the basis of a set of scattered nodes.

Definition 1

(Wendland 2005; Fasshauer 2006) A function $\Phi : \mathbb {R}^{d} \rightarrow \mathbb {R}$ is said to be radial if there exists a function $\phi :[0, \infty ) \rightarrow \mathbb {R}$ such that $\Phi (t)=$ $\phi \left( \Vert t\Vert _{2}\right)$, for all $t \in \mathbb {R}^{d}$.

In order to introduce the multivariate scattered data interpolation by radial basis functions, let us consider the following definition

Definition 2

(Wendland 2005) A real-valued continuous even function $\Phi$ is conditionally positive definite, if for all sets $\mathcal {X}=\left\{ t_{i}\right\} _{i=1}^{N} \subset \mathbb {R}^{d}$ of distinct points, and for all vectors $\lambda =\left[ \lambda _{1}, \ldots , \lambda _{N}\right] ^{T} \in \mathbb {R}^{N}$, the quadratic form

$$\begin{aligned} \sum _{i=1}^{N} \sum _{j=1}^{N} \lambda _{i} \lambda _{j} \Phi \left( t_{i}-t_{j}\right) , \end{aligned}$$

is positive.

Some of the well known RBFs are mentioned in Table 1. The RBF spaces are produced by $\phi _{j}(\cdot )=\phi \left( \left\| \cdot -t_{j}\right\| \right)$, where $\phi : \mathbb {R}_{+} \rightarrow \mathbb {R}$ is a given, continuous univariate function, and $\left\{ t_{j}\right\}$ are some nodes in the domain of the problem. Let the set $\mathcal {X}=\left\{ t_{j}\right\} _{j=1}^{N}$, where N is the number of data points. Given data $\left\{ t_{j}, u\left( t_{j}\right) \right\} _{j=1}^{N}$, in interpolation of the scattered data using RBFs, the approximation of a function u is generally presented in the form

$$\begin{aligned} u \left( t\right) \approx \mathcal {P}_{N} u(t)=\sum _{i=1}^{N} \lambda _{i} \phi \left( \left\| t-t_{i}\right\| \right) , \quad t \in \mathbb {R}^{d}. \end{aligned}$$

(3)

The interpolation problem is to find $\lambda _{i}, i=1, \ldots , N$ such that the interpolant $\mathcal {P}_{N} u$, all data satisfied

$$\begin{aligned} \mathcal {P}_{N} u \left( t_{i}\right) =u\left( t_{i}\right) , \quad i=1, \ldots , N. \end{aligned}$$

This can be lead to a system of equations for the unknown coefficients $\lambda _{i}$

$$\begin{aligned} A \varvec{\lambda }=\varvec{u}, \end{aligned}$$

where $\varvec{\lambda }=\left[ \lambda _{1}, \ldots , \lambda _{N}\right] ^{T},$ $\varvec{u}=\left[ u_{1}, \ldots , u_{N}\right] ^{T}$ and $A=\left( \phi \left( \left\| t_{k}-t_{j}\right\| \right) \right)$ is named the interpolation matrix or the system matrix.

Table 1 Some well-known functions that generate RBFs

We know that this system has only one solution when the matrix A is non-singular. If we apply positive definite RBFs, the generated coefficient matrix A is non-singular, and so the solution of the interpolation problem is unique.

Definition 3

(Wendland 2005; Fasshauer 2006) A function $\phi :[0, \infty ) \rightarrow \mathbb {R}$ that is in C[0, $\infty ) \cap C^{\infty }(0, \infty )$ and fulfills

$$\begin{aligned} (-1)^l \phi ^{(l)}(r) \ge 0, \quad r>0, \quad l=0,1,2, \ldots , \end{aligned}$$

is known as completely monotone on $[0, \infty )$.

The relation between positive definite RBFs and completely monotone functions is given by the following theorem (Wendland 2005; Schoenberg 1938).

Theorem 5

A function $\phi$ is completely monotone on $[0, \infty )$ if and only if $\Phi =\phi \left( \Vert \cdot \Vert ^{2}\right)$ is positive definite and radial basis on $\mathbb {R}^{s}$ for each s.

Theorem 6

A function $\phi$ is completely monotone on $[0, \infty )$ but not constant, then $\Phi =\phi \left( \Vert .\Vert ^2\right)$ is strictly positive definite and radial basis on $\mathbb {R}^s$ for each s.

There exists an associated Hilbert space where the radial basis function yields a better approximation of a chosen function. Every radial basis and strictly positive definite functions yield reproducing kernels with respect to certain Hilbert spaces or semi-Hilbert spaces. For this purpose, we define reproducing kernels.

Definition 4

(Buhmann 2003) Let H be a real Hilbert space of functions $u:\Omega \rightarrow \mathbb {R}$. A function $K:\Omega \times \Omega \rightarrow \mathbb {R}$ is known as reproducing kernel for H if

• $K(t,.) \in H$ for each $t \in \Omega ,$

• $u(t)=\langle u, K(., t)\rangle _H$ for each $u \in H$ and each $t \in \Omega$.

There is a connection between reproducing-kernel Hilbert spaces and positive definite kernels (Wendland 2005). In fact, if $K(t, s)=\Phi (t-s), t, s \in \mathbb {R}$, where $\Phi$ is a radial basis function, then K(t, s) is a symmetric reproducing kernel and

$$\begin{aligned} H_{\Phi }\Omega ={\text {span}}\{\Phi (\cdot -s): s \in \Omega \}, \end{aligned}$$

is the space with an associated bilinear form

$$\begin{aligned} \left\langle \sum _{i=1}^N c_i \Phi \left( \cdot -t_i\right) , \sum _{k=1}^N \lambda _k \Phi \left( \cdot -s_k\right) \right\rangle _{\Phi }=\sum _{i=1}^N \sum _{k=1}^N c_i \lambda _k \Phi \left( t_i, s_k\right) , \quad t_i, s_k \in \Omega . \end{aligned}$$

Theorem 7

(Wendland 2005) If $\Phi$ is a radial basis and strictly positive definite function, then the bilinear form $\langle ,\rangle _{\Phi }$ defines an inner product on $H_{\Phi }(\Omega )$. Moreover, $H_{\Phi }(\Omega )$ is a pre-Hilbert space with reproducing $\Phi$.

Definition 5

(Fasshauer 2006) The native space $\aleph _{\Phi }(\Omega )$ of $\Phi$ is now defined to be the completion of $H_{\Phi }(\Omega )$ with respect to the $\Phi$-norm $\Vert \cdot \Vert _{\Phi }$ so that $\Vert u\Vert _{\Phi }=\Vert u\Vert _{\aleph _{\Phi }(\Omega )}$ for all $u \in \aleph _{\Phi }(\Omega )$.

The RBFs contain a parameter c, called the shape parameter, which affects the accuracy of the solution and the conditioning of the collocation matrix. The shape parameter has been studied by many authors. For example,

• Hardy’s shape parameter (Hardy 1971)

  $$\begin{aligned} c=0.815 \textsf{d} \quad \text{ where } \quad \textsf{d}=\frac{1}{N} \sum _{i=1}^{N} \textsf{d}_{i}, \end{aligned}$$

  in which $\textsf{d}_{i}$ is the distance from ith center to the nearest neighbor and N is the total number of centers.

• Franke’s shape parameter (Franke 1982)

  $$\begin{aligned} c=\frac{1.25 \textbf{D}}{\sqrt{N}}, \end{aligned}$$

  in which $\textbf{D}$ is the diameter of smallest circle encompassing all the center locations and N is the total number of centers.

• Fasshauer’s shape parameter (Fasshauer 2002)

  $$\begin{aligned} c=\frac{2}{\sqrt{N}}, \end{aligned}$$

  in which N is the total number of centers.

However, in the cases of MQ, inverse IMQ and GA, the accuracy of the RBF solution depends largely on the choice of parameter c. In GA, for example, a fixed number of N and the smallest shape parameters provide the most accurate approximation. The choice of shape parameters is an essential task in the approximation of functions using RBF, and researchers have always been interested in choosing an appropriate shape parameter. We estimate the integral of f(t) on $[-1,1]$ by

$$\begin{aligned}{} & {} \int _{-1}^1 f(t) d t=\sum _{i=1}^N w_i f\left( t_i\right) , \\{} & {} w_i=\frac{2}{N(N+1)\left[ P_N\left( t_i\right) \right] ^2}, \quad i=1, \ldots , N, \end{aligned}$$

where $w_i$ are the Legendre–Gauss–Lobatto weights.

4 Description of the method

4.1 Formulation for class of linear Volterra integral equations of the third kind

This subsection presents an RBF scheme for solving a class of linear VIEs of the third kind. RBFs are computational means for approximating complicated functions or functions in several variables. The basic idea of the RBF method for solving a class of linear Volterra integral equations of the third kind is to employ a linear combination of RBFs to approximate the unknown function. Therefore, the integral equation is transformed into a combination of RBFs and their coefficients. Then, the weight coefficients of the RBFs can be computed using the collocation method. Finally, an approximate formula for the unknown function can be obtained. Let’s apply the RBF approximation method for solving (2). In order to do this, we require a RBF and nodes in [a, b]. Therefore, we put

$$\begin{aligned} \phi _j(t)=\Phi (r), \quad r=\left| t-t_j\right| . \end{aligned}$$

We can rewrite (2) as follows

$$\begin{aligned} u(t)=f(t)+\int _0^t t^{-\beta } s^{\beta -1} k(t, s) u(s) d s, \quad t \in I, \end{aligned}$$

(4)

To use the proposed new technique, based on the RBF collocation method, to find an approximate solution of the Eq. (2), it is necessary to transform the previous equation into an algebraic system of equations. To apply the suggested scheme, we estimate the unknown function u(t) by the RBFs method. For this, we can introduce

$$\begin{aligned} \tilde{u}(t)= \sum _{j=1}^{N} d_{j} \phi _{j}(t), \quad t \in [a, b], \end{aligned}$$

(5)

as an approximation of u(t). Now, by substituting (5) into (4) we obtain

$$\begin{aligned} \sum _{j=1}^{N} d_{j} \phi _{j}(t)- \int _{0}^{t}t^{-\beta } s^{\beta -1}k(t, s) \left[ \sum _{j=0}^{N} d_{j} \phi _{j}(s)\right] d s=f(t), \end{aligned}$$

by simplifying, we have

$$\begin{aligned} \sum _{j=1}^{N} d_{j}[\phi _{j}(t)- \int _{0}^{t} t^{-\beta } s^{\beta -1} k(t, s) \phi _{j}(s) d s]=f(t). \end{aligned}$$

(6)

In order to compute the integral in this equation, let the collocation points be the set of quadrature formula points $\left\{ t_{i}\right\} _{i=1}^{N}$. Suppose that Eq. (6) holds at collocation points, i.e.

$$\begin{aligned} \sum _{j=1}^{N} d_{j}[\phi _{j}(t_{i})- \int _{0}^{t_{i}}(t_{i})^{-\beta } s^{\beta -1} k(t_{i}, s) \phi _{j}(s) ds]=f(t_{i}). \end{aligned}$$

By using the Legendre–Gauss–Lobatto integration formula, we can evaluate the above integral. In order to do so, we apply the following transformation:

$$\begin{aligned} s(t, \eta )=\frac{t}{2} \eta +\frac{t}{2}, \quad -1 \le \eta \le 1. \end{aligned}$$

Hence, the above equation can be written as follows

$$\begin{aligned} \sum _{j=1}^{N} d_{j}[\phi _{j}(t_{i}) - \frac{1}{2} \int _{-1}^{1} (t_{i})^{1-\beta } (s \left( t_{i}, \eta \right) )^{\beta -1} k(t_{i}, s \left( t_{i}, \eta \right) )\phi _{j}(s \left( t_{i}, \eta \right) ) d\eta ]=f(t_{i}), \end{aligned}$$

we approximate the above integrals using the l points quadrature formula with the quadrature points $\left\{ \eta _{l}\right\} _{l=1}^{N}$ and the quadrature weights$\left\{ w_{l}\right\} _{l=1}^{N}$. Therefore, the above equation can be written as follows

$$\begin{aligned} \sum _{j=1}^{N} \hat{d}_{j} [\phi _{j}(t_{i}) -\frac{1}{2} \sum _{l=1}^{N} w_{l} (t_{i})^{1-\beta } (s \left( t_{i}, \eta _{l}\right) )^{\beta -1} k(t_{i}, s \left( t_{i}, \eta _{l}\right) )\phi _{j}(s \left( t_{i}, \eta _{l})\right) ]=f(t_{i}), \end{aligned}$$

(7)

where $\hat{d}_{j}$ are approximations for $d_{j}$, then by assuming that is exact for the collocation points, we get a system of linear equations $\Lambda \chi =\Delta$ where

$$\begin{aligned} \begin{aligned}&\Lambda =[\phi _{j}(t_{i}) -\frac{1}{2} \sum _{l=1}^{N} w_{l} (t_{i})^{1-\beta } (s \left( t_{i}, \eta _{l}\right) )^{\beta -1} k(t_{i}, s \left( t_{i}, \eta _{l}\right) )\phi _{j}(s \left( t_{i}, \eta _{l})\right) ]_{i, j},\\&\Delta =\left[ f\left( t_{1}\right) , f\left( t_{2}\right) , \ldots , f\left( t_{N}\right) \right] ^{T},\\&\chi =\left[ \hat{d}_{1},\hat{d}_{2}, \ldots , \hat{d}_{N}\right] ^{T}. \end{aligned} \end{aligned}$$

By solving the above system using mathematical software with a suitable numerical method, we obtain the values of the unknown coefficients $\hat{d}_{j}$. Then finally u(t) can be approximated at any point $t \in [a, b]$ by

$$\begin{aligned} \hat{u}(t)= \sum _{j=1}^{N} \hat{d}_{j} \phi _{j}(t). \end{aligned}$$

4.2 Formulation for class of nonlinear Volterra integral equation of the third kind

In this section, we use the RBF approximation to solve (1). We can rewrite (1) as follows

$$\begin{aligned} u(t)=f(t)+\int _0^t t^{-\beta } s^{\beta -1} k(t, s) G(u(s)) d s, \quad t \in I. \end{aligned}$$

(8)

First, we need a radial basis function and nodal points in the interval [a, b]. Therefore, let’s take

$$\begin{aligned} \phi _j(t)=\Phi (r), \quad r=\left| t-t_j\right| . \end{aligned}$$

By substituting

$$\begin{aligned} u_{h}(t)=\sum _{j=1}^N d_j \phi _j(t), \end{aligned}$$

as an estimation to u(t) in (8), we get

$$\begin{aligned} u_{h}(t)=f(t)+\int _0^t t^{-\beta } s^{\beta -1} k(t, s) G(u_{h}(s)) d s, \quad t \in I \end{aligned}$$

or

$$\begin{aligned} \sum _{j=1}^N d_j \phi _j(t)=f(t)+\int _0^t t^{-\beta } s^{\beta -1} k(t, s) G(\sum _{j=1}^N d_j \phi _j(s)) d s, \quad t \in I \end{aligned}$$

By using the Legendre–Gauss–Lobatto integration formula, we can calculate the above integral. So, we need to change the integration distance [0, t] to a fixed distance [0, 1]. To do this, we use the following transformation

$$\begin{aligned} s:=t x, \quad x \in [0,1], \quad s \in [0, t]. \end{aligned}$$

We obtain

$$\begin{aligned} \sum _{j=1}^N d_j \phi _j(t)=f(t)+ \int _0^1 t^{1-\beta } (t x)^{\beta -1} k(t, tx) G(\sum _{j=1}^N d_j \phi _j(tx)) d x, \quad t \in I. \end{aligned}$$

(9)

In order to solve the problem, let the collocation points be the set of quadrature formula points $t_i, i=0, \ldots , n$. Suppose (9) holds at the collocation points, we obtain the following system of nonlinear equations

$$\begin{aligned} \sum _{j=1}^N d_j \phi _j(t_i)=f(t_i)+\int _0^1 t_i^{1-\beta } (t_i x)^{\beta -1} k(t_i, t_i x) G(\sum _{j=1}^N d_j \phi _j(t_i x)) d x \quad i=0, \ldots , n. \end{aligned}$$

(10)

By using quadrature formula with the quadrature points $\left\{ \gamma _{l}\right\} _{l=1}^{N}$ and the quadrature weights $\left\{ w_{l}\right\} _{l=1}^{N}$ in (10), we obtain

$$\begin{aligned} \sum _{j=1}^N \hat{d}_j \phi _j\left( t_i\right) - \sum _{l=1}^N w_l t_i^{1-\beta } (t_i \gamma _l)^{\beta -1} k(t_i, t_i \gamma _l) G\left( \sum _{j=1}^N \hat{d}_j \phi _j(t_i \gamma _l)\right) =f(t_i) \quad i=0, \ldots , n, \end{aligned}$$

(11)

where $\hat{d}_j$ are approximations for $d_j$. This is a system of nonlinear equations that can be solved by an appropriate numerical method, which then provides the coefficients $\hat{d}_j$. By solving the above system using mathematical software, u(t) can be estimated by

$$\begin{aligned} \tilde{u}_{h}(t)=\sum _{j=1}^N \hat{d}_j \phi _j(t). \end{aligned}$$

(12)

5 Convergence analysis

In this section, we investigate the error analysis of the proposed method for solving a class of Volterra integral equations of the third kind. As mentioned in the previous sections, the coefficient matrix of the interpolation by RBFs is non-singular. This matrix has a very large condition number. Thus, a small perturbation of the problem input causes a large variation. Note that the condition number of the global RBFs increases as the number of N nodes in the domain increases to get accurate results. We introduce an estimation of the error of the proposed method based on strictly positive definite RBFs. A comparable approach can be used to get an estimate of the error for the suggested scheme based on strictly conditionally positive definite RBFs. We are interested in how the interpolation approaches the function u on $\Omega$ when the set of data $\mathcal {X}$ becomes denser in $\Omega$. We now move to the estimation of the RBF interpolation error, which is introduced in terms of the fill distance parameter $h_{\mathcal {X}, \Omega }$.

Definition 6

(Fasshauer 2006) The fill distance of a given set $\mathcal {X}=\left\{ t_{i}\right\} _{i=1}^{N}$ consisting of pairwise distinct points in $\Omega$ can be defined as

$$\begin{aligned} h_{\mathcal {X}, \Omega }=\sup _{t \in \Omega } \min _{t_{j} \in \mathcal {X}}\left\| t-t_{j}\right\| , \end{aligned}$$

which shows how well the data in the set $\mathcal {X}$ fill out the domain $\Omega$.

Definition 7

The separation distance of $\Omega =\left\{ t_{i}\right\} _{i=1}^{N} \subset \Omega$ is defined by

$$\begin{aligned} q_{\mathcal {X}}=\frac{1}{2} \min _{i \ne j}\left\| t_{i}-t_{j}\right\| . \end{aligned}$$

The set $\mathcal {X}$ is said to be quasi-uniform with respect to a constant $c>0$ if

$$\begin{aligned} q_{\mathcal {X}} \le h_{\mathcal {X},\Omega } \le c q_{\mathcal {X}}. \end{aligned}$$

We limit ourselves to domains that satisfy the specific interior cone condition as follows

Definition 8

(Wendland 2005) A set $\Omega$ is said to satisfy an interior cone condition if there exists an angle $\theta \in \left( 0, \frac{\pi }{2}\right)$ and a radius $r>0$ such that for every given $t \in \Omega$ a unit vector $\eta (t)$ exists such that the cone

$$\begin{aligned} C(t, \eta (t), \theta , r)=\left\{ t+\lambda s: s \in \mathbb {R}^{d},\Vert s\Vert _{2}=1, s^{T} \eta (t) \ge \cos (\theta ), \lambda \in [0, r]\right\} , \end{aligned}$$

is contained in $\Omega$.

Definition 9

(Wendland 2005) Suppose $\Phi \in C\left( \mathbb {R}^{d}\right) \cap L^{1}\left( \mathbb {R}^{d}\right)$ is a real-valued strictly positive definite function. Then the real native Hilbert space of $\Phi$ on $\mathbb {R}^{d}$ is inserted as

$$\begin{aligned} \aleph _{\Phi }\left( \mathbb {R}^{d}\right) =\left\{ u \in C\left( \mathbb {R}^{d}\right) \cap L^{2}\left( \mathbb {R}^{d}\right) : \frac{\hat{u}}{\sqrt{\hat{\Phi }}} \in L^{2}\left( \mathbb {R}^{d}\right) \right\} , \end{aligned}$$

with inner product

$$\begin{aligned} \langle u, \gamma \rangle _{\Phi }\left( \mathbb {R}^{d}\right) =\frac{1}{\sqrt{2 \pi }}\left\langle \frac{\hat{u}}{\sqrt{\hat{\Phi }}}, \frac{\hat{\gamma }}{\sqrt{\hat{\Phi }}}\right\rangle _{L^{2}\left( \mathbb {R}^{d}\right) }=\frac{1}{\sqrt{2 \pi }} \int _{\mathbb {R}^{d}} \frac{\hat{u}(w) \overline{\hat{\gamma }(w)}}{\sqrt{\hat{\Phi }}} \textrm{d} w, \end{aligned}$$

where $\hat{u}$ indicate Fourier transform of u. Moreover, each $u \in \aleph _{\Phi }\left( \mathbb {R}^{d}\right)$ has the representation

$$\begin{aligned} u(t)=\frac{1}{\sqrt{2 \pi }} \int _{\mathbb {R}^{d}} \hat{u}(w) e^{i t w} \mathrm {~d} w. \end{aligned}$$

Theorem 8

(Wendland 2005) Let $\Phi$ is positive definite RBF with infinitely smoothness. Assume that $\Omega \subset \mathbb {R}^{d}$ be open and bounded, satisfying an interior cone condition. Designate the interpolant of a function $u \in \aleph _{\Phi }(\Omega )$ based on this RBF and the distinct set $\mathcal {X}=\left\{ t_{1}, \ldots , t_{N}\right\}$ by $\mathcal {P}_{N} u$. Thus, for every $l \in \mathbb {N}$ there exist constants $h_{0}(l), C_{l}$ such that

$$\begin{aligned} \left\| u-\mathcal {P}_{N} u\right\| _{L^{\infty }(\Omega )} \leqslant C_{l} h_{\mathcal {X}, \Omega }^{l}\vert u\vert _{\aleph _{\Phi }(\Omega )}, \end{aligned}$$

for all $t \in \Omega$, provided $h_{\mathcal {X}, \Omega } \leqslant h_{0}(l)$.

As a conclusion from Theorem 8, for small enough $h_{\mathcal {X},\Omega }$, some positive constant c and $u \in \aleph _{\Phi }(\Omega )$, we give the error bound as follows For GAs, we have

Theorem 9

(Wendland 2005) The Enhanced error bound associated with Gaussian (GA)

$$\begin{aligned} \Phi (t)= e^{ \left( -c \Vert t\Vert ^2\right) }, \quad c>0 \end{aligned}$$

is computed in the following manner

$$\begin{aligned} \left\| u-\mathcal {P}_{N} u \right\| _{L^{\infty }(\Omega )} \le e^{\left( -\frac{c\left| \log h_{\mathcal {X}, \Omega }\right| }{h_{\mathcal {X}, \Omega }}\right) }\Vert u \Vert _{\aleph _{\Phi }(\Omega )}, \end{aligned}$$

where c is a constant, $h_{\mathcal {X}, \Omega }$ is sufficiently small, and $u \in \aleph _{\Phi }(\Omega )$.

For IMQs, we have

Theorem 10

(Wendland 2005) The Enhanced error bound associated with inverse multiquadrics (IMQ)

$$\begin{aligned} \Phi (t)=\left( \Vert t\Vert ^2+c^2\right) ^\beta , \quad c>0, \quad \beta <0, \quad or \quad \beta >0 \quad and \quad \beta \notin \mathbb {N} \end{aligned}$$

is calculated in the following way

$$\begin{aligned} \left\| u-\mathcal {P}_{N} u \right\| _{L_{\infty }(\Omega )} \le e^{\left( -\frac{c}{h_{\mathcal {X}, \Omega }}\right) }\Vert u \Vert _{\aleph _{\Phi }(\Omega )}. \end{aligned}$$

We can express (4) in abstract form as follows

$$\begin{aligned} (I-\mathcal {K}) u=f, \end{aligned}$$

where the integral operator $\mathcal {K}: C(\Omega ) \rightarrow C(\Omega )$ is defined as follows

$$\begin{aligned} \mathcal {K} u(t)= \int _0^t t^{-\beta } s^{\beta -1} k(t, s) u(s) d s. \end{aligned}$$

(13)

The Geometric Series Theorem (Atkinson 1997) involves that the operator $I- \mathcal {K}$ has a bounded inverse and

$$\begin{aligned} \left\| (I- \mathcal {K})^{-1}\right\| \leqslant \frac{1}{1-\Vert \mathcal {K}\Vert }. \end{aligned}$$

The projection operator $\mathcal {P}_{N}: C(\Omega ) \rightarrow C_{N}(\Omega )$ for the collocation points $\left\{ t_{1}, \ldots , t_{N}\right\} \subset \Omega$ is set as follows

$$\begin{aligned} \mathcal {P}_{N} u(t)=\sum _{k=1}^{N} \lambda _{k} \phi \left( \left\| t-t_{k}\right\| \right) , \quad t \in \Omega , \end{aligned}$$

where $C_{N}(\Omega )={\text {span}}\left\{ \Phi _{1}, \ldots , \Phi _{N}\right\}$ with the dimension $d_{N}$ and the coefficients $\left\{ \lambda _{k}\right\}$ determined by solving the linear system

$$\begin{aligned} \mathcal {P}_{N} u \left( t_{i}\right) =u \left( t_{i}\right) , \quad i=1, \ldots , N. \end{aligned}$$

As a result, the system associated with the collocation method is equivalent to the abstract form

$$\begin{aligned} \left( I-\mathcal {P}_{N} \mathcal {K}\right) u_{N}=\mathcal {P}_{N} f \text{. } \end{aligned}$$

(14)

We apply the quadrature rule relative to the coefficients $\left\{ \eta _{l}\right\}$ and weights $\left\{ w_{l}\right\}$, a sequence of numerical integral operators $\mathcal {K}_{N}$ is entered defined by

$$\begin{aligned} \mathcal {K}_{N} u(t)= \frac{1}{2} \sum _{l=1}^{N} w_{l} {t}^{1-\beta } (s \left( t, \eta _{l}\right) )^{\beta -1} k(t, s \left( t, \eta _{l}\right) )u(s \left( t, \eta _{l})\right) . \end{aligned}$$

(15)

Here are the assumptions for the approximation operators (Atkinson and Potra 1987; Atkinson 1997, 1993).

• $H_{1}: \mathcal {K}_{N}$ is a collectively compact family on $C(\Omega )$ i.e., for any bounded set $B \subset C(\Omega )$ the closure of the set $\cup _{N=1}^{\infty } \mathcal {K}_{N}(B)$ is compact in $C(\Omega )$.

• $H_{2}:$ $\mathcal {K}_{N}$ is pointwise convergent to $\mathcal {K}$ on $C(\Omega )$.

By using (15) and (3), therefore (7) becomes

$$\begin{aligned} \left( I-\mathcal {P}_{N} \mathcal {K}_{N}\right) \hat{u}_{N}=\mathcal {P}_{N} f. \end{aligned}$$

(16)

In order to achieve the most precise estimate solution, the iterated discrete collocation solution can be achieved.

$$\begin{aligned} \bar{u}_{N}=f+ \mathcal {P}_{N} \mathcal {K}_{N} \hat{u}_{N}, \end{aligned}$$

(17)

therefore, it is easy to notice that

$$\begin{aligned} \mathcal {P}_{N} \bar{u}_{N}=\hat{u}_{N}. \end{aligned}$$

Then, we have

$$\begin{aligned} \left( I-\mathcal {K}_{N} \mathcal {P}_{N}\right) \bar{u}_{N}=f. \end{aligned}$$

Theorem 11

(Atkinson 1997) Let $\left\{ \mathcal {P}_{N}\right\}$ be a family of interpolatory projection operators on $C(\Omega )$ to $C(\Omega )$, and assume that

$$\begin{aligned} \mathcal {P}_{N} u \rightarrow u \quad \text{ as } N \rightarrow \infty , \end{aligned}$$

for all $u \in C(\Omega )$ and $u_{0}$ be a unique solution of (4). Then for all sufficiently large N, say $N > M$, $\left( I- \mathcal {K}_{N} \mathcal {P}_{N}\right) ^{-1}$ exists and is uniformly bounded. Also, for the solution $\bar{u}_{N}$

$$\begin{aligned} \left\| \bar{u}_{N}-u_{0}\right\| _{L^{\infty }(\Omega )} \leqslant \left\| \left( I-\mathcal {K}_{N} \mathcal {P}_{N}\right) ^{-1}\right\| \left\| \mathcal {K} u_{0}-\mathcal {K}_{N} \mathcal {P}_{N} u_{0}\right\| _{L^{\infty }(\Omega )}, \quad N \geqslant M. \end{aligned}$$

This imposes a bound on the rate of convergence of the iterative solution $\bar{u}_N$ to $u_0$. Thus, the error analysis is completed by the next theorem

Theorem 12

Assume that the assumptions of Theorem 8 are satisfied. Also, suppose that $u_{0} \in \aleph _{\Phi }(\Omega )$ is the unique exact solution of Eq. (4) and the suggested method has been installed on the quasi-uniform set $\mathcal {X}=\left\{ t_{i}\right\} _{i=1}^{N} \subset \Omega$. So there is $M>0$ such that for every $N>M$, the method has a unique solution $\hat{u}_{N}$. Moreover, there exist constants $\eta _{1}$, $\eta _{2}$, $\eta _{3}$ and c such that for the Gaussians (GA), we have

$$\begin{aligned} \begin{aligned}&\left\| \hat{u}_{N}-u_{0}\right\| _{L{ }^{\infty }(\Omega )} \le \left( 1+\eta _{3}\right) e^{\left( -\frac{c\left| \log h_{\mathcal {X}, \Omega }\right| }{h_{\mathcal {X}, \Omega }}\right) } \left\| u_{0}\right\| _{\aleph _{\phi }(\Omega )} \\&\quad +\eta _{3}\left( \eta _{1}\left\{ \left\| \mathcal {K} u_{0}-\mathcal {K}_{N} u_{0}\right\| _{L^{\infty }(\Omega )}+\eta _{2}\left( 1+\eta _{3}\right) e^{\left( -\frac{c\left| \log h_{\mathcal {X}, \Omega }\right| }{h_{\mathcal {X}, \Omega }}\right) } \left\| u_{0}\right\| _{\aleph _{\phi }(\Omega )}\right\} \right) , \end{aligned} \end{aligned}$$

and for the inverse multiquadrics (IMQ), as a result

$$\begin{aligned} \begin{aligned}&\left\| \hat{u}_{N}-u_{0}\right\| _{L{ }^{\infty }(\Omega )} \le \left( 1+\eta _{3}\right) e^{\left( -\frac{c}{h_{\mathcal {X}, \Omega }}\right) }\left\| u_{0}\right\| _{\aleph _{\phi }(\Omega )} \\&\quad +\eta _{3}\left( \eta _{1}\left\{ \left\| \mathcal {K} u_{0}-\mathcal {K}_{N} u_{0}\right\| _{L^{\infty }(\Omega )}+\eta _{2}\left( 1+\eta _{3}\right) e^{\left( -\frac{c}{h_{\mathcal {X}, \Omega }}\right) } \left\| u_{0}\right\| _{\aleph _{\phi }(\Omega )}\right\} \right) . \end{aligned} \end{aligned}$$

Proof

According to Theorem 11, the iterated method has a solution $\bar{u}_{N}$ and as $\left( I-\mathcal {K}_{N} \mathcal {P}_{N}\right) ^{-1}$ exists and is uniformly bounded, i.e.

$$\begin{aligned} \left\| \left( I- \mathcal {K}_{N} \mathcal {P}_{N}\right) ^{-1}\right\| \leqslant \eta _{1}<\infty . \end{aligned}$$

From pointwise convergence of $\mathcal {K}_{N}$ for a certain great N, which means that there exists a certain $\eta _{2} >0$ so that we can suppose that

$$\begin{aligned} \left\| \mathcal {K}_{N}\right\| \leqslant \eta _{2}<\infty . \end{aligned}$$

Furthermore, according to the uniform boundedness principle for radial basis functions, it follows that

$$\begin{aligned} \left\| \mathcal {P}_{N}\right\| \leqslant \eta _{3}<\infty , \quad N \in \mathbb {N}. \end{aligned}$$

So, we get this

$$\begin{aligned} \begin{aligned} \left\| \bar{u}_{N}-u_{0}\right\| _{L^{\infty }(\Omega )}&\le \left\| \left( I-\mathcal {K}_{N} \mathcal {P}_{N}\right) ^{-1}\right\| \left\| \mathcal {K}u_{0}-\mathcal {K}_{N} \mathcal {P}_{N} u_{0}\right\| _{L^{\infty }(\Omega )}\\&\le \eta _{1}\left\| \mathcal {K} u_{0}-\mathcal {K}_{N} \mathcal {P}_{N} u_{0}\right\| _{L^{\infty }(\Omega )} \\&\le \eta _{1}\left\{ \left\| \mathcal {K} u_{0}-\mathcal {K}_{N} u_{0}\right\| _{L^{\infty }(\Omega )}+\left\| \mathcal {K}_{N}\left( u_{0}-\mathcal {P}_{N} u_{0}\right) \right\| _{L^{\infty }(\Omega )}\right\} \\&\le \eta _{1}\left\{ \left\| \mathcal {K} u_{0}-\mathcal {K}_{N} u_{0}\right\| _{L^{\infty }(\Omega )}+\eta _{2}\left\| u_{0}-\mathcal {P}_{N} u_{0}\right\| _{L^{\infty }(\Omega )}\right\} \\&\le \eta _{1}\left\{ \left\| \mathcal {K} u_{0}-\mathcal {K}_{N} u_{0}\right\| _{L^{\infty }(\Omega )}+\eta _{2}\left( \left\| u_{0}-\hat{u}_{0}\right\| _{L^{\infty }(\Omega )}+\left\| \mathcal {P}_{N} u_{0}-\mathcal {P}_{N} \hat{u}_{0}\right\| _{L^{\infty }(\Omega )}\right) \right\} \\&\le \eta _{1}\left\{ \left\| \mathcal {K} u_{0}-\mathcal {K}_{N} u_{0}\right\| _{L^{\infty }(\Omega )}+\eta _{2}\left( 1+\eta _{3}\right) \left\| u_{0}-\hat{u}_{0}\right\| _{L^{\infty }(\Omega )}\right\} . \end{aligned} \end{aligned}$$

Using the error bound of Theorem 10, we obtain

$$\begin{aligned} \left\| \bar{u}_{N}-u_{0}\right\| _{L^{\infty }(\Omega )} \le \eta _{1}\left\{ \left\| \mathcal {K} u_{0}-\mathcal {K}_{N} u_{0}\right\| _{L^{\infty }(\Omega )}+\eta _{2}\left( 1+\eta _{3}\right) e^{\left( -\frac{c}{h_{\mathcal {X}, \Omega }}\right) } \left\| u_{0}\right\| _{\aleph _{\phi }(\Omega )}\right\} . \end{aligned}$$

Furthermore, let $\hat{u}_{N}=\mathcal {P}_{N} \bar{u}_{N}$, and consider the decomposition

$$\begin{aligned} u_{0}-\hat{u}_{N}=u_{0}-\mathcal {P}_{N} \bar{u}_{N}=\left( u_{0}-\mathcal {P}_{N} u_{0}\right) +\mathcal {P}_{N}\left( u_{0}-\bar{u}_{N}\right) . \end{aligned}$$

This enables us to obtain

$$\begin{aligned} \left\| \hat{u}_{N}-u_{0}\right\| _{L^{\infty }(\Omega )} \leqslant \left\| u_{0}-\mathcal {P}_{N} u_{0}\right\| _{L^{\infty }(\Omega )}+\left\| \mathcal {P}_{N}\right\| \left\| u_{0}-\bar{u}_{N}\right\| _{L^{\infty }(\Omega )}. \end{aligned}$$

So, we can achieve

$$\begin{aligned} \begin{aligned}&\left\| \hat{u}_{N}-u_{0}\right\| _{L{ }^{\infty }(\Omega )} \le \left\| u_{0}-\mathcal {P}_{N} u_{0}\right\| _{L{ }^{\infty }(\Omega )}+\eta _{3}\left\| \bar{u}_{N}-u_{0}\right\| _{L^{\infty }(\Omega )} \\ {}&\quad \le \left( 1+\eta _{3}\right) e^{\left( -\frac{c}{h_{\mathcal {X}, \Omega }}\right) } \left\| u_{0}\right\| _{\aleph _{\phi }(\Omega )} \\&\qquad +\eta _{3}\left( \eta _{1}\left\{ \left\| \mathcal {K} u_{0}-\mathcal {K}_{N} u_{0}\right\| _{L^{\infty }(\Omega )}+\eta _{2}\left( 1+\eta _{3}\right) e^{\left( -\frac{c}{h_{\mathcal {X}, \Omega }}\right) } \left\| u_{0}\right\| _{\aleph _{\phi }(\Omega )}\right\} \right) , \end{aligned} \end{aligned}$$

the proof is complete. $\square$

6 Numerical results

In order to illustrate the performance of the RBFs method in solving a class of VIEs of the third kind and to demonstrate the accuracy, efficiency, and applicability of the proposed method, we consider both the linear and non-linear classes of the third kind of VIEs. In all examples, we use the Gaussian (GA) and inverse Multiquadric (IMQ) RBFs, whose applicability and efficiency strongly depend on the shape parameters. Also, the results obtained are compared with the method based on the use of the MLS scheme presented in Mirzaei and Dehghan (2010). For the tests in the MLS method, we use the linear case $(m = 1)$, the quadratic case $(m=2)$, and the degree 3 case $(m=3)$ and the Gaussian weight functions. Furthermore, the accuracy of the numerical solutions can be computed by measuring the maximum error and the mean error, which can be defined in the following way

$$\begin{aligned}{} & {} \Vert e_{N}\Vert _{2}=\left( \int _{0}^{1} |e(t) |^{2} d t\right) ^{\frac{1}{2}}, \\{} & {} \Vert e_{N}\Vert _{\infty }=\max _{t \in [0,1]} |e(t)|, \end{aligned}$$

where

$$\begin{aligned} e(t)=u(t)-\hat{u}_{N}(t), \end{aligned}$$

and the exact solution u(t) is evaluated by the numerical solution $\hat{u}_{N}(t)$ achieved by the current paper. All routines run on a Core(TM) i3-6006U CPU @ 2.00 GHz CPU and 4 GB RAM.

6.1 Class of linear VIEs of the third kind

Example 1

Consider the following class of third-kind VIE

$$\begin{aligned} t^{\beta } u(t)= t^{\beta } f(t)+\int _{0}^{t} s^{\beta -1} k(t, s)u(s) d s, \quad t \in [0,1], \end{aligned}$$

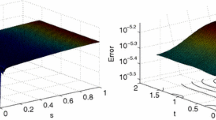
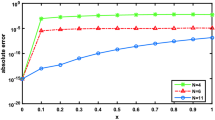
where $k(t, s)=s e^{t-s}$, $\beta =1$, the exact solution is $u(t)=e^{-t}$ and f(t) is defined accordingly. Table 2 reports numerical results in terms of $\left\| e_N\right\| _2$ and $\left\| e_N\right\| _{\infty }$ at different numbers of N for Gaussian and Inverse Multiquadric (IMQ) functions as radial basis functions with $\beta =1$. As indicated by the theoretical results presented in the Theorems 9 and 10, described in the previous section, we can see that the accuracy increases with the increase in the number of collocation points. Accuracy of the present approximation is examined in the $L_2$-error and $L_{\infty }$-error. The IMQ RBF method has a clear advantage over the Gaussian RBF method, which can be seen in the numerical results. With the superior interpolation performance of the IMQ function, the method can achieve greater accuracy with fewer nodes. In order to compare the method presented, we also solve Example 1 using the MLS method, and the numerical results are shown in Table 3. Table 4 describes the RBF error estimation; it is clear that the results progressively converge to the exact values as the number of nodes increases. Figures 1 and 2 depict the behavior of the absolute error function for $\beta =1$ on the interval [0, 1]. The computational efficiency of Example 1 for $\beta =1$ using the presented method and the MLS scheme is graphically plotted in semi-logarithmic representation in Fig. 3. We find that the new approach is very fast compared to other methods. The numerical results obtained demonstrate the accuracy and efficiency of the method compared to other existing methods. Figure 4 illustrates the curve of exact and approximate solutions for $\beta =1$. The numerical results indicate that the current approach to solving this problem is very practical and effective.

Table 2 Numerical results for Example 1 with $\beta =1$ by RBF method

Table 3 $\Vert e\Vert _{\infty }$ for Example 1 with different values of m, N and $\beta =1$ by MLS method

Table 4 Estimation of error by RBF (IMQ) for Example 1

Fig. 1

The absolute error function $\vert e(t)\vert$ for various values of N for Example 1 by RBF method

Fig. 2

The absolute error for Example 1 by RBF method

Fig. 3

$\vert e(t)\vert$ for various values of N and $\beta =1$ for Example 1

Fig. 4

The exact solution and RBF solution of Example 1 with $\beta = 1$

Example 2

Consider a class of linear third-kind VIEs of the form

$$\begin{aligned} t^{\beta } u(t)= t^{\beta } f(t)+\int _{0}^{t} s^{\beta -1} k(t, s)u(s) d s, \quad t \in [0,1], \end{aligned}$$

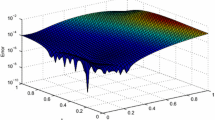
where $k(t, s)= \sqrt{s}\times sin(t)$, $\beta =\frac{4}{5}$, the exact solution is given by $u(t) = t^3$ and $f(t)=\frac{t^{5 / 2}(-10 \sin (t) t+43 \sqrt{t})}{43}$. Table 5 shows numerical results in terms of $\left\| e_N\right\| _2$ and $\left\| e_N\right\| _{\infty }$ at different numbers of N’s, and for GA and IMQ RBFs with $\beta =\frac{4}{5}$, it is clear the errors decrease as N increase, which proves the convergence of the proposed method. Therefore, as stated in the previous section, all the results of this example substantiate the theoretical analysis of the error achieved in Theorems 9 and 10. A comparison of the maximum absolute error of the suggested method with the MLS method is presented in Table 6. In Table 7, we summarize the estimation of error by RBF technique with $\beta =\frac{4}{5}$. This table indicates that as N increases, the error decreases more rapidly. Figures 5 and 6 depict the behavior of the absolute error function for $\beta =\frac{4}{5}$ on the interval [0, 1]. The computational efficiency of example 2 for $\beta =\frac{4}{5}$ using the presented method and the MLS scheme is shown in semi-logarithmic form in Fig. 7. The results obtained with the scheme presented are better than those given with the MLS method. Figure 8 illustrates the comparison between the exact and approximate solutions for $\beta =\frac{4}{5}$. The numerical results correspond well to the exact solution, which confirms the high accuracy of the considered approach.

Table 5 Numerical results for Example 2 with $\beta =\frac{4}{5}$ using RBF method

Table 6 $\Vert e\Vert _{\infty }$ for Example 2 with different values of m, N and $\beta =\frac{4}{5}$ by MLS method

Table 7 Estimation of error by RBF (IMQ) for Example 2

Fig. 5

The absolute error function $\vert e(t)\vert$ for various values of N for Example 2 by RBF method

Fig. 6

The absolute error for Example 2 by RBF method

Fig. 7

$\vert e(t)\vert$ for various values of N and $\beta =\frac{4}{5}$ for Example 2

Fig. 8

The exact solution and RBF solution of Example 2 with $\beta =\frac{4}{5}$

Example 3

We test a class of linear VIEs of the third kind of the form

$$\begin{aligned} t^{\beta } u(t)= f(t)+\int _{0}^{t} s^{\beta -1} k(t, s) u(s) d s, \quad t \in [0,1], \end{aligned}$$

where $k(t, s)=sin(s) t^\frac{2}{3}$, $\beta =\frac{3}{5}$, the exact solution is given by $u(t) = t^4$ and

$$\begin{aligned} \begin{aligned} f(t)=&\frac{\left( 5616 \cos (t) {\text {LommelS}} 1\left( \frac{1}{10}, \frac{1}{2}, t \right) +3510 \sin (t) {\text {LommelS}} 1\left( \frac{11}{10}, \frac{3}{2}, t \right) \right) t^{7 / 6}}{625}\\&-\frac{5616 \sin (t) {\text {LommelS}} 1\left( \frac{1}{10}, \frac{1}{2}, t \right) t^{1 / 6}}{625}+t^{64 / 15} \cos (t)-\frac{234 t^{34 / 15} \cos (t)}{25} \\&+\frac{234 t^{19 / 15} \sin (t)}{25}-\frac{18 t^{49 / 15} \sin (t)}{5}+t^{23 / 5}. \end{aligned} \end{aligned}$$

In order to demonstrate the effectiveness of the investigated scheme, $\Vert e\Vert _{\infty }$ and $\Vert e\Vert _2$ are displayed in Table 8 for various values of N for GA and IMQ functions as radial basis functions with $\beta =\frac{3}{5}$. Consequently, as the number of nodes increases, the results converge towards the exact values. We have also compared the maximum absolute error of the presented approach with that of the MLS method, as shown in Table 9. Table 10 illustrates the estimation of error by RBF, and Figs. 9 and 10 depict the behavior of the absolute error function for $\beta =\frac{3}{5}$ on the interval [0, 1]. According to these figures, the proposed method provides good precision for the numerical results. The computational efficiency of Example 3 for $\beta =\frac{3}{5}$ using the presented technique and the MLS scheme is graphically plotted in semi-logarithmic representation in Fig. 11. The results of the new method are much more effective. Figure 12 illustrates the curves of exact and approximate solutions for $\beta =\frac{3}{5}$.

Table 8 Numerical results for Example 3 with $\beta =\frac{3}{5}$ by RBF method

Fig. 9

The absolute error function $\vert e(t)\vert$ for various values of N for Example 3 by RBF method

Fig. 10

The absolute error for Example 3 by RBF method

Fig. 11

$\vert e(t)\vert$ for various values of N for Example 3 by RBF method

Table 9 $\Vert e\Vert _{\infty }$ for Example 3 with $\beta =\frac{3}{5}$ by MLS method

Table 10 Estimation of error by RBF (IMQ) for Example 3

Fig. 12

The exact solution and RBF solution of Example 3 with $\beta = \frac{3}{5}$

6.2 Class of nonlinear Volterra integral equations of the third kind

Example 4

We consider the following equation as in Dastjerdi and Shayanfard (2021)

$$\begin{aligned} t^{\beta } u(t)=t^{\beta }f(t)+\int _{0}^{ t} s^{\beta -1} k(t, s) G(u(s)) d s, \quad t \in I, \end{aligned}$$

(18)

where $G(u)= sin(u)$, $k(t, s)=s$. The exact solution is $u(t)=t^{2}$ and f(t) is defined accordingly. We have applied the RBF method to this equation for $\beta =\frac{4}{5}$ and $\beta =\frac{1}{3}$. To measure the accuracy of the method studied, $\Vert e\Vert _{\infty }$ and $\Vert e\Vert _2$ are depicted in Tables 11 and 12 for $\beta =\frac{1}{3}$ and $\beta =\frac{1}{4}$ and for different N’s. We can see that as the values of N increase, the results of the RBF approximation gradually converge to the real solution. To compare this approach, we also solved the Example 4 using the MLS method, and the numerical results are shown in Table 13. Table 14 presents the estimation of error by RBF for Example 4 with $\beta = \frac{4}{5}$. Figures 13 and 14 display the behavior of the absolute error function for $\beta =\frac{4}{5}$ and $\beta =\frac{1}{3}$ on the interval [0, 1]. The computational efficiency of example 1 using the presented method and the MLS scheme is depicted in semi-logarithmic representation in Fig. 15. As we can see, the approximation improves with increasing N and that the RBF approximation is very powerful and yields good results. The convergence of the proposed method is much higher than that of the MLS method. Figure 16 illustrates the comparison between the exact and approximate solutions for $\beta =\frac{4}{5}$. In this example, the approximate solution agrees well with the analytical solution. It is clear that the method provides accurate numerical solutions for a class of nonlinear Volterra integral equations of the third kind.

Table 11 Numerical results for Example 4 with $\beta =\frac{1}{3}$ using RBF method

Table 12 Numerical results for Example 4 with $\beta = \frac{4}{5}$ by RBF method

Table 13 $\Vert e\Vert _{\infty }$ for Example 4 using the MLS method

Table 14 Estimation of error by RBF (IMQ) for Example 4

Fig. 13

The absolute error function $\vert e(t)\vert$ for various values of N for Example 4 by RBF method

Fig. 14

The absolute error function for Example 4 by RBF method

Fig. 15

$\vert e(t)\vert$ for $\beta =\frac{4}{5}$ and $\beta =\frac{1}{3}$ and for various values of N for Example 4

Fig. 16

The exact solution and RBF solution of Example 4 with $\beta = \frac{4}{5}$

Example 5

Consider the following class of nonlinear third-kind VIE

$$\begin{aligned} t^{\beta } u(t)=t^{\beta }f(t)+\int _{0}^{ t} s^{\beta -1} k(t, s) G(u(s)) d s, \quad t \in I, \end{aligned}$$

(19)

where $G(u)= (u)^{2}$, $k(t,s)=t s$, $\beta =\frac{1}{2}$. The exact solution is $u(t)=\frac{3}{2}t^{3}$ and f(t) is defined accordingly. Table 15 displays $\Vert e\Vert _{\infty }$ and $\Vert e\Vert _2$ for different N’s, with $\beta =\frac{1}{2}$. We can see that when the values of N increase, the results of the MLS approximation converge progressively towards the real solution. To compare the presented method, we also solve the example 5 utilizing the MLS method, and the numerical results are displayed in Table 16. In Table 17, we summarize the estimation of error by RBF for example 5 with $\beta = \frac{1}{2}$, and Figs. 17 and 18 depict the behavior of the absolute error function for $\beta =\frac{1}{2}$ on the interval [0, 1]. The computational efficiency of example 5 for $\beta =\frac{1}{2}$ using the current method and the MLS scheme are drawn in semi-logarithmic representation in Fig. 19. As we can see, the new approach is very fast, and the algorithm of the suggested approach is simpler than the MLS method. Figure 20 graphically shows the comparison between exact and approximate solutions for $\beta =\frac{1}{2}$. It turns out that the proposed method gives good results and performs well for the considered class of Voterra integral equations of the third kind without significant loss of accuracy.

Table 15 Numerical results for Example 5 with $\beta = \frac{1}{2}$ using the RBF method

Table 16 $\Vert e\Vert _{\infty }$ for Example 5 with different values of m, N and $\beta = \frac{1}{2}$ using the MLS method

Table 17 Estimation of error by RBF (IMQ) for Example 5

Fig. 17

The absolute error function $\vert e(t)\vert$ for various values of N for Example 5 by RBF method

Fig. 18

The absolute error for Example 5 by RBF method

Fig. 19

$\vert e(t)\vert$ for various values of N and $\beta =\frac{1}{2}$ for Example 5

Fig. 20

The exact solution and RBF solution of Example 5 with $\beta = \frac{1}{2}$

Example 6

Consider a class of nonlinear VIEs of the third kind of the form

$$\begin{aligned} t^{\beta } u(t)=t^{\beta }f(t)+\int _{0}^{ t} s^{\beta -1} k(t, s) G(u(s)) d s, \quad t \in I, \end{aligned}$$

(20)

where $\beta =\frac{1}{4}$, $G(u)= e^{u}$, $k(t, s)=s^\frac{3}{4}cos(1+t^2)$, the exact solution is given by $u(t) = e^{-t}$ and

$$\begin{aligned} f(t)= \textrm{e}^{-t}+(\textrm{Ei}_1(-1) \cos (t+1)^2-\textrm{Ei}_1\left( -\textrm{e}^{-t}\right) \cos (t+1)^2 )t^{-1 / 4}. \end{aligned}$$

Table 18 displays numerical tests in terms of $\left\| e_N\right\| _2$ and $\left\| e_N\right\| _{\infty }$ at various numbers of N for GA and IMQ with $\beta =\frac{1}{4}$. The comparison of the maximum absolute error of the presented technique with the MLS method is given in Table 19. Table 20 summarizes the estimation of error by RBF, and Figs. 21 and 22 depict the behavior of the absolute error function for $\beta =\frac{1}{4}$ on the interval [0, 1]. These graphs indicate that the suggested approach is able to produce highly accurate numerical results. The computational efficiency of example 6 for $\beta =\frac{1}{4}$ using the presented technique and the MLS scheme is graphically plotted in semi-logarithmic representation in Fig. 23. Figure 24 illustrates the curves of exact and approximate solutions for $\beta =\frac{1}{4}$. The current approach yields accurate numerical solutions for this class of nonlinear VIEs of the third kind.

Table 18 Numerical results for Example 6 with $\beta =\frac{1}{4}$ by RBF method

Fig. 21

The absolute error function $\vert e(t)\vert$ for various values of N for Example 6 by RBF method

Fig. 22

The absolute error for Example 6 by RBF method

Fig. 23

$\vert e(t)\vert$ for various values of N for Example 6 by RBF method

Table 19 $\Vert e\Vert _{\infty }$ for Example 6 with $\beta =\frac{1}{4}$ by MLS method

Table 20 Estimation of error by RBF (GA) for Example 6

Fig. 24

The exact solution and RBF solution of Example 6 with $\beta = \frac{1}{4}$

7 Conclusion

In this current paper, a numerical scheme based on the RBF approach has been used for the approximate solution of a class of VIEs of the third kind. The algorithm of the scheme can be easily extended to other classes of Volterra integral equations of the third kind. The proposed scheme proved to be simple, computationally interesting, and attractive. The method is based on the zeros of Legendre–Gauss–Lobatto collocation points. The precision of the current method has been clearly proven by a series of numerical experiments. These verify the validity of the current method, which is efficient, accurate, and reliable for a class of VIEs of the third kind. Moreover, by comparing the RBF method with exact solutions and with the MLS collocation method, we show that RBF methods have good reliability and efficiency. The proposed scheme can produce highly accurate solutions with low memory requirements and high computing power. With the proposed method, high convergence rates and good accuracy can be achieved using relatively few data points. The presented method can easily be developed for other classes of integro-differential equations.