Global sensitivity analysis for mathematical models comparison

Abstract

The choice of an adequate mathematical model is a key step in solving problems in many different fields. When more than one model is available to represent a given phenomenon, a poor choice might result in loss of precision and efficiency. Well-known strategies for comparing mathematical models can be found in many previous works, but seldom regarding several models with uncertain parameters at once. In this work, we present a novel approach for measuring the similarity among any given number of mathematical models, so as to support decision making regarding model selection. The strategy consists in defining a new general model composed of all candidate models and a uniformly distributed random variable, whose sampling selects the candidate model employed to evaluate the response. Global Sensitivity Analysis (GSA) is then performed to measure the sensitivity of the response with respect to this random variable. The result indicates the level of discrepancy among the mathematical models in the stochastic context. We also demonstrate that the proposed approach is related to the Root Mean Square (RMS) error when only two models are compared. The main advantages of the proposed approach are: (i) the problem is cast in the sound framework of GSA, (ii) the approach also quantifies if the discrepancy among the mathematical models is significant in comparison to uncertainties/randomness of the parameters, an analysis that is not possible with RMS error alone. Numerical examples of different disciplines and degrees of complexity are presented, showing the kind of insight we can get from the proposed approach.

1 Introduction

In this work, we consider the following problem. Suppose a given phenomenon can be represented using different mathematical models $f_1$, $f_2$,..., $f_m$.¹ We then wish to measure the similarity/discrepancy among these mathematical models. Here, we propose a stochastic comparison approach wherein the problems parameters may be uncertain. In this way, we measure not only the discrepancy between the mathematical models but also if this discrepancy is significant in comparison to parameters uncertainties. This is an important question given that the discrepancy of the mathematical models may sometimes be overwhelmed by uncertainties and randomness on the problems parameters.

Due to its practical value, mathematical models comparisons have been extensively carried out in almost every field of science (see Heywood and Cheng (1984); Alberg and Berglund (2003); Allen et al. (2005); Fuina et al. (2011); Cazes and Moës (2015); Zhou et al. (2016); Henkel et al. (2016); Ooi and Ooi (2017); Malena et al. (2019); de Assis et al. (2020); den Boon et al. (2019); Vorel et al. (2021); Adnan et al. (2021); Bauer and Tyacke (2022) for some examples and discussions on the subject). The term “models comparison” is also frequently employed in the following contexts: i) comparison of regression models to empirical data (e.g. goodness of fit, R coefficient, likelihood estimates, among others); ii) stochastic models comparison (e.g. Bayesian models comparison, Akaike information criterion (AIC), Bayesian information criterion (BIC), among others). It is important to emphasize that the problem addressed here is different: we wish to compare if two or more deterministic mathematical representations (e.g. mathematical models) $f_1$, $f_2$,..., $f_m$ can be considered similar/discrepant even when they are subject to uncertainties in the parameters.

Here, we demonstrate that this problem can be formulated in the context of Global Sensitivity Analysis (GSA) (Saltelli et al. 2007) by defining a random variable that chooses which mathematical model is employed to evaluate the response. Sobol’ indices (Sobol’ 1990) (or some other GSA technique) can then be employed to measure the sensitivity of the response with respect to this random variable. The result indicates the similarity among the mathematical models in the stochastic context. The main advantage of the proposed approach is that the problem of mathematical models comparison is written as a GSA problem, for which a sound theoretical basis and efficient computational techniques exist. Other interesting properties of the proposed approach are discussed later on this paper.

Note that Borgonovo (2010) employed a similar approach to represent settings changes in a given mathematical model. In this case, a discrete random variable defines the current setting (i.e. current scenario) and different equations are employed for each setting. However, these different equations actually represent the response of the same theoretical model under different situations (e.g. before and after new information is included). Besides, Cannavó (2012) also employed GSA for a similar problem, that of comparison of theoretical models to empirical data (even though the empirical data was simulated with more accurate theoretical models in this case). The novelty of this work is that we address a different problem: employment of GSA for measuring similarity/discrepancy among mathematical models that represent the same phenomenon. The proposed formulation is also different from that proposed by Cannavó (2012). Finally, some preliminary results of the present work were presented in a conference paper by Begnini et al. (2022).

The rest of this paper is organized as follows. In the next section, we present a brief review of GSA and Sobol’ indices. We then present the proposed approach for mathematical models comparison. Numerical examples are presented in Section 4. The conclusions of this work are summarized in the last section.

2 Global sensitivity analysis and Sobol’ indices

In GSA, one quantifies the influence of input randomness on output randomness for a given mathematical model. The subject has been extensively studied in the past and is cast under solid mathematical foundations. Efficient computational techniques for GSA have also been developed. An overview of the subject is presented in Saltelli et al. (2007) and Borgonovo and Plischke (2016). See Tang et al. (2015); Yun et al. (2016); Zaicenco (2017); Jakeman et al. (2020); Hübler (2020); Ehre et al. (2020); Ökten and Liu (2021); Zhang et al. (2020); Zhu and Sudret (2021); Antoniadis et al. (2021); Goda (2021); Papaioannou and Straub (2021); Gilquin et al. (2021); Mwasunda et al. (2022) for some recent advances, applications and discussions on GSA.

GSA can be employed for several practical purposes (Saltelli et al. 2007; Borgonovo and Plischke 2016). In this work, we employ GSA in the context of factor fixing decision, i.e. we employ GSA to investigate whether or not some random factor can be fixed without affecting the results too much. In particular, we employ GSA to decide if we can take some particular mathematical model over a set of available ones without affecting the results too much.

Consider the random variable

$$\begin{aligned} Y = f({\textbf{X}}), \end{aligned}$$

(1)

where ${\textbf{X}} \in \mathbb {R}^n$ is a random vector and $f: \mathbb {R}^n \rightarrow \mathbb {R}$ is the mathematical model. Here, we say that Y is the response of the mathematical model f. Sobol’ first-order sensitivity index with respect to random variable $X_i$ is defined as Sobol’ (1990)

$$\begin{aligned} S_i = \frac{ \mathbb {V}\left[ \mathbb {E}\left[ Y \vert X_i \right] \right] }{ \mathbb {V}\left[ Y \right] }, \end{aligned}$$

(2)

where $\mathbb {E}$ and $\mathbb {V}$ represent the expected value and variance, respectively. In the above equation, $\mathbb {E}\left[ Y \vert X_i\right]$ represents the expected value of the response conditioned to $X_i$. Sobol’ total index can be written as Saltelli et al. (2007)

$$\begin{aligned} S_{Ti} = 1 - \frac{ \mathbb {V}\left[ \mathbb {E}\left[ Y \vert {\textbf{X}}_{\sim i} \right] \right] }{ \mathbb {V}\left[ Y \right] }, \end{aligned}$$

(3)

where $\mathbb {E}\left[ Y \vert {\textbf{X}}_{\sim i} \right]$ is the expected value of the response conditioned to all factors but $X_i$.

Sobol’ indices measure the relative impact on the variance of the model response when some factor $X_i$ is fixed. For this reason, Sobol’ indices are variance-based measures of sensitivity. The main difference between the indices $S_i$ and $S_{Ti}$ is that the latter also captures the interaction between $X_i$ and the other factors. Given that one variable may not directly influence the model variability but its interaction effects may be relevant, the total index $S_{Ti}$ is more appropriate for factor fixing decision. Sobol’ indices play a very important role in variance-based GSA and the reader is referred to Sobol’ (1990); Saltelli (2002); Saltelli et al. (2007); Sobol’ (2001) for more details on the subject.

3 Proposed approach for models comparison

In order to quantify the similarity among mathematical models $f_1$, $f_2$,..., $f_m$ using Sobol’ indices we employ the following strategy. We first take a discrete Uniform random variable W with mass function

$$\begin{aligned} p(w) = \left\{ \begin{array}{ll} 1/m, &{} \text {if } w = 1 \\ 1/m, &{} \text {if } w = 2 \\ \vdots &{} \\ 1/m, &{} \text {if } w = m \\ \end{array} \right. \end{aligned}$$

(4)

We then define the response as

$$\begin{aligned} Y = f({\textbf{X}},W) \equiv \left\{ \begin{array}{ll} f_1({\textbf{X}}), &{} \text {if } w = 1 \\ f_2({\textbf{X}}), &{} \text {if } w = 2 \\ \vdots &{} \\ f_m({\textbf{X}}), &{} \text {if } w = m \\ \end{array} \right. , \end{aligned}$$

(5)

i.e., we take $Y = f_i({\textbf{X}})$ with probability 1/m. In other words, the random variable W is employed to randomly select which mathematical model is employed to evaluate the response. Since W is uniform, the probability of employing each mathematical model $f_i$ is the same.

In this context, the sensitivity with respect to mathematical model choice can be measured by Sobol’ total index with respect to W², i.e.,

$$\begin{aligned} S_{TW} = 1 - \frac{\mathbb {V}\left[ \mathbb {E}\left[ Y \vert {\textbf{X}}_{\sim W}\right] \right] }{\mathbb {V}\left[ Y\right] }. \end{aligned}$$

(6)

A small sensitivity index $S_{TW}$ indicates that W does not influence $\mathbb {V}[Y]$ very much. This means that, from Sobol’ indices point of view, choosing between the different mathematical models $f_i$ has a small impact on the response. Thus, the index $S_{TW}$ can be viewed as a measure of discrepancy among the mathematical models $f_i$ in the stochastic context. The error estimates presented in Sobol’ et al. (2007) for factor fixing should also apply for the proposed approach, even though we do not pursue this topic further in this work.

The proposed approach has some interesting properties:

• 1. The problem of mathematical models comparison is written as a GSA problem, for which an extensive literature exists. This means that the proposed approach inherits the sound mathematical basis of Sobol’ indices (Sobol’ 2001; Sobol 2003; Sobol’ et al. 2007) and that efficient computational techniques are available (Saltelli 2002; Saltelli et al. 2007; Cannavó 2012; Gilquin et al. 2021).

• 2. The proposed approach measures the discrepancy between the mathematical models in the stochastic context. Even if the models are discrepant in the deterministic context, the discrepancy in the stochastic context may end-up being irrelevant if the influence of the random variables is too high. Several comparison techniques measure the discrepancy between models but do not identify if this discrepancy is significant with respect to the influence of the random variables. The opposite is also true. Two models may seem similar in the deterministic context but end-up being discrepant in the stochastic context, when subject to uncertainty or randomness.

• 3. The proposed approach allows for simultaneous comparison of several models at once.

3.1 Relation to RMS error

Suppose we wish to measure the discrepancy between two mathematical models $f_1$, $f_2$. A very popular approach in this case is to evaluate the Root Means Square (RMS) error

$$\begin{aligned} E_{RMS} = \sqrt{\mathbb {E}_X \left[ \left( f_2(X) - f_1(X) \right) ^2\right] }. \end{aligned}$$

(7)

The RMS error is likely the most popular approach for measuring discrepancies between models in practice, due to its computational and conceptual simplicity.

When only two mathematical models are compared, the proposed approach shares conceptual similarities to the RMS error. It can be demonstrated that (see the Appendix)

$$\begin{aligned} E_{RMS} = 2 \sqrt{ S_{TW} \mathbb {V}\left[ Y \right] } \end{aligned}$$

(8)

and

$$\begin{aligned} S_{TW} = \frac{E_{RMS}^2}{E_{RMS}^2 + 4 \mathbb {V}_X \left[ m(X) \right] }, \end{aligned}$$

(9)

where

$$\begin{aligned} m(X) = \frac{1}{2} \left( f_1(X) + f_2(X) \right) \end{aligned}$$

(10)

is the mean model (i.e. the point-wise mean between models $f_1$ and $f_2$). That is, the total index with respect to model choice $S_{TW}$ is closely linked to the RMS error in this case.

These results indicate that the Total Index $S_{TW}$ can be interpreted as a relation between the mean square error and the variance of the mean model. We also observe that the RMS error can be easily evaluated from the results obtained with GSA using Eq. (8). Finally, note that Eq. (9) is useful for computational purposes when one wishes to evaluate only $S_{TW}$, without measuring the sensitivity with respect to the other factors of the problem. All these conclusions hold when only two models $f_1$, $f_2$ are considered, because the RMS error is not defined when more than two models are compared. These are important conclusions, because the RMS error is very popular in practice.

4 Numerical examples

In this section, we present three numerical examples that illustrate the kind of insight we can gain from the proposed approach. The first example concerns the comparison of a quadratic function with its first order Taylor expansion. In the second example, we compare three well known head loss (i.e. pressure drop) formulas for a given range of situations. In the last example, we compare second order effects (i.e. bending moment amplification due to large displacements) for two reinforced concrete plane frames. Sobol’ total effect indices were evaluated with the MATLAB toolbox GSAT developed by Cannavó (2012).

4.1 Mathematical example

We first consider the mathematical models

$$\begin{aligned}{} & {} f_1(X_1,X_2) = X_1^2 + X_2^2 + X_1 X_2, \end{aligned}$$

(11)

$$\begin{aligned}{} & {} f_2(X_1,X_2) = 108 + 18 (X_1 - 6) + 18 (X_2 - 6). \end{aligned}$$

(12)

Note that the model $f_2$ is the first-order Taylor expansion of $f_1$ at $(x_1,x_2) = (6,6)$. The sensitivity indices were evaluated with a sample of size $N = 10^5$. This example was previously discussed by Begnini et al. (2022).

We start by taking $X_1, X_2$ as independent random variables with Normal distribution, expected value $\mathbb {E}[X_1] = \mathbb {E}[X_2] = 6$ and standard deviation $\sqrt{\mathbb {V}[X_1]} = \sqrt{\mathbb {V}[X_2]} = 1$. The results are presented in the first row of Table 1. Sensitivity with respect to the model choice (i.e. $S_{TW}$) is presented in the second column with bold letters. Sensitivity with respect to the other random variables are presented in the other columns.

Table 1 Sensitivity indices for Example 1

For $X_1, X_2 \sim \mathcal {N}(6,1)$, we observe that the random variable W has a small impact on the variance of the response (i.e. $S_{TW}$ close to 0.3%). This means that, in the stochastic context considered, the mathematical models $f_1$ and $f_2$ can be considered very similar since choosing between one or another does not affect the results significantly. This occurs because the Taylor expansion $f_2$ is centered at the expected value of the random variables and the variance of the random variables is small.

We now change the expected value of the random variables to $\mathbb {E}[X_1] = 9$, $\mathbb {E}[X_2] = 10$ and leave the other parameters unchanged. The results are presented in the second row of Table 1. The sensitivity index $S_{TW}$ is now close to 29%. This indicates that choosing between $f_1$ and $f_2$ now affects the results, i.e. the mathematical models are not similar for the new stochastic context. This basically occurs because the Taylor expansion $f_2$ is no longer centered on the expected value of the random variables.

In the last case, we take expected values $\mathbb {E}[X_1] = 9$, $\mathbb {E}[X_2] = 10$ and standard deviations $\sqrt{\mathbb {V}[X_1]} = 2$, $\sqrt{\mathbb {V}[X_2]} = 3$. Note that we keep the expected values from the previous case, but the standard deviations are significantly increased. The index $S_{TW}$ now results close to 13%, indicating that the models $f_1$ and $f_2$ are less discrepant than in the previous case (although the discrepancy is still relevant). This result is explained by the sensitivity index $S_{T2}$, that is now close to 65%. Since the standard deviation of $X_2$ was increased to $\sqrt{\mathbb {V}[X_2]} = 3$, the relative importance of this factor to the analysis was significantly increased. As a consequence, the relative importance of the other two factors W and $X_1$ was reduced. In other words, the discrepancy between the models is now overwhelmed by the variability of $X_2$. This puts in evidence an important conclusion: models comparison in the stochastic context must consider if the model discrepancy is relevant in comparison to the randomness caused by the random variables.

The total index $S_{TW}$ was also evaluated with Eq. (9) for all three cases presented in Table 1, in order to check the validity of the expression. In this case, we employed crude Monte Carlo Simulation (MCS) with a sample of size $10^6$ in order to evaluate $E_{RMS}$ and $\mathbb {V}\left[ m(X) \right]$. The indexes resulted $S_{TW} = 0.0035$, $S_{TW} = 0.2875$ and $S_{TW} = 0.1285$, respectively. These results are very similar to the ones obtained with GSA and presented in Table 1. This demonstrates that Eq. (9) can also be employed to evaluate $S_{TW}$ in practice. However, note that the indexes $S_{T1}$ and $S_{T2}$ cannot be accessed by this approach.

4.2 Head loss formulas

In the second example, we compare the well-known Darcy-Weisbach, Hazen-Williams and Chezy-Manning head loss formulas for a range of situations. These models are largely employed in the Engineering community to evaluate the pressure drop due to friction for flows in closed conduits. More details on the subject are presented in Larock et al. (2000). Here, we assume that all quantities are represented using SI units.

Darcy-Weisbach model is given by

$$\begin{aligned} Q_{DW}(D,S,e) = \frac{1}{\sqrt{f}} A \sqrt{2 g D S}, \end{aligned}$$

(13)

where Q is the flow, A is the pipe cross-sectional area, $g = 9.81\,m/s^2$ is the acceleration of gravity, D is the pipe diameter and S is the slope of the energy line. The friction factor f of Darcy-Weisbach model can be evaluated with Colebrook-White formula

$$\begin{aligned} \frac{1}{\sqrt{f}} = 1.14 - 2 \log _{10} \left( \frac{e}{D} + \frac{1}{\sqrt{f}} \frac{9.35}{Re} \right) , \end{aligned}$$

(14)

where e is the material roughness and

$$\begin{aligned} Re = \frac{V D}{\nu } \end{aligned}$$

(15)

is Reynolds number, where $V = Q/A$ is the flow velocity and $\nu$ is the kinematic viscosity (here we take $\nu = 10^{-6}$, representing water at 20$^o$C).

Darcy-Weisbach is a theoretical model derived from fluid mechanics fundamental equations. For this reason, the model is valid for a wide range of situations, including different flow regimes. It is also the model that better agrees with experimental data in general. However, the friction factor from Eq. (14) is defined implicitly, i.e. it depends on both Q (by means of Re) and on itself. Consequently, evaluation of the flow using Eq. (13) requires an iterative scheme. Here, we employ the following fixed point iteration

$$\begin{aligned}{} & {} Re^{(k)} = Q_k \frac{D}{A \nu }, \end{aligned}$$

(16)

$$\begin{aligned}{} & {} \frac{1}{\sqrt{f^{(k+1)}}} = 1.14 - 2 \log _{10} \left( \frac{e}{D} + \frac{1}{\sqrt{f^{(k)}}} \frac{9.35}{Re^{(k)}} \right) , \end{aligned}$$

(17)

$$\begin{aligned}{} & {} Q_{DW}^{(k+1)} = \frac{1}{\sqrt{f^{(k)}}} A \sqrt{2 g D S}, \end{aligned}$$

(18)

where indices (k) represent the current iteration and $(k+1)$ represents the updated values. Here, we take $f_0 = 0.5$, $Q_0 = 0.01$ and iterate until $\vert Q_{DW}^{(k+1)} - Q_{DW}^{(k)} \vert \le 10^{-6}$.

The Hazen–Williams model can be written as (using SI units)

$$\begin{aligned} Q_{HW}(R,S,C_{HW}) = 0.849 C_{HW} A R^{0.63} S^{0.54}, \end{aligned}$$

(19)

where $C_{HW}$ is the Hazen-Williams material roughness, $R = D/4$ for pipes with full flow and A, S are as defined above. Hazen-Williams is an empirical equation calibrated for turbulent flows. For this reason, its range of applications is limited in comparison to that of Darcy-Weisbach model. However, Hazen-Williams model is much easier to employ in practice, since it does not require an iterative scheme. Besides, Hazen-Williams model has been found to be very accurate for a wide range of situations of practical interest.

Finally, Chezy-Manning head loss model can be written as (using SI units)

$$\begin{aligned} Q_{CM}(R,S,n_{CM}) = \frac{1}{n_{CM}} A R^{2/3} \sqrt{S}, \end{aligned}$$

(20)

where $n_{CM}$ is the Manning material roughness and A, R, S are as defined above. The Chezy-Manning model is also empirical and was calibrated for wholly rough flow regimes. Even though it is also simple to employ, since no iterative scheme is required, some researchers argue that Hazen–Williams empirical model is more accurate in comparison to Darcy–Weisbach model and experimental data.

In this example, we compare these three classical models for parameters as defined in Table 2. Random variable $X_1$ is a multiplier for the material roughness of the pipe, with Gamma distribution, expected value equal to 1.0 and standard deviation equal to 0.2 (i.e. parameters (25.0, 0.04)). The expected values for $C_{HW}$, e and $n_{CM}$ correspond to cast iron pipes. The pipe diameter is defined by the Uniform random variable $X_2\sim \mathcal {U}(0.05,0.20)$ and the slope of the energy line is given by Uniform random variable $X_3\sim \mathcal {U}(0.01,0.20)$. In other words, the comparisons made here hold for cast iron pipes with uncertain roughness, diameter in the range 0.05m to 0.20m and slope of the energy line in the range 1/100 to 20/100. The sensitivity indices were evaluated with a sample of size $N = 10^5$.

Table 2 Random variables for head loss models

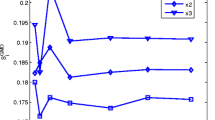
We first compare all three models by taking $f_1 = Q_{DW}$, $f_2 = Q_{HW}$ and $f_3 = Q_{CM}$. The results are given in the first row of Table 3. We observe that the variance of the response is mainly affected by uncertainties on the pipe diameter and slope of the energy line ($X_2$ and $X_3$, respectively). However, the response is also significantly affected by W, since we get $S_{TW}$ close to 16%. This indicates that the three models cannot be considered similar in this case. Note that this analysis is not able to quantify direct discrepancy between individual models. For this reason, we then proceed to comparison between two models at a time.

Table 3 Sensitivity indices for Example 2

We now compare only Darcy-Weisbach and Hazen–Williams models, by taking $f_1 = Q_{DW}$, $f_2 = Q_{HW}$. The results are given in the second row of Table 3. The results now indicate weak sensitivity with respect to W, with $S_{TW}$ close to 5%. This means that choosing between Darcy–Weisbach and Hazen–Williams models has little impact on the variance of the response in the stochastic context considered here. In other words, Darcy-Weisbach and Hazen–Williams models can be considered similar for the range of values considered.

The previous results indicate that Darcy–Weisbach and Hazen–Williams models are similar for the situation studied. This seems to indicate that Chezy-Manning model is not similar to the other two, because when all three models are compared simultaneously we get a significant sensitivity with respect to W (see the first row of Table 3). In order to confirm this assumption we now compare Darcy-Weisbach and Chezy-Manning models, by taking: $f_1 = Q_{DW}$, $f_2 = Q_{CM}$. The results are given in the third row of Table 3. Sensitivity with respect to W now indicates that Chezy-Manning model is not very similar to Darcy–Weisbach, since we get $S_{TW}$ close to 10%.

In order to understand what is really happening we finally compare Hazen-Williams and Chezy-Manning models, by taking: $f_1 = Q_{HW}$, $f_2 = Q_{CM}$. The results are given in the last row of Table  3 and indicate that the two models are very discrepant, since we get $S_{TW}$ close to 22%. This is the largest discrepancy identified among the three models.

These results lead to the following conclusions:

• Hazen–Williams model can be considered similar to Darcy-Weisbach model under the circumstances studied, with $S_{TW}$ close to 5%;

• Similarity between Chezzy-Manning and Darcy–Weisbach models is arguable under the circumstances studied, with $S_{TW}$ close to 10%;

• Hazen–Williams and Chezy-Manning models are very discrepant under the circumstances studied, with $S_{TW}$ close to 22%.

These conclusions are basically the same pointed out in the past by other researchers (see Jamil and Mujeebu (2019)) and indicate the kind of insight we can get from the proposed approach.

The total index $S_{TW}$ was also evaluated with Eq. (9) for the following comparisons: Darcy-Weisbach vs Hazen–Williams, Darcy–Weisbach vs Chezy-Manning and Hazen–Williams vs Chezy-Manning. Crude MCS with a sample of size $10^6$ was employed. The indexes resulted $S_{TW} = 0.0547$, $S_{TW} = 0.0909$ and $S_{TW} = 0.2257$, respectively. These results are again very similar to the ones obtained with GSA (see Table 3), demonstrating again that Eq. (9) can be employed in practice. However, simultaneous comparison of the three models is not possible in this case, since the RMS error can only be defined for two models at once. Finally, we again observe that the sensitivity with respect to the other random factors $S_{T1}$, $S_{T2}$ and $S_{T3}$ cannot be obtained from the RMS error alone.

4.3 Second-order effects on plane frames

In the last example, we consider a problem from Structural Engineering, concerning the Reinforced Concrete (RC) plane frames from Fig. 1. In particular, we compare two commonly employed mathematical models to represent the displacements of the structure. In the first case, the static equilibrium equations are written considering the original geometry of the structure. This approach is known as Linear Structural Analysis, since it leads to a system of linear equations. In the second case, the static equilibrium equations are written for the displaced configuration of the structure. This is known as Geometric Non-Linear Structural Analysis, since it leads to a system of non-linear equations. Geometric Non-Linear Structural Analysis is conceptually more accurate, since equilibrium indeed occurs in the displaced configuration. However, in several practical applications, the displacements are very small, due to design constraints, and Linear Structural Analysis is able to obtain accurate results. Since Linear Structural Analysis is much easier to employ, because it avoids the system of non-linear equations, engineers generally employ Linear Structural Analysis instead of Non-Linear Analysis, unless strictly necessary. See McGuire et al. (2000) for more details on the subject.

Here, we employ the proposed approach to identify if second order effects (i.e. bending moment amplification due to consideration of Geometric Non-Linearity) are significant. The first frame has two floors, while the second frame has four floors. Each story is 4 m height and 5 m long. All beams have rectangular cross-section with base equal to 20 cm and height equal to 40 cm. All columns have square cross-section with dimensions 20 cm $\times$ 20 cm. The cross-section moment of inertia of columns and beams are multiplied by 0.8 and 0.4, respectively, in order to represent loss of flexural stiffness due to cracking of the reinforced concrete. Structural analysis was made with the software MASTAN2 (McGuire et al. 2000) using a plane frame model and a single finite element for each structural member. Geometric non-linear analysis was made with the predictor corrector algorithm using 10 uniform load steps. The sensitivity indexes were evaluated with a sample of size $N = 10^4$.

Fig. 1

Reinforced Concrete (RC) plane frames

The random variables are as defined in Table 4. The Gamma-distributed random variables $X_1, X_2, X_3$ are multipliers for the Elastic Modulus E, the lateral forces P and the distributed loads q, respectively. These multipliers have expected value equal to 1.0 and standard deviation equal to 0.1 (i.e. parameters [100, 0.01]). Finally, random variable $X_4$ is normally distributed and defines the out-of-plumb angle $\theta$, as illustrated in Fig. 2.

In order to quantify the importance of second-order effects we consider the bending moment at the base of the lower right column (the region indicated in red in Fig. 1). We thus take

$$\begin{aligned}{} & {} f_1 = M_{L}, \end{aligned}$$

(21)

$$\begin{aligned}{} & {} f_2 = M_{NL}, \end{aligned}$$

(22)

where $M_{L}$ and $M_{NL}$ represent the bending moment at the base of the lower right column obtained with linear and geometric non-linear analysis, respectively. The results are presented in Table 5.

Table 4 Random variables for RC plane frames

Fig. 2

Out-of-plumb angle $\theta$

Table 5 Sensitivity indices for Example 3

For the two-story frame, the sensitivity with respect to model choice is close to 5%. This indicates a small influence of considering or not second order effects in this case. However, for the four-story frame the sensitivity index with respect to model choice is close to 20%, indicating that geometric non-linearity is now an important factor of the problem. These results indicate that linear structural analysis would likely be enough for most practical purposes concerning the two-story frame studied. However, the four-story frame studied is strongly subject to second-order effects that should be considered in practice.

We also observe that uncertainty on lateral loads ($X_2$) is the most important factor in this case. The out-of-plumb angle ($X_4$) is also significant for the variance of the response. Finally, uncertainties on the elastic modulus and distributed loads ($X_1$ and $X_3$, respectively) have a small impact on the variance of the response.

The total index $S_{TW}$ was also evaluated with Eq. (9) for the two RC plane frames. Crude MCS with a sample of size $10^3$ was employed. The indexes resulted $S_{TW} = 0.0583$ and $S_{TW} = 0.1941$, respectively. These results are again vary similar to the ones obtained with GSA.

5 Conclusions

In this work, we proposed an approach for mathematical models comparison in the stochastic context. The problem is stated in the framework of GSA, by defining a random variable that chooses which mathematical model is employed to evaluate the response. Sensitivity with respect to this random variable then indicates if the mathematical models are similar or not. We also demonstrated that the proposed approach is related to the RMS error. This is an important results since the RMS error is a very popular approach for measuring the discrepancy between two models. However, the main advantages of the proposed approach are: (i) the problem of mathematical models comparison is cast in the sound framework of GSA, (ii) the approach also quantifies if the discrepancy among the mathematical models is significant in comparison to uncertainties/randomness of the parameters, an analysis that is not possible with RMS error alone.

When only two mathematical models are compared, the sensitivity index with respect to model choice $S_{TW}$ can also be evaluated with Eq. (9), using the RMS error and the variance of the mean model. The results presented in the examples demonstrate that this expression can be easily employed in practice. However, it should be highlighted that this approach cannot be employed for simultaneous comparison of more than two models. Besides, this approach is unable to provide the sensitivity indexes with respect to the other random factors of the problem. For this reason, the proposed GSA approach is more general than the RMS error. Even though, Eq. (9) may be very useful in practice when only two models are compared and only $S_{TW}$ is required, a situation that may indeed be common in practice.

It is important to point out that a variance-based sensitivity index was employed in this work (Sobol’ total index). Thus, the approach proposed here shares the same limitations of standard variance-based approaches. First, the approach requires large computation effort in order to give accurate results. Besides, the approach is not recommended if higher order moments (e.g. skewness and kurtosis) or other probability measures (e.g. reliability) are important. However, it is important to highlight that several recent advancements on GSA could lead to a reduction of the required computational effort (see Hübler (2020); Ehre et al. (2020); Ökten and Liu (2021); Zhu and Sudret (2021); Papaioannou and Straub (2021)). Besides, the proposed approach can be adapted for reliability-based GSA using the concepts presented in Kala (2019); Fort et al. (2016). The numerical examples presented here illustrate the kind of insight we can get from this analysis. We observe that the proposed approach is valuable for identifying the level of discrepancy between mathematical models in a given stochastic context (i.e. considering randomness/uncertainties on the parameters of the models).

Appendix A relation to mean square error

The total index with respect to model choice can be written as

$$\begin{aligned} \begin{aligned} S_{TW}&= 1 - \frac{\mathbb {V}_X\left[ \mathbb {E}_W\left[ Y \vert {\textbf{X}}_{\sim W}\right] \right] }{\mathbb {V}\left[ Y\right] }\\&= \frac{\mathbb {E}_X\left[ \mathbb {V}_W\left[ Y \vert {\textbf{X}}_{\sim W}\right] \right] }{\mathbb {V}\left[ Y\right] }.\\ \end{aligned} \end{aligned}$$

(A1)

Let us define the auxiliary random variable

$$\begin{aligned} Z(X) = \mathbb {V}_W\left[ Y \vert {\textbf{X}}_{\sim W}\right] . \end{aligned}$$

(A2)

If only two mathematical models $f_1$, $f_2$ are considered, we then have

$$\begin{aligned} Z(X) = \frac{1}{2} \left( f_1(X) - \mathbb {E}_W\left[ Y \vert {\textbf{X}}_{\sim W}\right] \right) ^2 + \frac{1}{2} \left( f_2(X) - \mathbb {E}_W\left[ Y \vert {\textbf{X}}_{\sim W}\right] \right) ^2. \end{aligned}$$

(A3)

Besides

$$\begin{aligned} \mathbb {E}_W\left[ Y\vert {\textbf{X}}_{\sim W}\right] = \frac{1}{2} \left( f_1(X) + f_2(X) \right) . \end{aligned}$$

(A4)

Thus

$$\begin{aligned} \begin{aligned} f_1(X) - \mathbb {E}_W\left[ Y\vert {\textbf{X}}_{\sim W}\right]&= f_1(X) - \frac{1}{2} \left( f_1(X) + f_2(X) \right) \\&= \frac{1}{2} \left( f_1(X) - f_2(X) \right) \end{aligned} \end{aligned}$$

(A5)

and

$$\begin{aligned} \begin{aligned} \left( f_1(X) - \mathbb {E}_W\left[ Y\vert {\textbf{X}}_{\sim W}\right] \right) ^2&= \left( f_2(X) - \mathbb {E}_W\left[ Y\vert {\textbf{X}}_{\sim W}\right] \right) ^2\\&= \frac{1}{4} \left( f_2(X) - f_1(X) \right) ^2. \end{aligned} \end{aligned}$$

(A6)

Substitution of Eq. (A6) into Eq. (A3) gives

$$\begin{aligned} Z(X) = \frac{1}{4} \left( f_2(X) - f_1(X) \right) ^2. \end{aligned}$$

(A7)

Consequently

$$\begin{aligned} \begin{aligned} \mathbb {E}_X\left[ \mathbb {V}_W\left[ Y\vert {\textbf{X}}_{\sim W}\right] \right]&= \mathbb {E}_X \left[ Z(X)\right] \\&= \frac{1}{4} \mathbb {E}_X \left[ \left( f_2(X) - f_1(X) \right) ^2\right] . \end{aligned} \end{aligned}$$

(A8)

The total index with respect to model choice can then be written as

$$\begin{aligned} S_{TW} = \frac{1}{4} \frac{\mathbb {E}_X \left[ \left( f_2(X) - f_1(X) \right) ^2\right] }{\mathbb {V}\left[ Y \right] } \end{aligned}$$

(A9)

However, we observe that the Root Mean Square (RMS) Error is defined as

$$\begin{aligned} E_{RMS} = \sqrt{\mathbb {E}_X \left[ \left( f_2(X) - f_1(X) \right) ^2\right] }. \end{aligned}$$

(A10)

For this reason we can write

$$\begin{aligned} S_{TW} = \frac{1}{4} \frac{E_{RMS}^2}{\mathbb {V}\left[ Y \right] } \end{aligned}$$

(A11)

or, alternatively,

$$\begin{aligned} E_{RMS} = 2 \sqrt{ S_{TW} \mathbb {V}\left[ Y \right] }. \end{aligned}$$

(A12)

This demonstrates Eq. (8).

Also note that

$$\begin{aligned} \mathbb {V}\left[ Y \right] = \mathbb {E}_X\left[ \mathbb {V}_W\left[ Y\vert {\textbf{X}}_{\sim W}\right] \right] + \mathbb {V}_X\left[ \mathbb {E}_W\left[ Y\vert {\textbf{X}}_{\sim W}\right] \right] \end{aligned}$$

(A13)

and

$$\begin{aligned} \mathbb {V}_X\left[ \mathbb {E}_W\left[ Y\vert {\textbf{X}}_{\sim W}\right] \right] = \mathbb {V}_X\left[ \frac{1}{2} \left( f_1(X) + f_2(X) \right) \right] . \end{aligned}$$

(A14)

Thus

$$\begin{aligned} \mathbb {V}\left[ Y \right] = \frac{1}{4} \mathbb {E}_X \left[ \left( f_2(X) - f_1(X) \right) ^2\right] + \mathbb {V}_X\left[ \frac{1}{2} \left( f_1(X) + f_2(X) \right) \right] . \end{aligned}$$

(A15)

It is then possible to write

$$\begin{aligned} \mathbb {V}\left[ Y \right] = \frac{1}{4} E_{RMS}^2 + \mathbb {V}_X\left[ m(X) \right] , \end{aligned}$$

(A16)

where

$$\begin{aligned} m(X) = \frac{1}{2} \left( f_1(X) + f_2(X) \right) \end{aligned}$$

(A17)

is the mean model, i.e. the point-wise mean between models $f_1$ and $f_2$. From these results we can also write

$$\begin{aligned} S_{TW} = \frac{E_{RMS}^2}{E_{RMS}^2 + 4 \mathbb {V}_X\left[ m(X) \right] }, \end{aligned}$$

(A18)

that demonstrates Eq. (9).