1 Introduction

We consider the convex-constrained monotone nonlinear equations problem: finding \(x_* \in C\) such that

$$\begin{aligned} F(x_*)=0, \end{aligned}$$
(1)

where \(C \subset {\mathbb {R}}^n\) is a nonempty closed convex set and \(F : {\mathbb {R}}^n \rightarrow {\mathbb {R}}^n\) is a continuous and monotone nonlinear function, not necessarily differentiable. The monotonicity of \(F : {\mathbb {R}}^n \rightarrow {\mathbb {R}}^n\) here means \(\langle \,F(x)-F(y),x-y\rangle \ge 0,\) for all \(x,y \in {\mathbb {R}}^n\). We assume that the solution set of (1), denoted by \(C^*\), is nonempty. Problems of this nature appear in many applications such as power engineering, chemical equilibrium systems and economic equilibrium problems; see, e.g., (Dirkse and Ferris 1995; El-Hawary 1996; Meintjes and Morgan 1987; Wood and Wollenberg 1996).

Recently, many methods have been proposed for solving (1); see, for example, Liu and Feng (2019), Liu and Li (2015), Ou and Liu (2017), Wang and Wang (2009), Wang and Xu (2007), Yu et al. (2009). They are extensions of Newton, spectral gradient and conjugate gradient methods for solving the unconstrained case of (1). In general, these constrained (projected) methods require to compute the exact orthogonal projection of a point onto the constrained set C. However, it is well-known that, depending on the geometry of C, the projection onto it neither has a closed-form nor can be easily computed; for example, if C is a polyhedral or a spectrahedron. Therefore, one of the goals of this article is to present some improvements in existing projected methods for solving (1). Basically, we present some methods for solving (1) in which approximate projections are allowed. Moreover, a new algorithm with inexact projections is also proposed to solve (1). It is inspired by Solodov and Svaiter (1999a), Algorithm 2.1 for solving variational inequalities. In the context that the projection operator is computationally expensive, Solodov and Svaiter (1999a), Algorithm 2.1 was devised in order to minimize the total number of performed projection operations.

Toward the aforementioned goals, we first present a framework for solving convex-constrained monotone nonlinear equations. More precisely, at each iteration, the framework imposes a safeguard strategy on the search directions. A suitable linesearch procedure based on Solodov and Svaiter (1999b) is considered, which, in particular, provides a hyperplane that strictly separates the current iteration from zeroes of the system of equations. Then, we compute an approximate projection of a point, which belongs to the aforementioned hyperplane, onto the intersection between C and the hyperplane (or onto the constrained set C). Under mild assumptions, we prove that the sequence generated by the proposed framework converges to a solution of (1). Some examples of methods which fall into this framework are presented. In particular, inexact versions of steepest descent-based, spectral gradient-like, Newton-like and limited memory BFGS methods are discussed. A new algorithm inspired by Solodov and Svaiter (1999a), Algorithm 2.1 is also proposed and analyzed by means of the general framework.

In order to illustrate the robustness and effectiveness among the instances of the framework, we report some preliminary numerical experiments on a set of monotone nonlinear equations with polyhedral constraints problems. Moreover, we also applied the methods for solving the constrained absolute value equation and compare their performances with the inexact Newton method with feasible inexact projections Oliveira and Ferreira (2020).

The remainder of this paper is organized as follows. In Sect. 2, we list some notations and introduce a concept of an approximate solution for a specific quadratic problem with some of its properties. In Sect. 3, a framework, which combines a safeguard strategy on the search directions with approximate projections, is proposed and its global convergence is established. In Sect. 4, we present some instances of the framework by means of some examples of search directions \(d_k\) that satisfy the safeguard conditions. Some preliminary numerical experiments are reported in Sect. 5 and final remarks are given in Sect. 6.

2 Notation and preliminary results

This section presents some definitions and notations used in this paper. A concept of approximate solution for a specific quadratic problem is introduced and some of its useful properties are discussed.

Let \(L\in {\mathbb {R}}_{++}\). We denote by \({\mathbb {S}}_{n,L}({\mathbb {R}})\) be the set of \(n\times n\) symmetric positive definite matrices such that, for all \(B \in {\mathbb {S}}_{n,L}({\mathbb {R}})\)

$$\begin{aligned} \Vert B\Vert \le L \qquad \text{ and } \qquad \Vert B^{-1}\Vert \le L, \end{aligned}$$
(2)

where \(\Vert . \Vert \) is a sub-multiplicative matrix norm. Note that \({\mathbb {S}}_{n,L}({\mathbb {R}})\) is a compact set of \({\mathbb {R}}^{n \times n}\). Consider an inner product on \({\mathbb {R}}^n\) by setting \(\langle x,z \rangle _{B}=\langle x,Bz \rangle \), where \(B \in {\mathbb {S}}_{n,L}({\mathbb {R}})\) and \(\langle .,.\rangle \) denotes the usual inner product. Hence, the corresponding induced norm \(\Vert .\Vert _B\) is equivalent to the usual norm on \({\mathbb {R}}^n\), since the following inequalities hold

$$\begin{aligned} \frac{1}{\Vert B^{-1}\Vert }\Vert x\Vert ^2\le \Vert x\Vert ^2_B\le \Vert B\Vert \Vert x\Vert ^2. \end{aligned}$$
(3)

We next present the definition of an approximate solution for a specific quadratic problem.

Definition 1

Given \(B \in {\mathbb {S}}_{n,L}({\mathbb {R}})\), \(w\in {\mathbb {R}}^n\), \(\varepsilon \ge 0\) and a nonempty closed convex set \(\Omega \subset {\mathbb {R}}^n\), we say that \({{\tilde{y}}}^B_{\Omega }(w,\epsilon )\) is an \(\varepsilon \)–approximate solution for the problem

$$\begin{aligned} \min _{y\in \Omega }\; \frac{1}{2}\langle B y,y \rangle - \langle w, y \rangle , \end{aligned}$$
(4)

iff

$$\begin{aligned} {{\tilde{y}}}^B_{\Omega }(w,\epsilon ) \in \Omega \quad \text{ and } \quad \langle B {{\tilde{y}}}^B_{\Omega }(w,\epsilon ) - w, y - \tilde{y}^B_{\Omega }(w,\epsilon ) \rangle \ge -\varepsilon , \quad \forall \; y \in \Omega . \end{aligned}$$
(5)

Remark 1

Depending on the geometry of \(\Omega \), the exact solution of (4) neither has a closed-form nor can be easily computed; even for the case where (4) reduces to orthogonal projection onto \(\Omega \) (i.e., \(B=I\) in (4)). Since in (4) we are minimizing a strictly convex quadratic function over a convex set, (5) is a natural condition for an approximate solution. Indeed, the optimality condition for (4) is

$$\begin{aligned} \langle B {{\tilde{y}}}^B_{\Omega }(w,0) - w, y - {{\tilde{y}}}^B_{\Omega }(w,0) \rangle \ge 0, \quad \forall \; y \in \Omega , \end{aligned}$$

which can be obtained from (5) by setting \(\varepsilon =0\). Note that, if \({{\tilde{y}}}^B_{\Omega }(w,0)\) is a zero–approximate solution, then \({{\tilde{y}}}^B_{\Omega }(w,0)\) is the unique exact solution of (4), which we will denote by \(y^B_{\Omega }(w)\). Moreover, in situations in which an algorithm must be used to compute an approximate solution, Definition (1) is suitable since it provides a checkable criterion of inexactness for (4). In fact, as will be discussed below, if the conditional gradient method is used to solve (4), then the verifications of (5) come for free.

Note that if \(w := Bx-F(z)\) with \(x, z\in {\mathbb {R}}^n\), then problem (4) can be rewritten, ignoring constant terms, as

$$\begin{aligned} \min _{y \in \Omega } \frac{1}{2}\Vert y-(x -B^{-1}F(z))\Vert ^2_{B}. \end{aligned}$$
(6)

and (5) is equivalent to

$$\begin{aligned} \langle x - B^{-1}F(z) - {{\tilde{y}}}^B_{\Omega }(w,\epsilon ), y -\tilde{y}^B_{\Omega }(w,\epsilon ) \rangle _{B} \le \varepsilon , \quad \forall \; y \in \Omega . \end{aligned}$$
(7)

In this case, we can say that \(\tilde{y}^B_{\Omega }(Bx-F(z),\epsilon )\) is an approximate projection (in the norm \(\Vert \cdot \Vert _{B}\)) of the direction \(x - B^{-1}F(z)\).

Our condition (5) can be checked when, for example, \(\Omega \) is bounded and the conditional gradient (CondG) method, also known as Frank-Wolfe method (Dunn 1980; Frank and Wolfe 1956), is used to solve (4). The CondG method is designed to solve the convex optimization problem

$$\begin{aligned} \min _{z \in Z}f(z) \end{aligned}$$
(8)

where Z is a nonempty compact convex set and f is a differentiable convex function such that \(\nabla f \) is Lipschitz continuous on Z. Given \(z_{j-1}\in Z\), its j-th step first finds \(y_j\) as a minimum of the linear function \(\langle {\nabla f(z_{j-1})},{\cdot }\rangle \) over Z and then set \(z_j =(1-\alpha _k)z_{j-1}+\alpha _k {{\bar{z}}}_j \) for some \(\alpha _k \in [0,1]\). Its major distinguishing feature compared to other first-order algorithms such as the projected gradient method is that it replaces the usual projection onto Z by a linear oracle which computes \({{\bar{z}}}_j\) as above. Now, if we apply the CondG method to (4), we generate a sequence \(\{z_j\} \subset \Omega \), where \(z_{j} = z_{j-1} + \alpha _j ({\bar{z}}_j - z_{j-1})\), with \(\alpha _j \in (0,1)\), and \({\bar{z}}_j\) is a solution of the subproblem

$$\begin{aligned} \begin{aligned} \min&\quad \langle Bz_{j-1} - w, z - z_{j-1} \rangle .\\ \text {s.t.}&\quad z \in \Omega \end{aligned} \end{aligned}$$
(9)

If the CondG iterations are stopped when

$$\begin{aligned} \langle Bz_{j-1} - w, {\bar{z}}_j - z_{j-1} \rangle \ge -\varepsilon , \end{aligned}$$
(10)

then condition (5) holds with \(\tilde{y}^{B}_{\Omega }(w,\epsilon ) = {z}_{j-1} \).

We next establish a useful relationship between exact and inexact solutions of (4).

Lemma 1

For every \(w, {{\hat{w}}} \in {\mathbb {R}}^n\) and \(\varepsilon \ge 0\), we have

$$\begin{aligned} \Vert {{\tilde{y}}}^I_{\Omega }(w,\epsilon ) - y^I_{\Omega }({{\hat{w}}})\Vert ^2 \le \Vert w-{{\hat{w}}}\Vert ^2 + 2\varepsilon . \end{aligned}$$

Proof

Since \( {\tilde{y}}^I_{\Omega }(w,\epsilon )\in \Omega \) and \( y^I_{\Omega }({{\hat{w}}})\in \Omega \), it follows from Definition 1 that

$$\begin{aligned} \langle {{\tilde{y}}}^I_{\Omega }(w,\epsilon ) - w, \tilde{y}^I_{\Omega }(w,\epsilon ) - y^I_{\Omega }({{\hat{w}}}) \rangle \le {\varepsilon }, \quad \langle {{\hat{w}}} - y^I_{\Omega }({{\hat{w}}}),\tilde{y}^I_{\Omega }(w,\epsilon ) - y^I_{\Omega }({{\hat{w}}}) \rangle \le 0. \end{aligned}$$
(11)

On the other hand, after some simple algebraic manipulations we have

$$\begin{aligned} \begin{aligned} \Vert w - {{\hat{w}}}\Vert ^2 =&\Vert {\tilde{y}}^I_{\Omega }(w,\epsilon ) - y^I_{\Omega }({{\hat{w}}})\Vert ^2 + 2\langle w - {\tilde{y}}^I_{\Omega }(w,\epsilon ) - ({{\hat{w}}} - y^I_{\Omega }({{\hat{w}}})), ~{\tilde{y}}^I_{\Omega }(w,\epsilon ) \\&- y^I_{\Omega }({{\hat{w}}})\rangle + \Vert (w - {\tilde{y}}^I_{\Omega }(w,\epsilon ))-({{\hat{w}}} - y^I_{\Omega }({{\hat{w}}}))\Vert ^2, \end{aligned} \end{aligned}$$

which implies that

$$\begin{aligned} \begin{aligned} \Vert {\tilde{y}}^I_{\Omega }(w,\epsilon ) - y^I_{\Omega }({{\hat{w}}})\Vert ^2&\le \Vert w - {{\hat{w}}}\Vert ^2 + 2\langle {\tilde{y}}^I_{\Omega }(w,\epsilon ) - w,~{\tilde{y}}^I_{\Omega }(w,\epsilon ) - y^I_{\Omega }({{\hat{w}}})\rangle \\&\quad + 2\langle {{\hat{w}}} - y^I_{\Omega }({{\hat{w}}}),~\tilde{y}^I_{\Omega }(w,\epsilon ) - y^I_{\Omega }({{\hat{w}}}) \rangle . \end{aligned} \end{aligned}$$

By the last inequality, (11) and (2), it yields

$$\begin{aligned} \Vert {{\tilde{y}}}^I_{\Omega }(w,\epsilon ) - y^I_{\Omega }({{\hat{w}}})\Vert ^2 \le \Vert w-{{\hat{w}}}\Vert ^2 + 2\varepsilon , \end{aligned}$$

which is equivalent to the desired inequality. \(\square \)

3 A framework for solving convex-constrained monotone equations

This section describes a framework for solving (1) and presents its global convergence analysis. The framework imposes a safeguard strategy on the search directions which, combined with a suitable linesearch procedure, turns it a globalized scheme. Approximate projections are also considered in order to deal with the case where projecting exactly onto C is expensive. Formally, the framework is described as follows.

figure a

Remark 2

i) If F is the gradient of some function \(f:{\mathbb {R}}^n\rightarrow {\mathbb {R}}\), then condition (12) implies that \(d_k\) is a sufficient descent direction for f at \(x_k\). In its turn, condition (13) essentially says that the length of \(d(x_k)\) should be proportional to the length of \(F(x_k)\). The way to obtain \(d_k\) satisfying (12) and (13) will depend on the particular instance of the framework; see Sect. 4 for some examples. (ii) Note that condition (12) implies that there exists a nonnegative number \(m_k\) satisfying (14), for all \(k \ge 1\). Indeed, suppose that there exists \(k_0 \ge 1\) such that (14) is not satisfied for any nonnegative integer m, i.e.,

$$\begin{aligned} -\langle F(x_{k_0} + \gamma ^{m}d_{k_0}),~d_{k_0} \rangle < \sigma \gamma ^{m}\Vert d_{k_0}\Vert ^2, \; \forall ~m\ge 1. \end{aligned}$$

Let \(m \rightarrow \infty \) and by continuity of F, we have

$$\begin{aligned} -\langle F(x_{k_0}),~d_{k_0} \rangle \le 0. \end{aligned}$$
(16)

On the other hand, by (12), we obtain

$$\begin{aligned} -\langle F(x_{k_0}),~d_{k_0} \rangle \ge \eta _1 \Vert F(x_{k_0})\Vert ^2 > 0, \end{aligned}$$

which contradicts (16). Therefore, the linesearch procedure in Step 3 is well defined. iii) In Step 4, note that \(w_k\) is the projection of \(x_k\) in \(H_k \) (which has a closed-form) and \( x_{k + 1} \) is an \(\varepsilon _k\)–approximate solution of the problem (4) with \(B:=I\), \(w:=w_k\), \(\Omega :=C\cap H_k\) and \(\varepsilon := \mu _k^2\Vert \xi _k F(z_k)\Vert ^2\). Another choice of \(x_{k+1}\) in (15) would be

$$\begin{aligned} x_{k+1}:={{\tilde{y}}}^{I}_{C}(w_k, \varepsilon _k). \end{aligned}$$
(17)

For this choice, we mention that Lemma 2 and Theorem 1 also holds. iv) It will follow form (19) and (20) that the hyperplane \(H_k\) strictly separates the current iteration from the elements of the solution set \(C^*\).

In order to investigate the global convergence of Framework 1, the following properties of the sequences \(\{ x_k \}\) and \(\{ z_k\}\) will be needed.

Lemma 2

Let \(C \subset {\mathbb {R}}^n\) be a nonempty closed convex set and let \(F : {\mathbb {R}}^n \rightarrow {\mathbb {R}}^n\) be a continuous and monotone nonlinear function. Assume that \(C^*\) is nonempty. Then, the sequences \(\{x_k \}\) and \(\{z_k \}\) generated by Framework 1 are both bounded. Furthermore, it holds that

$$\begin{aligned} \displaystyle \lim _{k\rightarrow \infty } \Vert x_k - z_k\Vert = 0. \end{aligned}$$
(18)

Proof

From Step 3, we have

$$\begin{aligned} \langle F(z_k), ~ x_k-z_k \rangle = -\alpha _k \langle F(z_k),~d_k\rangle \ge \sigma \alpha _k^2\Vert d_k \Vert ^2 = \sigma \Vert x_k - z_k\Vert ^2. \end{aligned}$$
(19)

Note that \(\Vert x_k - z_k\Vert > 0\), for all \(k\ge 0\). Otherwise, since (12) and the Cauchy-Schwartz inequality imply that \(\eta _1\Vert F(x_k)\Vert \le \Vert d_k\Vert \), we would have \(F(x_k ) = 0\).

Let \(x_* \in C^*\) be given. By the monotonicity of F and the fact that \(F(x_*)=0\), we obtain

$$\begin{aligned} \langle F(z_k), ~x_* - z_k \rangle \le 0. \end{aligned}$$
(20)

Hence, \(x_* \in H_k\) (see the definition of \(H_k\) in Step 4). Since \(x_{k+1}={{\tilde{y}}}^{I}_{C\cap H_k}(w_k,\varepsilon _k)\), it follows from the fact that \(x^* \in C\cap H_k\) and Lemma 1 with \(x=w_k\) and \({\hat{x}}=x_*\) that

$$\begin{aligned} \begin{aligned} \Vert x_{k+1} - x_*\Vert ^2&= \Vert {{\tilde{y}}}^{I}_{C\cap H_k}(w_k,\varepsilon _k) - y^I_{C\cap H_k}(x_*)\Vert ^2 \le \Vert w_k- x_*\Vert ^2 + 2\varepsilon _k \\&= \Vert x_k - x_*\Vert ^2 -2\xi _k \langle F(z_k), ~x_k-x_*\rangle + \xi _k ^2\Vert F(z_k)\Vert ^2 + \mu _k^2\xi _k ^2\Vert F(z_k)\Vert ^2. \end{aligned}\nonumber \\ \end{aligned}$$
(21)

where we used that \(\varepsilon ^2_k=(\mu _k^2\Vert \xi _k F(z_k)\Vert ^2)/2\) in the last equality. It is easy to see that (21) also holds when \(x_{k+1}=\tilde{y}^{I}_{C}(w_k,\varepsilon _k)\). By the monotonicity of the mapping F and the fact that \(x_* \in C^*\), we get

$$\begin{aligned} \langle F(z_k), ~x_k - z_k\rangle&= \langle F(x_*), ~z_k-x_*\rangle + \langle F(z_k), ~x_k - z_k\rangle \nonumber \\&\le \langle F(z_k), ~z_k-x_*\rangle + \langle F(z_k), ~x_k - z_k\rangle \nonumber \\&= \langle F(z_k), ~x_k - x_*\rangle . \end{aligned}$$
(22)

By combining (21) and (22), we find

$$\begin{aligned} \begin{aligned} \Vert x_{k+1} - x_*\Vert ^2&\le \Vert x_k - x_*\Vert ^2 -2\xi _k \langle F(z_k), ~x_k-z_k\rangle + \xi _k ^2\Vert F(z_k)\Vert ^2 + \mu _k^2\xi _k ^2\Vert F(z_k)\Vert ^2\\&\le \Vert x_k - x_*\Vert ^2 +( \mu _k^2-1) \frac{\langle F(z_k), ~x_k-z_k\rangle ^2}{\Vert F(z_k)\Vert ^2} \\&\le \Vert x_k - x_*\Vert ^2 + ({\bar{\mu }}^2 - 1)\sigma ^2\frac{\Vert x_k - z_k\Vert ^4}{\Vert F(z_k)\Vert ^2}, \end{aligned} \end{aligned}$$
(23)

where the second inequality follows from the definition of \(\xi _k\) and the last inequality is due to the fact that \(\mu _k\le \bar{\mu }\) and (19). By (23) and the fact that \({\bar{\mu }} <1\), we have

$$\begin{aligned} \Vert x_{k+1} - x_*\Vert ^2 \le \Vert x_k - x_*\Vert ^2, \quad k\ge 0, \end{aligned}$$
(24)

which implies that the sequence \(\{x_k \}\) is bounded. It follows from the Cauchy-Schwartz inequality, the monotonicity of F and (19) that

$$\begin{aligned} \Vert F(x_k)\Vert \ge \frac{\langle F(x_k), ~x_k-z_k\rangle }{\Vert x_k-z_k\Vert } \ge \frac{\langle F(z_k), ~x_k-z_k\rangle }{\Vert x_k-z_k\Vert } \ge \sigma \Vert x_k - z_k\Vert . \end{aligned}$$

Therefore, by the continuity of F and the boundedness of \(\{ x_k \}\), we have that \(\{z_k \}\) is also bounded. Since \(\{z_k \}\) is bounded and F is continuous on \({\mathbb {R}}^n\), there exists a constant \(M>0\) such that \(\Vert F(z_k)\Vert \le M\) for all \(k \ge 0\), which, combined with (23), yields

$$\begin{aligned} \frac{(1 - {\bar{\mu }}^2)\sigma ^2}{M^2}\displaystyle \sum _{k = 0}^{\infty }\Vert x_k - z_k\Vert ^4 \le \displaystyle \sum _{k = 0}^{\infty } \left( \Vert x_k - x_*\Vert ^2 - \Vert x_{k+1} - x_*\Vert ^2 \right) < \infty , \end{aligned}$$

which implies \(\lim _{k\rightarrow \infty } \Vert x_k - z_k\Vert = 0\). \(\square \)

We are now ready to establish the global convergence of Framework 1.

Theorem 1

Let \(C \subset {\mathbb {R}}^n\) be a nonempty closed convex set and let \(F : {\mathbb {R}}^n \rightarrow {\mathbb {R}}^n\) be a continuous and monotone nonlinear function. Assume that \(C^*\) is nonempty. Then, the sequence \(\{ x_k\}\) generated by Framework 1 converges to a solution of (1).

Proof

Since \(z_k = x_k + \alpha _k d_k\), from Lemma 2, it holds that

$$\begin{aligned} \displaystyle \lim _{k\rightarrow \infty } \alpha _{k} \Vert d_{k} \Vert = \displaystyle \lim _{k\rightarrow \infty } \Vert x_{k} - z_{k}\Vert = 0. \end{aligned}$$
(25)

We also have, from Lemma 2, that \(\{ x_k \}\) is bounded and therefore \(\{ F(x_k)\}\) is bounded as well. Thus, it follows from the second inequality in (13) that \(\{ d_k \}\) is bounded. Consider now two different cases: (i) \(\liminf _{k\rightarrow \infty } \Vert d_{k} \Vert = 0\) or (ii) \(\liminf _{k\rightarrow \infty } \Vert d_{k} \Vert > 0\).

Case (i). Note that (12) and the Cauchy–Schwartz inequality imply that \(\eta _1\Vert F(x_k)\Vert \le \Vert d_k\Vert \). Hence, since \(\liminf _{k\rightarrow \infty } \Vert d_{k} \Vert = 0\), it follows that \(\liminf _{k\rightarrow \infty } \Vert F(x_k) \Vert = 0\). Since F is continuous, we have that the sequence \(\{ x_k\}\) has some cluster point \({\bar{x}}\) such that \(F({\bar{x}}) = 0\). Replacing \(x_*\) by \({\bar{x}}\) in (24), we obtain

$$\begin{aligned} \Vert x_{k+1} - {\bar{x}}\Vert ^2 \le \Vert x_k - {\bar{x}}\Vert ^2, \end{aligned}$$

which implies that \(\{ \Vert x_k - {\bar{x}}\Vert \}\) converges. Therefore, we can conclude that the whole sequence \(\{ x_k \}\) converges to \({\bar{x}}\), a solution of (1).

Case (ii). Since \(\liminf _{k\rightarrow \infty } \Vert d_{k} \Vert > 0\), it follows from (25) that there exists a subsequence of indices \(K \subset {\mathbb {N}}\) such that \(\lim _{k\rightarrow \infty } \alpha _{k} = 0\), where \(k \in K\). By (14), we have

$$\begin{aligned} -\langle F(x_{k} + \gamma ^{m_{k}-1}d_{k}),~d_{k} \rangle < \sigma \gamma ^{m_{k}-1}\Vert d_{k}\Vert ^2. \end{aligned}$$

Since \(\{ x_k \}\) and \(\{ d_k \}\) are bounded, we can choose a subsequence \(K_1 \subset K\) such that \(\{ (x_k,d_k) \} {\mathop {\longrightarrow }\limits ^{K_1}} ({{\bar{x}}}, {{\bar{d}}})\). Hence, using the continuity of F and taking the limit in the last inequality as \(k \rightarrow \infty \) with \(k \in K_1\), we have

$$\begin{aligned} -\langle F({\bar{x}}),~{\bar{d}} \rangle \le 0. \end{aligned}$$
(26)

On the other hand, by taking the limit in (12) as \(k \rightarrow \infty \) with \(k \in K_1\), we obtain

$$\begin{aligned} -\langle F({\bar{x}}),~{\bar{d}} \rangle \ge \delta \Vert F({{\bar{x}}})\Vert ^2 >0, \end{aligned}$$

where the last inequality is due to the inequality in (13) and the fact that \(\liminf _{k\rightarrow \infty } \Vert d_{k} \Vert > 0\). Thus, the last inequality contradicts (26). Hence, \(\liminf _{k\rightarrow \infty } \Vert d_{k} \Vert = 0\). Therefore, using a similar argument as in the first case, we conclude that the whole sequence \(\{ x_k \}\) converges to a solution of (1). This completes the proof. \(\square \)

4 Some instances of Framework 1

This section presents some examples of search directions \(d_k\) that satisfy the safeguard conditions (12) and (13) and, as a consequence, some instances of Framework 1. These instances of methods allow approximate projections onto \(C\cap H_k\), which can be advantageous when the exact projections are difficult (where the projection cannot be easily performed).

Let us begin by presenting inexact versions of two well-known methods.

1) Steepest descent-based method with approximate projections (SDM-AP). This method corresponds to Framework 1 with the direction \(d_k\) in the Step 2 defined by \(d_k = - F(x_k),\) for every \(k\ge 0\). It is easy to see that this choice of \(d_k\) satisfies the conditions (12) and (13) with \(\eta _1=1\) and \(\eta _2\ge 1\). Therefore, from Theorem 1, it holds that the sequence \(\{x_k\}\) generated by SDM-AP converges to a solution of (1).

2) Newton method with approximate projections (NM-AP). Assume that F is continuously differentiable. By taking \(d_k\) in the Step 2 of Framework 1 as \(d_k = - B(x_k)^{-1}F(x_k)\) for every \(k\ge 0\), where \(B(x_k)\) is a positive definite matrix, we obtain a variant of the Newton method proposed in Wang and Xu (2007) with approximate projections. Note that \(B(x_k)\) may be the Jacobian of F at \(x_k\) or an approximation of it. Assuming that there exist constants \(0<a\le b\) such that \(aI \prec B(x_k) \prec bI\), for every k, then \(d_k\) satisfies (12) and (13) with \(\eta _1= 1/b\) and \(\eta _2 = 1/a\). Indeed, since \(B_k d_k = -F(x_k)\), we obtain

$$\begin{aligned} \langle d_k,F(x_k) \rangle = \langle - B_k^{-1} F(x_k),F(x_k) \rangle = - \Vert F(x_k)\Vert _{B_k ^{-1}} ^2 \le -\left( \frac{1}{b } \right) \Vert F(x_k)\Vert ^2 \end{aligned}$$

and

$$\begin{aligned} a\Vert d_k \Vert ^2\le \Vert d_k \Vert ^2_{B_k} = \langle B_k d_k, ~d_k \rangle = - \langle F(x_k), ~d_k \rangle \le \Vert F(x_k)\Vert \Vert d_k \Vert , \end{aligned}$$

which proves the statement. Therefore, since this method can be seen as an instance of Framework 1, we trivially have, from Theorem 1, that the sequence \(\{x_k\}\) generated by it converges to a solution of (1).

We next present two examples of methods, in the spirit of the one in example 2, for the nonsmooth case. Recall that \(F : {\mathbb {R}}^n \rightarrow {\mathbb {R}}^n\) is said to be \(\tau \)-strongly monotone if there is a constant \(\tau >0\) such that \(\langle x - y,F(x)- F(y) \rangle \ge \tau \Vert x - y\Vert ^2,\) for all \(x,y \in {\mathbb {R}}^n\), and the function \(F : {\mathbb {R}}^n \rightarrow {\mathbb {R}}^n\) is said to be \({\mathcal {L}}\)-Lipschitz continuous if there is a constant \({\mathcal {L}} >0\) such that \(\Vert F(x)- F(y) \Vert \le {\mathcal {L}} \Vert x - y\Vert ,\) for all \(x,y \in {\mathbb {R}}^n\).

3) Spectral gradient-like methods with approximate projections (SGM-AP). Consider \(d_k= - \lambda _k F(x_k)\) for every \(k\ge 0\), where \(\lambda _k\) is the spectral coefficient which is related to the Barzilai-Borwein choice of the step-size (Barzilai and Borwein 1988). Firstly, let us discuss some existing choices of \(\lambda _k\).

  1. 3.1)

    In La Cruz and Raydan (2003), \(\lambda _k\) is defined by

    $$\begin{aligned} \lambda _k = \frac{\langle s_k, s_k\rangle }{\langle s_k, u_k\rangle }, \end{aligned}$$
    (27)

    where \(s_k := x_k - x_{k-1}\) and \(u_k:=F(x_k)- F(x_{k-1})\). Under the assumption that F is \(\tau \)-strongly monotone and \({\mathcal {L}}\)-Lipschitz continuous, we have that \(d_k= - \lambda _k F(x_k)\) satisfies (12) and (13) with \(\eta _1= 1/{\mathcal {L}} \) and \(\eta _2 = 1/\tau \). Indeed, using that F is \(\tau \)-strongly monotone, we have

    $$\begin{aligned} \begin{aligned} \langle s_k, u_k\rangle&= \langle x_k - x_{k-1},F(x_k)- F(x_{k-1}) \rangle \ge \tau \langle x_k - x_{k-1}, x_k - x_{k-1}\rangle = \tau \langle s_k , s_k \rangle > 0, \end{aligned} \end{aligned}$$

    for some \(\tau >0\), and therefore, \(\lambda _k \le 1/\tau \). Now, using the Cauchy-Schwarz inequality and that F is \({\mathcal {L}}\)-Lipschitz continuous, we obtain

    $$\begin{aligned} \begin{aligned} \langle s_k, u_k\rangle&= \langle s_{k},F(x_k)- F(x_{k-1}) \rangle \le \Vert F(x_k)- F(x_{k-1})\Vert \Vert s_{k}\Vert \le {\mathcal {L}} \langle s_k, s_{k}\rangle , \end{aligned} \end{aligned}$$

    which implies \(1/{\mathcal {L}} \le \lambda _k\). Thus, \(1/{\mathcal {L}} \le \lambda _k\le 1/\tau \) and, as a consequence, the statement trivially follows from the fact that \(d_k= - \lambda _k F(x_k)\).

  2. 3.2)

    In Yu et al. (2009), Zhang and Zhou (2006), the coefficient \(\lambda _k\) is as in (27) with \(s_k := x_k - x_{k-1}\) and \(u_k:=F(x_k)- F(x_{k-1}) + rs_{k}\), where \(r >0\) is a given scalar. Using that F is monotone, we have

    $$\begin{aligned} \begin{aligned} \langle s_k, u_k\rangle&= \langle s_{k},F(x_k)- F(x_{k-1}) + rs_{k}\rangle \\&= \langle x_k - x_{k-1},F(x_k)- F(x_{k-1}) \rangle + r \langle s_k, s_{k}\rangle \\&\ge r \langle s_k, s_{k}\rangle > 0, \end{aligned} \end{aligned}$$

    which implies that \(\lambda _k \le 1/r\). Now, by assuming that F is \({\mathcal {L}}\)-Lipschitz continuous, we obtain

    $$\begin{aligned} \begin{aligned} \langle s_k, u_k\rangle&= \langle s_{k},F(x_k)- F(x_{k-1}) + rs_{k}\rangle \\&= \langle x_k - x_{k-1},F(x_k)- F(x_{k-1}) \rangle + r \langle s_k, s_{k}\rangle \\&\le ({\mathcal {L}} + r) \langle s_k, s_{k}\rangle , \end{aligned} \end{aligned}$$

    which yields \(1/({\mathcal {L}}+r) \le \lambda _k\). Therefore, as \(1/({\mathcal {L}}+r) \le \lambda _k\le 1/r\), we can conclude, from the fact that \(d_k= - \lambda _k F(x_k)\), that \(d_k\) satisfies the conditions (12) and (13) with \(\eta _1= 1/({\mathcal {L}}+r) \) and \(\eta _2 = 1/r\).

  3. 3.3)

    In the works (Abubakar et al. 2020; Mohammad 2017) the coefficient \(\lambda _k\) is a convex combination of the default spectral coefficient in Barzilai and Borwein (1988) and the positive spectral coefficient in Dai et al. (2015). More specifically, \(\lambda _k\) is defined by

    $$\begin{aligned} \lambda _k = (1 - t )\theta ^*_k + t \theta ^{**}_k, \end{aligned}$$

    where \(t \in [0,1]\), \(\theta ^*_k = \Vert s_{k}\Vert ^2/\langle u_{k}, s_{k}\rangle \), \(\theta ^{**}_k = \Vert s_{k}\Vert /\Vert u_{k}\Vert \), \(s_k := x_k - x_{k-1}\), \(u_k:=F(x_k)- F(x_{k-1}) + rs_{k}\) and \(r >0\). In Abubakar et al. (2020), Lemma 2, it was shown that if F is \({\mathcal {L}}\)-Lipschitz continuous, then \(d_k= - \lambda _k F(x_k)\) satisfies (12) and (13) with \(\eta _1= \max \{1,1/({\mathcal {L}}+r)\} \) and \(\eta _2 = \min \{1,1/r\}\).

Since the search directions in examples 3.1, 3.2 and 3.3 satisfy (12) and (13) for specific values of \(\eta _1\) and \(\eta _2\), we can conclude, from Theorem 1, that the SGM-AP (i.e., Framework 1 with the above three choice of search directions) converges to a solution of (1).

4) Limited memory BFGS method with approximate projections (L-BFGS-AP). Consider the L-BFGS direction \(d_k\) proposed in Zhou and Li (2007), which is obtained by solving the system \(B_k d_k = -F(x_k)\), where the sequence \(\{ B_k\}\) is given by \(B_0 = I\) and \(B_{k+1}\) is computed by the following modified L-BFGS update process: let \(m>0\) be given and set \({\tilde{m}} = \min \{ k+1,m \}\), \(B^{(0)}_k = B_0=I\). Choose a set of increasing integers \(L_k = \{j_0,\dots ,j_{{\tilde{m}} - 1}\} \subset \{0,\dots ,k\}\). Update \(B_{k+1}\) by using the pairs \(\{y_{j_{l}}, s_{j_{l}}\} _{l = 0}^{{\tilde{m}}-1}\), i.e., for \(l = 0, \dots , {\tilde{m}}-1\),

$$\begin{aligned} B_{k+1}:=B^{(l+1)}_{k+1} = \left\{ \begin{array}{lc} B^{(l)}_{k} - \frac{B^{(l)}_{k}s_{j_{l}}s_{j_{l}}^TB^{(l)}_{k}}{s_{j_{l}}^TB^{(l)}_{k}s_{j_{l}}} + \frac{y_{j_{l}}y_{j_{l}}^T}{y_{j_{l}}^Ts_{j_{l}}}, &{}\quad if \; \frac{y_{j_{l}}^T s_{j_{l}}}{\Vert s_{j_{l}}\Vert ^2} \ge \varepsilon ,\\ B^{(l)}_{k}, &{}\quad \text{ otherwise }, \end{array} \right. \end{aligned}$$

where \(s_k := x_{k+1} - x_{k}\) and \(y_k:=F(x_{k+1})- F(x_{k})\). If \(d_k\) in the Step 2 of Framework 1 is defined as above, we obtain an L-BFGS method with approximate projections. Under the assumption that F is \({\mathcal {L}}\)-Lipschitz continuous, it was proven in Zhou and Li (2007) that \(B_k\) and \(B_k^{-1}\) are bounded for all \(k\ge 0\), i.e., \(\{ B_k\} \subset {\mathbb {S}}_{n,L}({\mathbb {R}})\). Since \(B_k d_k = -F(x_k)\) and using (3), we obtain

$$\begin{aligned} \langle d_k,F(x_k) \rangle = \langle - B_k^{-1} F(x_k),F(x_k) \rangle = - \Vert F(x_k)\Vert _{B_k ^{-1}} ^2 \le -\left( \frac{1}{\Vert B_k \Vert } \right) \Vert F(x_k)\Vert ^2, \end{aligned}$$

which yields \(\langle d_k,F(x_k) \rangle \le - 1/L \Vert F(x_k)\Vert ^2\). Now, from the Cauchy–Schwarz inequality, we have

$$\begin{aligned} \Vert d_k \Vert ^2_{B_k} = \langle B_k d_k, ~d_k \rangle = - \langle F(x_k), ~d_k \rangle \le \Vert F(x_k)\Vert \Vert d_k \Vert , \end{aligned}$$

which, combined with (3) and \( \Vert B_k^{-1}\Vert \le L\), yields \((1/L)\Vert d_k \Vert \le \Vert F(x_k)\Vert \). Thus, \(d_k\) satisfies (12) and (13) with \(\eta _1= 1/L\) and \(\eta _2 = L\). Therefore, we conclude, from Theorem 1, that the sequence \(\{x_k\}\) generated by L-BFGS-AP (i.e., Framework 1 with the above choice of search direction) converges to a solution of (1).

We end this section by proposing a new convergent method for solving (1), which is an instance of Framework 1. This method is inspired by Solodov and Svaiter (1999a), Algorithm 2.1 for solving variational inequalities. In the context that the projection operator is computationally expensive, the latter algorithm was devised in order to minimize the total number of performed projection operations. Let us now present our extension of Solodov and Svaiter (1999a), Algorithm 2.1 to the convex-constrained monotone nonlinear equations setting.

5) Modified Newton-like method with approximate projections (MNM-AP). Consider the direction \(d_k\) defined as follows: let \(\eta >0\), \({{\bar{\theta }}} \in [0,\eta )\) and \(\{ \theta _k\} \subset [0, {{\bar{\theta }}} ]\) be given. Let \( B_k \in {\mathbb {S}}_{n,L}({\mathbb {R}})\), and set \(w^1_k:=B_kx_k-F(x_k)\) and \(\varepsilon ^1_k := \theta _k^2\Vert F(x_k)\Vert ^2\). Compute \(s^1_k\) in \({\mathbb {R}}^n\) such that

$$\begin{aligned} s^1_k= {\tilde{y}}^{B_k}_C(w^1_k,\varepsilon ^1 _k) - x_k, \end{aligned}$$
(28)

where \({{\tilde{y}}}^{B_k}_C(w^1_k,\varepsilon ^1 _k)\) is an \(\varepsilon ^1_k\)–approximate solution of the problem (4). If \(\eta \Vert F(x_k)\Vert \le \Vert s_k^1\Vert _{B_k}\), then \(d_k := s^1_k\). Otherwise, compute \(s^2_k\) in \({\mathbb {R}}^n\) such that

$$\begin{aligned} F(x_k) + B_k s^2_k= 0, \end{aligned}$$
(29)

and set \(d_k:=s^2_k\). Note that the matrix \(B_k\) can be taken as those in the examples 3 and 4. We will now prove that the \(d_k\) described above satisfies (12) and (13), for all \(k \ge 0\). If \(~\eta \Vert F(x_k)\Vert \le \Vert s_k^1\Vert _{B_k}\), then \(d_k = {{\tilde{y}}}^{B_k}_C(w^1_k,\varepsilon ^1 _k) - x_k\). By (5) with \(B = B_k\), \(w = w_k^1\), \(\varepsilon = \varepsilon ^1 _k\) and \(y = x_k\), we have

$$\begin{aligned} \begin{aligned} \theta _k^2\Vert F(x_k)\Vert ^2 \ge&\langle B_k(x_k-{{\tilde{y}}}^{B_k}_C(w^1_k,\varepsilon ^1 _k)) -F(x_k), x_k - {{\tilde{y}}}^{B_k}_C(w^1_k,\varepsilon ^1 _k) \rangle \\ =&\Vert {{\tilde{y}}}^{B_k}_C(w^1_k,\varepsilon ^1 _k) - x_k\Vert _{B_k} ^2 - \langle F(x_k), ~x_k - {{\tilde{y}}}^{B_k}_C(w^1_k,\varepsilon ^1 _k) \rangle , \; \forall ~k \ge 0, \end{aligned} \end{aligned}$$

which, combined with the definition of \(d_k\), yields

$$\begin{aligned} \begin{aligned} - \langle F(x_k), d_k \rangle + \theta _k^2\Vert F(x_k)\Vert ^2&\ge \Vert d_k \Vert ^2_{B_k} \ge \Vert F(x_k)\Vert ^2 \eta ^2, \; \forall ~k \ge 0, \end{aligned} \end{aligned}$$
(30)

or, equivalently,

$$\begin{aligned} - \langle F(x_k), d_k \rangle \ge \Vert F(x_k)\Vert ^2 (\eta ^2 - \theta _k^2), \; \forall ~k \ge 0. \end{aligned}$$

Therefore, since \(~\theta _k \le {\bar{\theta }}\) for all \(k \ge 0\) and \({\bar{\theta }} \in [0,\eta )\), we have

$$\begin{aligned} \langle F(x_k), d_k \rangle \le - (\eta ^2 - {\bar{\theta }} ^2) \Vert F(x_k)\Vert ^2. \end{aligned}$$

Hence, (12) holds with \(\eta _1 = (\eta ^2 - {\bar{\theta }} ^2)\). From (30) and using the Cauchy–Schwarz inequality, we have

$$\begin{aligned} \Vert d_k \Vert ^2_{B_k} \le \theta _k^2\Vert F(x_k)\Vert ^2 - \langle B^{-1}_k F(x_k), d_k \rangle _{B_k} \le \theta _k^2\Vert F(x_k)\Vert ^2 + \Vert B^{-1}_k F(x_k)\Vert _{B_k} \Vert d_k \Vert _{B_k}, \end{aligned}$$

which, after some algebraic manipulations, yields

$$\begin{aligned} \Vert d_k \Vert ^2_{B_k} \le \theta _k^2\Vert F(x_k)\Vert ^2 + \frac{\Vert B^{-1}_k F(x_k)\Vert _{B_k}^2}{2} + \frac{\Vert d_k \Vert _{B_k}^2}{2}. \end{aligned}$$

Using the definition of scalar product \(\langle \cdot , \cdot \rangle _{B}=\langle \cdot ,B\cdot \rangle \) and (3), we obtain

$$\begin{aligned} \frac{\Vert d_k \Vert _{B_k}^2}{2}{} & {} \le \theta _k^2\Vert F(x_k)\Vert ^2 + \frac{\Vert F(x_k)\Vert _{B^{-1}_k}^2}{2} \le \theta _k^2\Vert F(x_k)\Vert ^2 + \frac{\Vert F(x_k)\Vert ^2 \Vert {B^{-1}_k}\Vert }{2} \\{} & {} = \left( \theta ^2_k + \frac{\Vert {B^{-1}_k}\Vert }{2}\right) \Vert F(x_k)\Vert ^2, \end{aligned}$$

which implies that

$$\begin{aligned} \Vert d_k \Vert _{B_k}^2 \le \left( 2\theta ^2_k + \Vert {B^{-1}_k}\Vert \right) \Vert F(x_k)\Vert ^2. \end{aligned}$$

Therefore, by (3), \(\Vert B_k^{-1}\Vert \le L\) and \(~\theta _k \le {\bar{\theta }}\) for all \(k \ge 0\), we have

$$\begin{aligned} \Vert d_k \Vert ^2 \le L \left( 2{\bar{\theta }}^2 + L \right) \Vert F(x_k)\Vert ^2, \end{aligned}$$

and hence (13) holds with \(\eta _2 = \sqrt{L \left( 2\bar{\theta }^2 + L \right) }\). On the other hand, if \(d_k:=s^2_k\), the proof is similar to the one in example 4. Therefore, we conclude, from Theorem 1, that the sequence \(\{x_k\}\) generated by the MNM-AP (i.e., Framework 1 with the above choice of search direction) converges to a solution of (1).

5 Numerical experiments

This section summarizes the numerical experiments carried out to verify the efficiency of the instances of Framework 1. Numerical experiments are divided into two sections. In Sect. 5.1, the methods are tested for a group of convex-constrained monotone nonlinear equations, whereas in Sect. 5.2 they are tested for solving the system of constrained absolute value equations (CAVE). The computational results are obtained using MATLAB R2018a on a 2.4 GHz Intel(R) i5 with 8GB of RAM and Windows 10 as ultimate system. The codes supporting the numerical experiments are freely available in https://maxlng.ime.ufg.br/p/17888-publications.

5.1 Monotone nonlinear equations with polyhedral constraints

In this subsection, our aim is to illustrate the behavior of the methods to solve 52 monotone nonlinear equations with polyhedral constraints (i.e., \(C=\{x\in {\mathbb {R}}^n: a\le x\le b, Ax\le c\}\), where \(a,b\in {\mathbb {R}}^n,\) \(c\in {\mathbb {R}}^m\) and \(A\in {\mathbb {R}}^{m \times n}\)); see Table 1. Some of these problems are originally unconstrained ones, for which constrains were added. In Pb11, the matrix \(A \in {\mathbb {R}}^{10\times n}\) is randomly generated so that a solution of the problem 11 belongs to the feasible set.

Table 1 Test problems
Full size table

The tolerance in the stopping criterion \(\Vert F(x_k)\Vert < \epsilon \) was set to \(\epsilon = 10^{-6}\). If the stopping criterion is not satisfied, the method stops when a maximum of 500 iterations has been performed. In this first group of test problems, we set \(\sigma = 10^{-4}\), \(\gamma = 1/2\) and \(\mu _k = {\bar{\mu }} = 0.25\), for every k, in all algorithms. Moreover, the \(\varepsilon _k\)–approximate solution in (15) was computed by the conditional gradient method, which stopped when either the stopping criterion is satisfied or a maximum of 300 iterations is performed. In order to avoid an excessive number of inner iterations, input \(\varepsilon _k\) was replaced by \(\max \{ \mu _k^2\Vert \xi _k F(z_k)\Vert ^2,10^{-2}\}\). Linear optimization subproblems in the conditional gradient method (see (9)) were solved via the MATLAB command linprog. We denote by SGM-AP1, SGM-AP2 and SGM-AP3, the method SGM-AP, with the coefficient \(\lambda _k\) given in examples 3.1, 3.2 and 3.3, respectively. In SGM-AP2, we set \(r = 0.01\), whereas, in SGM-AP3, we set \(t = 1/({exp(k + 1)}^{k + 1})\) and \(r = 1/(k + 1)^2\). In the L-BFGS-AP, we used \(m = 1\). Finally, we set \(\eta = 0.5\), \(\theta _k = {\bar{\theta }} = 0.25\) in the MNM-AP.

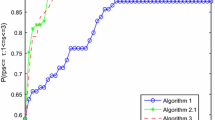
We consider 4 different starting points (following the suggestions from the original sources of the problems) for each problem of Table 1: For problem 1, \(x_1=(0.1, \dots , 0.1)\), \(x_2=(1,\dots , 1)\), \(x_3=((n-1)/n, 0.1,\dots , 0.1, (n-1)/n)\) and \(x_4=(-1,\dots , -1)\). For problem 2, \(x_1=(0.1,\dots , 0.1)\), \(x_2=(1,\dots , 1)\), \(x_3=(0, \dots , 0)\) and \(x_4=(-1,\dots , -1)\). For problem 3, \(x_1=(10, 0, \dots , 0)\), \(x_2=(9, 0, \dots , 0)\), \(x_3=(3, 0, 3, 0, 3)\) and \(x_4=(0, 2, 2, 2, 2)\). For problem 5, \(x_1=(0, \dots , 0)\), \(x_2=(3, 0, 0, 0)\), \(x_3=(1, 1, 1, 0)\) and \(x_4=(0, 1, 1, 1)\). For problems 14 and 16, \(x_1=(-1,\dots , -1)\), \(x_2=(-0.1, \dots , -0.1)\), \(x_3=(-1/2, -1/2^2,\dots , -1/2^n)\) and \(x_4=(-1, -1/2,\dots , -1/n)\). For problem 17, \(x_1=((n-1)/n, 0.1,\dots , 0.1, (n-1)/n)\), \(x_2=(0.1, \dots , 0.1)\), \(x_3=(1/2, 1/2^2,\dots , 1/2^n)\) and \(x_4=(1, 1/2, \dots , 1/n)\). For problems 4, 6 to 13, 15 and 18, \(x_1=(1,\dots , 1)\), \(x_2=(0.1, \dots , 0.1)\), \(x_3=(1/2, 1/2^2,\dots , 1/2^n)\) and \(x_4=(1, 1/2,\dots , 1/n)\). Figures 1, 2, 3 and 4 report the numerical results of SDM-AP, SGM-AP1, SGM-AP2, SGM-AP3, L-BFGS-

Table 2 Performance of the methods with \(x_{k+1}\) as in (15) for the first problem dimension n in Table 1 and \(x_1\) as initial point
Full size table
Table 3 Performance of the methods with \(x_{k+1}\) as in (17) for the first problem dimension n in Table 1 and \(x_1\) as initial point
Full size table

AP and MNM-AP for solving the 52 problems using performance profiles (Dolan and Moré 2002). Recall that in the performance profile, efficiency and robustness can be accessed on the left and right extremes of the graphic, respectively. We consider that a method is the most efficient if its number of iterations (resp. runtime) does not exceed in \(5\%\) the number of iterations (resp. CPU time) of the fastest one. We also display in Tables 2 and 3 the numerical results of the algorithms for the first problem dimension n in Table 1 and \(x_1\) as initial point. In the tables, It and Time denote the number of iterations and CPU time in seconds, respectively, whereas the symbol “-" indicates a failure.

Fig. 1
figure 1

Performance profile for the number of iterations of SDM-AP, SGM-AP1, SGM-AP2, SGM-AP3, L-BFGS-AP and MNM-AP with \(x_{k+1}\) as in (15)

Full size image
Fig. 2
figure 2

Performance profile for CPU time of SDM-AP, SGM-AP1, SGM-AP2, SGM-AP3, L-BFGS-AP and MNM-AP with \(x_{k+1}\) as in (15)

Full size image
Fig. 3
figure 3

Performance profile for the number of iterations of SDM-AP, SGM-AP1, SGM-AP2, SGM-AP3, L-BFGS-AP and MNM-AP with \(x_{k+1}\) as in (17)

Full size image
Fig. 4
figure 4

Performance for CPU time of SDM-AP, SGM-AP1, SGM-AP2, SGM-AP3, L-BFGS-AP and MNM-AP with \(x_{k+1}\) as in (17)

Full size image

From Figs. 1–4, we can see that all the variations of the SGM-AP achieved a better performance (in terms of efficiency and robustness) compared to L-BFGS-AP and MNM-AP. In the group of SGM-AP variants, SGM-AP1 and SGM-AP2 were better than the others.

5.2 Absolute value equations with polyhedral constraints

In this subsection, we consider the problem of finding a solution of the CAVE problem:

$$\begin{aligned} \text{ find } \; x \in C \; \text{ such } \text{ that } \; Ax - |x| = b, \end{aligned}$$
(31)

where \(C:= \{ x \in {\mathbb {R}}^n; \sum _{i = 1}^{n}x_i \le d, x_i\ge -1, i = 1, \dots , n\}\), \(A \in {\mathbb {R}}^{n\times n}\), \(b \in {\mathbb {R}}^n \equiv {\mathbb {R}}^{n\times 1}\), and |x| denotes the vector whose i-th component is equal to \(|x_i|\). The problem (31) draws attention for its simple formulation when compared to its equivalent linear complementarity problem (LCP) (see Cottle and Dantzig 1968; Cottle et al. 2009; Mangasarian and Meyer 2006) which in turn includes linear programs, quadratic programs, bimatrix games and other problems. Hence, interesting algorithms related to Newton-type methods to solve (31) have been developed; see, for example, Cruz et al. (2016), Mangasarian (2009) and Oliveira and Ferreira (2020) for the unconstrained and constrained case, respectively.

Under the assumption that \(\Vert A^{-1}\Vert \le 1\), it was proven in Mangasarian and Meyer (2006), Proposition 4 that the problem (31), with \(C = {\mathbb {R}}^n\), is uniquely solvable for any b. Now, if A is symmetric positive definite, then \(F(x) = Ax - |x| - b\) is monotone. In fact, for all \(x, y \in {\mathbb {R}}^n\), we have

$$\begin{aligned} \langle F(x) - F(y), x - y\rangle= & {} \langle Ax - |x| - Ay + |y|, x - y\rangle = \Vert x - y\Vert ^2_A + \langle |y| - |x|, x - y\rangle \nonumber \\\ge & {} \Vert x - y\Vert ^2\frac{1}{\Vert A^{-1}\Vert } + \langle |y| - |x|, x - y\rangle \nonumber \\\ge & {} \Vert x - y\Vert ^2 + \langle |y| - |x|, x - y\rangle . \end{aligned}$$
(32)

where in the second equality we use that \(\langle \cdot ,\cdot \rangle _{B}=\langle \cdot ,B\cdot \rangle \), (3) and \(\Vert A^{-1}\Vert \le 1\). Note that |x| can be written as \(|x| = P_{{\mathbb {R}}^n_{+}}(x) + P_{{\mathbb {R}}^n_{+}}(-x)\). So, from (32), the Cauchy-Schwarz inequality and the fact that \(P_{{\mathbb {R}}^n_{+}}(\cdot )\) is monotone and nonexpansive, we obtain

$$\begin{aligned} \begin{aligned} \langle F(x) - F(y),&x - y\rangle \\ \ge&\Vert x - y\Vert ^2 + \langle P_{{\mathbb {R}}^n_{+}}(y) + P_{{\mathbb {R}}^n_{+}}(-y) - P_{{\mathbb {R}}^n_{+}}(x) - P_{{\mathbb {R}}^n_{+}}(-x), x - y\rangle \\ =&\Vert x - y\Vert ^2 - \langle P_{{\mathbb {R}}^n_{+}}(x) - P_{{\mathbb {R}}^n_{+}}(y), x - y\rangle + \langle P_{{\mathbb {R}}^n_{+}}(-y) -P_{{\mathbb {R}}^n_{+}}(-x), x - y)\rangle \\ \ge&\Vert x- y\Vert ^2 - \Vert P_{{\mathbb {R}}^n_{+}}(x) - P_{{\mathbb {R}}^n_{+}}(y)\Vert \Vert x - y\Vert \\ \ge&\Vert x - y\Vert ^2 - \Vert x - y\Vert ^2 = 0, \end{aligned} \end{aligned}$$

which proves the statement. In our implementation, we used the Matlab routine sprandsym to construct matrix A randomly, which generates a symmetric positive definite sparse matrix with predefined dimension, density and singular values. For this process, the density of matrix A was set to 0.003 and the vector of singular values was randomly generated from a uniform distribution on (0, 1). In this case, as the vector of singular values (rc) is a vector of length n, then A has eigenvalues rc. Thus, if rc is a positive (nonnegative) vector, then A is a positive (nonnegative) definite matrix. We chose a random solution \(x_*\) from a uniform distribution on (0.1, 10) and computed \(b = Ax_* - |x_*|\) and \(d = \sum _{i = 1}^{n}(x_*)_i\), where \((x_*)_i\) denotes the i-th component of the vector \(x_*\). The initial points were defined as \(x_0=(0, \dots , 0, d/2, 0, \dots , 0, d/2, 0, \dots , 0) \in {\mathbb {R}}^n\), where the two positions of d/2 were generated randomly on the set \(\{1, 2, \dots , n\}\).

Fig. 5
figure 5

Performance profile for the number of iterations of SGM-AP2-C, SGM-AP2-CH and INM-InexP for CAVE

Full size image
Fig. 6
figure 6

Performance profile for the CPU time of SGM-AP2-C, SGM-AP2-CH and INM-InexP for CAVE

Full size image

For the CAVE problem, we consider only the SGM-AP2 since it was the best method in our first class of experiments described in Sect. 5.1. For a comparative purpose, we also run the inexact Newton method with feasible inexact projections (INM-InexP) of Oliveira and Ferreira (2020). INM-InexP is an algorithm designed for solving smooth and nonsmooth equations subject to a set of constraints. We rescale the vector of singular values to ensure that the condition \(\Vert A^{-1}\Vert \le 1/3 < 1\) is fulfilled and, consequently, ensure the good definition of INM-InexP (see Mangasarian 2009, Theorem 2 for more details). In INM-InexP, we set \(\theta = {\bar{\theta }} = {\bar{\mu }} = 0.25\) and the other parameters were set as in Oliveira and Ferreira (2020). For both algorithms, a failure was declared if the number of iterations was greater than 500. The procedure to obtain inexact projections used in the implementation of INM-InexP was also the CondG method and the procedure stopped when either the condition as in Oliveira and Ferreira (2020), Algorithm 1 was satisfied or a maximum of 10 iterations were performed. For our algorithms, the procedure stopped when either the stopping criterion was satisfied or a maximum of 10 iterations were performed.

As in Sect. 5.1, Figs. 5 and 6 report numerical results of algorithms using performance profiles. We generated 50 CAVEs of dimensions 1000, 5000 and 10000 and for each of them we test the algorithm for 5 different initial points. The numerical results of the algorithms are also displayed in Table 4, where “% solve" indicates the percentage of runs that has reached a solution, and for the successful runs It and Time denote the number of iterations and CPU time in seconds, respectively. We see, from Figs. 5 and 6 , that the SGM-AP2-C (with \(x_{k+1}\) as in (17)) was the most robust one whereas INM-InexP was more efficient than SGM-AP2-C and SGM-AP2-CH (with \(x_{k+1}\) as in (15)).

Table 4 Performance of the SGM-AP2-C, SGM-AP2-CH and INM-InexP for CAVE
Full size table

6 Final remarks

In this paper, we proposed and analyzed some methods with approximate projections for solving constrained monotone equations. When necessary, such inexact projections can be obtained by using suitable iterative algorithms; for example, the conditional gradient (Frank-Wolfe) method (Dunn 1980; Frank and Wolfe 1956). Inexact versions of steepest descent-based, spectral gradient-like, Newton-like and limited memory BFGS methods were discussed. A new algorithm inspired by Solodov and Svaiter (1999a), Algorithm 2.1 for solving variational inequalities was also presented. The global convergences of the aforementioned methods were obtained by first presenting and establishing the global convergence of a framework and then showing that the new methods fall in this framework. Preliminary numerical experiments showed that the proposed methods performed well to solve constrained monotone nonlinear equations, and they are competitive in terms of robustness with the Inexact Newton method with feasible inexact projections in Oliveira and Ferreira (2020) for solving absolute value equations with polyhedral constraints.