Robust Output Feedback Stabilization for Uncertain Discrete-Time Stochastic Neural Networks with Time-Varying Delay

Abstract

This paper investigates the problem of robust exponential stabilization of uncertain discrete-time stochastic neural networks with time-varying delay based on output feedback control. By choosing an augmented Lyapunov–Krasovskii functional, we established the sufficient conditions of the delay-dependent asymptotical stabilization in the mean square for a class of discrete-time stochastic neural networks with time-varying delay. Furthermore, we obtain the criteria of robust global exponential stabilization in the mean square for uncertain discrete-time stochastic neural networks with time-varying delay. Finally, we give numerical examples to illustrate the effectiveness of the proposed results.

1 Introduction

Over the past decades, neural networks have attracted considerable attention owing to their wide applications in various fields such as signal and image processing, pattern recognition, associative memory, parallel computing and so on [1,2,3,4,5,6]. Dynamical behaviors such as stability, instability, periodic oscillatory and chaos of the neural networks are known to be crucial in applications. Stability of neural networks is a prerequisite for many engineering problems, it received much research attention in recent years and many elegant results have been reported, for details see [5, 7, 8]. On the other hand, the stabilization of neural networks has been attracting considerable attention and several feedback stabilizing control methods have been proposed, for details see [9,10,11].

The time delays are commonly encountered in various engineering systems such as chemical processes, hydraulic and rolling mill systems, etc. The existence of time delay worsens the dynamic performance of a system and even leads to instability of the system. It is quintessential to understand the impact of time delays on dynamic systems theoretically so that, when using time delays to solve real-world problems, the unfavorable consequences of them can be circumvented. Therefore, the dynamic problem of delayed neural networks has been widely studied recently [5,6,7, 12,13,14]. Huang et al. [7] proposed a class of asymptotically almost periodic shunting inhibitory cellular neural networks with mixed delays and nonlinear decay functions. Tian et al. [8] gave an improved delay-partitioning method to stability analysis for neural networks with discrete and distributed time-varying delays. Park et al. [12] given the synchronization criterion for coupled discrete-time neural networks with interval time-varying delays. In [13], the dynamics of switched cellular neural networks with mixed delays were investigated. Dong et al. [15] investigated the robust stability and H_∞ control for nonlinear discrete-time switched systems with interval time-varying delay.

However, it should be noted that most of the neural networks that have been studied are continuous-time systems. However, in the application of neural networks, discrete-time neural networks have surpassed the continuous-time networks in their importance because when implementing continuous-time networks for computer-based simulation, experimentation or computation, the continuous-time networks are usually discretized. Besides, discrete-time networks are more suitable to model digitally transmitted signals in a dynamical way. These two features of the discrete-time networks have inspired researchers to study the stability and stabilization analysis problems for discrete-time neural networks, and some stability and stabilization criteria have been proposed in the literature, see [16,17,18,19,20] and the references therein. Yu et al. [16] investigated exponential stability criteria for discrete-time recurrent neural networks with time-varying delay. Luo et al. [18] studied the robust stability for discrete-time stochastic neural networks systems with time-varying delays. In [20], the stability analysis for discrete-time stochastic neural networks with time-varying delays was given.

During the modeling process of real nervous systems, stochastic disturbances and parameters uncertainties are identified as the two main sources of performance degradations of the implemented neural networks. Therefore, it is significant to solve the stability analysis problem for stochastic neural networks, and some academic efforts devoted to this problem have recently been published, see e.g. [21,22,23,24] and the references therein. In [21], the mean square exponential stability of uncertain stochastic delayed neural networks was considered. In [22], stochastic stability of uncertain Hopfield neural networks with discrete and distributed delays was investigated. Zhou et al. [24] considered robust exponential stability of uncertain stochastic neural networks with distributed delays and reaction–diffusions. However, these papers mainly concern continuous-time neural networks. To the best of our knowledge, the robust output feedback stabilization problem for uncertain stochastic discrete-time neural networks with time-varying delays has not been adequately investigated.

In this paper, the static output feedback stabilization problem for uncertain discrete-time stochastic neural networks with time-varying delay is studied. By constructing a new augmented Lyapunov–Krasovskii functional, the delay-dependent stabilization criterion, which guarantees the asymptotical stability of the closed-loop system of a class of discrete-time stochastic neural networks with time-varying delays in the mean square sense, is obtained. Then, by static output feedback control, the sufficient conditions of robust global exponential stabilization in the mean square for uncertain discrete-time stochastic neural networks with time-varying delay is presented. Finally, some simulation examples are given to illustrate the effectiveness of our results.

The remainder of this paper is organized as follows. In Sect. 2, formulation and preliminaries are presented. In Sect. 3, robust exponential stabilization criteria in the mean square is derived for uncertain discrete-time stochastic neural networks with time-varying delays. In Sect. 4, numerical examples are given to demonstrate our results. Finally, some conclusions are given in Sect. 5.

Notation

Throughout this paper, $N^{ + }$ stands for the set of nonnegative integers. $R^{n}$ and $R^{n \times m}$ denote the $n$ dimensional Euclidean space and the set of all $n \times m$ real matrices respectively. The superscript “$T$” denotes the transpose and the notation $X \ge Y$ (respectively $X > Y$), where $X$ and $Y$ are symmetric matrices, means that $X - Y$ is positive semi-definite (respectively positive definite).$I$ is the identity matrix with compatible dimension. $E\{ \cdot \}$ stands for the mathematical expectation operator with respect to the given probability measure $P$, $\left\| {\, \cdot \,} \right\|$ stands for the Euclidean vector norm. The asterisk $( * )$ in a matrix is used to denote term that is induced by symmetry. We use $\lambda_{\hbox{min} } ( \cdot )$ and $\lambda_{\hbox{max} } ( \cdot )$ to denote the minimum and maximum eigenvalue of the real symmetric matrix.

2 Problem Formulation and Preliminaries

Consider the following uncertain discrete-time stochastic neural networks with time-varying delay:

$$ \begin{aligned} x (k + 1 )& = (A + \Delta A(k))x (k )+ (C + \Delta C(k))x(k - \tau (k)) + (B + \Delta B(k))f (x (k ) )\\ & \quad + (D + \Delta D(k))g(x(k - \tau (k))) + Nu(k) + \delta (k,x(k),x(k - \tau (k)))\omega (k), \\ y(k) & = Kx(k), \\ x(\theta ) & = \varphi (\theta ),\;\theta = - \tau_{M} , - \tau_{M} + 1, \ldots ,0, \\ \end{aligned} $$

(1)

where $x(k) = [x_{1} (k),x_{ 2} (k), \cdots ,x_{n} (k)]^{T} \in R^{n}$ is the state vector, $u(k) \in R^{m}$ is the control input. $f(x(k)) = [f_{1} (x_{1} (k)), \ldots ,f_{n} (x_{n} (k))]^{T}{\kern-2pt,}\;g(x(k - \tau (k))) = [g_{1} (x_{1} (k - \tau (k))), \ldots ,g_{n} (x_{n} (k - \tau (k)))]^{T}$ denote the neuron activation functions. $\varphi (\theta )$ is an initial condition, the positive integer $\tau (k)$ denotes the time-varying delay satisfying

$$ 0 < \tau_{m} \le \tau (k) \le \tau_{M} , $$

(2)

where $\tau_{m}$ and $\tau_{M}$ are known positive integers. The diagonal matrix $A = diag(a_{1} ,a_{2} , \ldots ,a_{n} )$ is real constant diagonal matrix, $C,B,D,N$ and K are the suitable dimension constant matrices. $B = (b_{ij} )_{n \times n}$ and $D = (d_{ij} )_{n \times n}$ are the connection weight matrix and the delayed connection weight matrix.$\Delta A(k),\Delta B(k),\Delta C(k),\Delta D(k)$ denote the parameter uncertainties, and assume to satisfy the following admissible condition

$$ [\Delta A(k),\Delta B(k),\Delta C(k),\Delta D(k)] = GF(k)[E_{a} ,E_{b} ,E_{c} ,E_{d} ], $$

(3)

where $G,E_{a} ,E_{b} ,E_{\text{c}} ,E_{d}$ are known matrices of appropriate dimensions, $F(k)$ is an unknown time-varying matrix function satisfying

$$ F^{\text{T}} (k)F(k) \le I,\quad \forall k \in N^{ + } . $$

$\omega (k)$ is a scalar Wiener process on a probability space $(\Omega ,\Gamma ,P)$ with

$$ E\{ \omega (k)\} = 0,\;E\{ \omega^{2} (k)\} = 1,\;E\{ \omega (i)\omega (j)\} = 0\;(i \ne j). $$

We make following assumptions for the neuron activation functions in (1).

Assumption 1

[25] For $i \in {\text{\{ }}1,2, \ldots ,n{\text{\} }},$ the neuron activation functions $f_{i} ( \cdot )$ and $g_{i} ( \cdot )$ are continuous and bounded, and for any $s_{1} ,s_{2} \in R$$(s_{1} \ne s_{2} )$ satisfy the following conditions:

$$ \begin{aligned} l_{i}^{ - } & \le \frac{{f_{i} (s_{1} ) - f_{i} (s_{2} )}}{{s_{1} - s_{2} }} \le l_{i}^{ + } , \\ v_{i}^{ - } & \le \frac{{g_{i} (s_{1} ) - g_{i} (s_{2} )}}{{s_{1} - s_{2} }} \le v_{i}^{ + } , \\ f_{i} (0) & = g_{i} (0) = 0, \\ \end{aligned} $$

(4)

where $l_{i}^{ - } ,l_{i}^{ + } ,v_{i}^{ - } ,v_{i}^{ + }$ are known constants.

Remark 1

The Assumption 1 on the activation functions has been made in many other papers dealing with the stability problem for neural networks; see, for example, [6, 13, 25, 26]. We note that this assumption is weak in comparison with those made under the Lipschitz condition [27,28,29]. In Assumption 1, the constants $l_{i}^{ - } ,l_{i}^{ + } ,v_{i}^{ - } ,v_{i}^{ + }$ are allowed to be positive, negative or zero. Hence, the resulting activation functions could be nonmonotonic, and are more general than the usual sigmoid functions and the recently commonly used Lipschitz conditions.

Assumption 2

$\delta :Z \times R^{n} \times R^{n} \to R^{n}$ is the continuous function, and satisfies

$$ \delta^{T} (k,x(k),x(k - \tau (k)))\delta (k,x(k),x(k - \tau (k))) \le \rho_{1} x^{T} (k)x(k) + \rho_{2} x^{T} (k - \tau (k))x(k - \tau (k)), $$

(5)

where $\rho_{ 1} > 0$ and $\rho_{2} > 0$ are known constant scalars.

For obtaining the main results of this paper, the following lemma will be useful for the proofs.

Lemma 1

[30] For any constant matrix$M \in R^{{n \times {\text{n}}}}$, $M = M^{T} \ge 0$, integers$r_{2} \ge r_{1} ,$vector function$\omega :{\text{\{ }}r_{1} ,r_{1} + 1, \ldots ,r_{2} \} \to R^{n}$such that the sums in the following are well defined, then

$$ - (r_{2} - r_{1} + 1)\sum\limits_{{i = r_{1} }}^{{r_{2} }} {\omega^{T} (i)M\omega (i) \le - \left( {\sum\limits_{{i = r_{1} }}^{{r_{2} }} {\omega (i)} } \right)^{T} M\left( {\sum\limits_{{i = r_{1} }}^{{r_{2} }} {\omega (i)} } \right)} . $$

Definition 1

[31] The system (1) is said to be robustly exponentially stable in the mean square if there exist constants $\alpha > 0$ and $\mu \in ( 0, 1 ),$ such that every solution of the system (1) satisfies that

$$ E\{ \left\| {x(k)} \right\|^{2} \} \le \alpha \mu^{k} \mathop {\hbox{max} }\limits_{{ - \tau_{M} \le i \le 0}} E\{ \left\| {x(i)} \right\|^{2} {\text{\} ,}}\;\quad \forall k \ge 0. $$

for all parameter uncertainties satisfying the admissible condition.

For presentation convenience, in the following, we denote

$$ \begin{aligned} A(k) & = A + \Delta A(k),\;B(k) = B + \Delta B(k),\;C(k) = C + \Delta C(k),\,\;D(k) = D + \Delta D(k), \\ \Lambda_{ 1} & = diag(l_{1}^{ + } l_{1}^{ - } ,l_{2}^{ + } l_{2}^{ - } , \ldots ,l_{n}^{ + } l_{n}^{ - } ),\quad \Lambda_{2} = diag\left( {\frac{{l_{1}^{ + } + l_{1}^{ - } }}{2},\frac{{l_{2}^{ + } + l_{2}^{ - } }}{2}, \ldots ,\frac{{l_{n}^{ + } + l_{n}^{ - } }}{2}} \right), \\ \Omega_{ 1} & = diag(v_{1}^{ + } v_{1}^{ - } ,v_{2}^{ + } v_{2}^{ - } , \ldots ,v_{n}^{ + } v_{n}^{ - } ),\quad \Omega_{ 2} = diag\left( {\frac{{v_{1}^{ + } + v_{1}^{ - } }}{2},\frac{{v_{2}^{ + } + v_{2}^{ - } }}{2}, \ldots ,\frac{{v_{n}^{ + } + v_{n}^{ - } }}{2}} \right). \\ \end{aligned} $$

(6)

3 Main Results

In this section, we aim to provide new delay dependent sufficient conditions which ensure the exponential stabilization in the mean square of the neural networks (1).

Firstly, we consider following neural networks with time-varying delay

$$ \begin{aligned} x (k + 1 )& = Ax (k )+ Cx(k - \tau (k)) + Bf (x (k ))+ Dg(x(k - \tau (k))) + Nu(k)\\&\quad + \delta (k,x(k),x(k - \tau (k)))\omega (k), \\ y(k) & = Kx(k), \\ x(\theta ) & = \varphi (\theta ),\quad \theta = - \tau_{M} , - \tau_{M} + 1, \ldots ,0. \\ \end{aligned} $$

(7)

For system (7), we consider the following static output feedback controller

$$ u(k) = My(k). $$

(8)

Under the controller (8), the corresponding closed-loop system for (7) is given by

$$ x (k + 1 )= \bar{A}x (k )+ Cx(k - \tau (k)) + Bf (x (k ) )+ Dg(x(k - \tau (k))) + \delta (k,x(k),x(k - \tau (k)))\omega (k), $$

(9)

where $\bar{A} = A + NMK.$

Theorem 1

Suppose that Assumptions 1 and 2 hold. For given scalars$\tau_{m}$and$\tau_{M}$, satisfying$0< \tau_{m} \le \tau_{M}$, the discrete-time system (9) is asymptotical stability in the mean square, if there exist matrices$\psi = diag(s_{1} ,s_{2} , \ldots ,s_{n} ) > 0,$$\Gamma = diag(h_{1} ,h_{2} , \ldots ,h_{n} ) > 0,$positive definite matrices$P,Z,Q_{1} ,Q_{2} ,R$, $T = \left[ {\begin{array}{*{20}c} {T_{11} } & {T_{12} } \\ * & {T_{22} } \\ \end{array} } \right],$and scalars$\varepsilon > 0$, $\lambda^{*} > 0$such that the following matrix inequalities hold:

$$ \left[ {\begin{array}{*{20}c} {\Theta_{ 1 1} } & {\text{Z}} & 0& 0& {\Theta_{ 1 5} } & 0& {\psi \Lambda_{2} } & 0& {\bar{A}^{T} P} \\ * & {\Theta_{ 2 2} } & 0& 0& 0& 0& 0& 0& 0 \\ * & * & {\Theta_{ 3 3} } & 0& {{\text{C}}^{\text{T}} P} & { - T_{ 1 2} } & 0& {\Gamma \Omega_{2} } & {C^{T} P} \\ * & * & * & { - Q_{2} - R} & 0& 0& 0& 0& 0 \\ * & * & * & * & {\Theta_{ 5 5} } & 0& {PB} & {PD} & 0 \\ * & * & * & * & * & { - T_{ 2 2} } & 0& 0& 0 \\ * & * & * & * & * & * & { - \psi } & 0& {B^{\text{T}} P} \\ * & * & * & * & * & * & * & { - \Gamma } & {D^{T} P} \\ * & * & * & * & * & * & * & * & { - P} \\ \end{array} } \right] < 0, $$

(10)

$$ P < \lambda^{*} I, $$

(11)

where

$$ \begin{aligned} \Theta_{11} & = - P + Q_{1} + Q_{2} + (\tau_{M} - \tau_{m} + 1)T_{11} + R + \lambda^{*} \rho_{1} I - Z - \psi \Lambda_{ 1} , \\ \Theta_{ 1 5} & = (\tau_{M} - \tau_{m} + 1)T_{12} + (\bar{A} - I)^{T} P, \\ \end{aligned} $$

$$ \begin{aligned} \Theta_{ 2 2} & = - Q_{1} - Z,\quad \Theta_{ 3 3} = \lambda^{ *} \rho_{ 2} I - T_{11} - \Gamma \Omega_{1} , \\ \Theta_{ 5 5} & = (\tau_{M} - \tau_{m} + 1)T_{22} + \tau_{m}^{2} Z - 2P. \\ \end{aligned} $$

Proof

Choose the following Lyapunov–Krasovskii functional candidate:

$$ V(k) = \sum\limits_{i = 1}^{4} {V_{i} (k)} , $$

(12)

where

$$ \begin{aligned} V_{1} (k) & = x^{T} (k)Px(k), \\ V_{ 2} (k) & = \sum\limits_{{i = k - \tau_{m} }}^{k - 1} {x^{T} (i)Q_{1} x(i) + \sum\limits_{{i = k - \tau_{M} }}^{k - 1} {x^{T} (i)Q_{2} x(i)} } + \sum\limits_{{i = k - \tau (k)_{{}} }}^{k - 1} {\lambda^{T} (i)T\lambda (i)} , \\ V_{3} (k) & = \sum\limits_{{i = - \tau_{M} + 1}}^{{ - \tau_{m} }} {\sum\limits_{j = k + i}^{k - 1} {\lambda^{T} (j)T\lambda (j)} } , \\ V_{4} (k) & = \tau_{m} \sum\limits_{{i = - \tau_{m} }}^{ - 1} {\sum\limits_{j = k + i}^{k - 1} {\eta^{T} (j)Z\eta (j)} } + \sum\limits_{{i = k - \tau_{M} }}^{k - 1} {x^{T} (i)Rx(i)} , \\ \lambda (k) & = \left[ {\begin{array}{*{20}c} {x^{T} (k)} & {\eta^{T} (k)} \\ \end{array} } \right]^{T} ,\quad \eta (k) = x(k + 1) - x(k). \\ \end{aligned} $$

(13)

Define $\Delta V(k) = V(k + 1) - V(k)$, then along the solution of (9) we have

$$ \begin{aligned} & E\{ \Delta V_{1} (k)\} = E\{ V_{1} (k + 1) - V_{1} (k)\} \\ & \quad = E\{ [\bar{A}x(k) + Cx(k - \tau (k)) + Bf(x(k)) + Dg(x(k - \tau (k)))]^{T} P[\bar{A}x(k) + Cx(k - \tau (k)) + Bf(x(k)) \\ & \quad \;\; + Dg(x(k - \tau (k)))] + (\delta (k,x(k),x(k - \tau (k)))\omega (k))^{T} P(\delta (k,x(k),x(k - \tau (k)))\omega (k)) - x^{T} (k)Px(k)\} \\ & \quad \le E\{ [\bar{A}x(k) + Cx(k - \tau (k)) + Bf(x(k)) + Dg(x(k - \tau (k)))]^{T} P[\bar{A}x(k) + Cx(k - \tau (k)) + Bf(x(k)) \\ & \quad \;\; + Dg(x(k - \tau (k)))] + \lambda^{*} \rho_{1} x^{T} (k)x(k) + \lambda^{*} \rho_{2} x^{T} (k - \tau (k))x(k - \tau (k)) - x^{T} (k)Px(k)\} , \\ \end{aligned} $$

(14)

$$ \begin{aligned} E\{ \Delta V_{2} (k)\} & = E\left\{ {\sum\limits_{{i = k - \tau_{m} + 1}}^{k} {x^{T} (i)Q_{1} } x(i) - \sum\limits_{{i = k - \tau_{m} }}^{k - 1} {x^{T} (i)Q_{1} } x(i)} \right. \\ & \quad \left. + \sum\limits_{{i = k - \tau_{M} + 1}}^{k} {x^{T} (i)Q_{2} } x(i) - \sum\limits_{{i = k - \tau_{M} }}^{k - 1} {x^{T} (i)Q_{2} } x(i) + \sum\limits_{i = k - \tau (k + 1) + 1}^{k} {\lambda^{T} (i)T} \lambda (i) - \sum\limits_{i = k - \tau (k)}^{k - 1} {\lambda^{T} (i)T} \lambda (i)\right\} \\ & = E\left\{\vphantom{\sum\limits_{{i = k - \tau_{m} + 1}}^{k}} x^{T} (k)(Q_{1} + Q_{2} )x(k) + \lambda^{T} (k)T\lambda (k) - x^{T} (k - \tau_{m} )Q_{1} x(k - \tau_{m} ) \right. \\ & \quad \left. { - x^{T} (k - \tau_{M} )Q_{2} x(k - \tau_{M} ) - \lambda^{T} (k - \tau (k))T\lambda (k - \tau (k)) + \sum\limits_{j = k + 1 - \tau (k + 1)}^{k - \tau (k)} {\lambda^{T} (j)} T\lambda (j)} \right\} \\ & \le E\left\{\vphantom{\sum\limits_{{i = k - \tau_{m} + 1}}^{k}} {x^{T} (k)(Q_{1} + Q_{2} )x(k) + \lambda^{T} (k)T\lambda (k) - x^{T} (k - \tau_{m} )Q_{1} x(k - \tau_{m} )} \right. \\ & \quad - \left. {x^{T} (k - \tau_{M} )Q_{2} x(k - \tau_{M} ) - \lambda^{T} (k - \tau (k))T\lambda (k - \tau (k)) + \sum\limits_{{j = k + 1 - \tau_{M} }}^{{k - \tau_{m} }} {\lambda^{T} (j)} T\lambda (j)} \right\} \\ & \le E\left\{\vphantom{\sum\limits_{{i = k - \tau_{m} + 1}}^{k}} {x^{T} (k)(Q_{1} + Q_{2} )x(k) + x^{T} (k)T_{11} x(k) + 2x^{T} (k)T_{12} \eta (k)} \right. \\ & \quad + \eta^{T} (k)T_{ 2 2} \eta (k) - x^{T} (k - \tau_{m} )Q_{1} x(k - \tau_{m} ) - x^{T} (k - \tau_{M} )Q_{2} x(k - \tau_{M} ) \\ & \quad - x^{T} (k - \tau (k))T_{11} x(k - \tau (k)) - 2x^{T} (k - \tau (k))T_{12} \eta (k - \tau (k)) \\ & \quad - \left. {\eta^{T} (k - \tau (k))T_{22} \eta (k - \tau (k)) + \sum\limits_{{j = k + 1 - \tau_{M} }}^{{k - \tau_{m} }} {\lambda^{T} (j)} T\lambda (j)} \right\}, \\ \end{aligned} $$

(15)

$$ \begin{aligned} E\{ \Delta V_{3} (k)\} & = E\{ V_{3} (k + 1) - V_{3} (k)\} = E\left\{ {\sum\limits_{{i = - \tau_{M} + 1}}^{{ - \tau_{m} }} {(\lambda^{T} (k)T} \lambda (k) - \lambda^{T} (k + i)T\lambda (k + i))} \right\} \\ & = E\left\{ {(\tau_{M} - \tau_{m} )\lambda^{T} (k)T\lambda (k) - \sum\limits_{{i = k - \tau_{M} + 1}}^{{k - \tau_{m} }} {\lambda^{T} (j)T\lambda (j)} } \right\} \\ & = E\left\{ {(\tau_{M} - \tau_{m} )[x^{T} (k)T_{11} x(k) + 2x^{T} (k)T_{12} \eta (k) + \eta^{T} (k)T_{22} \eta (k)] - \sum\limits_{{i = k - \tau_{M} + 1}}^{{k - \tau_{m} }} {\lambda^{T} (j)T\lambda (j)} } \right\}, \\ \end{aligned} $$

(16)

$$ \begin{aligned} E\{ \Delta V_{4} (k)\} & = E\{ V_{4} (k + 1) - V_{4} (k)\} \\ & = E\left\{ {\tau_{m} \sum\limits_{{i = - \tau_{m} }}^{ - 1} {\sum\limits_{j = k + 1 + i}^{k} {\eta^{T} (j)Z\eta (j)} } - \tau_{m} \sum\limits_{{i = - \tau_{m} }}^{ - 1} {\sum\limits_{j = k + i}^{k - 1} {\eta^{T} (j)Z\eta (j)} } } \right. \\ & \quad \; + \left. {\sum\limits_{{i = k - \tau_{M} + 1}}^{k} {x^{T} (i)Rx(i)} - \sum\limits_{{i = k - \tau_{M} }}^{k - 1} {x^{T} (i)Rx(i)} } \right\} \\ & = E\left\{ {\tau_{m} \sum\limits_{{i = - \tau_{m} }}^{ - 1} {[\eta^{T} (k)Z\eta (k) - \eta^{T} (k + i)Z\eta (k + i)} ] + x^{T} (k)Rx(k)} \right. \\ & \quad \; - \left. {x^{T} (k - \tau_{M} )Rx(k - \tau_{M} )} \vphantom{\sum\limits_{{i = k - \tau_{m} + 1}}^{k}}\right\} \\ & \le E\left\{ \tau_{m}^{2} \eta^{T} (k)Z\eta (k) - \tau_{m} \sum\limits_{{i = k - \tau_{m} }}^{k - 1} {(\eta^{T} (j)Z\eta (j))}\right. \\ &\left. \quad \; + x^{T} (k)Rx(k) - x^{T} (k - \tau_{M} )Rx(k - \tau_{M} ) \vphantom{\sum\limits_{{i = k - \tau_{m} + 1}}^{k}}\right\} . \\ \end{aligned} $$

(17)

From Lemma 1, it’s easy to find

$$ \begin{aligned} - \tau_{m} \sum\limits_{{j = k - \tau_{m} }}^{k - 1} {\eta^{T} (j)Z\eta (j)} & \le - \left( {\sum\limits_{{j = k - \tau_{m} }}^{k - 1} {\eta^{T} (j)} } \right)Z\left( {\sum\limits_{{j = k - \tau_{m} }}^{k - 1} {\eta (j)} } \right) \\ & \le - (x(k) - x(k - \tau_{m} ))^{T} Z\;(x(k) - x(k - \tau_{m} )). \\ \end{aligned} $$

So, (17) can replaced that

$$ \begin{aligned} E\{ \Delta V_{4} (k)\} & \le E\left\{ {\tau_{m}^{2} \eta^{T} (k)Z\eta (k) - \tau_{m} \sum\limits_{{i = k - \tau_{m} }}^{k - 1} {(\eta^{T} (j)Z\eta (j))} + x^{T} (k)Rx(k) - x^{T} (k - \tau_{M} )Rx(k - \tau_{M} )} \right\} \\ & \le E\left\{ {\tau_{m}^{2} \eta^{T} (k)Z\eta (k) + x^{T} (k)Rx(k) - x^{T} (k - \tau_{M} )Rx(k - \tau_{M} )} \right. \\ & \quad \;\left. { - (x(k) - x(k - \tau_{m} ))^{T} Z(x(k) - x(k - \tau_{m} ))} \right\}. \\ \end{aligned} $$

(18)

It is easy to see

$$ E\eta (k) = E(x(k + 1) - x(k)) = E((\bar{A} - I)x(k) + Cx(k - \tau (k)) + Bf(x(k)) + Dg(x(k - \tau (k)))). $$

So, for any matrices P, we have

$$ 2E\left[ {\eta^{T} (k)P\left( {(\bar{A} - I)x(k) + Cx(k - \tau (k)) + Bf(x(k)) + Dg(x(k - \tau (k))) - \eta (k)} \right)} \right] = 0 $$

(19)

From (14)–(19), it follows that

$$ \begin{aligned} E\{ \Delta V(k)\} & \le E\left\{ {x^{T} (k)[ - P + Q_{1} + Q_{2} + (\tau_{M} - \tau_{m} + 1)T_{11} + \lambda^{*} \rho_{1} I - Z + R]x(k)} \right. \\ & \quad + 2x^{T} (k)Zx(k - \tau_{m} ) - x^{T} (k - \tau_{m} )(Q_{1} + Z)x(k - \tau_{m} ) \\ & \quad - x^{T} (k - \tau_{M} )(Q_{2} + R)x(k - \tau_{M} ) + x^{T} (k - \tau (k))(\lambda^{*} \rho_{2} I - T_{11} )x(k - \tau (k)) \\ & \quad - 2x^{T} (k - \tau (k))T_{12} \eta (k - \tau (k)) - \eta^{T} (k - \tau (k))T_{22} \eta (k - \tau (k)) \\ & \quad + 2x^{T} (k)[(\tau_{M} - \tau_{m} + 1)T_{12} + (\bar{A} - I)^{T} P]\eta (k) \\ & \quad + 2x^{T} (k - \tau (k))(C^{T} P)\eta (k) + 2\eta^{T} (k)(PB)f(x(k)) + 2\eta^{T} (k)(PD)g(x(k - \tau (k))) \\ & \quad + \left. {\eta^{T} (k)[(\tau_{M} - \tau_{m} + 1)T_{22} + \tau_{m}^{2} Z - 2P]\eta (k) + \xi^{T} (k)\varUpsilon^{T} P\varUpsilon \xi (k)} \right\}, \\ \end{aligned} $$

(20)

where

$$ \begin{aligned} \varUpsilon & = \left[ {\begin{array}{*{20}c} {\bar{A}} & 0 & C & 0 & 0 & 0 & B & D \\ \end{array} } \right], \\ \xi^{T} (k) & = [x^{T} (k),x^{T} (k - \tau_{m} ),x^{T} (k - \tau (k)),x^{T} (k - \tau_{M} ),\eta^{T} (k),\eta^{T} (k - \tau (k)),f^{T} (x(k)), \\ & \quad \quad \quad g^{T} (x(k - \tau (k)))]. \\ \end{aligned} $$

In addition, from Assumption 1, we have

$$ \begin{aligned} & (f_{i} (x_{i} (k)) - l_{i}^{ + } x_{i} (k))^{T} (f_{i} (x_{i} (k)) - l_{i}^{ - } x_{i} (k)) \le 0,\;i = 1,2, \ldots ,n, \\ & (g_{i} (x_{i} (k - \tau (k))) - v_{i}^{ + } x_{i} (k - \tau (k)))^{T} (g_{i} (x_{i} (k - \tau (k)) - v_{i}^{ - } x_{i} (k - \tau (k))) \le 0,\;i = 1,2, \ldots ,n. \\ \end{aligned} $$

So, it follows that for any matrices $\psi = diag(s_{1} ,s_{2} , \ldots ,s_{n} ) > 0,$$\Gamma = diag(h_{1} ,h_{2} , \ldots ,h_{n} ) > 0,$

$$ \begin{aligned} 0 & \le - \sum\limits_{i = 1}^{n} {s_{i} } (f_{i} (x_{i} (k)) - l_{i}^{ + } x_{i} (k))^{T} (f_{i} (x_{i} (k)) - l_{i}^{ - } x_{i} (k)) - \sum\limits_{i = 1}^{n} {h_{i} } (g_{i} (x_{i} (k - \tau (k))) \\ & \quad \; - v_{i}^{ + } x_{i} (k - \tau (k)))^{T} (g_{i} (x_{i} (k - \tau (k)) - v_{i}^{ - } x_{i} (k - \tau (k))) \\ & = - x^{T} (k)\psi \Lambda_{1} x(k) + 2x^{T} (k)\psi \Lambda_{2} f(x(k)) - f^{T} (x(k))\psi f(x(k)) \\ & \quad \; - x^{T} (k - \tau (k))\Gamma \Omega_{1} x(k - \tau (k)) + 2x^{T} (k - \tau (k))\Gamma \Omega_{2} g(k - \tau (k)) \\ & \quad \; - g^{T} (k - \tau (k))\Gamma g(k - \tau (k)). \\ \end{aligned} $$

(21)

Combining (20) and (21), we can get

$$ \begin{aligned} E\left\{ {\Delta V(k)} \right\} & \le E\left\{ {x^{T} (k)[ - P + Q_{1} + Q_{2} + (\tau_{M} - \tau_{m} + 1)T_{11} + R + \lambda^{*} \rho_{1} I - Z]x(k)} \right. \\ & \quad \;\; + 2x^{T} (k)Zx(k - \tau_{m} ) - x^{T} (k - \tau_{m} )(Q_{1} + Z)x(k - \tau_{m} ) \\ & \quad \;\; - x^{T} (k - \tau_{M} )(Q_{2} + R)x(k - \tau_{M} ) + x^{T} (k - \tau (k))(\lambda^{*} \rho_{2} I - T_{11} )x(k - \tau (k)) \\ & \quad \;\; - 2x^{T} (k - \tau (k))T_{12} \eta (k - \tau (k)) - \eta^{T} (k - \tau (k))T_{22} \eta (k - \tau (k)) \\ & \quad \;\; + 2x^{T} (k)[(\tau_{M} - \tau_{m} + 1)T_{12} + (A - I + NMK)^{T} P]\eta (k) \\ & \quad \;\; + 2x^{T} (k - \tau (k))(PC)^{T} \eta (k) + 2\eta^{T} (k)(PB)f(x(k)) + 2\eta^{T} (k)(PD)g(x(k - \tau (k))) \\ & \quad \;\; - x^{T} (k)\psi \Lambda_{1} x(k) + 2x^{T} (k)\psi \Lambda_{2} f(x(k)) - f^{T} (x(k))\psi f(x(k)) \\ & \quad \;\; - x^{T} (k - \tau (k))\Gamma \Omega_{1} x(k - \tau (k)) + 2x^{T} (k - \tau (k))\Gamma \Omega_{2} g(x(k - \tau (k))) \\ & \quad \;\; - g^{T} (x(k - \tau (k)))\Gamma g(x(k - \tau (k))) + \eta^{T} (k)[(\tau_{M} - \tau_{m} + 1)T_{22} + \tau_{m}^{2} Z - 2P]\eta (k) \\ & \quad \;\; + \left. {\xi^{T} (k)\varUpsilon^{T} P\varUpsilon \xi (k)} \right\} \\ & = E\{ \xi^{T} (k)[\varXi_{ 1} + \varUpsilon^{T} P\varUpsilon ]\xi (k)\} , \\ \end{aligned} $$

(22)

where

$$ \varXi_{ 1} = \left[ {\begin{array}{*{20}c} {\Theta_{11} } & Z & 0 & 0 & {\Theta_{ 1 5} } & 0 & {\psi \Lambda_{2} } & 0 \\ * & {\Theta_{ 2 2} } & 0 & 0 & 0 & 0 & 0 & 0\\ * & * & {\Theta_{ 3 3} } & 0 & {C^{T} P} & { - T_{12} } & 0 & {\Gamma \Omega_{2} } \\ * & * & * & { - Q_{2} - R} & 0 & 0 & 0 & 0 \\ * & * & * & * & {\Theta_{ 5 5} } & 0 & {PB} & {PD} \\ * & * & * & * & * & { - T_{22} } & 0 & 0 \\ * & * & * & * & * & * & { - \psi } & 0 \\ * & * & * & * & * & * & * & { - \Gamma } \\ \end{array} } \right], $$

$$ \begin{aligned} \Theta_{11} & = - P + Q_{1} + Q_{2} + (\tau_{M} - \tau_{m} + 1)T_{11} + R + \lambda^{*} \rho_{1} I - Z - \psi \Lambda_{ 1} , \\ \Theta_{ 1 5} & = (\tau_{M} - \tau_{m} + 1)T_{12} + (\bar{A} - I)^{T} P,\quad \Theta_{ 2 2} = - Q_{1} - Z, \\ \Theta_{ 3 3} & = \lambda^{ *} \rho_{ 2} I - T_{11} - \Gamma \Omega_{1} ,\quad \Theta_{ 5 5} = (\tau_{M} - \tau_{m} + 1)T_{22} + \tau_{m}^{2} Z - 2P. \\ \end{aligned} $$

Applying Schur complement to (10) yields,

$$ \varXi_{ 1} + \varUpsilon^{T} P\varUpsilon < 0. $$

(23)

Therefore, there exists a sufficient small scalar $c > 0$, such that,

$$ E\{ \Delta V(k)\} \le - cE\left\| {x(k)} \right\|^{2} < 0. $$

(24)

This means that the discrete-time system (9) is asymptotically stable. This completes the proof of Theorem 1.

Now, we consider the uncertain discrete-time stochastic neural networks (1) under the control (8). The closed-loop system for (1) with (8) is rewritten to

$$ \begin{aligned} x (k + 1 )& = (A + NMK)x (k )+ Cx(k - \tau (k)) + Bf (x (k ) )+ Dg(x(k - \tau (k))) + Gm(k) \\ & \quad \quad \quad \;\; + \delta (k,x(k),x(k - \tau (k)))\omega (k), \\ m(k) & = F(k)(E_{a} x(k) + E_{c} x(k - \tau (k)) + E_{b} f (x (k ) )+ E_{d} g(x(k - \tau (k)))). \\ \end{aligned} $$

(25)

Theorem 2

Suppose that Assumptions 1 and 2 hold. For given scalars$\tau_{m}$and$\tau_{M}$satisfying (2), the closed-loop system (25) is robustly globally exponentially stable in the mean square, if there exist matrices$\psi = diag(s_{1} ,s_{2} , \ldots ,s_{n} ) > 0,$$\Gamma = diag(h_{1} ,h_{2} , \ldots ,h_{n} ) > 0,$positive definite matrices$P,$$Z,Q_{1} ,Q_{2} ,R,$$T = \left[ {\begin{array}{*{20}c} {T_{11} } & {T_{12} } \\ * & {T_{22} } \\ \end{array} } \right],$and scalars$\varepsilon > 0$and$\lambda^{*} > 0$such that the following matrix inequalities hold:

$$ \left[ {\begin{array}{*{20}c} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 1 1} } & Z & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 1 3} } & 0& {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 1 5} } & 0& {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 1 7} } & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 1 8} } & 0& {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{1 1 0} } \\ * & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 2 2} } & 0& 0& 0& 0& 0& 0& 0& 0\\ * & * & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 3 3} } & 0& {C^{T} P} & { - T_{12} } & {\varepsilon E_{c}^{T} E_{b} } & {\Gamma \Omega_{2} + \varepsilon E_{c}^{T} E_{d} } & 0& {C^{T} P} \\ * & * & * & { - Q_{2} - R} & 0& 0& 0& 0& 0& 0\\ * & * & * & * & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 5 5} } & 0& {PB} & {PD} & {PG} & 0\\ * & * & * & * & * & { - T_{22} } & 0& 0& 0& 0\\ * & * & * & * & * & * & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 7 7} } & {\varepsilon E_{b}^{T} E_{d} } & 0& {B^{T} P} \\ * & * & * & * & * & * & * & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{8 8} } & 0& {D^{T} P} \\ * & * & * & * & * & * & * & * & { - \varepsilon I} & {G^{T} P} \\ * & * & * & * & * & * & * & * & * & { - P} \\ \end{array} } \right] < 0, $$

(26)

$$ P < \lambda^{*} I, $$

(27)

where

$$ \begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 1 1} & = - P + Q_{1} + Q_{2} + (\tau_{M} - \tau_{m} + 1)T_{11} + R + \varepsilon E_{a}^{T} E_{a} + \lambda^{*} \rho_{1} I - Z - \psi \Lambda_{ 1} , \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 1 3} & = \varepsilon E_{a}^{T} E_{c} ,\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 1 5} = (\tau_{M} - \tau_{m} + 1)T_{12} + (A - I)^{T} P + (NMK)^{T} P, \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 1 7} & = \psi \Lambda_{2} + \varepsilon E_{a}^{T} E_{b} ,\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 1 8} = \varepsilon E_{a}^{T} E_{d} ,\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 1 1 0} = A^{T} P + (NMK)^{T} P, \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 2 2} & = - Q_{1} - Z,\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 3 3} = \lambda^{*} \rho_{2} I - T_{11} - \Gamma \Omega_{1} + \varepsilon E_{c}^{T} E_{c} , \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 5 5} & = (\tau_{M} - \tau_{m} + 1)T_{22} + \tau_{m}^{2} Z - 2P, \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 7 7} & = - \psi + \varepsilon E_{b}^{T} E_{b} ,\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 8 8} = - \Gamma + \varepsilon E_{d}^{T} E_{d} . \\ \end{aligned} $$

(28)

Proof

From (25), we have

$$ 2E\{ \eta^{T} (k)P[(A + NMK - I)x(k) + Cx(k - \tau (k)) + Bf(x(k)) + Dg(x(k - \tau (k))) + Gm(k) - \eta (k)]\} = 0, $$

where $\eta (k) = x(k + 1) - x(k).$

Choose the Lyapunov–Krasovskii functional candidate (12). Calculating the difference of $V(k)$ along the system (25), and taking the mathematical expectation, we have

$$ \begin{aligned} E\left\{ {\Delta V(k)} \right\} & \le E\left\{ {x^{T} (k)[ - P + Q_{1} + Q_{2} + (\tau_{M} - \tau_{m} + 1)T_{11} + R + \lambda^{*} \rho_{1} I - Z]x(k)} \right. \\ & \quad + 2x^{T} (k)Zx(k - \tau_{m} ) - x^{T} (k - \tau_{m} )(Q_{1} + Z)x(k - \tau_{m} ) \\ & \quad - x^{T} (k - \tau_{M} )(Q_{2} + R)x(k - \tau_{M} ) + x^{T} (k - \tau (k))(\lambda^{*} \rho_{2} I - T_{11} )x(k - \tau (k)) \\ & \quad - 2x^{T} (k - \tau (k))T_{12} \eta (k - \tau (k)) - \eta^{T} (k - \tau (k))T_{22} \eta (k - \tau (k)) \\ & \quad + 2x^{T} (k)[(\tau_{M} - \tau_{m} + 1)T_{12} + (A - I + NMK)^{T} P]\eta (k) \\ & \quad + 2\eta^{T} (k)PCx(k - \tau (k)) + 2\eta^{T} (k)PBf(x(k)) + 2\eta^{T} (k)PDg(x(k - \tau (k))) \\ & \quad + 2\eta^{T} (k)PGm(k) - x^{T} (k)\psi \Lambda_{1} x(k) + 2x^{T} (k)\psi \Lambda_{2} f(x(k)) - f^{T} (x(k))\psi f(x(k)) \\ & \quad - x^{T} (k - \tau (k))\Gamma \Omega_{1} x(k - \tau (k)) + 2x^{T} (k - \tau (k))\Gamma \Omega_{2} gx(k - \tau (k)) \\ & \quad - g^{T} x(k - \tau (k))\Gamma gx(k - \tau (k)) + \eta^{T} (k)[(\tau_{M} - \tau_{m} + 1)T_{22} + \tau_{m}^{2} Z - 2P]\eta (k) \\ & \quad + \left. {\bar{\xi }^{T} (k)\bar{\varUpsilon }^{T} P\bar{\varUpsilon }\bar{\xi }(k)} \right\} \\ & = E\{ \bar{\xi }^{T} (k)(\tilde{\varXi }_{ 1} + \bar{\varUpsilon }^{T} P\bar{\varUpsilon }\;)\bar{\xi }(k)\} , \\ \end{aligned} $$

(29)

where

$$ \begin{aligned} \bar{\varUpsilon } & = \left[ {\begin{array}{*{20}c} {A + NMK} & 0& C & 0 & 0 & 0 & B & D & G \\ \end{array} } \right], \\ \bar{\xi }^{T} (k) & = [x^{T} (k),x^{T} (k - \tau_{m} ),x^{T} (k - \tau (k)),x^{T} (k - \tau_{\text{M}} ),\eta^{\text{T}} (k),\eta^{\text{T}} (k - \tau (k)),f^{T} (x(k)) \\ & \;\;\;\;\;\;\;\;\;\;g^{T} (x(k - \tau (k))),m(k)], \\ \end{aligned} $$

$$ \tilde{\varXi }_{ 1} = \left[ {\begin{array}{*{20}c} {\Theta_{ 1 1} } & Z & 0 & 0 & {\Theta_{ 1 5} } & 0 & {\psi \Lambda_{2} } & 0 & 0 \\ *& {\Theta_{ 2 2} } & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ *& *& {\Theta_{ 3 3} } & 0 & {C^{T} P} & { - T_{12} } & 0 & {\Gamma \Omega_{2} } & 0 \\ *& *& *& { - Q_{2} - R} & 0 & 0 & 0 & 0 & 0 \\ *& *& *& *& {\Theta_{ 5 5} } & 0 & {PB} & {PD} & {PG} \\ *& *& *& *& *& { - T_{22} } & 0 & 0 & 0 \\ *& *& *& *& *& *& { - \psi } & 0 & 0 \\ *& *& *& *& *& *& *& { - \Gamma } & 0 \\ *& *& *& *& *& *& *& *& 0 \\ \end{array} } \right], $$

$$ \begin{aligned} \Theta_{11} & = - P + Q_{1} + Q_{2} + (\tau_{M} - \tau_{m} + 1)T_{11} + R + \lambda^{*} \rho_{1} I - Z - \psi \Lambda_{ 1} , \\ \Theta_{ 1 5} & = (\tau_{M} - \tau_{m} + 1)T_{12} + (\bar{A} - I)^{T} P,\quad \quad \Theta_{ 2 2} = - Q_{1} - Z, \\ \Theta_{ 3 3} & = \lambda^{ *} \rho_{ 2} I - T_{11} - \Gamma \Omega_{1} ,\quad \Theta_{ 5 5} = (\tau_{M} - \tau_{m} + 1)T_{22} + \tau_{m}^{2} Z - 2P. \\ \end{aligned} $$

From (3) and (25), it follows that

$$ \begin{aligned} & \varepsilon x^{T} (k)(E_{a}^{T} E_{a} )x(k) + 2\varepsilon x^{T} (k)(E_{a}^{T} E_{c} )x(k - \tau (k)) \\ & \quad + 2\varepsilon x^{T} (k)(E_{a}^{T} E_{b} )f(x(k)) + 2\varepsilon x^{T} (k)(E_{a}^{T} E_{d} )g(x(k - \tau (k))) \\ & \quad + \varepsilon x^{T} (k - \tau (k))(E_{c}^{T} E_{c} )x(k - \tau (k)) + 2\varepsilon x^{T} (k - \tau (k))(E_{c}^{T} E_{b} )f(x(k)) \\ & \quad + 2\varepsilon x^{T} (k - \tau (k))(E_{c}^{T} E_{d} )g(x(k - \tau (k))) + \varepsilon f^{T} (x(k))(E_{b}^{T} E_{b} )f(x(k)) \\ & \quad + 2\varepsilon f^{T} (x(k))(E_{b}^{T} E_{d} )g(x(k - \tau (k))) \\ & \quad + \varepsilon g^{T} (x(k - \tau (k)))(E_{d}^{T} E_{d} )g(x(k - \tau (k))) - \varepsilon m^{T} (k)m(k) \ge 0 \\ \end{aligned} $$

(30)

From (29) and (30), we have

$$ \begin{aligned} E\left\{ {\Delta V(k)} \right\} & \le E\left\{ {\bar{\xi }^{T} (k)\tilde{\varXi }_{ 1} (k)\bar{\xi }(k) + \bar{\xi }^{T} (k)\bar{\varUpsilon }^{T} P\bar{\varUpsilon }\bar{\xi }(k)} \right. \\ & \quad + \varepsilon x^{T} (k)(E_{a}^{T} E_{a} )x(k) + 2\varepsilon x^{T} (k)(E_{a}^{T} E_{c} )x(k - \tau (k)) \\ & \quad + 2\varepsilon x^{T} (k)(E_{a}^{T} E_{b} )f(x(k)) + 2\varepsilon x^{T} (k)(E_{a}^{T} E_{d} )g(x(k - \tau (k))) \\ & \quad + \varepsilon x^{T} (k - \tau (k))(E_{c}^{T} E_{c} )x(k - \tau (k)) + 2\varepsilon x^{T} (k - \tau (k))(E_{c}^{T} E_{b} )f(x(k)) \\ & \quad + 2\varepsilon x^{T} (k - \tau (k))(E_{c}^{T} E_{d} )g(x(k - \tau (k))) + \varepsilon f^{T} (x(k))(E_{b}^{T} E_{b} )f(x(k)) \\ & \quad + 2\varepsilon f^{T} (x(k))(E_{b}^{T} E_{d} )g(x(k - \tau (k))) \\ & \quad + \left. {\varepsilon g^{T} (x(k - \tau (k)))(E_{d}^{T} E_{d} )g(x(k - \tau (k))) - \varepsilon m^{T} (k)m(k)} \right\} \\ & = E\{ \bar{\xi }^{T} (k)[\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\varXi }_{ 1} + \bar{\varUpsilon }^{T} P\bar{\varUpsilon }]\bar{\xi }(k)\} , \\ \end{aligned} $$

(31)

where

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\varXi }_{ 1} = \left[ {\begin{array}{*{20}c} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 1 1} } & Z & {\varepsilon E_{a}^{T} E_{c} } & 0 & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 1 5} } & 0 & {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 1 7} } & {\varepsilon E_{a}^{T} E_{d} } & 0 \\ *& { - Q_{1} - Z} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ *& *& {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 3 3} } & 0 & {C^{T} P} & { - T_{12} } & 0 & {\Gamma \Omega_{2} { + }\varepsilon E_{c}^{T} E_{d} } & 0 \\ *& *& *& { - Q_{2} - R} & 0 & 0 & 0 & 0 & 0 \\ *& *& *& *& {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 5 5} } & 0 & {PB} & {PD} & {PG} \\ *& *& *& *& *& { - T_{22} } & 0 & 0 & 0 \\ *& *& *& *& *& *& {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 7 7} } & {\varepsilon E_{b}^{T} E_{d} } & 0 \\ *& *& *& *& *& *& *& { - \Gamma + \varepsilon E_{d}^{T} E_{d} } & 0 \\ *& *& *& *& *& *& *& *& { - \varepsilon I} \\ \end{array} } \right], $$

$$ \begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 1 1} & = - P + Q_{1} + Q_{2} + (\tau_{M} - \tau_{m} + 1)T_{11} + R + \varepsilon E_{a}^{T} E_{a} + \lambda^{*} \rho_{1} I - Z - \psi \Lambda_{ 1} , \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 1 5} & = (\tau_{M} - \tau_{m} + 1)T_{12} + (A - I + NMK)^{T} P,\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 1 7} = \psi \Lambda_{2} + \varepsilon E_{a}^{T} E_{b} , \\ \end{aligned} $$

$$ \begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 2 2} & = - Q_{1} - Z,\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 3 3} = \lambda^{*} \rho_{2} I - T_{11} - \Gamma \Omega_{1} + \varepsilon E_{c}^{T} E_{c} , \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 5 5} & = (\tau_{M} - \tau_{m} + 1)T_{22} + \tau_{m}^{2} Z - 2P, \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 7 7} & = - \psi + \varepsilon E_{b}^{T} E_{b} ,\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{ 8 8} = - \Gamma + \varepsilon E_{d}^{T} E_{d} . \\ \end{aligned} $$

Using Schur complement and (26), we have

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\varXi }_{ 1} + \bar{\varUpsilon }^{T} P\bar{\varUpsilon } < 0. $$

So, there exists a sufficient small scalar $c > 0$ such that,

$$ E\{ \Delta V(k)\} \le - cE\left\| {x(k)} \right\|^{2} < 0, $$

this means that system (25) is asymptotically stable for any time-varying delay $\tau (k)$ satisfying (2).

Now, we prove the global exponential stability of system (25), it is easy to get that

$$ V(k) \le \lambda_{\hbox{max} } (P)\left\| {x(k)} \right\|^{2} + \gamma_{1} \sum\limits_{{i = k - \tau_{M} }}^{k - 1} {\left\| {x(i)} \right\|^{2} } + \gamma_{ 2} \sum\limits_{{i = k - \tau_{M} }}^{k - 1} {\left\| {x(i + 1)} \right\|^{2} } , $$

(32)

where

$$ \begin{aligned} \gamma_{1} & = \lambda_{\hbox{max} } (Q_{1} + Q_{2} + R) + (\tau_{M} - \tau_{m} + 1)(\lambda_{\hbox{max} } (T_{11} ) + \lambda_{\hbox{max} } (T_{12} ) + 2\lambda_{\hbox{max} } (T_{22} )) + 2\tau_{m}^{2} \lambda_{\hbox{max} } (Z), \\ \gamma_{2} & = (\tau_{M} - \tau_{m} + 1)((\lambda_{\hbox{max} } (T_{11} ) + \lambda_{\hbox{max} } (T_{12} ) + 2\lambda_{\hbox{max} } (T_{22} )) + 2\tau_{m}^{2} \lambda_{\hbox{max} } (Z). \\ \end{aligned} $$

For any $\mu > 1$, it seen that

$$\begin{aligned} E\{ \mu ^{{j + 1}} V(j + 1) - \mu ^{j} V(j)\} & = E\{ \mu ^{{j + 1}} \Delta V(j) + \mu ^{j} (\mu - 1)V(j)\} \\ & \le E\left\{ {[ - c\mu + (\mu - 1)\lambda _{{{\text{max}}}} P]\mu ^{j} \left\| {x(i)} \right\|^{2} } \right. \\ & \quad + \left. (\mu - 1){\left[ {\gamma _{1} \mu ^{j} \sum\limits_{{i = j - \tau _{M} }}^{{j - 1}} {\left\| {x(i)} \right\|^{2} } + \gamma _{2} \mu ^{j} \sum\limits_{{i = j - \tau _{M} }}^{{j - 1}} {\left\| {x(i + 1)} \right\|^{2} } } \right]} \right\}. \\ \end{aligned}$$

(33)

Now, we sum up both side of (33) from 0 to $k - 1$ and obtain

$$ \begin{aligned} E\{ \mu^{k} V(k) - V( 0)\} & \le E\left\{ {[ - c\mu + (\mu - 1)\lambda_{\hbox{max} } P]\sum\limits_{j = 0}^{k - 1} {\mu^{j} \left\| {x(j)} \right\|^{ 2} } } \right. \\ & \quad + \left. {(\mu - 1)\left( {\gamma_{1} \sum\limits_{j = 0}^{k - 1} {\sum\limits_{{i = j - \tau_{M} }}^{j - 1} {\mu^{j} \left\| {x(j)} \right\|^{ 2} } } + \gamma_{2} \sum\limits_{j = 0}^{k - 1} {\sum\limits_{{i = j - \tau_{M} }}^{j - 1} {\mu^{j} \left\| {x(j + 1)} \right\|^{ 2} } } } \right)} \right\}. \\ \end{aligned} $$

(34)

According to the method in [16], it is easy to have

$$ \begin{aligned} \sum\limits_{j = 0}^{k - 1} {\sum\limits_{{i = j - \tau_{M} }}^{j - 1} {\mu^{j} \left\| {x(j)} \right\|^{ 2} } } & \le \left( {\sum\limits_{{i = - \tau_{M} }}^{ - 1} {\sum\limits_{j = 0}^{{i + \tau_{M} }} + } \sum\limits_{i = 0}^{{k - 1 + \tau_{M} }} {\sum\limits_{j = i + 1}^{{i + \tau_{M} }} + } \sum\limits_{{i = k - \tau_{M} }}^{k - 1} {\sum\limits_{j = i + 1}^{k - 1} {} } } \right)\mu^{j} \left\| {x(j)} \right\|^{2} \\ & \le \tau_{M}^{2} \mu^{{\tau_{M} }} \mathop {\hbox{max} }\limits_{{ - \tau_{M} \le s \le 0}} \left\| {x(s)} \right\|^{2} + \tau_{M} \mu^{{\tau_{M} }} \sum\limits_{i = 0}^{k} {\mu^{i} \left\| {x(i)} \right\|^{2} ,} \\ \sum\limits_{j = 0}^{k - 1} {\sum\limits_{{i = j - \tau_{M} }}^{j - 1} {\mu^{j} \left\| {x(j + 1)} \right\|^{ 2} } } & \le \tau_{M}^{2} \mu^{{\tau_{M} }} \mathop {\hbox{max} }\limits_{{ - \tau_{M} \le s \le 0}} \left\| {x(s)} \right\|^{2} + \tau_{M} \mu^{{\tau_{M} }} \sum\limits_{i = 1}^{k} {\mu^{i} \left\| {x(i)} \right\|^{2} } . \\ \end{aligned} $$

Meanwhile, from (32), we can easily get

$$ \begin{aligned} V( 0) & \le \lambda_{\hbox{max} } (P)\left\| {x(0)} \right\|^{2} + \left[ {\gamma_{1} \sum\limits_{{i = - \tau_{M} }}^{ - 1} {\left\| {x(i)} \right\|^{2} } + \gamma_{2} \sum\limits_{{i = - \tau_{M} }}^{ - 1} {\left\| {x(i + 1)} \right\|^{2} } } \right] \\ & \le [\lambda_{\hbox{max} } (P) + \tau_{M} (\gamma_{1} + \gamma_{2} )]\mathop {\sup }\limits_{{ - \tau_{M} \le s \le 0}} \left\| {x(s)} \right\|^{2} . \\ \end{aligned} $$

(35)

Thus from (32)–(35), it can be obtained that

$$ E\{ \mu^{k} V(k)\} \le E\left\{ {\vartheta_{ 0} (\mu )\mathop {\hbox{max} }\limits_{{ - \tau_{M} \le s \le 0}} \left\| {x(s)} \right\|^{2} + \vartheta_{1} (\mu )\sum\limits_{i = 0}^{k} {\mu^{i} } \left\| {x(i)} \right\|^{2} } \right\}, $$

where

$$ \begin{aligned} \vartheta_{ 0} (\mu ) & = \lambda_{\hbox{max} } (P) + (\mu - 1)\tau_{M}^{2} \mu^{{\tau_{M} }} (\gamma_{1} + \gamma_{2} ) + \tau_{M} (\gamma_{1} + \gamma_{2} ), \\ \vartheta_{1} (\mu ) & = (\mu - 1)\lambda_{\hbox{max} } (P) - c\mu + (\mu - 1)\tau_{M} \mu^{{\tau_{M} }} (\gamma_{1} + \gamma_{2} ). \\ \end{aligned} $$

Because $\vartheta_{ 1} (1) = - c < 0$, there must be a positive scalar $\mu_{0} > 1$, such that $\vartheta_{ 1} (\mu_{0} ) < 0$, so

$$ E\{ V(k)\} \le E\left\{ {\vartheta_{ 0} (\mu_{0} )\left( {\frac{1}{{\mu_{0} }}} \right)^{k} \mathop {\hbox{max} }\limits_{{ - \tau_{M} \le s \le 0}} \left\| {x(s)} \right\|^{2} } \right\}. $$

From definition of $V(k),$ we also get that

$$ V(k) \ge \lambda_{\hbox{min} } (P)\left\| {x(k)} \right\|^{2} . $$

So,

$$ E\{ \left\| {x(k)} \right\|^{2} \} \le \frac{{\vartheta_{ 0} (\mu_{0} )}}{{\lambda_{ \hbox{min} } (P)}}\left( {\frac{1}{{\mu_{0} }}} \right)^{k} \mathop {\hbox{max} }\limits_{{ - \tau_{M} \le s \le 0}} E\left\| {x(s)} \right\|^{2} . $$

Then closed-loop system (25) is globally exponentially stable. This completes the proof of Theorem 2.

Remark 2

According to the proof of Theorem 2 and Definition 1, we have

$$ \begin{aligned} \alpha & = \frac{{\vartheta_{ 0} (\mu_{0} )}}{{\lambda_{ \hbox{min} } (P)}} \\ & = 1 + \frac{{(\mu - 1)\tau_{M}^{2} \mu^{{\tau_{M} }} (\gamma_{1} + \gamma_{2} ) + \tau_{M} (\gamma_{1} + \gamma_{2} )}}{{\lambda_{ \hbox{min} } (P)}} \\ & > 1 + \frac{{\tau_{M} (\gamma_{1} + \gamma_{2} )}}{{\lambda_{ \hbox{min} } (P)}} \\ \end{aligned} $$

Remark 3

The steps of calculating the gain matrix M of the static output feedback controller are as follows:

Step 1 Let $\varPi = (NMK)^{T} P.$ Using MATLAB LMI Toolbox to solve (26) and (27), we can obtain matrices $\varPi ,\quad \psi = diag(s_{1} ,s_{2} , \ldots ,s_{n} ),$$\Gamma = diag(h_{1} ,h_{2} , \ldots ,h_{n} ),$ positive definite matrices $P,Z,Q_{1} ,$$Q_{2} ,R,$$T = \left[ {\begin{array}{*{20}c} {T_{11} } & {T_{12} } \\ * & {T_{22} } \\ \end{array} } \right],$ and positive scalars $\varepsilon$ and $\lambda^{*} .$

Step 2 From P and $\varPi$, we calculate $M = N^{ - 1} P^{ - 1} \varPi^{T} K^{ - 1} .$

When $\tau (k) = d,$ where $d$ is a constant, the closed-loop system (25) can be written as:

$$ \begin{aligned} x (k + 1 )& = (A + NMC)x (k )+ Cx(k - d) + Bf (x (k ) )+ Dg(x(k - d)) + Gm(k) \\ & \quad \; + \delta (k,x(k),x(k - d))\omega (k), \\ m(k) & = F(k)(E_{a} x(k) + E_{c} x(k - d) + E_{b} f (x (k ) )+ E_{d} g(x(k - d))). \\ \end{aligned} $$

(36)

The following corollary can be obtained.

Corollary 1

Suppose that Assumptions 1 and 2 hold. The discrete-time system (36) is globally exponentially stable in the mean square, if there exist matrices$Z > 0,Q > 0,R > 0,P > 0,$$\psi = diag(s_{1} ,s_{2} , \ldots ,s_{n} ) > 0,$$\Gamma = diag(h_{1} ,h_{2} , \ldots ,h_{n} ) > 0$, and scalars$\varepsilon > 0$and$\lambda^{*} > 0$such that the following matrix inequalities hold:

$$ \tilde{\varXi } = \left[ {\begin{array}{*{20}c} {\tilde{\Theta }_{ 1 1} } & {\tilde{\Theta }_{ 12} } & {\tilde{\Theta }_{ 13} } & {\tilde{\Theta }_{ 1 4} } & {\tilde{\Theta }_{ 1 5} } & 0& {\tilde{\Theta }_{ 1 7} } \\ * & {\tilde{\Theta }_{ 2 2} } & {C^{T} P} & {\varepsilon E_{c}^{T} E_{b} } & {\Gamma \Omega_{2} + \varepsilon E_{b}^{T} E_{d} } & 0 & {C^{T} P} \\ * & * & {\tilde{\Theta }_{ 3 3} } & {PB} & {PD} & {PG} & 0 \\ * & * & * & { - \psi + \varepsilon E_{b}^{T} E_{b} } & {\varepsilon E_{b}^{T} E_{d} } & 0 & {B^{T} P} \\ * & * & * & * & { - \Gamma + \varepsilon E_{d}^{T} E_{d} } & 0 & {D^{T} P} \\ * & * & * & * & * & { - \varepsilon I} & {G^{T} P} \\ * & * & * & * & * & * & { - P} \\ \end{array} } \right] < 0, $$

(37)

$$ P < \lambda^{*} I, $$

(38)

where

$$ \begin{aligned} \tilde{\Theta }_{ 1 1} & = Q + R + \lambda^{*} \rho_{1} I - Z - \psi \Lambda_{ 1} - P + \varepsilon E_{a}^{T} E_{a} ,\quad \tilde{\Theta }_{ 1 2} = Z + \varepsilon E_{a}^{T} E_{c} ,\quad \\ \tilde{\Theta }_{ 13} & = (A - I)^{T} P + (NMK)^{T} P,\quad \tilde{\Theta }_{ 1 4} = \psi \Lambda_{2} + \varepsilon E_{a}^{T} E_{b} ,\quad \\ \tilde{\Theta }_{ 1 5} & = \varepsilon E_{a}^{T} E_{d} ,\quad \tilde{\Theta }_{ 1 7} = A^{T} P + (NMK)^{T} P \\ \tilde{\Theta }_{ 3 3} & = d^{2} Z - 2P,\quad \tilde{\Theta }_{ 2 2} = - Q - Z + \lambda^{*} \rho_{ 2} I - R - \Gamma \Omega_{1} + \varepsilon E_{c}^{T} E_{c} . \\ \end{aligned} $$

(39)

Proof

Choose the following Lyapunov–Krasovskii functional candidate:

$$ V(k) = \sum\limits_{i = 1}^{3} {V_{i} (k)} , $$

where

$$ \begin{aligned} V_{1} (k) & = x^{T} (k)Px(k), \\ V_{ 2} (k) & = \sum\limits_{i = k - d}^{k - 1} {x^{T} (i)Qx(i)} , \\ V_{3} (k) & = d\sum\limits_{i = - d}^{ - 1} {\sum\limits_{j = k + i}^{k - 1} {\eta^{T} (j)Z\eta (j)} } + \sum\limits_{i = k - d}^{k - 1} {x^{T} (i)Rx(i)} , \\ \eta (k) & = x(k + 1) - x(k). \\ \end{aligned} $$

(40)

Calculating the difference of $V(k)$ along the system (36), and taking the mathematical expectation, we have

$$ \begin{aligned} E\left\{ {\Delta V(k)} \right\} & \le E\left\{ {x^{T} (k)[ - P + Q + R + \lambda^{*} \rho_{1} I - Z]x(k) + 2x^{T} (k)Zx(k - d)} \right. \\ & \quad - x^{T} (k - d)(Q + Z + R - \lambda^{*} \rho_{2} I + \Gamma \Omega_{1} )x(k - d) \\ & \quad + 2x^{T} (k)[(A - I + NMK)^{T} P]\eta (k) + 2\eta^{T} (k)PCx(k - d) \\ & \quad + 2\eta^{T} (k)PBf(x(k)) + 2\eta^{T} (k)PDg(x(k - d)) + 2\eta^{T} (k)PGm(k) \\ & \quad - x^{T} (k)\psi \Lambda_{1} x(k) + 2x^{T} (k)\psi \Lambda_{2} f(x(k)) - f^{T} (x(k))\psi f(x(k)) \\ & \quad + 2x^{T} (k - d)\Gamma \Omega_{2} g(k - d) - g^{T} (k - d)\Gamma g(k - d) \\ & \quad + \eta^{T} (k)[d^{2} Z - 2P]\eta (k) + \hat{\xi }^{T} (k)\hat{\zeta }^{T} (k)P\hat{\zeta }(k))\hat{\xi }(k) \\ & \quad + \varepsilon x^{T} (k)(E_{a}^{T} E_{a} )x(k) + 2\varepsilon x^{T} (k)(E_{a}^{T} E_{c} )x(k - d) \\ & \quad + 2\varepsilon x^{T} (k)(E_{a}^{T} E_{b} )f(x(k)) + 2\varepsilon x^{T} (k)(E_{a}^{T} E_{d} )g(x(k - d)) \\ & \quad + \varepsilon x^{T} (k - d)(E_{c}^{T} E_{c} )x(k - d) + 2\varepsilon x^{T} (k - d)(E_{c}^{T} E_{b} )f(x(k)) \\ & \quad + 2\varepsilon x^{T} (k - d)(E_{c}^{T} E_{d} )g(x(k - d)) + \varepsilon f^{T} (x(k))(E_{b}^{T} E_{b} )f(x(k)) \\ & \quad + 2\varepsilon f^{T} (x(k))(E_{b}^{T} E_{d} )g(x(k - d)) \\ & \quad + \left. {\varepsilon g^{T} (x(k - d))(E_{d}^{T} E_{d} )g(x(k - d)) - \varepsilon m^{T} (k)m(k)} \right\} \\ & = E\{ \hat{\xi }^{T} (k)\tilde{\varXi }_{ 1} (k)\hat{\xi }(k)\} + \hat{\xi }^{T} (k)\hat{\zeta }^{T} P\hat{\zeta }\hat{\xi }(k)\} , \\ \end{aligned} $$

where

$$ \begin{aligned} \hat{\zeta } & = \left[ {\begin{array}{*{20}c} {\bar{A}} & C & 0 & B & D & G \\ \end{array} } \right], \\ \hat{\xi }^{T} (k) & = [x^{T} (k),x^{T} (k - d),\eta^{T} (k),f^{T} (x(k)),g^{T} (x(k - d)),m(k)], \\ \end{aligned} $$

$$ \hat{\varXi } = \left[ {\begin{array}{*{20}c} {\tilde{\Theta }_{ 1 1} } & {\tilde{\Theta }_{ 12} } & {\tilde{\Theta }_{ 13} } & {\tilde{\Theta }_{ 1 4} } & {\tilde{\Theta }_{ 1 5} } & 0 \\ * & {\tilde{\Theta }_{ 2 2} } & {C^{T} P} & {\varepsilon E_{c}^{T} E_{b} } & {\Gamma \Omega_{2} + \varepsilon E_{b}^{T} E_{d} } & 0 \\ * & * & {\tilde{\Theta }_{ 3 3} } & {PB} & {PD} & {PG} \\ * & * & * & { - \psi + \varepsilon E_{b}^{T} E_{b} } & {\varepsilon E_{b}^{T} E_{d} } & 0 \\ * & * & * & * & { - \Gamma + \varepsilon E_{d}^{T} E_{d} } & 0 \\ * & * & * & * & * & { - \varepsilon I} \\ \end{array} } \right]. $$

From (36) and Schur complement, it follows that

$$ E\{ \Delta (V(x(k))\} \le 0. $$

The rest proofs are omitted as they are similar to the proof of Theorem 2.□.

4 Numerical Examples

In this section, numerical examples are given to demonstrate the high performance of the proposed approach.

Example 1

Consider the uncertain discrete-time neural networks system (1) with the following parameters:

$$ \begin{aligned} A & = \left[ {\begin{array}{*{20}c} { - 1. 1 5} & 0 \\ 0 & { - 0. 3} \\ \end{array} } \right],\quad B = \left[ {\begin{array}{*{20}c} { - 0.0 4} & {0. 02} \\ {0. 0 3} & { - 0. 1} \\ \end{array} } \right],\quad C = \left[ {\begin{array}{*{20}c} {0.0 5} & {0. 3 6} \\ { - 0.06} & {0.0 4} \\ \end{array} } \right],K = \left[ {\begin{array}{*{20}c} {0.2} & 0 \\ 0 & {0.3} \\ \end{array} } \right], \\ D & = \left[ {\begin{array}{*{20}c} {0.16} & { - 0.19} \\ {0.04} & {0.01} \\ \end{array} } \right],\quad G = \left[ {\begin{array}{*{20}c} {0.02} & 0 \\ 0 & { - 0.01} \\ \end{array} } \right],\quad N = \left[ {\begin{array}{*{20}c} {1.42} & { - 0.06} \\ 0 & {0.13} \\ \end{array} } \right],\;I = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right], \\ E_{a} & = \left[ {\begin{array}{*{20}c} {0.01} & 0 \\ { - 0.1} & { - 0.12} \\ \end{array} } \right],\;E_{b} = \left[ {\begin{array}{*{20}c} {1.1} & {0.1} \\ 0 & {0.03} \\ \end{array} } \right],\quad E_{d} = \left[ {\begin{array}{*{20}c} {0.1 3} & 0 \\ {0.0 1} & {0.2} \\ \end{array} } \right],\quad E_{c} = \left[ {\begin{array}{*{20}c} { - 0.23} & {0.36} \\ {0.15} & {0.01} \\ \end{array} } \right], \\ \end{aligned} $$

$$ \begin{aligned} \tau_{m} & = 2,\tau_{M} = 4 ,\quad \rho_{1} = 0. 0 1,\quad \rho_{2} = 0. 0 2,\quad \\ f_{1} (s) & = \tanh (0.6s),\quad f_{2} (s) = \tanh (0.4s),\quad g_{1} (s) = \tanh (0. 2s),\quad g_{2} (s) = \tanh (0. 6s). \\ \end{aligned} $$

We have $l_{1}^{ - } = 0,l_{1}^{ + } = 0. 6,l_{2}^{ - } = 0,l_{2}^{ + } = 0. 4,v_{1}^{ - } = 0,v_{1}^{ + } = 0.2,v_{2}^{ - } = 0,v_{2}^{ + } = 0. 6.$

Solving (26) and (27) gives feasible solutions as follows:

$$ \begin{aligned} Q_{1} & = \left[ {\begin{array}{*{20}c} { 5. 9 1 2 3} & { - 0. 4 2 5 8} \\ { - 0. 4 2 5 8} & { 7. 9 4 0 6} \\ \end{array} } \right],Q_{2} = \left[ {\begin{array}{*{20}c} { 4. 7 9 2 4 { }} & { - 0. 3 5 4 6} \\ { - 0. 3 5 4 6} & {{ 6} . 6 0 7 5 { }} \\ \end{array} } \right],Z = \, \left[ {\begin{array}{*{20}c} {{ 1} . 6 4 1 4} & { - 0. 0 3 6 2} \\ { - 0. 0 3 6 2} & {{ 6} . 7 1 7 9} \\ \end{array} } \right], \\ P & = \left[ {\begin{array}{*{20}c} {{ 70} . 3 2 3 8 { }} & { 4. 0 8 1 5} \\ {{ 4} . 0 8 1 5} & {{ 150} . 2 8 4 2} \\ \end{array} } \right], \, \psi = \left[ {\begin{array}{*{20}c} {{ 31} . 1 9 8 2} & 0\\ 0& { 3 2. 5 1 0 5} \\ \end{array} } \right],\Gamma = \left[ {\begin{array}{*{20}c} { 4 8. 6 0 9 5 { }} & 0\\ 0& { 3 2. 1 9 3 9} \\ \end{array} } \right], \\ T & = \left[ {\begin{array}{*{20}c} { 9. 5 8 1 0} & { 1. 0 1 0 3 { }} & {{ 5} . 0 0 9 6} & { - 0. 6 1 1 3} \\ { 1. 0 1 0 3} & { 3 2. 3 3 7 9} & { - 0. 6 1 1 3} & { 2 2. 3 3 8 2} \\ {{ 5} . 0 0 9 6} & { - 0. 6 1 1 3 { }} & {{ 13} . 4 1 6 3} & { - 1. 2 4 2 9} \\ { - 0. 6 1 1 3} & { 2 2. 3 3 8 2} & { - 1. 2 4 2 9} & { 5 8. 9 6 5 3} \\ \end{array} } \right],R = \left[ {\begin{array}{*{20}c} { 4. 7 9 2 4 { }} & { - 0. 3 5 4 6} \\ { - 0. 3 5 4 6} & {{ 6} . 6 0 7 5 { }} \\ \end{array} } \right] \\ \varPi & = \, \left[ {\begin{array}{*{20}c} {{ 105} . 0 4 2 8 { }} & { 2. 5 5 9 6} \\ { 2. 5 5 9 6} & { 9 7. 9 3 3 6} \\ \end{array} } \right],\quad \varepsilon = 6. 1 6 5 9,\quad \lambda^{*} = 1 6 3. 5 2 1 3.\\ \end{aligned} $$

The output feedback controller gain matrix is

$$ M = \, \left[ {\begin{array}{*{20}c} {{ 5} . 2 2 6 0 { }} & { 0. 7 0 2 7} \\ { - 0. 9 0 6 6} & { 1 6. 7 1 0 1} \\ \end{array} } \right]. $$

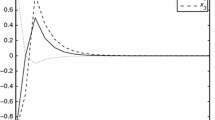
Therefore, it follows from Theorem 2 the closed-loop system (25) is robustly globally exponentially stable in the mean square. The state trajectory of closed-loop system is shown in Fig. 1.

Fig. 1

State trajectories of the closed-loop system in Example 1

Example 2

Consider the uncertain discrete-time system (1) with the following parameters:

$$ \begin{aligned} A & = \left[ {\begin{array}{*{20}c} {0. 4} & 0 & 0 \\ 0 & {0.2} & 0 \\ 0 & 0 & {0.45} \\ \end{array} } \right],\;B = \left[ {\begin{array}{*{20}c} {0.0 4} & {0. 2 5} & 0 \\ 0 & { - 0.0 1 5} & { - 0. 0 2} \\ {0. 1} & {0.0 2} & {0. 0 1} \\ \end{array} } \right],\;C = \left[ {\begin{array}{*{20}c} { 0. 0 2} & 0& 0\\ 0& { 0. 0 3} & { 0. 1} \\ 0& { 0. 0 5 5} & { - 0. 1} \\ \end{array} } \right] \\ N & = \left[ {\begin{array}{*{20}c} {0.07} & 0 & 0 \\ 0 & {0.08} & 0 \\ 0 & 0 & {0.02} \\ \end{array} } \right],\;D = \left[ {\begin{array}{*{20}c} 0 & {0.2} & {0.01} \\ {0.2} & {0.01} & {0.1} \\ {0.2} & { - 0.4} & { - 0.03} \\ \end{array} } \right],\;E_{a} = \left[ {\begin{array}{*{20}c} {0.01} & 0 & 0 \\ 0 & {0.01} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right], \\ E_{b} & = \left[ {\begin{array}{*{20}c} {0.01} & {0.03} & 0 \\ {0.02} & 0 & {0.1} \\ {0.01} & {0.02} & {0.2} \\ \end{array} } \right],\;E_{c} = \left[ {\begin{array}{*{20}c} {0.07} & 0 & 0 \\ 0 & {0.03} & 0 \\ {0.19} & {0.2} & {0.04} \\ \end{array} } \right],\;E_{d} = \left[ {\begin{array}{*{20}c} {0.02} & 0 & 0 \\ {0.02} & 0 & {0.24} \\ {0.2} & {0.1} & {0.03} \\ \end{array} } \right], \\ \end{aligned} $$

$$ \begin{aligned} G & = \left[ {\begin{array}{*{20}c} {0.026} & 0 & {0.06} \\ {0.11} & {0.023} & {0.1} \\ {0.3} & {0.03} & {0.14} \\ \end{array} } \right],\;\quad K = \left[ {\begin{array}{*{20}c} {0.2} & 0 & 0 \\ 0 & {0.1} & 0 \\ 0 & 0 & {1.2} \\ \end{array} } \right], \\ \tau_{m} & = 2,\;\tau_{M} = 4,\rho_{1} = 0.0 1,\;\rho_{2} = 0. 02,\; \\ f_{1} (s) & = \tanh (0.6s),f_{2} (s) = \tanh ( - 0.4s),f_{ 3} (s) = \tanh ( - 0. 2s), \\ g_{1} (s) & = \tanh ( - 0. 4s),g_{2} (s) = \tanh (0.2s),g_{ 3} (s) = \tanh (0. 4s). \\ \end{aligned} $$

We have

$$ \begin{aligned} l_{1}^{ - } & = 0,\;l_{1}^{ + } = 0. 6,\;l_{2}^{ - } = - 0. 4,\;l_{2}^{ + } = 0,\;l_{ 3}^{ - } = - 0. 2,\;l_{ 3}^{ + } = 0, \\ v_{1}^{ - } & = - 0. 4,\;v_{1}^{ + } = 0,\;v_{2}^{ - } = 0,\;v_{2}^{ + } = 0. 2,\;v_{3}^{ - } = 0,\;v_{3}^{ + } = 0. 4. \\ \end{aligned} $$

Solving (26) and (27) gives feasible solutions as follows:

$$ \begin{aligned} Q_{ 1} & = \left[ {\begin{array}{*{20}c} { 1. 0 2 3 0} & { - 0. 0 9 8 2} & { - 0. 1 5 1 1} \\ { - 0. 0 9 8 2} & { 0. 4 0 2 8} & { - 0. 0 6 0 6} \\ { - 0. 1 5 1 1} & { - 0. 0 6 0 6 { }} & { 0. 1 1 5 9} \\ \end{array} } \right],\quad Q_{ 2} = \left[ {\begin{array}{*{20}c} { 0. 7 0 5 2} & { - 0. 0 6 9 3} & { - 0. 1 0 6 5} \\ { - 0. 0 6 9 3} & {{ 0} . 3 0 5 4} & { - 0. 0 4 9 6} \\ { - 0. 1 0 6 5} & { - 0. 0 4 9 6 { }} & { 0. 0 8 6 2} \\ \end{array} } \right], \\ R & = \left[ {\begin{array}{*{20}c} { 0. 7 0 5 2} & { - 0. 0 6 9 3} & { - 0. 1 0 6 5} \\ { - 0. 0 6 9 3} & {{ 0} . 3 0 5 4} & { - 0. 0 4 9 6} \\ { - 0. 1 0 6 5} & { - 0. 0 4 9 6 { }} & { 0. 0 8 6 2} \\ \end{array} } \right],\quad Z = \left[ {\begin{array}{*{20}c} { 1. 6 2 8 2} & { - 0. 1 5 1 3} & { \, - 0. 2 2 1 1} \\ { - 0. 1 5 1 3} & { 0. 4 1 3 8} & { - 0. 0 3 2 3} \\ { \, - 0. 2 2 1 1} & { - 0. 0 3 2 3} & {{ 0} . 1 2 4 5} \\ \end{array} } \right], \\ \varPi & = \left[ {\begin{array}{*{20}c} { - 1. 8 9 2 9} & { - 0. 0 6 8 0} & { \, - 1. 1 3 4 4} \\ { - 0. 0 6 8 0} & { 3. 7 4 8 0} & { - 0. 1 7 3 6} \\ { \, - 1. 1 3 4 4} & { - 0. 1 7 3 6} & {{ 2} . 8 0 0 7} \\ \end{array} } \right],\quad \psi = \left[ {\begin{array}{*{20}c} { 3 2. 5 4 1 5} & 0& 0\\ 0& { 2 1. 5 8 8 5} & 0\\ 0& 0& { 2 1. 2 5 1 9} \\ \end{array} } \right], \\ \Gamma & = \left[ {\begin{array}{*{20}c} { 6 7. 5 7 1 9} & 0& 0\\ 0& { 1 2 9. 0 8 7 6} & 0\\ 0& 0& { 6. 5 8 0 3} \\ \end{array} } \right],\quad P = \left[ {\begin{array}{*{20}c} { 3 4. 3 9 4 8} & { 0. 8 2 6 8} & { 1. 7 8 9 1} \\ { 0. 8 2 6 8} & { 3 0. 3 3 7 8} & { - 1. 4 0 4 1} \\ { 1. 7 8 9 1} & { - 1. 4 0 4 1} & { 3 3. 0 2 3 6} \\ \end{array} } \right] \\ \end{aligned} $$

$$ \begin{aligned} T & = \left[ {\begin{array}{*{20}c} { 7. 3 5 5 4} & { 0. 3 0 4 4} & { 0. 3 0 3 3} & { 5. 0 2 9 4} & { - 0. 1 8 1 4} & { - 0. 5 7 2 2} \\ { 0. 3 0 4 4} & { 5. 7 8 9 7} & { - 0. 1 6 1 5} & { - 0. 1 8 1 4} & { 0. 5 7 4 5} & { - 0. 0 4 8 2} \\ { 0. 3 0 3 3} & { - 0. 1 6 1 5} & { 3. 2 9 5 6} & { - 0. 5 7 2 2} & { - 0. 0 4 8 2} & { 0. 2 0 4 0} \\ { 5. 0 2 9 4} & { - 0. 1 8 1 4} & { - 0. 5 7 2 2} & { 1 3. 6 4 8 9} & { - 0. 5 7 0 4} & { - 1. 5 4 0 3} \\ { - 0. 1 8 1 4} & { 0. 5 7 4 5} & { - 0. 0 4 8 2} & { - 0. 5 7 0 4} & { 1. 4 6 5 8} & { - 0. 0 7 8 9} \\ { - 0. 5 7 2 2} & { - 0. 0 4 8 2} & { 0. 2 0 4 0} & { - 1. 5 4 0 3} & { - 0. 0 7 8 9} & { 0. 5 2 6 3} \\ \end{array} } \right] \\ \varepsilon & = 9. 2 0 0 1,\quad \lambda^{*} = 3 6. 0 6 0 3.\\ \end{aligned} $$

The output feedback controller gain matrix is

$$ M = \left[ {\begin{array}{*{20}c} { - 3. 8 0 9 9 { }} & { - 0. 7 0 9 1} & { - 0. 3 3 8 3} \\ { - 0. 1 4 0 5} & { 1 5. 4 6 1 2} & { - 0. 0 9 1 9} \\ { - 7. 8 8 9 1 { }} & { 0. 1 3 5 3} & { - 3. 4 8 5 2} \\ \end{array} } \right], $$

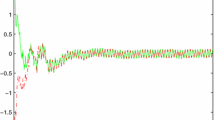
Therefore, it follows from Theorem 2 the closed-loop system is robustly globally exponentially stable in the mean square. The state trajectory of closed-loop system is shown in Fig. 2.

Fig. 2

State trajectories of the closed-loop system in Example 2

Example 3

Consider the uncertain discrete-time system (1) with the following parameters

$$ \begin{aligned} A & = \left[ {\begin{array}{*{20}c} {1.4} & 0 \\ 0 & {1. 3} \\ \end{array} } \right],B = \left[ {\begin{array}{*{20}c} { - 0.0 4} & {0. 02} \\ {0. 0 3} & { - 0. 1} \\ \end{array} } \right],C = \left[ {\begin{array}{*{20}c} {0.0 5} & {0. 3 6} \\ { - 0.06} & {0.0 4} \\ \end{array} } \right],D = \left[ {\begin{array}{*{20}c} {0.01} & { - 0.02} \\ {0.04} & {0.01} \\ \end{array} } \right], \\ G & = \left[ {\begin{array}{*{20}c} {0.02} & 0 \\ 0 & { - 0.01} \\ \end{array} } \right],N = \left[ {\begin{array}{*{20}c} {1.42} & { - 0.06} \\ {0.1} & {3.13} \\ \end{array} } \right],K = \left[ {\begin{array}{*{20}c} {0.2} & 0 \\ 0 & {0.3} \\ \end{array} } \right],E_{a} = \left[ {\begin{array}{*{20}c} {0.01} & 0 \\ { - 0.} & { - 0.12} \\ \end{array} } \right], \\ E_{b} & = \left[ {\begin{array}{*{20}c} {0.1} & {0.01} \\ 0 & {0.3} \\ \end{array} } \right],E_{d} = \left[ {\begin{array}{*{20}c} {0.0 3} & 0 \\ {0.0 1} & {0.02} \\ \end{array} } \right],E_{c} = \left[ {\begin{array}{*{20}c} { - 0.02} & {0.03} \\ {0.01} & {0.01} \\ \end{array} } \right],I = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right], \\ \end{aligned} $$

$$ f_{1} (s) = \tanh (0.06s),f_{2} (s) = \tanh (0.04s),\quad g_{1} (s) = \tanh (0.0 2s),g_{2} (s) = \tanh (0.0 6s), $$

$$\begin{aligned} &l_{1}^{ - } = 0,l_{1}^{ + } = 0. 6,l_{2}^{ - } = 0,l_{2}^{ + } = 0. 4,v_{1}^{ - } = 0,v_{1}^{ + } = 0.2,v_{2}^{ - } = 0,v_{2}^{ + } = 0. 6,\tau_{m} = 2,\\&\tau_{M} = 4 ,\rho_{1} = 0. 0 1,\rho_{2} = 0. 0 2. \end{aligned}$$

It is easy to know that the above discrete-time system with $u(k) = 0$ is unstable.

Solving (26) and (27) gives feasible solutions as follows:

$$ \begin{aligned} Q_{1} & = \left[ {\begin{array}{*{20}c} { 4. 1 5 1 7} & { - 0. 3 1 4 6} \\ { - 0. 3 1 4 6} & { 6. 6 8 9 0} \\ \end{array} } \right],\;Q_{2} = \left[ {\begin{array}{*{20}c} { 3. 3 3 1 9 { }} & { - 0. 2 5 5 6} \\ { - 0. 2 5 5 6} & {{ 4} . 8 7 3 3 { }} \\ \end{array} } \right],\;Z = \, \left[ {\begin{array}{*{20}c} {{ 2} . 7 6 9 0} & { - 0. 2 8 2 8} \\ { - 0. 2 8 2 8} & {{ 10} . 0 2 7 3} \\ \end{array} } \right], \\ \, P & = \left[ {\begin{array}{*{20}c} { 5 0. 4 6 8 6} & { 2. 5 4 7 6} \\ {{ 2} . 5 4 7 6} & {{ 154} . 2 7 3 1} \\ \end{array} } \right], \, \psi = \left[ {\begin{array}{*{20}c} {{ 33} . 5 3 4 5} & 0\\ 0& { 4 1. 7 2 5 9} \\ \end{array} } \right],\;\Gamma = \left[ {\begin{array}{*{20}c} { 3 3. 2 8 2 1 { }} & 0\\ 0& { 3 0. 8 6 3 9} \\ \end{array} } \right], \\ T & = \left[ {\begin{array}{*{20}c} { 7. 4 5 6 4} & { 0. 5 8 9 0 { }} & {{ 2} . 6 5 4 5} & { - 0. 6 7 6 5} \\ { 0. 5 8 9 0} & { 2 6. 1 4 6 4} & { - 0. 6 7 6 5} & { 1 9. 3 6 9 7} \\ {{ 2} . 6 5 4 5} & { - 0. 6 7 6 5 { }} & {{ 6} . 5 2 0 2 { }} & { - 1. 2 4 2 9} \\ { - 0. 6 7 6 5} & { 1 9. 3 6 9 7} & { - 1. 2 4 2 9} & { 5 1. 7 2 4 7} \\ \end{array} } \right],\;R = \left[ {\begin{array}{*{20}c} { 3. 3 3 1 9 { }} & { - 0. 2 5 5 6} \\ { - 0. 2 5 5 6} & {{ 4} . 8 7 3 3 { }} \\ \end{array} } \right], \\ \varPi & = \, \left[ {\begin{array}{*{20}c} { - 5 3. 0 5 3 3 { }} & { - 2. 5 6 8 0} \\ { - 2. 5 6 8 0} & { - 1 4 4. 9 0 1 3} \\ \end{array} } \right],\quad \varepsilon = { 0} . 1 6 4 2,\quad \lambda^{*} = 1 6 4. 5 9 3 5.\\ \end{aligned} $$

The output feedback controller gain matrix is

$$ M = \, \left[ {\begin{array}{*{20}c} { - 3. 6 9 6 5 { }} & { - 0. 0 5 0 3} \\ { 0. 1 1 9 2} & { - 0. 9 9 8 6} \\ \end{array} } \right]. $$

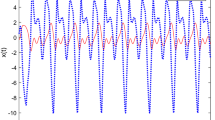
Therefore, it follows from Theorem 2 the closed-loop system is robustly globally exponentially stable in the mean square. The state trajectory of closed-loop system is shown in Fig. 3.

Fig. 3

State trajectories of the closed-loop system in Example 3

Example 4

Consider the uncertain discrete-time system (1) with the following parameters

$$ \begin{aligned} A & = \left[ {\begin{array}{*{20}c} {0.9} & 0 \\ 0 & {0.2 3} \\ \end{array} } \right],\;B = \left[ {\begin{array}{*{20}c} { - 0. 4} & {0. 0 1} \\ {0. 0 4} & { - 0. 1} \\ \end{array} } \right],\;C = \left[ {\begin{array}{*{20}c} {0.03} & {0. 0 6} \\ { - 0.06} & {0.0 4} \\ \end{array} } \right],\;D = \left[ {\begin{array}{*{20}c} {0.26} & { - 0.19} \\ {0.04} & {0.1} \\ \end{array} } \right], \\ G & = \left[ {\begin{array}{*{20}c} {0.02} & 0 \\ 0 & {0.01} \\ \end{array} } \right],N = \left[ {\begin{array}{*{20}c} { - 0.42} & { - 0.6} \\ 0 & {0.13} \\ \end{array} } \right],K = \left[ {\begin{array}{*{20}c} {0.2} & 0 \\ 0 & {0.3} \\ \end{array} } \right],\;E_{a} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right], \\ E_{b} & = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right],E_{d} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right],E_{c} = \left[ {\begin{array}{*{20}c} {0.13} & 0 \\ {0.01} & {0.2} \\ \end{array} } \right],\Lambda_{1} = \left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & 0 \\ \end{array} } \right],\Lambda_{2} = \left[ {\begin{array}{*{20}c} {0.2} & 0 \\ 0 & {0.3} \\ \end{array} } \right], \\ \Omega_{1} & = \left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & 0 \\ \end{array} } \right],\Omega_{2} = \left[ {\begin{array}{*{20}c} { 0. 3} & 0 \\ 0 & {0.1} \\ \end{array} } \right],I = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right],\;\rho_{1} = 0. 0 1,\rho_{2} = 0. 0 2, \\ \end{aligned} $$

$$ f_{1} (s) = \tanh (0.4s),f_{2} (s) = \tanh (0.6s),g_{1} (s) = \tanh (0.6s),g_{2} (s) = \tanh (0.2s). $$

For different values of $\tau_{m}$, we give the upper bounds $\tau_{M}$ of time-varying delay in Table 1, which guarantee the robust global exponential stability in the mean square of the system (25).

Table 1 Value of the upper bound $\tau_{M}$ for given $\tau_{m}$

5 Conclusion

In this paper, we investigate robust exponential stabilization for uncertain discrete-time stochastic neural networks with time-varying delay. Using the Lyapunov–Krasovskii functional approach, we propose the delay-dependent stabilization criteria to guarantee that the closed-loop system of a class of discrete-time stochastic neural networks with time-varying delays is asymptotical stable in the mean square. Then, we give sufficient conditions of robust global exponential stabilization for a class of discrete-time stochastic neural networks with time-varying delays via output feedback control. Finally, some examples are given to show the superiority of our proposed stability conditions.