New approaches to the robust 1-center location problems on tree networks

Abstract

This paper is concerned with the robust 1-center location problems on the tree networks under minmax and minmax regret criteria, where the vertex weights and edge lengths of the underlying tree are considered as dynamic data or discrete set of scenarios. In the problem under minmax criterion, the aim is to find a point on the tree such that it minimizes the maximum cost. The problem under minmax regret asks to find a point on the tree such that minimizes the maximum regret. We develop the first optimal solution algorithms with polynomial time complexities for the problems under investigation.

1 Introduction

Location problems have received strong theoretical interest due to their relevance in practice. In a location problem on the network, the aim is to find the best locations for establishing one or several facilities such that these facilities serve all clients on the network. One of the most important location problems is the p-center location problem, which has many applications in practice. In this problem the task is to find p locations for facilities which minimize the maximum of weighted distances of each customer to its closest facility.

The classical p-center location problem was first investigated by Hakimi (1965). Hakimi showed that this problem on general networks can not be solved in a polynomial time. Kariv and Hakimi (1979) proposed a combinatorial algorithm with $O(mn\log n)$ time complexity for the 1-center location problem on general graphs with m edges and n vertices. For the case that the underlying graph is a tree, they reduced this time to $O(n\log n)$. Megiddo designed a linear time algorithm for solving the 1-center location problem on trees (Megiddo 1983). Megiddo and Tamir also considered this problem in Megiddo and Tamir (1983) and proposed an $O(n\log ^3 n)$ time algorithm for the continuous p-center location problem on tree networks. Also, they presented an $O(n\log ^2 n\log \log n)$ time algorithm for a weighted discrete p-center location problem.

Kouvelis et al. introduced the idea of minmax and minmax regret approaches to obtain a robust solution of the 1-median problem (Kouvelis et al. 1993). These methods minimize the maximum cost of decision maker’s decision and maximum difference between the cost of decision-maker’s decision and the cost of optimal decision, respectively. In the minmax and minmax regret criteria on networks, vertex weights and edge lengths are uncertain, and this uncertainty can be consider as interval, discrete set of scenarios, dynamic, polyhedral, etc.

Averbakh showed that the minmax regret 1-center location problem on general graphs with interval edge lengths is NP-hard (Averbakh 2003). This problem on general graphs with uncertain vertex weights can be solved in a polynomial time. Averbakh and Berman considered the minmax regret 1-center location problem with interval vertex weights on general graphs and tree networks and presented combinatorial algorithms with $O(m^{2}n\log n)$ and $O(n^{2})$ running times, respectively (Averbakh and Berman 1997). Lin et al. improved these times to $O(mn\log n)$ and $O(n\log ^{2}n)$, respectively (Lin et al. 2006). The robust 1-center location problem on tree networks with interval vertex weights and edge lengths was solved in $O(n^{6})$ time by Averbakh and Berman (2000). They reduced this time to $O(n^{2}\log n)$ on un-weighted trees. Burkard and Dollani considered this problem and proposed combinatorial algorithms for the problem with $O(n^{3}\log n)$ and $O(n\log n)$ times on weighted trees and un-weighted trees, respectively (Burkard and Dollani 2002). Aloulou et al. (2005) presented an algorithm with $O(mn(\log n +\vert S\vert )\vert S\vert )$ time complexity for the robust 1-center location problem with uncertain vertex weights on general graphs and an algorithm with $O(n(n+\log n)\vert S\vert )$ time complexity with uncertain vertex weights on tree graphs, where the type of uncertainty is the discrete set of scenarios and S is the set of scenarios.

Bhattacharya et al. proposed algorithms with O(n) , $O(n\log n)$ and $O(n\log ^{2}n)$ times for the minmax regret 1-center location problem on path, cycle and tree networks with interval vertex weights, respectively (Bhattacharya et al. 2012). Also, Bhattacharya et al. considered the minmax regret 1-center location problem on tree, unicycle and cactus graphs with interval vertex weights and obtained algorithms with $O(n\log n)$, $O(n\log n)$ and $O(n\log ^{2}n)$ on these graphs, respectively (Bhattacharya et al. 2015). This problem on cactus networks with c cycles solved in Bhattacharya et al. (2014).

In this paper, we consider the robust vertex and absolute 1-center location problems on the tree networks. We use the minmax and minmax regret criteria for obtaining the robust solution. The vertex weights and the edge lengths of the tree network are considered as dynamic data and discrete set of scenarios. These problems have not been investigated up to now with these types of data for the vertex weights and edge lengths. This paper is organized as follows. Section 2 introduces the basic definitions, preliminaries and reviews some facts that are used throughout the paper. In Sect. 3, we consider the robust vertex 1-center location problem on dynamic tree networks with minmax criterion and present a polynomial time algorithm for this problem. In Sect. 4, we solve this problem with minmax regret criterion in a polynomial time. In Sects. 5 and 6, we consider the robust absolute 1-center location problem on the dynamic tree networks and solve this problem under minmax and minmax regret criteria, respectively. Section 7 considers the robust 1-center location problem on tree networks with discrete set of scenarios for vertex weights and edge lengths. Finally, we present the concludes of paper in Sect. 8.

2 Problem statement

Let $T=(V, E)$ be a tree network with vertex set $V=\left\{ v_{1}, \ldots , v_{n} \right\}$ and edge set E. Each vertex $v \in V$ is associated with a weight $w_{i}$ and each edge e is associated with a non-negative length $l_{e}$. Notice that the negative weights are allowed for vertices of tree T. For all $x, y \in T$, let d(x, y) be the length of shortest path between x, y. The classical absolute (vertex) 1-center location problem wants to find $x \in T$ ($x\in V$) such that it minimizes the following objective function:

$$\begin{aligned} f(x)=\max _{i=1,\ldots , n} w_{i}d(v_{i}, x) \end{aligned}$$

(1)

in Kariv and Hakimi (1979) showed that $d(v_{i}, x)$, $x\in e$ on general graphs is a linear function or contains two linear functions. Therefore f(x) is a piecewise linear and continuous function on each edge e on the graph. They used this property and solved the classical 1-center location problem on general graphs and tree networks. The following Lemma is a conclusion of their article.

Lemma 2.1

(Kariv and Hakimi 1979) An optimal solution of the classical absolute 1-center location problem on the tree network is obtained in $O(n\log n)$ time.

Dearing and Francis considered the center location problem on networks and obtained some properties of this problem (Dearing and Francis 1974). We use one of these results, i.e., Lemma 2.1 in this paper.

Lemma 2.2

(Dearing and Francis 1974) The optimal value of the classical absolute 1-center location problem equals to

$$\begin{aligned} \max _{ 1\le i, j\le n}\dfrac{w_{i}w_{j}d(v_{i}, v_{j})}{w_{i}+w_{j}}. \end{aligned}$$

Also, if

$$\begin{aligned} \dfrac{w_{i^{*}}w_{j^{*}}d(v_{i^{*}}, v_{j^{*}})}{w_{i^{*}}+w_{j^{*}}}= \max _{ 1\le i, j\le n}\dfrac{w_{i}w_{j}d(v_{i}, v_{j})}{w_{i}+w_{j}}, \end{aligned}$$

then $x^{*}$ is an absolute 1-center location, where

$$\begin{aligned} d(x^{*}, v_{i^{*}})=\frac{w_{j^{*}}d(v_{i^{*}}, v_{j^{*}})}{w_{i^{*}}+w_{j^{*}}}. \end{aligned}$$

In the real-life problems, the input data are not characterized precisely and many factors have effect on these parameters. Therefore, the input data of problems may be uncertain. In the robust optimization problems, this uncertainty is considered as interval data, discrete set of scenarios, dynamic data and etc.

In the next sections, the vertex and absolute 1-center location problems are investigated such that these problems contains dynamic data and discrete set of scenarios. First we introduce the robust 1-center location problem under general uncertainty. Consider tree network T. Suppose that the weight of vertices and length of edges in T are uncertain. Let S represents the set of all realizations of the vertex weights and edge lengths. This set is called the set of scenarios and each $s\in S$ is a scenario. The classical 1-center location problem under scenario $s\in S$ is defined as

$$\begin{aligned} \min _{x\in T} (\min _{x\in V}) f(x, s), \end{aligned}$$

in which

$$\begin{aligned} f(x, s)=\max _{i=1,\ldots , n}w_{i}^{s}d^{s}(v_{i}, x). \end{aligned}$$

The robust 1-center location problem on uncertain trees can be consider under two criteria, i.e. minmax criterion (worst case criterion) and minmax regret criterion (robust deviation and relative robustness). The first one selects a point on tree T such that it minimizes the maximum value of the objective function on all scenarios. If we use this criterion for absolute (vertex) 1-center location problem, then we have the following formulation:

$$\begin{aligned} \min _{x \in T}(\min _{x\in V}) \max _{s \in S} f(x, s). \end{aligned}$$

(2)

The optimal solution of this problem is called absolute robust solution. If the difference between f(x, s) and $f(x^{*}, s)$ is considered by R(x, s) for all $x \in T$ and $s \in S$, i.e. $R(x, s)=f(x, s) - f(x^{*}, s)$, then the robust deviation criterion for the absolute (vertex) 1-center location problem is defined as follows:

$$\begin{aligned} \min _{x \in T}(\min _{x\in V}) \max _{s \in S} R(x, s). \end{aligned}$$

(3)

Furthermore, the relative robustness criterion for the described problem is defined as

$$\begin{aligned} \min _{x \in T}(\min _{x\in V}) \max _{s \in S} \dfrac{R(x, s)}{f(x^{*},s)}. \end{aligned}$$

(4)

In the deviation and relative robustness the regret for a specific location is computed by calculating either the difference or the ratio between the maximum transportation cost of the specific location under a scenario and the maximum transportation cost of the optimal location for this scenario.

3 Dynamic robust vertex 1-center location problem with minmax criterion

Suppose that the vertex weights and the edge lengths of tree T are linear functions of parameter t and t varying in the interval $\left[ l, u\right]$. Assume that the weight of vertex $v_{i}$ equals to $w_{i}(t)=a_{i}t+b_{i}$, $1\le i\le n$, and the length of edge e equals to $l_{e}(t)=a_{e}t+b_{e}$, $e \in E$ with $l_{e}(t)>0$ for any value of t on interval $\left[ l, u\right]$. Notice that the vertex weights are allowed to become negative. The dynamic robust vertex 1-center location problem under the minmax criterion is formulated as follows:

$$\begin{aligned} \min _{x\in V}\max _{t\in \left[ l,u\right] }f(x,t), \end{aligned}$$

(5)

where

$$\begin{aligned} f(x,t)=\max _{i=1,..., n}w_{i}(t)d^{t}(x,v_{i}). \end{aligned}$$

According to the definition of vertex weights and edges lengths, we can rewrite f(x, t) at given vertex x as follows:

$$\begin{aligned} f(x, t)&= \max _{i = 1, \ldots , n} w_{i}(t)d^{t}(x,v_{i}) \\&= \max _{i = 1, \ldots , n}\left( a_{i}t + b_{i}\right) \left( \left( \sum _{e \in E(P_{i})} a_{e}\right) t + \sum _{e \in E(P_{i})} b_{e} \right) \\&= \max _{i = 1, \ldots , n}\left( A_{i}t^{2} + B_{i}t + C_{i}\right) , \end{aligned}$$

where $P_{i}$ is the unique path between x and $v_{i}$, $A_{i}=a_{i}(\sum _{e \in E(P_{i})} a_{e})$, $B_{i} =(a_{i}(\sum _{e \in E(P_{i})} b_{e})+b_{i}(\sum _{e \in E(P_{i})} a_{e}))$ and $C_{i}=b_{i}(\sum _{e \in E(P_{i})} b_{e})$. If we define $f_{i}(t)=A_{i}t^{2}+B_{i}t+C_{i}$, $i=1,\ldots \ldots , n$, then

$$\begin{aligned} f(x,t)=\max _{i = 1, \ldots , n} f_{i}(t). \end{aligned}$$

The functions $f_{i}(t)$, $i=1,\ldots , n$ have the following properties:

• 1. $f_{i}(t)$ is a continuous function on interval $\left[ l, u\right]$.

• 2. $f_{i}(t)$ is a totally defined on interval $\left[ l, u\right]$.

• 3. $f_{i}(t)$ is a univariate function. Also, for each $1\le i\ne j \le n$, $f_{i}(t)$ and $f_{j}(t)$ intersect in at most two points.

Consequently, for all $x \in V$, f(x, t) is the upper envelope of n continuous, totally defined and univariate functions which each pair of them intersect at most two points. Therefore, f(x, t) is a continuous piecewise function such that each piece of it is either a quadratic function or linear function (see Fig. ). If we want to obtain an optimal solution for (5) first, we must compute f(x, t) on interval $\left[ l, u\right]$, for every vertex $x\in V$. For this purpose, we can use the following Lemma, which it has been proven in Agarwal et al. (1996), because $f_{i}(t)$, $1\le i\le n$ satisfy in the conditions of Lemma 3.1.

Lemma 3.1

(Agarwal et al. 1996) Let ${\mathcal {F}}=\left\{ f_{1}, f_{2}, \ldots , f_{n}\right\}$ be a collection of n continuous, totally defined and univariate functions that each pair of them intersect in at most s points. Then, the total pieces of upper envelope of these n functions are equal to $\lambda _{s}(n)$.

The value of $\lambda _{s}(n)$ can be calculated using the following theorem, which is described in Agarwal et al. (1996).

Fig. 1

The upper envelope of functions $f_{1}, f_{2}, f_{3}$

Theorem 3.2

(Agarwal et al. 1996) Let n be the number of univariate and continuous functions. Then we have

• i. $\lambda _{1}(n)=n$,

• ii. $\lambda _{2}(n)=2n-1$,

• iii. $\lambda _{3}(n)=O(n\alpha (n) )$

in which $\alpha (n)$ is the inverse of Ackerman’s function.

For more information about Ackerman’s function, see Ackermann (1928). According to Lemma 3.1 and Theorem 3.2, for each vertex $v\in V$, the number of pieces for the piecewise function f(x, t) on the interval $\left[ l,u\right]$ is $O(\lambda _{2}(n))=O(n)$. Suppose that this number is denoted by m. In Agarwal et al. (1996), a method is presented that explains how to calculate these pieces and their corresponding intervals with required time complexity. The important results of this method are mentioned in the following two theorems.

Theorem 3.3

(Agarwal et al. 1996) The upper envelope of an arbitrary collection contains n continuous, totally defined and univariate functions that each pair of them intersect in at most s points, can be constructed in $O(\lambda _{s}(n)\log n)$ time.

We use from Theorem 3.3 and the proposed method presented in its proof to compute the pieces of function f(x, t) as follows. For a given vertex $x \in V$, let $\left\{ i_{1}, \ldots ,i_{m} \right\}$ be a permutation of the index of $\left\{ f_{1}(t), \ldots , f_{n}(t)\right\}$ such that

$$\begin{aligned} f(x,t)=&f_{i_{1}}(t),~~~~~~\forall t\in I_{1}=[t_{0},t_{1}],\\ f(x,t)=&f_{i_{2}}(t),~~~~~~ \forall t\in I_{2}=[t_{1},t_{2}],\\ \vdots&\\ f(x,t)=&f_{i_{m}}, ~~~~~~~~~\forall t \in I_{m}=[t_{m-1}, t_{m}], \end{aligned}$$

where $[l,u]=\bigcup _{j=1}^{m}I_{j}$. The used process is described in Example 3.6. After calculating the upper envelope and breakpoints, we must find the points that maximize the each piece of upper envelope.

If the first derivative of the function $f_{i_{j}}$ is denoted by $f^{'}_{i_{j}}$, then one of the points that this function obtains its maximum, is $t_{j}^{*}$ such that, $f^{'}_{i_{j}}(t_{j}^{*})=0$. Point $t_{j}^{*}$ is called a critical point of $f^{'}_{i_{j}}(t)$. For example, if $f(t)=at^{2}+bt+c$, then

$$\begin{aligned} f^{'}(t)=0 \Rightarrow 2at+b=0 \Rightarrow t^{*}=-b/2a. \end{aligned}$$

However, we know that the maximum of $f_{i_{j}}(t)$ on interval $I_{j}$ is achieved at $t=t_{j-1}$ or $t=t_{j}$. If $t_{j-1}\le t_{j}^{*}\le t_{j}$, then we get the following theorem.

Theorem 3.4

For a given vertex x on tree T, the value of objective function of the robust vertex $1-$center location problem with minmax criterion is obtained as

$$\begin{aligned} \max _{l\le t\le u}f(x,t)=\max \{&f_{i_{1}}(x,t_{0}), f_{i_{1}}(x,t_{1}^{*}),f_{i_{1}}(x,t_{1}),\ldots ,\\&f_{i_{m}}(x,t_{m-1}),f_{i_{m}}(x,t_{m}^{*}),f_{i_{m}}(x,t_{m})\} . \end{aligned}$$

Thus, $\max _{l\le t\le u}f(x,t)$ is equivalent to choosing the largest member of a set with O(n) members. This selection is performed in linear time. Consequently, for a vertex x on tree T, $\max _{l\le t\le u}f(x,t)$ is calculated in $O(n\log n)$ time. If these operations are repeated for all vertices of tree T, then we get the following Lemma.

Lemma 3.5

An optimal solution for the dynamic robust vertex 1-center location problem under minmax criterion on tree networks with linear vertex weights and linear positive edge lengths can be computed in $O(n^{2}\log n)$ time.

Example 3.6

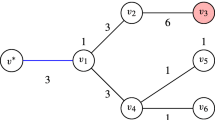
Consider the given tree network in Fig. with dynamic edge lengths and dynamic vertex weights.

Fig. 2

The tree network of Example 3.6

Assume that the vertex weights and edge lengths are given in Table . Using Theorem 3.3, we can obtain maps of f(x, t) on interval $[-1, 3]$ for each $x\in \lbrace v_{1}, v_{2}, ..., v_{6}\rbrace$. These computed maps are given in Table . For example, we explain how to calculate f(x, t) for $x=v_1$ on interval $[-1, 3]$. First we compute $f_{i}(v_1, t)$ for $i=1,..., 6$. We set

$$\begin{aligned} {\mathcal {F}}=\lbrace 0, 12t+20, 3t^{2}-3, 8t^{2}+12t+4, 12t+15, 6t+6\rbrace . \end{aligned}$$

Then we partition set ${\mathcal {F}}$ into two sets ${\mathcal {F}}_{1}$ and ${\mathcal {F}}_{2}$ such that $\vert {\mathcal {F}}_{i}\vert \le 3$, $i=1, 2$. We calculate the breakpoints of all functions in set ${\mathcal {F}}_{i}$, $i=1,2$ and we put all these points in set $V=\lbrace -1, 0.25, 1, \frac{\sqrt{352}}{16}, 3\rbrace$ so that $v_i \le v_i+1$ for $i=1, ..., t-1$. There are functions $f_{i}^{(1)}\in {\mathcal {F}}_{1}$ and $f_{i}^{(2)} \in {\mathcal {F}}_{2}$ that have the highest value on the interval $\left[ v_i , v_i+1\right]$, for $i=1,..., t-1$. In this example, $f_{i}^{(1)}=12t+20$ and $f_{i}^{(2)}= 12t+15$ for $i=1,..., t-1$. Next, we find the roots of $f_{i}^{(1)}-f_{i}^{(2)}$ on interval $\left[ v_i , v_i+1\right]$. We add these roots to set V and call the new set $V^{'}=\lbrace v^{'}_1 , ..., v^{'}_{t^{'}} \rbrace$. Here, $V^{'}=V$. It is clear that for $i=1, ..., t^{'}$, there is a unique function $f_i \in {\mathcal {F}}$ such that $f(v_1 , t)=f_i$ on interval $\left[ v^{'}_i , v^{'}_{i+1} \right]$ for $i=1, ..., t^{'}$. Here, $f_i =12t+20$, for $i=1,..., t-1$. Therefore, $f(v_1 ,t)=12t+20$ on interval $\left[ -1, 3\right]$.

Table 1 The data of dynamic tree

As a result, a robust solution of the robust vertex 1-center location problem with minmax criterion is obtained as

$$\begin{aligned}&\min _{x\in \lbrace v_1 , ..., v_6 \rbrace }\max _{t\in \left[ -1, 3\right] }f(x,t)=\min \{f(v_1 ,-1), f(v_1 ,3), f(v_2 , -1), f\left( v_2 , \frac{-15+\sqrt{477}}{18}\right) ,\\&\quad f(v_2 , 3), f(v_3 , -1), f(v_3 , \frac{1}{3}), f(v_3 , 3), f(v_4 , -1), f\left( v_4 , \frac{-3+\sqrt{33}}{6}\right) , f(v_4 , 3),\\&\quad f(v_5 , -1), f\left( v_5 , \frac{-19+\sqrt{753}}{24}\right) , f(v_5 , 3), f(v_6 , -1),\\&\quad f\left( v_6 , \frac{-12+\sqrt{1152}}{32}\right) , f(v_6 , 3)\} =f(v_5 , 3). \end{aligned}$$

Then $v_5$ is a location of robust vertex 1-center location on described tree.

Table 2 The values of f(x, t)

4 Dynamic robust vertex 1-center location problem with minmax regret criterion

In this section, we use the minmax regret criterion to obtain a robust solution of the vertex 1-center location problem on tree networks with dynamic edge lengths and dynamic vertex weights. Suppose that the vertex weights and the edge lengths of tree T are the linear functions of parameter t. Using these assumptions, the minmax regret vertex 1-center location problem is written as follows:

$$\begin{aligned} \min _{x\in V}\max _{t\in [l,u]}(f(x,t)-f(x^{*},t)), \end{aligned}$$

(6)

where

$$\begin{aligned} f(x^{*},t)=\min _{y\in V}f(y,t). \end{aligned}$$

Therefore, we can rewrite the minmax regret vertex 1-center location problem as

$$\begin{aligned} \min _{x\in V}\max _{y\in V}\max _{t\in [l,u]}(f(x,t)-f(y,t)). \end{aligned}$$

(7)

Now we wants to find a vertex such ${\bar{x}}$ on tree T so that it minimizes this function:

$$\begin{aligned} \max _{y\in V(T)}\max _{t\in [l,u]}(f({\bar{x}},t)-f(y,t)). \end{aligned}$$

Averbakh (2003) proved that the robust 1-center location problem with minmax regret criterion on general networks is NP-hard, if the edge lengths be as interval. Moreover, he proved that this problem can be solved on tree networks in a polynomial time (Averbakh and Berman 2000).

Lemma 4.1

The minmax regret 1-center location problem on general networks with dynamic edge lengths is NP-hard.

Proof

The length of edges are linear functions. Therefore, the length of edge $e\in E$ is belong to interval $\left[ l_{e}(l), l_{e}(u) \right]$. $\square$

Assume that for $x \in e=(u,v)$ the ratio

$$\begin{aligned} \dfrac{d^{t}(x,v)}{l_{e}(t)} \end{aligned}$$

remains constant for every $t \in [l,u]$. For every vertex x and y on tree T, we know that $f(x,t)=\max _{1\le i\le n}f_{i}(x,t)$ and $f(y,t)=\max _{1\le i\le n}f_{i}(y,t)$, where $f_{i}(x,t)=A_{xi}t^{2}+B_{xi}t+C_{xi}$ and $f_{i}(y,t)=A_{yi}t^{2}+B_{yi}t+C_{yi}$. Notice that $A_{xi}, A_{yi}$, $B_{xi}, B_{yi}$ and $C_{xi}, C_{yi}$ are defined similar to $A_{i}$, $B_{i}$ and $C_{i}$ introduced in Sect. 3. Now to calculate the robust solution, $f(x,t) - f(y,t)$ must be computed for each pair of vertices x and y. This is done as the following two steps.

Step 1. For every $x\in V$, compute the upper envelope of the functions

$$\begin{aligned} f_{i}(x,t)=A_{xi}t^{2}+B_{xi}t+C_{xi} , ~~~ 1\le i\le n \end{aligned}$$

using the presented method in Theorem 3.2. Notice that for each $x\in V$ and $i\in \left\{ 1,... , n\right\}$, $f_{i}(x,t)$ is an univariate, continuous and totally defined function on all points of interval $\left[ l, u\right]$, also, $f_{i}(x,t)$ is a quadratic or linear function. Then for each pair $i, j \in \left\{ 1,... , n\right\}$, $i\ne j$, the graph of $f_{i}(x,t)$ and $f_{j}(x,t)$ cut each other off at most in two points. The time complexity of computing the upper envelope for a given vertex is $O(n\log n)$. Consequently, for all vertices, this time increases to $O(n^{2}\log n)$.

Step 2. This step computes $f(x,t)-f(y,t)$ for all $x,y\in V$ . Suppose that $\left\{ x1, x2,...,xm_{x}\right\}$ and $\left\{ y1, y2,...,ym_{y}\right\}$ are permutations of $\left\{ 1, 2, ..., n\right\}$ such that

$$\begin{aligned} f(x,t)=&f_{x1}(x,t), ~~~\forall t\in [l, t_{x1}],\\ f(x,t)=&f_{x2}(x,t), ~~~\forall t\in [t_{x1}, t_{x2}],\\&.\\&.\\&.\\ f(x,t)=&f_{xm_{x}+1}(x,t), ~~~\forall t\in [t_{xm_{x}},u]. \end{aligned}$$

and

$$\begin{aligned} f(y,t)=&f_{y1}(y,t), ~~~\forall t\in [l, t_{y1}],\\ f(y,t)=&f_{y2}(y,t), ~~~\forall t\in [t_{y1}, t_{y2}],\\&.\\&.\\&.\\ f(y,t)=&f_{ym}(y,t), ~~~\forall t\in [t_{ym_{y}},u]. \end{aligned}$$

Notice that $m=\lambda _{2}(n)$. Now we want to characterize $f(x,t)-f(y,t)$ on interval $\left[ l, u\right]$. Let ${\bar{t}}_{i} =\min \left\{ t_{xi}, t_{yi}\right\}$, $m_x$ be the number of breakpoints of f(x, t) and $m_y$ be the number of breakpoints of f(y, t) . Also, assume that $k=\min \{m_x ,m_y\}$.

Lemma 4.2

If $t \in \left[ {\bar{t}}_{0}, {\bar{t}}_{1}\right]$, then $f(x,t)-f(y,t)=f_{x1}(x,t)-f_{y1}(y,t)$.

Proof

For every $t\in \left[ {\bar{t}}_{0}, t_{x1}\right]$, $f(x,t)=f_{x1}(x,t)$ and for every $t\in \left[ {\bar{t}}_{0}, t_{y1}\right]$, $f(y,t)=f_{y1}(y,t)$. By considering ${\bar{t}}_{1}$ is less than $t_{y1}$, the desired goal can be concluded. $\square$

Lemma 4.3

For $i=1,..., k-1$, we have

• 1. If ${\bar{t}}_{i}=t_{xi}$ and $t_{yi} \le {\bar{t}}_{i+1},$ then for every $t\in [{\bar{t}}_{i}, t_{yi}]$,

  $$\begin{aligned} f(x,t)-f(y,t)=f_{xi+1}(x,t)-f_{yi}(y,t) \end{aligned}$$

  and for every $t\in [ t_{yi}, {\bar{t}}_{i+1}]$,

  $$\begin{aligned} f(x,t)-f(y,t)=f_{xi+1}(x,t)-f_{yi+1}(y,t). \end{aligned}$$

• 2. If ${\bar{t}}_{i}=t_{xi}$ and $t_{yi} > {\bar{t}}_{i+1},$ then for every $t\in [{\bar{t}}_{i}, {\bar{t}}_{i+1}]$,

  $$\begin{aligned} f(x,t)-f(y,t)=f_{xi+1}(x,t)-f_{yi}(y,t) \end{aligned}$$

• 3. If ${\bar{t}}_{i}=t_{yi}$ and $t_{xi} \le {\bar{t}}_{i+1},$ then for every $t\in [{\bar{t}}_{i}, t_{xi}]$,

  $$\begin{aligned} f(x,t)-f(y,t)=f_{xi}(x,t)-f_{yi+1}(y,t) \end{aligned}$$

  and for every $t\in [ t_{xi}, {\bar{t}}_{i+1}]$,

  $$\begin{aligned} f(x,t)-f(y,t)=f_{xi+1}(x,t)-f_{yi+1}(y,t). \end{aligned}$$

• 4. If ${\bar{t}}_{i}=t_{yi}$ and $t_{xi} > {\bar{t}}_{i+1},$ then for every $t\in [{\bar{t}}_{i}, {\bar{t}}_{i+1}]$,

  $$\begin{aligned} f(x,t)-f(y,t)=f_{xi}(x,t)-f_{yi+1}(y,t) . \end{aligned}$$

Proof

Case 1 can be proved as follows. For every $t\in \left[ t_{xi}, t_{xi+1}\right]$, $f(x,t)=f_{xi+1}(x,t)$ and for every $t\in \left[ t_{yi}, t_{yi+1}\right]$, $f(y,t)=f_{yi+1}(y,t)$. If ${\bar{t}}_{i}=t_{xi}$ and $t_{yi}\le {\bar{t}}_{i+1}$, then on interval $\left[ {\bar{t}}_{i}, t_{yi}\right]$, $f(x,t)=f_{xi+1}(x,t)$ and $f(y,t)=f_{yi}(y,t)$. Therefore,

$$\begin{aligned} f(x,t)-f(y,t)=f_{xi+1}(x,t)-f_{yi}(y,t) . \end{aligned}$$

Also, for every $t\in \left[ t_{yi},{\bar{t}}_{i+1}\right]$, $f(x,t)=f_{xi+1}(x,t)$ and $f(y,t)=f_{yi+1}(y,t)$. Then

$$\begin{aligned} f(x,t)-f(y,t)=f_{xi+1}(x,t)-f_{yi+1}(y,t) . \end{aligned}$$

The other cases can be proved in an analogous way as Case 1. $\square$

Now based on Lemma 4.2 and Lemma 4.3 we get the following algorithm.

Algorithm 1: Find $f(x,t)-f(y,t)$ for each given pairs of vertices x, y.

• 1. For every $t \in \left[ {\bar{t}}_{0}, {\bar{t}}_{1}\right]$, set

  $$\begin{aligned} f(x,t)-f(y,t)=f_{x1}(x,t)-f_{y1}(y,t). \end{aligned}$$

• 2. Set $i=1$.

• 3. Repeat the following steps for $1\le i\le k$ :

• 4. If ${\bar{t}}_{i}=t_{xi}$ and $t_{yi} \le {\bar{t}}_{i+1},$ then for every $t\in [{\bar{t}}_{i}, t_{yi}]$ set

  $$\begin{aligned} ~~~~f(x,t)-f(y,t)=f_{xi+1}(x,t)-f_{yi}(y,t), \end{aligned}$$

  and for every $t\in [ t_{yi}, {\bar{t}}_{i+1}]$ set

  $$\begin{aligned} ~~~~f(x,t)-f(y,t)=f_{xi+1}(x,t)-f_{yi+1}(y,t). \end{aligned}$$

• 5. If ${\bar{t}}_{i}=t_{xi}$ and $t_{yi} > {\bar{t}}_{i+1},$ then for every $t\in [{\bar{t}}_{i}, {\bar{t}}_{i+1}]$ set

  $$\begin{aligned} ~~~~f(x,t)-f(y,t)=f_{xi+1}(x,t)-f_{yi}(y,t), \end{aligned}$$

• 6. If ${\bar{t}}_{i}=t_{yi}$ and $t_{xi} \le {\bar{t}}_{i+1},$ then for every $t\in [{\bar{t}}_{i}, t_{xi}]$ set

  $$\begin{aligned} ~~~~f(x,t)-f(y,t)=f_{xi}(x,t)-f_{yi+1}(y,t), \end{aligned}$$

  and for every $t\in [ t_{xi}, {\bar{t}}_{i+1}]$ set

  $$\begin{aligned} ~~~~f(x,t)-f(y,t)=f_{xi+1}(x,t)-f_{yi+1}(y,t). \end{aligned}$$

• 7. If ${\bar{t}}_{i}=t_{yi}$ and $t_{xi} > {\bar{t}}_{i+1},$ then for every $t\in [{\bar{t}}_{i}, {\bar{t}}_{i+1}]$ set

  $$\begin{aligned} ~~~~f(x,t)-f(y,t)=f_{xi}(x,t)-f_{yi+1}(y,t), \end{aligned}$$

• 8. Set $i=i+1$ and go to 3.

These steps are repeated until the function $f(x,t)-f(y,t)$ are specified over the entire interval $\left[ l, u\right]$. In an iteration of Algorithm 1, the total time complexity is a constant value. Thus, we can conclude the following lemma.

Lemma 4.4

For the given vertices x and y on tree T, the function $f(x,t)-f(y,t)$ on interval $\left[ l, u\right]$ is computed in a linear time. Moreover, the maximum value of this function occurs at one of the breakpoints.

Proof

The functions f(x, t) and f(y, t) are piecewise linear or quadratic functions, where are computed in Step 1. Therefore $f(x,t)-f(y,t)$ is also a piecewise linear or quadratic function. According to Theorem 3.3 maximum and minimum point of this function is obtained in its breakpoints. Therefore,

$$\begin{aligned}&\max _{t\in [l, u]}(f(x,t)-f(y,t))\\ {}&\quad =\max _{1\le i\le m} \left\{ f_{xi-1}(x,t_{xi-1})-f_{yi}(y,t_{xi-1}), f_{xi}(x,t_{xi-1})\right. \\ {}&\qquad \quad -f_{yi-1} (y,t_{xi-1}), f_{xi}(x,t_{xi-1})-f_{yi}(y,t_{xi-1}), f_{xi-1}(x,t_{xi-1})\left. \right. \\ {}&\qquad \quad -f_{yi-1}(y,t_{xi-1}),f_{xi-1}(x,t_{xi}) -f_{yi}(y,t_{xi}),f_{xi}(x,t_{xi})-f_{yi-1}(y,t_{xi}), f_{xi}(x,t_{xi})\left. \right. \\ {}&\qquad \quad -f_{yi}(y,t_{xi}), f_{xi-1}(x,t_{xi}) -f_{yi-1}(y,t_{xi}), f_{xi-1}(x,t_{yi-1}) \left. \right. \\ {}&\qquad \quad -f_{yi}(y,t_{yi-1}), f_{xi}(x,t_{yi-1}) -f_{yi-1} (y,t_{yi-1}), f_{xi}(x,t_{yi-1})\left. \right. \\ {}&\qquad \quad -f_{yi}(y,t_{yi-1}), f_{xi-1}(x,t_{yi-1})-f_{yi-1}(y,t_{yi-1}), f_{xi-1}(x,t_{yi})\left. \right. \\ {}&\qquad \quad -f_{yi}(y,t_{yi}), f_{xi}(x,t_{yi}) -f_{yi-1}(y,t_{yi}), f_{xi} (x, t_{yi})-f_{yi}(y,t_{yi}), f_{xi-1}(x,t_{yi})\left. \right. \\ {}&\qquad \quad -f_{yi-1}(y,t_{yi}), f_{xi-1}\left( x,\frac{-B_{xi-1}-B_{yi}}{2A_{xi-1}+2A_{yi}}\right) \left. \right. \\ {}&\qquad \quad -f_{yi}\left( y,\frac{-B_{xi-1}-B_{yi}}{2A_{xi-1}+2A_{yi}}\right) , f_{xi}\left( x,\frac{-B_{xi}-B_{yi-1}}{2A_{xi}+2A_{yi-1}}\right) \left. \right. \\ {}&\qquad \quad -f_{yi-1} \left( y,\frac{-B_{xi}-B_{yi-1}}{2A_{xi}+2A_{yi-1}}\right) , f_{xi}\left( x,\frac{-B_{xi}-B_{yi}}{2A_{xi}+2A_{yi}}\right) \left. \right. \\ {}&\qquad \quad -f_{yi}\left( y,\frac{-B_{xi}-B_{yi}}{2A_{xi}+2A_{yi}}\right) , f_{xi-1}\left( x,\frac{-B_{xi-1}-B_{yi-1}}{2A_{xi-1}+2A_{yi-1}}\right) \left. \right. \\ {}&\qquad \quad \left. -f_{yi-1}\left( y,\frac{-B_{xi-1}-B_{yi-1}}{2A_{xi-1}+2A_{yi-1}}\right) \right\} . \end{aligned}$$

$\square$

Thus, we get the following Lemma.

Theorem 4.5

An optimal solution of the dynamic robust vertex 1-center location problem under minmax regret criterion is obtained in $O(n^{3})$ time.

Proof

Step 1 is performed in $O(n^{2}\log n)$ time. Step 2 is done in a linear time for every vertices x and y on tree T. Then the total time complexity of Step 2 and consequently, the total time complexity of Algorithm 1 is $o(n^{3})$. $\square$

Example 4.6

Consider the given dynamic tree network of Example 3.6. We want to find a vertex that minimizes the robust 1-center location problem with minmax regret criterion. We first compute $f(x,t)-f(y,t)$ for every pair of vertices x and y. The computed values of $f(x,t)-f(y,t)$ is written in Table . The procedure of finding $f(x,t)-f(y,t)$ with $x=v_1$ and $y=v_2$ is as follows. Let $x=v_1$ and $y=v_2$. Therefore, $m_x =2$ and $m_y =3$. Also, $l=m_x =2$, ${\bar{t}}_{0}=-1$ and ${\bar{t}}_{1}=\frac{-15+\sqrt{477}}{18}$. For every $t\in \left[ {\bar{t}}_{0}, {\bar{t}}_{1}\right]$, $f(x,t)-f(y,t)=12t+20 - (3t+12)=9t+8$. For every $t\in \left[ {\bar{t}}_{1}, \max \{2, \frac{-15+\sqrt{477}}{18}\}\right]$, $f(x,t)-f(y,t)=12t+20 - (9t^2 +18t+5)=15-9t^2 -6t$ since $\max \left\{ 2, \frac{-15+\sqrt{477}}{18}\right\} =2=t_{x1}$. For other pair of vertices, the maps are determined in an analogous way. Now we use Lemma 4.4 and obtain an optimal solution for the robust vertex 1-center location problem. Thus, we have

$$\begin{aligned} \min _{x\in \lbrace v_1 , ..., v_6 \rbrace }\max _{x\in \lbrace v_1 , ..., v_6 \rbrace }(f(x,t)-f(y,t))=\min \{16,84, 64, 104, 50,184\}=16 \end{aligned}$$

Therefore, $v_1$ is a robust solution of the robust 1-center location problem with minmax regret criterion. The optimal value of objective function is equal to 16.

Table 3 The values of $f(x,t)-f(y,t)$

Corollary 4.7

If $A_{xi}=0$ for all $i=1,\ldots , n$ and $x\in V$, then the time complexity of the dynamic robust vertex 1-center location problem under minmax regret criterion is reduced to $O(n^{2}\alpha (n)\log n)$.

5 Dynamic robust absolute 1-center location problem under minmax criterion

If we use the worst case criterion for the absolute 1-center location problem, then we must find a point on T such that this point minimizes the maximum value of the objective function on interval [l, u] . To do this, first we can find a point on each edge of the tree T that minimizes the worst case criterion. These points are called the local minimums and their number are equal to number of edges of T (i.e., $n-1$). Then among these points we select a point as an optimal solution for the robust absolute 1-center location problem under minmax criterion. This solution is called the global minimum. This criterion on edge $e\in E$ is considered as follows:

$$\begin{aligned} \min _{x \in e}\max _{t \in [l, u]}f(x,t), \end{aligned}$$

(8)

where

$$\begin{aligned} f(x,t)= \max _{i = 1, \ldots , n}(A_{i}t^{2} + B_{i}t + C_{i}). \end{aligned}$$

It is clear that there is an one-to-one correspondence between the length of edge $e=(u, v) \in E$ and the interval [0, 1] , where 0 is corresponding to $d^{t}(u, u)$ and 1 is corresponding to $d^{t}(u, v)$, for all $t\in [l, u]$. Therefore, if we assume that $x \in [0, 1]$, then $A_{i}$, $B_{i}$ and $C_{i}$ for $i = 1, \ldots , n$ are as linear functions of x.

Then f(x, t) is an upper envelope of n continuous, totally defined and bivariate functions. Consequently, f(x, t) is a piecewise bivariate function where each piece of this function is a plane or a parabola. Let the number of pieces of this function be m and define

$$\begin{aligned} f_{i}(x,t) = A_{i}t^{2} + B_{i}t + C_{i},~~~ \forall i = 1, \ldots , n. \end{aligned}$$

We want to compute f(x, t) on intervals [l, u] and [0, 1] in which $t\in [l,u]$ and $x\in [0,1]$. To calculate this function, we first examine its properties.

Lemma 5.1

• 1. At one point of the domain, the function with maximum value is equal to upper envelope in this point.

• 2. If $(x_{k}, t_{k})$ is the starting point of domain for function $f_{k}(x,t)$, then the domain of this function is $\left[ x_{k}, x_{k+1}\right] \times \left[ t_{k}, t_{k+1}\right]$, where $(x_{k+1}, t_{k+1})$ is the smallest intersection point of this function with other functions.

Proof

• 1. It is obvious.

• 2. Let $(x_{k+1}, t_{k+1})$ and $(x_{k+2}, t_{k+2})$ be the intersection points of function $f_{k}(x,t)$ with functions $f_{i}(x,t)$ and $f_{j}(x,t)$. Also, $x_{k+1}<x_{k+2}$ and $t_{k+1}<t_{k+2}$.

  $$\begin{aligned} f_{k}(x,t)>f_{i}(x,t),~~f_{k}(x,t)>f_{j}(x,t)~~~\forall (x,t) \in \left[ x_{k}, x_{k+1}\right] \times \left[ t_{k}, t_{k+1}\right] \end{aligned}$$

  and

  $$\begin{aligned} f_{k}(x_{k+1},t_{k+1})=f_{i}(x_{k+1},t_{k+1}). \end{aligned}$$

  Given that $f_{k}(x,t)$ is decreasing and $f_{i}(x,t)$ is increasing in this interval, thus

  $$\begin{aligned} f_{k}(x, t)<f_{i}(x, t),~~~\forall x>x_{k+1} and t>t_{k+1}. \end{aligned}$$

$\square$

For obtaining function f(x, t) , we perform the following algorithm:

Algorithm 2: Find f(x, t) on intervals [l, u] and [0, 1]

• 1. Set $k=0$, $k'=k+1$, $t_{0}=l$ and $x_{0}=0$.

• 2. Calculate the value of functions $f_{i}(x,t) = A_{i}t^{2} + B_{i}t + C_{i}$ for $i = 1, \ldots , n$ at point $t_{k}$, $x_{k}$.

• 3. Select the function with maximum value in specified point and denote the selected function by $f_{i_{k}}(x,t)$.

• 4. Let $\left( x_{j}, t_{j} \right)$ be the intersection of $f_{i_{k}}(x,t)$ with $f_{j}(x, t)$ for $2\le j\le n$ such that $x_{k+1}\le x_{j}$ and $t_{k+1}\le t_{j}$ for $1\le j\le n$. Show the domain of $f_{i_{k}}(x,t)$ with $P_{k}=I_{k}\times J_{k}$, where $I_{k}=\left[ t_{k}, t_{k+1}\right]$ and $J_{k}=\left[ x_{k}, x_{k+1}\right]$.

• 5. If $\left( x_{k+1},t_{k+1} \right)$, $x_{k+1}< 1$ and $t_{k+1}< u$, is the intersection of $f_{i_{k}}(x,t)$ with the one of functions $f_{j}(x,t)$, then call it $f_{i_{k+1}}(x,t)$. Set $k=k+1$ and go to step 2.

• 6. Otherwise, call the first one $f_{i_{k+1}}(x,t)$ and the second function $f_{i_{k'+1}}(x,t)$. Set $k=k+1$ and repeat the steps 2-6 for $f_{i_{k+1}}(x,t)$ and $f_{i_{k'+1}}(x,t)$ separately. In this case, $J_{k'+1}=J_{k}$, $I_{k'+1}=\left[ t_{k}, t_{k+1} \right]$ and $J_{k+1}=\left[ x_{k}, x_{k+1}\right]$, $I_{k+1}=I_{k}$, respectively.

This procedure performs at most n iteration and any time contains O(n) operations. Therefore, the total time for performing the characterized procedure is $O(n^{2})$.

Lemma 5.2

An optimal solution of the absolute robust absolute 1-center location problem on T is obtained in $O(n^{3})$ time.

Proof

For each edge of tree T run Algorithm 2. Thus the time complexity of problem is equal to $O(n^{3})$. $\square$

6 Dynamic robust absolute 1-center location problem with minmax regret criterion

Consider now the robust deviation absolute 1-center location problem in which the length of edges and the weight of vertices are linear functions of parameter t. This problem is written as follows:

$$\begin{aligned} \min _{x \in T}\max _{t \in [l, u]} (f(x,t)-f(x^{*},t)). \end{aligned}$$

(9)

According to Lemma 2.2, we have

$$\begin{aligned} f(x^{*},t)=\max _{i,j=1, \ldots , n}\frac{w_{i}(t)w_{j}(t)d^{t}(v_{i},v_{j})}{w_{i}(t)+w_{j}(t)}. \end{aligned}$$

Similar to Sect. 5, we consider this problem on each edge $e\in E$ and solve this problem on described edge. Let

$$\begin{aligned} f(x^{*},t)=\max _{i,j=1, \ldots , n}\frac{\alpha _{ij}t^{3}+\beta _{ij}t^{2} +\gamma _{ij}t+\delta _{ij}}{(a_{i}+a_{j})t+(b_{i}+b_{j})}, \end{aligned}$$

where

$$\begin{aligned}{} & {} \alpha _{ij}=a_{i}a_{j}\left( \sum _{e\in P_{ij}}a_{e}\right) , \\ {}{} & {} \beta _{ij}=\left( a_{i}a_{j}\left( \sum _{e\in P_{ij}}b_{e}\right) +a_{i}b_{j} \left( \sum _{e\in P_{ij}}a_{e}\right) +b_{i}a_{j}\left( \sum _{e\in P_{ij}}a_{e}\right) \right) , \\ {}{} & {} \gamma _{ij}=\left( a_{i}b_{j}\left( \sum _{e\in P_{ij}}b_{e}\right) +b_{i}a_{j} \left( \sum _{e\in P_{ij}}b_{e}\right) +b_{i}b_{j}\left( \sum _{e\in P_{ij}}a_{e}\right) \right) \end{aligned}$$

and

$$\begin{aligned} \delta _{ij}=b_{i}b_{j}\left( \sum _{e\in P_{ij}}b_{e}\right) .\end{aligned}$$

Notice that $P_{ij}$ represents the unique path between the vertices $v_{i}$ and $v_{j}$ on tree T.

Therefore, $f(x^{*},t)$ is the maximum of $O( n^{2})$ univariate fractional functions. for solving problem (9), first we must compute the upper envelope of $O(n^{2})$ univariate fractional functions on interval [l, u] . To compute the upper envelope we distinguish the following two cases:

Case 1. Let the denominator of functions

$$\begin{aligned} f_{ij}(t)=\frac{\alpha _{ij}t^{3} + \beta _{ij}t^{2} + \gamma _{ij}t + \delta _{ij}}{(a_{i} + a_{j})t + b_{i} + b_{j}} \end{aligned}$$

be a scaler, for all $1\le i,j \le n$, i.e,

$$\begin{aligned} a_{i}+a_{j}=0. \end{aligned}$$

In this case, $f(x^{*},t)$ is the upper envelope of $O( n^{2})$ continuous, totally defined, univariate functions such that the maximum degree of each of them is three. Furthermore, each disjoint pair $f_{ij}(t)$ and $f_{kh}(t)$ intersect in at most three points on interval [l, u] , $1\le i,j,k,h\le n$. (We know that each polynomial with degree n has at most n real roots). Therefore, we can use Theorem 3.3 and calculate $f(x^{*},t)$ on interval [l, u] . Thus, we conclude the following Lemma.

Lemma 6.1

The upper envelope of $\left\{ f_{ij}:1\le i,j\le n \right\}$ is obtained in $O(n^{2}\alpha (n^{2})\log n)$ time. It has at most $m=O(n^{2}\alpha (n^{2}) )$ subinterval.

Proof

In Lemma 3.1 and Theorem 3.3, if we set $s=3$ and $n^{2}$ instead n, we can conclude this Lemma. $\square$

Now we have to solve the dynamic robust absolute 1-center location problem on each obtained subinterval.

It can be solved separately on every edge of tree in $O(n^{2})$ time using Algorithm 2. Therefore, the number of local minimums on tree T and interval [l, u] is at most $O(n^{3}\alpha (n^{2}))$. Consequently, we can select an optimal solution for the dynamic robust absolute 1-center location problem on interval [l, u] between the obtained optimal solutions.

Lemma 6.2

Time complexity of computing an optimal solution for the dynamic robust absolute 1-center location problem under minmax regret criterion in the case of $a_i +a_j =0$ is $O(n^{5}\alpha (n^{2}))$.

Case 2. Let $a_{i}+a_{j} \ne 0$, for all i, j. In this case we use Algorithm 2 two times. In the first time we use this algorithm for computing $\max _{i,j=1,\ldots , n}f_{ij}(t)$ on interval [l, u] . In the following we present a brief description of how to calculate $\max _{i,j=1,\ldots , n}f_{ij}(t)$ using Algorithm 2 on interval [l, u] . It should be noted that Algorithm 2 is used for bivariate functions, but we want to use it for univariate functions.

• 1. Set $t_{0}=l$ and compute the value of functions $f_{ij}(t)$ at point $t_{0}$.

• 2. Select the function that has maximum value at this point. Denote this function with $f_{ij_{1}}(t)$.

• 3. Compute the intersection of $f_{ij_{1}}(t)$ with the remaining functions.

• 4. Choose the minimum intersection point and consider this point with $t_{1}$. Denote the function corresponding to this point by $f_{ij_{2}}$.

• 5. Repeat steps 1 to 4 until $t_{k}\ge u$.

If this approach is repeated, then $f(x^{*},t)$ is computed. In this case, at most $O(n^{2})$ pieces and their corresponding intervals are obtained in $O(n^{4})$ time.

Again, the dynamic robust absolute 1-center location problem on each edge $e\in E$ and each interval is computed, separately using the Algorithm 2. On each interval and each edge the dynamic robust absolute 1-center location problem under minmax regret criterion can be calculated in $O(n^{2})$ time. Then we can conclude the following Lemma.

Lemma 6.3

Dynamic robust absolute 1-center location problem under minmax regret criterion on T in case $a_{i}+a_{j}\ne 0$ can be solved in $O(n^{5})$ time.

If we compare case 1 and case 2 together, we see that the used method used in the second case has less time complexity. Therefore, the second case method is more efficient.

Remark 6.4

By the same process, we can obtain an optimal solution for relative robust absolute(vertex) 1-center location problem on tree T.

7 Robust deviation 1-center location problem on trees

In this section, we assume that T is a weighted tree and the edge lengths and vertex weights of T correspond to a finite set of positive real and real numbers, respectively. Denote the set of all possible events for the edge lengths and vertex weights of tree T with a finite number of scenarios, which is denoted by S. We now consider the robust deviation 1-center location problem. For obtaining the optimal solution of this problem, first we have to compute the 1-centers on the tree T for all scenarios. Using Lemma 2.1, we get the following Lemma:

Lemma 7.1

Under all scenarios in S, the time complexity of computing $f(x^{*}, s)$ is equal to $O(n\log n\vert S\vert )$.

For solving the minmax regret 1-center location problem with the candidate locations E, it is sufficient to solve this problem on each edge of tree T, separately. Therefore, we first compute the optimal solution of this problem for every edge $e\in E$.

$$\begin{aligned} \min _{x \in e}(\min _{x\in V}) \max _{s \in S} R(x, s). \end{aligned}$$

(10)

We can obtain the optimal solution of this problem at $O(\vert S\vert )$ time using the Kouvelis’s algorithm (Kouvelis et al. 1993). Then we have

Lemma 7.2

The robust deviation 1-center location problem on tree networks can be solved in $O(\vert S\vert n\log n)$ time.

Suppose now that the weights of all vertices of tree T are equal to one. Also, for each $s \in S$, let $p[a_{s},b_{s}]$ be a longest path on T under scenario s which is computed in linear time by Handler’s algorithm (Handler 1973). On the other hand, we know that the middle point of this path indicates the absolute 1-center under scenario $s\in S$. Then, for all $x \in T$ we have

$$\begin{aligned} R(x,s)=\max _{i=1, \ldots , n}d^{s}(v_{i},x)-\frac{d^{s}(a_{s}, b_{s})}{2}. \end{aligned}$$

Furthermore, we know that the furthest vertex from each point x on T is the endpoint of longest path on T. Therefore, $\max _{i=1,\ldots , n}d^{s}(v_{i},x)=\max \left\{ d^{s}(a_{s},x), d^{s}(b_{s},x)\right\}$. It follows that

$$\begin{aligned} R(x,s)=\max \left\{ d^{s}(a_{s},x) -\frac{d^{s}(a_{s}, b_{s})}{2}, d^{s}(b_{s},x)-\frac{d^{s}(a_{s}, b_{s})}{2}\right\} . \end{aligned}$$

Now we solve the minmax regret 1-center location problem on each edge $e=(u,v) \in E$. If we define a mapping on edge $e=(u,v)$ such that in this map the points u and v correspond to 0 and 1, respectively, and the distance between u and each point x on edge e except u and v is equal to $xd^{s}(u,v)$, where $x=\frac{d^{s}(u,x)}{d^{s}(u,v)}$, then we conclude that

$$\begin{aligned} d^{s}(a_{s},x)-\frac{d^{s}(a_{s}, b_{s})}{2}=\frac{2d^{s}(a_{s},u)-d^{s}(a_{s},b_{s})}{2}+xd^{s}(u,v). \end{aligned}$$

It is clear that $d^{s}(a_{s},x)-\frac{d^{s}(a_{s}, b_{s})}{2}$ and $d^{s}(b_{s},x)-\frac{d^{s}(a_{s}, b_{s})}{2}$ are the linear functions which are defined on interval [0, 1] . Therefore, an optimal solution for the robust deviation 1-center location problem on edge e can be computed in $O(\vert S\vert )$ time using the presented algorithm in Kouvelis et al. (1993).

Lemma 7.3

An optimal solution for the robust deviation 1-center location problem on the un-weighted tree T is obtained in $O(n\vert S\vert )$ time.

8 Conclusion

In this paper, we considered the robust vertex (absolute) 1-center location problem on tree networks in which vertex weights and edge lengths have been considered as dynamic data or as a discrete set of scenarios. We considered the problems with minmax and minmax regret criteria and developed combinatorial algorithms which solve the problems under investigation in polynomial times.

We showed that in all problems, the optimal solution was located in one of the breakpoints. The dynamic robust vertex 1-center problem under minmax and minmax regret criteria were solved in times $O(n^{2}\log n)$ and $O(n^{3})$. Also, an optimal solution for the dynamic robust absolute 1-center problem under minmax and minmax regret criteria were computed in times $O(n^{3})$ and $O(n^{5})$. In the two first problems, the objective functions are univariable, but in the next two problems, the objective functions are bivariables. Finally, we considered the robust deviation 1-center problem and obtained an algorithm for this problem in $O(\vert S\vert n\log n)$ time complexity. In this problem, the vertex weights and edge lengths were considered as discrete set of scenarios.

For further research, we can consider the robust inverse (reverse) location problems. We can investigate the robust inverse 1-center problem. Furthermore, we can also study the minmax reverse 1-center problem.